Three-Dimensional Lower-Limb Kinematics from Accelerometers and Gyroscopes with Simple and Minimal Functional Calibration Tasks: Validation on Asymptomatic Participants
Abstract
:1. Introduction
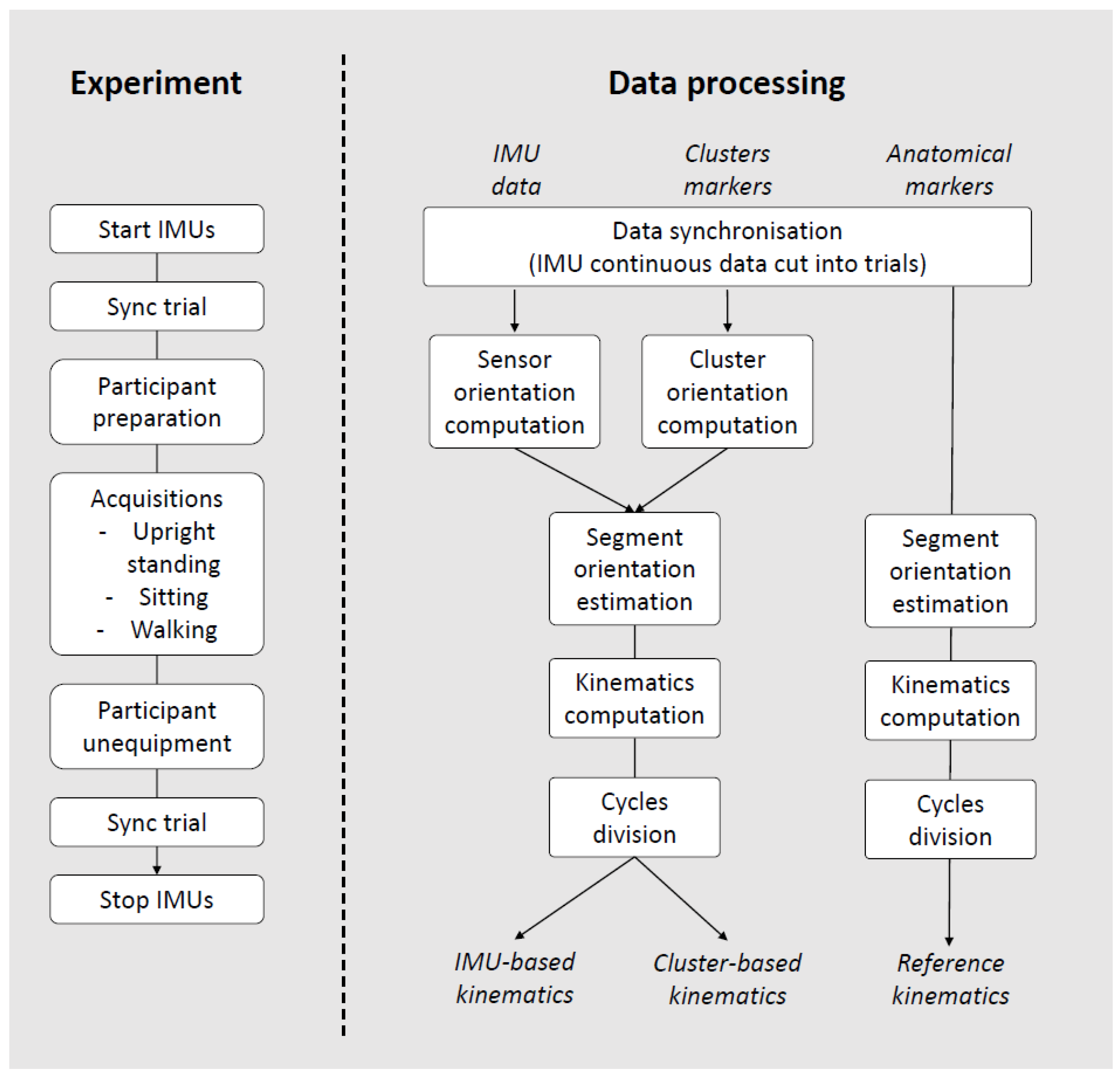
2. Materials and Methods
2.1. Participants
2.2. Equipment
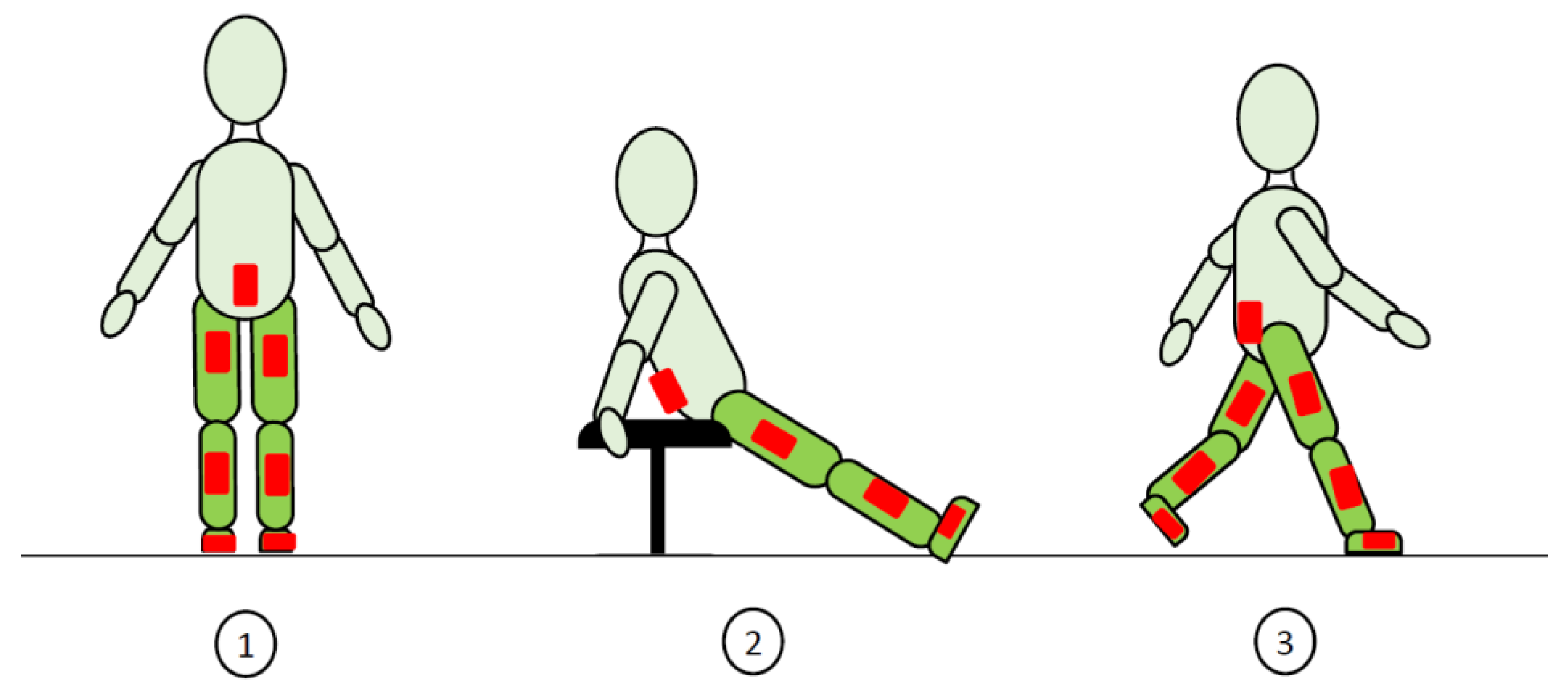
2.3. Protocol
2.4. Data Processing
2.4.1. Pre-Processing
2.4.2. Sensor Orientations
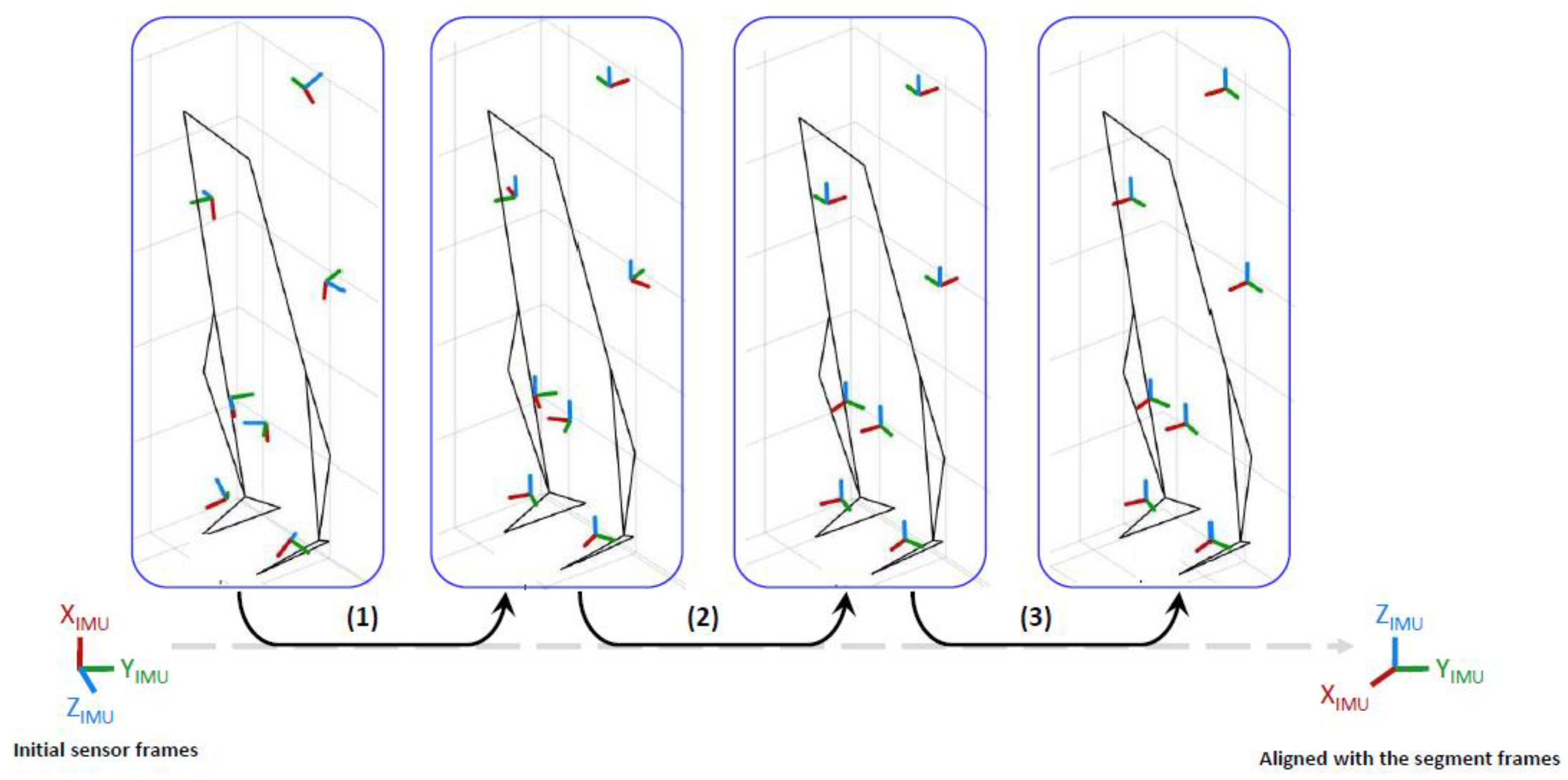
2.4.3. Sensor-to-Segment (S2S) Calibration
- Alignment with gravity: During the first calibration standing posture, the segment’s vertical axis (Z) is supposed to be aligned with gravity measured by the accelerometer. A rotation was applied to the sensor data to align the vertical axis of the sensor with the vertical axis of the segment. This rotation was also applied to the cluster-based quaternions.
- Alignment with the segment’s mediolateral (Y) axis: During the walking trials, the feet, shanks and thighs’ mediolateral axis was determined by the principal axis of the measured angular velocity, supposing that the movement occurs mainly in the sagittal plane for these segments. A rotation was applied to the corresponding sensor data to align the mediolateral axis of the sensor with the principal axis of movement during gait. This same rotation was applied to the cluster-based quaternions. The mediolateral axis of the pelvis was supposed to be manually aligned with the mediolateral axis of the sensor since no assumption could be made on the principal axis of movement during gait for this segment.
- Mediolateral axis correction: The cross product of the 2 detected sensors’ vertical axes during standing and sitting postures allows one to know the direction of the mediolateral axis. The correction of the sign of the mediolateral axis previously determined was applied on the sensor and cluster-based orientations if necessary.
RThigh segment->IFt = RThigh segment→Thigh sensor/cluster * RThigh sensor/cluster→IFt,
RShank segment->IFs = RShank segment→Shank sensor/cluster * RShank sensor/cluster→IFs,
RFoot segment->IFf = RFoot segment→Foot sensor/cluster * RFoot sensor/cluster→IFf,
2.4.4. Sensors Common Frame Setting
RThigh segment->CF = RThigh segment->IFh * RIFh→CF,
RShank segment->CF = RShank segment->IFs * RIFs→CF,
RFoot segment->CF = RFoot segment->IFf * RIFf→CF,
2.4.5. Sensor-to-Global Calibration
RThigh segment->GF = RThigh segment->CFtdrifted * R CFtdrifted→CF * RCF→GF,
RShank segment->GF = RShank segment->CFsdrifted * R CFsdrifted→CF * RCF→GF,
RFoot segment->GF = RFoot segment->CFfdrifted * R CFfdrifted→CF * RCF→GF,
2.4.6. Kinematics Computation and Cycle Division
RKnee = RThigh segment→Shank segment = RThigh segment→GF * R−1Shank segment→GF,
RAnkle = RShank segment→Foot segment = RShank segment→GF * R−1Foot segment→GF,
2.5. Data Analysis
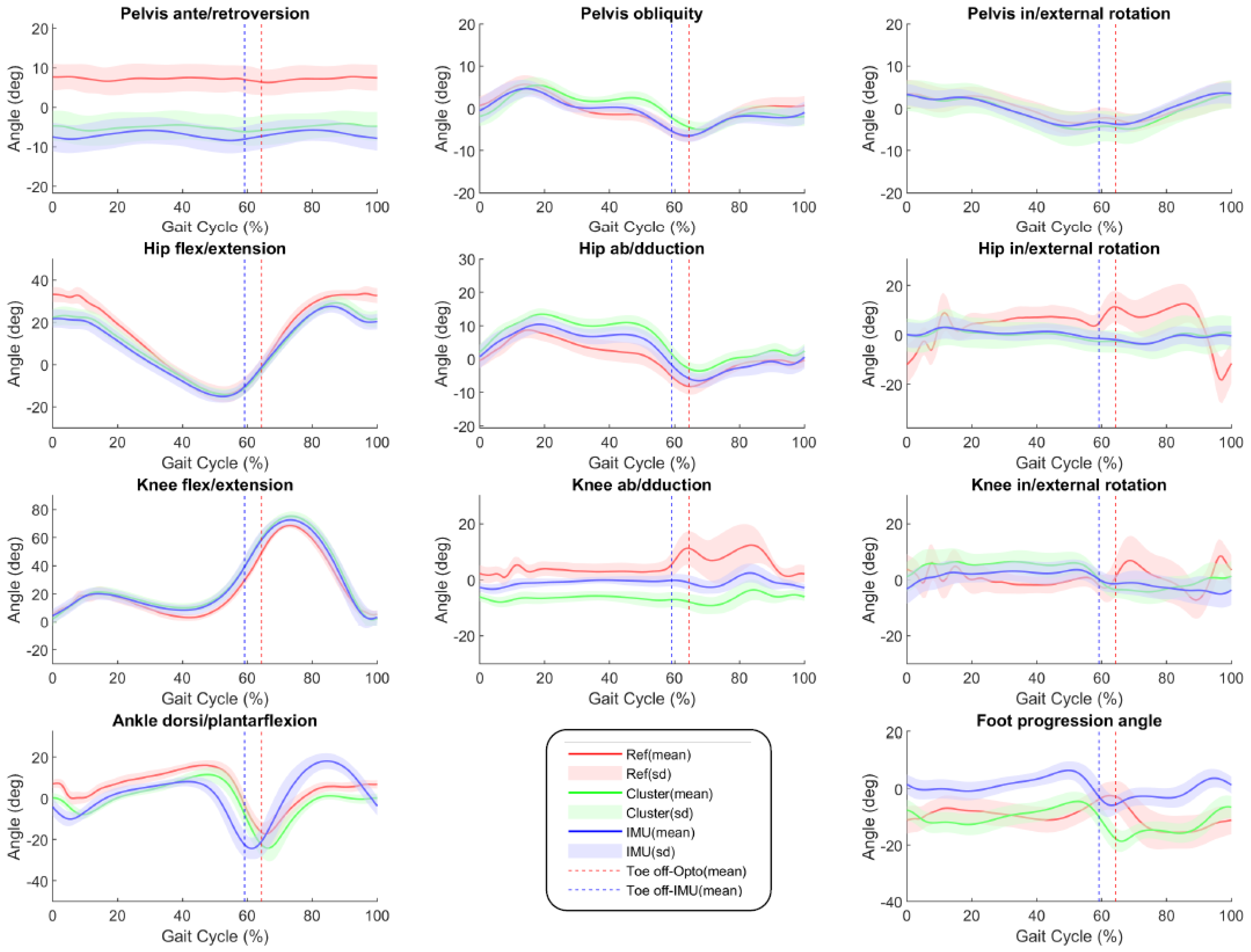
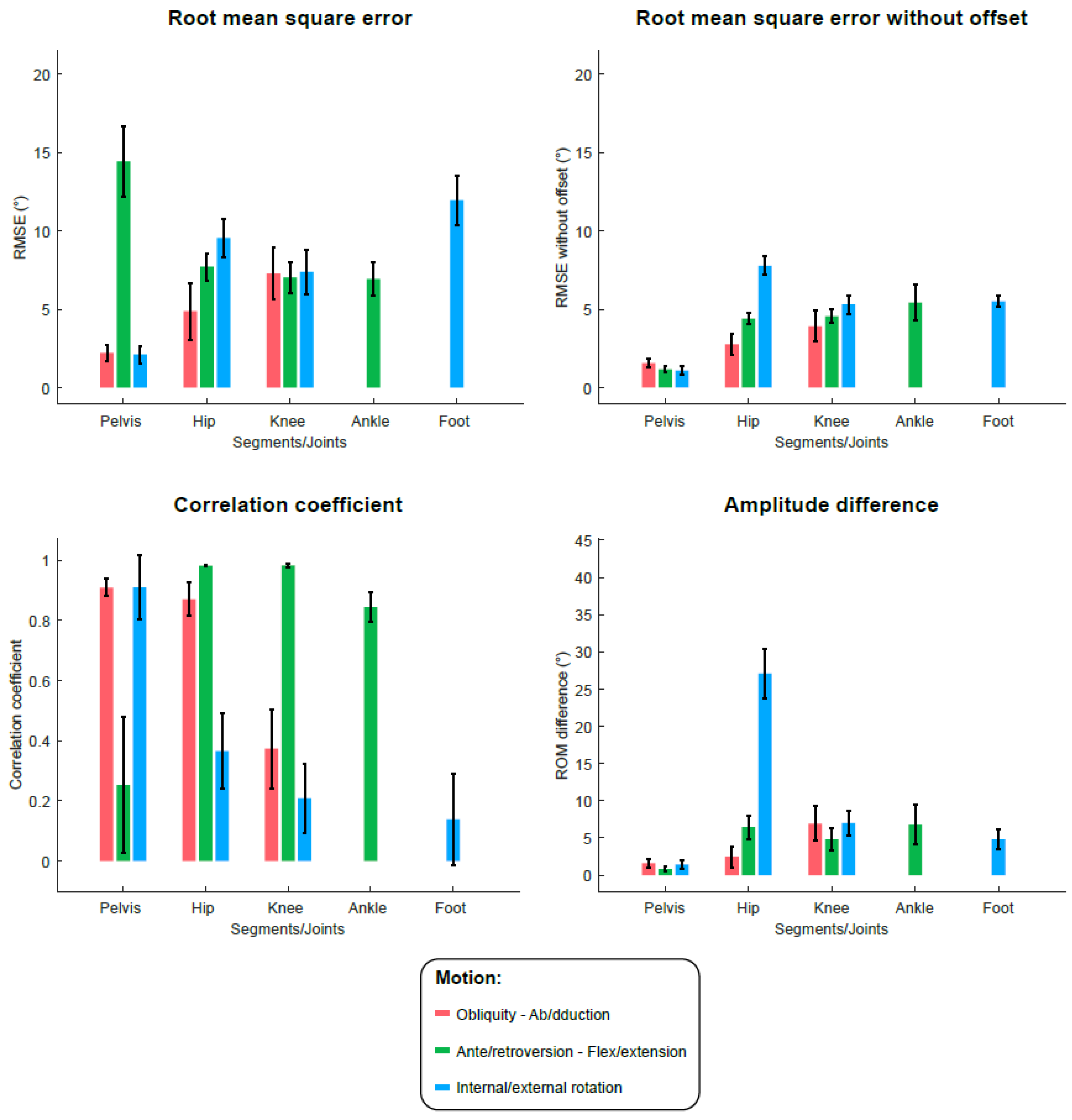
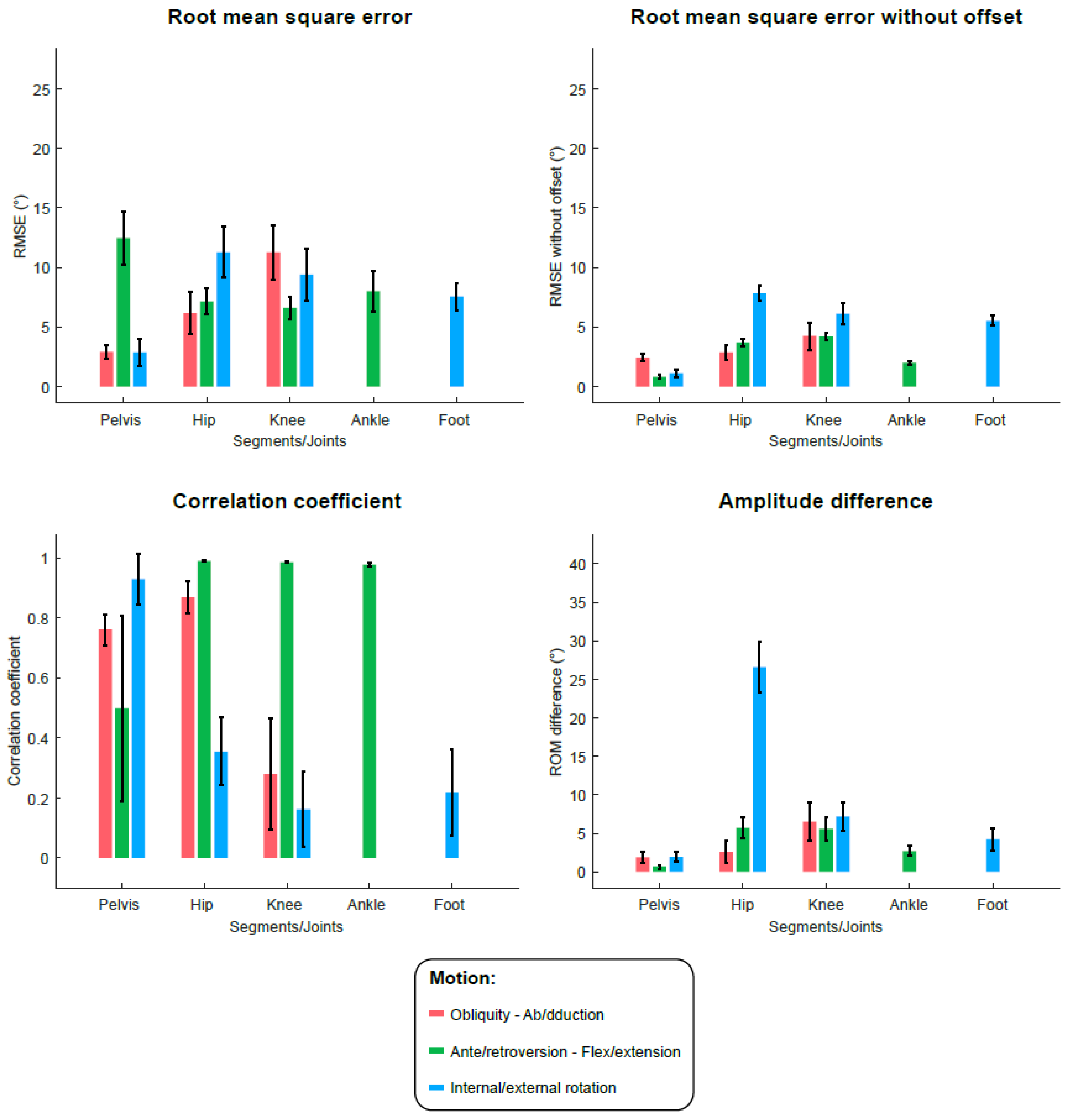
3. Results
4. Discussion
4.1. Study Limitations
4.2. Clinical Relevance
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Storm, F.A.; Cesareo, A.; Reni, G.; Biffi, E. Wearable Inertial Sensors to Assess Gait during the 6-Minute Walk Test: A Systematic Review. Sensors 2020, 20, 2660. [Google Scholar] [CrossRef]
- Nazarahari, M.; Rouhani, H. 40 Years of Sensor Fusion for Orientation Tracking via Magnetic and Inertial Measurement Units: Methods, Lessons Learned, and Future Challenges. Inf. Fusion 2020, 68, 67–84. [Google Scholar] [CrossRef]
- Al Borno, M.; O’Day, J.; Ibarra, V.; Dunne, J.; Seth, A.; Habib, A.; Ong, C.; Hicks, J.; Uhlrich, S.; Delp, S. OpenSense: An Open-Source Toolbox for Inertial-Measurement-Unit-Based Measurement of Lower Extremity Kinematics over Long Durations. J. NeuroEngineering Rehabil. 2022, 19, 22. [Google Scholar] [CrossRef]
- Vitali, R.V.; Perkins, N.C. Determining Anatomical Frames via Inertial Motion Capture: A Survey of Methods. J. Biomech. 2020, 106, 109832. [Google Scholar] [CrossRef] [PubMed]
- Pacher, L.; Chatellier, C.; Vauzelle, R.; Fradet, L. Sensor-to-Segment Calibration Methodologies for Lower-Body Kinematic Analysis with Inertial Sensors: A Systematic Review. Sensors 2020, 20, 3322. [Google Scholar] [CrossRef]
- Poitras, I.; Dupuis, F.; Bielmann, M.; Campeau-Lecours, A.; Mercier, C.; Bouyer, L.J.; Roy, J.S. Validity and Reliability Ofwearable Sensors for Joint Angle Estimation: A Systematic Review. Sensors 2019, 19, 1555. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kobsar, D.; Charlton, J.; Tse, C.; Esculier, J.F.; Graffos, A.; Krowchuk, N.M.; Thatcher, D.; Hunt, M.A. Validity and Reliability of Wearable Inertial Sensors in Healthy Adult Walking: A Systematic Review and Meta-Analysis. J. Neuroeng. Rehabil. 2020, 17, 62. [Google Scholar] [CrossRef]
- Baker, R. Gait Analysis Methods in Rehabilitation. J. Neuroeng. Rehabil. 2006, 3, 4. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Favre, J.; Aissaoui, R.; Jolles, B.M.; De Guise, J.A.; Aminian, K. Functional Calibration Procedure for 3D Knee Joint Angle Description Using Inertial Sensors. J. Biomech. 2009, 42, 2330–2335. [Google Scholar] [CrossRef]
- Picerno, P.; Cereatti, A.; Cappozzo, A. Joint Kinematics Estimate Using Wearable Inertial and Magnetic Sensing Modules. Gait Posture 2008, 28, 588–595. [Google Scholar] [CrossRef]
- Armand, S.; De Coulon, G.; Bonnefoy-Mazure, A. Gait Analysis in Children with Cerebral Palsy. EFORT Open Rev. 2016, 1, 448–460. [Google Scholar] [CrossRef]
- Cloete, T.; Scheffer, C. Benchmarking of a Full-Body Inertial Motion Capture System for Clinical Gait Analysis. In Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Vancouver, BC, Canada, 20–25 August 2008; pp. 4579–4582. [Google Scholar] [CrossRef]
- Zhang, J.T.; Novak, A.C.; Brouwer, B.; Li, Q. Concurrent Validation of Xsens MVN Measurement of Lower Limb Joint Angular Kinematics. Physiol. Meas. 2013, 34, N63–N69. [Google Scholar] [CrossRef]
- Scalera, G.M.; Ferrarin, M.; Marzegan, A.; Rabuffetti, M. Assessment of Stability of MIMU Probes to Skin-Marker-Based Anatomical Reference Frames During Locomotion Tasks: Effect of Different Locations on the Lower Limb. Front. Bioeng. Biotechnol. 2021, 9, 721900. [Google Scholar] [CrossRef] [PubMed]
- Leboeuf, F.; Baker, R.; Barré, A.; Reay, J.; Jones, R.; Sangeux, M. The Conventional Gait Model, an Open-Source Implementation That Reproduces the Past but Prepares for the Future. Gait Posture 2019, 69, 235–241. [Google Scholar] [CrossRef]
- Gløersen, Ø.; Federolf, P. Predicting Missing Marker Trajectories in Human Motion Data Using Marker Intercorrelations. PLoS ONE 2016, 11, e0152616. [Google Scholar] [CrossRef] [PubMed]
- Zeni, J.A.; Richards, J.G.; Higginson, J.S.; Zeni, J.A., Jr.; Richards, J.G.; Higginson, J.S.; Zeni, J.A.; Richards, J.G.; Higginson, J.S. Two Simple Methods for Determining Gait Events during Treadmill and Overground Walking Using Kinematic Data. Gait Posture 2008, 27, 710–714. [Google Scholar] [CrossRef] [Green Version]
- Madgwick, S.O.H.; Harrison, A.J.L.; Vaidyanathan, R. Estimation of IMU and MARG Orientation Using a Gradient Descent Algorithm. In Proceedings of the 2011 IEEE International Conference on Rehabilitation Robotics, Zurich, Switzerland, 29 June–1 July 2011. [Google Scholar] [CrossRef]
- Mariani, B.; Rochat, S.; Christophe, J.B.; Aminian, K. Heel and Toe Clearance Estimation for Gait Analysis Using Wireless Inertial Sensors. IEEE Trans. Biomed. Eng. 2012, 59, 3162–3168. [Google Scholar] [CrossRef]
- Baker, R. Measuring Walking: A Handbook of Clinical Gait Analysis; Mac Keith Press: London, UK, 2013; ISBN 978-1-908316-66-0. [Google Scholar]
- Nuesch, C.; Roos, E.; Pagenstert, G.; Mundermann, A.; Nüesch, C.; Roos, E.; Pagenstert, G.; Mündermann, A. Measuring Joint Kinematics of Treadmill Walking and Running: Comparison Be- Tween an Inertial Sensor Based System and a Camera-Based System. J. Biomech. 2017, 57, 32–38. [Google Scholar] [CrossRef] [Green Version]
- Altman, D.G.; Altman, E. Practical Statistics for Medical Research; Chapman: Orange, CA, USA, 1999. [Google Scholar]
- Lebel, K.; Hamel, M.; Duval, C.; Nguyen, H.; Boissy, P. Camera Pose Estimation to Improve Accuracy and Reliability of Joint Angles Assessed with Attitude and Heading Reference Systems. Gait Posture 2018, 59, 199–205. [Google Scholar] [CrossRef] [PubMed]
- Robert-Lachaine, X.; Parent, G.; Fuentes, A.; Hagemeister, N.; Aissaoui, R. Inertial Motion Capture Validation of 3D Knee Kinematics at Various Gait Speed on the Treadmill with a Double-Pose Calibration. Gait Posture 2020, 77, 132–137. [Google Scholar] [CrossRef]
- Li, G.; Liu, T.; Yi, J.; Wang, H.; Li, J.; Inoue, Y. The Lower Limbs Kinematics Analysis by Wearable Sensor Shoes. IEEE Sens. J. 2016, 16, 2627–2638. [Google Scholar] [CrossRef]
- Palermo, E.; Rossi, S.; Marini, F.; Patanè, F.; Cappa, P. Experimental Evaluation of Accuracy and Repeatability of a Novel Body-to-Sensor Calibration Procedure for Inertial Sensor-Based Gait Analysis. Meas. J. Int. Meas. Confed. 2014, 52, 145–155. [Google Scholar] [CrossRef]
- Dorschky, E.; Nitschke, M.; Seifer, A.K.; van den Bogert, A.J.; Eskofier, B.M. Estimation of Gait Kinematics and Kinetics from Inertial Sensor Data Using Optimal Control of Musculoskeletal Models. J. Biomech. 2019, 95, 109278. [Google Scholar] [CrossRef]
- Lebleu, J.; Gosseye, T.; Detrembleur, C.; Mahaudens, P.; Cartiaux, O.; Penta, M. Lower Limb Kinematics Using Inertial Sensors during Locomotion: Accuracy and Reproducibility of Joint Angle Calculations with Different Sensor-to-Segment Calibrations. Sensors 2020, 20, 715. [Google Scholar] [CrossRef] [Green Version]
- Nazarahari, M.; Rouhani, H. Semi-Automatic Sensor-to-Body Calibration of Inertial Sensors on Lower Limb Using Gait Recording. IEEE Sens. J. 2019, 19, 12465–12474. [Google Scholar] [CrossRef]
- Teufl, W.; Miezal, M.; Taetz, B.; Fröhlich, M.; Bleser, G. Validity, Test-Retest Reliability and Long-Term Stability of Magnetometer Free Inertial Sensor Based 3D Joint Kinematics. Sensors 2018, 18, 1980. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tadano, S.; Takeda, R.; Miyagawa, H. Three Dimensional Gait Analysis Using Wearable Acceleration and Gyro Sensors Based on Quaternion Calculations. Sensors 2013, 13, 9321–9343. [Google Scholar] [CrossRef]
- Cho, Y.S.; Jang, S.H.; Cho, J.S.; Kim, M.J.; Lee, H.D.; Lee, S.Y.; Moon, S.B. Evaluation of Validity and Reliability of Inertial Measurement Unit-Based Gait Analysis Systems. Ann. Rehabil. Med. 2018, 42, 872–883. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lee, J.K.; Jeon, T.H. IMU-Based but Magnetometer-Free Joint Angle Estimation of Constrained Links. In Proceedings of the 2018 IEEE SENSORS, New Delhi, India, 28–31 October 2018; pp. 41–44. [Google Scholar] [CrossRef]
- McGrath, T.; Stirling, L. Body-Worn IMU-Based Human Hip and Knee Kinematics Estimation during Treadmill Walking. Sensors 2022, 22, 2544. [Google Scholar] [CrossRef] [PubMed]
- Ligorio, G.; Bergamini, E.; Truppa, L.; Guaitolini, M.; Raggi, M.; Mannini, A.; Sabatini, A.M.; Vannozzi, G.; Garofalo, P. A Wearable Magnetometer-Free Motion Capture System: Innovative Solutions for Real-World Applications. IEEE Sens. J. 2020, 20, 8844–8857. [Google Scholar] [CrossRef]
- Marín, J.; Blanco, T.; de la Torre, J.; Marín, J.J. Gait Analysis in a Box: A System Based on Magnetometer-Free IMUs or Clusters of Optical Markers with Automatic Event Detection. Sensors 2020, 20, 3338. [Google Scholar] [CrossRef] [PubMed]
- Berner, K.; Cockcroft, J.; Morris, L.D.; Louw, Q. Concurrent Validity and Within-Session Reliability of Gait Kinematics Measured Using an Inertial Motion Capture System with Repeated Calibration. J. Bodyw. Mov. Ther. 2020, 24, 251–260. [Google Scholar] [CrossRef] [PubMed]
- Pacher, L.; Fradet, L.; Tarent, Y.; Retailleau, M.; Colloud, F.; Chatellier, C.; Vauzelle, R. Pelvis and Hip Calibration Methods for Movement Analysis with Inertial Sensors. Comput. Methods Biomech. Biomed. Eng. 2019, 22, S166–S168. [Google Scholar] [CrossRef]
- Al-Amri, M.; Nicholas, K.; Button, K.; Sparkes, V.; Sheeran, L.; Davies, J.L. Inertial Measurement Units for Clinical Movement Analysis: Reliability and Concurrent Validity. Sensors 2018, 18, 719. [Google Scholar] [CrossRef] [Green Version]
- Shull, P.B.; Jirattigalachote, W.; Hunt, M.A.; Cutkosky, M.R.; Delp, S.L. Quantified Self and Human Movement: A Review on the Clinical Impact of Wearable Sensing and Feedback for Gait Analysis and Intervention. Gait Posture 2014, 40, 11–19. [Google Scholar] [CrossRef]
- Huang, Y.; Jirattigalachote, W.; Cutkosky, M.R.; Zhu, X.; Shull, P.B. Novel Foot Progression Angle Algorithm Estimation via Foot-Worn, Magneto-Inertial Sensing. IEEE Trans. Biomed. Eng. 2016, 63, 2278–2285. [Google Scholar] [CrossRef]
- Karatsidis, A.; Richards, R.E.; Konrath, J.; van den Noort, J.C.; Schepers, H.M.; Bellusci, G.; Harlaar, J.; Veltink, P.H. Validation of Wearable Visual Feedback for Retraining Foot Progression Angle Using Inertial Sensors and an Augmented Reality Headset. J. Neuroeng. Rehabil. 2018, 15, 78. [Google Scholar] [CrossRef]
- Hassani, R.H.; Willi, R.; Rauter, G.; Bolliger, M.; Seel, T. Validation of Non-Restrictive Inertial Gait and Kinematic Analysis of Incomplete Spinal Cord Injured Patients in Clinical Settings. Sensors 2022, 22, 4237. [Google Scholar] [CrossRef]
- Bailey, C.A.; Uchida, T.K.; Nantel, J.; Graham, R.B. Validity and Sensitivity of an Inertial Measurement Unit-Driven Biomechanical Model of Motor Variability for Gait. Sensors 2021, 21, 7690. [Google Scholar] [CrossRef]
- Glowinski, S.; Krzyzynski, T.; Bryndal, A.; Maciejewski, I. A Kinematic Model of a Humanoid Lower Limb Exoskeleton with Hydraulic Actuators. Sensors 2020, 20, 6116. [Google Scholar] [CrossRef]
- Nieuwenhuys, A.; Õunpuu, S.; Van Campenhout, A.; Theologis, T.; De Cat, J.; Stout, J.; Molenaers, G.; De Laet, T.; Desloovere, K. Identification of Joint Patterns during Gait in Children with Cerebral Palsy: A Delphi Consensus Study. Dev. Med. Child Neurol. 2016, 58, 306–313. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- McGinley, J.L.; Baker, R.; Wolfe, R.; Morris, M.E. The Reliability of Three-Dimensional Kinematic Gait Measurements: A Systematic Review. Gait Posture 2009, 29, 360–369. [Google Scholar] [CrossRef] [PubMed]
- Cappozzo, A.; Catani, F.; Della Croce, U.; Leardini, A. Position and Orientation in Space of Bones during Movement: Anatomical Frame Definition and Determination. Clin. Biomech. 1995, 10, 171–178. [Google Scholar] [CrossRef]
- Leardini, A.; Sawacha, Z.; Paolini, G.; Ingrosso, S.; Nativo, R.; Benedetti, M.G. A New Anatomically Based Protocol for Gait Analysis in Children. Gait Posture 2007, 26, 560–571. [Google Scholar] [CrossRef] [PubMed]
- Sangeux, M.; Peters, A.; Baker, R. Hip Joint Centre Localization: Evaluation on Normal Subjects in the Context of Gait Analysis. Gait Posture 2011, 34, 324–328. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Carcreff, L.; Payen, G.; Grouvel, G.; Massé, F.; Armand, S. Three-Dimensional Lower-Limb Kinematics from Accelerometers and Gyroscopes with Simple and Minimal Functional Calibration Tasks: Validation on Asymptomatic Participants. Sensors 2022, 22, 5657. https://doi.org/10.3390/s22155657
Carcreff L, Payen G, Grouvel G, Massé F, Armand S. Three-Dimensional Lower-Limb Kinematics from Accelerometers and Gyroscopes with Simple and Minimal Functional Calibration Tasks: Validation on Asymptomatic Participants. Sensors. 2022; 22(15):5657. https://doi.org/10.3390/s22155657
Chicago/Turabian StyleCarcreff, Lena, Gabriel Payen, Gautier Grouvel, Fabien Massé, and Stéphane Armand. 2022. "Three-Dimensional Lower-Limb Kinematics from Accelerometers and Gyroscopes with Simple and Minimal Functional Calibration Tasks: Validation on Asymptomatic Participants" Sensors 22, no. 15: 5657. https://doi.org/10.3390/s22155657
APA StyleCarcreff, L., Payen, G., Grouvel, G., Massé, F., & Armand, S. (2022). Three-Dimensional Lower-Limb Kinematics from Accelerometers and Gyroscopes with Simple and Minimal Functional Calibration Tasks: Validation on Asymptomatic Participants. Sensors, 22(15), 5657. https://doi.org/10.3390/s22155657





