Definition of Optimized Indicators from Sensors Data for Damage Detection of Instrumented Roadways
Abstract
:1. Introduction
2. Theoretical Background of the Optimized Indicators Method (OIM)
3. Description of the Experiment
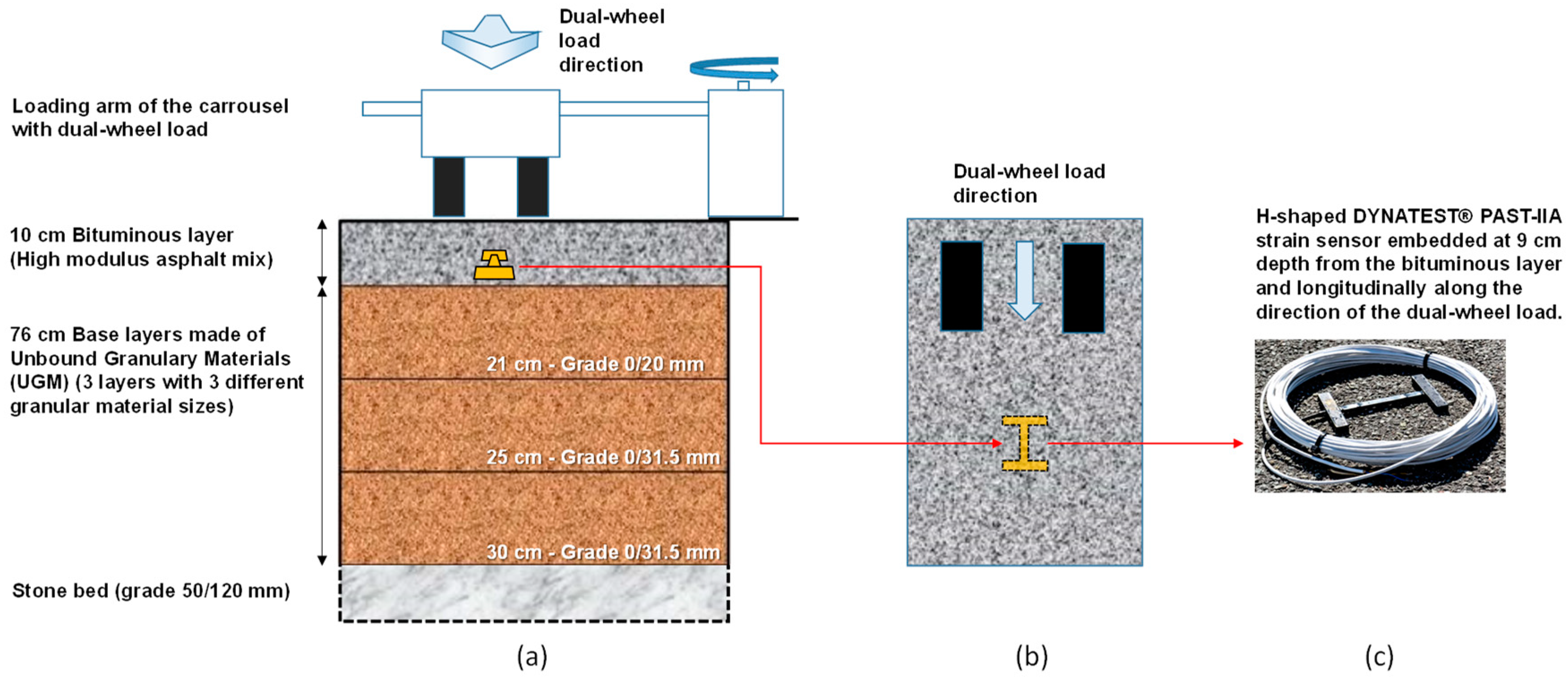
3.1. The Pavement Fatigue Carousel
3.2. Tested Instrumented Structure
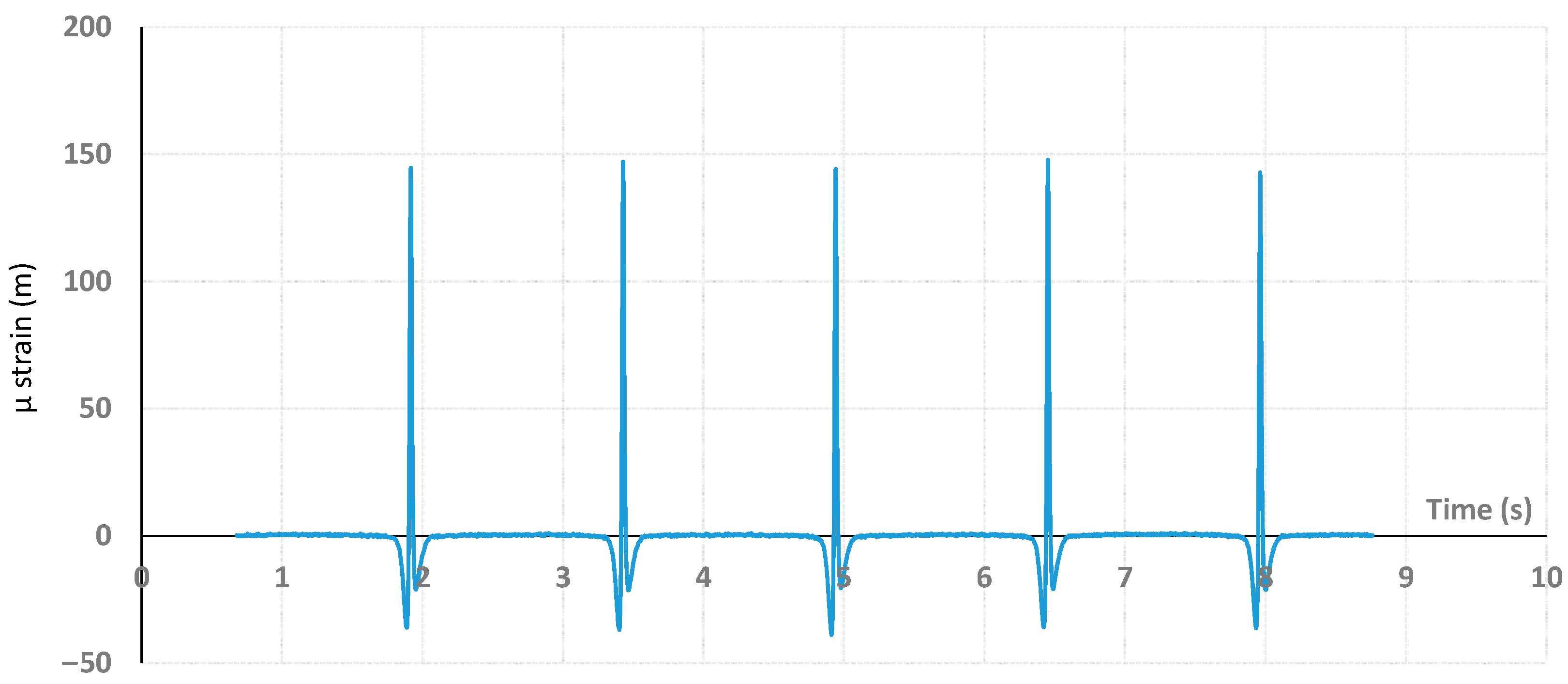
3.3. Loading Characteristics and Data Acquisition
4. Modelling
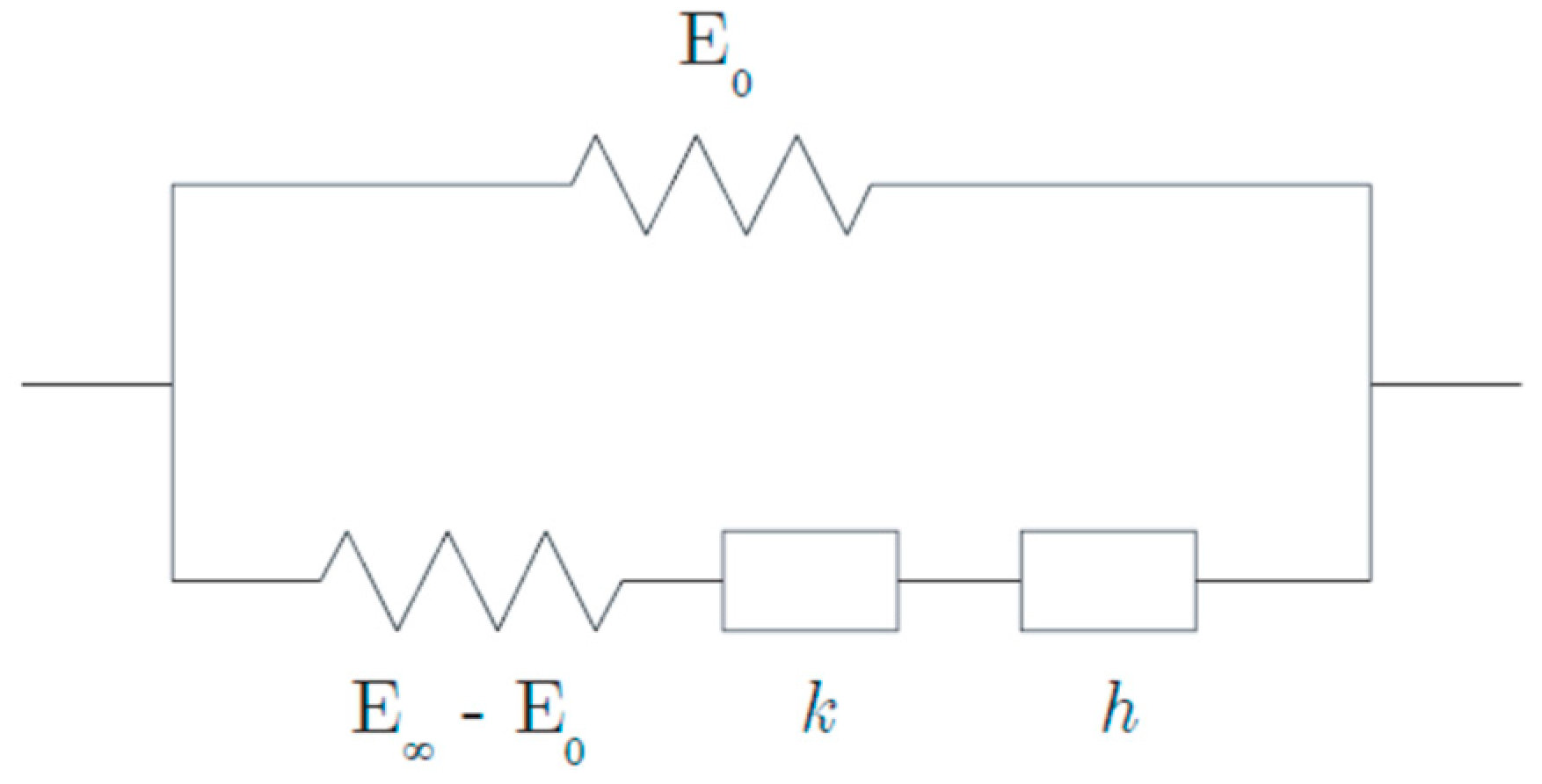
4.1. Huet-Sayegh Model
4.2. VISCOROUTE© Software
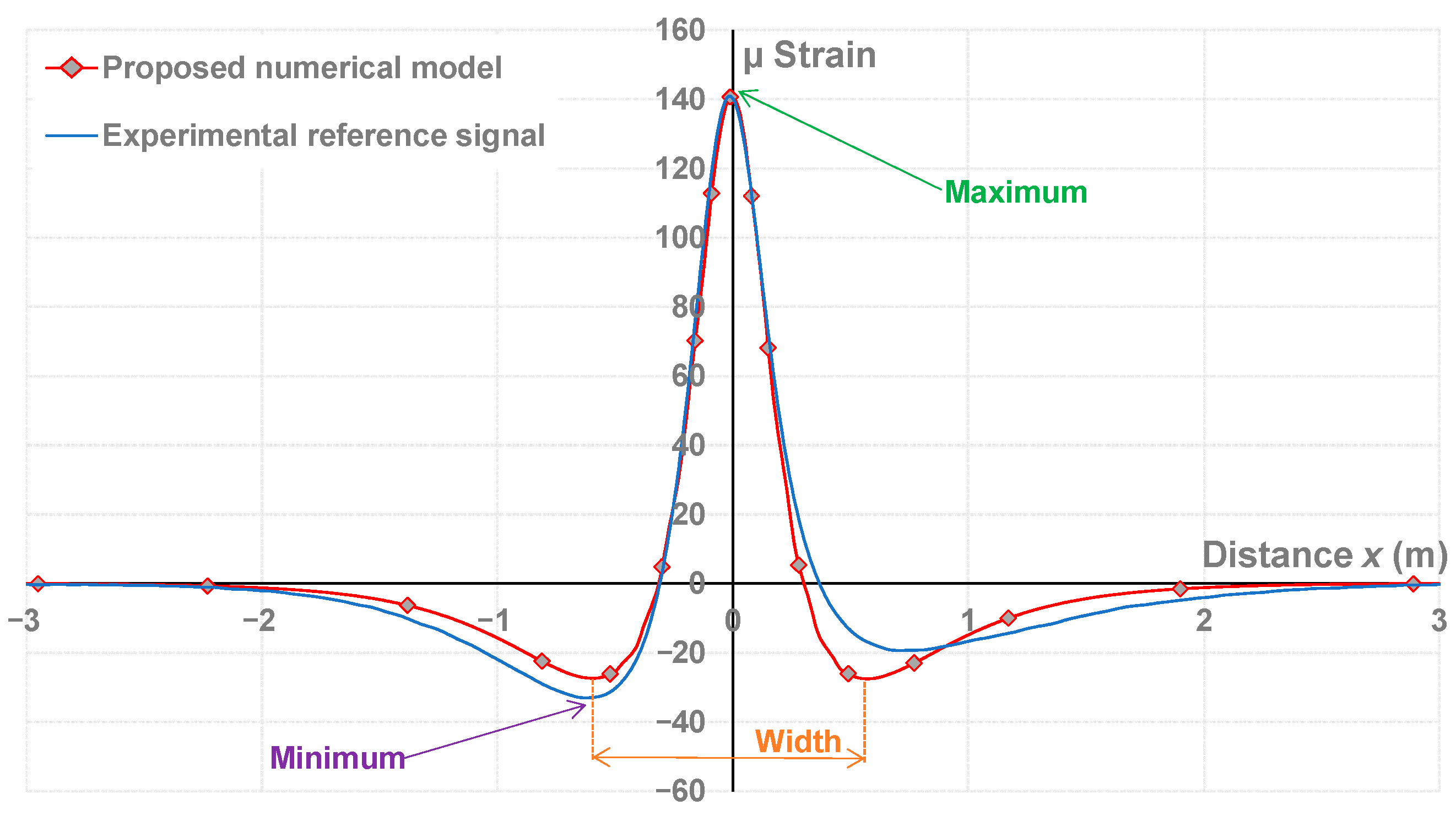
5. Calculation of the Optimized Indicators and the Weighting Functions
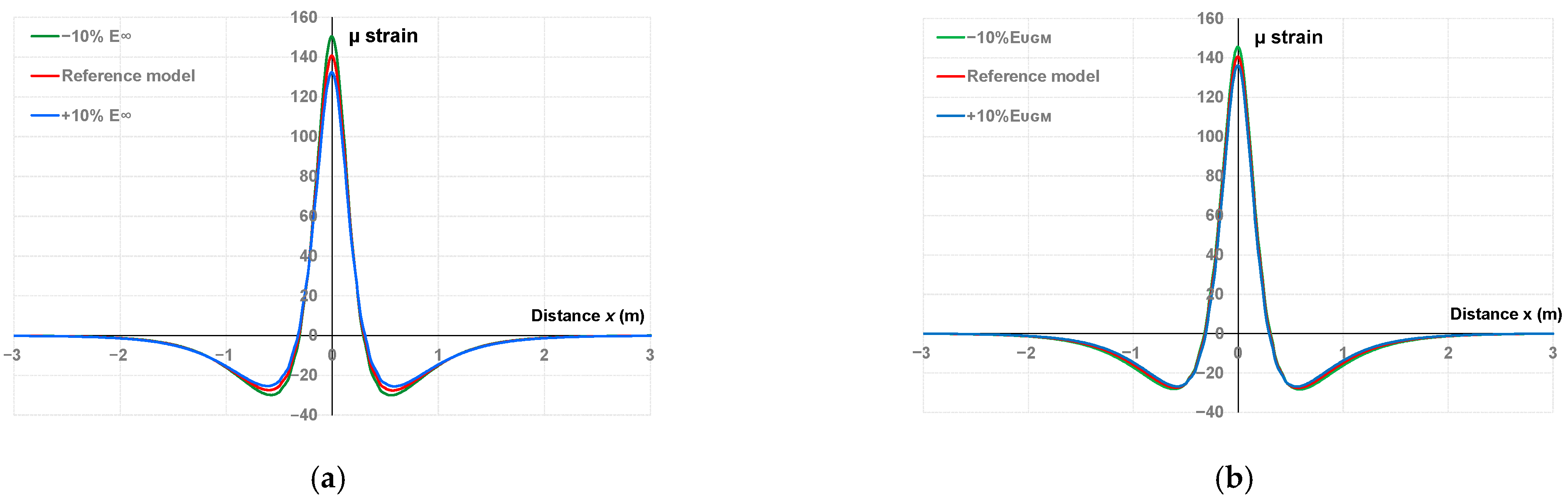
5.1. Choice of the Construction Parameters of the Optimized Indicators
5.2. Choice of the Construction Parameters of the Optimized Indicators
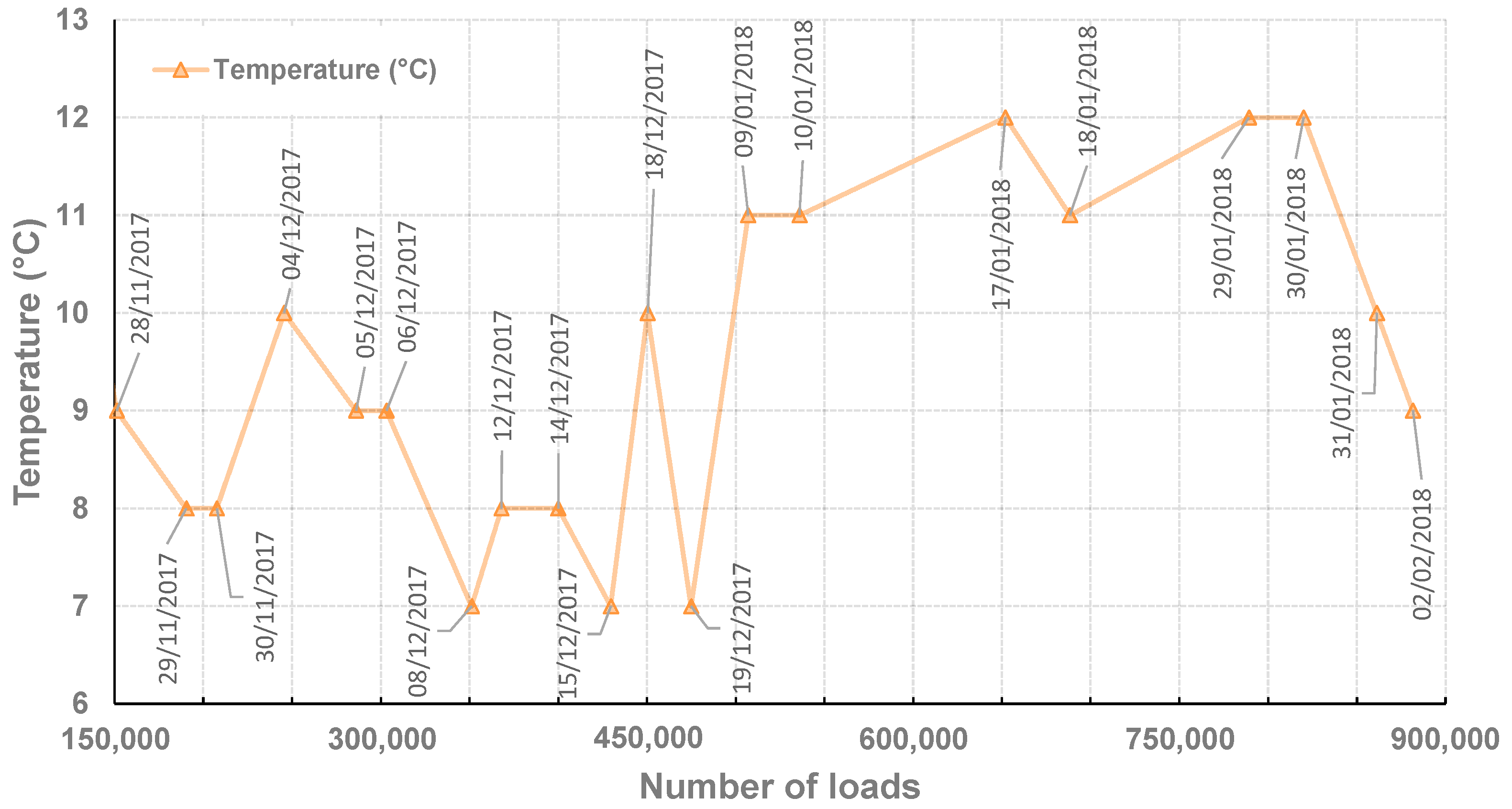
6. Data Processing of the Carousel Test
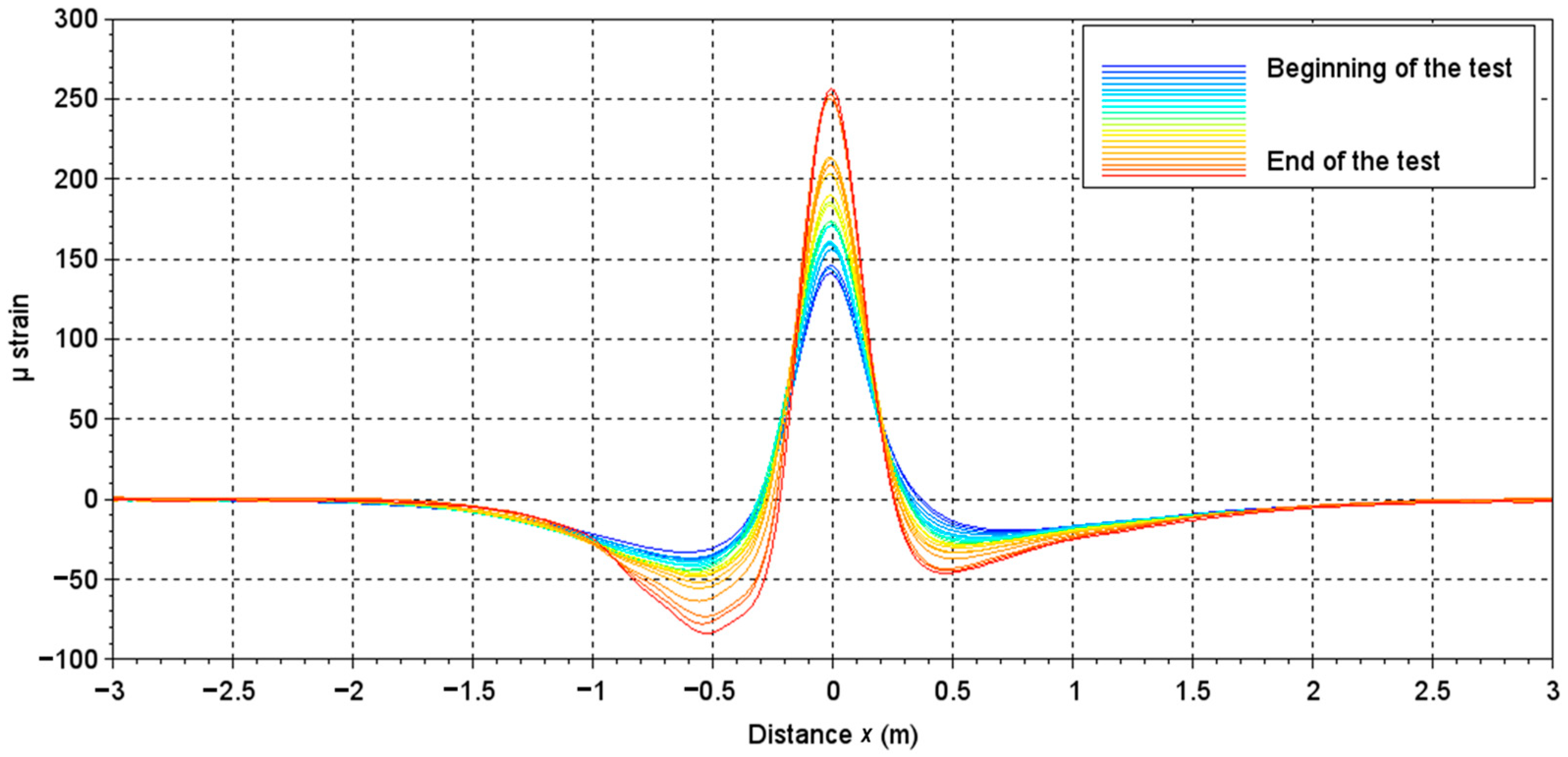
6.1. Evolution of Signals’ Values with Loadings
6.2. Implementation of the OIM
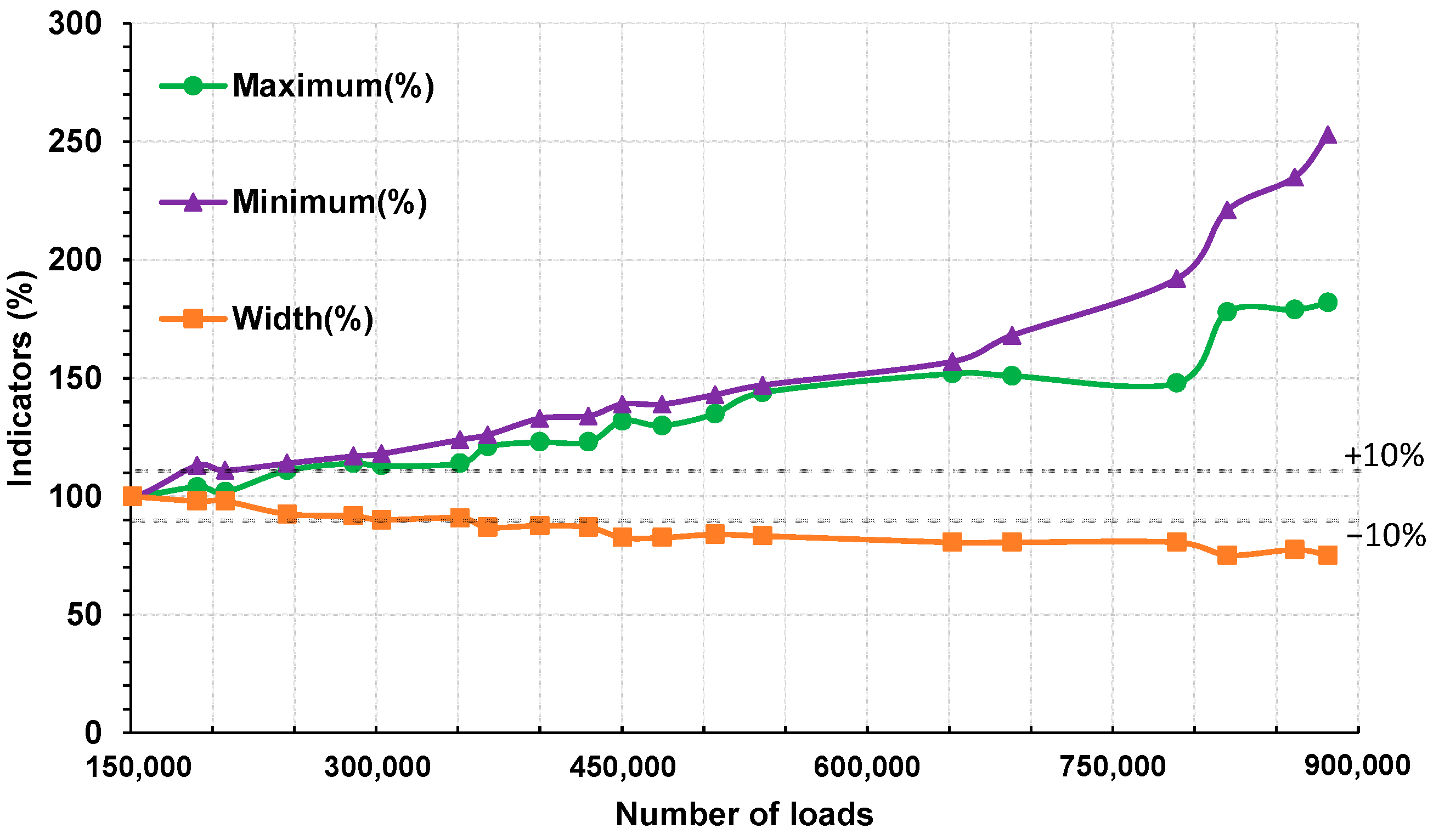
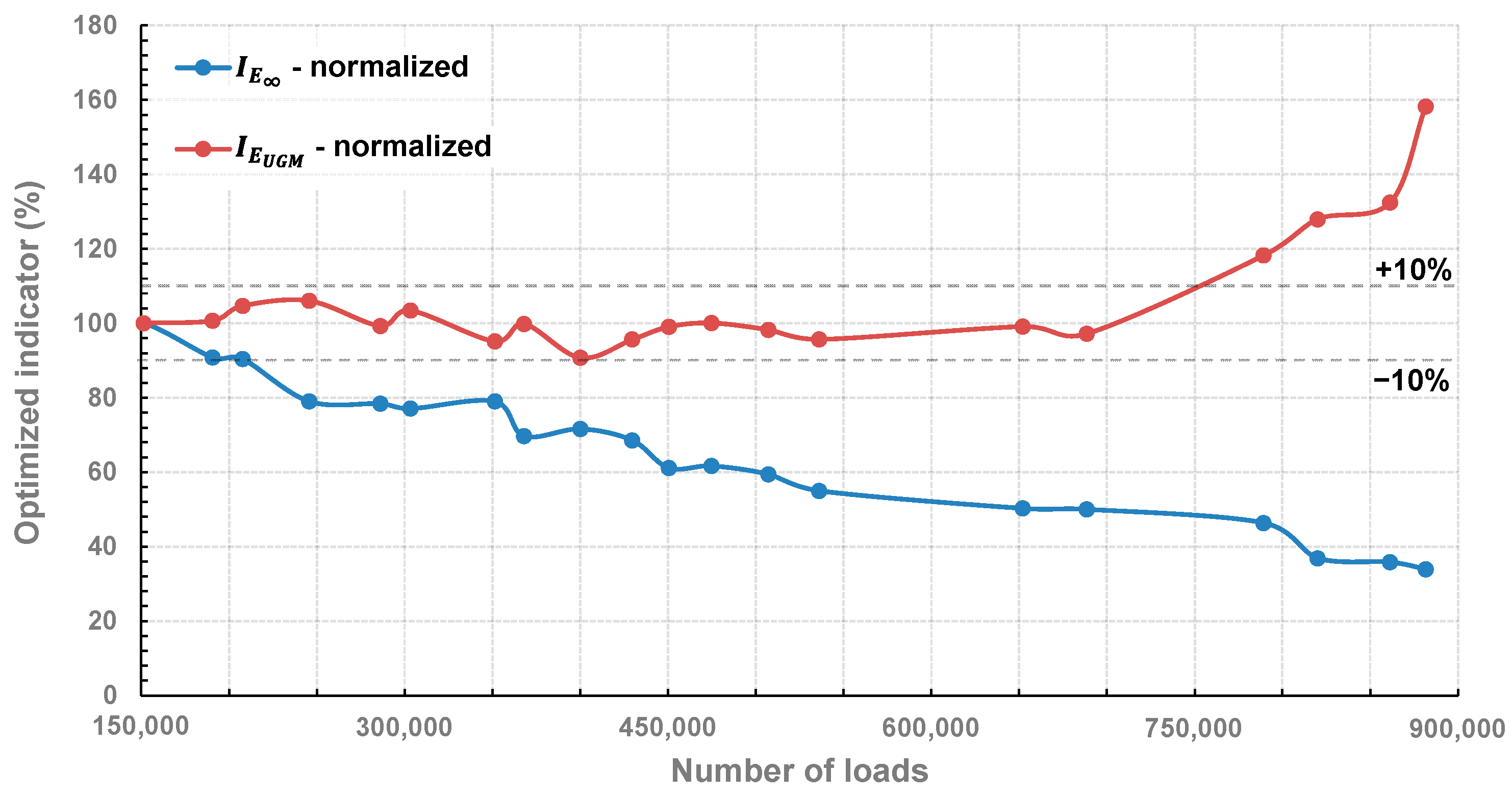
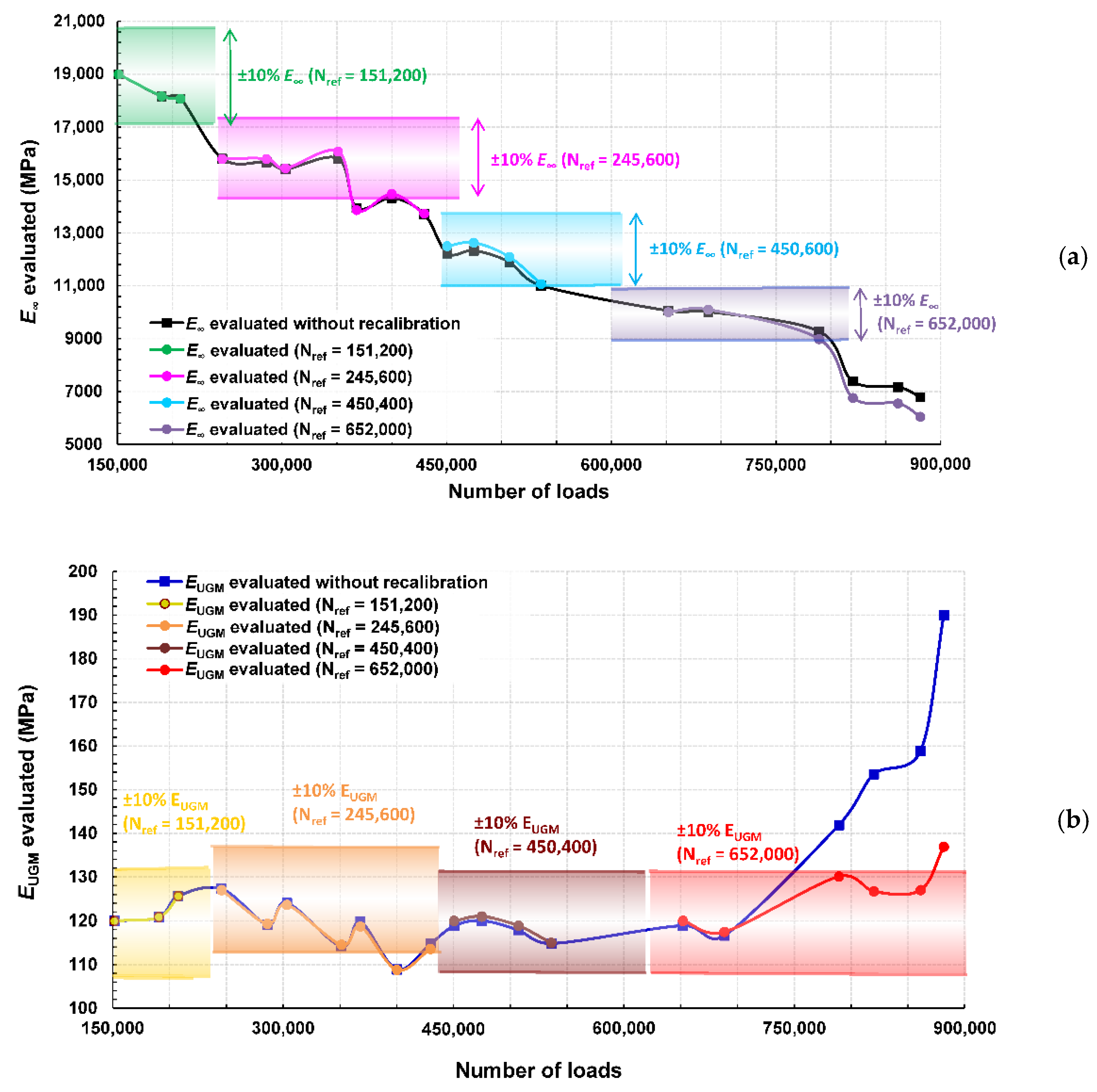
6.3. Data Processing through Regular Recalibration of the OIM
6.4. Discussion and Prospects
- -
- The bituminous layer is progressively damaged during the complete experimental campaign, this damage leading to a decrease of its instantaneous elastic modulus. After a regular decrease from 152,200 to 536,000 loadings, this characteristic remained nearly constant in the range of 652,000 to 789,200 loadings and noticeably decreased at 820,000 loadings.
- -
- The base layer, composed of unbound granular materials, kept a nearly constant 120 MPa elastic modulus from 151,200 to 688,400 loadings, before a net increase evaluated up to 130 MPa at N = 789,200. As the elastic modulus of the bituminous layer is reduced due to the repeated 65 kN-loadings, we assume that a slight compaction of the base layer may occur through compressive stress transmission. Afterwards, the damaging of the bituminous layer continued at 820,000 loadings, while the base layer was unaffected.
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, Y.; Su, P.; Li, M.; You, Z.; Zhao, M. Review on evolution and evaluation of asphalt pavement structures and materials. J. Traffic Transp. Eng. 2020, 7, 573–599. [Google Scholar] [CrossRef]
- Peraka, N.S.P.; Biligiri, K.P. Pavement asset management systems and technologies: A review. Autom. Constr. 2020, 119, 103336. [Google Scholar] [CrossRef]
- Marecos, V.; Solla, M.; Fontul, S.; Antunes, V. Assessing the pavement subgrade by combining different non-destructive methods. Constr. Build. Mater. 2017, 135, 76–85. [Google Scholar] [CrossRef] [Green Version]
- Chengchao, G.; Pengfei, X.; Yanhui, Z. Nondestructive Testing Method to Assess and Detect Road Performance. Strateg. Study CAE 2017, 19, 72–79. [Google Scholar] [CrossRef]
- Kamruzaman, N.; Mohd Kamaruddin, D.N.H. Non-destructive Method for Asphalt Pavement Evaluation: A Review. RTCEBE 2021, 2, 315–322. Available online: https://publisher.uthm.edu.my/periodicals/index.php/rtcebe/article/view/1500 (accessed on 13 July 2022).
- Guo, S.; Xu, Z.; Li, X.; Zhu, P. Detection and Characterization of Cracks in Highway Pavement with the Amplitude Variation of GPR Diffracted Waves: Insights from Forward Modeling and Field Data. Remote Sens. 2022, 14, 976. [Google Scholar] [CrossRef]
- Diamantia, N.; Redmanb, D. Field observations and numerical models of GPR response from vertical pavement cracks. J. Appl. Geophy. 2012, 81, 106–116. [Google Scholar] [CrossRef]
- Horak, E. Benchmarking the structural condition of flexible pavements with deflection bowl parameters. J. S. Afr. Inst. Civ. Eng. 2008, 50, 2–9. Available online: http://hdl.handle.net/2263/6317 (accessed on 13 July 2022).
- Khan, Z.H.; Tarefder, R.A.; Hasan, M.A. Field Characterization of Pavement Materials using Falling Weight Deflectometer and Sensor Data from an Instrumented Pavement Section. Transp. Res. Rec. 2020, 2674, 205–221. [Google Scholar] [CrossRef]
- Di Graziano, A.; Marchetta, V.; Cafiso, S. Structural health monitoring of asphalt pavements using smart sensor networks: A comprehensive review. J. Traffic Transp. Eng. 2020, 7, 639–651. [Google Scholar] [CrossRef]
- Le Boursicaud, V. New Uses of Deflection Bowls Measurements to Characterize the Structural Conditions of Pavements. Ph.D. Thesis, Ecole Centrale de Nantes, Nantes University, Nantes, France, 2018. [Google Scholar]
- Simonin, J.-M.; Piau, J.-M.; Le-Boursicault, V.; Freitas, M. Orthogonal Set of Indicators for the Assessment of Flexible Pavement Stiffness from Deflection Monitoring: Theoretical Formalism and Numerical Study. Remote Sens. 2022, 14, 500. [Google Scholar] [CrossRef]
- Chailleux, E.; Bessmann, E.; Hornych, P.; Blanc, J.; Gaudefroy, V.; Sotoodeh-Nia, Z.; Manke, N.; Williams, C.; Cochran, E.; Lo Presti, D.; et al. BioRePavation: Innovation in bio-recycling of old asphalt pavements, comparison between EU and US mix design specification systems. In Proceedings of the 13th ISAP Conference, Fortaleza, Brazil, 19–21 June 2018. [Google Scholar]
- Blanc, J.; Chailleux, E.; Hornych, P.; Williams, C.; Sotoodeh-Niab, Z.; Porot, L.; Pouget, S.; Olard, F.; Planche, J.-P.; Lo Presti, D.; et al. From laboratory mixes evaluation to full scale test: Fatigue behavior of bio-materials recycled asphalt mixtures. In Accelerated Pavement Testing to Transport Infrastructure Innovation; Chabot, A., Hornych, P., Harvey, J., Loria-Salazar, L.G., Eds.; Springer International Publishing: Cham, Switzerland, 2000; pp. 261–269. [Google Scholar] [CrossRef]
- Blanc, J.; Chailleux, E.; Hornych, P.; Williams, C.; Lo Presti, D.; Jimenez Del Barco Carrion, A.; Porot, L.; Planche, J.-P.; Pouget, S. Bio materials with reclaimed asphalt: From lab mixes properties to non-damaged full scale monitoring and mechanical simulation. Road Mater. Pavement Des. 2019, 20, S95–S111. [Google Scholar] [CrossRef]
- The Pavement Fatigue Carrousel. Available online: https://lames.univ-gustave-eiffel.fr/en/equipments/the-pavement-fatigue-carrousel (accessed on 11 July 2022).
- Nguyen, M.L.; Balay, J.M.; Sauzéat, C.; Di Benedeto, H.; Bilodeau, K.; Olard, F.; Ficheroulle, B. Accelerated pavement testing experiment of a pavement made of fiber-reinforced roller-compacted concrete. In Proceedings of the 4th International Conference on Accelerated Pavement Testing, Davis, CA, USA, 19–21 September 2012; pp. 299–311. Available online: https://trid.trb.org/view/1225105 (accessed on 13 June 2022).
- Blanc, J.; Hornych, P.; Sotoodeh-Niab, Z.; Williams, C.; Porot, L.; Pouget, S.; Boysen, R.; Planche, J.-P.; Lo Presti, D.; Jimenez, A.; et al. Full-scale validation of bio-recycled asphalt mixtures for road pavements. J. Clean. Prod. 2019, 227, 1068–1078. [Google Scholar] [CrossRef] [Green Version]
- Precision Transducers-Dynatest. Available online: https://dynatest.com/wp-content/uploads/2021/06/PAST-1.pdf (accessed on 11 July 2022).
- Xu, Q.; Solaimanian, M. Modelling linear viscoelastic properties of asphalt concrete by the Huet–Sayegh model. Int. J. Pavement Eng. 2009, 10, 401–422. [Google Scholar] [CrossRef]
- Huet, C. Etude Par Une Méthode D’impédance du Comportement Viscoélastiques des Matériaux Hydrocarbonnées. Ph.D. Thesis, Université de Paris, Paris, France, 1965. [Google Scholar]
- Sayegh, G. Viscoelastic Properties of Bituminous Mixtures. In Proceedings of the Second International Conference on Structural Design of Asphalt Pavement, Ann Arbor, MI, USA, 7–11 August 1967; pp. 743–755. [Google Scholar]
- Adams, Y.E.; Zeghal, M.; Mohamed, E.H. Complex Modulus Test Protocol and Procedure for Determining Huet-Sayegh Model Parameters; Internal Report no. IRC-IR-871; National Research Council of Canada, Institute for Research in Construction: Ottawa, ON, Canada, 2006. [Google Scholar] [CrossRef]
- Chabot, A.; Chupin, O.; Deloffre, L.; Duhamel, D. Viscoroute 2.0 A tool for the simulation of moving load effects on asphalt pavement. Road Mater. Pavement Des. 2010, 11, 227–250. [Google Scholar] [CrossRef] [Green Version]
- Chupin, O.; Chabot, A.; Piau, J.-M.; Duhamel, D. Influence of sliding interfaces on the response of a layered viscoelastic medium under moving load. Int. J. Solids Struct. 2010, 47, 3435–3446. [Google Scholar] [CrossRef] [Green Version]
- Chupin, O.; Piau, J.-M.; Chabot, A. Evaluation of the structure-induced rolling resistance (SRR) for pavement including viscoelastic material layers. Mater. Struct. 2013, 46, 683–696. [Google Scholar] [CrossRef]
- Ritter, J.; Rabe, R.; Wolf, A. Accelerated pavement testing of two flexible road pavements to assess long-term structural performance. In Proceedings of the 4th International Conference on Accelerated Pavement Testing, Davis, CA, USA, 19–21 September 2012; pp. 225–236. Available online: https://trid.trb.org/view/1245198 (accessed on 13 July 2022).
- Kerzrého, J.-P.; Hornych, P.; Chabot, A.; Trichet, S.; Gouy, T.; Coirier, G.; Deloffre, L. Evaluation of the agressiveness of different multi-axle loads using accelerated pavement tests. In Proceedings of the 4th International Conference on Accelerated Pavement Testing, Davis, CA, USA, 19–21 September 2012; pp. 505–517. Available online: https://trid.trb.org/view/1262595 (accessed on 13 July 2022).



| E0 (MPa) | (MPa) | (MPa) | δ | h | k | τ | A0 | A1 | A2 |
|---|---|---|---|---|---|---|---|---|---|
| 150 | 19,000 | 120 | 1.35 | 0.54 | 0.11 | 1.30 | 8.9 | −0.44 | 0.0016 |
| Parameter | E0 | δ | h | k | A0 | A1 | A2 | ||
|---|---|---|---|---|---|---|---|---|---|
| (%) | 0 | 11 | 10 | 3 | 1 | 3 | 3 | 3 | 0 |
| Deviation of the Indicator (%) | Deviation of the Indicator (%) | |||
|---|---|---|---|---|
| Reference signal | −18,098.81 | 0 | −133.90 | 0 |
| −10% | −20,161.25 | −11.46 | −133.57 | +0.25 |
| +10% | −16,361.25 | +9.67 | −133.57 | +0.25 |
| −10% | −18,075.03 | +0.13 | −146.71 | −9.34 |
| +10% | −18,075.03 | +0.13 | −122.71 | +8.19 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Souriou, D.; Simonin, J.-M.; Schmidt, F. Definition of Optimized Indicators from Sensors Data for Damage Detection of Instrumented Roadways. Sensors 2022, 22, 5572. https://doi.org/10.3390/s22155572
Souriou D, Simonin J-M, Schmidt F. Definition of Optimized Indicators from Sensors Data for Damage Detection of Instrumented Roadways. Sensors. 2022; 22(15):5572. https://doi.org/10.3390/s22155572
Chicago/Turabian StyleSouriou, David, Jean-Michel Simonin, and Franziska Schmidt. 2022. "Definition of Optimized Indicators from Sensors Data for Damage Detection of Instrumented Roadways" Sensors 22, no. 15: 5572. https://doi.org/10.3390/s22155572
APA StyleSouriou, D., Simonin, J.-M., & Schmidt, F. (2022). Definition of Optimized Indicators from Sensors Data for Damage Detection of Instrumented Roadways. Sensors, 22(15), 5572. https://doi.org/10.3390/s22155572







