Authenticated Semi-Quantum Key Distribution Protocol Based on W States
Abstract
:1. Introduction
- (1)
- It reduces the quantum hardware equipment when compared to other ASQKD protocols.
- (2)
- It does not require pre-share keys.
- (3)
- Wen et al. demonstrated that the proposed ASQKD protocol is robust against typical attacks.
- (4)
- It is highly efficient than some of the existing ASQKD protocols.
- The proposed ASQKD protocol ensures the procedure is functional.
- The proposed ASQKD protocol does not require quantum memory and legally fulfills a semi-quantum environment [17].
- The proposed ASQKD protocol, based on W states, only reduces the quantum hardware requirements.
- The qubit efficiency of the proposed ASQKD protocol is 1.6 times higher than that of Wen et al.’s ASQKD protocol.
- The proposed ASQKD protocol does not require classical cryptography (i.e., the hash function), which does not show the potential menace of the advance quantum computing.
2. Review of Wen et al.’s ASQKD Protocol
- Step W1.
- Alice prepares n GHZ-like states as shown in Equation (1) and divides these states into three sequences: . Every photon in represents all the first particles in GHZ-like states, and and represent all the second and third particles in GHZ-like states. Then, she inserts random decoy states into and obtains as follows:
- Step W2.
- Alice encodes state string according to the specific coding rule (see also Table 1), generates a binary message string , then recodes the binary string according to the following rules: binary message {0,1} recodes into the Z-basis . Eventually, Alice obtains the new particle string | = {}. Alice performs W-basis measurement on and and performs Bell measurement on Then, Alice can obtain the measurement results respectively. Alice informs Bob of the measurement results via a classical channel. It should be noted that is presented in notation format
- Step W3.
- Bob receives the measurement results, from Alice. He can perform the unitary operation on to recover the states based on the measurement result . Bob measures in using a Z-basis. Then, he records the measurement results as . According to the notation and the measurement result of , Bob applies the corresponding coding rule and obtains as shown in Table 2 below.
- Step W4.
- Bob obtains and returns based on If or , then he measures in the Z-basis, prepares the same photon as , and resends it back to Alice. If or , then Bob returns as directly to Alice. Furthermore, Alice checks the received decoy states using the correct corresponding basis.
- Step W5.
- Alice measures on the correct basis and checks if equals to the original Alice then announces the position of and decoy photons in to Bob via the classical channel. According to this announcement, Bob removes the decoy state in and recovers sequence Then, Bob measures on the Z-basis to check its correlation with .
- Step W6.
- Based on the measurement results of , Bob generates binary string according to the following coding rules: if the measurement result is , then he encodes . Furthermore, while the measurement result is , he encodes . Bob hashes to obtain the hash value H(). Bob then sends H() to Alice.
- Step W7.
- Alice calculates H() and checks if H() equals H().
3. Security Issues in Wen et al.’s ASQKD Protocol
3.1. Teleportation of W States in Wen et al.’s ASQKD Protocol
3.2. Quantum Environment Issue in Wen et al.’s ASQKD Protocol
4. Proposed Measure-Resend ASQKD Protocol
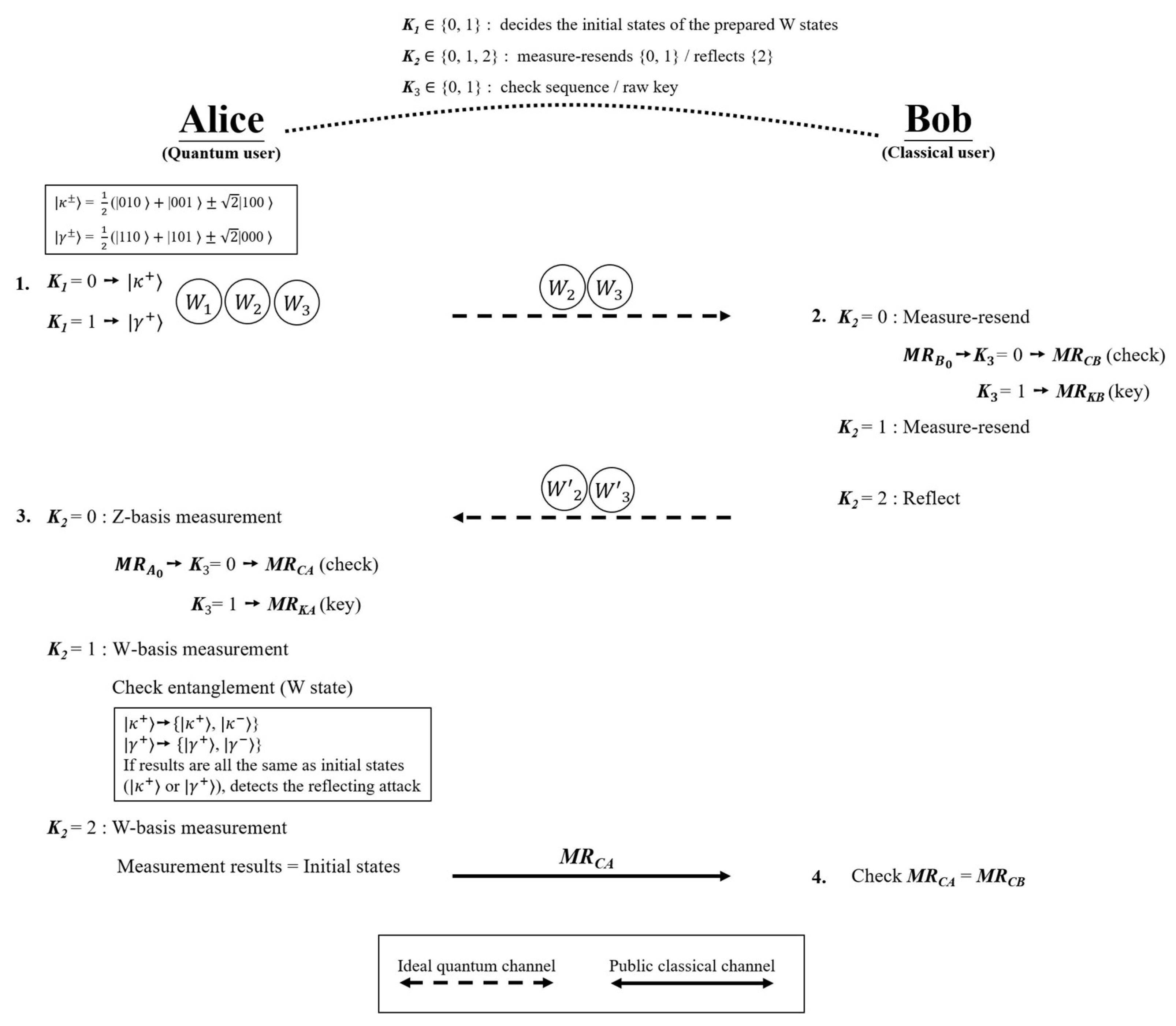
- Step 1.
- Alice prepares the initial W states based on If , then Alice prepares , and while , she prepares . Alice then divides the W states into three sequences: , , and represents all the first particles of W states. Similarly, and represent all the second and third particles of W states, respectively. Alice sends and to Bob one photon at a time.
- Step 2.
- For every received photon, Bob performs measure-resending or reflects photons based on .
- If , then Bob measures the received photon on a Z-basis, prepares the same photon as the measurement result, and resends it to Alice. For the measured sequence at , if , then Bob records the measurement results to the check sequence ; if , then Bob records the measurement results to the key sequence .
- If , then Bob measures the received photon on a Z-basis, prepares the same photon as the measurement result, and resends it to Alice.
- If , then Bob reflects the received photon back to Alice without any influence.
- Step 3.
- Alice receives and from Bob. She performs Z-basis or W-basis measurements based on .
- If , then Alice performs a Z-basis measurement and classifies it into two measured sequences based on . If , then Alice records the measurement results as a check sequence , whereas if , Alice records the measurement results to the key sequence .
- If , then Alice performs a W-basis measurement to check the entanglement correlation of the W states. Hence, according to the uncertainty principle, if the initial state is or , then the measured states should collapse into } or }. Otherwise, if the states remain the same as the initial state, then it is inferred that Bob does not measure the photons and Alice will detect that the protocol may suffer from the reflecting attack.
- If , then Alice performs a W-basis measurement for the eavesdropping check. Alice compares the measurement results with the initial states. This implies that if the states remain the same as the original states, neither Bob nor Eve measure the photons, proving the security of the transmission.
After the eavesdropping check, Alice announces to Bob.
- Step 4.
- Bob checks if to secure the channel. Eventually, Alice and Bob share a raw key as the measurement result of (i.e., if one measures , represents classical bits “00”, “01”, “10”, “11”, respectively.). Then, they perform a privacy amplification process [67,68] on the raw key to distill the private key.
5. Security Analysis
5.1. Impersonation Attack
5.1.1. Assume Eve Essayed to Impersonate Alice
5.1.2. Assume Eve Essayed to Impersonate Bob
5.2. Reflecting Attack
5.3. Man-in-the-Middle Attack
5.4. Collective Attack
5.5. Key Leakage Problem
6. Efficiency Analysis
- The proposed ASQKD protocol ensures the procedure is functional.
- The proposed ASQKD protocol does not require quantum memory and legally fulfills a semi-quantum environment [17].
- The proposed ASQKD protocol, based on W states, only reduces the quantum hardware requirements.
- The qubit efficiency of the proposed ASQKD protocol is 1.6 times higher than that of Wen et al.’s ASQKD protocol.
- The proposed ASQKD protocol does not require classical cryptography (i.e., the hash function), which does not show the potential menace of the advance quantum computing.
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Shor, P.W. Algorithms for quantum computation: Discrete logarithms and factoring. In Proceedings of the 35th Annual Symposium on the Foundations of Computer Science, Los Alamitos, CA, USA, 20–22 November 1994; pp. 124–134. [Google Scholar]
- Bennett, C.H.; Brassard, G. Quantum Cryptography: Public Key Distribution and Coin Tossing. In Proceedings of the IEEE International Conference on Computers, Systems and Signal Processing, Bangalore, India, 9–12 December 1984; pp. 175–179. [Google Scholar]
- Boström, K.; Felbinger, T. Deterministic Secure Direct Communication Using Entanglement. Phys. Rev. Lett. 2002, 89, 187902. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Deng, F.-G.; Long, G.; Liu, X.-S. Two-step quantum direct communication protocol using the Einstein-Podolsky-Rosen pair block. Phys. Rev. A 2003, 68, 042317. [Google Scholar] [CrossRef] [Green Version]
- Man, Z.X.; Zhang, Z.J.; Li, Y. Deterministic secure direct communication by using swapping quantum entanglement and local unitary operations. Chin. Phys. Lett. 2005, 22, 18–21. [Google Scholar]
- Zhang, Z.J.; Jun, L.; Liu, Y.M.; Cao, H.J.; Shi, S.H. Revisiting quantum secure direct communication with W state. Chin. Phys. Lett. 2006, 23, 2652–2655. [Google Scholar]
- Zhang, Z.J.; Yuan, H.; Liu, Y.M.; Zhang, W. Eavesdropping on quantum secure direct communication with W state in noisy channel. Commun. Theor. Phys. 2008, 49, 103–106. [Google Scholar]
- Zhang, Z.J.; Li, Y.; Man, Z.X. Multiparty quantum secret sharing. Phys. Rev. A 2005, 71, 044301. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.J.; Man, Z.X. Multiparty quantum secret sharing of classical messages based on entanglement swapping. Phys. Rev. A 2005, 72, 022303. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.J.; Liu, Y.M.; Fang, M.; Wang, D. Multiparty quantum secret sharing scheme of classical messages by swapping qudit-state entanglement. Int. J. Mod. Phys. C 2007, 18, 1885–1901. [Google Scholar] [CrossRef]
- Han, L.F.; Liu, Y.M.; Liu, J.; Zhang, Z.J. Multiparty quantum secret sharing of secure direct communication using single photons. Opt. Commun. 2008, 281, 2690–2694. [Google Scholar] [CrossRef]
- Wang, X.; Liu, Y.M.; Han, L.F.; Zhang, Z.J. Multiparty Quantum Secret Sharing of Secure Direct Communication with High-Dimensional Quantum Superdense Coding. Int. J. Quantum Inf. 2008, 6, 1155–1163. [Google Scholar] [CrossRef]
- Zeng, G.H.; Zhang, W.P. Identity verification in quantum key distribution. Phys. Rev. A 2000, 61, 5. [Google Scholar] [CrossRef]
- Hwang, T.; Lee, K.C.; Li, C.M. Provably secure three-party authenticated quantum key distribution protocols. IEEE Trans. Dependable Secur. Comput. 2007, 4, 71–80. [Google Scholar] [CrossRef]
- Shih, H.C.; Lee, K.C.; Hwang, T. New Efficient Three-Party Quantum Key Distribution Protocols. IEEE J. Sel. Top. Quantum 2009, 15, 1602–1606. [Google Scholar] [CrossRef]
- Boyer, M.; Kenigsberg, D.; Mor, T. Quantum Key Distribution with Classical Bob. Phys. Rev. Lett. 2007, 99, 140501. [Google Scholar] [CrossRef] [Green Version]
- Boyer, M.; Gelles, R.; Kenigsberg, D.; Mor, T. Semiquantum key distribution. Phys. Rev. A 2009, 79, 032341. [Google Scholar] [CrossRef] [Green Version]
- Zou, X.; Qiu, D.; Li, L.; Wu, L.; Li, L. Semiquantum-key distribution using less than four quantum states. Phys. Rev. A 2009, 79, 052312. [Google Scholar] [CrossRef]
- Krawec, W.O. Restricted attacks on semi-quantum key distribution protocols. Quantum Inf. Process. 2014, 13, 2417–2436. [Google Scholar] [CrossRef]
- Krawec, W.O. Mediated semiquantum key distribution. Phys. Rev. A 2015, 91, 032323. [Google Scholar] [CrossRef] [Green Version]
- Krawec, W.O. Security of a semi-quantum protocol where reflections contribute to the secret key. Quantum Inf. Process. 2016, 15, 2067–2090. [Google Scholar] [CrossRef] [Green Version]
- Li, Q.; Chan, W.H.; Zhang, S. Semiquantum key distribution with secure delegated quantum computation. Sci. Rep. 2016, 6, 19898. [Google Scholar] [CrossRef] [Green Version]
- Boyer, M.; Katz, M.; Liss, R.; Mor, T. Experimentally feasible protocol for semiquantum key distribution. Phys. Rev. A 2017, 96, 062335. [Google Scholar] [CrossRef] [Green Version]
- Tsai, C.-W.; Yang, C.-W.; Lee, N.-Y. Lightweight mediated semi-quantum key distribution protocol. Mod. Phys. Lett. A 2019, 34, 1950281. [Google Scholar] [CrossRef]
- Wang, M.-M.; Gong, L.-M.; Shao, L.-H. Efficient semiquantum key distribution without entanglement. Quantum Inf. Process. 2019, 18, 260. [Google Scholar] [CrossRef]
- Hajji, H.; El Baz, M. Qutrit-based semi-quantum key distribution protocol. Quantum Inf. Process. 2021, 20, 4. [Google Scholar] [CrossRef]
- Han, S.; Huang, Y.; Mi, S.; Qin, X.; Wang, J.; Yu, Y.; Wei, Z.; Zhang, Z. Proof-of-principle demonstration of semi-quantum key distribution based on the Mirror protocol. EPJ Quantum Technol. 2021, 8, 28. [Google Scholar] [CrossRef]
- Tsai, C.-W.; Yang, C.-W. Lightweight mediated semi-quantum key distribution protocol with a dishonest third party based on Bell states. Sci. Rep. 2021, 11, 23222. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.; Chan, W.H.; Long, D.Y. Semiquantum secret sharing using entangled states. Phys. Rev. A 2010, 82, 022303. [Google Scholar] [CrossRef] [Green Version]
- Gheorghiu, V. Generalized semiquantum secret-sharing schemes. Phys. Rev. A 2012, 85, 052309. [Google Scholar] [CrossRef] [Green Version]
- Li, L.Z.; Qiu, D.W.; Mateus, P. Quantum secret sharing with classical Bobs. J. Phys. A-Math. Theor. 2013, 46, 045304. [Google Scholar] [CrossRef] [Green Version]
- Xie, C.; Li, L.; Qiu, D. A Novel Semi-Quantum Secret Sharing Scheme of Specific Bits. Int. J. Theor. Phys. 2015, 54, 3819–3824. [Google Scholar] [CrossRef]
- Li, Z.; Li, Q.; Liu, C.; Peng, Y.; Chan, W.H.; Li, L. Limited resource semiquantum secret sharing. Quantum Inf. Process. 2018, 17, 285. [Google Scholar] [CrossRef]
- Yin, A.H.; Tong, Y. A novel semi-quantum secret sharing scheme using entangled states. Mod. Phys. Lett. B 2018, 32, 1850256. [Google Scholar] [CrossRef]
- Tsai, C.-W.; Yang, C.-W.; Lee, N.-Y. Semi-quantum secret sharing protocol using W-state. Mod. Phys. Lett. A 2019, 34, 1950213. [Google Scholar] [CrossRef]
- Xiang, Y.; Liu, J.; Bai, M.-q.; Yang, X.; Mo, Z.-w. Limited Resource Semi-Quantum Secret Sharing Based on Multi-Level Systems. Int. J. Theor. Phys. 2019, 58, 2883–2892. [Google Scholar] [CrossRef]
- Li, C.; Ye, C.; Tian, Y.; Chen, X.-B.; Li, J. Cluster-state-based quantum secret sharing for users with different abilities. Quantum Inf. Process. 2021, 20, 385. [Google Scholar] [CrossRef]
- Tian, Y.; Li, J.; Chen, X.-B.; Ye, C.-Q.; Li, H.-J. An efficient semi-quantum secret sharing protocol of specific bits. Quantum Inf. Process. 2021, 20, 217. [Google Scholar] [CrossRef]
- Tsai, C.-W.; Yang, C.-W.; Lin, J. Multiparty mediated quantum secret sharing protocol. Quantum Inf. Process. 2022, 21, 63. [Google Scholar] [CrossRef]
- Zhang, M.-H.; Li, H.-F.; Xia, Z.-Q.; Feng, X.-Y.; Peng, J.-Y. Semiquantum secure direct communication using EPR pairs. Quantum Inf. Process. 2017, 16, 117. [Google Scholar] [CrossRef]
- Xie, C.; Li, L.; Situ, H.; He, J. Semi-quantum Secure Direct Communication Scheme Based on Bell States. Int. J. Theor. Phys. 2018, 57, 1881–1887. [Google Scholar] [CrossRef]
- Yan, L.; Sun, Y.; Chang, Y.; Zhang, S.; Wan, G.; Sheng, Z. Semi-quantum protocol for deterministic secure quantum communication using Bell states. Quantum Inf. Process. 2018, 17, 315. [Google Scholar] [CrossRef]
- Sun, Y.; Yan, L.; Chang, Y.; Zhang, S.; Shao, T.; Zhang, Y. Two semi-quantum secure direct communication protocols based on Bell states. Mod. Phys. Lett. A 2019, 34, 1950004. [Google Scholar] [CrossRef]
- Tao, Z.; Chang, Y.; Zhang, S.; Dai, J.; Li, X. Two Semi-Quantum Direct Communication Protocols with Mutual Authentication Based on Bell States. Int. J. Theor. Phys. 2019, 58, 2986–2993. [Google Scholar] [CrossRef]
- Wang, M.-M.; Liu, J.-L.; Gong, L.-M. Semiquantum secure direct communication with authentication based on single-photons. Int. J. Quantum Inf. 2019, 17, 1950024. [Google Scholar] [CrossRef]
- Rong, Z.; Qiu, D.; Zou, X. Semi-Quantum Secure Direct Communication Using Entanglement. Int. J. Theor. Phys. 2020, 59, 1807–1819. [Google Scholar] [CrossRef]
- Yang, C.-W. Efficient and secure semi-quantum secure direct communication protocol against double CNOT attack. Quantum Inf. Process. 2020, 19, 50. [Google Scholar] [CrossRef]
- Yang, C.-W.; Tsai, C.-W. Advanced semi-quantum secure direct communication protocol based on bell states against flip attack. Quantum Inf. Process. 2020, 19, 126. [Google Scholar] [CrossRef]
- Zhang, X.; Zhou, R.-G. An Efficient and Novel Semi-Quantum Deterministic Secure Quantum Communication Protocol. Int. J. Theor. Phys. 2022, 61, 94. [Google Scholar] [CrossRef]
- Liu, W.-J.; Chen, Z.-Y.; Ji, S.; Wang, H.-B.; Zhang, J. Multi-party Semi-quantum Key Agreement with Delegating Quantum Computation. Int. J. Theor. Phys. 2017, 56, 3164–3174. [Google Scholar] [CrossRef]
- Shukla, C.; Thapliyal, K.; Pathak, A. Semi-quantum communication: Protocols for key agreement, controlled secure direct communication and dialogue. Quantum Inf. Process. 2017, 16, 295. [Google Scholar] [CrossRef] [Green Version]
- Yan, L.; Zhang, S.; Chang, Y.; Sheng, Z.; Yang, F. Mutual semi-quantum key agreement protocol using Bell states. Mod. Phys. Lett. A 2019, 34, 1950294. [Google Scholar] [CrossRef]
- Li, H.-H.; Gong, L.-H.; Zhou, N.-R. New semi-quantum key agreement protocol based on high-dimensional single-particle states. Chin. Phys. B 2020, 29, 110304. [Google Scholar] [CrossRef]
- Ye, T.-Y.; Ye, C.-Q. Measure-Resend Semi-Quantum Private Comparison Without Entanglement. Int. J. Theor. Phys. 2018, 57, 3819–3834. [Google Scholar] [CrossRef]
- Jiang, L.-Z. Semi-quantum private comparison based on Bell states. Quantum Inf. Process. 2020, 19, 180. [Google Scholar] [CrossRef]
- Tsai, C.-W.; Lin, J.; Yang, C.-W. Cryptanalysis and improvement in semi-quantum private comparison based on Bell states. Quantum Inf. Process. 2021, 20, 120. [Google Scholar] [CrossRef]
- Yan, L.; Zhang, S.; Chang, Y.; Wan, G.; Yang, F. Semi-quantum private comparison protocol with three-particle G-like states. Quantum Inf. Process. 2021, 20, 17. [Google Scholar] [CrossRef]
- Tian, Y.; Li, J.; Ye, C.; Chen, X.-B.; Li, C. W-state-based Semi-quantum Private Comparison. Int. J. Theor. Phys. 2022, 61, 18. [Google Scholar] [CrossRef]
- Yu, K.-F.; Yang, C.-W.; Liao, C.-H.; Hwang, T. Authenticated semi-quantum key distribution protocol using Bell states. Quantum Inf. Process. 2014, 13, 1457–1465. [Google Scholar] [CrossRef]
- Li, C.-M.; Yu, K.-F.; Kao, S.-H.; Hwang, T. Authenticated semi-quantum key distributions without classical channel. Quantum Inf. Process. 2016, 15, 2881–2893. [Google Scholar] [CrossRef]
- Meslouhi, A.; Hassouni, Y. Cryptanalysis on authenticated semi-quantum key distribution protocol using Bell states. Quantum Inf. Process. 2016, 16, 18. [Google Scholar] [CrossRef]
- Tsai, C.-W.; Yang, C.-W. Lightweight authenticated semi-quantum key distribution protocol without trojan horse attack. Laser Phys. Lett. 2020, 17, 075202. [Google Scholar] [CrossRef]
- Zebboudj, S.; Djoudi, H.; Lalaoui, D.; Omar, M. Authenticated semi-quantum key distribution without entanglement. Quantum Inf. Process. 2020, 19, 77. [Google Scholar] [CrossRef]
- Chang, C.-H.; Lu, Y.-C.; Hwang, T. Measure-resend authenticated semi-quantum key distribution with single photons. Quantum Inf. Process. 2021, 20, 272. [Google Scholar] [CrossRef]
- Wang, H.-W.; Tsai, C.-W.; Lin, J.; Huang, Y.-Y.; Yang, C.-W. Efficient and Secure Measure-Resend Authenticated Semi-Quantum Key Distribution Protocol against Reflecting Attack. Mathematics 2022, 10, 1241. [Google Scholar] [CrossRef]
- Wen, X.-J.; Zhao, X.-Q.; Gong, L.-H.; Zhou, N.-R. A semi-quantum authentication protocol for message and identity. Laser Phys. Lett. 2019, 16, 075206. [Google Scholar] [CrossRef]
- Bennett, C.H.; Brassard, G.; Robert, J.M. Privacy Amplification by Public Discussion. SIAM J. Comput. 1988, 17, 210–229. [Google Scholar] [CrossRef]
- Bennett, C.H.; Brassard, G.; Crepeau, C.; Maurer, U.M. Generalized privacy amplification. IEEE Trans. Inf. Theory 1995, 41, 1915–1923. [Google Scholar] [CrossRef] [Green Version]
| Yu et al.’s ASQKD Protocol [59] | Li et al.’s ASQKD Protocol [60] | Zebboudj et al.’s ASQKD Protocol [63] | Chang et al.’s ASQKD Protocol [64] | Wang et al.’s ASQKD Protocol [65] | Wen et al.’s ASQKD Protocol [66] | The Proposed ASQKD Protocol | |
|---|---|---|---|---|---|---|---|
| Quantum resource | Bell states | Bell states, Single photons | Single photons | Single photons | Single photons | GHZ-like states W states | W states |
| Qubit efficiency | 10% | 11% | 14% | 17% | 14% | ||
| Required pre-shared keys (in bits) | 6n | 4n | 3n | 3n | 3n | 4n | 5n |
| Classical participant’s quantum capabilities | Generate Reflect Measure | Generate Reflect Measure | Generate Reflect Measure | Generate Reflect Measure | Generate Reflect Measure | Generate Reflect Measure Quantum memory | Generate Reflect Measure |
| Classical participant does not require quantum memory | Yes | Yes | Yes | Yes | Yes | No | Yes |
| Legal semi-quantum environment | Yes | Yes | Yes | Yes | Yes | No | Yes |
| The protocol does not require the hash function | Yes | No | No | No | No | No | Yes |
| Runnable protocol | Yes | Yes | Yes | Yes | Yes | No | Yes |
| Required classical channel | Yes | Yes | Yes | Yes | No | Yes | Yes |
| Robustness of the reflecting attack | Yes | Yes | Yes | No | Yes | Yes | Yes |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.-W.; Tsai, C.-W.; Lin, J.; Yang, C.-W. Authenticated Semi-Quantum Key Distribution Protocol Based on W States. Sensors 2022, 22, 4998. https://doi.org/10.3390/s22134998
Wang H-W, Tsai C-W, Lin J, Yang C-W. Authenticated Semi-Quantum Key Distribution Protocol Based on W States. Sensors. 2022; 22(13):4998. https://doi.org/10.3390/s22134998
Chicago/Turabian StyleWang, Hung-Wen, Chia-Wei Tsai, Jason Lin, and Chun-Wei Yang. 2022. "Authenticated Semi-Quantum Key Distribution Protocol Based on W States" Sensors 22, no. 13: 4998. https://doi.org/10.3390/s22134998
APA StyleWang, H.-W., Tsai, C.-W., Lin, J., & Yang, C.-W. (2022). Authenticated Semi-Quantum Key Distribution Protocol Based on W States. Sensors, 22(13), 4998. https://doi.org/10.3390/s22134998









