Anisotropy of the ΔE Effect in Ni-Based Magnetoelectric Cantilevers: A Finite Element Method Analysis
Abstract
:1. Introduction
2. Model Details
2.1. Analytic Description of the ΔE Effect in Nickel
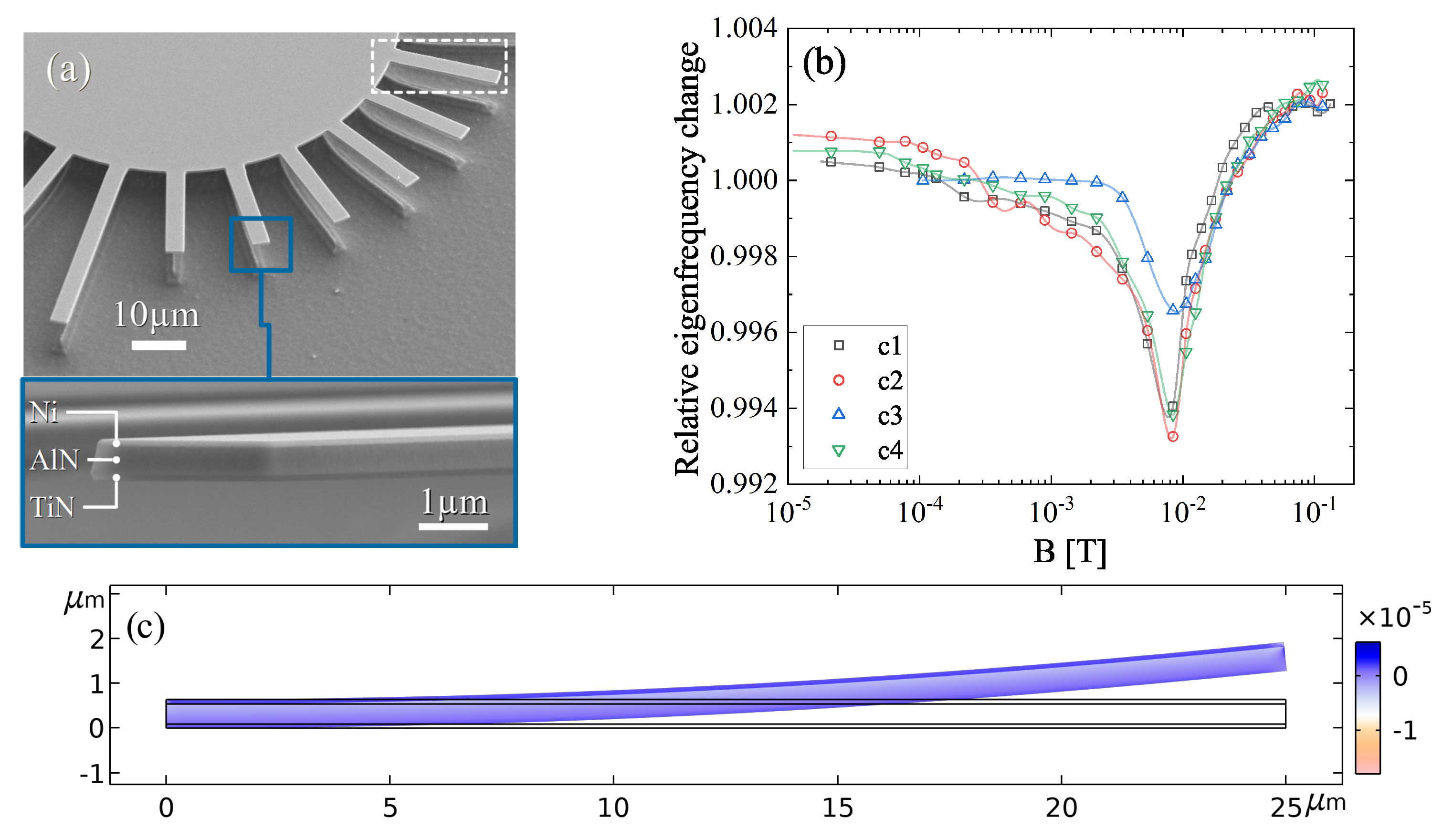
2.2. Description of the Finite Element Model
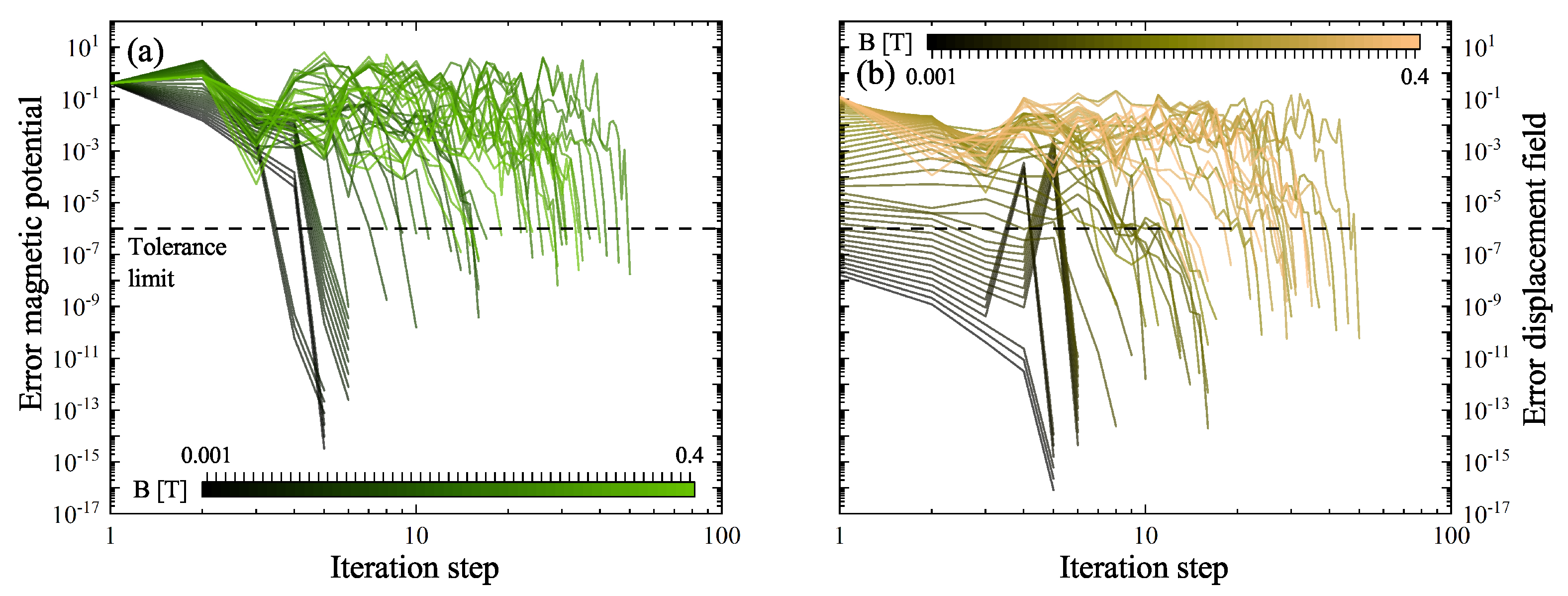
2.3. Limits of the Proposed Model
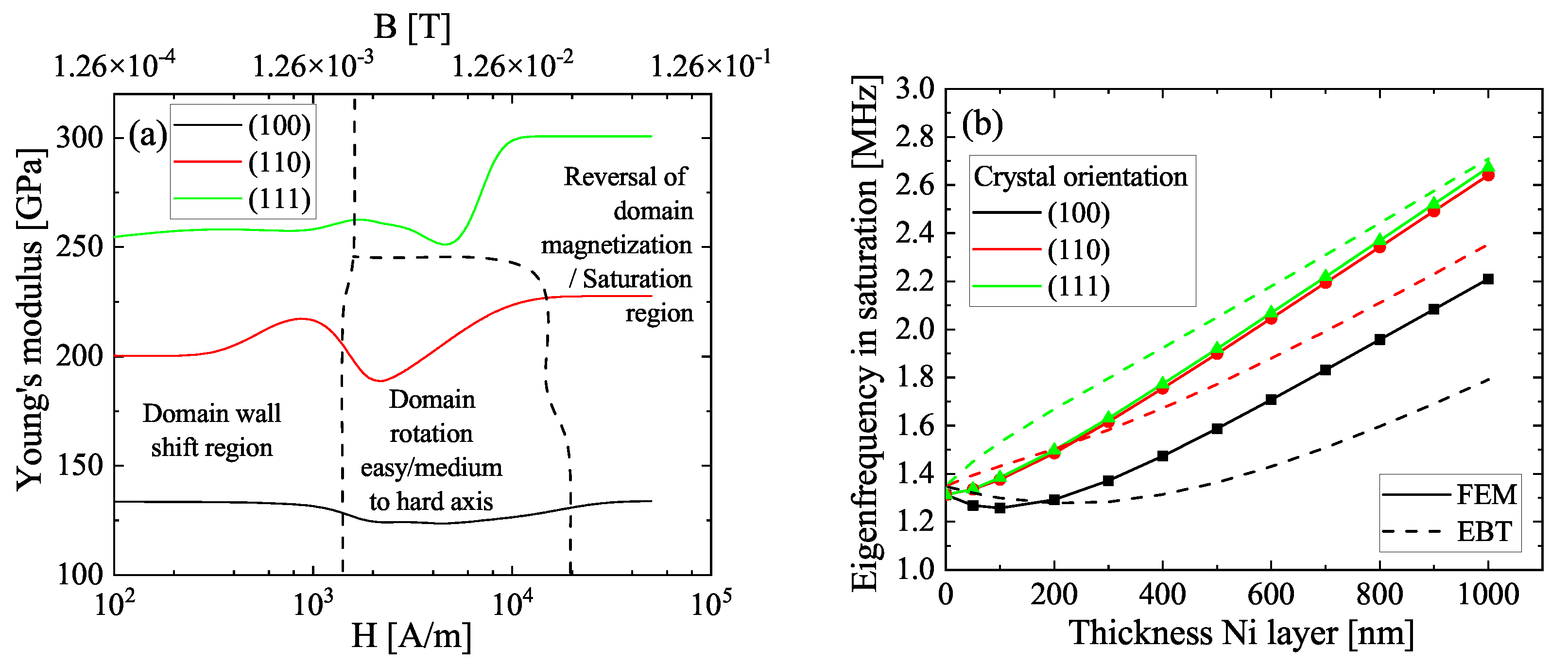
3. Results
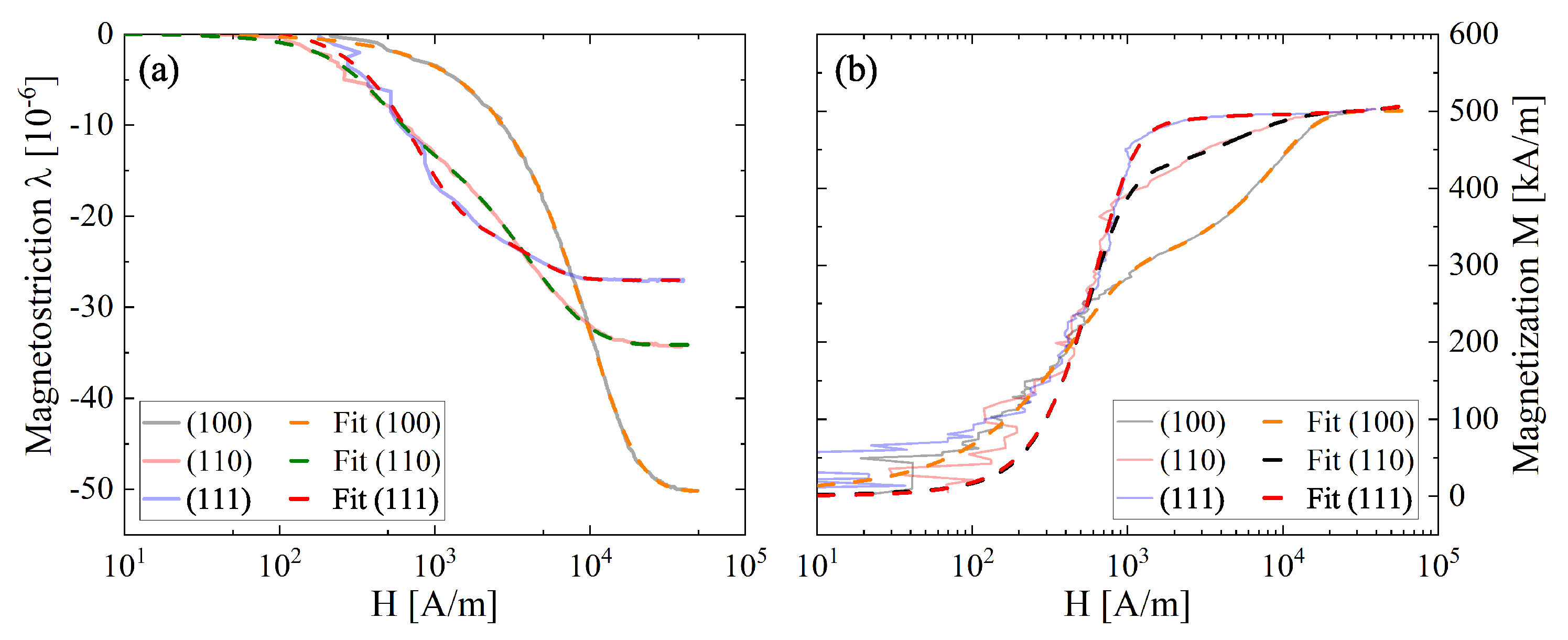
3.1. Magnetostriction and Bending
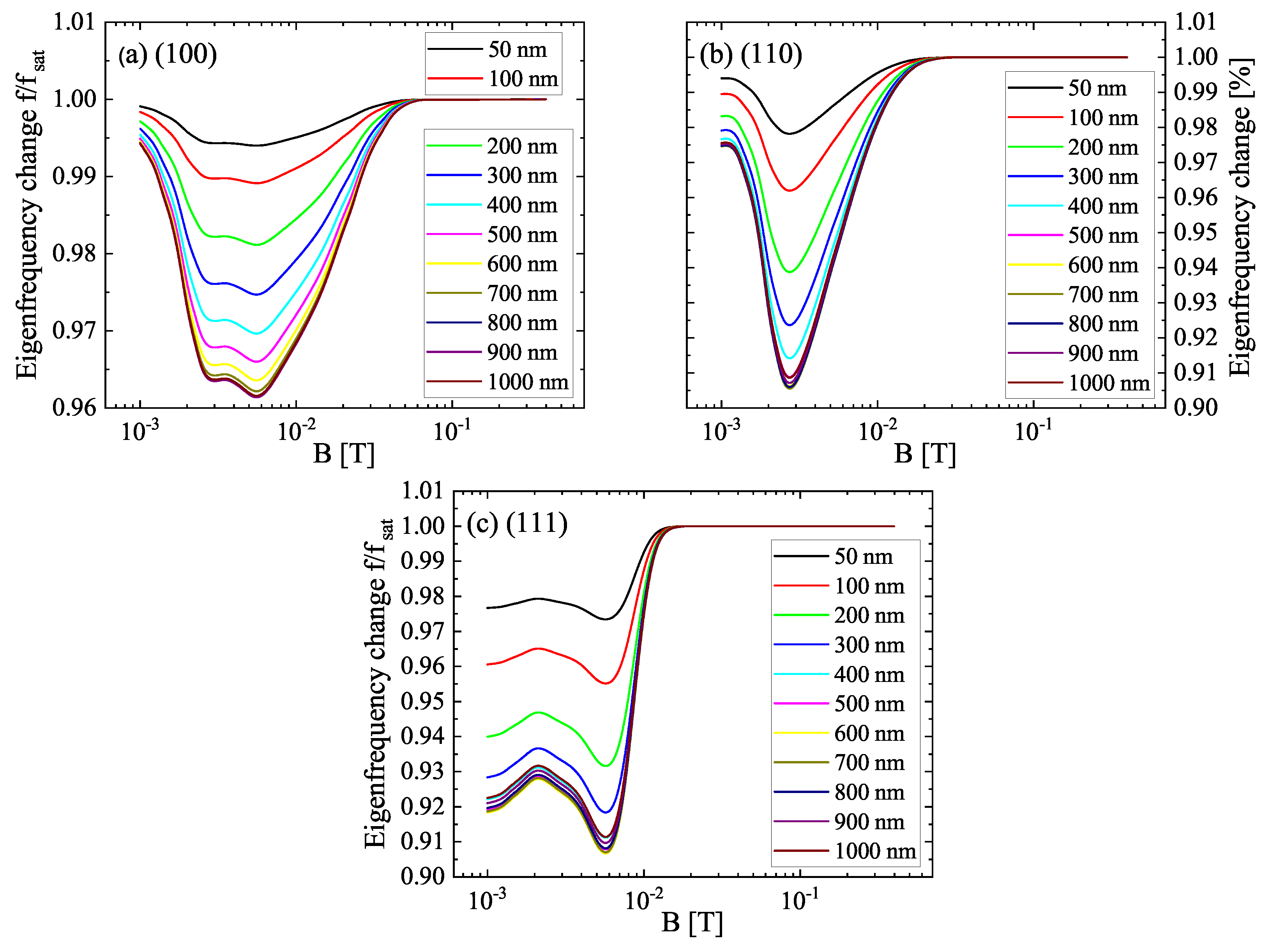
3.2. Eigenfrequency Behavior in the Magnetic Field
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Parameter | ( m/A) | ( m/A) | (A/m) | (A/m) | ||
|---|---|---|---|---|---|---|
| −1.61 | −1.34 | 2.17 | 1.40 | 0 | −22,132 | |
| −7.95 | −1.27 | −52.4 | 2.80 | 0 | −11,500 | |
| −2.24 | −7.16 | −26.2 | −5.35 | −200 | −500 | |
| 260,000 | 276,100 | −2.08 | 9.43 | −5000 | 0 | |
| 403,234 | 248,314 | 42.8 | −2.50 | 0 | −10,000 | |
| 10,621 | 483,372 | 8.86 | 37.9 | 0 | 0 |
| Reference | (Pa) | (Pa) | (Pa) |
|---|---|---|---|
| Honda et al. | 2.52 | 1.51 | 1.04 |
| Bozorth1 et al. | 2.5 | 1.6 | 1.19 |
| Bozorth2 et al. Saturated | 2.52 | 1.57 | 1.23 |
| Neighbours et al. | 2.53 | 1.52 | 1.24 |
| Yamamoto et al. | 2.44 | 1.58 | 1.02 |
| Levy et al. | 2.47 | 1.52 | 1.21 |
| DeKlerk et al. Saturated | 2.46 | 1.47 | 1.24 |
| Shirakawa et al. | 2.55 | 1.69 | 0.90 * |
| DeKlerk2 et al. Saturated | 2.46 | 1.48 | 1.22 |
| Alers et al. | 2.51 | 1.5 | 1.24 |
| Sakurai et al. | 2.51 | 1.53 | 1.24 |
| Epstein et al. Saturated | 2.5 | 1.54 | 1.24 |
| Vintaikin et al. | 2.47 | 1.44 | 1.24 |
| Salama et al. | 2.52 | 1.54 | 1.22 |
| Shirakawa2 et al. | 2.88 | 1.81 | 1.24 |
| Average | 2.52 | 1.55 | 1.2 |
Appendix B
Appendix C
Appendix D
References
- Wang, Y.; Gray, D.; Berry, D.; Gao, J.; Li, M.; Li, J.; Viehland, D. An Extremely Low Equivalent Magnetic Noise Magnetoelectric Sensor. Adv. Mater. 2011, 23, 4111–4114. [Google Scholar] [CrossRef] [PubMed]
- Gun Lee, D.; Man Kim, S.; Kyung Yoo, Y.; Hyun Han, J.; Won Chun, D.; Kim, Y.C.; Kim, J.; Seon Hwang, K.; Song Kim, T.; Woo Jo, W.; et al. Ultra-sensitive magnetoelectric microcantilever at a low frequency. Appl. Phys. Lett. 2012, 101, 182902. [Google Scholar] [CrossRef]
- Piorra, A.; Jahns, R.; Teliban, I.; Gugat, J.L.; Gerken, M.; Knöchel, R.; Quandt, E. Magnetoelectric thin film composites with interdigital electrodes. Appl. Phys. Lett. 2013, 103, 032902. [Google Scholar] [CrossRef]
- Zhai, J.; Xing, Z.; Dong, S.; Li, J.; Viehland, D. Detection of pico-Tesla magnetic fields using magneto-electric sensors at room temperature. Appl. Phys. Lett. 2006, 88, 062510. [Google Scholar] [CrossRef] [Green Version]
- Schmelz, M.; Stolz, R.; Zakosarenko, V.; Schönau, T.; Anders, S.; Fritzsch, L.; Mück, M.; Meyer, H.G. Field-stable SQUID magnetometer with sub-fT/Hz1/2-resolution based on sub-micrometer cross-type Josephson tunnel junctions. Supercond. Sci. Technol. 2011, 24, 065009. [Google Scholar] [CrossRef]
- Su, J.; Niekiel, F.; Fichtner, S.; Kirchhof, C.; Meyners, D.; Quandt, E.; Wagner, B.; Lofink, F. Frequency tunable resonant magnetoelectric sensors for the detection of weak magnetic field. J. Micromech. Microeng. 2020, 30, 075009. [Google Scholar] [CrossRef]
- Fetisov, L.Y.; Serov, V.N.; Chashin, D.V.; Makovkin, S.A.; Srinivasan, G.; Viehland, D.; Fetisov, Y.K. A magnetoelectric sensor of threshold DC magnetic fields. J. Appl. Phys. 2017, 121, 154503. [Google Scholar] [CrossRef]
- PourhosseiniAsl, M.J.; Chu, Z.; Gao, X.; Dong, S. A hexagonal-framed magnetoelectric composite for magnetic vector measurement. Appl. Phys. Lett. 2018, 113, 092902. [Google Scholar] [CrossRef]
- Zhang, J.; Li, P.; Wen, Y.; He, W.; Yang, A.; Lu, C. Packaged current-sensing device with self-biased magnetoelectric laminate for low-frequency weak-current detection. Smart Mater. Struct. 2014, 23, 095028. [Google Scholar] [CrossRef]
- Filippov, D.; Firsova, T.; Laletin, V.; Poddubnaya, N. The magnetoelectric effect in Nickel–GaAs–Nickel structures. Tech. Phys. Lett. 2017, 43, 313–315. [Google Scholar] [CrossRef]
- Spetzler, B.; Kirchhof, C.; Quandt, E.; McCord, J.; Faupel, F. Magnetic Sensitivity of Bending-Mode Delta-E-Effect Sensors. Phys. Rev. Appl. 2019, 12, 064036. [Google Scholar] [CrossRef]
- Hui, Y.; Nan, T.; Sun, N.X.; Rinaldi, M. High Resolution Magnetometer Based on a High Frequency Magnetoelectric MEMS-CMOS Oscillator. J. Microelectromech. Syst. 2015, 24, 134–143. [Google Scholar] [CrossRef]
- Kiser, J.; Finkel, P.; Gao, J.; Dolabdjian, C.; Li, J.; Viehland, D. Stress reconfigurable tunable magnetoelectric resonators as magnetic sensors. Appl. Phys. Lett. 2013, 102, 042909. [Google Scholar] [CrossRef] [Green Version]
- Shen, Y.; Gao, J.; Wang, Y.; Li, J.; Viehland, D. High non-linear magnetoelectric coefficient in Metglas/PMN-PT laminate composites under zero direct current magnetic bias. J. Appl. Phys. 2014, 115, 094102. [Google Scholar] [CrossRef] [Green Version]
- Mandal, S.K.; Sreenivasulu, G.; Petrov, V.M.; Srinivasan, G. Magnetization-graded multiferroic composite and magnetoelectric effects at zero bias. Phys. Rev. B 2011, 84, 014432. [Google Scholar] [CrossRef]
- Bichurin, M.I.; Petrov, R.V.; Leontiev, V.S.; Sokolov, O.V.; Turutin, A.V.; Kuts, V.V.; Kubasov, I.V.; Kislyuk, A.M.; Temirov, A.A.; Malinkovich, M.D.; et al. Self-Biased Bidomain LiNbO3/Ni/Metglas Magnetoelectric Current Sensor. Sensors 2020, 20, 7142. [Google Scholar] [CrossRef]
- Nguyen, T.; Fleming, Y.; Bender, P.; Grysan, P.; Valle, N.; El Adib, B.; Adjeroud, N.; Arl, D.; Emo, M.; Ghanbaja, J.; et al. Low-Temperature Growth of AlN Films on Magnetostrictive Foils for High-Magnetoelectric-Response Thin-Film Composites. ACS Appl. Mater. Interfaces 2021, 13, 30874–30884. [Google Scholar] [CrossRef]
- Gojdka, B.; Jahns, R.; Meurisch, K.; Greve, H.; Adelung, R.; Quandt, E.; Knöchel, R.; Faupel, F. Fully integrable magnetic field sensor based on delta-E effect. Appl. Phys. Lett. 2011, 99, 223502. [Google Scholar] [CrossRef] [Green Version]
- Kim, H.J.; Wang, S.; Xu, C.; Laughlin, D.; Zhu, J.; Piazza, G. Piezoelectric/magnetostrictive MEMS resonant sensor array for in-plane multi-axis magnetic field detection. In Proceedings of the 2017 IEEE 30th International Conference on Micro Electro Mechanical Systems (MEMS), Las Vegas, NV, USA, 22–26 January 2017; pp. 109–112. [Google Scholar] [CrossRef]
- Zhang, Z.; Wu, H.; Sang, L.; Takahashi, Y.; Huang, J.; Wang, L.; Toda, M.; Akita, I.M.; Koide, Y.; Koizumi, S.; et al. Enhancing Delta E Effect at High Temperatures of Galfenol/Ti/Single-Crystal Diamond Resonators for Magnetic Sensing. ACS Appl. Mater. Interfaces 2020, 12, 23155–23164. [Google Scholar] [CrossRef]
- Giallonardo, J.; Erba, U.; Austa, K.; Palumbo, G. The influence of grain size and texture on the Young’s modulus of nanocrystalline Nickel and Nickel-iron alloys. Philos. Mag. 2011, 91, 4594–4605. [Google Scholar] [CrossRef]
- Ishizaki, T.; Yatsugi, K.; Akedo, K. Effect of Particle Size on the Magnetic Properties of Ni Nanoparticles Synthesized with Trioctylphosphine as the Capping Agent. Nanomaterials 2016, 6, 172. [Google Scholar] [CrossRef]
- Hähnlein, B.; Schaaf, P.; Pezoldt, J. Size effect of Young’s modulus in AlN thin layers. J. Appl. Phys. 2014, 116, 124306. [Google Scholar] [CrossRef]
- Hähnlein, B.; Kovac, J., Jr.; Pezoldt, J. Size effect of the silicon carbide Young’s modulus. Phys. Status Solidi A 2017, 214, 1600390. [Google Scholar] [CrossRef]
- Krey, M.; Hähnlein, B.; Tonisch, K.; Krischok, S.; Töpfer, H. Automated Parameter Extraction Of ScAlN MEMS Devices Using An Extended Euler-Bernoulli Beam Theory. Sensors 2020, 20, 1001. [Google Scholar] [CrossRef] [Green Version]
- Haehnlein, B.; Kellner, M.; Krey, M.; Nikpourian, A.; Pezoldt, J.; Michael, S.; Toepfer, H.; Krischok, S.; Tonisch, K. The Angle Dependent Δe Effect in Tin/Aln/Ni Micro Cantilevers. Available online: https://ssrn.com/abstract=4112978 (accessed on 18 May 2022).
- Cullity, B.D.; Graham, C.D. Introduction to Magnetic Materials; John Wiley & Sons: Hoboken, NJ, USA, 2008; pp. 197–273. [Google Scholar] [CrossRef]
- Carr, W. Invar and volume magnetostriction. J. Magn. Magn. Mater. 1979, 10, 197–204. [Google Scholar] [CrossRef]
- Masiyama, Y. On the magnetostriction of a single crystal of Nickel. Sci. Rep. Tohoku Imp. Univ. 1928, 17, 945–961. [Google Scholar]
- Spetzler, B.; Golubeva, E.V.; Müller, C.; McCord, J.; Faupel, F. Frequency Dependency of the Delta-E Effect and the Sensitivity of Delta-E Effect Magnetic Field Sensors. Sensors 2019, 19, 4769. [Google Scholar] [CrossRef] [Green Version]
- Rösler, J.; Harders, H.; Bäker, M. Mechanisches Verhalten der Werkstoffe; Vieweg+Teubner: Wiesbaden, Germany, 2019; pp. 51–53. [Google Scholar] [CrossRef]
- Ledbetter, H.; Reed, R. Elastic Properties of Metals and Alloys, I. Iron, Nickel, and Iron-Nickel Alloys. J. Phys. Chem. Ref. Data 1973, 2, 531–617. [Google Scholar] [CrossRef] [Green Version]
- Yamamoto, M. The Elastic Constants of Nickel Single Crystals. J. Jpn. I. Met. Mater. 1942, 6, 331–338. [Google Scholar] [CrossRef]
- McCarthy, E.; Bellew, A.; Sader, J.; Boland, J. Poisson’s ratio of individual metal nanowires. Nat. Commun. 2014, 5, 4336. [Google Scholar] [CrossRef] [Green Version]
- Zhou, H.; Pei, Y.; Fang, D. Magnetic Field Tunable Small-scale Mechanical Properties of Nickel Single Crystals Measured by Nanoindentation Technique. Sci. Rep. 2014, 4, 4583. [Google Scholar] [CrossRef] [PubMed]
- Baxy, A.; Sarkar, A. Natural frequencies of a rotating curved cantilever beam: A perturbation method-based approach. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2020, 234, 1706–1719. [Google Scholar] [CrossRef]
- Greve, H.; Woltermann, E.; Quenzer, H.J.; Wagner, B.; Quandt, E. Giant magnetoelectric coefficients in (Fe90Co10)78Si12B10-AlN thin film composites. Appl. Phys. Lett. 2010, 96, 182501. [Google Scholar] [CrossRef]
- Lou, J.; Insignares, R.E.; Cai, Z.; Ziemer, K.S.; Liu, M.; Sun, N.X. Soft magnetism, magnetostriction, and microwave properties of FeGaB thin films. Appl. Phys. Lett. 2007, 91, 182504. [Google Scholar] [CrossRef]
- Yang, P.; Peng, S.; Wu, X.B.; Wan, J.G.; Zhu, J.S. Magnetoelectric study in Terfenol-D/PFNT laminate composite. Integr. Ferroelectr. 2008, 99, 86–92. [Google Scholar] [CrossRef]
- Nan, T.; Hui, Y.; Rinaldi, M.; Sun, N.X. Self-Biased 215 MHz Magnetoelectric NEMS Resonator for Ultra-Sensitive DC Magnetic Field Detection. Sci. Rep. 2013, 3, 1985. [Google Scholar] [CrossRef] [Green Version]
- Kirchner, H. Über den Einfluß von Zug, Druck und Torsion auf die Längsmagnetostriktion. Ann. Phys. 1936, 419, 49–69. [Google Scholar] [CrossRef]
- Ludwig, A.; Quandt, E. Optimization of the Delta-E effect in thin films and multilayers by magnetic field annealing. IEEE Trans. Magn. 2002, 38, 2829–2831. [Google Scholar] [CrossRef]
- Coey, J.M. Magnetism and Magnetic Materials; Cambridge University Press: Cambridge, UK, 2010; pp. 264–304. [Google Scholar] [CrossRef] [Green Version]
- Ciria, M.; Arnaudas, J.I.; Benito, L.; de la Fuente, C.; del Moral, A.; Ha, J.K.; O’Handley, R.C. Magnetoelastic coupling in thin films with weak out-of-plane anisotropy. Phys. Rev. B 2003, 67, 024429. [Google Scholar] [CrossRef]
- Liang, X.; Dong, C.; Chen, H.; Wang, J.; Wei, Y.; Zaeimbashi, M.; He, Y.; Matyushov, A.; Sun, C.; Sun, N. A Review of Thin-Film Magnetoelastic Materials for Magnetoelectric Applications. Sensors 2020, 20, 1532. [Google Scholar] [CrossRef] [Green Version]
- Spetzler, B.; Golubeva, E.V.; Friedrich, R.M.; Zabel, S.; Kirchhof, C.; Meyners, D.; McCord, J.; Faupel, F. Magnetoelastic Coupling and Delta-E Effect in Magnetoelectric Torsion Mode Resonators. Sensors 2021, 21, 2022. [Google Scholar] [CrossRef]
- Durdaut, P.; Rubiola, E.; Friedt, J.M.; Müller, C.; Spetzler, B.; Kirchhof, C.; Meyners, D.; Quandt, E.; Faupel, F.; McCord, J.; et al. Fundamental Noise Limits and Sensitivity of Piezoelectrically Driven Magnetoelastic Cantilevers. J. Microelectromechanical Syst. 2020, 29, 1347–1361. [Google Scholar] [CrossRef]
- Li, M.; Matyushov, A.; Dong, C.; Chen, H.; Lin, H.; Nan, T.; Qian, Z.; Rinaldi, M.; Lin, Y.; Sun, N.X. Ultra-sensitive NEMS magnetoelectric sensor for picotesla DC magnetic field detection. Appl. Phys. Lett. 2017, 110, 143510. [Google Scholar] [CrossRef]
- Linzen, S.; Schmidt, F.; Schmidl, F.; Mans, M.; Hesse, O.; Nitsche, F.; Kaiser, G.; Müller, S.; Seidel, P. A thin film HTSC-Hall magnetometer - development and application. Phys. C Supercond. 2002, 372–376, 146–149. [Google Scholar] [CrossRef]
- Webster, W.L. Magnetostriction and change of resistance in single crystals of iron and Nickel. Proc. Phys. Soc. 1930, 42, 431–440. [Google Scholar] [CrossRef]
- Daniel, L. An analytical model for the magnetostriction strain of ferromagnetic materials subjected to multiaxial stress. Eur. Phys. J. Appl. Phys. 2018, 83, 30904. [Google Scholar] [CrossRef] [Green Version]
- Namazu, T.; Inoue, S.; Takemoto, H.; Koterazawa, K. Mechanical Properties of Polycrystalline Titanium Nitride Films Measured by XRD Tensile Testing. IEEJ Trans. Sens. Micromachines 2005, 125, 374–379. [Google Scholar] [CrossRef] [Green Version]



| Material | Reference | Sensitivity (1/T) |
|---|---|---|
| Ni(100)/AlN/TiN | this work | −14.9 |
| Ni(110)/AlN/TiN | this work | −41.3 |
| Ni(111)/AlN/TiN | this work | 8.8 |
| poly-Ni/AlN/TiN | [26] | −0.9 …−1.4 |
| FeCoSiB/poly-Si/AlN | [11] | 10 |
| FeCoSiB/poly-Si/AlN | [11] | 13 * |
| FeCoSiB/poly-Si/AlN | [11] | 48 * |
| FeCoB/Al/AlN/Pt | [19] | −0.7 |
| FeGaB/AlN/Pt | [48] | −2.2 |
| FeGa/Ti/Diamond | [20] | 0.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hähnlein, B.; Sagar, N.; Honig, H.; Krischok, S.; Tonisch, K. Anisotropy of the ΔE Effect in Ni-Based Magnetoelectric Cantilevers: A Finite Element Method Analysis. Sensors 2022, 22, 4958. https://doi.org/10.3390/s22134958
Hähnlein B, Sagar N, Honig H, Krischok S, Tonisch K. Anisotropy of the ΔE Effect in Ni-Based Magnetoelectric Cantilevers: A Finite Element Method Analysis. Sensors. 2022; 22(13):4958. https://doi.org/10.3390/s22134958
Chicago/Turabian StyleHähnlein, Bernd, Neha Sagar, Hauke Honig, Stefan Krischok, and Katja Tonisch. 2022. "Anisotropy of the ΔE Effect in Ni-Based Magnetoelectric Cantilevers: A Finite Element Method Analysis" Sensors 22, no. 13: 4958. https://doi.org/10.3390/s22134958
APA StyleHähnlein, B., Sagar, N., Honig, H., Krischok, S., & Tonisch, K. (2022). Anisotropy of the ΔE Effect in Ni-Based Magnetoelectric Cantilevers: A Finite Element Method Analysis. Sensors, 22(13), 4958. https://doi.org/10.3390/s22134958






