Rational Design of Field-Effect Sensors Using Partial Differential Equations, Bayesian Inversion, and Artificial Neural Networks
Abstract
1. Introduction
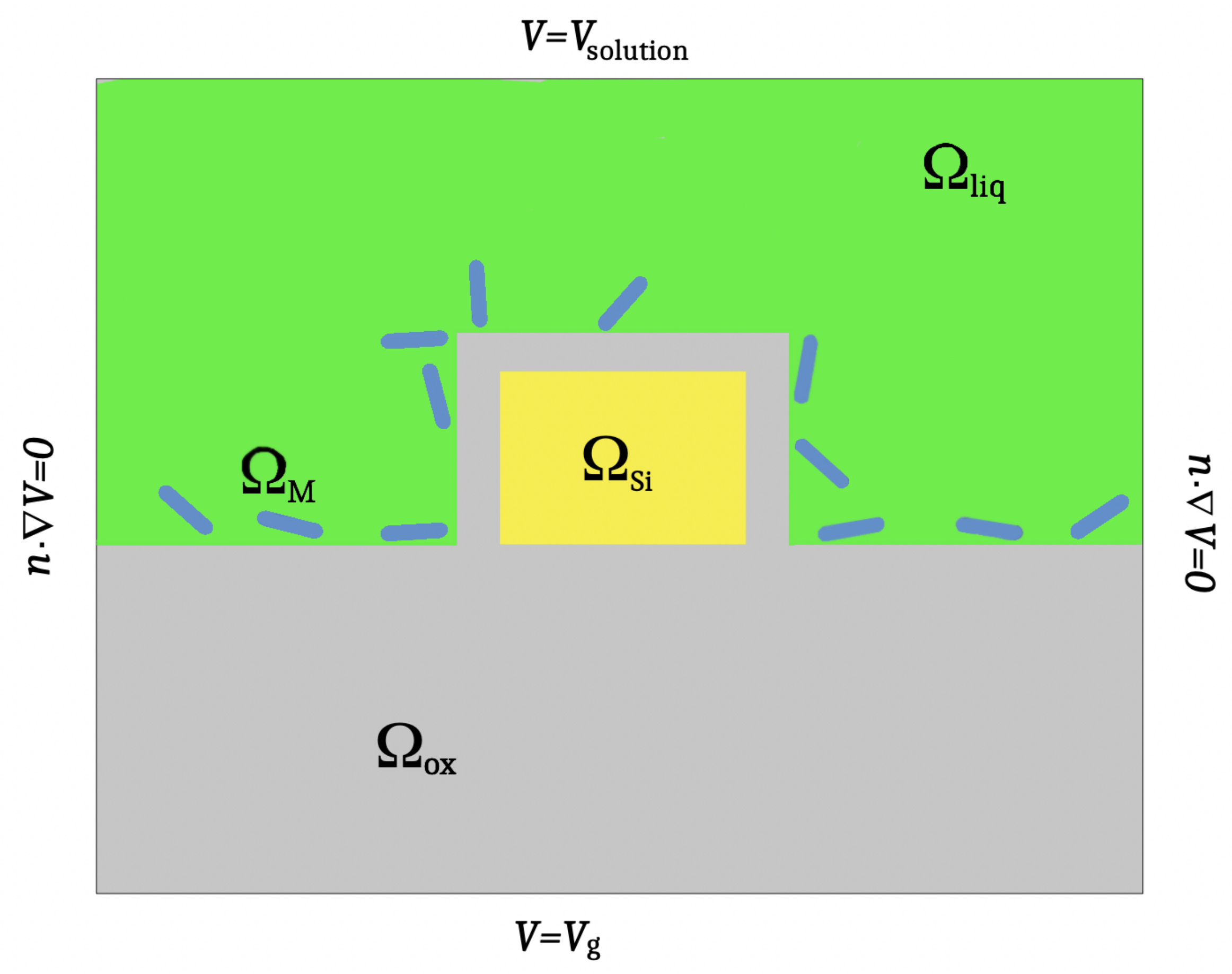
2. The Model Equations
3. Parameter Estimation Based on Bayesian Inference
| Algorithm 1 The Metropolis–Hastings algorithm. |
| Initialization: Start the process with the initial guess and number of samples N. |
| while |
| 1. Propose a new sample according to the proposal density . |
| 2. Compute the acceptance/rejection ratio
|
| 3. Sample . |
| 4. then |
| accept and set |
| else |
| reject and set |
| end if |
| 5. Set |
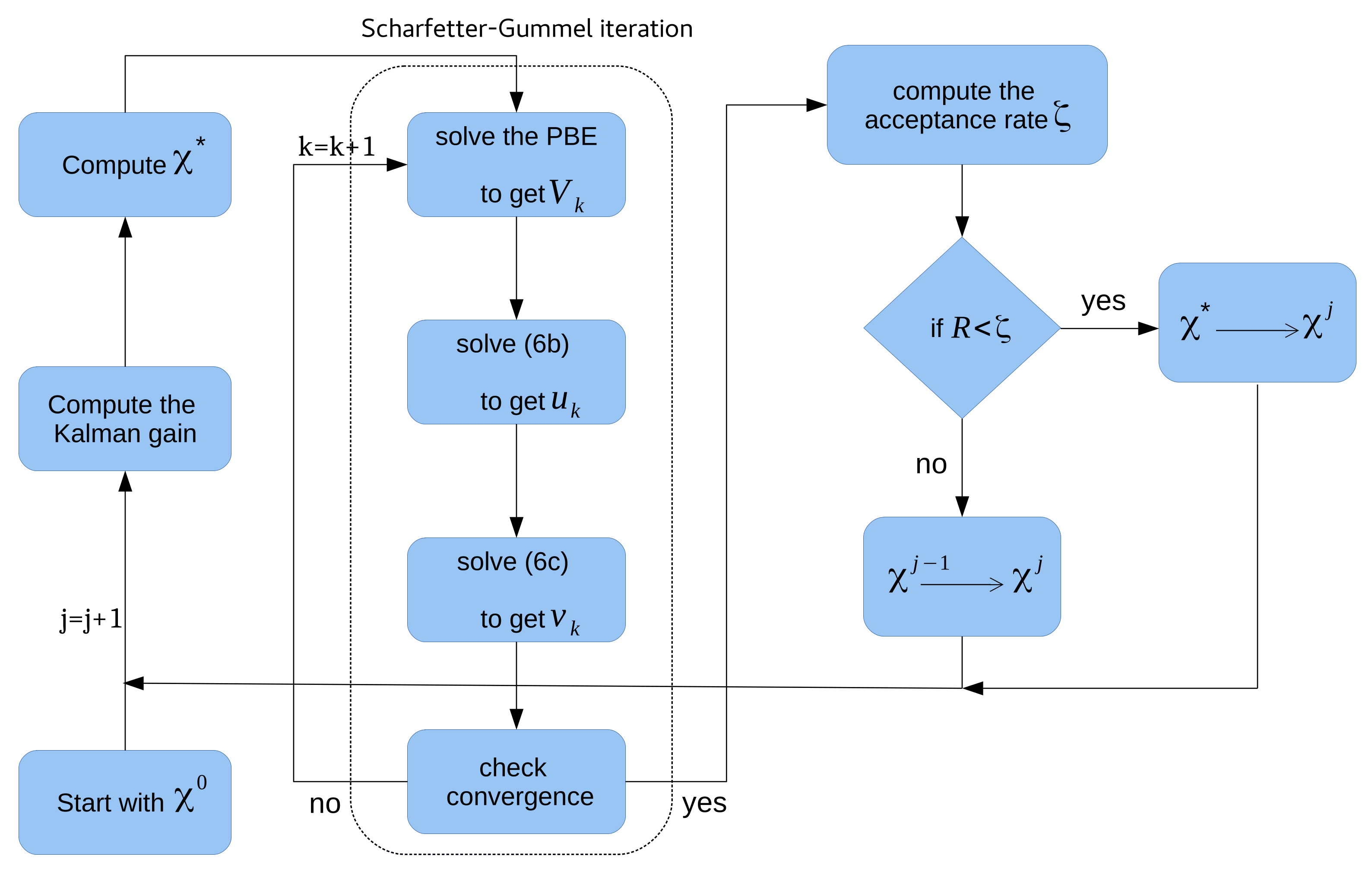
Mcmc with Ensemble-Kalman Filter (EnKF-MCMC)
| Algorithm 2 Bayesian inference using EnKF-MCMC |
| Initialization (): Start the process with the initial guess and number of samples N. |
| while |
| 1. Estimate the model response with respect to |
| 2. Compute the Kalman gain |
| 3. Produce the new proposal using the shift |
| 4. Accepted/rejected |
| 5. Set . |
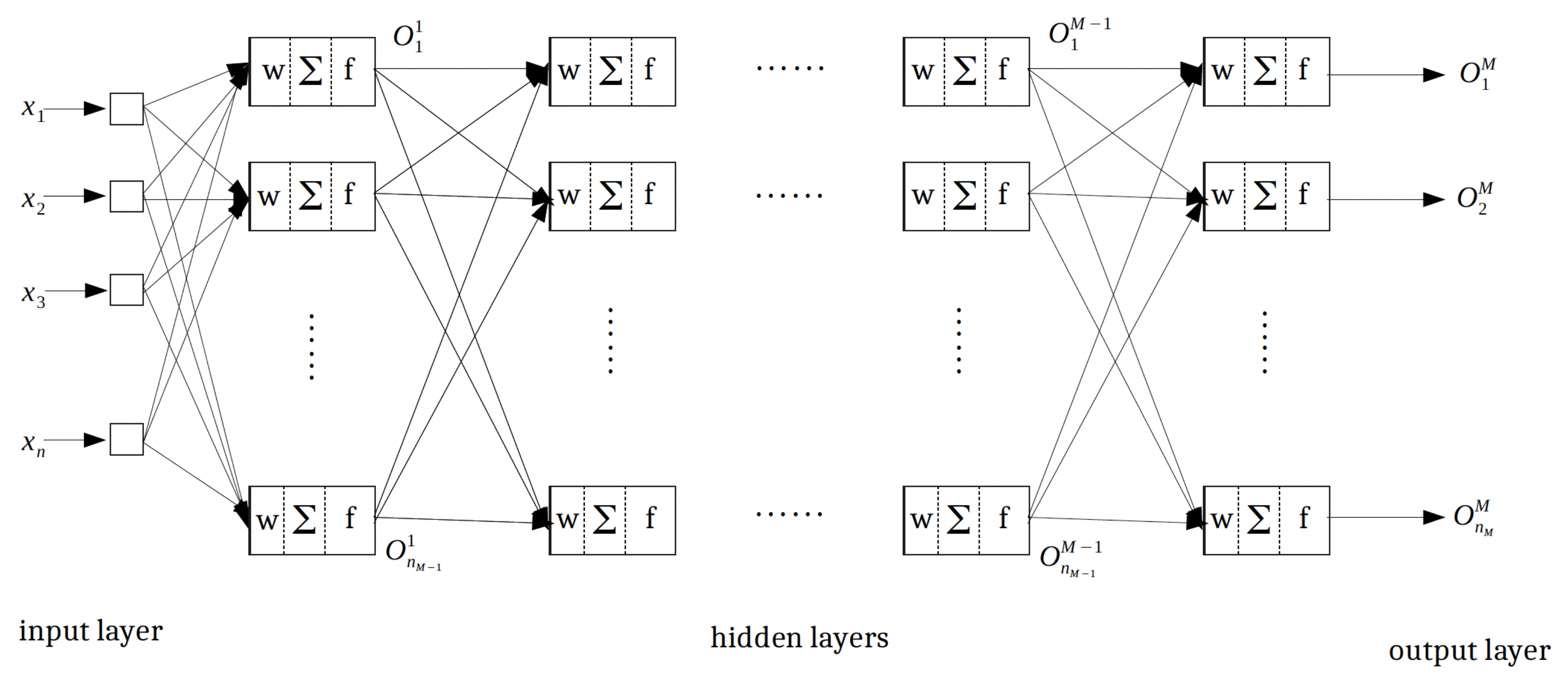
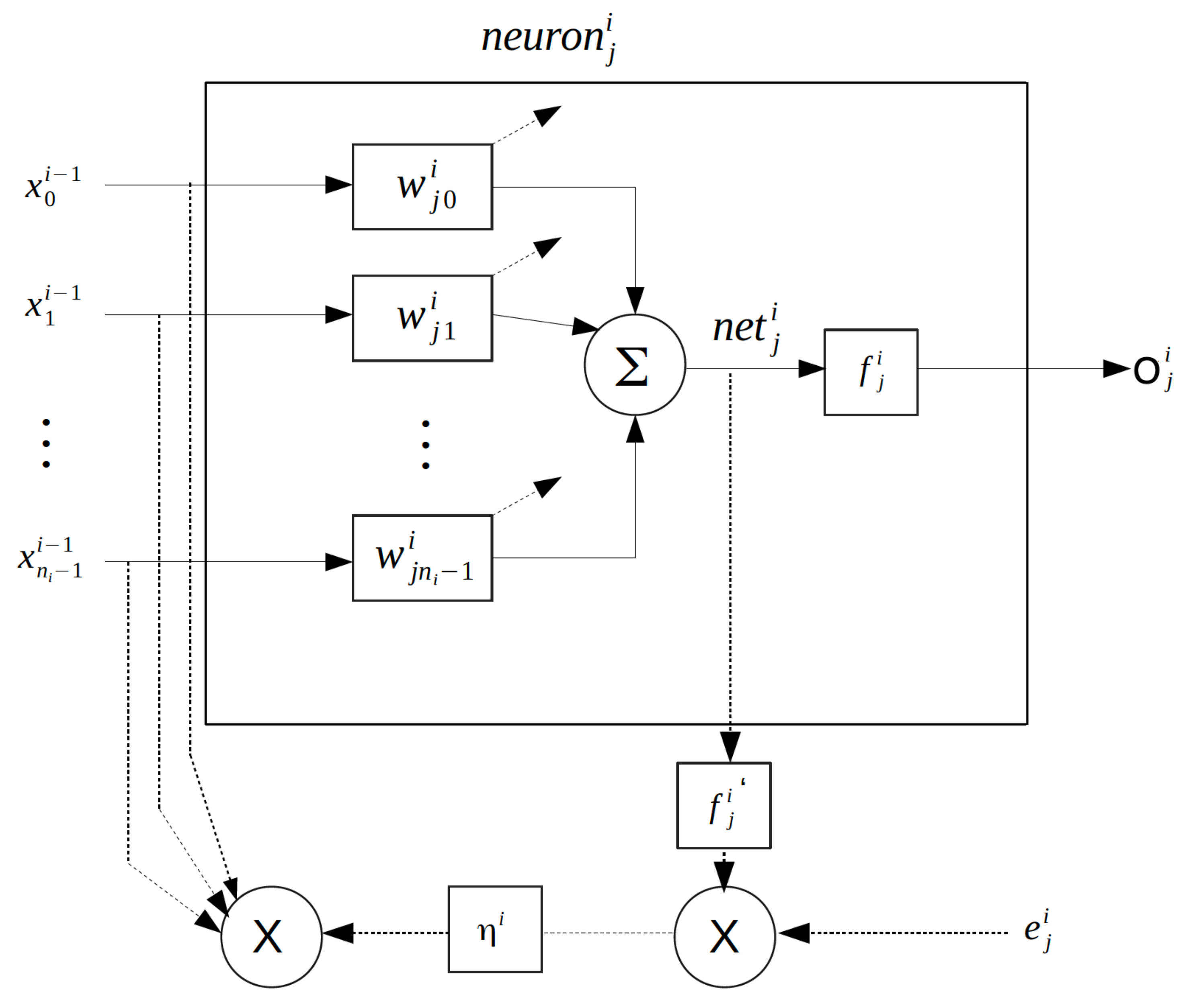
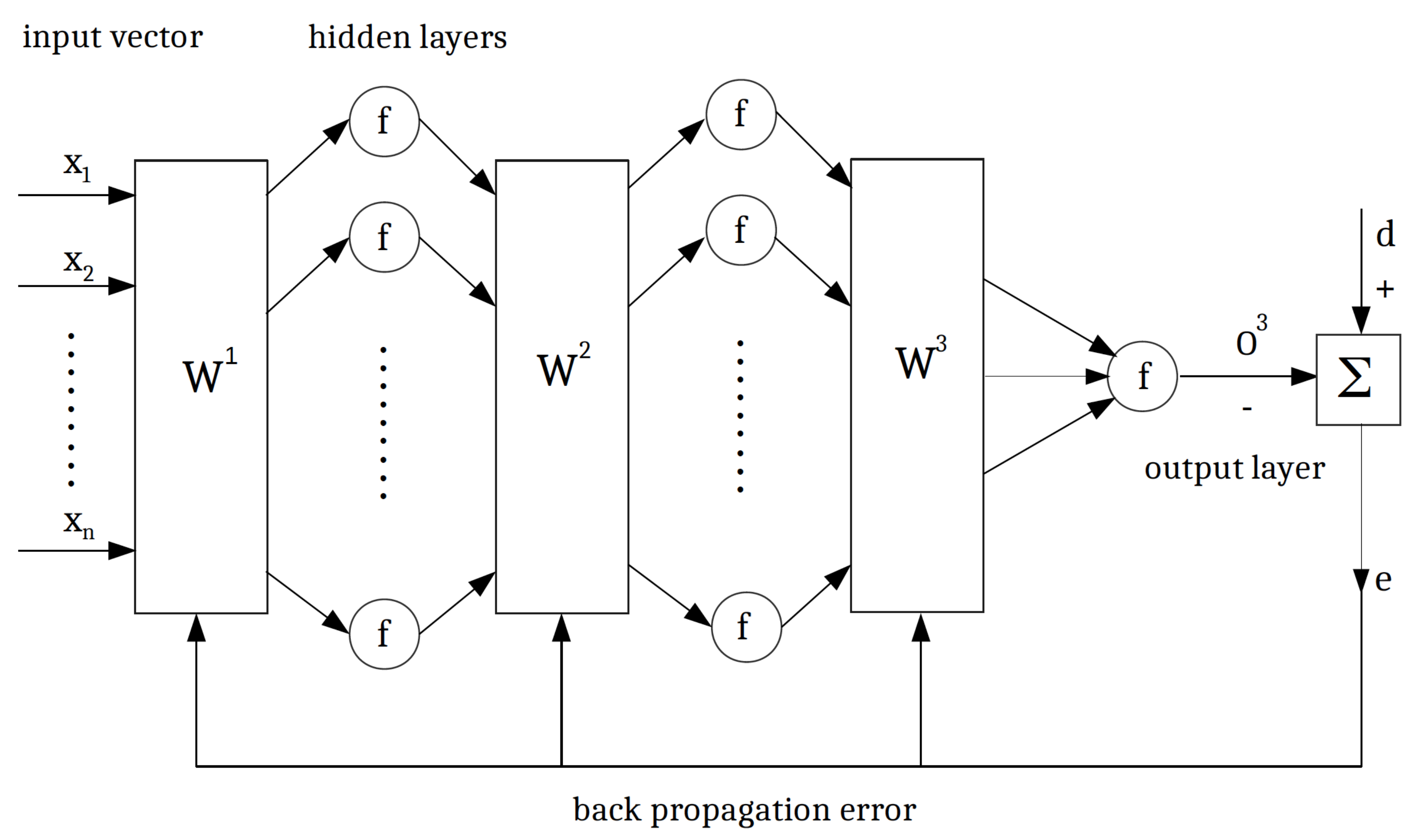
4. Multilayer Feed-Forward Neural Networks
5. Numerical Experiments
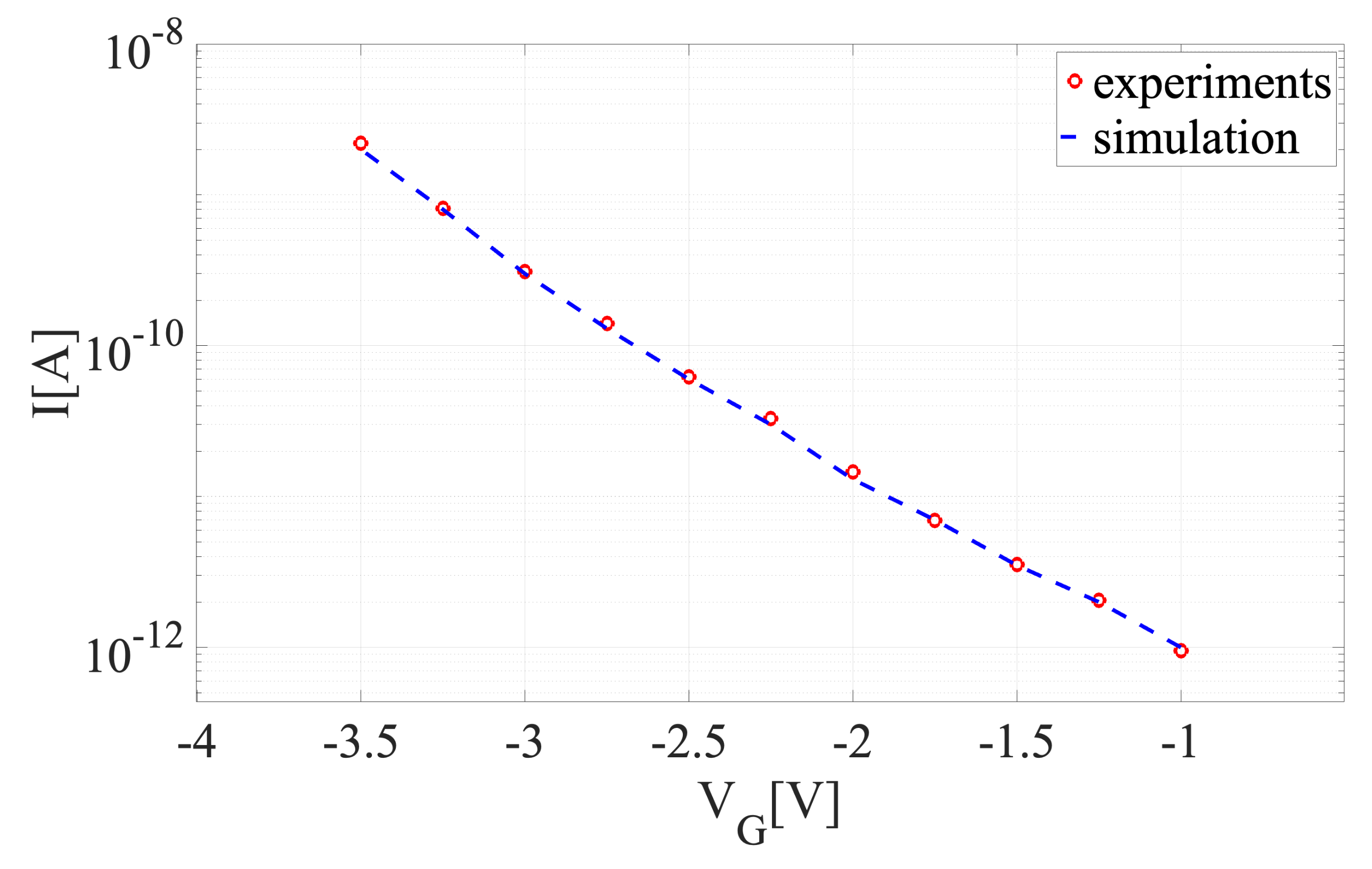
5.1. Model Verification
5.2. Bayesian Inversion
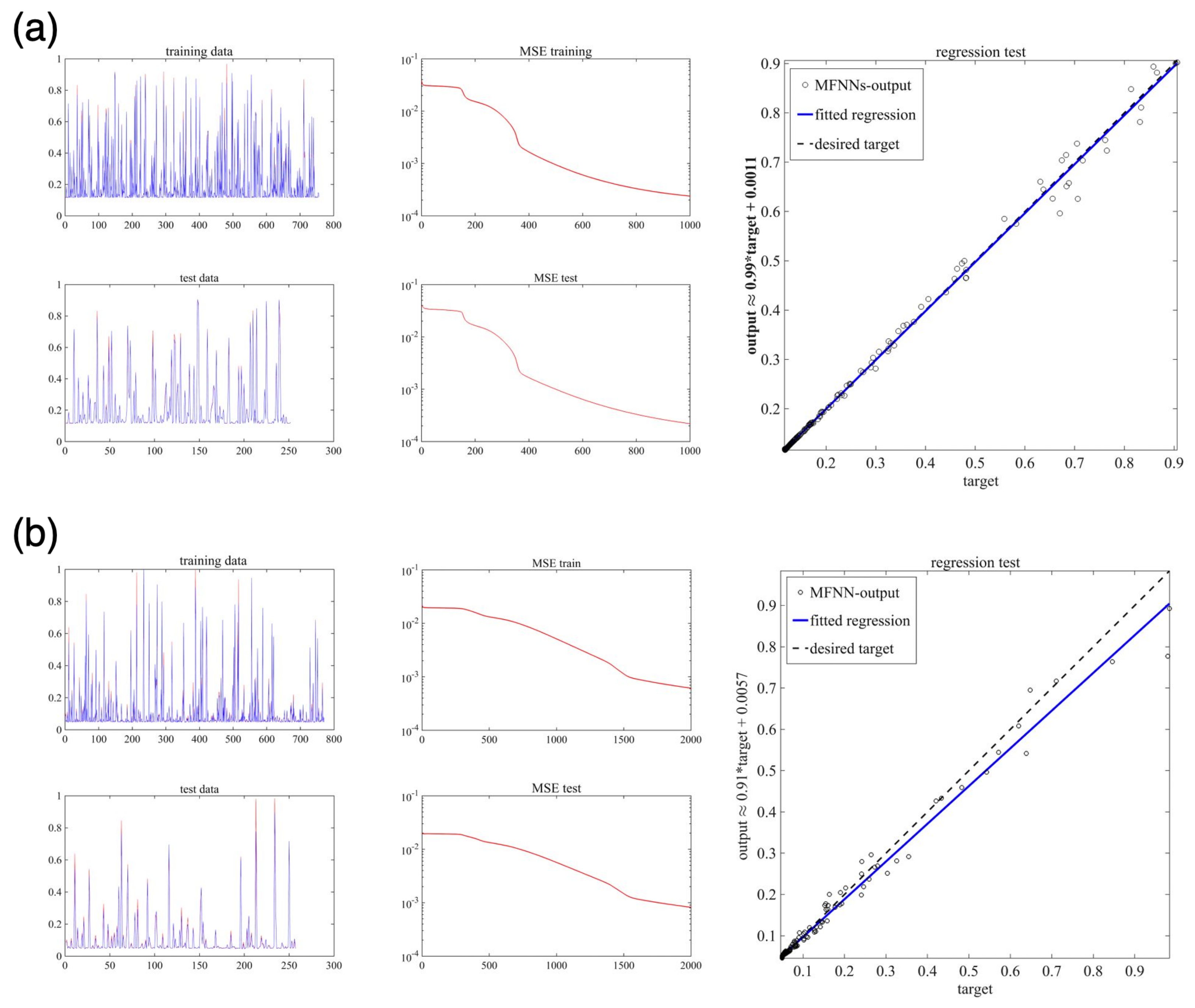
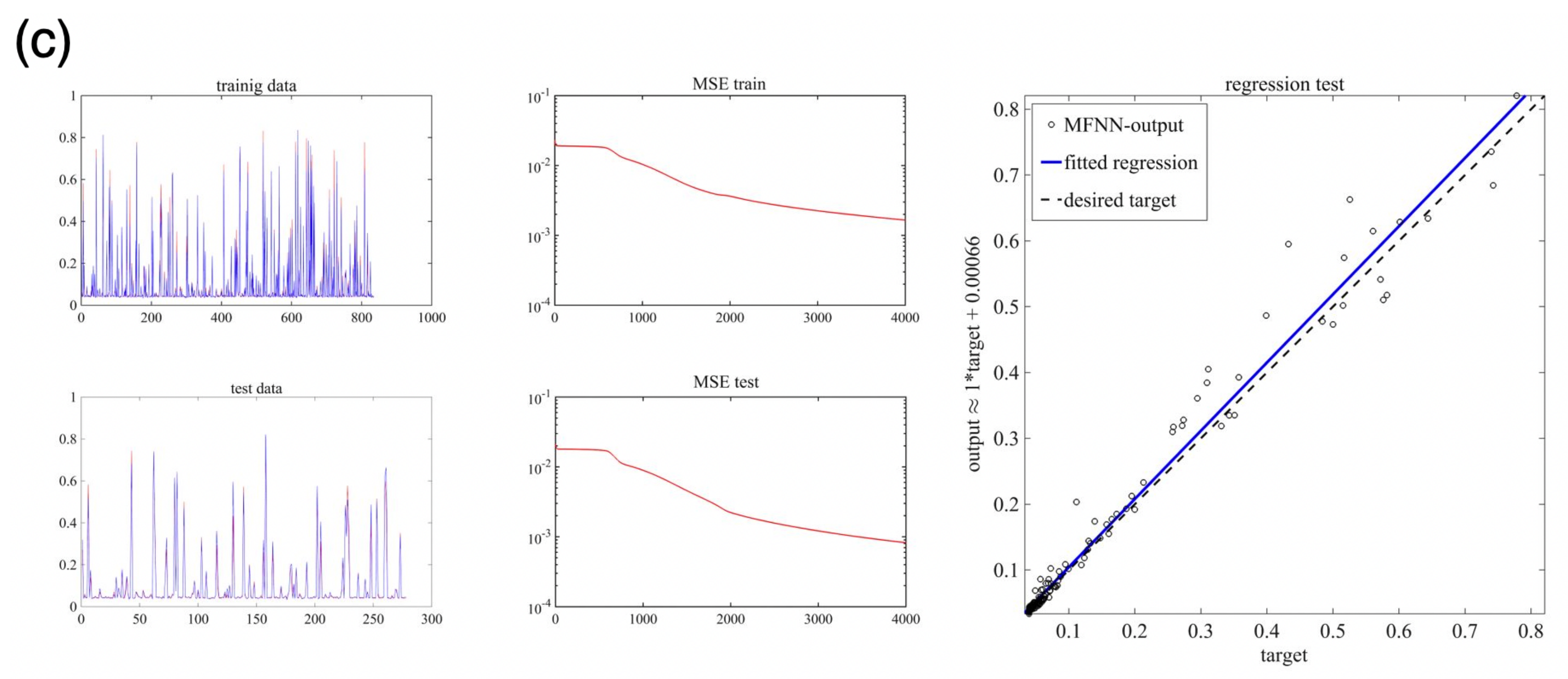
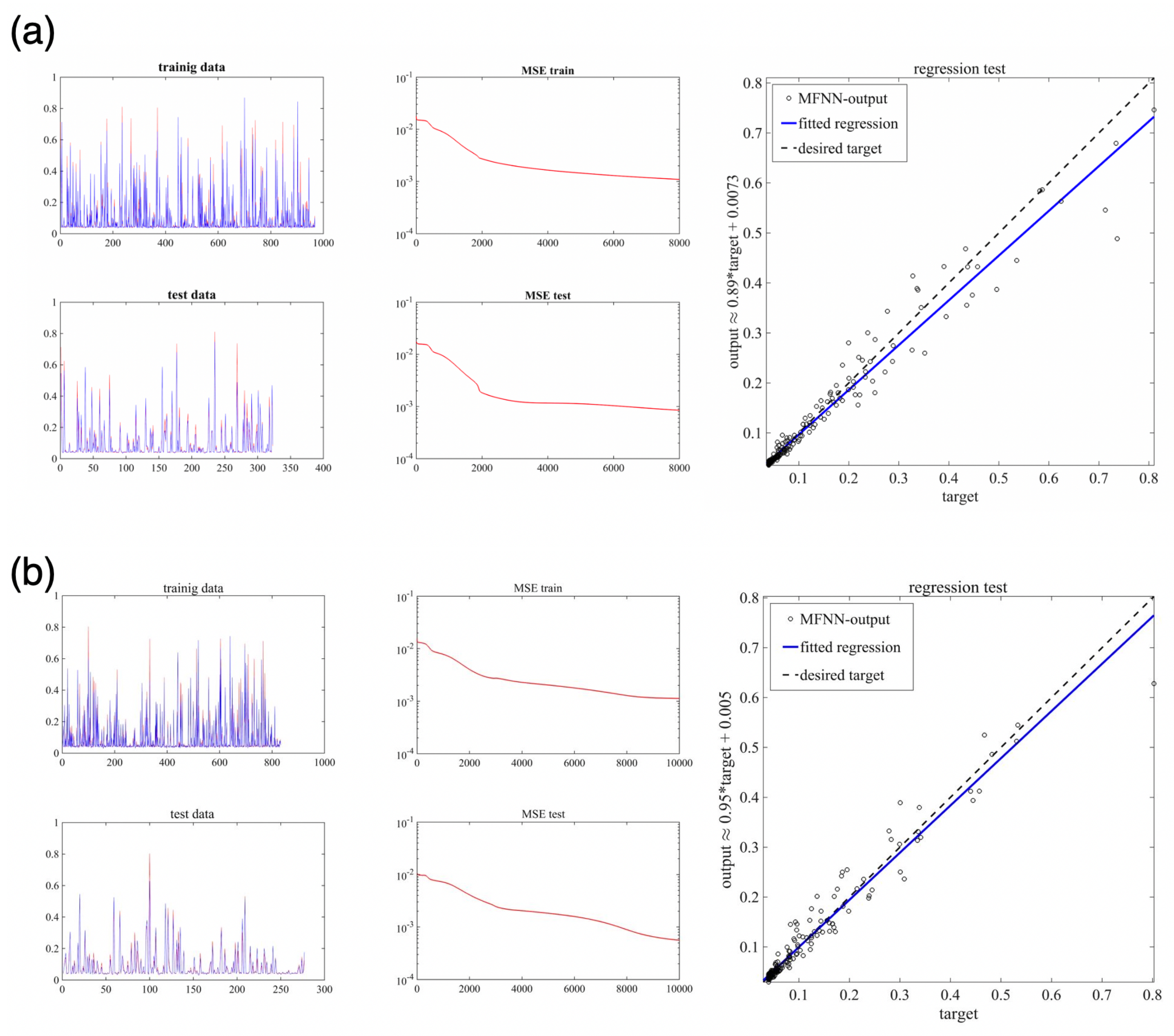
5.3. Machine Learning Based on MFNNs
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mirsian, S.; Khodadadian, A.; Hedayati, M.; Manzour-ol Ajdad, A.; Kalantarinejad, R.; Heitzinger, C. A new method for selective functionalization of silicon nanowire sensors and Bayesian inversion for its parameters. Biosens. Bioelectron. 2019, 142, 111527. [Google Scholar] [CrossRef]
- Kuang, T.; Chang, L.; Peng, X.; Hu, X.; Gallego-Perez, D. Molecular beacon nano-sensors for probing living cancer cells. Trends Biotechnol. 2017, 35, 347–359. [Google Scholar] [CrossRef]
- Hahm, J.i.; Lieber, C.M. Direct ultrasensitive electrical detection of DNA and DNA sequence variations using nanowire nanosensors. Nano Lett. 2004, 4, 51–54. [Google Scholar] [CrossRef]
- Zhang, G.J.; Chua, J.H.; Chee, R.E.; Agarwal, A.; Wong, S.M. Label-free direct detection of MiRNAs with silicon nanowire biosensors. Biosens. Bioelectron. 2009, 24, 2504–2508. [Google Scholar] [CrossRef] [PubMed]
- Choi, J.H.; Kim, H.; Kim, H.S.; Um, S.H.; Choi, J.W.; Oh, B.K. MMP-2 detective silicon nanowire biosensor using enzymatic cleavage reaction. J. Biomed. Nanotechnol. 2013, 9, 732–735. [Google Scholar] [CrossRef] [PubMed]
- De Santiago, F.; Trejo, A.; Miranda, A.; Salazar, F.; Carvajal, E.; Pérez, L.; Cruz-Irisson, M. Carbon monoxide sensing properties of B-, Al-and Ga-doped Si nanowires. Nanotechnology 2018, 29, 204001. [Google Scholar] [CrossRef]
- Song, X.; Hu, R.; Xu, S.; Liu, Z.; Wang, J.; Shi, Y.; Xu, J.; Chen, K.; Yu, L. Highly sensitive ammonia gas detection at room temperature by integratable silicon nanowire field-effect sensors. ACS Appl. Mater. Interfaces 2021, 13, 14377–14384. [Google Scholar] [CrossRef]
- Duan, X.; Li, Y.; Rajan, N.K.; Routenberg, D.A.; Modis, Y.; Reed, M.A. Quantification of the affinities and kinetics of protein interactions using silicon nanowire biosensors. Nat. Nanotechnol. 2012, 7, 401–407. [Google Scholar] [CrossRef]
- Patolsky, F.; Zheng, G.; Lieber, C.M. Fabrication of silicon nanowire devices for ultrasensitive, label-free, real-time detection of biological and chemical species. Nat. Protoc. 2006, 1, 1711–1724. [Google Scholar] [CrossRef]
- Stern, E.; Vacic, A.; Rajan, N.K.; Criscione, J.M.; Park, J.; Ilic, B.R.; Mooney, D.J.; Reed, M.A.; Fahmy, T.M. Label-free biomarker detection from whole blood. Nat. Nanotechnol. 2010, 5, 138–142. [Google Scholar] [CrossRef]
- Chua, J.H.; Chee, R.E.; Agarwal, A.; Wong, S.M.; Zhang, G.J. Label-free electrical detection of cardiac biomarker with complementary metal-oxide semiconductor-compatible silicon nanowire sensor arrays. Anal. Chem. 2009, 81, 6266–6271. [Google Scholar] [CrossRef]
- Chen, K.I.; Li, B.R.; Chen, Y.T. Silicon nanowire field-effect transistor-based biosensors for biomedical diagnosis and cellular recording investigation. Nano Today 2011, 6, 131–154. [Google Scholar] [CrossRef]
- Gao, A.; Lu, N.; Wang, Y.; Dai, P.; Li, T.; Gao, X.; Wang, Y.; Fan, C. Enhanced sensing of nucleic acids with silicon nanowire field effect transistor biosensors. Nano Lett. 2012, 12, 5262–5268. [Google Scholar] [CrossRef]
- Khodadadian, A.; Stadlbauer, B.; Heitzinger, C. Bayesian inversion for nanowire field-effect sensors. J. Comput. Electron. 2020, 19, 147–159. [Google Scholar] [CrossRef]
- Taghizadeh, L.; Khodadadian, A.; Heitzinger, C. The optimal multilevel Monte-Carlo approximation of the stochastic drift–diffusion-Poisson system. Comput. Methods Appl. Mech. Eng. 2017, 318, 739–761. [Google Scholar] [CrossRef]
- Khodadadian, A.; Hosseini, K.; Manzour-ol Ajdad, A.; Hedayati, M.; Kalantarinejad, R.; Heitzinger, C. Optimal design of nanowire field-effect troponin sensors. Comput. Biol. Med. 2017, 87, 46–56. [Google Scholar] [CrossRef]
- Pittino, F.; Selmi, L. Use and comparative assessment of the CVFEM method for Poisson–Boltzmann and Poisson–Nernst–Planck three dimensional simulations of impedimetric nano-biosensors operated in the DC and AC small signal regimes. Comput. Methods Appl. Mech. Eng. 2014, 278, 902–923. [Google Scholar] [CrossRef]
- Khodadadian, A.; Heitzinger, C. Basis adaptation for the stochastic nonlinear Poisson–Boltzmann equation. J. Comput. Electron. 2016, 15, 1393–1406. [Google Scholar] [CrossRef]
- Khodadadian, A.; Taghizadeh, L.; Heitzinger, C. Three-dimensional optimal multi-level Monte–Carlo approximation of the stochastic drift–diffusion–Poisson system in nanoscale devices. J. Comput. Electron. 2018, 17, 76–89. [Google Scholar] [CrossRef]
- Baumgartner, S.; Heitzinger, C.; Vacic, A.; Reed, M.A. Predictive simulations and optimization of nanowire field-effect PSA sensors including screening. Nanotechnology 2013, 24, 225503. [Google Scholar] [CrossRef]
- Hastings, W.K. Monte Carlo sampling methods using Markov chains and their applications. Biometrika 1970, 57, 97–109. [Google Scholar] [CrossRef]
- Haario, H.; Saksman, E.; Tamminen, J. Adaptive proposal distribution for random walk Metropolis algorithm. Comput. Stat. 1999, 14, 375–395. [Google Scholar] [CrossRef]
- Green, P.J.; Mira, A. Delayed rejection in reversible jump Metropolis–Hastings. Biometrika 2001, 88, 1035–1053. [Google Scholar] [CrossRef]
- Haario, H.; Laine, M.; Mira, A.; Saksman, E. DRAM: Efficient adaptive MCMC. Stat. Comput. 2006, 16, 339–354. [Google Scholar] [CrossRef]
- Evensen, G. The ensemble Kalman filter for combined state and parameter estimation. IEEE Control Syst. Mag. 2009, 29, 83–104. [Google Scholar] [CrossRef]
- Noii, N.; Khodadadian, A.; Ulloa, J.; Aldakheel, F.; Wick, T.; François, S.; Wriggers, P. Bayesian Inversion with Open-Source Codes for Various One-Dimensional Model Problems in Computational Mechanics. Arch. Comput. Methods Eng. 2022, 1–34. [Google Scholar] [CrossRef]
- Schackart, K.E.; Yoon, J.Y. Machine learning enhances the performance of bioreceptor-free biosensors. Sensors 2021, 21, 5519. [Google Scholar] [CrossRef] [PubMed]
- Cui, F.; Yue, Y.; Zhang, Y.; Zhang, Z.; Zhou, H.S. Advancing biosensors with machine learning. ACS Sens. 2020, 5, 3346–3364. [Google Scholar] [CrossRef] [PubMed]
- Albrecht, T.; Slabaugh, G.; Alonso, E.; Al-Arif, S.M.R. Deep learning for single-molecule science. Nanotechnology 2017, 28, 423001. [Google Scholar] [CrossRef] [PubMed]
- Jin, X.; Liu, C.; Xu, T.; Su, L.; Zhang, X. Artificial intelligence biosensors: Challenges and prospects. Biosens. Bioelectron. 2020, 165, 112412. [Google Scholar] [CrossRef] [PubMed]
- Raji, H.; Tayyab, M.; Sui, J.; Mahmoodi, S.R.; Javanmard, M. Biosensors and machine learning for enhanced detection, stratification, and classification of cells: A review. arXiv 2021, arXiv:2101.01866. [Google Scholar]
- Rivera, E.C.; Swerdlow, J.J.; Summerscales, R.L.; Uppala, P.P.T.; Maciel Filho, R.; Neto, M.R.; Kwon, H.J. Data-driven modeling of smartphone-based electrochemiluminescence sensor data using artificial intelligence. Sensors 2020, 20, 625. [Google Scholar] [CrossRef]
- Khodadadian, A.; Parvizi, M.; Heitzinger, C. An adaptive multilevel Monte Carlo algorithm for the stochastic drift–diffusion–Poisson system. Comput. Methods Appl. Mech. Eng. 2020, 368, 113163. [Google Scholar] [CrossRef]
- Khodadadian, A.; Taghizadeh, L.; Heitzinger, C. Optimal multilevel randomized quasi-Monte-Carlo method for the stochastic drift–diffusion-Poisson system. Comput. Methods Appl. Mech. Eng. 2018, 329, 480–497. [Google Scholar] [CrossRef]
- Baumgartner, S.; Heitzinger, C. Existence and local uniqueness for 3d self-consistent multiscale models of field-effect sensors. Commun. Math. Sci. 2012, 10, 693–716. [Google Scholar] [CrossRef]
- Cockburn, B.; Triandaf, I. Convergence of a finite element method for the drift-diffusion semiconductor device equations: The zero diffusion case. Math. Comput. 1992, 59, 383–401. [Google Scholar] [CrossRef]
- Chen, Z.; Cockburn, B. Analysis of a finite element method for the drift-diffusion semiconductor device equations: The multidimensional case. Numer. Math. 1995, 71, 1–28. [Google Scholar] [CrossRef]
- Zlámal, M. Finite element solution of the fundamental equations of semiconductor devices. I. Math. Comput. 1986, 46, 27–43. [Google Scholar] [CrossRef][Green Version]
- Zhang, J.; Vrugt, J.A.; Shi, X.; Lin, G.; Wu, L.; Zeng, L. Improving Simulation Efficiency of MCMC for Inverse Modeling of Hydrologic Systems with a Kalman-Inspired Proposal Distribution. Water Resour. Res. 2020, 56, e2019WR025474. [Google Scholar] [CrossRef]
- Bebis, G.; Georgiopoulos, M. Feed-forward neural networks. IEEE Potentials 1994, 13, 27–31. [Google Scholar] [CrossRef]
- Svozil, D.; Kvasnicka, V.; Pospichal, J. Introduction to multi-layer feed-forward neural networks. Chemom. Intell. Lab. Syst. 1997, 39, 43–62. [Google Scholar] [CrossRef]
- Sazli, M.H. A brief review of feed-forward neural networks. Commun. Fac. Sci. Univ. Ank. Ser. A2-A3 Phys. Sci. Eng. 2006, 50. [Google Scholar] [CrossRef]
- Dolinsky, T.J.; Czodrowski, P.; Li, H.; Nielsen, J.E.; Jensen, J.H.; Klebe, G.; Baker, N.A. PDB2PQR: Expanding and upgrading automated preparation of biomolecular structures for molecular simulations. Nucleic Acids Res. 2007, 35, W522–W525. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Robertson, A.D.; Jensen, J.H. Very fast empirical prediction and rationalization of protein pKa values. Proteins Struct. Funct. Bioinform. 2005, 61, 704–721. [Google Scholar] [CrossRef] [PubMed]
- Søndergaard, C.R.; Olsson, M.H.; Rostkowski, M.; Jensen, J.H. Improved treatment of ligands and coupling effects in empirical calculation and rationalization of pKa values. J. Chem. Theory Comput. 2011, 7, 2284–2295. [Google Scholar] [CrossRef] [PubMed]
- Olsson, M.H.; Søndergaard, C.R.; Rostkowski, M.; Jensen, J.H. PROPKA3: Consistent treatment of internal and surface residues in empirical pKa predictions. J. Chem. Theory Comput. 2011, 7, 525–537. [Google Scholar] [CrossRef] [PubMed]
- Bulyha, A.; Heitzinger, C. An algorithm for three-dimensional Monte-Carlo simulation of charge distribution at biofunctionalized surfaces. Nanoscale 2011, 3, 1608–1617. [Google Scholar] [CrossRef]
- Heitzinger, C.; Liu, Y.; Mauser, N.J.; Ringhofer, C.; Dutton, R.W. Calculation of fluctuations in boundary layers of nanowire field-effect biosensors. J. Comput. Theor. Nanosci. 2010, 7, 2574–2580. [Google Scholar] [CrossRef]
- Punzet, M.; Baurecht, D.; Varga, F.; Karlic, H.; Heitzinger, C. Determination of surface concentrations of individual molecule-layers used in nanoscale biosensors by in situ ATR-FTIR spectroscopy. Nanoscale 2012, 4, 2431–2438. [Google Scholar] [CrossRef]

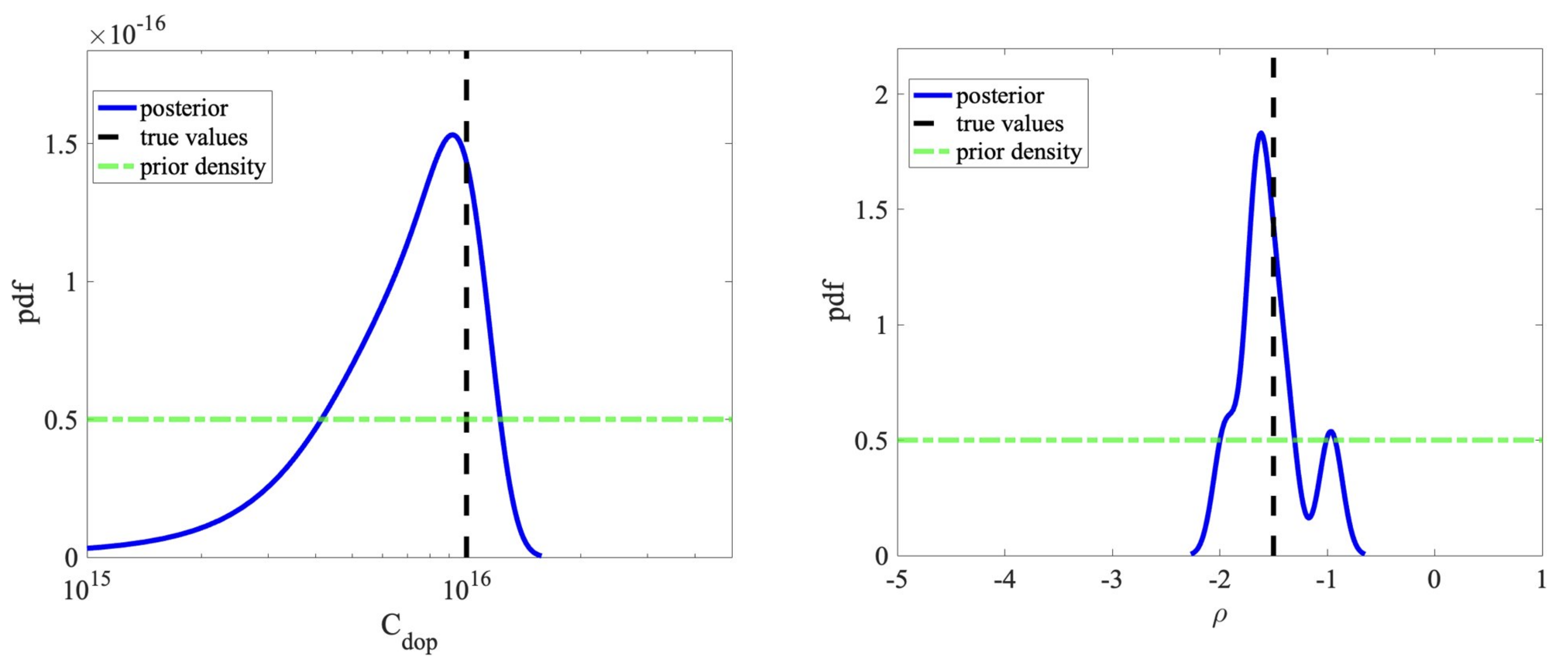
| Parameter | Min | Max | EnKF (Median) | True Values | Acceptance Rate |
|---|---|---|---|---|---|
| C(cm) | 1 | 5 | 9.4 | 1 | 91% |
| (q/nm) | −5 | 1 | −1.55 | −1.5 | 86% |
| Cases | Inputs | [V] | SiO [nm] | N [nm] | N [nm] | |
|---|---|---|---|---|---|---|
| Case 1 | 1 | 8 | 100 | 1 | 50 | |
| Case 2 | 2 | 100 | 1 | 50 | ||
| Case 3 | 3 | 1 | 50 | |||
| Case 4 | 4 | 50 | ||||
| Case 5 | 5 |
| Case | No. Neurons in 1st Hidden Layer | No. Neurons in 2nd Hidden Layer | MSE-Train | MSE-Test | No. Epochs | |
|---|---|---|---|---|---|---|
| 1 | 10 | 4 | 0.00057 | 0.00061 | 1000 | 0.1 |
| 2 | 20 | 7 | 0.00147 | 0.00184 | 2000 | 0.2 |
| 3 | 20 | 7 | 0.00181 | 0.000836 | 4000 | 0.2 |
| 4 | 20 | 7 | 0.000842 | 0.000517 | 8000 | 0.2 |
| 5 | 20 | 7 | 0.0011 | 0.000058 | 10,000 | 0.2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khodadadian, A.; Parvizi, M.; Teshnehlab, M.; Heitzinger, C. Rational Design of Field-Effect Sensors Using Partial Differential Equations, Bayesian Inversion, and Artificial Neural Networks. Sensors 2022, 22, 4785. https://doi.org/10.3390/s22134785
Khodadadian A, Parvizi M, Teshnehlab M, Heitzinger C. Rational Design of Field-Effect Sensors Using Partial Differential Equations, Bayesian Inversion, and Artificial Neural Networks. Sensors. 2022; 22(13):4785. https://doi.org/10.3390/s22134785
Chicago/Turabian StyleKhodadadian, Amirreza, Maryam Parvizi, Mohammad Teshnehlab, and Clemens Heitzinger. 2022. "Rational Design of Field-Effect Sensors Using Partial Differential Equations, Bayesian Inversion, and Artificial Neural Networks" Sensors 22, no. 13: 4785. https://doi.org/10.3390/s22134785
APA StyleKhodadadian, A., Parvizi, M., Teshnehlab, M., & Heitzinger, C. (2022). Rational Design of Field-Effect Sensors Using Partial Differential Equations, Bayesian Inversion, and Artificial Neural Networks. Sensors, 22(13), 4785. https://doi.org/10.3390/s22134785






