Absolute Quantitation of Serum Antibody Reactivity Using the Richards Growth Model for Antigen Microspot Titration
Abstract
:1. Introduction
2. Materials and Methods
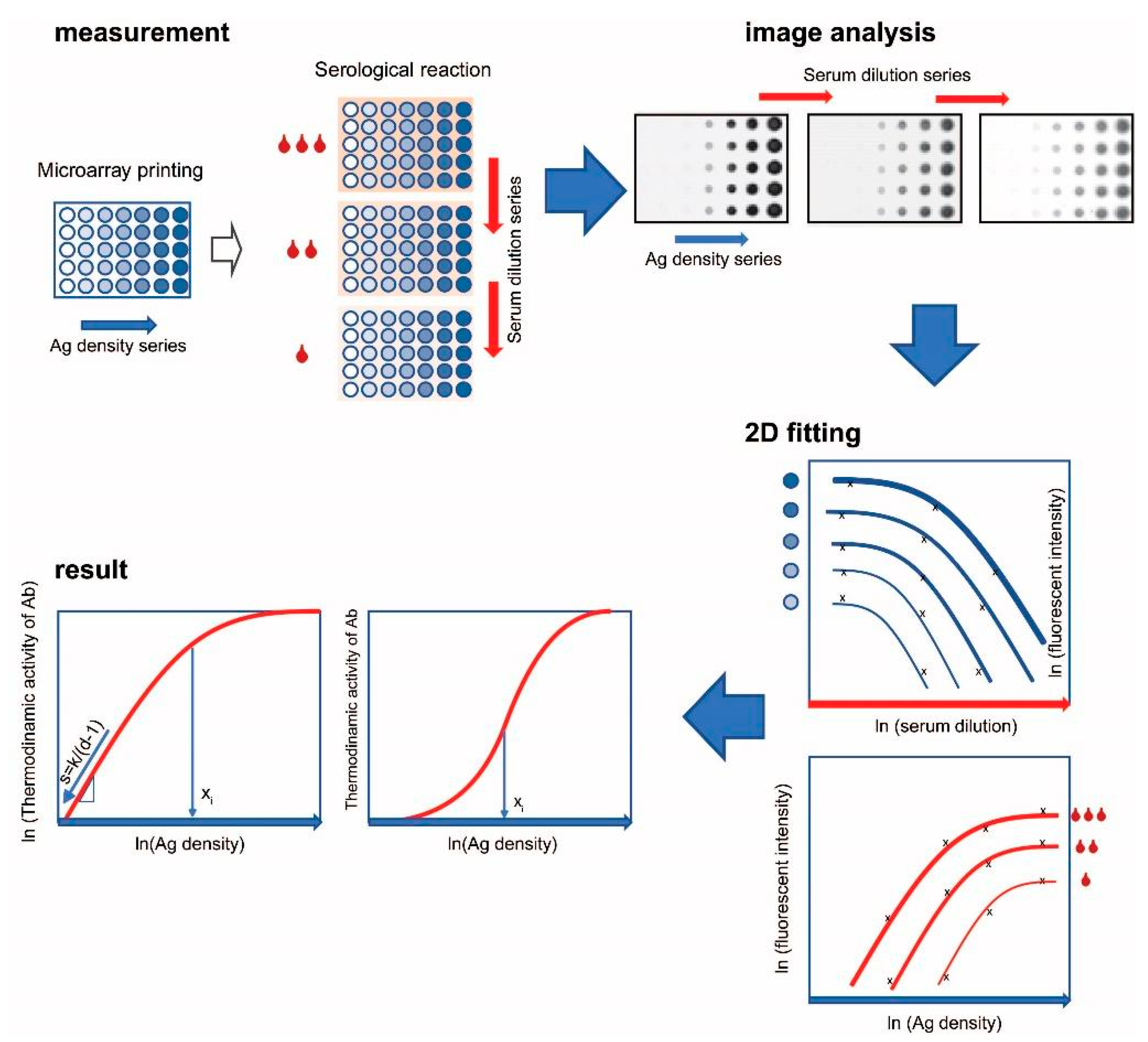
2.1. Microarray Production and Measurements
2.2. Sample Handling and Signal Detection
2.3. Measurements with 14D5 Monoclonal Antibody
2.4. Analysis of the Microarray Data
2.5. Fitting of Binding Curves
3. Results
3.1. Experimental Setup and Properties of the Measurement System
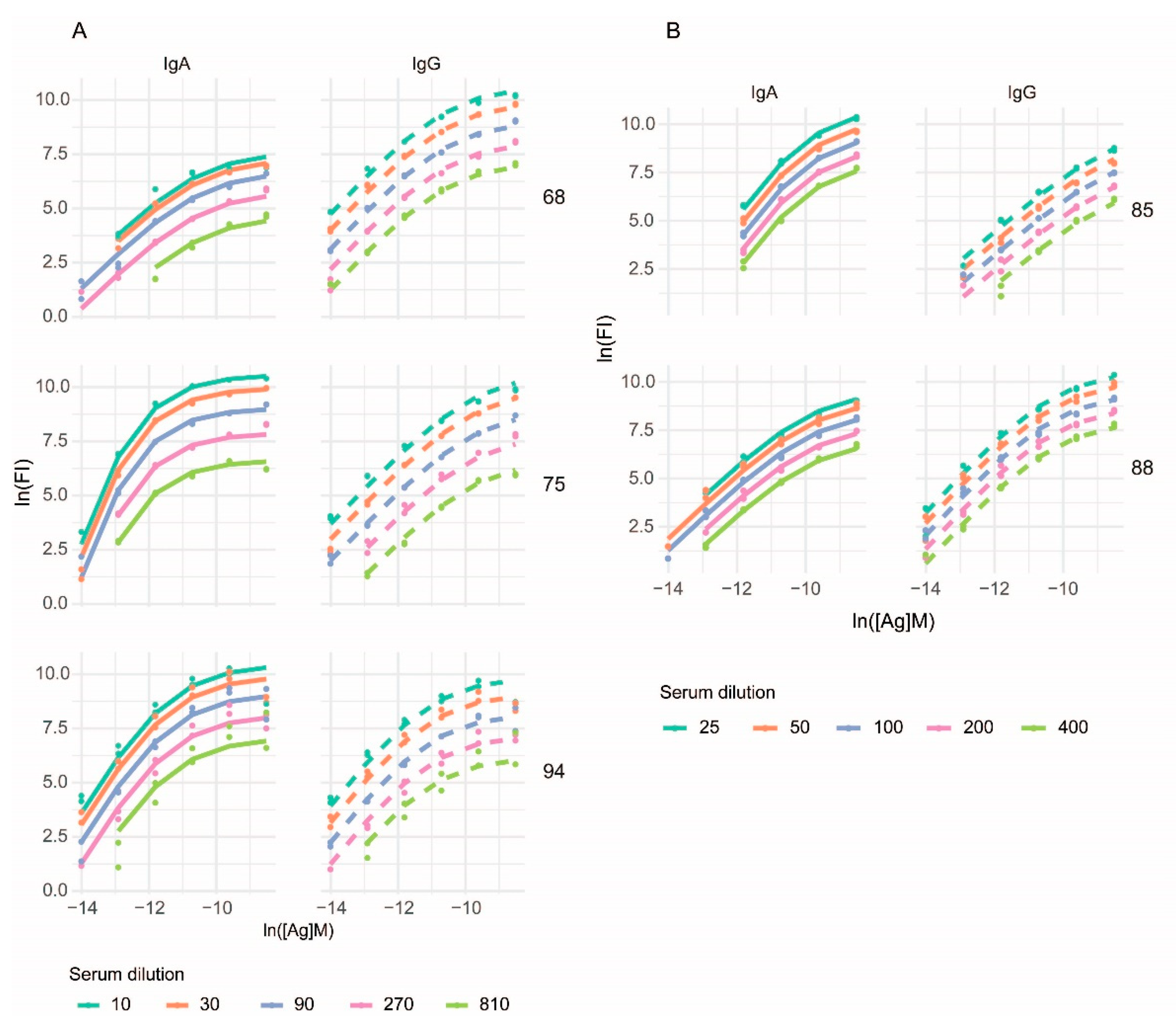
3.2. Curve Fitting
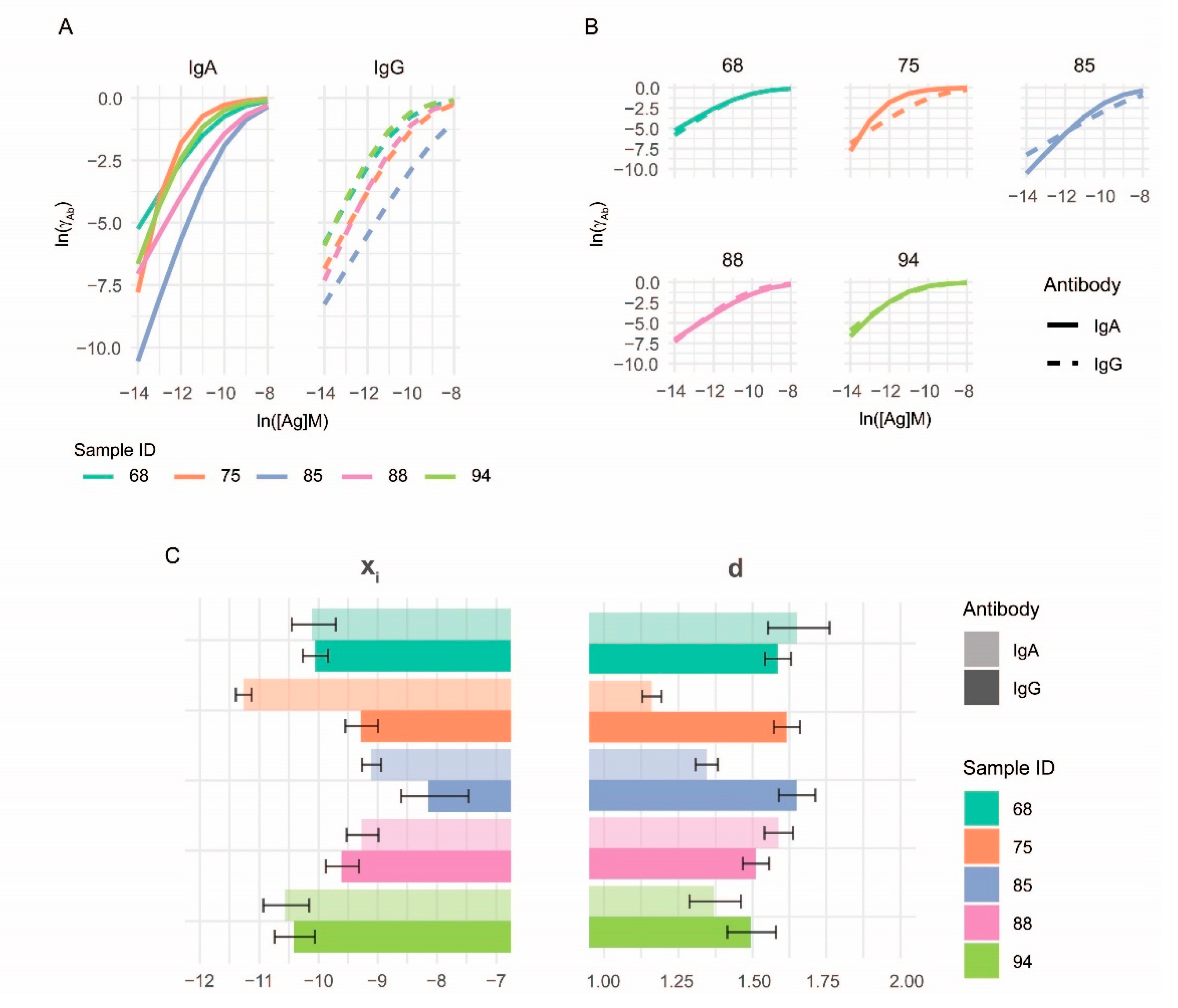
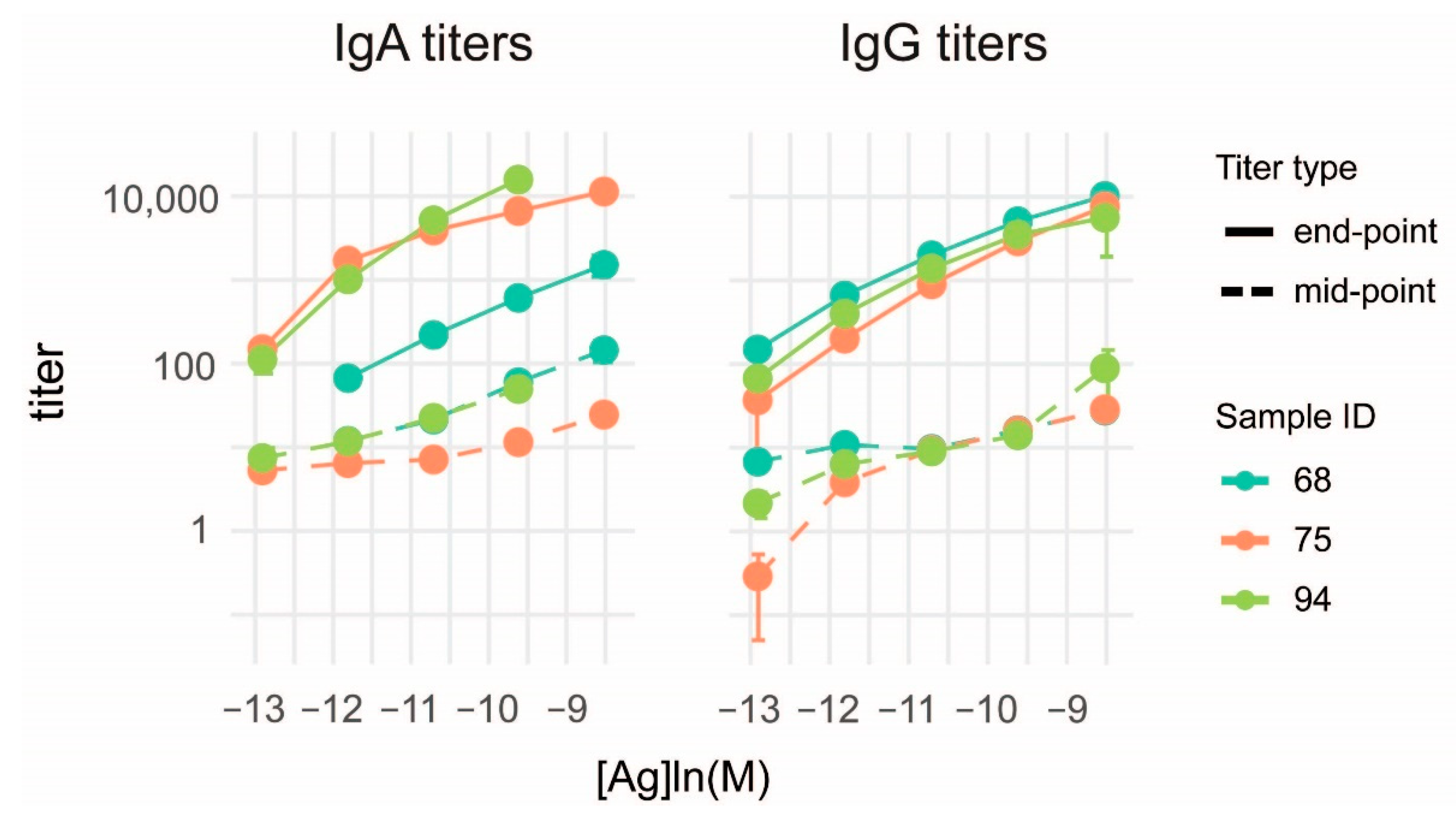
3.3. Characterization of Anti-Deamidated Gliadin Peptide Serum Antibodies
3.4. Measurement of Reference Monoclonal Antibody Properties
4. Discussion
5. Conclusions
6. Patents
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| A | relative thermodynamic activity |
| A | antibody binding capacity [FI] |
| Ab | antibody |
| [Ab] | antibody concentration [mol/L] |
| AbAg | antibody–antigen complex |
| [AbAg] | antibody–antigen complex concentration [mol/L] |
| Ag | antigen |
| [Ag] | antigen concentration [mol/L] |
| B | auxiliary parameter |
| BSA | Bovine Serum Albumin |
| c | molar concentration [mol/L] |
| C | auxiliary parameter |
| d | shape parameter that determines asymmetry |
| D | positive constant [L/mol] |
| ELISA | Enzyme-Linked Immunosorbent Assay |
| γ | thermodynamic activity coefficient |
| IgA | immunoglobulin A |
| IgG | immunoglobulin G |
| k | rate of exponential growth |
| KD | equilibrium dissociation constant |
| m | auxiliary parameter |
| μ | chemical potential [J/mol] |
| μ° | standard chemical potential [J/mol] |
| mAb | monoclonal antibody |
| PBS | Phosphate-Buffered Saline |
| R | ideal gas constant [~8.314 J/K·mol] |
| R(x) | Richards function |
| RFI | Relative Fluorescence Intensity |
| RIA | Radioimmunoassay |
| s | slope of lnR(x) at minus infinity |
| T | temperature [K] |
| xi | value of x at inflection point |
| yi | value of y at inflection point |
| z | serum dilution factor [1/dilution] |
References
- Imkeller, K.; Wardemann, H. Assessing human B cell repertoire diversity and convergence. Immunol. Rev. 2018, 284, 51–66. [Google Scholar] [CrossRef]
- Briney, B.; Inderbitzin, A.; Joyce, C.; Burton, D.R. Commonality despite exceptional diversity in the baseline human antibody repertoire. Nature 2019, 566, 393–397. [Google Scholar] [CrossRef] [Green Version]
- Prechl, J. A generalized quantitative antibody homeostasis model: Antigen saturation, natural antibodies and a quantitative antibody network. Clin. Transl. Immunol. 2017, 6, e131. [Google Scholar] [CrossRef]
- Marillet, S.; Lefranc, M.-P.; Boudinot, P.; Cazals, F. Novel Structural Parameters of Ig-Ag Complexes Yield a Quantitative Description of Interaction Specificity and Binding Affinity. Front. Immunol. 2017, 8, 34. [Google Scholar] [CrossRef] [Green Version]
- Prechl, J. A generalized quantitative antibody homeostasis model: Maintenance of global antibody equilibrium by effector functions. Clin. Transl. Immunol. 2017, 6, e161. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bacarese-Hamilton, T.; Bistoni, F.; Crisanti, A. Protein microarrays: From serodiagnosis to whole proteome scale analysis of the immune response against pathogenic microorganisms. BioTechniques 2002, 33, S24–S29. [Google Scholar] [CrossRef]
- Meyer, P.W.A.; Ally, M.M.T.M.; Anderson, R. Reliable and cost-effective serodiagnosis of rheumatoid arthritis. Rheumatol. Int. 2016, 36, 751–758. [Google Scholar] [CrossRef]
- Chokshi, N.Y.; Sicherer, S.H. Interpreting IgE sensitization tests in food allergy. Expert Rev. Clin. Immunol. 2016, 12, 389–403. [Google Scholar] [CrossRef]
- Bozsóky, S. The problem of standardization in rheumatoid arthritis serology. Arthritis Rheumatism 1963, 6, 641–649. [Google Scholar] [CrossRef]
- Meroni, P.L.; Biggioggero, M.; Pierangeli, S.S.; Sheldon, J.; Zegers, I.; Borghi, M.O. Standardization of autoantibody testing: A paradigm for serology in rheumatic diseases. Nat. Rev. Rheumatol. 2014, 10, 35–43. [Google Scholar] [CrossRef]
- Stanley, C.; Lew, A.M.; Steward, M.W. The measurement of antibody affinity: A comparison of five techniques utilizing a panel of monoclonal anti-DNP antibodies and the effect of high affinity antibody on the measurement of low affinity antibody. J. Immunol. Methods 1983, 64, 119–132. [Google Scholar] [CrossRef]
- Macdonald, R.A.; Hosking, C.S.; Jones, C.L. The measurement of relative antibody affinity by ELISA using thiocyanate elution. J. Immunol. Methods 1988, 106, 191–194. [Google Scholar] [CrossRef]
- Bruderer, U.; Deusinger, M.; Schürch, U.; Lang, A.B. Analyses of affinity distributions within polyclonal populations of antigen-specific antibodies. Evaluation of their accuracy in population detection using monoclonal antibodies. J. Immunol. Methods 1992, 151, 157–164. [Google Scholar] [CrossRef]
- Nieto, A.; Gaya, A.; Jansa, M.; Moreno, C.; Vives, J. Direct measurement of antibody affinity distribution by hapten-inhibition enzyme immunoassay. Mol. Immunol. 1984, 21, 537–543. [Google Scholar] [CrossRef]
- Beatty, J.D.; Beatty, B.G.; Vlahos, W.G. Measurement of monoclonal antibody affinity by non-competitive enzyme immunoassay. J. Immunol. Methods 1987, 100, 173–179. [Google Scholar] [CrossRef]
- Sem, D.S.; McNeeley, P.A.; Linnik, M.D. Antibody affinities and relative titers in polyclonal populations: Surface plasmon resonance analysis of anti-DNA antibodies. Arch. Biochem. Biophys. 1999, 372, 62–68. [Google Scholar] [CrossRef]
- Abdiche, Y.; Malashock, D.; Pinkerton, A.; Pons, J. Determining kinetics and affinities of protein interactions using a parallel real-time label-free biosensor, the Octet. Anal. Biochem. 2008, 377, 209–217. [Google Scholar] [CrossRef]
- Jerabek-Willemsen, M.; Wienken, C.J.; Braun, D.; Baaske, P.; Duhr, S. Molecular interaction studies using microscale thermophoresis. Assay Drug Dev. Technol. 2011, 9, 342–353. [Google Scholar] [CrossRef] [Green Version]
- Ekins, R.; Chu, F.; Biggart, E. Multispot, multianalyte, immunoassay. Ann. Biol. Clin. 1990, 48, 655–666. [Google Scholar]
- Saviranta, P.; Okon, R.; Brinker, A.; Warashina, M.; Eppinger, J.; Geierstanger, B.H. Evaluating sandwich immunoassays in microarray format in terms of the ambient analyte regime. Clin. Chem. 2004, 50, 1907–1920. [Google Scholar] [CrossRef] [Green Version]
- Larsson, A. Assessment of polyclonal antibody binding of ligand by Sips’ equation or by the exact polyclonal equation. Comparison of models. Mol. Immunol. 1988, 25, 1239–1249. [Google Scholar] [CrossRef]
- Kallay, N.; Preočanin, T.; Kovačević, D.; Lützenkirchen, J.; Villalobos, M. Thermodynamics of the reactions at solid/liquid interfaces. Croat. Chem. Acta 2011, 84, 1–10. [Google Scholar] [CrossRef]
- Moradi, O. Thermodynamics of Interfaces. In Thermodynamics-Interaction Studies-Solids, Liquids and Gases; Moreno Pirajn, J.C., Ed.; InTech: London, UK, 2011; ISBN 978-953-307-563-1. [Google Scholar]
- Pfeil, T.; Herbály, B. A linear model for polyclonal antibody–antigen reactions. Math. Comput. Simul. 2022, 198, 20–30. [Google Scholar] [CrossRef]
- De Michele, C.; De Los Rios, P.; Foffi, G.; Piazza, F. Simulation and Theory of Antibody Binding to Crowded Antigen-Covered Surfaces. PLoS Comput. Biol. 2016, 12, e1004752. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Edwards, D.A. Steric hindrance effects on surface reactions: Applications to BIAcore. J. Math. Biol. 2007, 55, 517–539. [Google Scholar] [CrossRef] [PubMed]
- Gottschalk, P.G.; Dunn, J.R. The five-parameter logistic: A characterization and comparison with the four-parameter logistic. Anal. Biochem. 2005, 343, 54–65. [Google Scholar] [CrossRef]
- Tsoularis, A.; Wallace, J. Analysis of logistic growth models. Math. Biosci. 2002, 179, 21–55. [Google Scholar] [CrossRef] [Green Version]
- Tjørve, E.; Tjørve, K.M.C. A unified approach to the Richards-model family for use in growth analyses: Why we need only two model forms. J. Theor. Biol. 2010, 267, 417–425. [Google Scholar] [CrossRef]
- Hadzhieva, M.; Pashov, A.D.; Kaveri, S.; Lacroix-Desmazes, S.; Mouquet, H.; Dimitrov, J.D. Impact of antigen density on the binding mechanism of igg antibodies. Sci. Rep. 2017, 7, 3767. [Google Scholar] [CrossRef] [Green Version]
- Lew, A.M. The effect of epitope density and antibody affinity on the ELISA as analysed by monoclonal antibodies. J. Immunol. Methods 1984, 72, 171–176. [Google Scholar] [CrossRef]
- Kusnezow, W.; Syagailo, Y.V.; Rüffer, S.; Baudenstiel, N.; Gauer, C.; Hoheisel, J.D.; Wild, D.; Goychuk, I. Optimal design of microarray immunoassays to compensate for kinetic limitations: Theory and experiment. Mol. Cell. Proteomics 2006, 5, 1681–1696. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Engelmann, B.W.; Kim, Y.; Wang, M.; Peters, B.; Rock, R.S.; Nash, P.D. The development and application of a quantitative peptide microarray based approach to protein interaction domain specificity space. Mol. Cell. Proteomics 2014, 13, 3647–3662. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rizwan, M.; Rönnberg, B.; Cistjakovs, M.; Lundkvist, Å.; Pipkorn, R.; Blomberg, J. Serology in the Digital Age: Using Long Synthetic Peptides Created from Nucleic Acid Sequences as Antigens in Microarrays. Microarrays 2016, 5, 22. [Google Scholar] [CrossRef] [Green Version]
- Achenbach, P.; Schlosser, M.; Williams, A.J.K.; Yu, L.; Mueller, P.W.; Bingley, P.J.; Bonifacio, E. Combined testing of antibody titer and affinity improves insulin autoantibody measurement: Diabetes Antibody Standardization Program. Clin. Immunol. 2007, 122, 85–90. [Google Scholar] [CrossRef] [PubMed]
- Szarka, E.; Aradi, P.; Huber, K.; Pozsgay, J.; Végh, L.; Magyar, A.; Gyulai, G.; Nagy, G.; Rojkovich, B.; Kiss, É.; et al. Affinity Purification and Comparative Biosensor Analysis of Citrulline-Peptide-Specific Antibodies in Rheumatoid Arthritis. Int. J. Mol. Sci. 2018, 19, 326. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Real-Fernández, F.; Rossi, G.; Panza, F.; Pratesi, F.; Migliorini, P.; Rovero, P. Surface Plasmon Resonance Method to Evaluate Anti-citrullinated Protein/Peptide Antibody Affinity to Citrullinated Peptides. Methods Mol. Biol. 2015, 1348, 267–274. [Google Scholar] [CrossRef]
- Sakakibara, S.; Arimori, T.; Yamashita, K.; Jinzai, H.; Motooka, D.; Nakamura, S.; Li, S.; Takeda, K.; Katayama, J.; El Hussien, M.A.; et al. Clonal evolution and antigen recognition of anti-nuclear antibodies in acute systemic lupus erythematosus. Sci. Rep. 2017, 7, 16428. [Google Scholar] [CrossRef] [Green Version]
- Poulsen, T.R.; Jensen, A.; Haurum, J.S.; Andersen, P.S. Limits for antibody affinity maturation and repertoire diversification in hypervaccinated humans. J. Immunol. 2011, 187, 4229–4235. [Google Scholar] [CrossRef] [Green Version]
- Reddy, S.B.; Anders, R.F.; Cross, N.; Mueller, I.; Senn, N.; Stanisic, D.I.; Siba, P.M.; Wahlgren, M.; Kironde, F.; Beeson, J.G.; et al. Differences in affinity of monoclonal and naturally acquired polyclonal antibodies against Plasmodium falciparum merozoite antigens. BMC Microbiol. 2015, 15, 133. [Google Scholar] [CrossRef] [Green Version]
- Pratesi, F.; Caruso, T.; Testa, D.; Tarpanelli, T.; Gentili, A.; Gioè, D.; Migliorini, P. BNT162b2 mRNA SARS-CoV-2 Vaccine Elicits High Avidity and Neutralizing Antibodies in Healthcare Workers. Vaccines 2021, 9, 672. [Google Scholar] [CrossRef]
- Xiong, H.; Dolpady, J.; Wabl, M.; Curotto de Lafaille, M.A.; Lafaille, J.J. Sequential class switching is required for the generation of high affinity IgE antibodies. J. Exp. Med. 2012, 209, 353–364. [Google Scholar] [CrossRef] [Green Version]
- Mita, H.; Yasueda, H.; Akiyama, K. Affinity of IgE antibody to antigen influences allergen-induced histamine release. Clin. Exp. Allergy 2000, 30, 1583–1589. [Google Scholar] [CrossRef]
- Wang, J.; Lin, J.; Bardina, L.; Goldis, M.; Nowak-Wegrzyn, A.; Shreffler, W.G.; Sampson, H.A. Correlation of IgE/IgG4 milk epitopes and affinity of milk-specific IgE antibodies with different phenotypes of clinical milk allergy. J. Allergy Clin. Immunol. 2010, 125, 695–702.e1. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pierson, L.; Allauzen, S.; Blumenthal, M.; Rosenberg, A. An automated method for determination of antibody affinity distribution functions with nanogram quantities. J. Immunol. Methods 1998, 211, 97–109. [Google Scholar] [CrossRef]
- Péterfy, F.; Kuusela, P.; Mäkelä, O. Affinity requirements for antibody assays mapped by monoclonal antibodies. J. Immunol. 1983, 130, 1809–1813. [Google Scholar] [PubMed]
- Alessi, P.; Fermeglia, M.; Kikic, I. Significance of dilute regions. Fluid Phase Equilib. 1991, 70, 239–250. [Google Scholar] [CrossRef]
- Thomas, A.; Messer, W.B.; Hansel, D.E.; Streblow, D.N.; Kazmierczak, S.C.; Lyski, Z.L.; Lu, Z.; Slifka, M.K. Establishment of Monoclonal Antibody Standards for Quantitative Serological Diagnosis of SARS-CoV-2 in Low-Incidence Settings. Open Forum Infect. Dis. 2021, 8, ofab061. [Google Scholar] [CrossRef]
- Dimitrov, D.S. Therapeutic antibodies, vaccines and antibodyomes. MAbs 2010, 2, 347–356. [Google Scholar] [CrossRef] [Green Version]
- Prechl, J. Network organization of antibody interactions in sequence and structure space: The RADARS model. Antibodies 2020, 9, 13. [Google Scholar] [CrossRef]
- Prechl, J. Why current quantitative serology is not quantitative and how systems immunology could provide solutions. Biol. Futura 2021, 72, 37–44. [Google Scholar] [CrossRef]
- Pratesi, F.; Tommasi, C.; Anzilotti, C.; Puxeddu, I.; Sardano, E.; Di Colo, G.; Migliorini, P. Antibodies to a new viral citrullinated peptide, VCP2: Fine specificity and correlation with anti-cyclic citrullinated peptide (CCP) and anti-VCP1 antibodies. Clin. Exp. Immunol. 2011, 164, 337–345. [Google Scholar] [CrossRef] [PubMed]
- Mukkur, T.K.S.; Szewczuk, M.R.; Schmidt, D.E. Determination of total affinity constant for heterogeneous hapten-antibody interactions. Immunochemistry 1974, 11, 9–13. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Papp, K.; Kovács, Á.; Orosz, A.; Hérincs, Z.; Randek, J.; Liliom, K.; Pfeil, T.; Prechl, J. Absolute Quantitation of Serum Antibody Reactivity Using the Richards Growth Model for Antigen Microspot Titration. Sensors 2022, 22, 3962. https://doi.org/10.3390/s22103962
Papp K, Kovács Á, Orosz A, Hérincs Z, Randek J, Liliom K, Pfeil T, Prechl J. Absolute Quantitation of Serum Antibody Reactivity Using the Richards Growth Model for Antigen Microspot Titration. Sensors. 2022; 22(10):3962. https://doi.org/10.3390/s22103962
Chicago/Turabian StylePapp, Krisztián, Ágnes Kovács, Anita Orosz, Zoltán Hérincs, Judit Randek, Károly Liliom, Tamás Pfeil, and József Prechl. 2022. "Absolute Quantitation of Serum Antibody Reactivity Using the Richards Growth Model for Antigen Microspot Titration" Sensors 22, no. 10: 3962. https://doi.org/10.3390/s22103962
APA StylePapp, K., Kovács, Á., Orosz, A., Hérincs, Z., Randek, J., Liliom, K., Pfeil, T., & Prechl, J. (2022). Absolute Quantitation of Serum Antibody Reactivity Using the Richards Growth Model for Antigen Microspot Titration. Sensors, 22(10), 3962. https://doi.org/10.3390/s22103962






