Improved Grey Wolf Optimization Algorithm and Application
Abstract
:1. Introduction
- An improved GWO algorithm based on a multi-strategy hybrid is proposed.
- The improved GWO algorithm is applied to the path planning of mobile robot.
- The performance of the proposed approach is compared with standard GWO, Sparrow Search Algorithm (SSA), Mayfly Algorithm (MA), Modified Grey Wolf Optimization Algorithm (MGWO) [10], Novel Grey Wolf Optimization Algorithm (NGWO) [11], A Fuzzy Hierarchical Operator in the Grey Wolf Optimizer Algorithm (GWO-fuzzy) [12], and Evolutionary population dynamics and grey wolf optimizer (GWO-EPD) [13].
2. Related Work
2.1. Research Situation
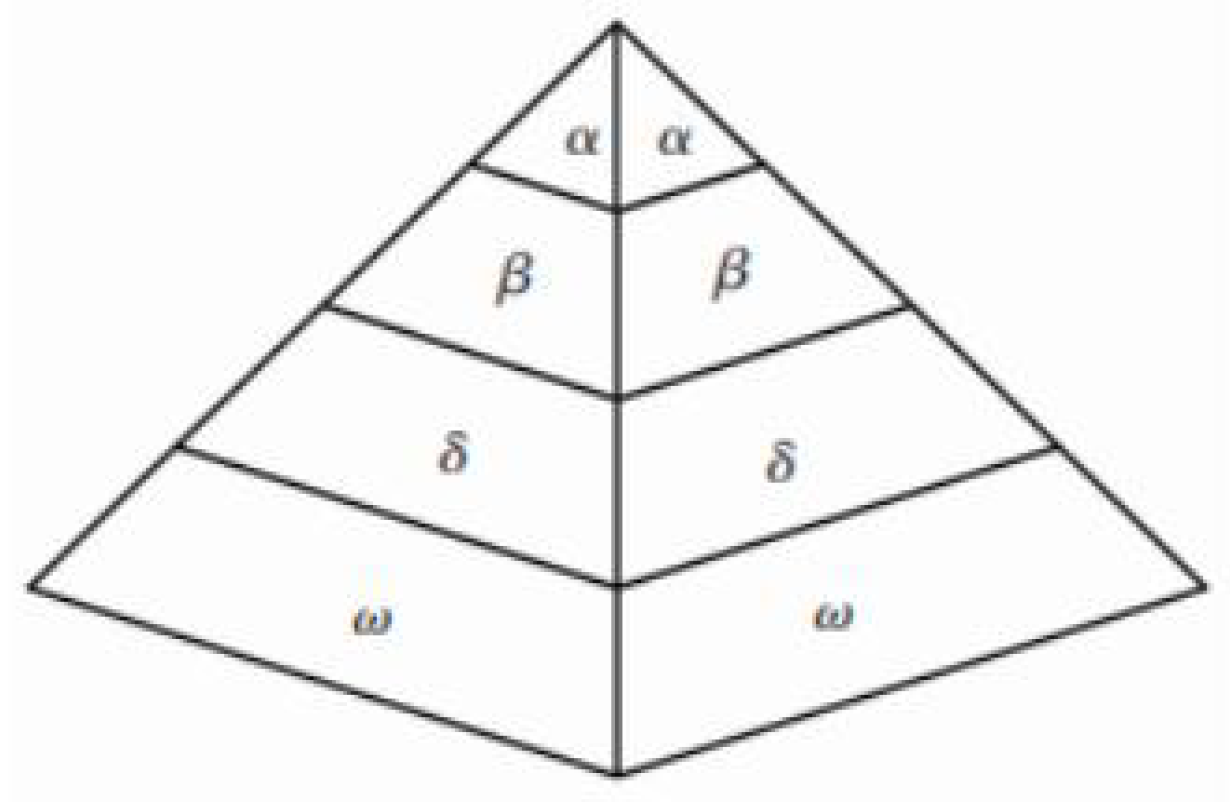
2.2. GWO Algorithm
3. Improved GWO Algorithm
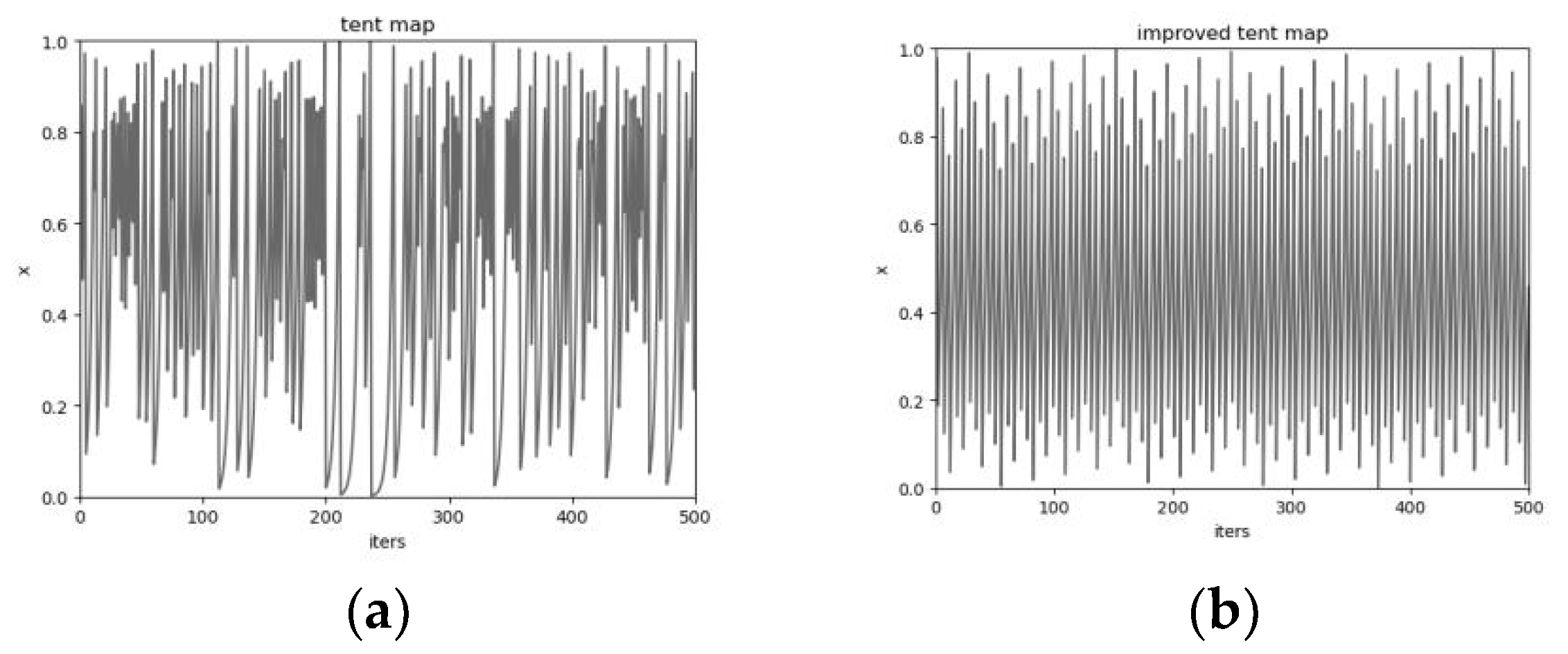
3.1. Wolf Pack Initialization
- Produce random initial values y0 in (0, 1) with i = 0.
- Calculate iteratively using Equation (9) to produce the sequence.
- Stop iterating when the iteration reaches the maximum value and saves the sequence.
3.2. Nonlinear Convergence Factor
3.3. Dynamic Proportional Weighting Strategy
| Algorithm 1: Pseudo Code of Improved GWO | |
| 1 | Initialize (Xi (i = 1, 2…, n)) t, Tmax, a, A, C |
| 2 | Initialize Tent map x0 |
| 3 | Calculate the fitness of each wolf |
| 4 | Xa = best wolf. Xβ = second wolf. Xw = third wolf. |
| 5 | While t < Tmax |
| 6 | Sort fitness of each wolf |
| 7 | Update chaotic number, a |
| 8 | for each search agent |
| 9 | Update position current wolf using |
| 10 | end |
| 11 | Calculate fitness of each wolf |
| 12 | Update Xa, Xβ, Xw |
| 13 | t = t + 1 |
| 14 | end |
4. Result
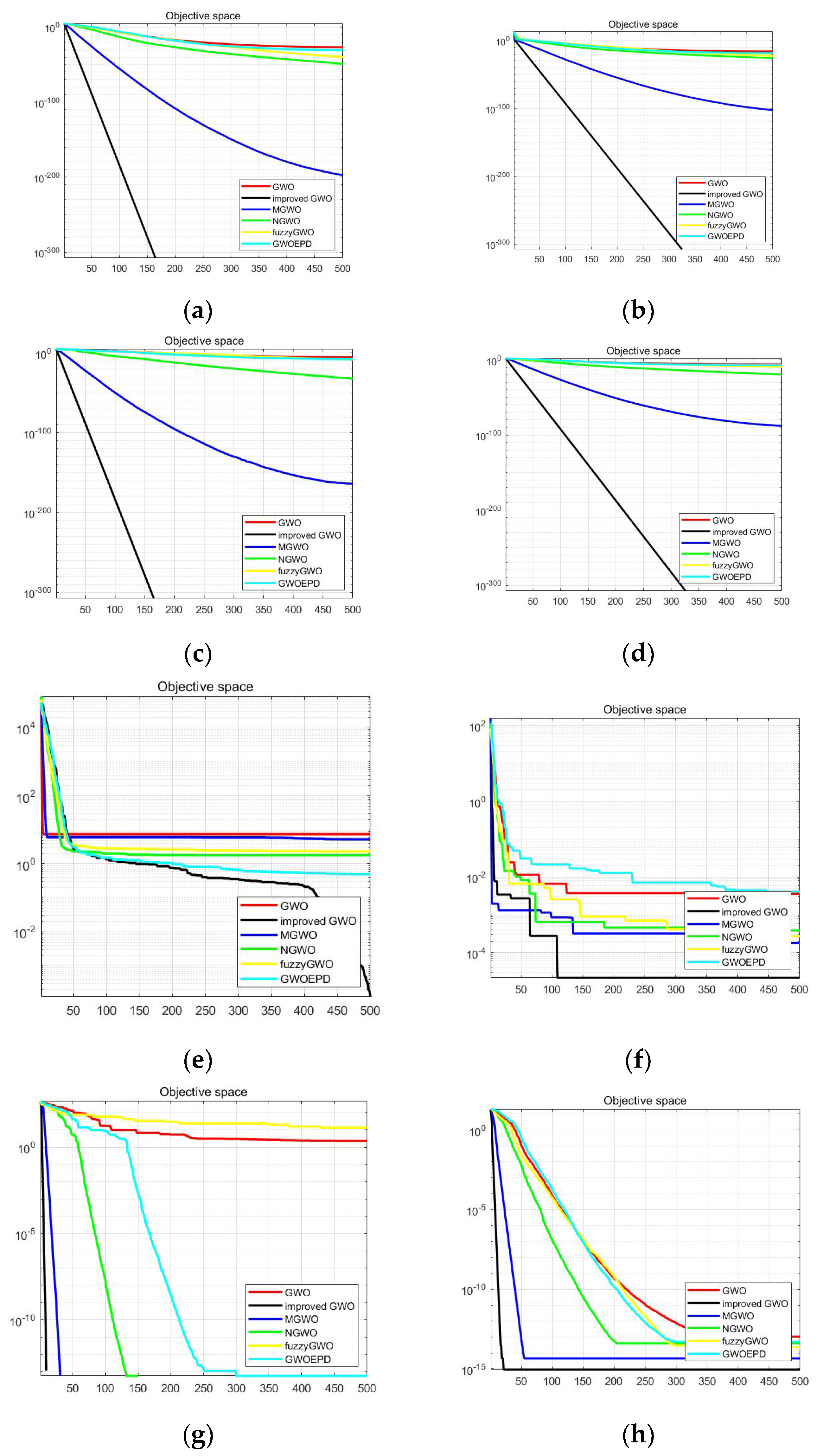
4.1. Comparison with GWO and Other Improvement GWO
4.1.1. Convergence Accuracy Analysis
4.1.2. Convergence Speed Analysis
4.2. Comparison with Other Intelligent Optimization Algorithms
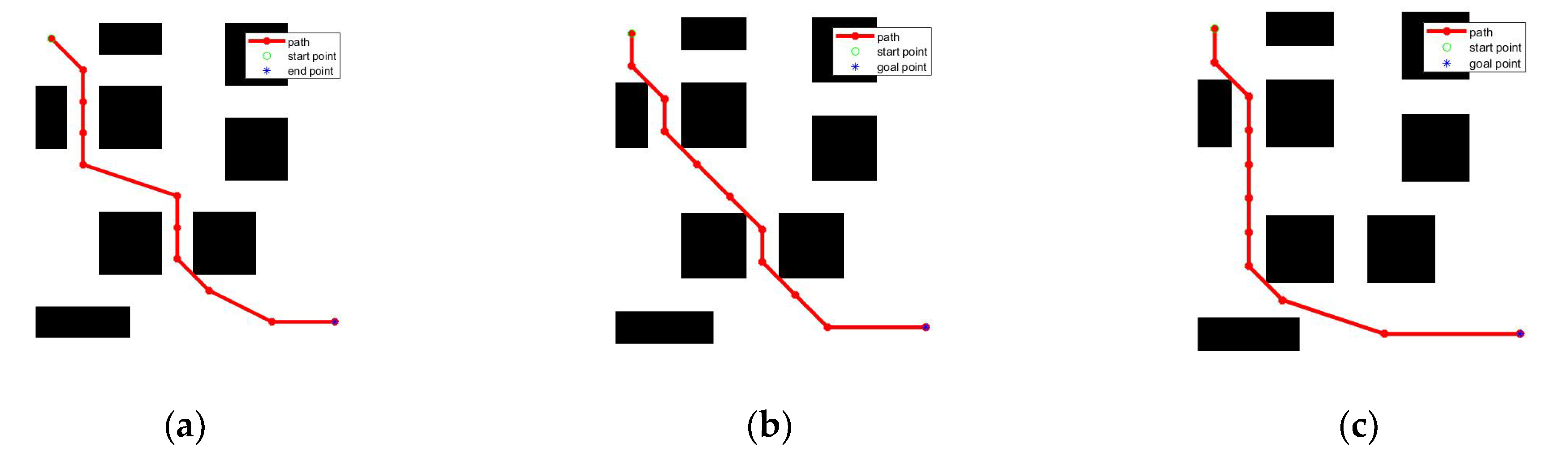
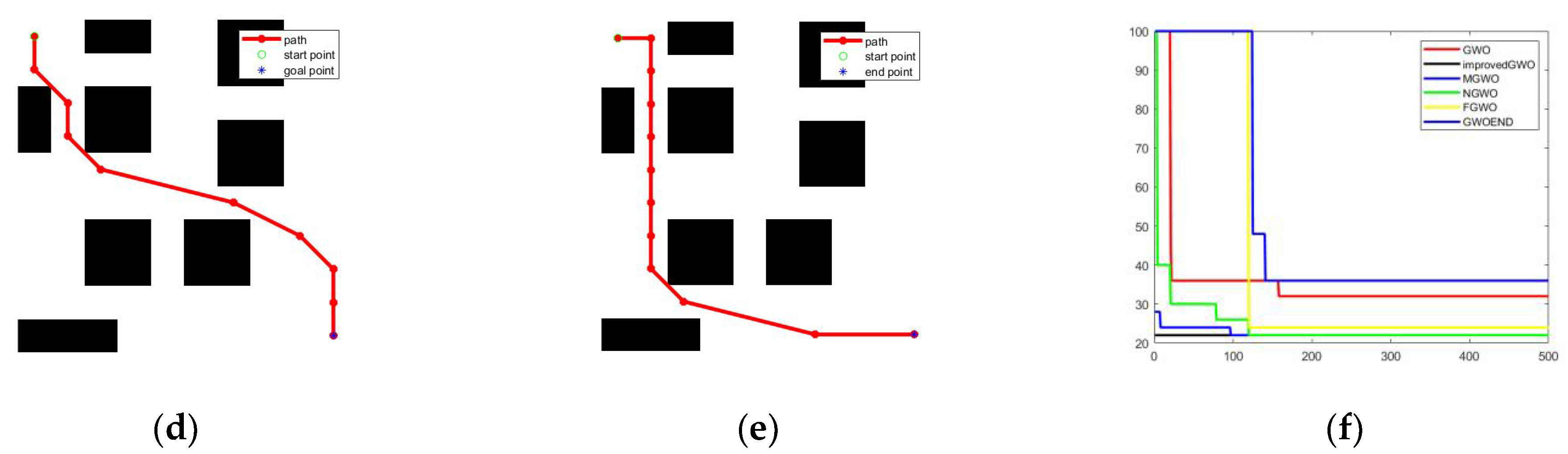
4.3. Path Planning Application
4.3.1. Problem Description
- Maximum cornering angle constraint
- 2.
- Threat area constraints
4.3.2. Path Planning
- Establish the search space according to the actual environment, and set the starting point and target point.
- Initialize the parameters of grey wolf algorithm, including the number of wolves, the maximum number of iterations, tent mapping parameters, and upper and lower bounds for parameter values.
- Initialize the grey wolf’s position and objective function according to the utilization mapping.
- Calculate each grey wolf’s fitness and select the top three grey wolves as wolf α, wolf β, and wolf w for the fitness ranking.
- Compare with the objective function to update the position and the objective function.
- Update the convergence factor at each iteration.
- Calculate the next position of other wolves according to the positions of wolf α, wolf β, and wolf w.
- Reach the maximum number of iterations and output the optimal path.
5. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zafar, M.N.; Mohanta, J.C. Methodology for path planning and optimization of mobile robots: A review. Procedia Comput. Sci. 2018, 133, 141–152. [Google Scholar] [CrossRef]
- Zhao, X. Mobile robot path planning based on an improved A* algorithm. Robot 2018, 40, 903–910. [Google Scholar]
- Chongqing, T.Z. Path planning of mobile robot with A* algorithm based on the artificial potential field. Comput. Sci. 2021, 48, 327–333. [Google Scholar]
- Eberhart, R.C. Guest editorial special issue on particle swarm optimization. IEEE Trans. Evol. Comput. 2004, 8, 201–203. [Google Scholar] [CrossRef]
- Zhangfang, H. Improved particle swarm optimization algorithm for mobile robot path planning. Comput. Appl. Res. 2021, 38, 3089–3092. [Google Scholar] [CrossRef]
- Wang, H. Robot Path Planning Based on Improved Adaptive Genetic Algorithm. Electro Optics & Control: 1–7. Available online: http://kns.cnki.net/kcms/detail/41.1227.TN.20220105.1448.015.html (accessed on 21 March 2022).
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef] [Green Version]
- Saxena, A.; Kumar, R.; Das, S. β-chaotic map-enabled grey wolf optimizer. Appl. Soft Comput. 2019, 75, 84–105. [Google Scholar] [CrossRef]
- Cai, J. Non-linear grey wolf optimization algorithm based on Tent mapping and elite Gauss perturbation. Comput. Eng. Des. 2022, 43, 186–195. [Google Scholar] [CrossRef]
- Zhang, Y. Modified grey wolf optimization algorithm for global optimization problems. J. Univ. Shanghai Sci. Techol. 2021, 43, 73–82. [Google Scholar] [CrossRef]
- Wang, M. Novel grey wolf optimization algorithm based on nonlinear convergence factor. Appl. Res. Comput. 2016, 33, 3648–3653. [Google Scholar]
- Rodríguez, L.; Castillo, O.; Soria, J.; Melin, P.; Valdez, F.; Gonzalez, C.I.; Martinez, G.E.; Soto, J. A fuzzy hierarchical operator in the grey wolf optimizer algorithm. Appl. Soft Comput. 2017, 57, 315–328. [Google Scholar] [CrossRef]
- Saremi, S.; Zahra, M.S.; Mohammad, M.S. Evolutionary population dynamics and grey wolf optimizer. Neural Comput. Appl. 2015, 26, 1257–1263. [Google Scholar] [CrossRef]
- Wang, Q. Improved grey wolf optimizer with convergence factor and proportion weight. Comput. Eng. Appl. 2019, 55, 60–65+98. [Google Scholar]
- Yue, Z.; Zhang, S.; Xiao, W. A novel hybrid algorithm based on grey wolf optimizer and fireworks algorithm. Sensors 2020, 20, 2147. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, S.; Yang, X.; Wang, X.; Qian, Z. A virtual force algorithm-lévy-embedded grey wolf optimization algorithm for wireless sensor network coverage optimization. Sensors 2019, 19, 2735. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mahdy, A.M.S.; Lotfy, K.; Hassan, W.; El-Bary, A.A. Analytical solution of magneto-photothermal theory during variable thermal conductivity of a semiconductor material due to pulse heat flux and volumetric heat source. Waves Random Complex Media 2021, 31, 2040–2057. [Google Scholar] [CrossRef]
- Khamis, A.K.; Lotfy, K.; El-Bary, A.A.; Mahdy, A.M.; Ahmed, M.H. Thermal-piezoelectric problem of a semiconductor medium during photo-thermal excitation. Waves Random Complex Media 2021, 31, 2499–2513. [Google Scholar] [CrossRef]
- Yin, L. Path Planning Combined with Improved Grey Wolf Optimization Algorithm and Artificial Potential Filed Method. Elector Measurement Technology: 1–11. Available online: https://kns.cnki.net/kcms/detail/detail.aspx?doi=10.19651/j.cnki.emt.2108659 (accessed on 21 March 2022).
- You, D. A path planning method for mobile robot based on improved grey wolf optimizer. Mach. Tool Hydraul. 2021, 49, 6. [Google Scholar]
- Kumar, R.; Singh, L.; Tiwari, R. Path planning for the autonomous robots using modified grey wolf optimization approach. J. Intell. Fuzzy Syst. 2021, 40, 9453–9470. [Google Scholar] [CrossRef]
- Ge, F.; Li, K.; Xu, W. Path planning of UAV for oilfield inspection based on improved grey wolf optimization algorithm. In Proceedings of the 2019 Chinese Control and Decision Conference (CCDC), Nanchang, China, 3–5 June 2019. [Google Scholar]
- Kumar, R.; Singh, L.; Tiwari, R. Comparison of two meta–heuristic algorithms for path planning in robotics. In Proceedings of the 2020 International Conference on Contemporary Computing and Applications (IC3A), Lucknow, India, 5–7 February 2020. [Google Scholar]
- Shrivastava, V.K.; Makhija, P.; Raj, R. Joint optimization of energy efficiency and scheduling strategies for side-link relay system. In Proceedings of the 2017 IEEE Wireless Communications and Networking Conference (WCNC), San Francisco, CA, USA, 19–22 March 2017. [Google Scholar]



| Parameter Symbols | Meaning | Take Value |
|---|---|---|
| N | Population size | 30 |
| Tmax | Maximum Iteration | 500 |
| a1 | Initial value of convergence factor | 2 |
| a2 | Final value of convergence factor | 0 |
| Function | Dim | Scope | Solution |
|---|---|---|---|
| 30 | [−100, 100] | 0 | |
| 30 | [−10, 10] | 0 | |
| 30 | [−100, 100] | 0 | |
| 30 | [−100, 100] | 0 | |
| 30 | [−30, 30] | 0 | |
| 30 | [−100, 100] | 0 | |
| 30 | [−1.28, 1.28] | 0 | |
| 30 | [−5.12, 5.12] | 0 | |
| 30 | [−32, 32] | 0 | |
| 30 | [−600, 600] | 0 | |
| 30 | [−50, 50] | 0.398 | |
| 30 | [−50, 50] | 3 | |
| 30 | [−10, 10] | 0 | |
| 30 | [−100, 100] | 0 | |
| 30 | [−15, 15] | 0 |
| Function | Algorithm | Average Value | Standard Deviation |
|---|---|---|---|
| f1 | GWO | 4.389 × 10−27 | 1.056 × 10−27 |
| Improved GWO | 0 | 0 | |
| MGWO | 5.996 × 10−199 | 0 | |
| NGWO | 9.939 × 10−49 | 4.754 × 10−48 | |
| GWO-fuzzy | 9.887 × 10−40 | 4.977 × 10−40 | |
| GWO-EPD | 1.501 × 10−31 | 2.289 × 10−30 | |
| f2 | GWO | 2.167 × 10−5 | 3.958 × 10−6 |
| Improved GWO | 0 | 0 | |
| MGWO | 1.617 × 10−102 | 2.154 × 10−102 | |
| NGWO | 2.133 × 10−26 | 1.143 × 10−26 | |
| GWO-fuzzy | 1.572 × 10−24 | 1.374 × 10−23 | |
| GWO-EPD | 1.893 × 10−19 | 2.358 × 10−20 | |
| f3 | GWO | 1.115 × 10−7 | 3.463 × 10−5 |
| Improved GWO | 0 | 0 | |
| MGWO | 6.982 × 10−166 | 0 | |
| NGWO | 1.015 × 10−33 | 3.789 × 10−31 | |
| GWO-fuzzy | 5.981 × 10−8 | 3.753 × 10−7 | |
| GWO-EPD | 4.505 × 10−8 | 2.456 × 10−6 | |
| f4 | GWO | 8.423 × 10−7 | 4.583 × 10−7 |
| Improved GWO | 0 | 0 | |
| MGWO | 5.368 × 10−90 | 9.664 × 10−89 | |
| NGWO | 4.414 × 10−20 | 1.104 × 10−19 | |
| GWO-fuzzy | 4.995 × 10−9 | 8.259 × 10−7 | |
| GWO-EPD | 3.395 × 10−7 | 7.652 × 10−6 | |
| f5 | GWO | 2.706 × 101 | 6.824 × 10−1 |
| Improved GWO | 2.867 × 101 | 2.611 × 10−2 | |
| MGWO | 2.761 × 101 | 3.917 × 10−1 | |
| NGWO | 2.719 × 101 | 5.836 × 10−1 | |
| GWO-fuzzy | 2.855 × 101 | 8.518 × 10−1 | |
| GWO-EPD | 2.818 × 101 | 8.075 × 10−1 | |
| f6 | GWO | 1.013 | 2.816 × 10−1 |
| Improved GWO | 6.533 × 10−1 | 2.860 × 10−1 | |
| MGWO | 5.261 | 6.381 × 10−1 | |
| NGWO | 1.829 | 3.763 × 10−1 | |
| GWO-fuzzy | 2.324 | 5.052 × 10−1 | |
| GWO-EPD | 1.238 | 4.725 × 10−1 | |
| f7 | GWO | 1.154 × 10−3 | 1.226 × 10−3 |
| Improved GWO | 2.961 × 10−7 | 2.373 × 10−7 | |
| MGWO | 1.914 × 10−4 | 1.369 × 10−4 | |
| NGWO | 1.347 × 10−3 | 2.747 × 10−4 | |
| GWO-fuzzy | 1.744 × 10−3 | 1.047 × 10−3 | |
| GWO-EPD | 1.646 × 10−3 | 1.031 × 10−3 | |
| f8 | GWO | 6.934 × 10−12 | 4.701 |
| Improved GWO | 0 | 0 | |
| MGWO | 0 | 0 | |
| NGWO | 5.684 × 10−14 | 2.017 × 10−1 | |
| GWO-fuzzy | 6.130 × 10−1 | 1.657 × 10−1 | |
| GWO-EPD | 1.715 × 10−13 | 3.852 | |
| f9 | GWO | 1.103 × 10−13 | 1.633 × 10−14 |
| Improved GWO | 8.811 × 10−16 | 1.164 × 10−16 | |
| MGWO | 4.440 × 10−15 | 6.486 × 10−15 | |
| NGWO | 2.930 × 10−14 | 2.420 × 10−15 | |
| GWO-fuzzy | 2.930 × 10−14 | 3.923 × 10−15 | |
| GWO-EPD | 4.352 × 10−14 | 6.4963 × 10−15 | |
| f10 | GWO | 7.558 × 10−3 | 1.412 × 10−2 |
| Improved GWO | 0 | 0 | |
| MGWO | 0 | 0 | |
| NGWO | 0 | 0 | |
| GWO-fuzzy | 7.2159 × 10−4 | 3.0047 × 10−3 | |
| GWO-EPD | 5.6751 × 10−3 | 5.7892 × 10−3 | |
| f11 | GWO | 3.8124 × 10−1 | 6.7824 × 10−2 |
| Improved GWO | 2.1331 × 10−3 | 6.8945 × 10−3 | |
| MGWO | 5.3122 × 10−1 | 3.1121 × 10−2 | |
| NGWO | 1.1021 × 101 | 3.0031 | |
| GWO-fuzzy | 1.3811 | 8.3221 | |
| GWO-EPD | 1.2254 × 10−2 | 4.2214 × 10−1 | |
| f12 | GWO | 7.3712 | 4.1077 × 10−1 |
| Improved GWO | 1.2922 × 10−2 | 7.6012 × 10−2 | |
| MGWO | 8.3211 | 3.2454 × 10−1 | |
| NGWO | 1.6722 × 101 | 3.1207 | |
| GWO-fuzzy | 6.1545 × 10−1 | 4.5512 | |
| GWO-EPD | 8.21475 × 102 | 8.1542 × 102 | |
| f13 | GWO | 4.5214 × 10−3 | 2.5784 × 10−3 |
| Improved GWO | 2.4457 × 10−6 | 6.3641 × 10−6 | |
| MGWO | 7.7541 × 10−5 | 8.2231 × 10−4 | |
| NGWO | 2.1441 × 101 | 8.1601 | |
| GWO-fuzzy | 1.2215 × 101 | 2.2232 × 101 | |
| GWO-EPD | 1.2014 × 10−2 | 1.2424 × 101 | |
| f14 | GWO | 1.4125 × 10−2 | 2.3622 × 10−3 |
| Improved GWO | 3.1337 × 10−3 | 1.1184 × 10−3 | |
| MGWO | 4.3221 × 10−3 | 1.4752 × 10−3 | |
| NGWO | 4.8842 × 10−1 | 2.4821 × 10−3 | |
| GWO-fuzzy | 1.3315 × 10−2 | 2.4774 × 10−1 | |
| GWO-EPD | 3.9454 × 10−1 | 1.7424 × 10−1 | |
| f15 | GWO | 1.2547 × 10−10 | 7.2242 × 10−11 |
| Improved GWO | 2.4467 × 10−13 | 1.0871 × 10−14 | |
| MGWO | 7.2101 × 10−4 | 7.9945 × 10−5 | |
| NGWO | 1.5547 × 101 | 9.0141 | |
| GWO-fuzzy | 2.4875 × 10−13 | 1.0401 × 101 | |
| GWO-EPD | 7.2154 × 102 | 9.4012 × 101 |
| Function | Algorithm | Average Value | Standard Deviation |
|---|---|---|---|
| f1 | Improved GWO | 0 | 0 |
| PSO | 3.125 × 10−2 | 2.716 × 10−2 | |
| SSA | 1.891 × 10−257 | 0 | |
| MA | 1.711 × 10−43 | 4.254 × 10−43 | |
| f2 | Improved GWO | 0 | 0 |
| PSO | 1.416 × 10−1 | 3.581−1 | |
| SSA | 1.435 × 10−93 | 8.487 × 10−93 | |
| MA | 2.255 × 102 | 8.183 × 102 | |
| f3 | Improved GWO | 0 | 0 |
| PSO | 7.225 × 10−2 | 5.331 × 10−1 | |
| SSA | 2.821 × 10−180 | 0 | |
| MA | 7.318 × 10−5 | 5149 × 10−4 | |
| f4 | Improved GWO | 0 | 0 |
| PSO | 9.225 × 10−2 | 1.153 × 10−1 | |
| SSA | 1.354 × 10−93 | 6.81 × 10−93 | |
| MA | 8.154 × 10−7 | 6.518 × 10−5 | |
| f5 | Improved GWO | 2.867 × 101 | 2.611 × 10−2 |
| PSO | 1.314 × 102 | 1.795 × 102 | |
| SSA | 2.327 × 10−3 | 2.189 × 10−3 | |
| MA | 4.501 × 10−1 | 5.587 × 10−1 | |
| f6 | Improved GWO | 6.533 | 2.801 × 10−1 |
| PSO | 8.792 × 105 | 9.782 × 105 | |
| SSA | 1.047 × 101 | 4.772 | |
| MA | 3.128 × 101 | 8.791 × 102 | |
| f7 | Improved GWO | 2.961 × 10−7 | 2.373 × 10−7 |
| PSO | 2.561 × 10−1 | 7.844 × 10−1 | |
| SSA | 1.144 × 10−4 | 3.581 × 10−3 | |
| MA | 3.254 × 10−2 | 4.358 × 10−1 | |
| f8 | Improved GWO | 0 | 0 |
| PSO | 3.015 | 2.641 | |
| SSA | 8.161 × 10−185 | 1.254 × 10−186 | |
| MA | 2.271 × 10−45 | 5.174 × 10−44 | |
| f9 | Improved GWO | 8.881 × 10−16 | 1.604 × 10−16 |
| PSO | 3.712 × 10−2 | 2.816 × 10−1 | |
| SSA | 8.881 × 10−16 | 0 | |
| MA | 4.213 × 10−10 | 1.576 × 10−9 | |
| f10 | Improved GWO | 0 | 0 |
| PSO | 5.001 × 10−3 | 2.655 × 10−1 | |
| SSA | 4.114 × 10−210 | 3.241 × 10−211 | |
| MA | 5.260 × 10−140 | 0 | |
| f11 | Improved GWO | 2.1331 × 10−3 | 6.8945 × 10−3 |
| PSO | 1.8741 | 4.4411 | |
| SSA | 1.496 × 10−2 | 2.106 × 10−2 | |
| MA | 2.714 × 10−1 | 1.954 × 10−17 | |
| f12 | Improved GWO | 1.292 × 10−2 | 7.6012 × 10−2 |
| PSO | 8.4152 | 8.3372 | |
| SSA | 7.346 × 10−1 | 1.355 × 10−2 | |
| MA | 8.214 | 1.245 × 10−2 | |
| f13 | Improved GWO | 2.4457 × 10−6 | 6.3641 × 10−6 |
| PSO | 1.052 × 102 | 1.2362 | |
| SSA | 1.232 × 10−3 | 1.571 × 10−4 | |
| MA | 3.247 × 10−3 | 5.014 × 10−3 | |
| f14 | Improved GWO | 3.1337 × 10−3 | 1.1184 × 10−3 |
| PSO | 3.958 × 10−1 | 1.541 × 10−2 | |
| SSA | 9.001 × 10−2 | 0 | |
| MA | 3.971 × 10−1 | 6.051 × 10−1 | |
| f15 | Improved GWO | 2.4467 × 10−13 | 1.0871 × 10−14 |
| PSO | 7.1522 | 9.142 × 101 | |
| SSA | 4.701 × 10−7 | 3.147 × 10−8 | |
| MA | 5.445 × 10−2 | 4.401 × 10−2 |
| Function | GWO | MGWO | NGWO | GWO-Fuzzy | GWO-EPD | SSA | MA | PSO | |
|---|---|---|---|---|---|---|---|---|---|
| f1 | P | 6.52 × 10−12 | 8.78 × 10−8 | 5.05 × 10−12 | 6.52 × 10−12 | 6.52 × 10−12 | 6.01 × 10−5 | 6.52 × 10−12 | 6.52 × 10−12 |
| R | + | + | + | + | + | + | + | + | |
| f2 | P | 2.07 × 10−11 | 1.40 × 10−11 | 2.07 × 10−11 | 2.07 × 10−11 | 2.07 × 10−11 | 2.07 × 10−11 | 2.07 × 10−11 | 2.07 × 10−11 |
| R | + | + | + | + | + | + | + | + | |
| f3 | P | 3.77 × 10−10 | 6.52 × 10−12 | 6.52 × 10−12 | 6.52 × 10−12 | 6.52 × 10−12 | 3.77 × 10−10 | 6.52 × 10−12 | 6.52 × 10−12 |
| R | + | + | + | + | + | + | + | + | |
| f4 | P | 6.52 × 10−12 | 5.05 × 10−11 | 6.52 × 10−12 | 6.52 × 10−12 | 6.52 × 10−12 | 3.77 × 10−11 | 6.52 × 10−12 | 6.52 × 10−12 |
| R | + | + | + | + | + | + | + | + | |
| f5 | P | 4.60 × 10−3 | 1.20 × 10−5 | 6.01 × 10−3 | 1.09 × 10−2 | 1.68 × 10−4 | 2.05 × 10−2 | 4.23 × 10−1 | 1.20 × 10−6 |
| R | + | + | + | + | + | - | - | + | |
| f6 | P | 2.07 × 10−11 | 1.41 × 10−11 | 2.07 × 10−11 | 2.07 × 10−11 | 2.07 × 10−11 | 2.07 × 10−11 | 2.07 × 10−11 | 2.07 × 10−11 |
| R | + | + | + | + | + | + | + | + | |
| f7 | P | 3.01 × 10−11 | 5.24 × 10−9 | 3.01 × 10−11 | 2.07 × 10−11 | 2.07 × 10−11 | 2.07 × 10−11 | 2.07 × 10−11 | 2.07 × 10−11 |
| R | + | + | + | + | + | + | + | + | |
| f8 | P | 6.52 × 10−12 | NaN | 6.52 × 10−12 | 6.52 × 10−12 | 6.52 × 10−12 | 2.07 × 10−11 | 6.52 × 10−12 | 6.52 × 10−12 |
| R | + | = | + | + | + | + | + | + | |
| f9 | P | 2.07 × 10−11 | 2.07 × 10−11 | 2.07 × 10−11 | 2.07 × 10−11 | 2.07 × 10−11 | 3.77 × 10−10 | 2.07 × 10−11 | 2.07 × 10−11 |
| R | + | + | + | + | + | + | + | + | |
| f10 | P | 6.52 × 10−12 | NaN | NaN | 6.52 × 10−12 | 6.52 × 10−12 | 2.07 × 10−11 | 2.07 × 10−11 | 6.52 × 10−12 |
| R | + | = | = | + | + | + | + | + | |
| f11 | P | 6.52 × 10−12 | 2.07 × 10−11 | 2.07 × 10−11 | 2.07 × 10−11 | 6.52 × 10−12 | 2.07 × 10−11 | 2.07 × 10−11 | 6.52 × 10−12 |
| R | + | + | + | + | + | + | + | + | |
| f12 | P | 6.52 × 10−12 | 2.07 × 10−11 | 2.07 × 10−11 | 2.07 × 10−11 | 6.52 × 10−12 | 2.07 × 10−11 | 2.07 × 10−11 | 6.52 × 10−12 |
| R | + | + | + | + | + | + | + | + | |
| f13 | P | 6.52 × 10−12 | 1.20e−06 | 6.52 × 10−12 | 6.52 × 10−12 | 2.07 × 10−11 | 2.07 × 10−11 | 2.07 × 10−11 | 6.52 × 10−12 |
| R | + | + | + | + | + | + | + | + | |
| f14 | P | 6.52 × 10−12 | 2.07 × 10−11 | 2.07 × 10−11 | 2.07 × 10−11 | 2.07 × 10−11 | 2.07 × 10−11 | 2.07 × 10−11 | 6.52 × 10−12 |
| R | + | + | + | + | + | + | + | + | |
| f15 | P | 2.07 × 10−11 | 6.52 × 10−12 | 6.52 × 10−12 | 2.07 × 10−11 | 6.52 × 10−12 | 6.52 × 10−12 | 6.52 × 10−12 | 6.52 × 10−12 |
| R | + | + | + | + | + | + | + | + | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hou, Y.; Gao, H.; Wang, Z.; Du, C. Improved Grey Wolf Optimization Algorithm and Application. Sensors 2022, 22, 3810. https://doi.org/10.3390/s22103810
Hou Y, Gao H, Wang Z, Du C. Improved Grey Wolf Optimization Algorithm and Application. Sensors. 2022; 22(10):3810. https://doi.org/10.3390/s22103810
Chicago/Turabian StyleHou, Yuxiang, Huanbing Gao, Zijian Wang, and Chuansheng Du. 2022. "Improved Grey Wolf Optimization Algorithm and Application" Sensors 22, no. 10: 3810. https://doi.org/10.3390/s22103810
APA StyleHou, Y., Gao, H., Wang, Z., & Du, C. (2022). Improved Grey Wolf Optimization Algorithm and Application. Sensors, 22(10), 3810. https://doi.org/10.3390/s22103810





