Discovering Stick-Slip-Resistant Servo Control Algorithm Using Genetic Programming
Abstract
1. Introduction
2. Materials and Methods
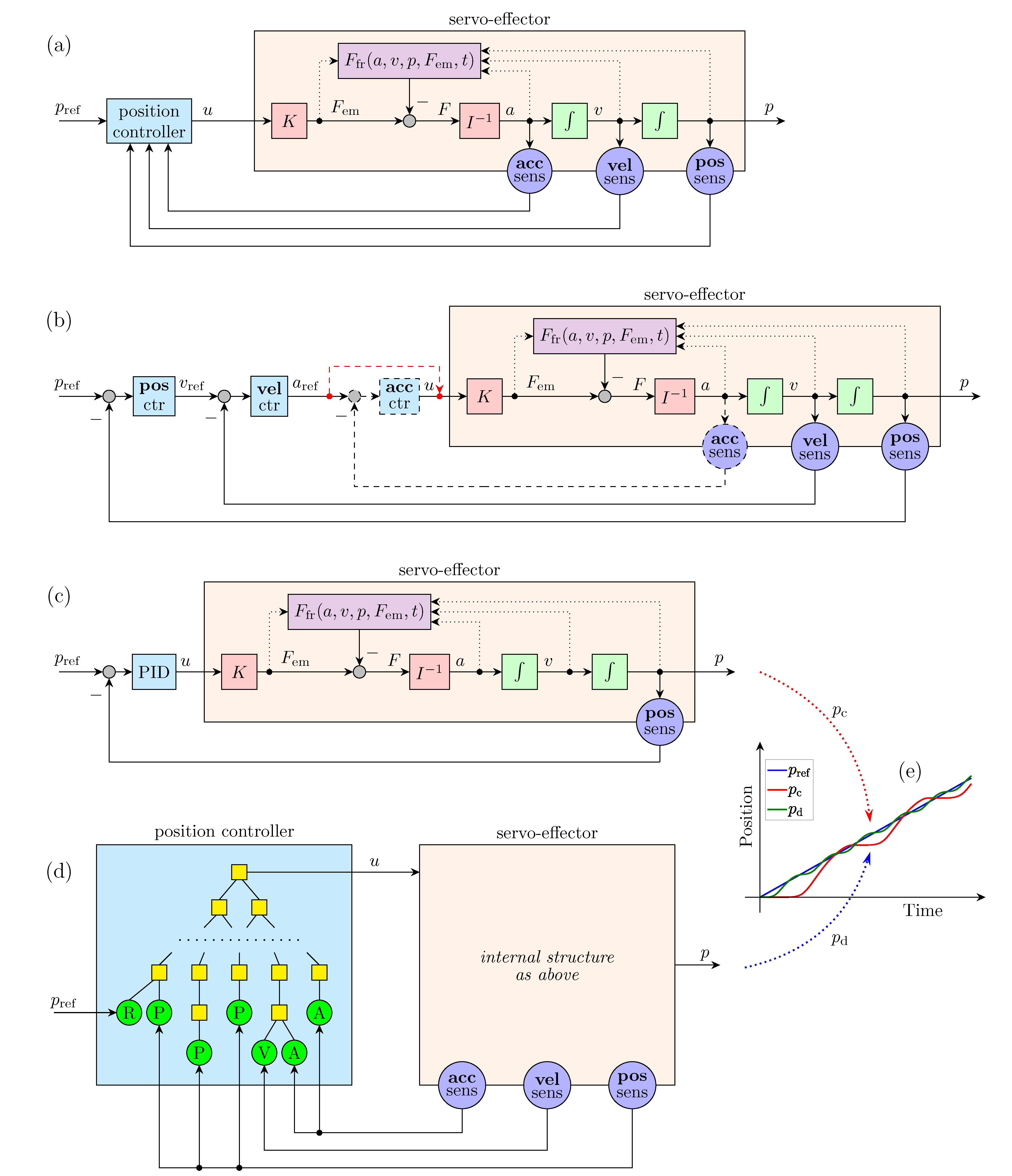
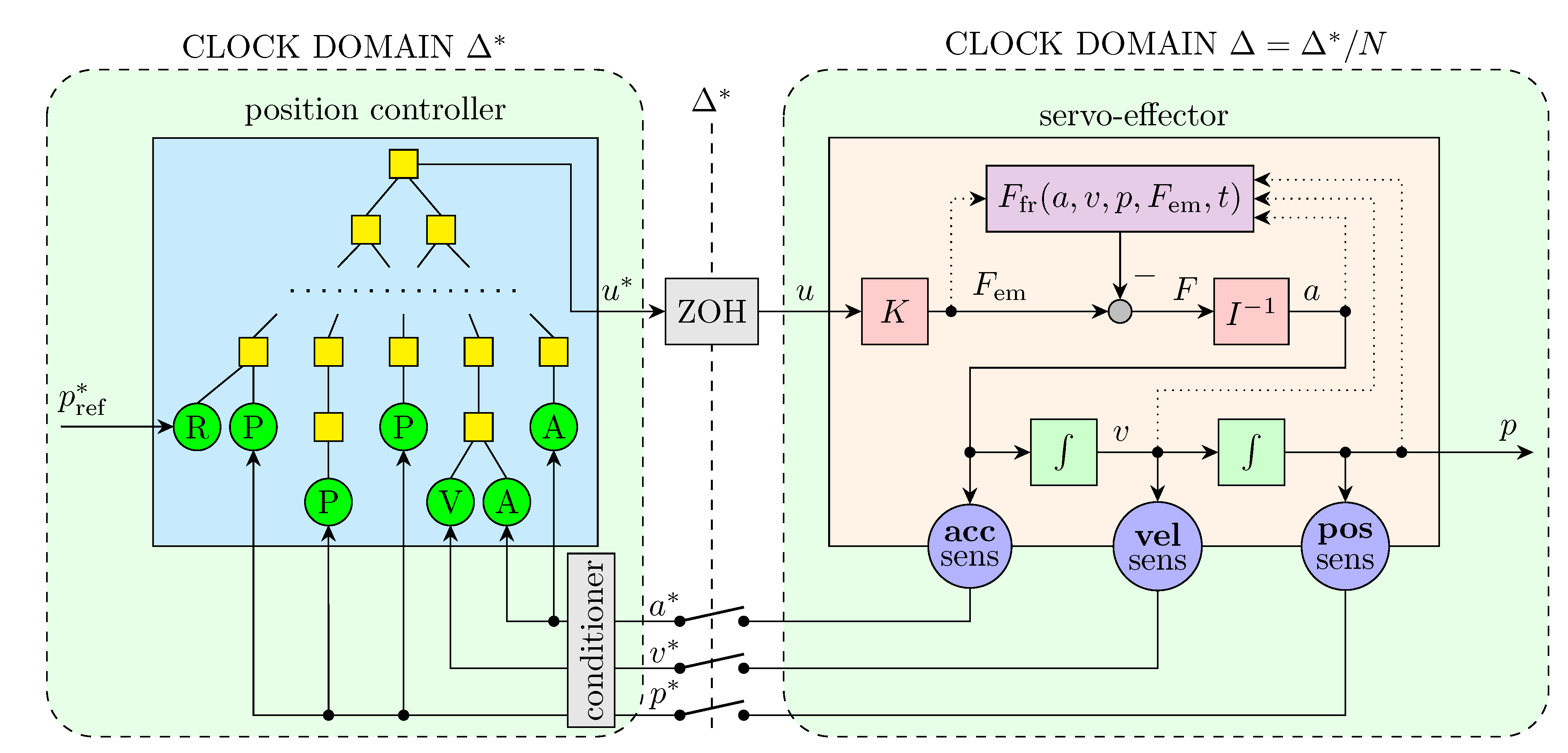
2.1. Structure of an Experimental Simulation System
2.2. Friction Model
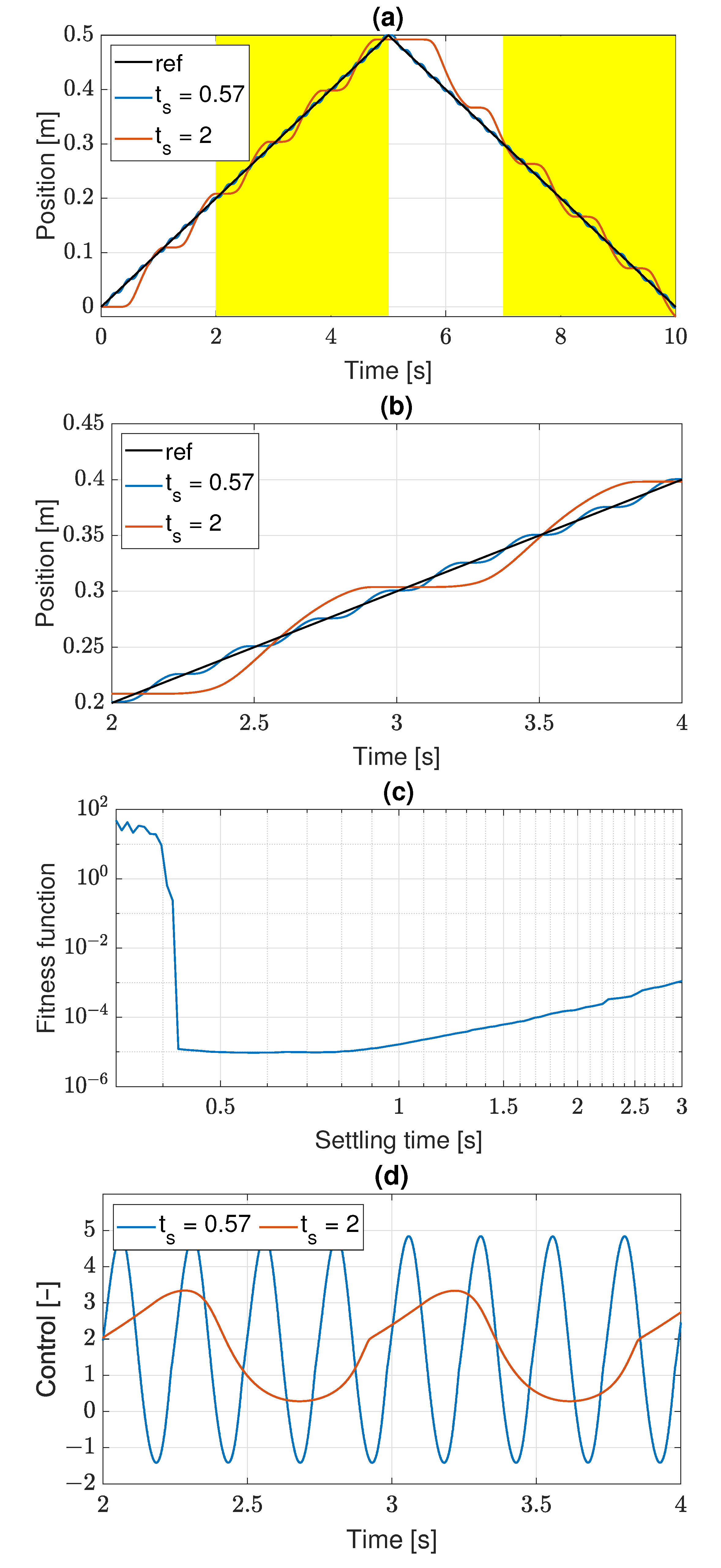
2.3. Learning Trajectory and Fitness Function
2.4. Fitness of the PID Algorithm
2.5. Implementation and Configuration of the Genetic Programming Process
3. Results
3.1. Unconstrained Bang-Bang Control Algorithms
3.2. Control Algorithms for Servo with Ideal Measurement
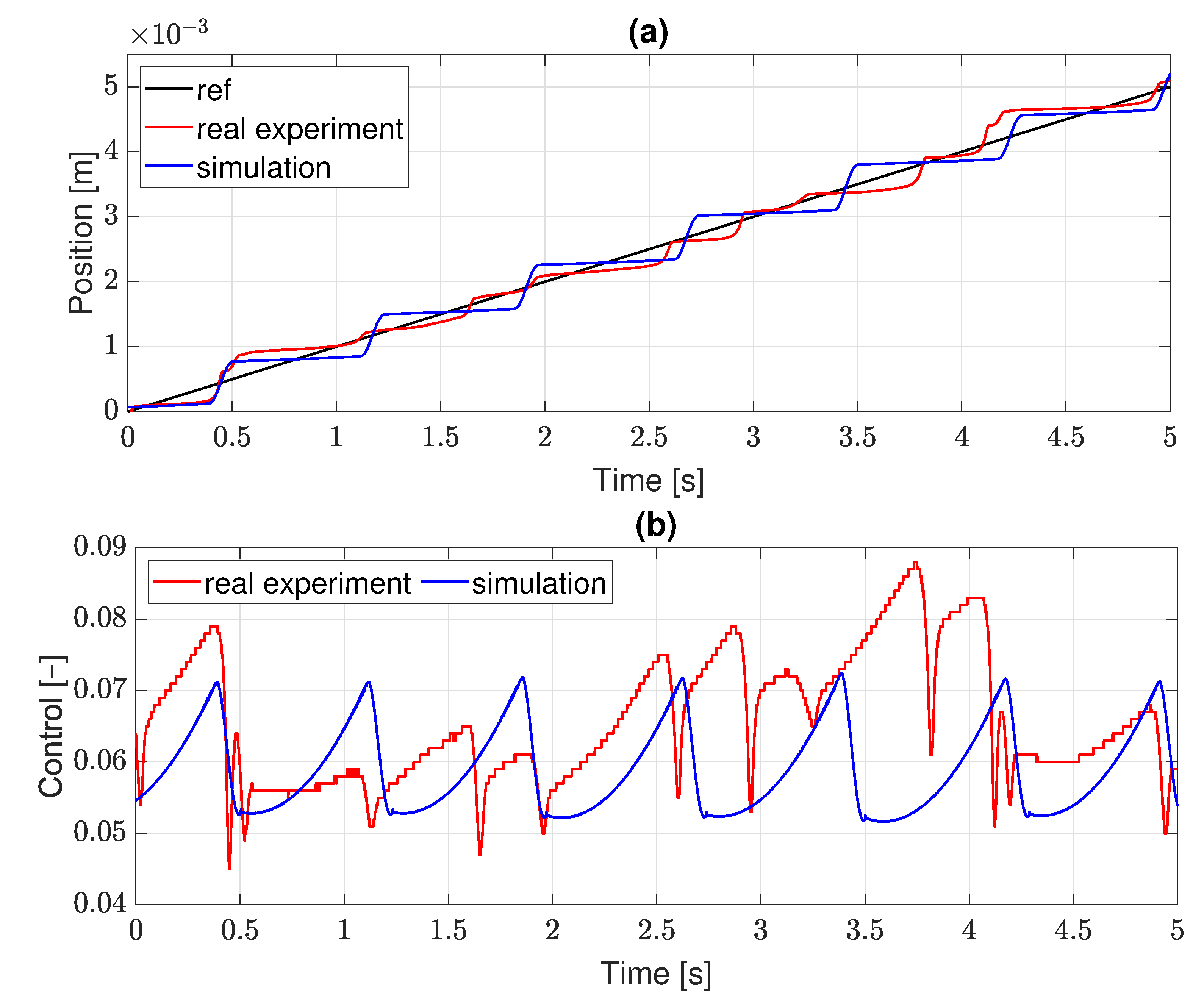
3.3. Control Algorithms for Servo with Real Position Sensor
4. Discussion
5. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| GP | Genetic Programming |
| ECJ | Evolutionary Computation [research system written in] Java |
References
- Koza, J.R. Genetic Programming: On the Programming of Computers by Means of Natural Selection; MIT Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Niranjan, P.; Karinka, S.; Sairam, K.V.S.S.S.S.; Upadhya, A.; Shetty, S. Friction modeling in servo machines: A review. Int. J. Dyn. Control 2017, 6, 893–906. [Google Scholar] [CrossRef]
- Dahl, P.R. A Solid Friction Model. TOR 158 (3107-18). The Aerospace Corporation. El Segundo 1968. Available online: https://www.academia.edu/41171280/_A_Solid_Friction_Model_THE_AEROSPACE_CORPORATION_APPROVED_FOR_PUBLIC_RELEASE_Reproduced_From_Best_Available_Copy (accessed on 21 November 2021).
- Stribeck, R. Die wesentlichen Eigenschaften der Gleit- und Rollenlager—The key qualities of sliding and roller bearings. Z. Des. Vereins Dtsch. Ingenieure 1902, 46, 1432–1437. [Google Scholar]
- Marton, L.; Lantos, B. Modeling, Identification, and Compensation of Stick-Slip Friction. IEEE Trans. Ind. Electron. 2007, 54, 511–521. [Google Scholar] [CrossRef]
- Jeon, J.Y.; Lee, S.W.; Chae, H.K.; Kim, J.H. Low velocity friction identification and compensation using accelerated evolutionary programming. In Proceedings of the IEEE International Conference on Evolutionary Computation, IEEE, Nayoya, Japan, 20–22 May 1996. [Google Scholar] [CrossRef]
- Astrom, K.J.; de Wit, C.C. Revisiting the LuGre friction model. IEEE Control Syst. 2008, 28, 101–114. [Google Scholar] [CrossRef]
- Chen, Q.; Tao, L.; Nan, Y.; Ren, X. Adaptive Nonlinear Sliding Mode Control of Mechanical Servo System with LuGre Friction Compensation. J. Dyn. Syst. Meas. Control 2015, 138, 021003. [Google Scholar] [CrossRef]
- de Wit, C.C.; Olsson, H.; Astrom, K.J.; Lischinsky, P. A new model for control of systems with friction. IEEE Trans. Autom. Control 1995, 40, 419–425. [Google Scholar] [CrossRef]
- Kim, S. Moment of Inertia and Friction Torque Coefficient Identification in a Servo Drive System. IEEE Trans. Ind. Electron. 2019, 66, 60–70. [Google Scholar] [CrossRef]
- Liu, L.; Wu, Z. Comprehensive parameter identification of feed servo systems with friction based on responses of the worktable. Mech. Syst. Signal Process. 2015, 64–65, 257–265. [Google Scholar] [CrossRef]
- Dumanli, A.; Sencer, B. Pre-compensation of servo tracking errors through data-based reference trajectory modification. CIRP Ann. 2019, 68, 397–400. [Google Scholar] [CrossRef]
- Li, K.; Zhang, Y.; Wei, S.; Yue, H. Evolutionary Algorithm-Based Friction Feedforward Compensation for a Pneumatic Rotary Actuator Servo System. Appl. Sci. 2018, 8, 1623. [Google Scholar] [CrossRef]
- Lu, Y.; Yan, D.; Levy, D. Friction coefficient estimation in servo systems using neural dynamic programming inspired particle swarm search. Appl. Intell. 2015, 43, 1–14. [Google Scholar] [CrossRef]
- Wang, S.; Na, J. Parameter Estimation and Adaptive Control for Servo Mechanisms With Friction Compensation. IEEE Trans. Ind. Inform. 2020, 16, 6816–6825. [Google Scholar] [CrossRef]
- Maeda, Y.; Harata, K.; Iwasaki, M. A Friction Model-Based Frequency Response Analysis for Frictional Servo Systems. IEEE Trans. Ind. Inform. 2018, 14, 5146–5155. [Google Scholar] [CrossRef]
- Dumanli, A.; Sencer, B. Optimal high-bandwidth control of ball-screw drives with acceleration and jerk feedback. Precis. Eng. 2018, 54, 254–268. [Google Scholar] [CrossRef]
- Cao, F. PID controller optimized by genetic algorithm for direct-drive servo system. Neural Comput. Appl. 2018, 32, 23–30. [Google Scholar] [CrossRef]
- Jaen-Cuellar, A.Y.; de J. Romero-Troncoso, R.; Morales-Velazquez, L.; Osornio-Rios, R.A. PID-Controller Tuning Optimization with Genetic Algorithms in Servo Systems. Int. J. Adv. Robot. Syst. 2013, 10, 324. [Google Scholar] [CrossRef]
- Wang, S. Asymptotic Tracking Control for Nonaffine Systems with Disturbances. In IEEE Transactions on Circuits and Systems II: Express Briefs; IEEE Press: Piscataway, NJ, USA, 2021; p. 1. [Google Scholar] [CrossRef]
- Sharma, S.; Tambe, S.S. Soft-sensor development for biochemical systems using genetic programming. Biochem. Eng. J. 2014, 85, 89–100. [Google Scholar] [CrossRef]
- Chion, C.; Landry, J.A.; Costa, L.D. A Genetic-Programming-Based Method for Hyperspectral Data Information Extraction: Agricultural Applications. IEEE Trans. Geosci. Remote Sens. 2008, 46, 2446–2457. [Google Scholar] [CrossRef]
- Santos, J.A.; Faria, F.; Calumby, R.; da S. Torres, R.; Lamparelli, R.A.C. A Genetic Programming approach for coffee crop recognition. In Proceedings of the 2010 IEEE International Geoscience and Remote Sensing Symposium, IEEE, Honolulu, HI, USA, 25–30 July 2010. [Google Scholar] [CrossRef]
- Ciglarič, I.; Kidrič, A. Computer-aided derivation of the optimal mathematical models to study gear-pair dynamic by using genetic programming. Struct. Multidiscip. Optim. 2006, 32, 153–160. [Google Scholar] [CrossRef]
- Behbahani, S.; de Silva, C.W. Automated Identification of a Mechatronic System Model Using Genetic Programming and Bond Graphs. J. Dyn. Syst. Meas. Control 2013, 135, 051007. [Google Scholar] [CrossRef]
- Romero, J.; Santos, A.; Carballal, A.; Rodriguez-Fernandez, N.; Santos, I.; Torrente-Patiño, A.; Tuñas, J.; Machado, P. A Genetic Programming-Based Low-Level Instructions Robot for Realtimebattle. Entropy 2020, 22, 1362. [Google Scholar] [CrossRef]
- Schmidt, P.B.; Lorenz, R.D. Design principles and implementation of acceleration feedback to improve performance of DC drives. IEEE Trans. Ind. Appl. 1992, 28, 594–599. [Google Scholar] [CrossRef]
- Butler, H. Acceleration feedback in a lithographic tool. Control Eng. Pract. 2012, 20, 453–464. [Google Scholar] [CrossRef]
- Ding, F.; Luo, X.; Cai, Y.; Chang, W. Acceleration feedback control for enhancing dynamic stiffness of fast tool servo system considering the sensor imperfections. Mech. Syst. Signal Process. 2020, 141, 106429. [Google Scholar] [CrossRef]
- Żabiński, T.; Trybus, L. Tuning P-PI and PI-PI controllers for electrical servos. Bull. Pol. Acad. Sciences. Tech. Sci. 2010, 58, 51–58. [Google Scholar] [CrossRef][Green Version]
- Karnopp, D. Computer Simulation of Stick-Slip Friction in Mechanical Dynamic Systems. J. Dyn. Syst. Meas. Control 1985, 107, 100–103. [Google Scholar] [CrossRef]
- Xia, H.; Han, L.; Pan, C.; Jia, H.; Yu, L. Simulation of Motion Interactions of a 2-DOF Linear Piezoelectric Impact Drive Mechanism with a Single Friction Interface. Appl. Sci. 2018, 8, 1400. [Google Scholar] [CrossRef]
- Luke, S. The ECJ Owner’s Manual. A User Manual for the ECJ Evolutionary Computation Library. Version 27; George Mason University: Fairfax, VA, USA, 2019. [Google Scholar]
- Luke, S.; Panait, L. A Survey and Comparison of Tree Generation Algorithms. In Proceedings of the Genetic and Evolutionary Computation Conference (GECCO-2001), San Francisco, CA, USA, 7–11 July 2001. [Google Scholar]
- Merry, R.J.E.; van de Molengraft, M.J.G.; Steinbuch, M. Velocity and acceleration estimation for optical incremental encoders. Mechatronics 2010, 20, 20–26. [Google Scholar] [CrossRef]
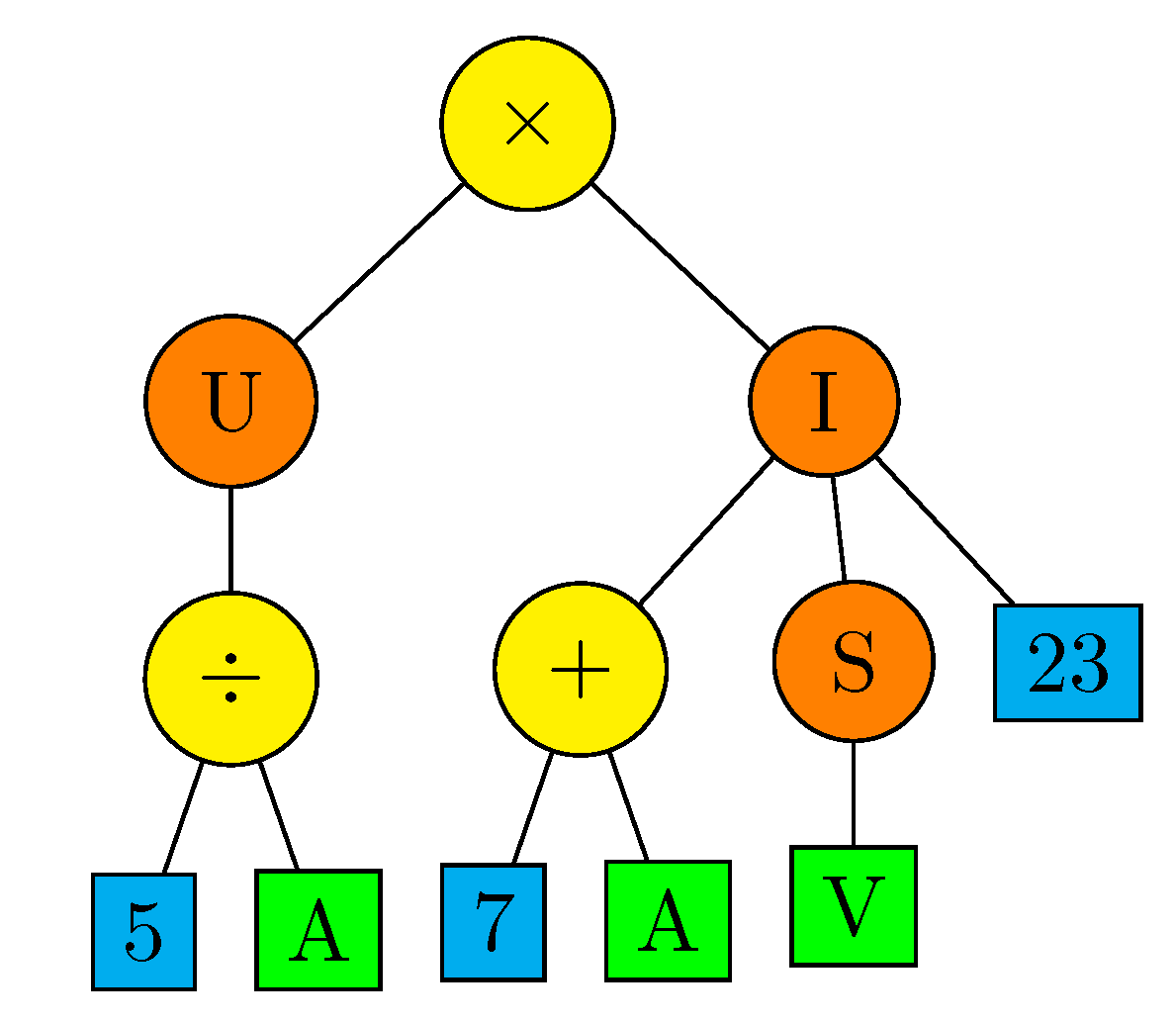
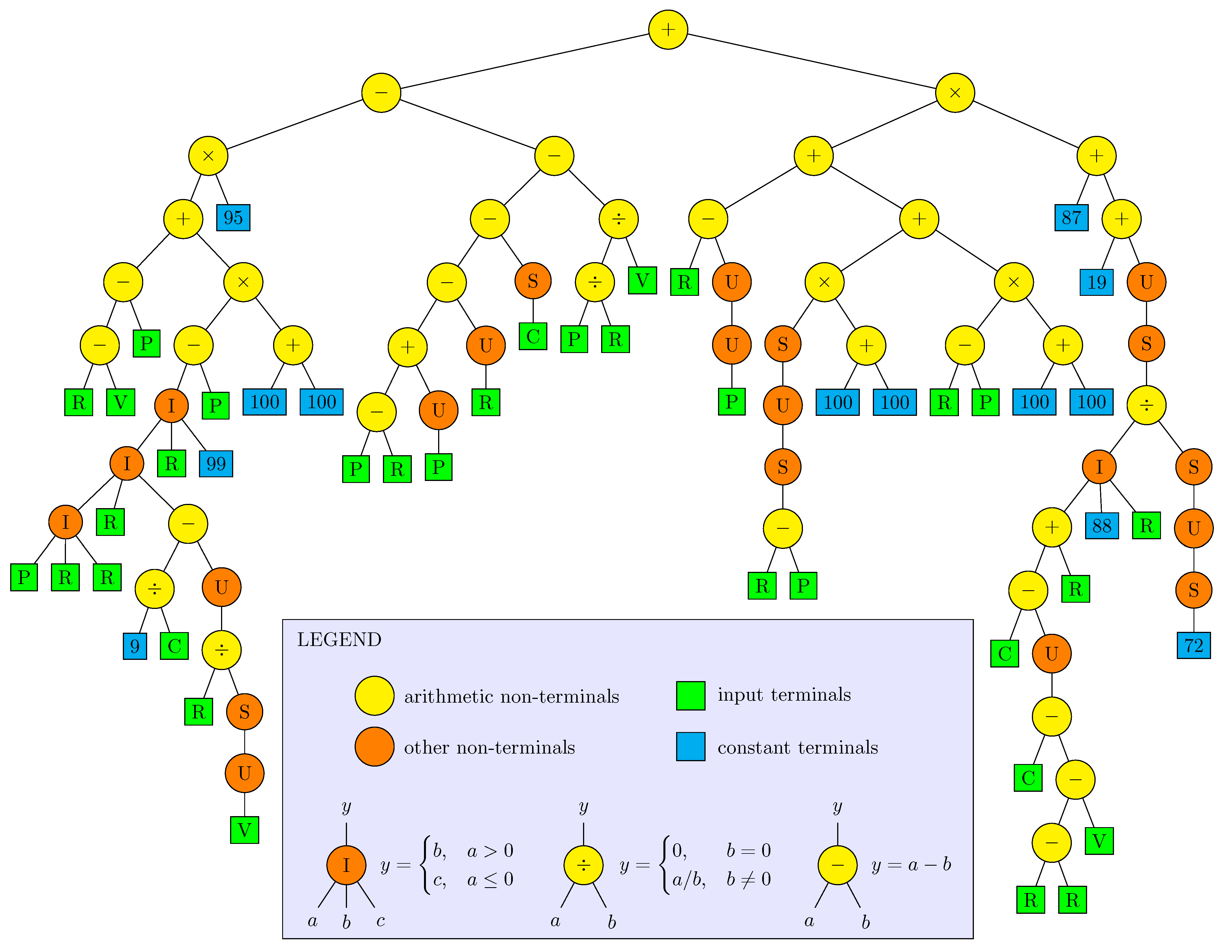
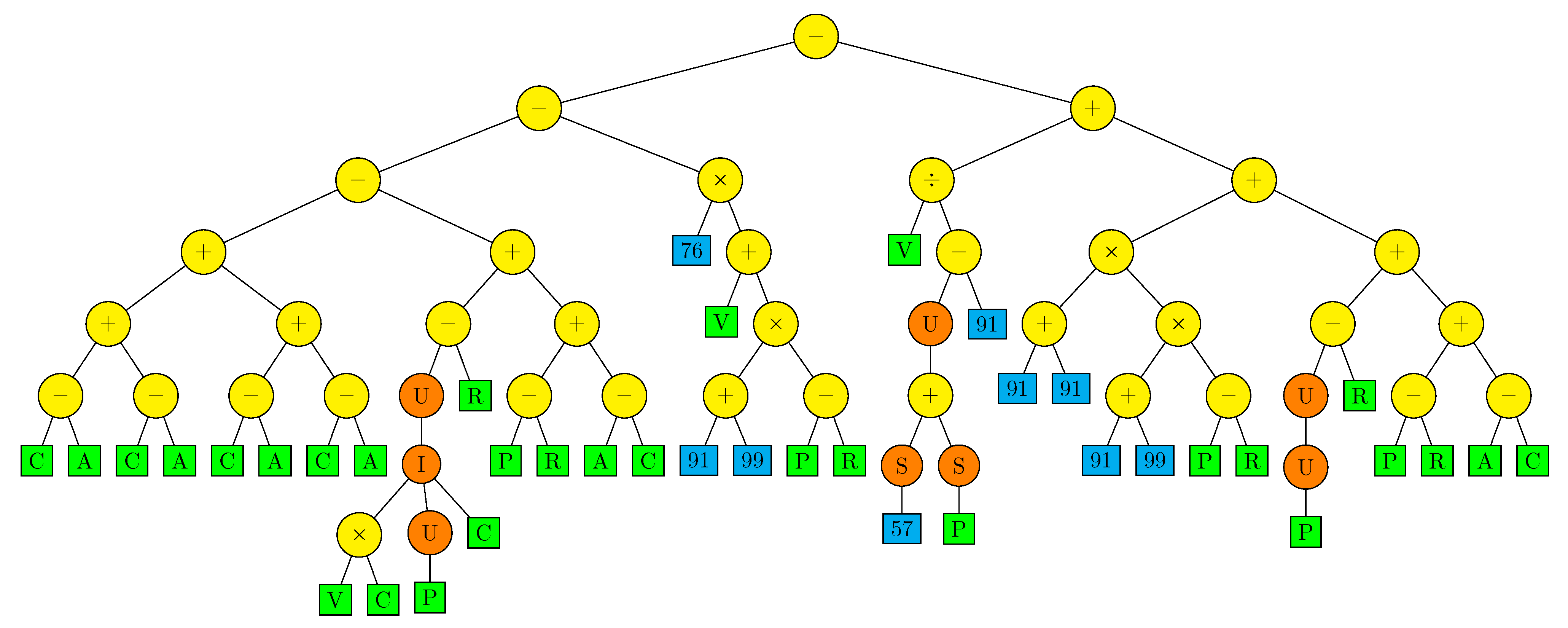
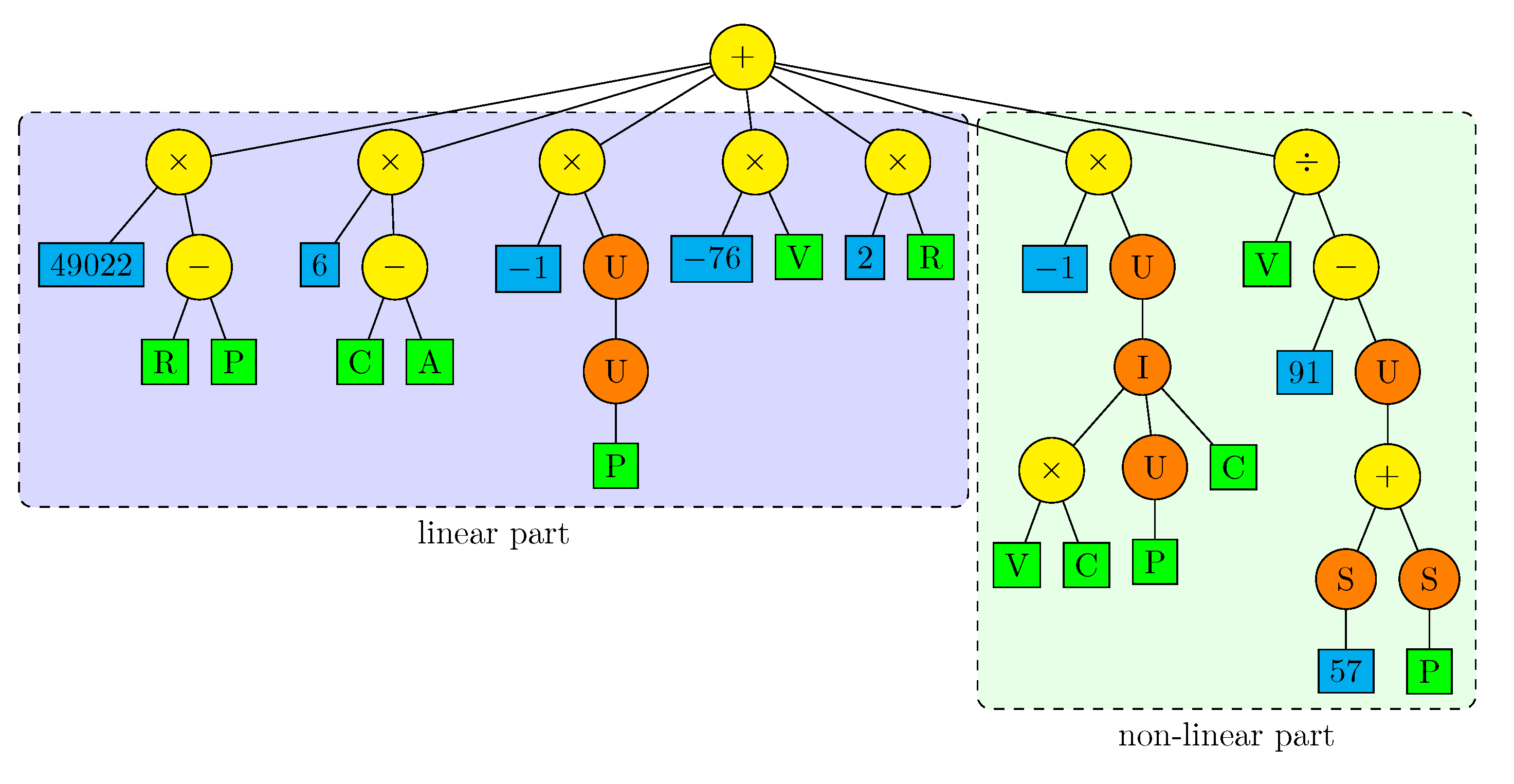
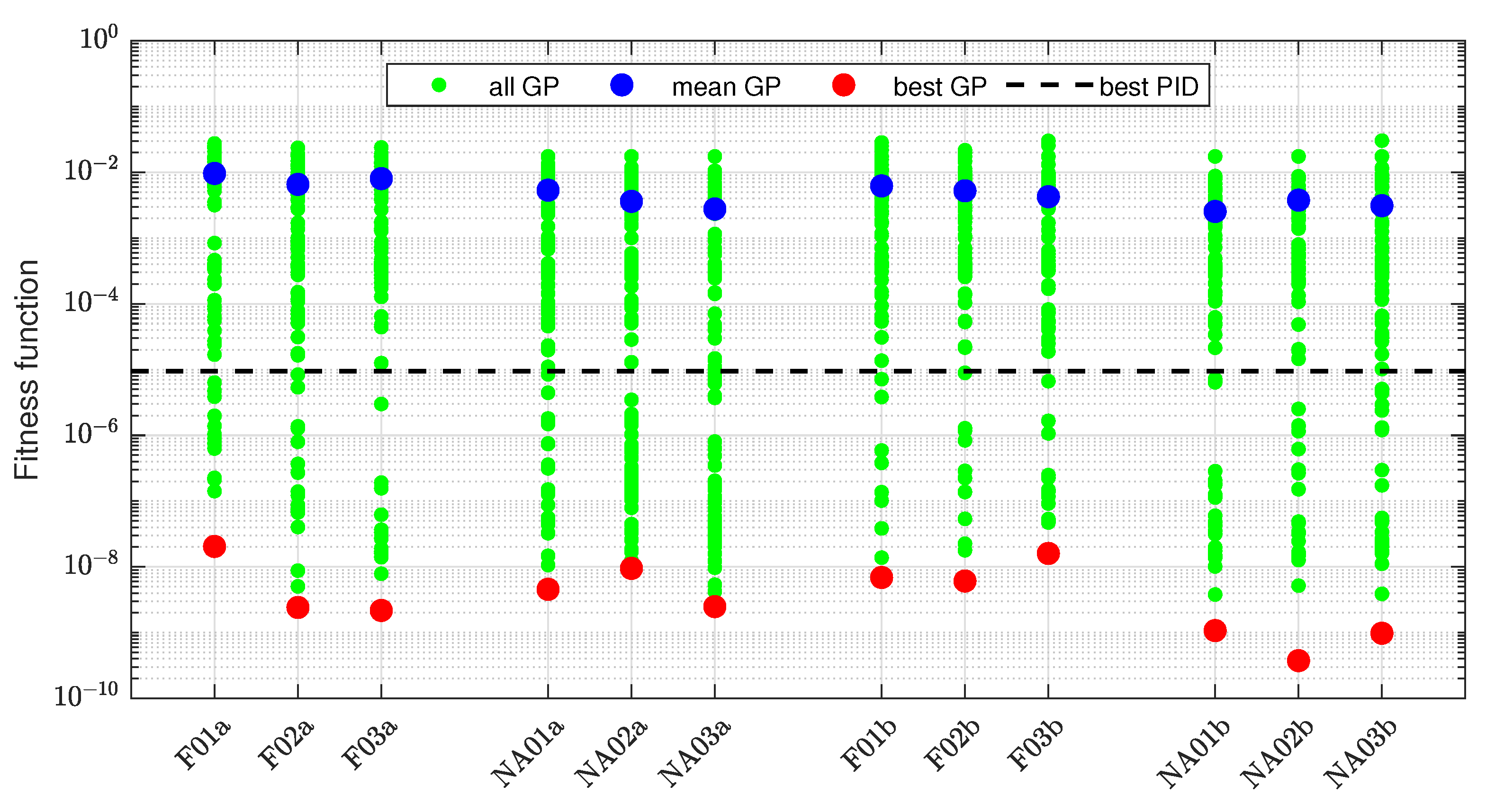
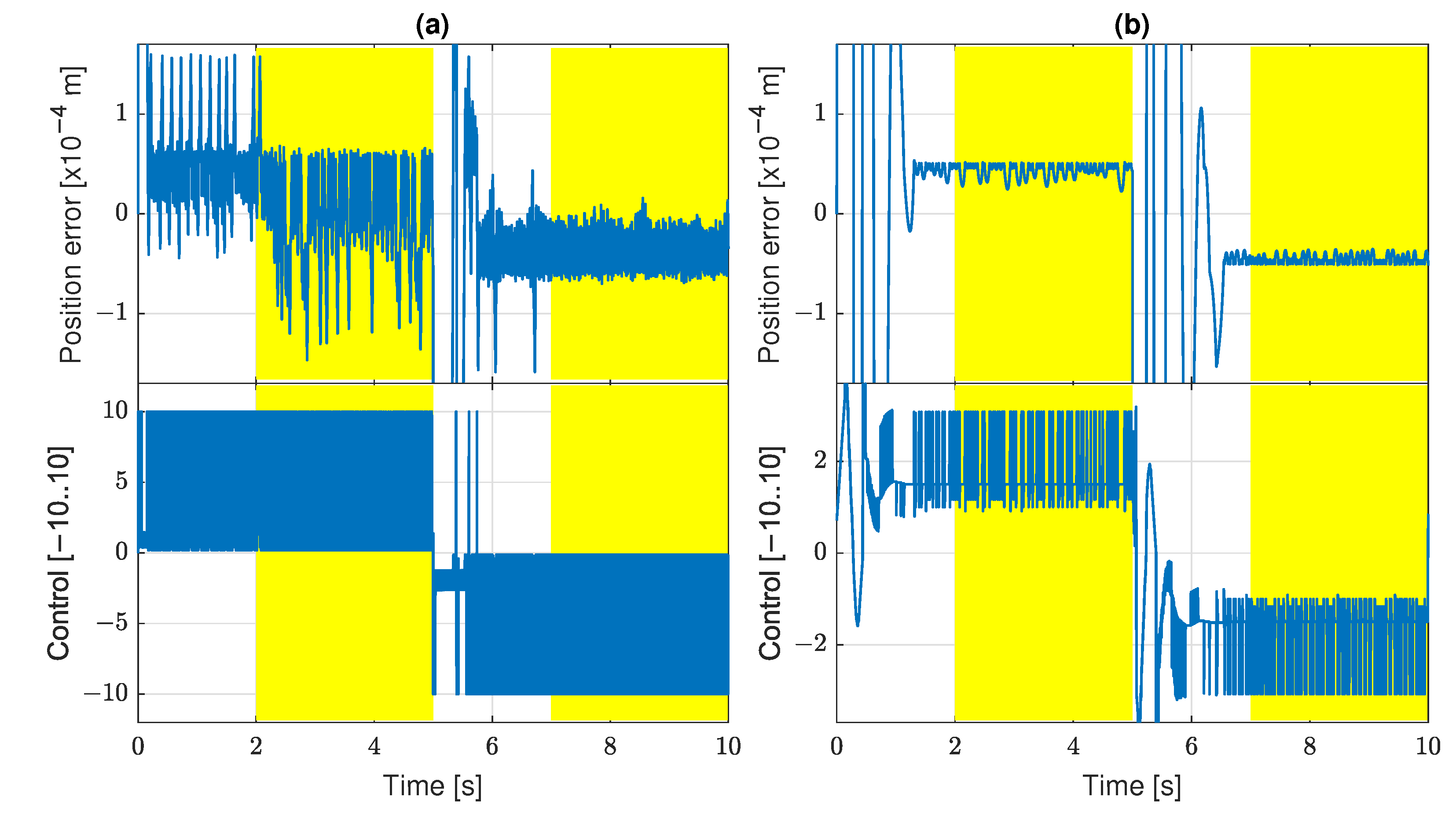
| Symbol | Arity | Operation | Explanation |
|---|---|---|---|
| + | 2 | arithmetic addition | |
| − | 2 | arithmetic subtraction | |
| * | 2 | arithmetic multiplication | |
| ÷ | 2 | safe arithmetic division | |
| I | 3 | if-else expression | |
| S | 1 | sin function | |
| U | 1 | unit delay | |
| 0 | integer constant | randomly initialized and mutated | |
| R | 0 | reference position | from trajectory generator |
| C | 0 | control signal | from previous control cycle |
| P | 0 | actual position | from position sensor |
| V | 0 | actual velocity | from velocity sensor (or estimator) |
| A | 0 | actual acceleration | from acceleration sensor (or estimator) |
| Parameter | Setting |
|---|---|
| Initial population | ramped half-and-half (2:6) algorithm |
| Breeding pipelines | reproduction, crossover, mutation |
| Reproduction probability | 0.1 |
| Crossover probability | 0.9 |
| Mutation probability | 0.1, 0.2, 0.3 |
| Selection method | tournament without elitism |
| Tournament size | 7 |
| Size of population | 1000 |
| Number of generations | 500 |
| Mutation Probability | Full Input | No Acc | No Vel | No Acc, No Vel | No Acc, No Vel, No Ctr |
|---|---|---|---|---|---|
| 0.1 | F01 | NA01 | NV01 | NAV01 | NAVC01 |
| 0.2 | F02 | NA02 | NV02 | NAV02 | NAVC02 |
| 0.3 | F03 | NA03 | NV03 | NAV03 | NAVC03 |
| No. | Parameter | F01 | F02 | F03 | NA01 | NA02 | NA03 | NV01 | NV02 | NV03 | NAV01 | NAV02 | NAV03 | NAVC01 | NAVC02 | NAVC03 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 44 | 30 | 30 | 28 | 19 | 13 | 16 | 31 | 22 | 5 | 9 | 5 | ||||
| 2 | 27 | 29 | 30 | 27 | 24 | 31 | 24 | 16 | 20 | 14 | 11 | 11 | 4 | 2 | ||
| 3 | 13 | 18 | 15 | 19 | 14 | 15 | 32 | 28 | 29 | 66 | 68 | 63 | 93 | 97 | 94 | |
| 4 | 2 | 5 | 1 | 2 | 5 | 8 | 12 | 7 | 9 | 6 | 4 | 4 | 2 | |||
| 5 | 2 | 2 | 3 | 1 | 7 | 6 | 5 | 9 | 6 | 5 | 5 | 11 | 1 | 1 | ||
| 6 | 2 | 3 | 6 | 5 | 7 | 3 | 9 | 5 | 6 | 4 | 1 | 2 | 2 | 3 | 1 | |
| 7 | 6 | 6 | 8 | 7 | 9 | 12 | 1 | 1 | 2 | 2 | ||||||
| 8 | 1 | 1 | 1 | 3 | 8 | 7 | 1 | 2 | 2 | |||||||
| 9 | 1 | 1 | 1 | 1 | 2 | 1 | 2 | 2 | ||||||||
| 10 | 2 | 2 | 1 | 1 | 1 | 1 | ||||||||||
| 11 | 1 | 1 | 1 | 1 | ||||||||||||
| 12 | 1 | |||||||||||||||
| 13 | 2 | 1 | ||||||||||||||
| 14 | 1 | 2 | ||||||||||||||
| 15 | 1 | 1 | 1 | |||||||||||||
| 16 | 1 | 1 | ||||||||||||||
| 17 | 1 | 1 | 1 | |||||||||||||
| 18 | 1 | 1 | 2 | |||||||||||||
| 19 | 1 | |||||||||||||||
| 20 | 1 | |||||||||||||||
| 21 | 14 | 18 | 24 | 24 | 38 | 33 | 16 | 18 | 20 | 9 | 8 | 17 | 3 | 3 | 2 | |
| 22 | ||||||||||||||||
| 23 |
| No. | Parameter | F01a | F02a | F03a | NA01a | NA02a | NA03a | F01b | F02b | F03b | NA01b | NA02b | NA03b |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 48 | 32 | 43 | 24 | 14 | 9 | 24 | 17 | 5 | 5 | 11 | 8 | |
| 2 | 15 | 21 | 14 | 22 | 30 | 20 | 41 | 41 | 56 | 33 | 38 | 32 | |
| 3 | 15 | 24 | 24 | 23 | 16 | 17 | 21 | 25 | 15 | 31 | 25 | 21 | |
| 4 | 8 | 7 | 4 | 10 | 7 | 8 | 5 | 5 | 10 | 8 | 5 | 11 | |
| 5 | 6 | 4 | 1 | 4 | 5 | 7 | 2 | 3 | 3 | 3 | 4 | 7 | |
| 6 | 7 | 5 | 2 | 7 | 17 | 12 | 4 | 5 | 5 | 7 | 5 | 2 | |
| 7 | 1 | 4 | 10 | 9 | 9 | 23 | 2 | 3 | 6 | 11 | 10 | 17 | |
| 8 | 3 | 2 | 1 | 2 | 4 | 1 | 1 | 2 | 1 | 1 | |||
| 9 | 1 | 1 | |||||||||||
| 10 | 14 | 16 | 15 | 21 | 33 | 46 | 9 | 12 | 14 | 23 | 21 | 28 | |
| 11 | |||||||||||||
| 12 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bożek, A. Discovering Stick-Slip-Resistant Servo Control Algorithm Using Genetic Programming. Sensors 2022, 22, 383. https://doi.org/10.3390/s22010383
Bożek A. Discovering Stick-Slip-Resistant Servo Control Algorithm Using Genetic Programming. Sensors. 2022; 22(1):383. https://doi.org/10.3390/s22010383
Chicago/Turabian StyleBożek, Andrzej. 2022. "Discovering Stick-Slip-Resistant Servo Control Algorithm Using Genetic Programming" Sensors 22, no. 1: 383. https://doi.org/10.3390/s22010383
APA StyleBożek, A. (2022). Discovering Stick-Slip-Resistant Servo Control Algorithm Using Genetic Programming. Sensors, 22(1), 383. https://doi.org/10.3390/s22010383






