Modeling and Calibration for Dithering of MDRLG and Time-Delay of Accelerometer in SINS
Abstract
1. Introduction
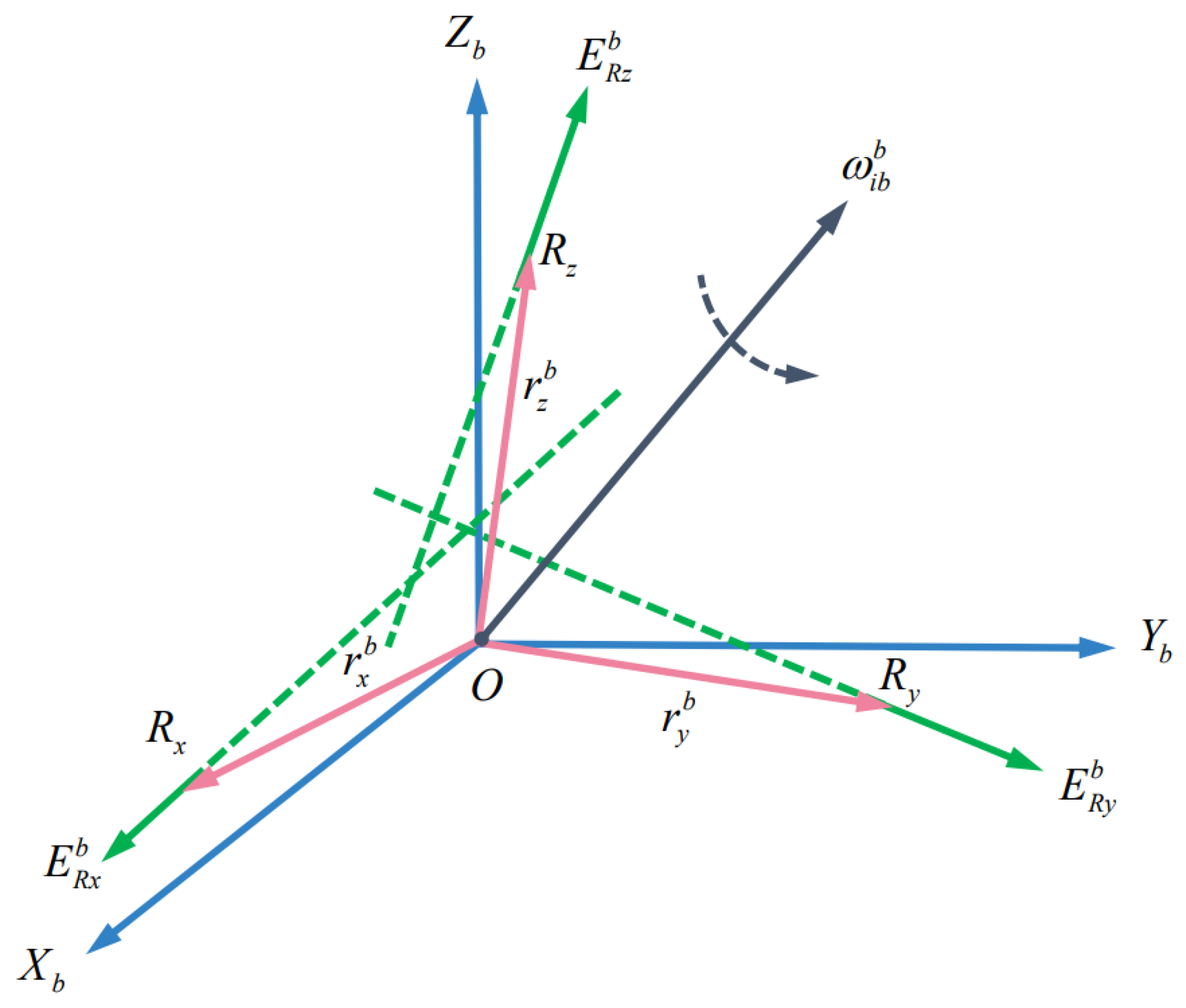
2. Reference Frame Definition
3. Modeling and Error Analysis for Systematic Calibration of Sins
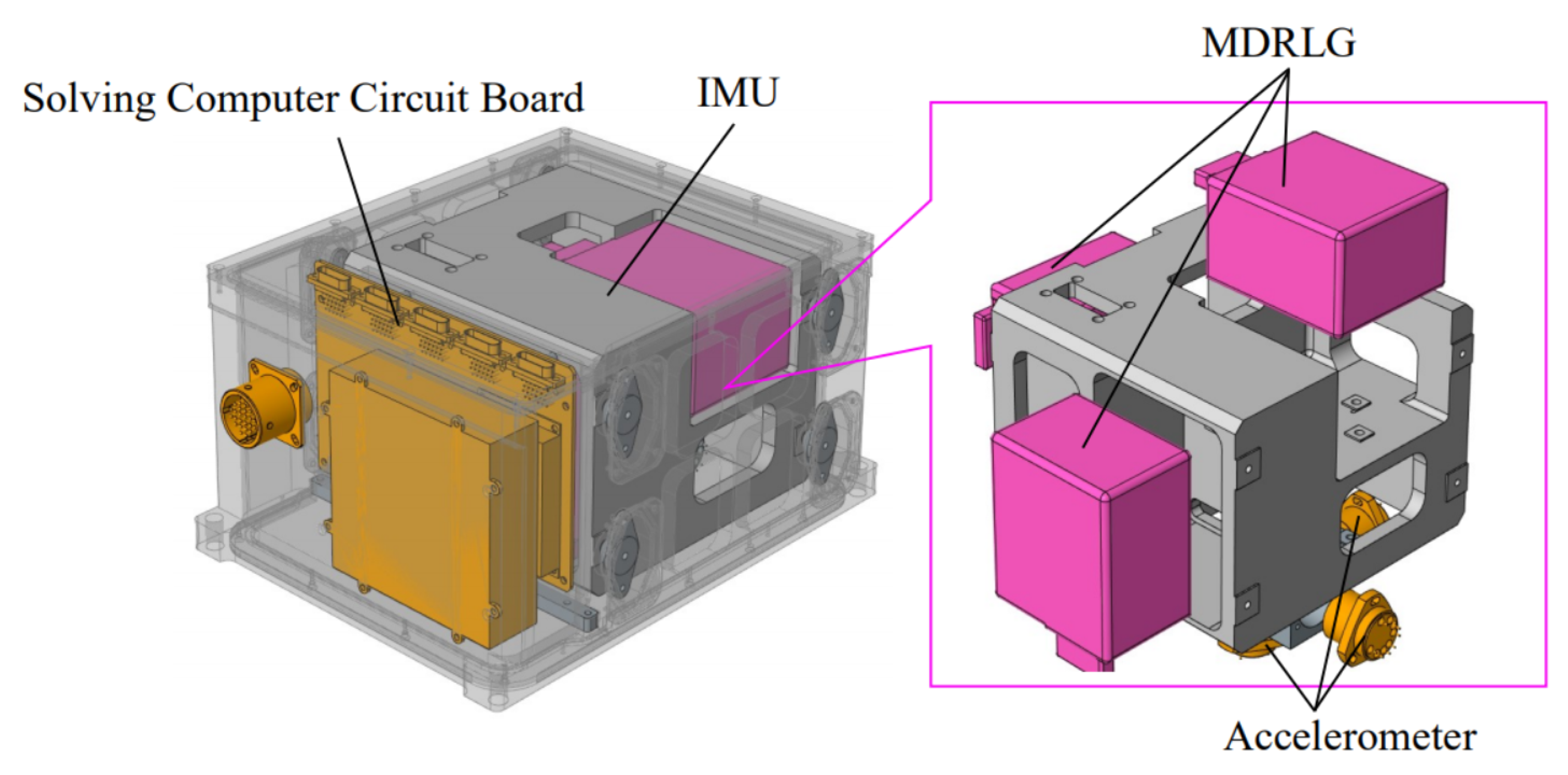
3.1. System Configuration of the SINS
3.2. Modeling and Error Analysis for Dithering of the MDRLG
3.3. Modeling and Error Analysis for Time Delay of Accelerometer
3.3.1. Error Modeling
3.3.2. Analysis of Time Delay Error of Accelerometer
3.4. IMU Calibration Parameters and Model of Inertial Device Output Error
3.4.1. Model of IMU Calibration Parameters
3.4.2. Output Error Model of the MDRLG
3.4.3. Output Error Model of the Accelerometer
4. Design of Systematic Calibration Based on Kalman Filter
4.1. Outer Lever Arm Effect
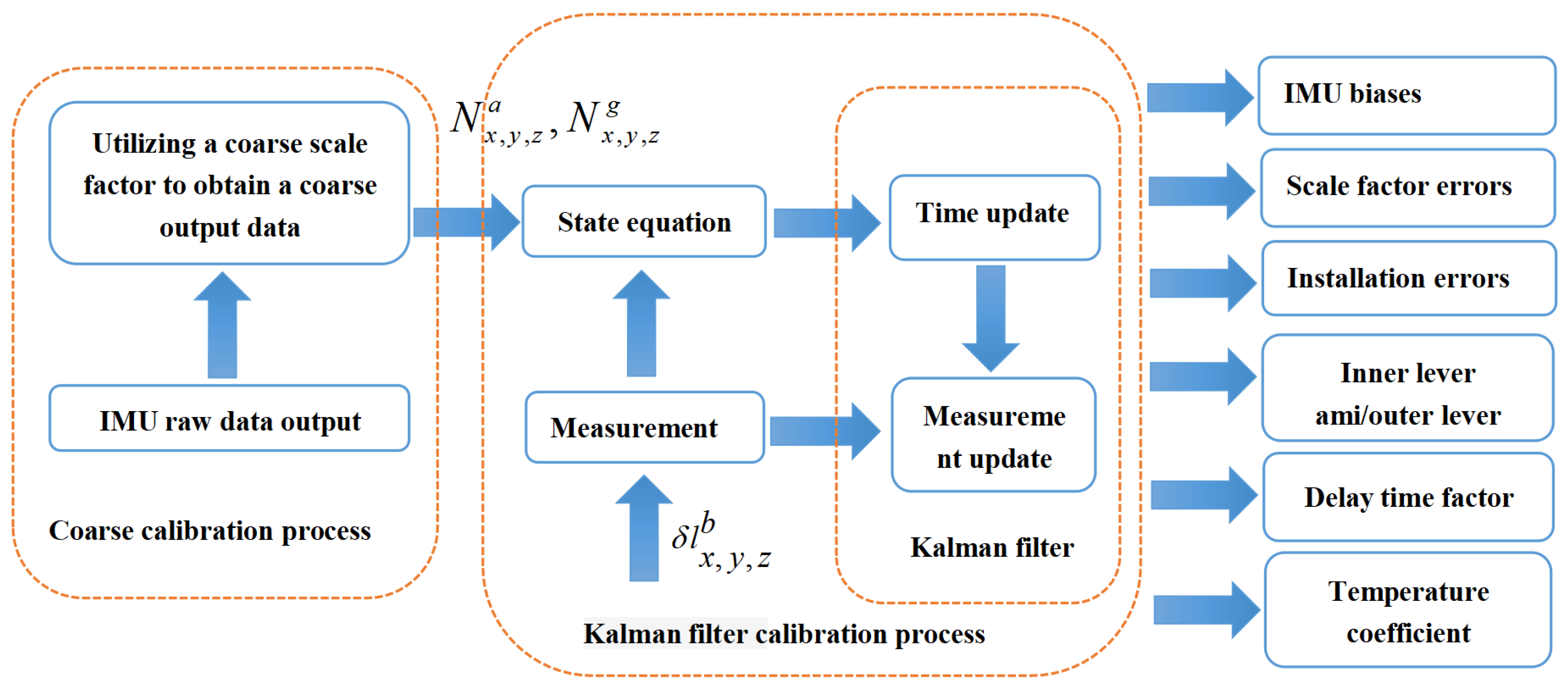
4.2. Calibration Filter Design for SINS
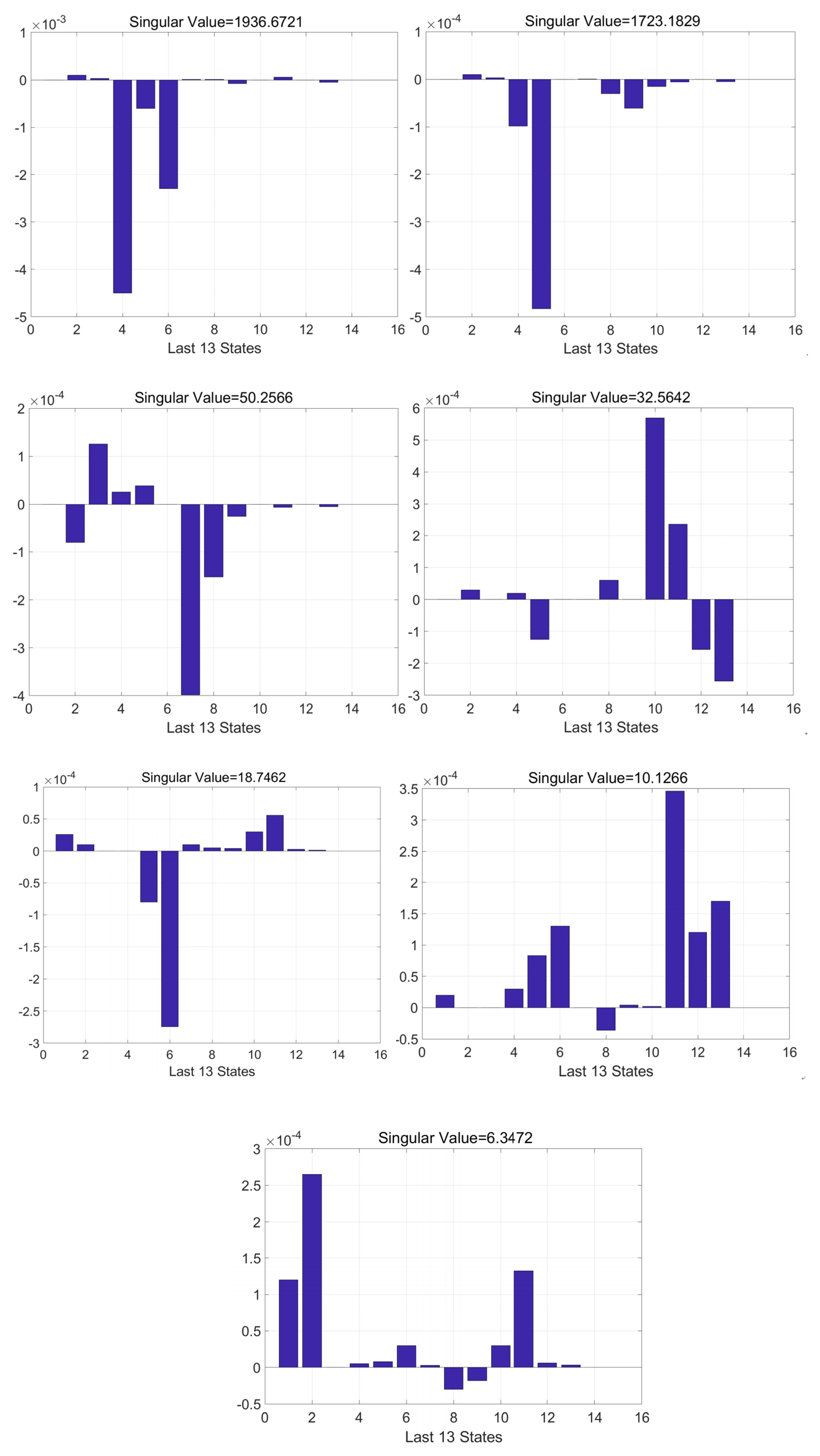
4.3. Analysis of Observable Degree
5. Test Results and Analysis
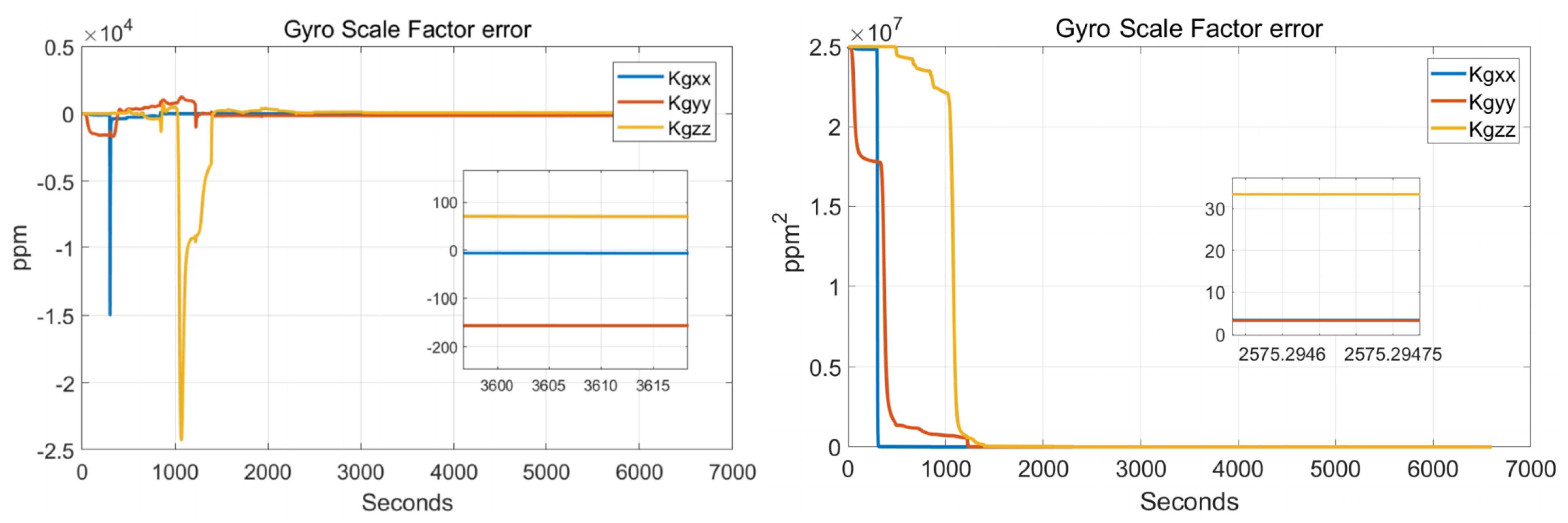
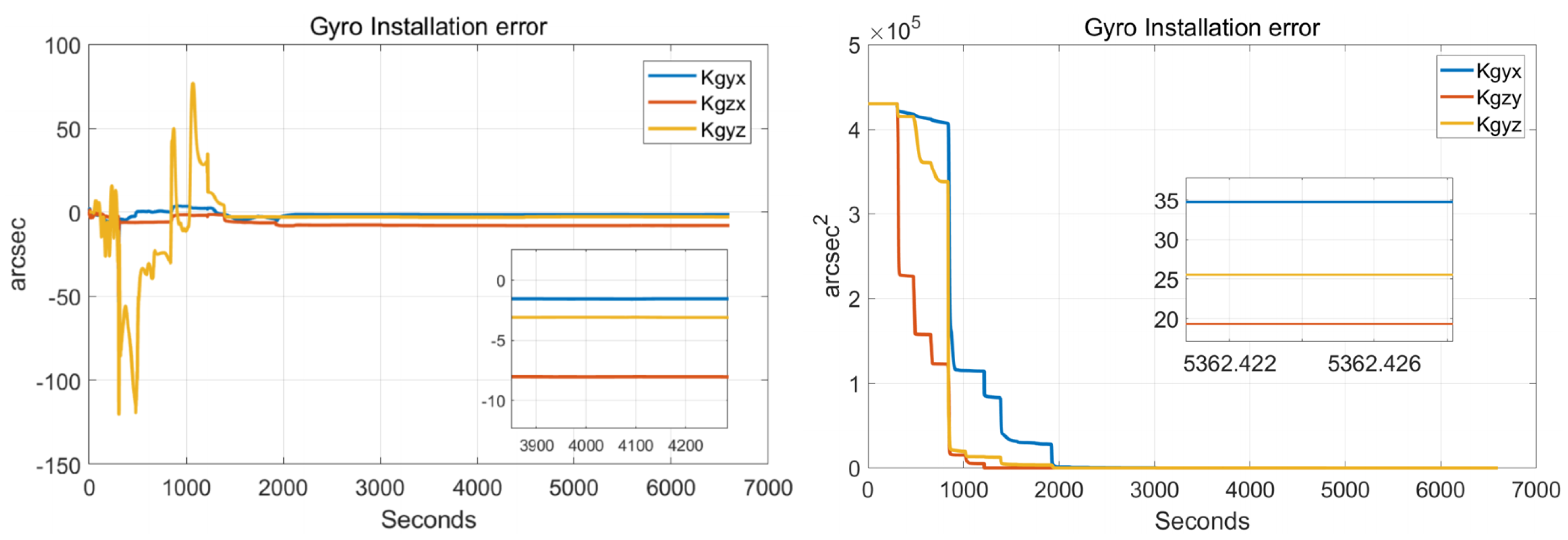
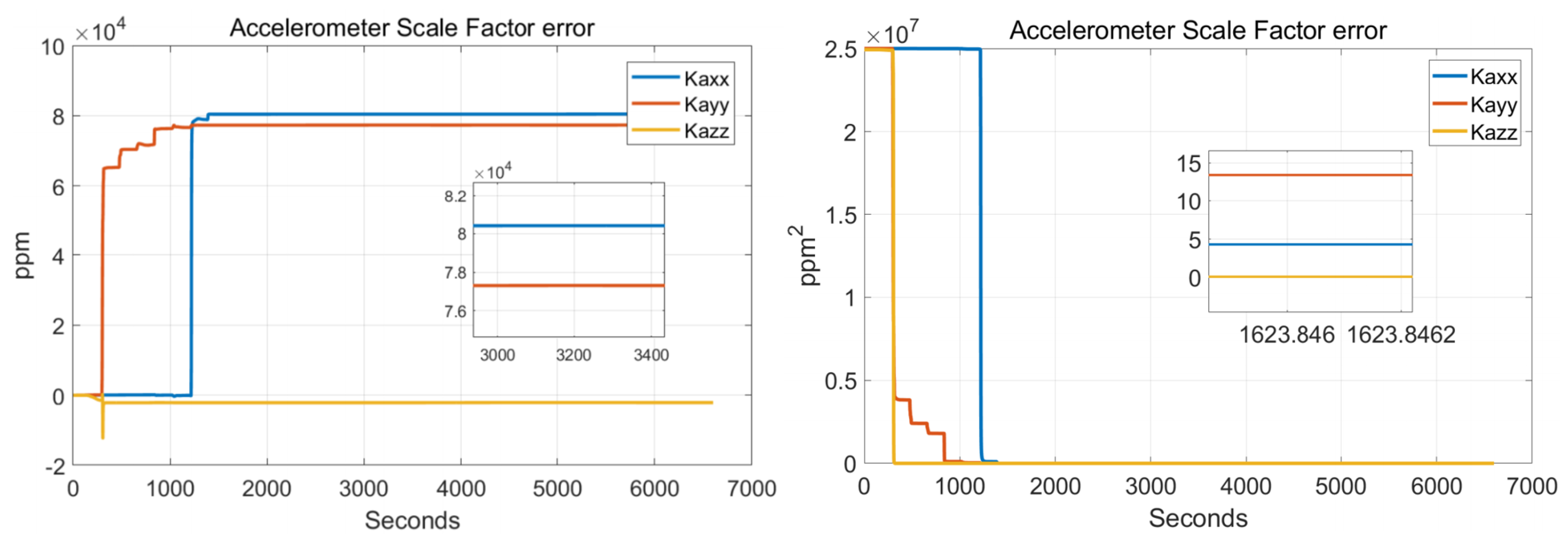
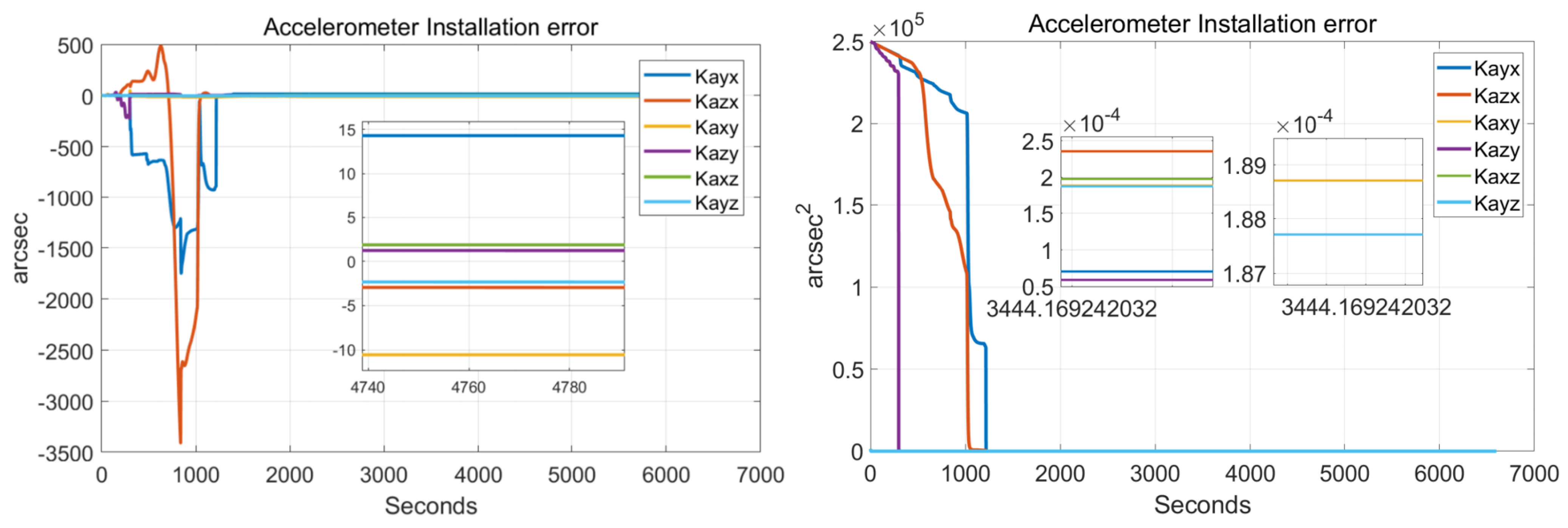
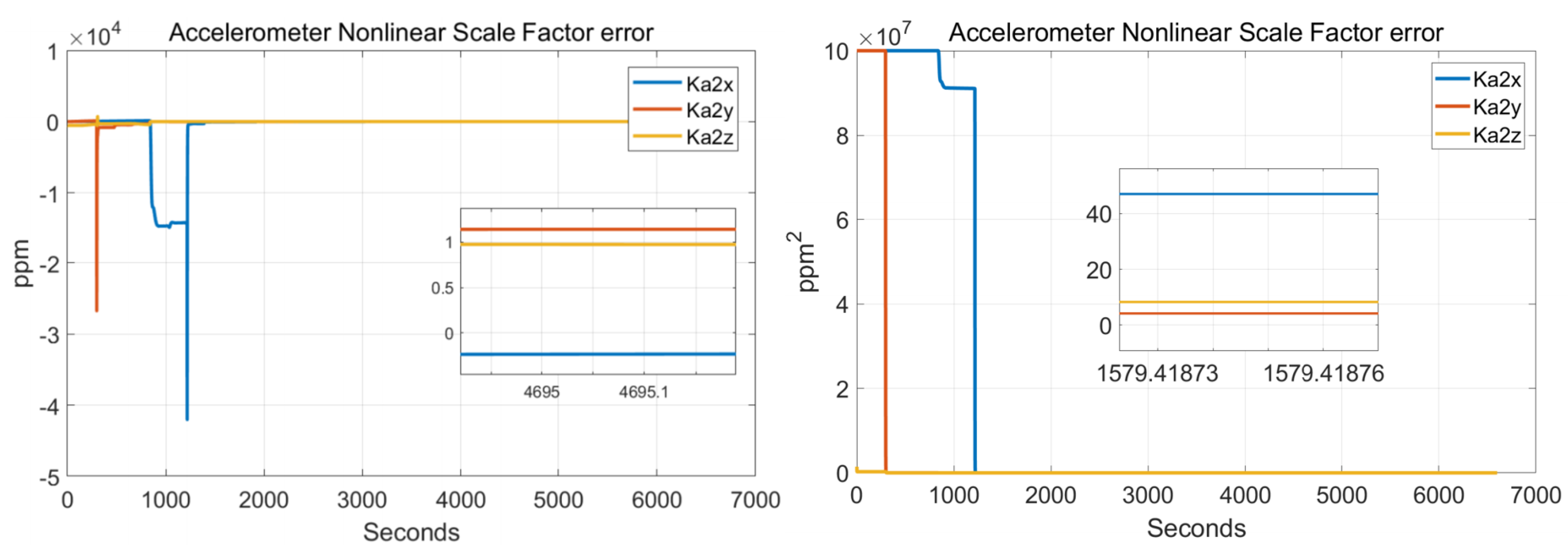
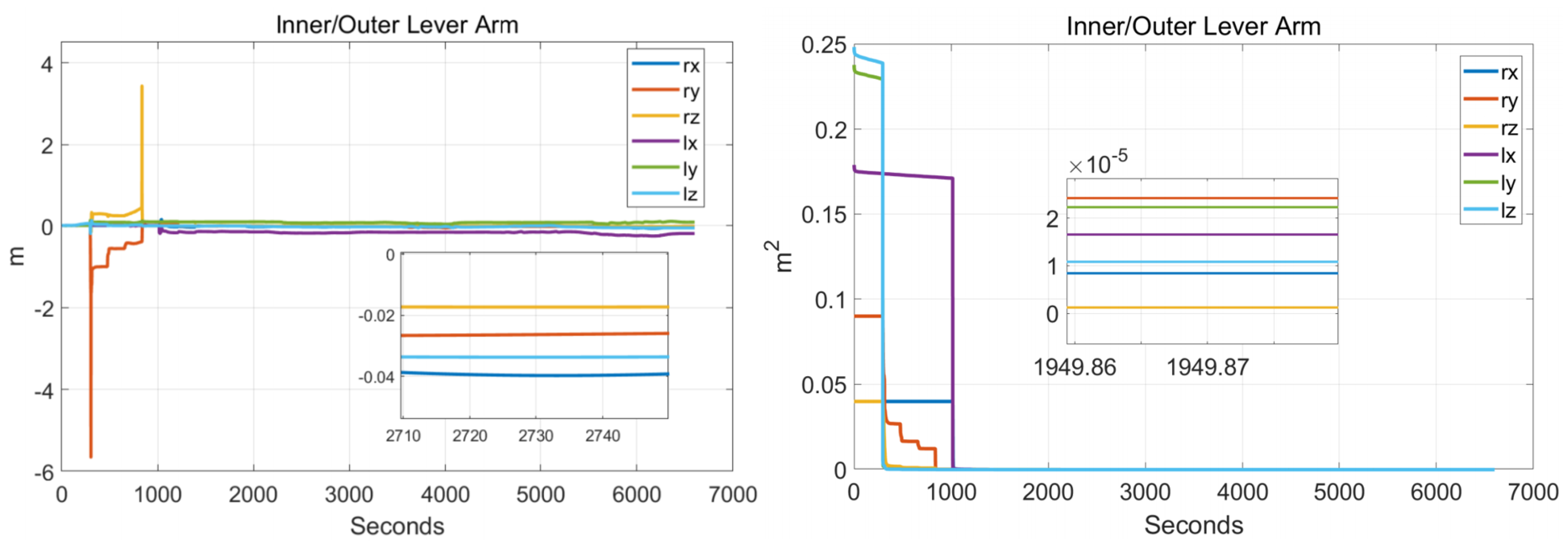
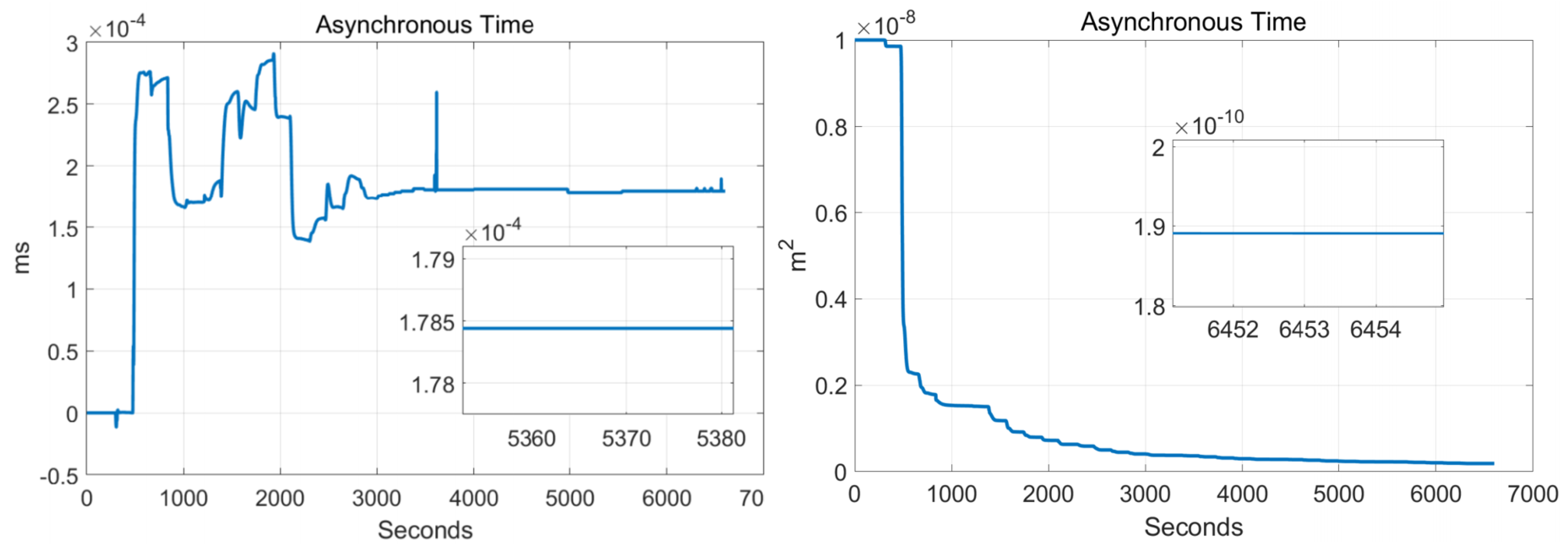
5.1. Calibration Test
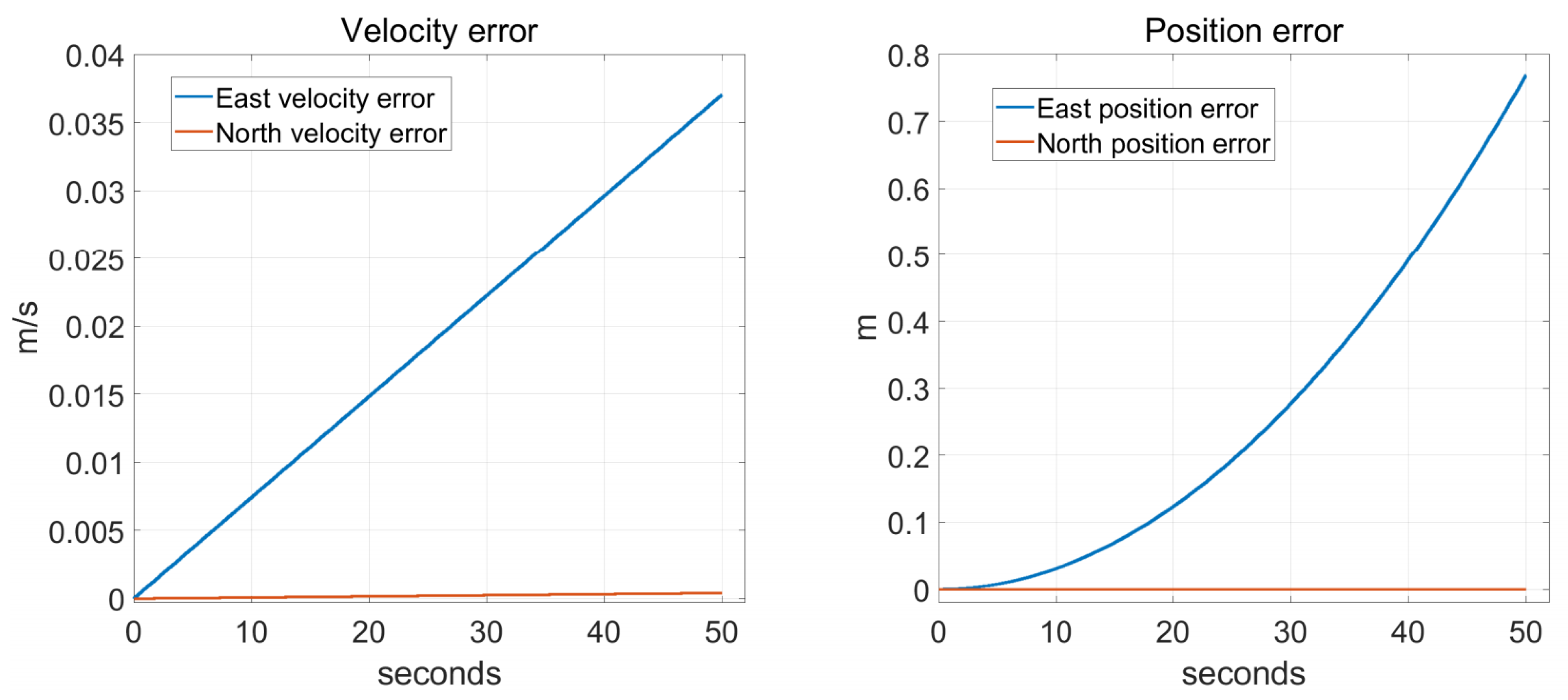
5.2. Static Swing Navigation Test
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Sample Availability
References
- Ren, Q.; Wang, B.; Deng, Z.; Fu, M. Amulti-position self-calibration method for dual-axis rotational inertial navigation system. Sens. Actuators A Phys. 2014, 219, 24–31. [Google Scholar] [CrossRef]
- Nieminen, T.; Kangas, J.; Suuriniemi, S.; Kettunen, L. An enhanced multi-position calibration method for consumer-grade inertial measurement units applied and tested. Meas. Sci. Technol. 2010, 21, 105204. [Google Scholar] [CrossRef]
- Zhang, H.; Wu, Y.; Wu, W.; Wu, M.; Hu, X. Improved multi-position calibration for inertial measurement units. Meas. Sci. Technol. 2010, 21, 015107. [Google Scholar] [CrossRef]
- Pittman, D.N.; Roberts, C.E. Determining Inertial Errors from Navigation-in-Place Data. In Proceedings of the IEEE Position Location and Navigation Symposium, Monterey, CA, USA, 24–27 March 1992. [Google Scholar]
- Savage, P.G. Strapdown Analytics; Strapdown Associates, Inc.: Maple Plain, MN, USA, 2007; pp. 56–59. [Google Scholar]
- Zhou, Z.H.; Qiu, H.B.; Li, Y.; Lian, T.; Wang, T. Systematic calibration method for SINS with low-precision two-axis turntable. J. Chin. Inert. Technol. 2010, 18, 503–507. [Google Scholar]
- Camberlein, L.; Mazzanti, F. Calibration technique for laser gyro strapdown inertial navigation systems. In Proceedings of the Symposium Gyro Technology, Stuttgart, Germany, 24–25 September 1985. [Google Scholar]
- Joos, D.K.; Hunsanger, W. High Accuracy Laboratory Tests on an Orbital-Microgravity-Sensor-System. In Proceedings of the Symposium Gyro Technology, Stuttgart, Germany, 19–20 September 1989. [Google Scholar]
- Grewal, M.S.; Henderson, V.D.; Miyasako, R.S. Application of Kalman Filtering to the Calibration and Alignment of Inertial Navigation Systems. IEEE Trans. Autom. Control. 1991, 36, 4–13. [Google Scholar] [CrossRef]
- Cai, Q.; Yang, G.; Song, N.; Liu, Y. Systematic Calibration for Ultra-High Accuracy Inertial Measurement Units. Sensors 2016, 16, 940. [Google Scholar] [CrossRef] [PubMed]
- Yu, X.D.; Wang, Y.; Zhang, P.F.; Xie, Y.P.; Tang, J.X.; Long, X.W. Calibration of RLG drift in single-axis rotation INS. Opt. Precis. Eng. 2012, 20, 1201–1207. [Google Scholar]
- Liu, B.; Ren, J.; Bai, H. Systematic Calibration Method Based on High-order Kalman Filter for Laser Gyro SINS. Missilesand Space Veh. 2017, 4, 90–94. [Google Scholar]
- Shi, W.; Wang, X.; Zheng, J.; Wang, Y. Multi-position systematic calibration method for RLG-SINS. Infrared Laser Eng. 2016, 45, 99–106. [Google Scholar]
- Yu, H. Research on the Methods for Improving the Accuracy of Laser Gyro SINS in Vibration Environment. Ph.D. Thesis, National University of Defense Technology, Changsha, China, 2012. [Google Scholar]
- Weng, J. Multi-position continuous rotate-stop fast temperature parameters estimation method of flexible pendulum accelerometer triads. Measurement 2020, 169, 108372. [Google Scholar] [CrossRef]
- Gao, P.; Li, K.; Song, T.; Liu, Z. An accelerometers-size-effect self-calibration method for triaxis rotational inertial navigation system. IEEE Trans. Ind. Electron. 2017, 65, 1655–1664. [Google Scholar] [CrossRef]
- Song, T.; Li, K.; Wu, Q.; Li, Q.; Xue, Q. An improved self-calibration method with consideration of inner lever- arm effect for dual-axis RINS. Meas. Sci. Technol. 2020, 31, 074001. [Google Scholar] [CrossRef]
- Xu, C.; Miao, L.; Zhou, Z. A self-calibration method of inner lever arms for dual-axis rotation INS. Meas. Sci. Technol. 2019, 30, 125110. [Google Scholar] [CrossRef]
- Jiang, Q.; Tang, J.; Han, S.; Bao, Y. Systematic calibration method based on 36-dimension Kalman filter for laser gyro SINS. Infrared Laser Eng. 2015, 44, 1110–1114. [Google Scholar]
- Gao, J.M.; Zhang, K.B.; Chen, F.B.; Yang, H.B. Temperature characteristics and error compensation for quartz flexible accelerometer. Int. J. Autom. Comput. 2015, 12, 540–550. [Google Scholar] [CrossRef][Green Version]
- Pan, Y.; Li, L.; Ren, C.; Luo, H. Study on the compensation for a quartz accelerometer based on a wavelet neural network. Meas. Sci. Technol. 2010, 21, 105202. [Google Scholar] [CrossRef]
- Ban, J.; Wang, L.; Liu, Z.; Zhang, L. Self-calibration method for temperature errors in multi-axis rotational inertial navigation system. Opt. Express 2020, 28, 8909–8923. [Google Scholar] [CrossRef] [PubMed]

| Number | Rotation Angle/Axis | Attitude after Rotation (XYZ) |
|---|---|---|
| 1 | +90Y | NED |
| 2 | +180Y | UEN |
| 3 | +180Y | DES |
| 4 | +90Z | UEN |
| 5 | +180Z | EDN |
| 6 | +180Z | WUN |
| 7 | +90X | EDN |
| 8 | +180X | ENU |
| 9 | +180X | ESD |
| 10 | +90X | ENU |
| 11 | +90X | EUS |
| 12 | +90X | ESD |
| 13 | +90Z | EDN |
| 14 | +90Z | DWN |
| 15 | +90Z | WUN |
| 16 | +90Y | UEN |
| 17 | +90Y | SEU |
| 18 | +90Y | DES |
| Vibration Axis (IMU) | Amplitude | Frequency |
|---|---|---|
| x-axis | 2° | 0.4 |
| y-axis | 3° | 0.3 |
| z-axis | 4° | 0.4 |
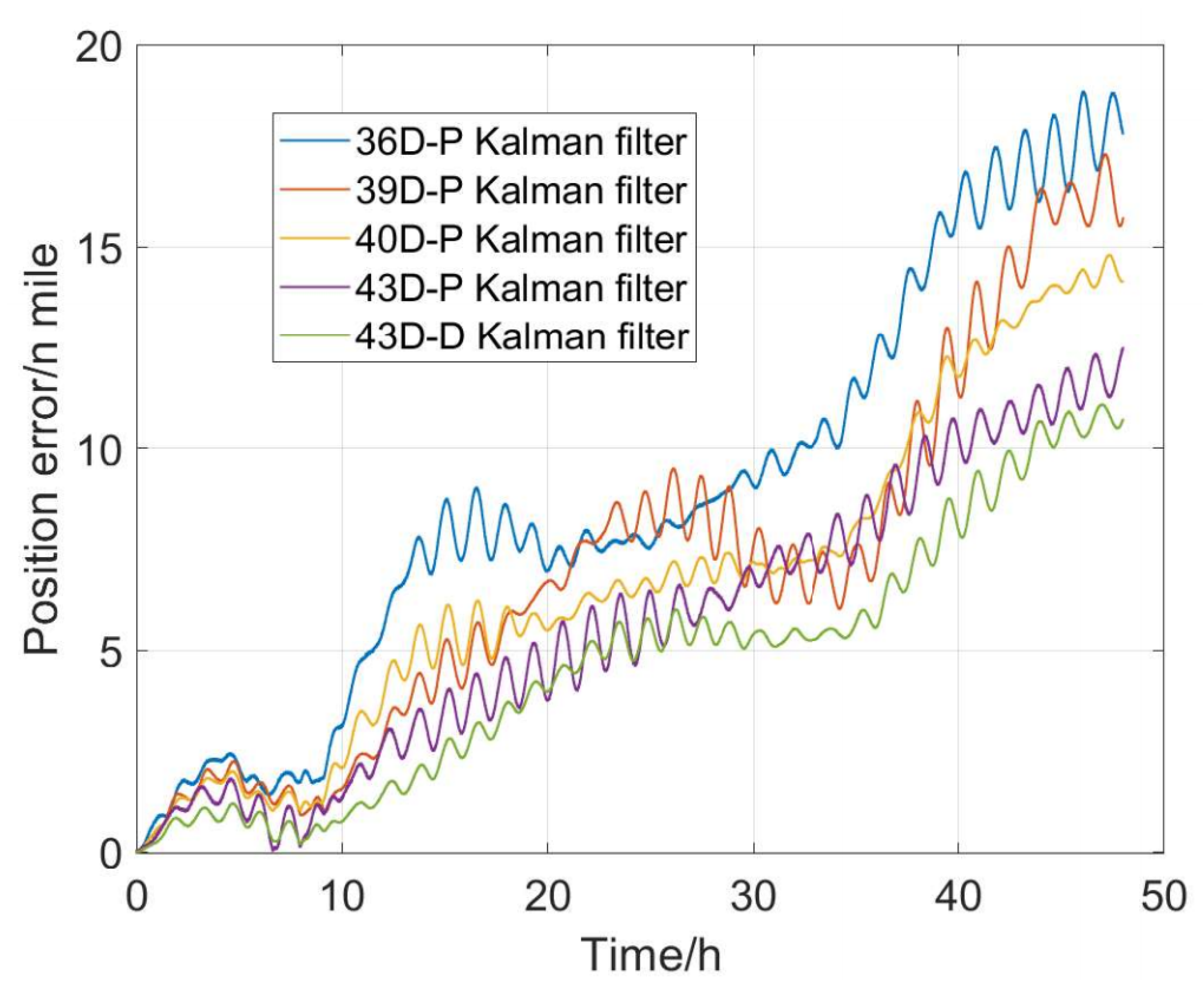
| Filter Model | Contains Error Components |
|---|---|
| 36D-P Kalman filter | IMU scale factor error, installation error, zero offset, outer lever arm error |
| 39D-P Kalman filter | IMU scale factor error, installation error, zero offset, outer lever arm error |
| inner lever arm error | |
| 40D-P Kalman filter | IMU scale factor error, installation error, zero offset, outer lever arm error |
| inner lever arm error , time delay factor | |
| 43D-P Kalman filter | IMU scale factor error, installation error, zero offset, outer lever arm error |
| inner lever arm error , time delay factor | |
| Temperature error coefficient | |
| 43D-B Kalman filter | IMU scale factor error, installation error, zero offset, outer lever arm error |
| (Consider the dithering | inner lever arm error , time delay factor |
| of MDRLG | Temperature error coefficient |
| compensation model) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xing, J.; Yang, G.; Cai, T. Modeling and Calibration for Dithering of MDRLG and Time-Delay of Accelerometer in SINS. Sensors 2022, 22, 278. https://doi.org/10.3390/s22010278
Xing J, Yang G, Cai T. Modeling and Calibration for Dithering of MDRLG and Time-Delay of Accelerometer in SINS. Sensors. 2022; 22(1):278. https://doi.org/10.3390/s22010278
Chicago/Turabian StyleXing, Jinlong, Gongliu Yang, and Tijing Cai. 2022. "Modeling and Calibration for Dithering of MDRLG and Time-Delay of Accelerometer in SINS" Sensors 22, no. 1: 278. https://doi.org/10.3390/s22010278
APA StyleXing, J., Yang, G., & Cai, T. (2022). Modeling and Calibration for Dithering of MDRLG and Time-Delay of Accelerometer in SINS. Sensors, 22(1), 278. https://doi.org/10.3390/s22010278





