Sensor Modeling for Underwater Localization Using a Particle Filter
Abstract
1. Introduction
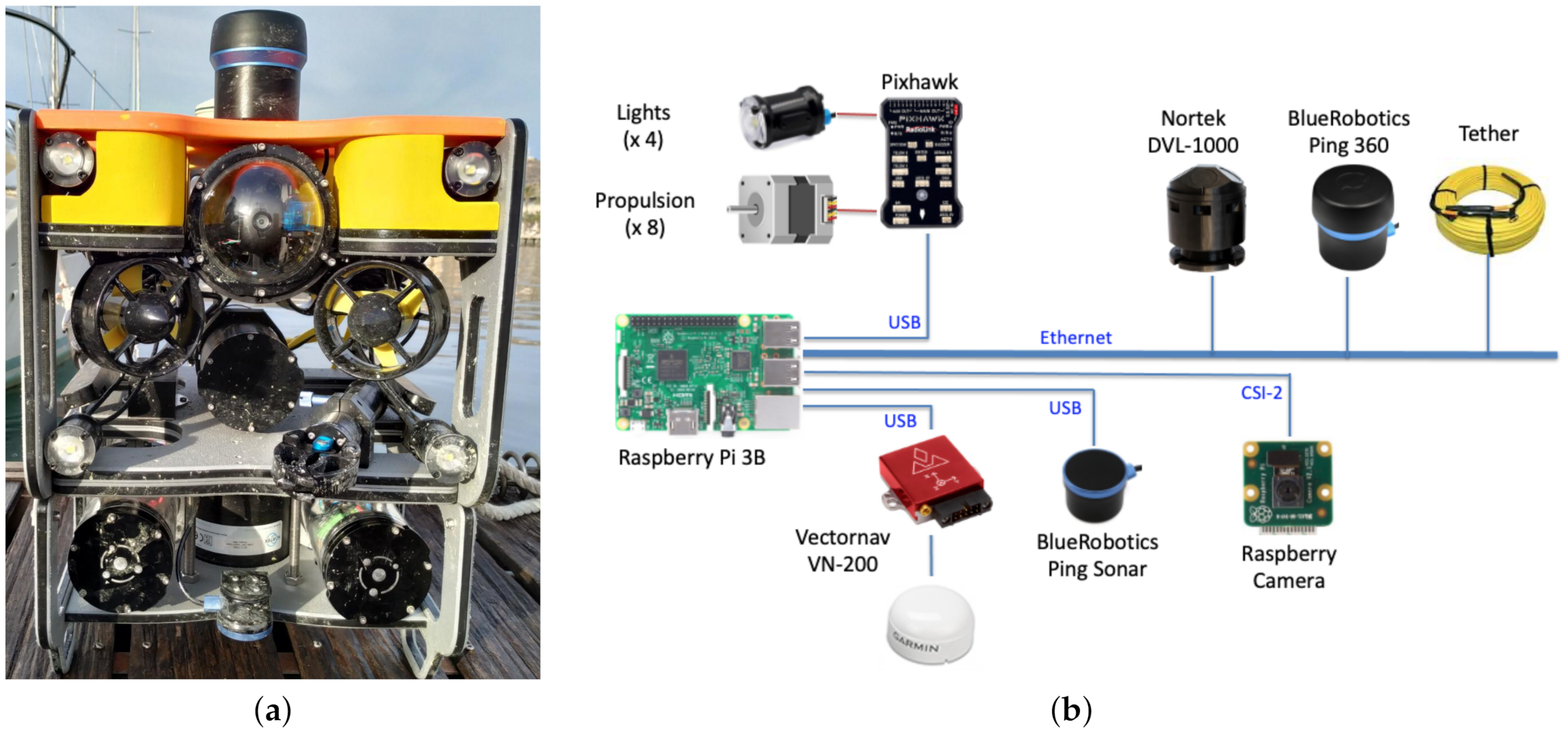
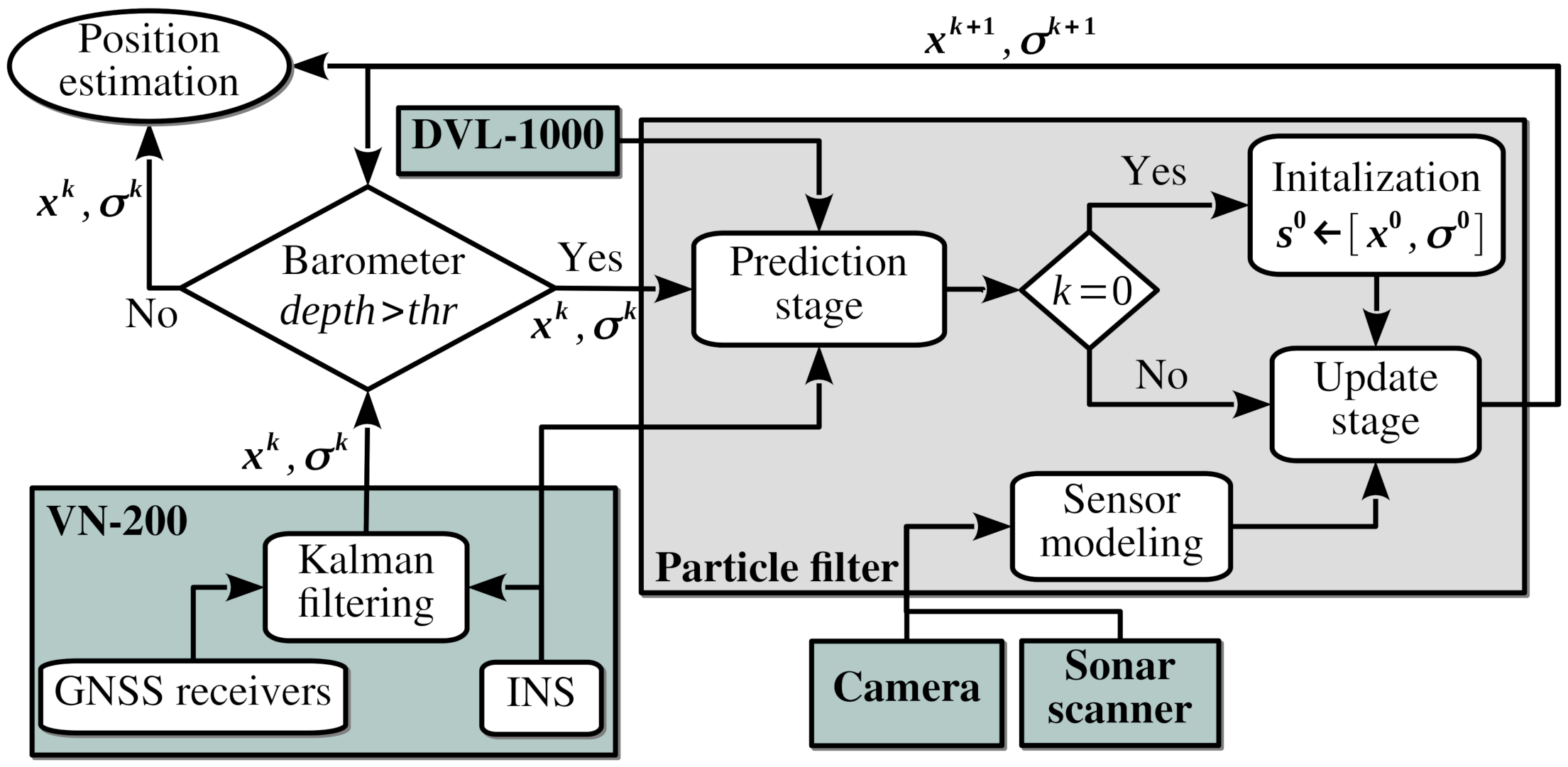
2. Underwater Platform
3. Sensor Modeling
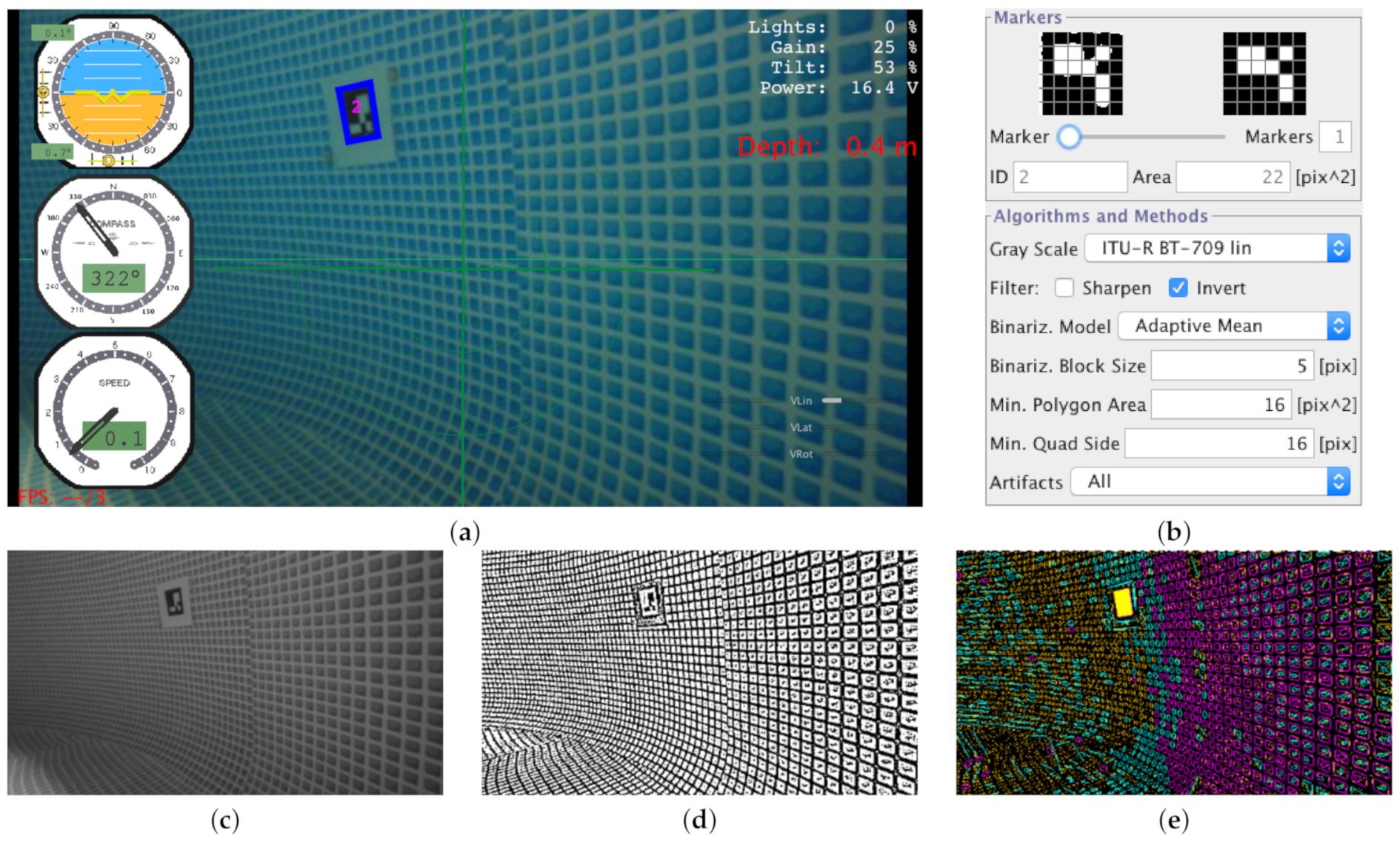
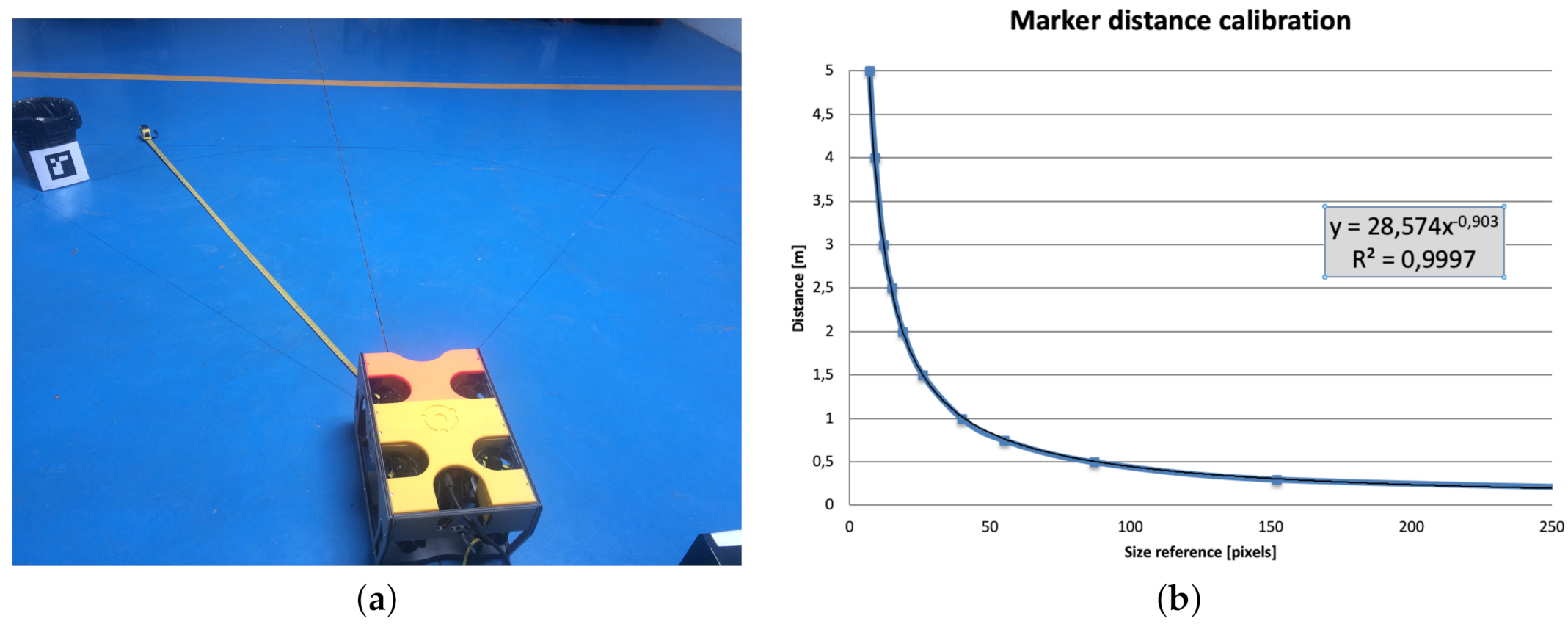
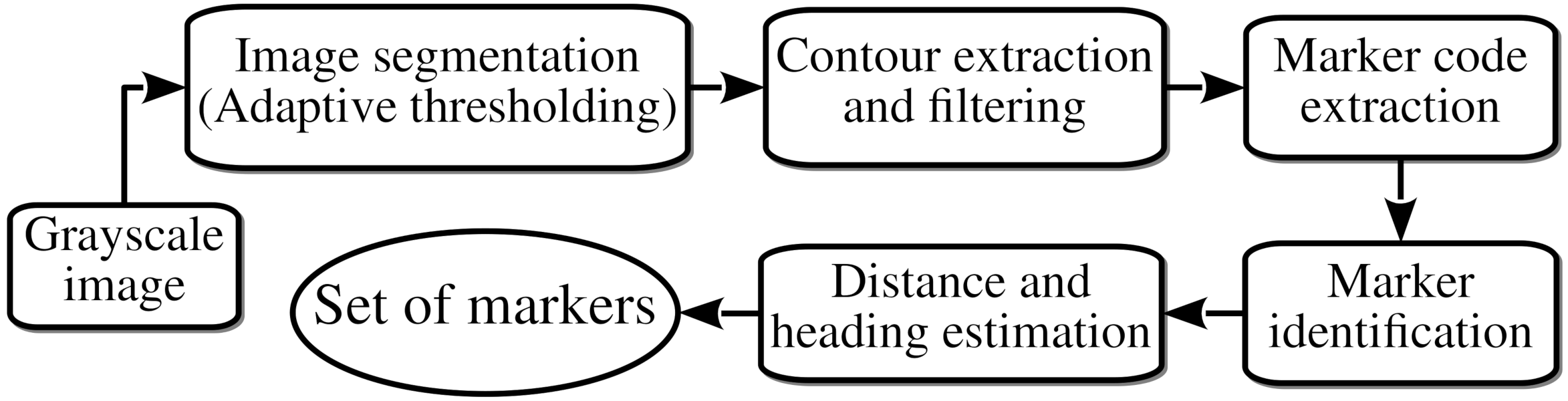
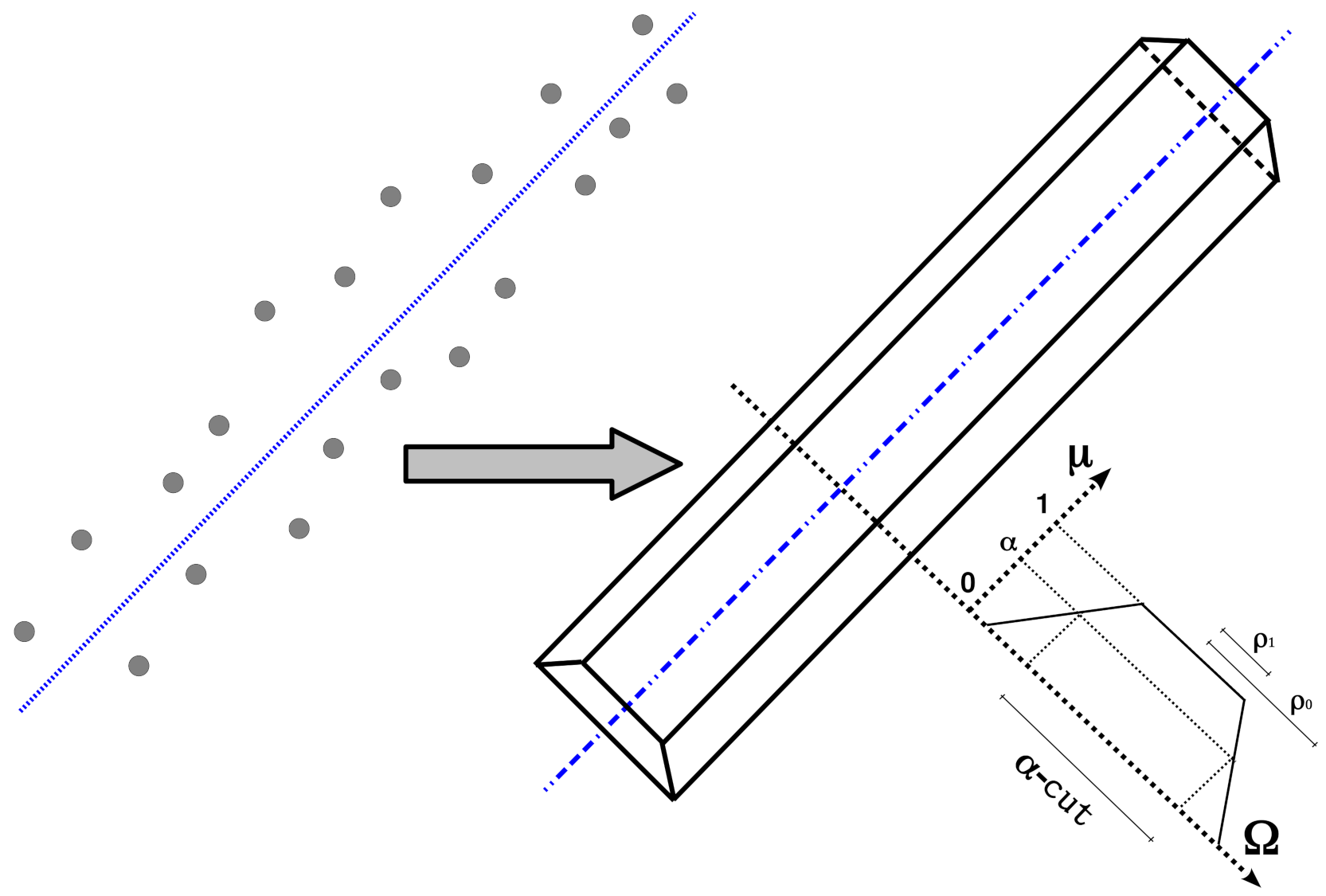
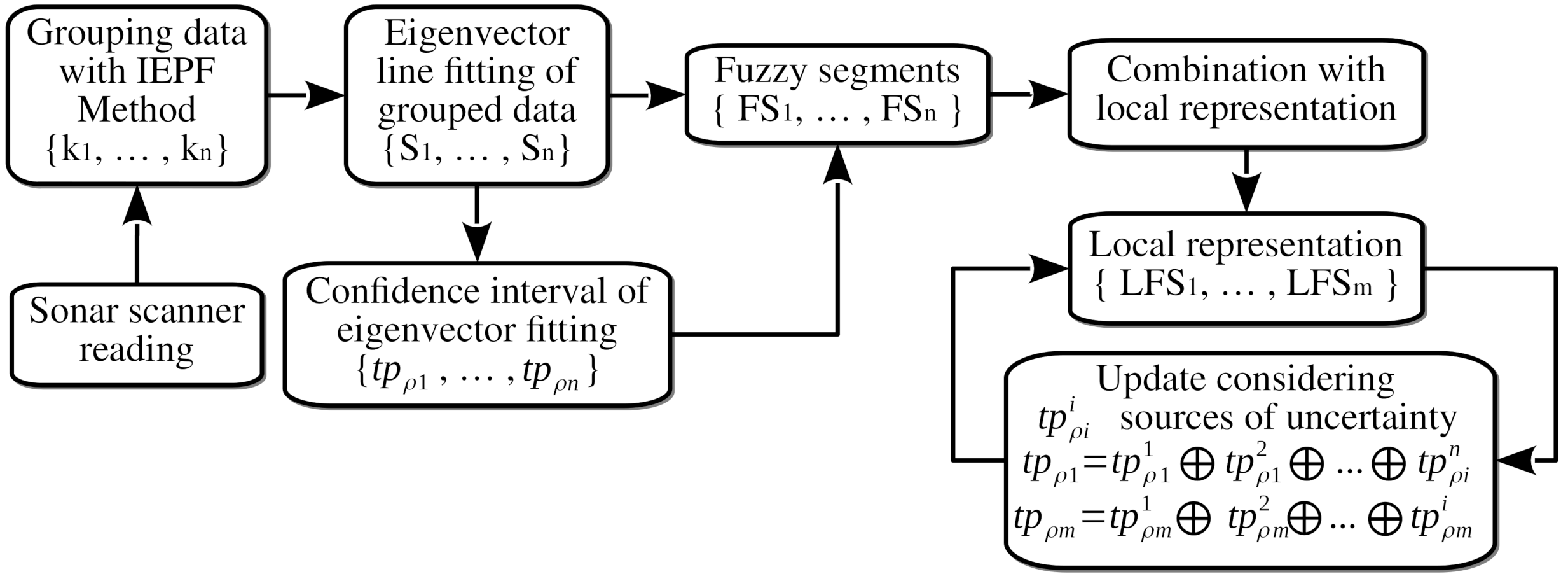
3.1. Visual Perception of Landmarks
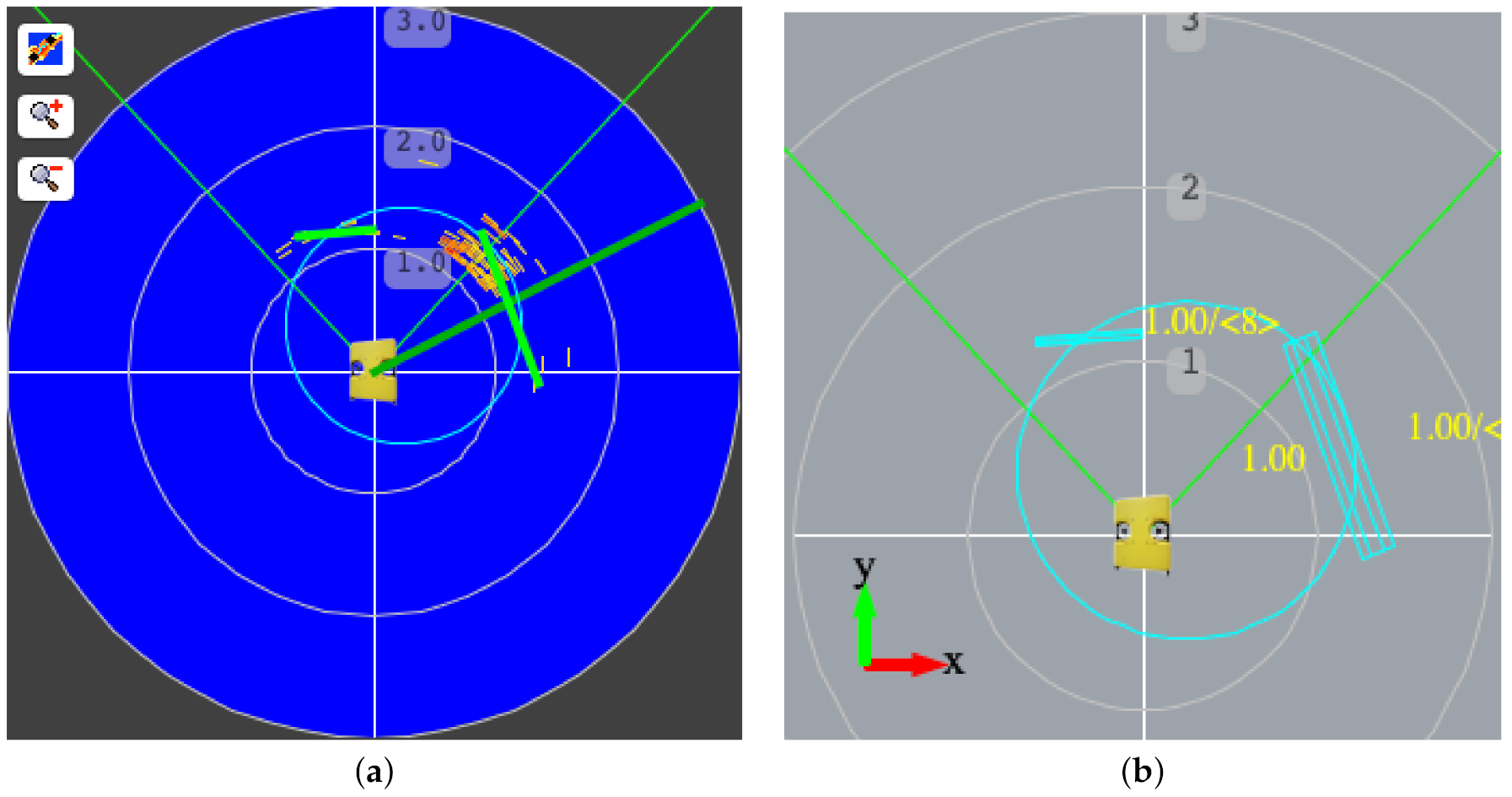
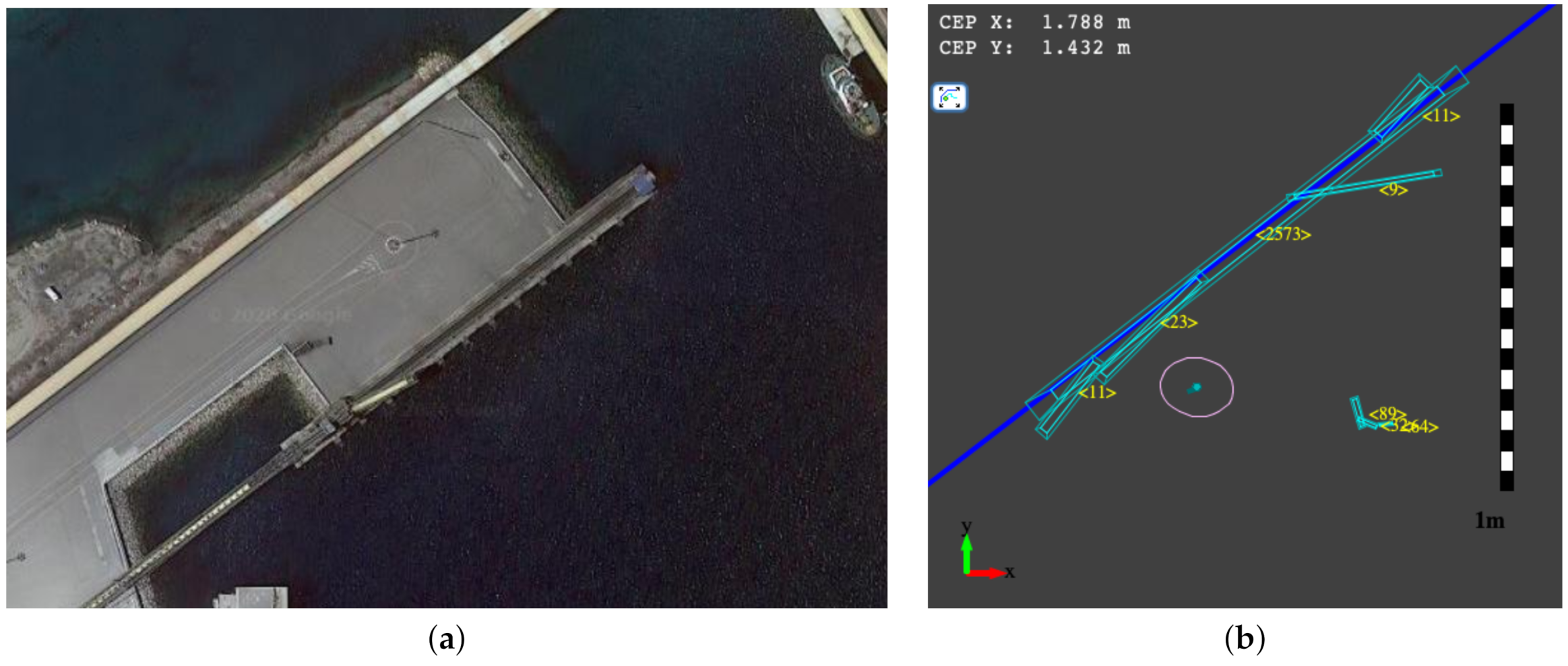
3.2. Feature Extraction Using Sonar Scanner Readings
- Aging. We remove from the buffer those echoes that are older than a given amount of time. This filter is of paramount importance because the uncertainty of the local position of the sonar echoes grows unbounded with time.
- Motion. Whenever the vehicle moves, all the echoes stored in the buffer have to be translated and rotated correspondingly. This update is key to maintaining a coherent representation of the environment.
- Blanking. When a new scan is available, remove previous echoes that lie inside the scanning zone. The application of this filter is crucial for eliminating noise from the sonar buffer.
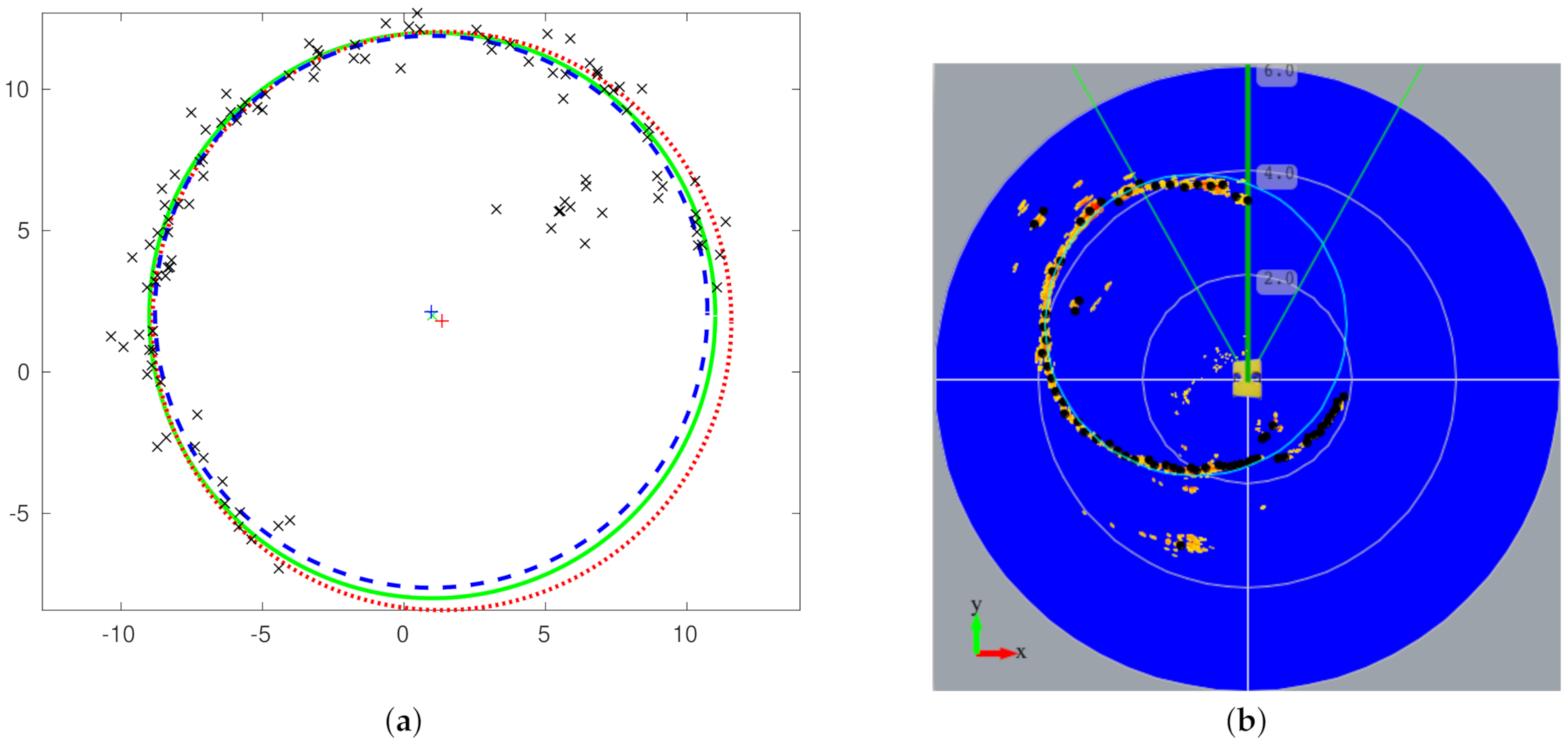
3.2.1. Circular Model-Fitting
| Algorithm 1 Circular model-fitting with outlier rejection | |
| Input: | |
| points | ▹ Set of points to be fitted |
| T | ▹ Threshold used to compute the cost function |
| FAILURE_PROBABILITY | ▹ Probability of not finding a correct model |
| INLIER_PROPORTION | ▹ Proportion of inliers in data |
| Output: | |
| ▹ Best model parameters found | |
| Initialization | |
| 1: | ▹ Initialize to a large number |
| 2: | |
| Find model | |
| 3: for to N do | |
| Find possible model | |
| 4: Take 3 points randomly | |
| 5: Build matrices and using equations (4) and (5) and the 3 sampled points | |
| 6: Find model parameters using equations (6) and (7) | |
| 7: Compute the cost function C using equations (8) to () | |
| If this possible model is better than the previous one, we keep it | |
| 8: if () then | |
| 9: | |
| 10: | |
| 11: end if | |
| 12: end for | |
| Refine the model using inliers | |
| 13: Select the points such that using (8) | |
| 14: Build matrices and using equations (4) and (5) and the selected inliers | |
| 15: Find model parameters using equations (6) to (7) | |
| 16: return | |
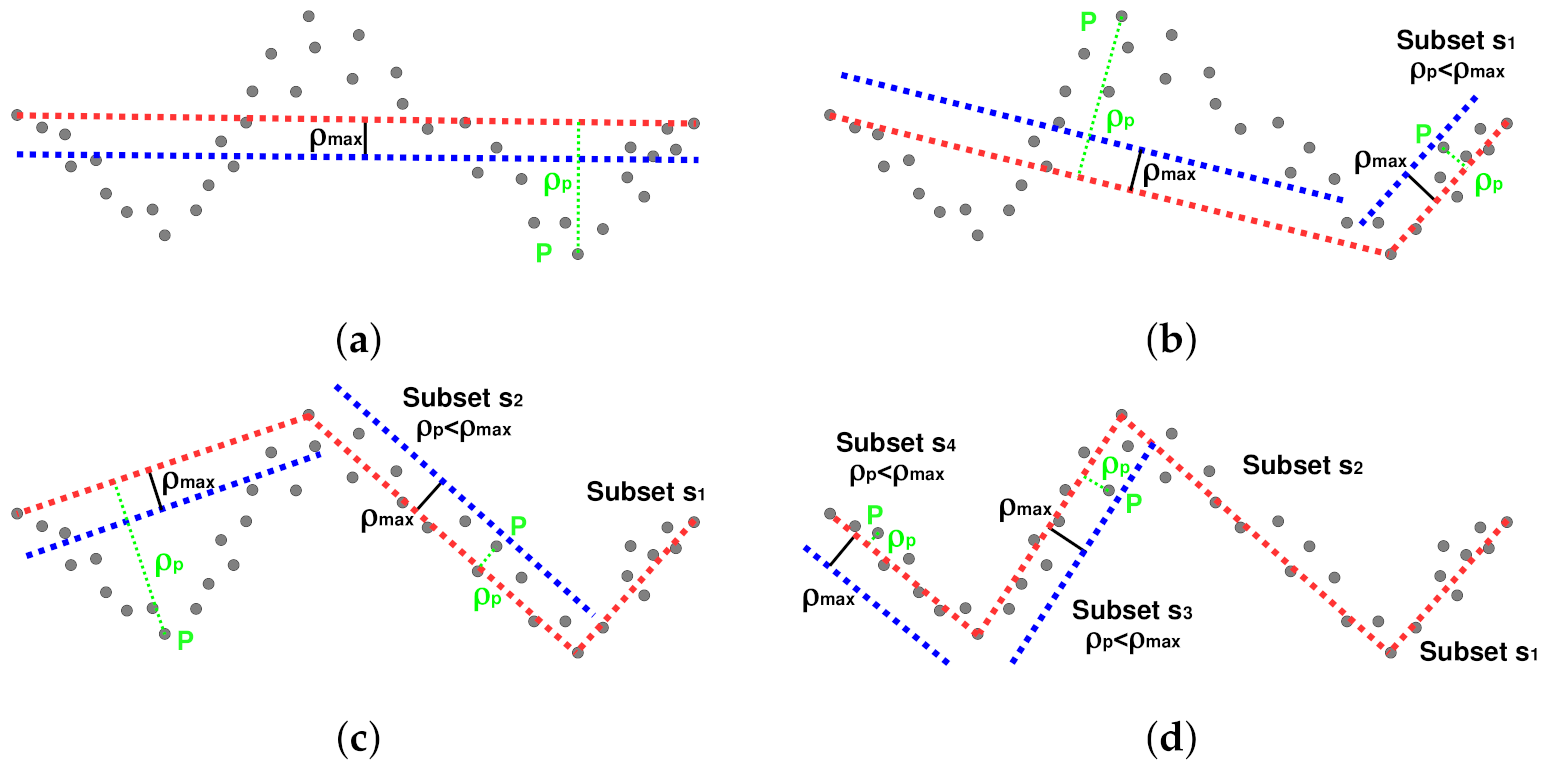
3.2.2. Line Segment Model-Fitting
- Initialization. We initialize the algorithm with a set s containing all the ordered observations.
- Step 1. If the set s is composed of more than observations, draw a line segment between the first and last data (end-points), otherwise reject the set s.
- Step 2. Detect the point P with maximum distance to the fitted line segment between the end-points.
- Step 3. If splits the set s at P into two subsets and and goes to Step 1 for both subsets. Otherwise, the set s is a candidate to be a line segment.
- Stopping criteria. We finalize the search when all the subsets are a candidate to be a line segment satisfying the condition or are rejected because they have fewer than observations.
4. Particle Filter
| Algorithm 2: Particle filtering for localization. | |
| Initialization | |
| 1: | ▹ Randomly initialization of particles from location p |
| 2: | ▹ Initialization of distribution from the position |
| 3: | ▹ Initialization of samples within the uncertain location |
| Recursive loop for localization | |
| 4: while true do | |
| 5: k++ | |
| 6: ENP = | ▹ Effective number of particles |
| 7: if ENP < then | ▹ Condition of particle population depletion () |
| 8: | ← Resampling() |
| 9: end if | |
| 10: Prediction stage | |
| 11: ← | ▹ Include action (dead-reckoning displacements) |
| 12: ←+· | ▹ Include ramdom noise to the variable of interest |
| 13: Update stage | |
| 14: = | ▹ Update with sensing |
| 15: Normalization of the weights | |
| 16: for j← 1 to n do | |
| 17: = | |
| 18: end for | |
| 19: end while | |
5. Experimental Results
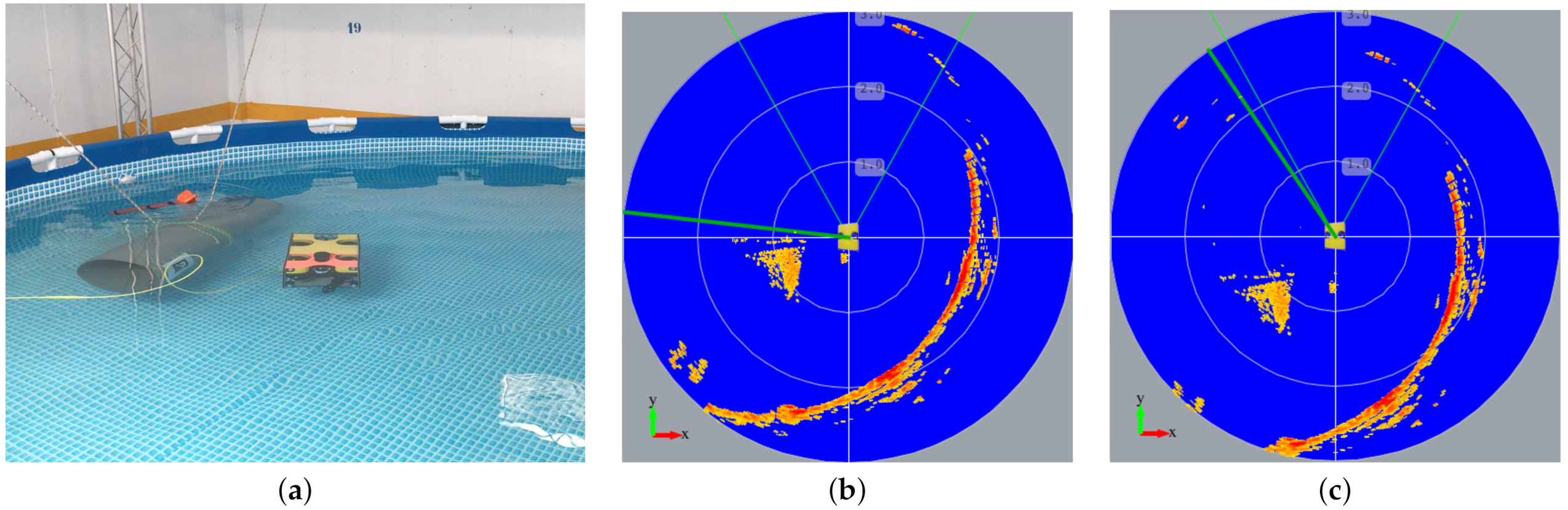
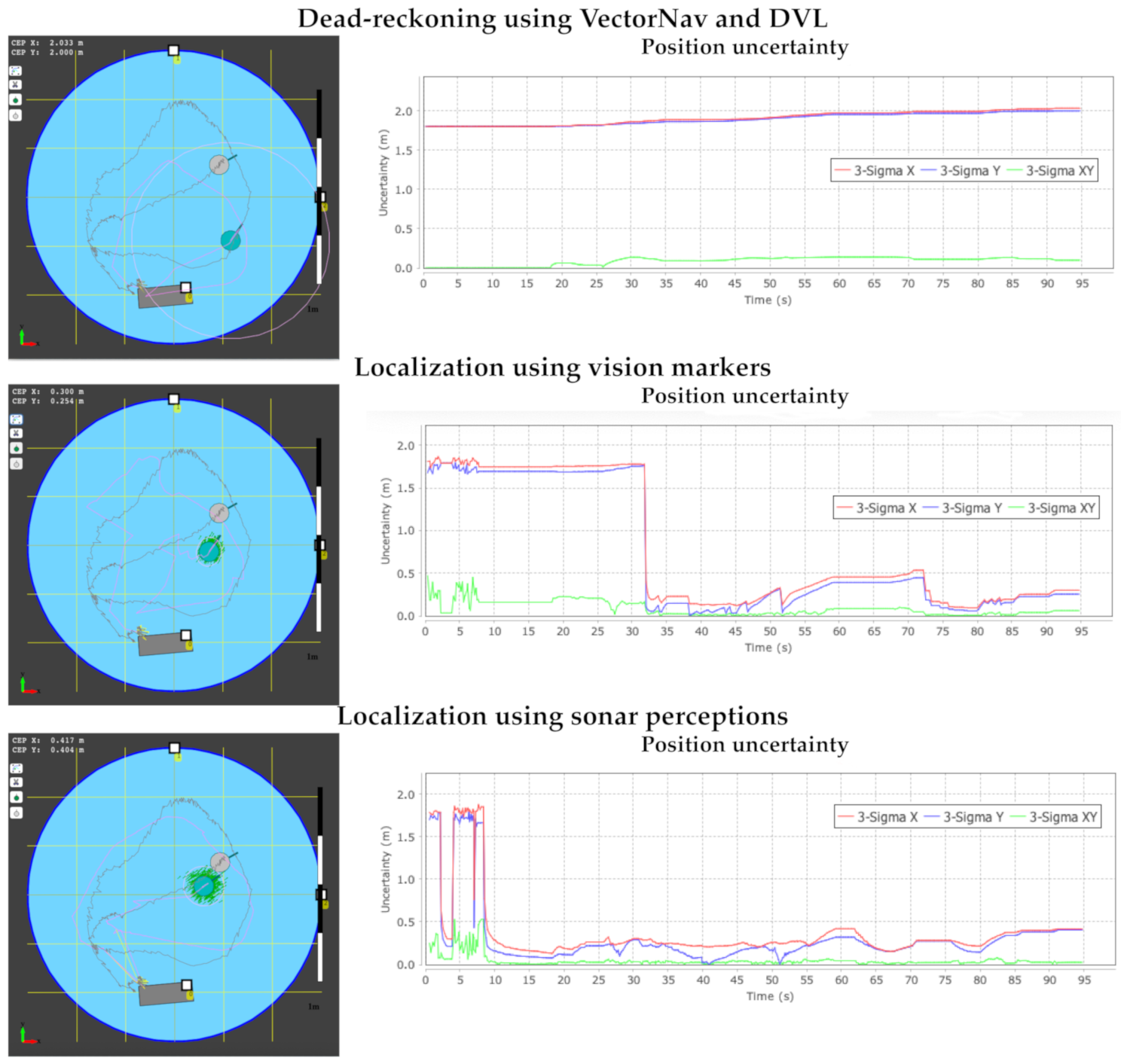
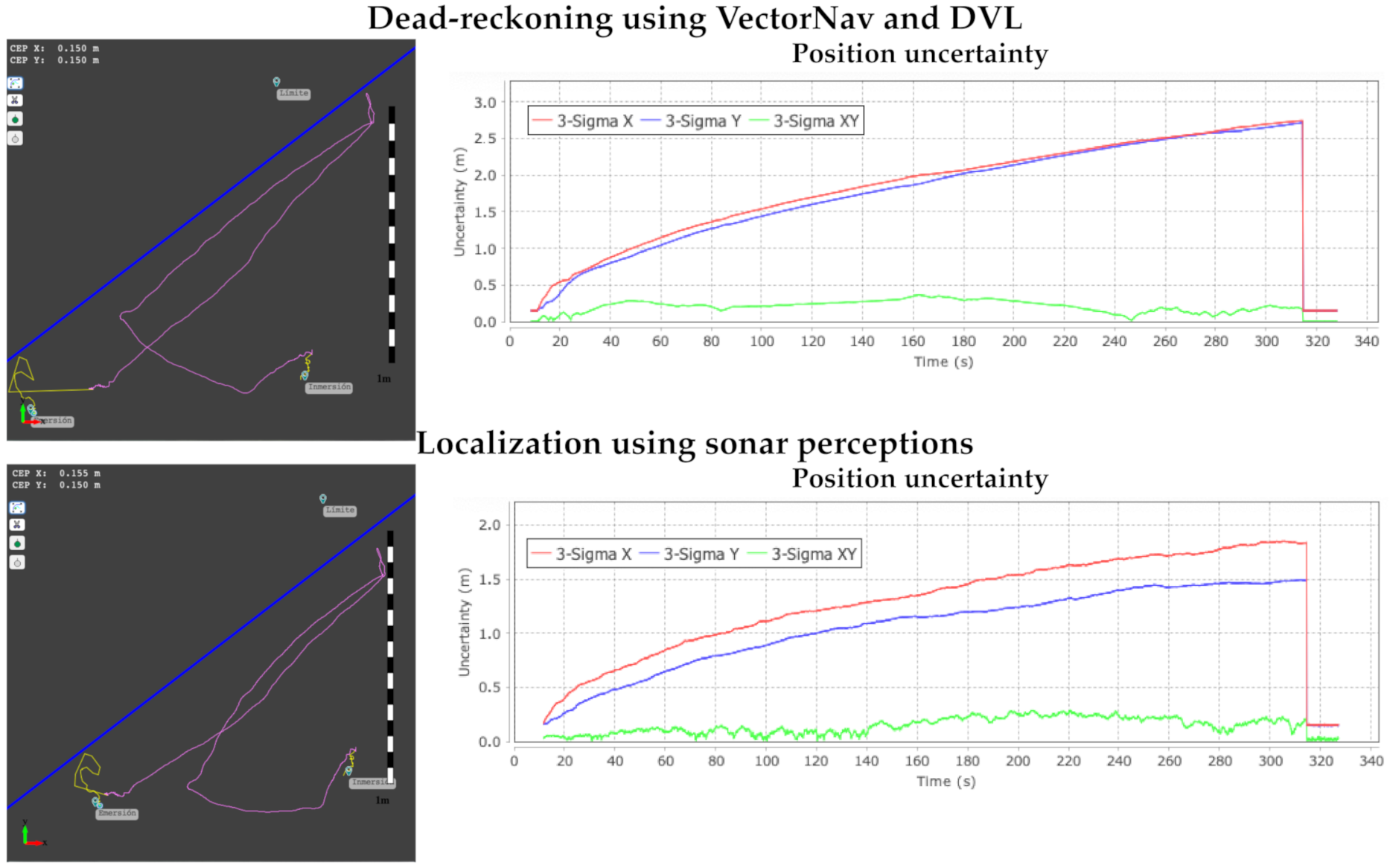
5.1. Experiments in the Swimming Pool Scenario
5.2. Experiments in the Dock Harbor Scenario
6. Conclusions and Future Works
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Petillot, Y.R.; Antonelli, G.; Casalino, G.; Ferreira, F. Underwater Robots: From Remotely Operated Vehicles to Intervention-Autonomous Underwater Vehicles. IEEE Robot. Autom. Mag. 2019, 26, 94–101. [Google Scholar] [CrossRef]
- Chitta, S.; Vemaza, P.; Geykhman, R.; Lee, D.D. Proprioceptive localization for a quadrupedal robot on known terrain. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Roma, Italy, 10–14 April 2007; pp. 4582–4587. [Google Scholar]
- Tal, A.; Klein, I.; Katz, R. Inertial Navigation System/Doppler Velocity Log (INS/DVL) Fusion with Partial DVL Measurements. Sensors 2017, 17, 415. [Google Scholar] [CrossRef]
- Melo, J.; Matos, A. Survey on advances on terrain based navigation for autonomous underwater vehicles. Ocean Eng. 2017, 139, 250–264. [Google Scholar] [CrossRef]
- Whitcomb, L.; Yoerger, D.; Singh, H. Advances in Doppler-based navigation of underwater robotic vehicles. In Proceedings 1999 IEEE International Conference on Robotics and Automation (ICRA), Detroit, MI, USA, 10–15 May 1999; pp. 399–406. [Google Scholar]
- Larsen, M.B. Synthetic long baseline navigation of underwater vehicles. In In Proceedings of the OCEANS 2000 MTS/IEEE Conference and Exhibition. Conference Proceedings (Cat. No.00CH37158), Providence, RI, USA, 11–14 September 2000; pp. 2043–2050. [Google Scholar]
- Zhang, J.; Han, Y.; Zheng, C.; Sun, D. Underwater target localization using long baseline positioning system. Appl. Acoust. 2016, 111, 129–134. [Google Scholar] [CrossRef]
- Smith, S.M.; Kronen, D. Experimental results of an inexpensive short baseline acoustic positioning system for AUV navigation. In Proceedings of the Oceans ’97. MTS/IEEE Conference Proceedings, Halifax, NS, Canada, 6–9 October 1997; pp. 714–720. [Google Scholar]
- Allotta, B.; Caiti, A.; Costanzi, R.; Fanelli, F.; Fenucci, D.; Meli, E.; Ridolfi, A. A new AUV navigation system exploiting unscented Kalman filter. Ocean Eng. 2016, 113, 121–132. [Google Scholar] [CrossRef]
- Khan, R.R.; Taher, T.; Hover, F.S. Accurate geo-referencing method for AUVs for oceanographic sampling. In Proceedings of the OCEANS 2010 MTS/IEEE SEATTLE, Seattle, WA, USA, 20–23 September 2010; pp. 1–5. [Google Scholar]
- Leonard, J.J.; Bennett, A.A.; Smith, C.M.; Feder, H.J.S. Autonomous Underwater Vehicle Navigation; Technical Memorandum 98-1; Technical Report; MIT Marine Robotics Laboratory: Cambridge, MA, USA, 1998. [Google Scholar]
- Morgado, M.; Batista, P.; Oliveira, P.; Silvestre, C. Position USBL/DVL sensor-based navigation filter in the presence of unknown ocean currents. Automatica 2011, 47, 2604–2614. [Google Scholar] [CrossRef]
- Bosch, J.; Gracias, N.; Ridao, P.; Istenič, K.; Ribas, D. Close-Range Tracking of Underwater Vehicles Using Light Beacons. Sensors 2016, 16, 429. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Shi, C.; Sun, D.; Han, Y. High-precision, limited-beacon-aided AUV localization algorithm. Ocean Eng. 2018, 149, 106–112. [Google Scholar] [CrossRef]
- Han, Y.; Wang, B.; Deng, Z.; Fu, M. A Combined Matching Algorithm for Underwater Gravity-Aided Navigation. IEEE/ASME Trans. Mechatronics 2018, 23, 233–241. [Google Scholar] [CrossRef]
- Gustafsson, F.; Gunnarsson, F.; Bergman, N.; Forssell, U.; Jansson, J.; Karlsson, R.; Nordlund, P.J. Particle filters for positioning, navigation, and tracking. IEEE Trans. Signal Process. 2002, 50, 425–437. [Google Scholar] [CrossRef]
- Li, Z.; Dosso, S.E.; Sun, D. Motion-Compensated Acoustic Localization for Underwater Vehicles. IEEE J. Ocean. Eng. 2016, 41, 840–851. [Google Scholar] [CrossRef]
- Masmitja, I.; Bouvet, P.-J.; Gomariz, S.; Aguzzi, J.; del Rio, J. Underwater mobile target tracking with particle filter using an autonomous vehicle. In Proceedings of the OCEANS 2017-Aberdeen, Aberdeen, UK, 19–22 June 2017; pp. 1–5. [Google Scholar]
- Garrido-Jurado, S.; Muñoz-Salinas, R.; Madrid-Cuevas, F.J.; Marín-Jiménez, M.J. Automatic generation and detection of highly reliable fiducial markers under occlusion. Pattern Recognit. 2014, 47, 2280–2292. [Google Scholar] [CrossRef]
- Garrido-Jurado, S.; Muñoz-Salinas, R.; Madrid-Cuevas, F.J.; Medina-Carnicer, R. Generation of fiducial marker dictionaries using mixed integer linear programming. Pattern Recognit. 2016, 51, 481–491. [Google Scholar] [CrossRef]
- Nurunnabi, A.; Sadahiro, Y.; Laefer, D. Robust statistical approaches for circle fitting in laser scanning three-dimensional point cloud data. Pattern Recognit. 2018, 81, 417–431. [Google Scholar] [CrossRef]
- Coope, I.D. Circle fitting by linear and nonlinear least squares. J. Optim. Theory Appl. 1993, 76, 381–388. [Google Scholar] [CrossRef]
- Fischler, M.A.; Bolles, R.C. Random sample consensus: A paradigm for model fitting with applications to image analysis and automated cartography. Commun. ACM 1981, 24, 381–395. [Google Scholar] [CrossRef]
- Torr, P.H.S.; Zisserman, A. MLESAC: A New Robust Estimator with Application to Estimating Image Geometry. Comput. Vis. Image Underst. 2000, 78, 138–156. [Google Scholar] [CrossRef]
- Gasós, J.; Martín, A. Mobile Robot Localization using fuzzy maps. In Fuzzy Logic in Artificial Intelligence: Towards Intelligent Systems; Lecture Notes in Computer Science; Martin, T.P., Ralescu, A.L., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; Volume 1188, pp. 271–341. [Google Scholar]
- Herrero-Pérez, D.; Alcaraz-Jimenez, J.; Martínez-Barberá, H. Mobile Robot Localization Using Fuzzy Segments. Int. J. Adv. Robot. Syst. 2013, 10, 1–16. [Google Scholar] [CrossRef]
- Saffiotti, A.; Konolige, K.; Ruspini, E. A multivalued-logic approach to integrating planning and control. Artif. Intell. 1995, 76, 481–526. [Google Scholar] [CrossRef]
- Zadeh, L. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Zhang, L.; Ghosh, B. Line Segment Based Map Building and Localization Using 2D Laser Rangefinder. In Proceedings of the Proceedings 2000 ICRA. Millennium Conference. IEEE International Conference on Robotics and Automation. Symposia Proceedings (Cat. No.00CH37065), San Francisco, CA, USA, 24–28 April 2000; pp. 2538–2543. [Google Scholar]
- Borges, G.; Aldon, M. Line Extraction in 2D Range Images for Mobile Robotics. Intell. Robot. Syst. 2004, 40, 267–297. [Google Scholar] [CrossRef]
- Rekleitis, I.M. A Particle Filter Tutorial for Mobile Robot Localization. Technical; Report TR-CIM-04-02; Technical Report; Centre for Intelligent Machines, McGill University: Montreal, QC, Canada, 2004. [Google Scholar]
- Vallicrosa, G.; Ridao, P. Sum of gaussian single beacon range-only localization for AUV homing. Annu. Rev. Control 2016, 42, 177–187. [Google Scholar] [CrossRef]
- Liu, J.S.; Chen, R.; Logvinenko, T. Theoretical Framework for Sequential Importance Sampling with Resampling. In Sequential Monte Carlo Methods in Practice; Doucet, A., de Freitas, N., Gordon, N., Eds.; Springer: New York, NY, USA, 2001; pp. 225–246. [Google Scholar]
- Campos, R.; Gracias, N.; Ridao, P. Underwater Multi-Vehicle Trajectory Alignment and Mapping Using Acoustic and Optical Constraints. Sensors 2016, 16, 387. [Google Scholar] [CrossRef] [PubMed]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Martínez-Barberá, H.; Bernal-Polo, P.; Herrero-Pérez, D. Sensor Modeling for Underwater Localization Using a Particle Filter. Sensors 2021, 21, 1549. https://doi.org/10.3390/s21041549
Martínez-Barberá H, Bernal-Polo P, Herrero-Pérez D. Sensor Modeling for Underwater Localization Using a Particle Filter. Sensors. 2021; 21(4):1549. https://doi.org/10.3390/s21041549
Chicago/Turabian StyleMartínez-Barberá, Humberto, Pablo Bernal-Polo, and David Herrero-Pérez. 2021. "Sensor Modeling for Underwater Localization Using a Particle Filter" Sensors 21, no. 4: 1549. https://doi.org/10.3390/s21041549
APA StyleMartínez-Barberá, H., Bernal-Polo, P., & Herrero-Pérez, D. (2021). Sensor Modeling for Underwater Localization Using a Particle Filter. Sensors, 21(4), 1549. https://doi.org/10.3390/s21041549







