Symmetry Analysis of Oriental Polygonal Pagodas Using 3D Point Clouds for Cultural Heritage
Abstract
:1. Introduction
2. Methods
2.1. Preprocessing
2.1.1. Data Collection
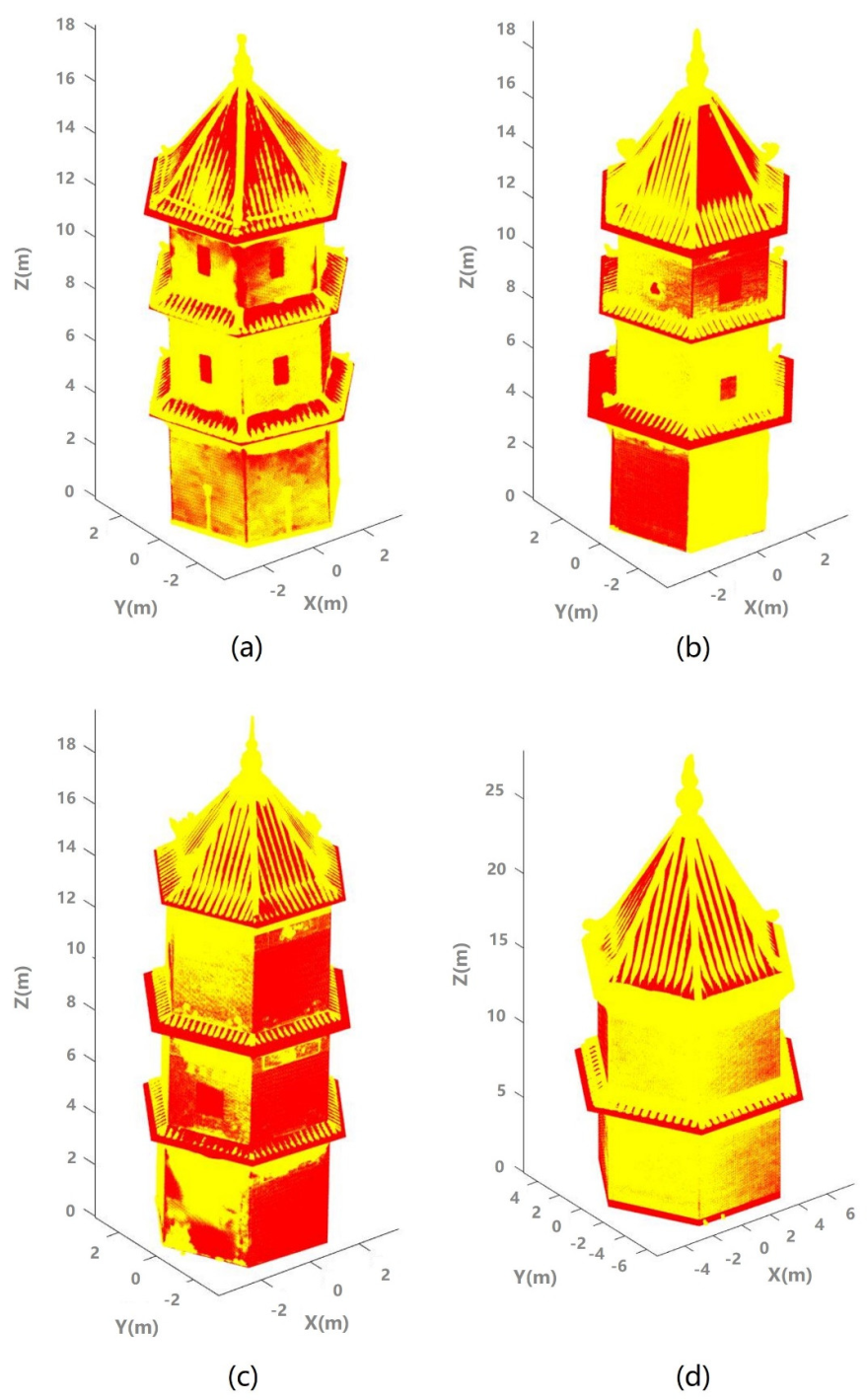
2.1.2. Pagoda Extraction
2.2. Model Parameter Estimation
2.2.1. Planar Patch Extraction Based on the PCA
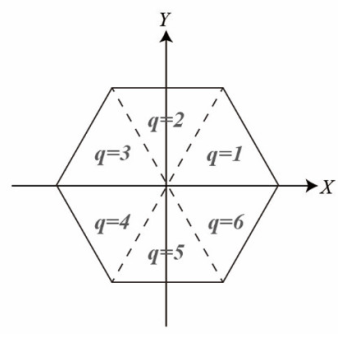
2.2.2. Geometric Model
Polygonal Prism/Pyramid for Different Components of the Pagodas
Geometric Model for the Entire Pagoda
2.2.3. Least-Squares Estimation
2.2.4. Initial Value Estimation
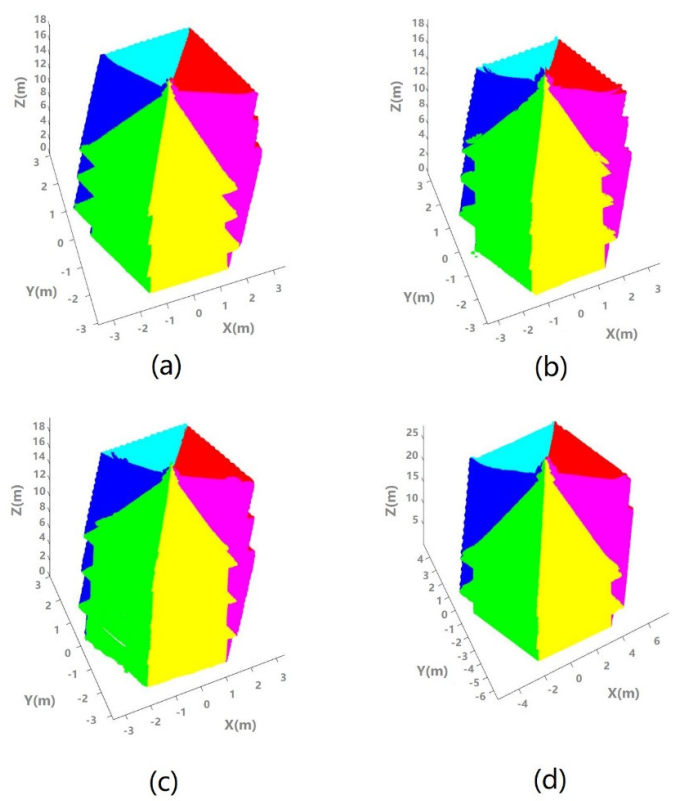
2.3. Sysmmetry Analysis
2.3.1. Rigid Body Transformation
2.3.2. ICP-Based Sector Matching
3. Experiment
4. Results
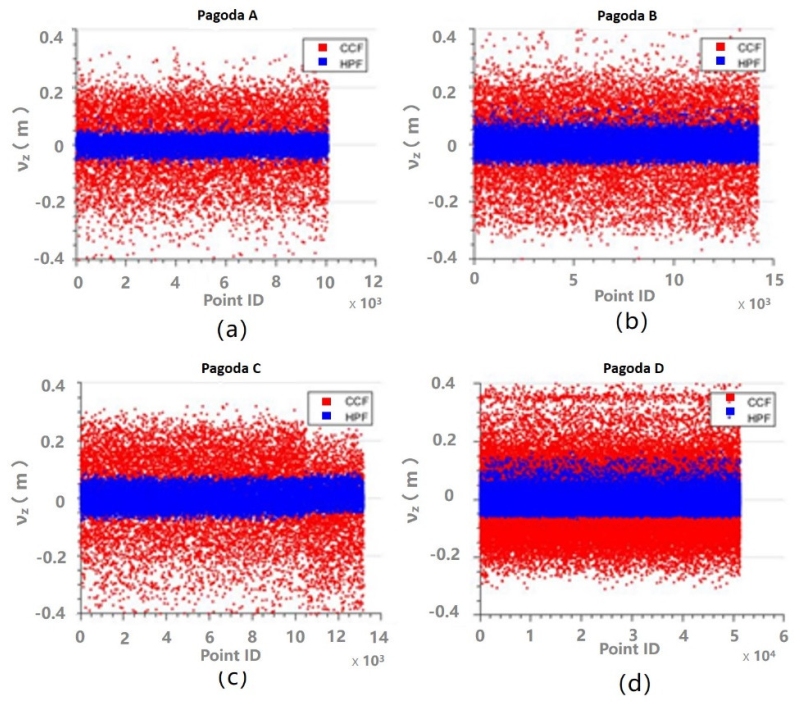
4.1. Fitting Estimates Compared to the Conventional Cylindrical/Conic Models
4.2. Geometric Fitting of the Proposed Pagoda Model
4.3. Symmetry Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tang, X.X.; Chen, C.J. The Symmetry in the Traditional Chinese Architecture. Appl. Mech. Mater. 2014, 488, 669–675. [Google Scholar] [CrossRef]
- Lu, Y. A History of Chinese Science and Technology; Springer: Berlin, Germany, 2015; Volume 3, pp. 1–624. [Google Scholar]
- Heritage, E. 3D Laser Scanning for Heritage: Advice and Guidance to Users on Laser Scanning in Archaeology and Architecture; Historic England: Swindon, UK, 2007; pp. 1–44. [Google Scholar]
- Lindenbergh, R. Engineering applications. In Airborne and Terrestrial Laser Scanning; Vosselman, G., Maas, H.-G., Eds.; Whittles Publishing: Scotland, UK, 2010; pp. 237–269. [Google Scholar]
- Luhmann, T.; Robson, S.; Kyle, S.A.; Harley, I.A. Close Range Photogrammetry: Principles, Techniques and Applications; Blackwell Publishing Ltd: Oxford, UK, 2006. [Google Scholar]
- Remondino, F. Heritage Recording and 3D Modeling with Photogrammetry and 3D Scanning. Remote Sens. 2011, 3, 1104–1138. [Google Scholar] [CrossRef] [Green Version]
- Aicardi, I.; Chiabrando, F.; Lingua, A.M.; Noardo, F. Recent trends in cultural heritage 3D survey: The photogrammetric computer vision approach. J. Cult. Herit. 2017, 32, 257–266. [Google Scholar] [CrossRef]
- Berner, A.; Bokeloh, M.; Wand, M.; Schilling, A.; Seidel, H.P. A graph-based approach to symmetry detection. In Proceedings of the IEEE/ EG Symposium on Volume and Point-Based Graphics (2008), Los Angeles, CA, USA, 10–11 August 2008; Volume 23, pp. 1–8. [Google Scholar]
- Combes, B.; Hennessy, R.; Waddington, J.; Roberts, N.; Prima, S. Automatic symmetry plane estimation of bilateral objects in point clouds. In Proceedings of the 2008 IEEE Conference on Computer Vision and Pattern Recognition, Anchorage, AK, USA, 23–28 June 2008; pp. 1–8. [Google Scholar] [CrossRef] [Green Version]
- Benoît, C.; Sylvain, P. New algorithms to map asymmetries of 3D surfaces. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention—MICCAI 2008, New York, NY, USA, 6–10 September 2008; Volume 11. [Google Scholar] [CrossRef]
- Jiang, W.; Xu, K.; Cheng, Z.Q.; Zhang, H. Skeleton-based intrinsic symmetry detection on point clouds. Graph. Models 2013, 75, 177–188. [Google Scholar] [CrossRef]
- Li, E.; Zhang, X.P.; Chen, Y.Y. Symmetry based Chinese Ancient Architecture Reconstruction from Incomplete Point Cloud. In Proceedings of the 5th International Conference on Digital Home, Guangzhou, China, 28–30 November 2014; pp. 157–161. [Google Scholar] [CrossRef]
- Shao, J.; Gong, T.; Yang, T.; Xu, J. Incomplete Surface Reconstruction for Statue Point Cloud based on Symmetry. In Proceedings of the ITM Web of Conferences, Hangzhou, China, 29–31 July 2016; Volume 7, p. 07002. [Google Scholar]
- Xue, F.; Chen, K.; Lu, W. Architectural symmetry detection from 3D urban point clouds: A derivative-free optimization (DFO) approach. In Advances in Informatics and Computing in Civil and Construction Engineering; Springer: Berlin/Heidelberg, Germany, 2019; pp. 513–519. [Google Scholar]
- Xue, F.; Lu, W.; Webster, C.J.; Chen, K. A derivative-free optimization-based approach for detecting architectural symmetries from 3D point clouds. Isprs J. Photogramm. Remote Sens. 2019, 148, 32–40. [Google Scholar] [CrossRef]
- Li, H.; Zhu, Q.; Huang, M.; Guo, Y.; Qin, J. Pose Estimation of Sweet Pepper through Symmetry Axis Detection. Sensors 2018, 18, 3083. [Google Scholar] [CrossRef] [Green Version]
- Cheng, L.; Wu, Y.; Chen, S.; Zong, W.; Yuan, Y.; Sun, Y.; Zhuang, Q.; Li, M. A Symmetry-Based Method for LiDAR Point Registration. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 285–299. [Google Scholar] [CrossRef]
- Liang, H.; Li, W.; Lai, S.; Zhu, L.; Jiang, W.; Zhang, Q. The integration of terrestrial laser scanning and terrestrial and unmanned aerial vehicle digital photogrammetry for the documentation of Chinese classical gardens –A case study of Huanxiu Shanzhuang, Suzhou, China. J. Cult. Herit. 2018, 33, 222–230. [Google Scholar] [CrossRef]
- Jo, Y.; Hong, S. Three-Dimensional Digital Documentation of Cultural Heritage Site Based on the Convergence of Terrestrial Laser Scanning and Unmanned Aerial Vehicle Photogrammetry. Int. J. Geo-Inf. 2019, 8, 53. [Google Scholar] [CrossRef] [Green Version]
- Martínez-Carricondo, P.; Carvajal-Ramírez, F.; Yero-Paneque, L.; Agüera-Vega, F. Combination of nadiral and oblique UAV photogrammetry and HBIM for the virtual reconstruction of cultural heritage. Case study of Cortijo del Fraile in Níjar, Almería (Spain). Build. Res. Inf. 2019, 48, 140–159. [Google Scholar] [CrossRef]
- Manajitprasert, S.; Tripathi, N.K.; Arunplod, S. Three-dimensional (3D) Modeling of cultural heritage site using UAV imagery: A case study of the pagodas in Wat Maha That, Thailand. Appl. Sci. 2019, 9, 3640. [Google Scholar] [CrossRef] [Green Version]
- Chan, T.O.; Lichti, D.D.; Belton, D.; Klingseisen, B.; Helmholz, P. Survey Accuracy Analysis of a Hand-held Mobile LiDAR Device for Cultural Heritage Documentation. Photogramm. Fernerkund. Geoinf. 2016, 2016, 153–165. [Google Scholar] [CrossRef]
- Erenoglu, R.C.; Akcay, O.; Erenoglu, O. An UAS-Assisted multi-Sensor approach for 3D modeling and reconstruction of cultural heritage site. J. Cult. Herit. 2017, 26, 79–90. [Google Scholar] [CrossRef]
- Herrero-Tejedor, T.R.; Arqués Soler, F.; López-Cuervo Medina, S.; de la O Cabrera, M.R.; Martín Romero, J.L. Documenting a cultural landscape using point-cloud 3d models obtained with geomatic integration techniques. The case of the El Encín atomic garden, Madrid (Spain). PLoS ONE 2020, 15, e0235169. [Google Scholar] [CrossRef] [PubMed]
- Andriasyan, M.; Moyano, J.; Nieto-Julián, J.E.; Antón, D. From Point Cloud Data to Building Information Modelling: An Automatic Parametric Workflow for Heritage. Remote Sens. 2020, 12, 1094. [Google Scholar] [CrossRef] [Green Version]
- Chan, T.O.; Xia, L.; Tang, J.; Liu, M.; Lang, W.; Chen, T.; Xiao, H. Central axis estimation for ancient Chinese pagodas based on geometric modelling and UAV-based photogrammetry. Int. Arch. Photogramm. Remote Sens. Spatial Inf. Sci. 2020, 43, 751–756. [Google Scholar] [CrossRef]
- Yanagi, H.; Chikatsu, H. Performance evaluation of 3D modeling software for UAV photogrammetry. Isprs Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 41, 147–152. [Google Scholar] [CrossRef]
- Zhang, W.; Qi, J.; Wan, P.; Wang, H.; Xie, D.; Wang, X.; Yan, G. An Easy-to-Use Airborne LiDAR Data Filtering Method Based on Cloth Simulation. Remote Sens. 2016, 8, 501. [Google Scholar] [CrossRef]
- Luo, D.; Wang, Y. Rapid extracting pillars by slicing point clouds. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2008, 37 Pt B3, 215–218. [Google Scholar]
- Chan, T.O.; Lichti, D.D. Automatic In Situ Calibration of a Spinning Beam LiDAR System in Static and Kinematic Modes. Remote Sens. 2015, 7, 10480–10500. [Google Scholar] [CrossRef] [Green Version]
- El-Halawany, S.I.; Lichti, D.D. Detecting road poles from mobile terrestrial laser scanning data. GIsci. Remote Sens. 2013, 50, 704–722. [Google Scholar] [CrossRef]
- Demantké, J.; Mallet, C.; David, N.; Vallet, B. Dimensionality based scale selection in 3D LiDAR point cloud. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2011, 38, 97–102. [Google Scholar] [CrossRef] [Green Version]
- Chan, T.O.; Lichti, D.D.; Belton, D.; Nguyen, H.L. Automatic point cloud registration using a single octagonal lamp pole. Photogramm. Eng. Remote Sens. 2016, 82, 257–269. [Google Scholar] [CrossRef]
- Förstner, W.; Wrobel, B. Mathematical Concepts in Photogrammetry. In Manual of Photogrammetry, 5th ed.; McGlone, J.C., Mikhail, E.M., Bethel, J., Mullen, R., Eds.; American Society of Photogrammetry and Remote Sensing: Bethesda, MA, USA, 2004; pp. 15–180. [Google Scholar]
- Besl, P.J.; Mckay, H.D. A method for registration of 3-D shapes. IEEE Trans. Pattern Anal. Mach. Intell. 1992, 14, 239–256. [Google Scholar] [CrossRef]









| Pagoda Name | Location | Approx. No. of Images | No. of Floor | Survey Platform | Sensor Dimension/ Focal Length | Fly Height | Capture Period |
|---|---|---|---|---|---|---|---|
| A (Wenfeng) | Pengyu District, Guangzhou, China | 102 | 3 | UAV | 13.20 mm/ 10.26 mm | 3–8 m | July, 2017 |
| B (Wenchang) | Pengyu District, Guangzhou, China | 99 | 3 | UAV | 13.20 mm/ 10.26 mm | 3–8 m | Oct, 2020 |
| C (Shenjing Wen) | Huangpu District, Guangzhou, China | 117 | 3 | UAV | 13.20 mm/ 10.26 mm | 3–8 m | Oct, 2020 |
| D (Liwan Wen) | Liwan District, Guangzhou, China | 37 | 2 | Hand-held | 23.50 mm/ 18.00 mm | - | Oct, 2020 |
| Pagoda A | Pagoda B | Pagoda C | Pagoda D | |||||
|---|---|---|---|---|---|---|---|---|
| Param. | CCF | HPF | CCF | HPF | CCF | HPF | CCF | HPF |
| Est. ± σ | Est. ± σ | Est. ± σ | Est. ± σ | Est. ± σ | Est. ± σ | Est. ± σ | Est. ± σ | |
| Xc (m) | −0.108 ± 4.9 × 10−5 | −0.108 ± 3.0 × 10−7 | 0.035 ± 3.6 × 10−5 | 0.036 ± 2.2 × 10−7 | −0.013 ± 4.2 × 10−5 | −0.019 ± 2.4 × 10−7 | 0.235 ± 1.9 × 10−5 | 0.245 ± 1.1 × 10−7 |
| Yc (m) | −0.018 ± 5.0 × 10−5 | −0.018 ± 2.9 × 10−7 | −0.088 ± 3.6 × 10−5 | −0.090 ± 2.1 × 10−7 | −0.043 ± 4.3 × 10−5 | −0.046 ± 2.4 × 10−7 | −0.243 ± 1.9 × 10−5 | −0.246 ± 1.1 × 10−7 |
| Ω (°) | −0.558 ± 1.6 × 10−3 | −0.448 ± 9.9 × 10−6 | 0.401 ± 2.8 × 10−5 | 0.401 ± 1.7 × 10−7 | 1.661 ± 3.0 × 10−5 | 1.604 ± 1.8 × 10−7 | 0.573 ± 6.7 × 10−6 | 0.401 ± 4.1 × 10−8 |
| Φ (°) | −1.803 ± 1.66 × 10−3 | −1.792 ± 9.9 × 10−6 | 1.031 ± 2.8 × 10−5 | 1.089 ± 1.7 × 10−7 | 0.458 ± 3.1 × 10−5 | 0.229 ± 1.9 × 10−7 | 3.896 ± 6.8 × 10−6 | 0.516 ± 4.2 × 10−8 |
| Ψ (°) | n/a | −12.832 ± 1.6 × 10−5 | n/a | −11.517 ± 2.6 × 10−7 | n/a | −1.203 ± 2.5 × 10−7 | n/a | −2.177 ± 6.2 × 10−8 |
| k | 0.661 ± 2.8 × 10−5 | 0.719 ± 2.0 × 10−7 | 0.535 ± 2.5 × 10−5 | 0.581 ± 1.8 × 10−7 | 0.649 ± 3.1 × 10−5 | 0.694 ± 2.2 × 10−7 | 0.520 ± 6.2 × 10−6 | 0.566 ± 4.4 × 10−8 |
| R0 (m) | 1.672 ± 2.7 × 10−5 | 1.824 ± 1.9 × 10−7 | 1.540 ± 2.2 × 10−5 | 1.674 ± 1.5 × 10−7 | 1.589 ± 2.2 × 10−5 | 1.727 ± 1.6 × 10−7 | 3.020 ± 1.1 × 10−5 | 3.319 ± 7.6 × 10−8 |
| Pagoda A | Pagoda B | Pagoda C | Pagoda D | |||||
|---|---|---|---|---|---|---|---|---|
| Param. | CCF | HPF | CCF | HPF | CCF | HPF | CCF | HPF |
| Est. ± σ | Est. ± σ | Est. ± σ | Est. ± σ | Est. ± σ | Est. ± σ | Est. ± σ | Est. ± σ | |
| Xc (m) | −0.286 ± 1.7 × 10−3 | −0.099 ± 2.0 × 10−6 | 0.006 ± 5.9 × 10−4 | 0.155 ± 1.3 × 10−6 | −0.133 ± 9.3 × 10−4 | 0.061 ± 1.5 × 10−6 | 1.591 ± 4.8 × 10−4 | 0.871 ± 9.7 × 10−7 |
| Yc (m) | 0.351 ± 1.7 × 10−3 | −0.006 ± 1.9 × 10−6 | −0.121 ± 6.2 × 10−4 | −0.120 ± 1.2 × 10−6 | −0.223 ± 8.8 × 10−4 | 0.014 ± 1.6 × 10−6 | −1.134 ± 4.8 × 10−4 | −0.851 ± 9.7 × 10−7 |
| Ω (°) | −3.328 ± 1.4 × 10−2 | −0.552 ± 3.6 × 10−5 | 0.745 ± 1.8 × 10−4 | 0.630 ± 4.8 × 10−7 | 4.011 ± 1.6 × 10−4 | 1.948 ± 4.6 × 10−7 | −2.292 ± 6.7 × 10−5 | 0.859 ± 2.8 × 10−7 |
| Φ (°) | −3.947 ± 1.4 × 10−2 | −2.683 ± 3.7 × 10−5 | −2.349 ± 1.7 × 10−4 | 0.172 ± 4.8 × 10−7 | −2.578 ± 1.7 × 10−4 | −0.745 ± 4.4 × 10−7 | 5.500 ± 6.9 × 10−5 | 0.802 ± 2.9 × 10−7 |
| Ψ (°) | n/a | −12.839 ± 2.8 × 10−5 | n/a | −9.339 ± 3.6 × 10−7 | n/a | −3.266 ± 4.1 × 10−7 | n/a | −1.948 ± 1.6 × 10−7 |
| k | 2.483 ± 1.9 × 10−3 | 1.237 ± 5.5 × 10−6 | 1.307 ± 3.5 × 10−4 | 1.145 ± 2.0 × 10−6 | 2.026 ± 8.1 × 10−4 | 1.472 ± 3.4 × 10−6 | 1.481 ± 2.7 × 10−4 | 0.816 ± 1.0 × 10−6 |
| R0 (m) | 2.817 ± 5.5 × 10−4 | 3.159 ± 5.4 × 10−7 | 2.644 ± 7.8 × 10−5 | 2.913 ± 3.5 × 10−7 | 2.674 ± 2.4 × 10−4 | 2.988 ± 4.2 × 10−7 | 4.608 ± 1.4 × 10−4 | 5.126 ± 3.2 × 10−7 |
| Pagoda A | Pagoda B | Pagoda C | Pagoda D | |||||
|---|---|---|---|---|---|---|---|---|
| Param. | CCF | HPF | CCF | HPF | CCF | HPF | CCF | HPF |
| Est. ± σ | Est. ± σ | Est. ± σ | Est. ± σ | Est. ± σ | Est. ± σ | Est. ± σ | Est. ± σ | |
| Xc (m) | 0.003 ± 1.0 × 10−4 | 0.000 ± 2.6 × 10−7 | 0.098 ± 4.2 × 10−5 | 0.088 ± 2.6 × 10−7 | −0.102 ± 3.3 × 10−5 | −0.104 ± 2.1 × 10−7 | 0.862 ± 8.5 × 10−6 | 0.885 ± 5.3 × 10−8 |
| Yc (m) | −0.019 ± 1.0 × 10−4 | −0.018 ± 2.6 × 10−7 | −0.203 ± 4.3 × 10−5 | −0.199 ± 2.7 × 10−7 | −0.033 ± 3.2 × 10−5 | −0.035 ± 2.0 × 10−7 | −0.896 ± 8.5 × 10−6 | −0.929 ± 5.3 × 10−8 |
| Ω (°) | 0.222 ± 8.6 × 10−3 | 0.241 ± 2.2 × 10−5 | 0.057 ± 5.7 × 10−5 | 0.401 ± 3.5 × 10−7 | 1.203 ± 3.1 × 10−5 | 1. 261 ± 2.0 × 10−7 | −0.229 ± 5.6 × 10−6 | −0.401 ± 3.0 × 10−8 |
| Φ (°) | −1.506 ± 8.5 × 10−3 | −1.424 ± 2.1 × 10−5 | 0.115 ± 5.6 × 10−5 | 0.344 ± 3.5 × 10−7 | 0.458 ± 3.2 × 10−5 | 0.401 ± 2.0 × 10−7 | −0.057 ± 5.5 × 10−6 | −0.115 ± 3.0 × 10−8 |
| Ψ (°) | n/a | −12.863 ± 1.3 × 10−5 | n/a | −9.053 ± 2.3 × 10−7 | n/a | −3.381 ± 1.7 × 10−7 | n/a | −1.834 ± 2.0 × 10−8 |
| k | n/a | n/a | 0.002 ± 4.1 × 10−5 | n/a | −0.004 ± 2.2 × 10−5 | n/a | 0.001 ± 4.5 × 10−6 | n/a |
| R0 (m) | 2.426 ± 7.3 × 10−5 | 2.653 ± 2.1 × 10−7 | 2.531 ± 3.0 × 10−5 | 2.769 ± 2.2 × 10−7 | 2.654 ± 2.3 × 10−5 | 2.909 ± 1.7 × 10−7 | 5.046 ± 6.8 × 10−6 | 5.522 ± 4.8 × 10−8 |
| Param. | Pagoda A | Pagoda B | Pagoda C | Pagoda D |
|---|---|---|---|---|
| Est. ± σ | Est. ± σ | Est. ± σ | Est. ± σ | |
| Xc (m) | 0.049 ± 3.5 × 10−4 | −0.007 ± 8.7 × 10−4 | −0.137 ± 4.0 × 10−4 | 1.004 ± 4.8 × 10−4 |
| Yc (m) | −0.015 ± 3.5 × 10−4 | 0.076 ± 9.6 × 10−4 | 0.141 ± 4.0 × 10−4 | −0.902 ± 5.0 × 10−4 |
| Ω (°) | 0.097 ± 4.5 × 10−3 | 1.089 ± 1.1 × 10−4 | 1.203 ± 4.3 × 10−5 | −0.172 ± 6.5 × 10−5 |
| Φ (°) | −1.901 ± 4.4 × 10−3 | 0.516 ± 1.1 × 10−4 | 0.458 ± 4.3 × 10−5 | −0.115 ± 6.3 × 10−5 |
| Ψ (°) | −12.800 ± 1.7 × 10−2 | −9.282 ± 3.9 × 10−4 | −3.438 ± 1.6 × 10−4 | −1.834 ± 1.1 × 10−4 |
| k1 | 0.721 ± 6.6 × 10−4 | 0.586 ± 1.6 × 10−3 | 0.705 ± 6.5 × 10−4 | 0.569 ± 1.2 × 10−3 |
| R1 (m) | 5.474 ± 3.3 × 10−3 | 10.074 ± 2.3 × 10−2 | 12.491 ± 1.0 × 10−2 | 13.926 ± 2.1 × 10−2 |
| k2 | 1.216 ± 1.5 × 10−2 | 1.197 ± 2.3 × 10−2 | 1.544 ± 1.3 × 10−2 | 1.008 ± 1.7 × 10−2 |
| R2 (m) | 7.374 ± 5.0 × 10−2 | 18.063 ± 2.9 × 10−1 | 24.267 ± 1.8 × 10−1 | 20.986 ± 2.5 × 10−1 |
| R3 (m) | 2.653 ± 5.3 × 10−4 | 2.769 ± 5.9 × 10−4 | 2.908 ± 2.3 × 10−4 | 5.523 ± 3.4 × 10−4 |
| k4 | 1.667 ± 2.1 × 10−2 | 2.426 ± 3.1 × 10−1 | 1.928 ± 4.9 × 10−2 | 1.694 ± 3.4 × 10−2 |
| R4 (m) | 2.679 ± 8.5 × 10−3 | 24.733 ± 2.7 × 100 | 20.255 ± 4.3 × 10−1 | 18.653 ± 2.5 × 10−1 |
| R5 (m) | 2.768 ± 5.4 × 10−4 | 2.774 ± 7.1 × 10−4 | 2.959 ± 2.9 × 10−4 | 5.520 ± 2.9 × 10−4 |
| k6 | 1.608 ± 2.7 × 10−2 | 3.016 ± 3.0 × 10−1 | 1.692 ± 3.6 × 10−2 | n/a |
| R6 (m) | −3.840 ± 1.2 × 10−1 | 17.982 ± 1.5 × 100 | 10.896 ± 1.6 × 10−1 | n/a |
| R7 (m) | 2.878 ± 5.3 × 10−4 | 2.854 ± 6.7 × 10−4 | 3.050 ± 3.3 × 10−4 | n/a |
| Pagoda A | Pagoda B | Pagoda C | Pagoda D | Mean | |
|---|---|---|---|---|---|
| RMSErot (m) | 0.0424 | 0.0572 | 0.0389 | 0.0632 | 0.0504 |
| RMSEref (m) | 0.0486 | 0.0548 | 0.0451 | 0.0597 | 0.0520 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chan, T.O.; Xia, L.; Chen, Y.; Lang, W.; Chen, T.; Sun, Y.; Wang, J.; Li, Q.; Du, R. Symmetry Analysis of Oriental Polygonal Pagodas Using 3D Point Clouds for Cultural Heritage. Sensors 2021, 21, 1228. https://doi.org/10.3390/s21041228
Chan TO, Xia L, Chen Y, Lang W, Chen T, Sun Y, Wang J, Li Q, Du R. Symmetry Analysis of Oriental Polygonal Pagodas Using 3D Point Clouds for Cultural Heritage. Sensors. 2021; 21(4):1228. https://doi.org/10.3390/s21041228
Chicago/Turabian StyleChan, Ting On, Linyuan Xia, Yimin Chen, Wei Lang, Tingting Chen, Yeran Sun, Jing Wang, Qianxia Li, and Ruxu Du. 2021. "Symmetry Analysis of Oriental Polygonal Pagodas Using 3D Point Clouds for Cultural Heritage" Sensors 21, no. 4: 1228. https://doi.org/10.3390/s21041228
APA StyleChan, T. O., Xia, L., Chen, Y., Lang, W., Chen, T., Sun, Y., Wang, J., Li, Q., & Du, R. (2021). Symmetry Analysis of Oriental Polygonal Pagodas Using 3D Point Clouds for Cultural Heritage. Sensors, 21(4), 1228. https://doi.org/10.3390/s21041228













