Automatic Identification System (AIS) Dynamic Data Integrity Monitoring and Trajectory Tracking Based on the Simultaneous Localization and Mapping (SLAM) Process Model
Abstract
1. Introduction
- a.
- Fault Tree Analysis (FTA)—the method of analysis designed to determine which type of unfitness, damage of the object, an external event or a combination thereof can generate an object failure. This method is presented in the form of a failure tree [15];
- b.
- Multivariate statistical analysis—a method that examines the confidence degree of received information. The method is based on the analysis of recorded data detailing the study of information affecting the safety of navigation. It is possible to determine integrity and availability of binary channel transmission. Multivariate statistical estimation is used in this method [16];
- c.
- Operating states graph—the method of presentation for the reliability structure of the object. This method is used for reliability evaluation. On the basis of stochastic processes, this method is an effective way for reliability estimation of renewable objects [15];
- d.
- Stochastic methods with the use of Markov and semi-Markov process—provide a convenient mathematical apparatus enabling the description and investigation of actual random processes. They are an important class of stochastic processes, which allows a mathematical description of the change of random quantities in time [15,16];
- e.
- Probability model based on the chi-square test presented in [10]. The chi-square test is used to test hypotheses. The value of the test is assessed using the chi-square distribution. The test most often used in practice. We can use it to test the compliance of both measurable and immeasurable features.
- f.
- Generalized likelihood ratio (GLR) control method for detecting changes in the parameters of system for individual observations. The method usually used for monitoring system is based on taking a sample of n observations at each sampling time point, where n is large enough that a regression model can be fitted at each sampling point using these n observations [17,18].
2. Materials and Methods
2.1. Simulation of Automatic Identification System (AIS) Dynamic Data
- -
- based on EKF-SLAM estimator, on the basis of radar bearing and distance to fixed navigation aid;
- -
- based on the mathematical count of the ship’s movement (Dead Reckoning);
- -
- based on the simulated position of the object using the GPS system.
2.2. Trajectory Tracking Process Models
2.2.1. Dead Reckoning (DR)
2.2.2. RADAR Extended Kalman Filter (EKF) Simultaneous Localization and Mapping (SLAM)
2.2.3. Motion Model
2.2.4. Measurement Model
2.2.5. Integrity Model
2.3. Simulated Trajectories
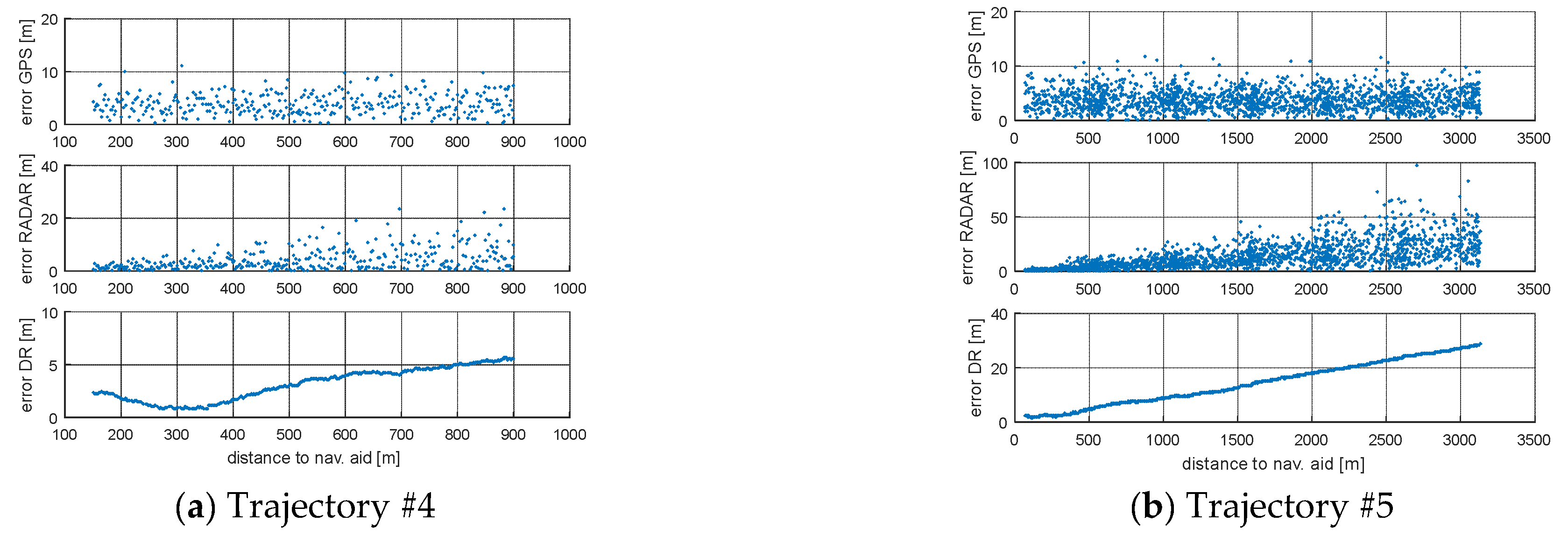
3. Results
- ship position—GPS receiver;
- bearing and distance—Navigation radar.
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Specht, C. Radio navigation systems: Definitions and classifications. J. Navig. 2021, 74, 945–954. [Google Scholar] [CrossRef]
- Jaskólski, K. Automatic Identification System (AIS) dynamic data estimation based on discrete Kalman Filter (KF) algorithm. Zesz. Nauk. Akad. Mar. Wojennej 2017, 58, 71–87. [Google Scholar] [CrossRef]
- Jaskólski, K. The Availability of Automatic Identification System (AIS) Based on Latency Position Reports in The Gulf of Gdansk. Annu. Navig. 2014, 21, 59–74. [Google Scholar] [CrossRef][Green Version]
- Specht, C.; Rudnicki, J. A Method for The Assessing of Reliability Characteristics Relevant to an Assumed Position-Fixing Accuracy in Navigational Positioning Systems. Polish Marit. Res. 2016, 23, 20–27. [Google Scholar] [CrossRef]
- Specht, M. Method of Evaluating the Positioning System Capability for Complying with the Minimum Accuracy Requirements for the International Hydrographic Organization Orders. Sensors 2019, 19, 3860. [Google Scholar] [CrossRef]
- Felski, A.; Jaskólski, K.; Banyś, P. Comprehensive Assessment of Automatic Identification System (AIS) Data Application to Anti-collision Manoeuvring. J. Navig. 2015, 68, 697–717. [Google Scholar] [CrossRef]
- Fossen, S.; Fossen, T.I. Extended Kalman Filter Design and Motion Prediction of Ships Using Live Automatic Identification System (AIS) Data. In Proceedings of the 2018 2nd European Conference on Electrical Engineering and Computer Science (EECS), Bern, Switzerland, 20–22 December 2018; pp. 464–470. [Google Scholar]
- Kaniewski, P. Structures, Models and Algorithms in Integrated Positioning and Navigation Systems (Struktury, Modele i Algorytmy w Zintegrowanych Systemach Pozycjonujących i Nawigacyjnych); Military University of Technology: Warsaw, Poland, 2010. [Google Scholar]
- Särkkä, S.; Tamminen, T.; Vehtari, A.; Lampinen, J. Probabilistic Methods in Multiple Target. Tracking—Review and Bibliography; Aalto University: Espoo, Finland, 2004. [Google Scholar]
- Siegert, G.; Banys, P.; Martinez, C.S.; Heymann, F. EKF based trajectory tracking and integrity monitoring of AIS data. In Proceedings of the 2016 IEEE/ION Position, Location and Navigation Symposium (PLANS), Savannah, GA, USA, 11–14 April 2016; pp. 887–897. [Google Scholar]
- Konatowski, S.; Kaniewski, P.; Matuszewski, J. Comparison of Estimation Accuracy of EKF, UKF and PF Filters. Annu. Navig. 2016, 23, 69–87. [Google Scholar] [CrossRef]
- Xu, T.; Liu, X.; Yang, X. Ship Trajectory Online Prediction Based on BP Neural Network Algorithm. In Proceedings of the 2011 International Conference of Information Technology, Computer Engineering and Management Sciences, Nanjing, China, 24–25 September 2011; pp. 103–106. [Google Scholar]
- Guo, S.; Zhang, X.; Zheng, Y.; Du, Y. An Autonomous Path Planning Model for Unmanned Ships Based on Deep Reinforcement Learning. Sensors 2020, 20, 426. [Google Scholar] [CrossRef]
- Yang, F.; Qiao, Y.; Wei, W.; Wang, X.; Wan, D.; Damaševičius, R.; Woźniak, M. DDTree: A Hybrid Deep Learning Model for Real-Time Waterway Depth Prediction and Smart Navigation. Appl. Sci. 2020, 10, 2770. [Google Scholar] [CrossRef]
- Jakubowski, B. Niezawodnościowe Aspekty Przetwarzania Informacji w Zintegrowanym Systemie Nawi-Gacyjnym (Reliability-Based Aspects of Data Processing in an Integrated Navigational System); Polish Naval Academy: Gdynia, Poland, 2003. [Google Scholar]
- Jaskólski, K. Availability and Integrity Model of Automatic Identification System (AIS) Information; GRIN Publishing GmbH: Munich, Germany, 2014; ISBN 9783656707899. [Google Scholar]
- Chang, Y.; Chen, C. A Kullback-Leibler information control chart for linear profiles monitoring. Qual. Reliab. Eng. Int. 2020, 36, 2225–2248. [Google Scholar] [CrossRef]
- Abba, S.I.; Gaya, M.S.; Yakubu, M.L.; Zango, M.U.; Abdulkadir, R.A.; Saleh, M.A.; Hamza, A.N.; Abubakar, U.; Tukur, A.I.; Wahab, N.A. Modelling of Uncertain System: A comparison study of Linear and Non-Linear Approaches. In Proceedings of the 2019 IEEE International Conference on Automatic Control and Intelligent Systems (I2CACIS), Selangor, Malaysia, 29 June 2019; pp. 1–6. [Google Scholar]
- Harati-Mokhtari, A.; Wall, A.; Brooks, P.; Wang, J. Automatic Identification System (AIS): Data Reliability and Human Error Implications. J. Navig. 2007, 60, 373–389. [Google Scholar] [CrossRef]
- Felski, A.; Jaskolski, K. The Integrity of Information Received by Means of AIS During Anti-collision Manoeuvring. TransNav Int. J. Mar. Navig. Saf. Sea Transp. 2013, 7, 95–100. [Google Scholar] [CrossRef][Green Version]
- Lensu, M.; Goerlandt, F. Big maritime data for the Baltic Sea with a focus on the winter navigation system. Mar. Policy 2019, 104, 53–65. [Google Scholar] [CrossRef]
- Fournier, M.; Casey Hilliard, R.; Rezaee, S.; Pelot, R. Past, present, and future of the satellite-based automatic identification system: Areas of applications (2004–2016). WMU J. Marit. Aff. 2018, 17, 311–345. [Google Scholar] [CrossRef]
- Yang, D.; Wu, L.; Wang, S.; Jia, H.; Li, K.X. How big data enriches maritime research—A critical review of Automatic Identification System (AIS) data applications. Transp. Rev. 2019, 39, 755–773. [Google Scholar] [CrossRef]
- Wang, J.; Zhu, C.; Zhou, Y.; Zhang, W. Vessel Spatio-temporal Knowledge Discovery with AIS Trajectories Using Co-clustering. J. Navig. 2017, 70, 1383–1400. [Google Scholar] [CrossRef]
- Alizadeh, D.; Alesheikh, A.A.; Sharif, M. Vessel Trajectory Prediction Using Historical Automatic Identification System Data. J. Navig. 2021, 74, 156–174. [Google Scholar] [CrossRef]
- Sun, Y.; Chen, X.; Jun, L.; Zhao, J.; Hu, Q.; Fang, X.; Yan, Y. Ship trajectory cleansing and prediction with historical ais data using an ensemble ann framework. Int. J. Innov. Comput. Inf. Control. 2021, 17, 443–459. [Google Scholar]
- International Telecommunication Union. Technical Characteristics for an Automatic Identification System Using Time Division Multiple Access in the VHF Maritime Mobile Band (Recommendation ITU-R M.1371-4); International Telecommunication Union: Geneva, Switzerland, 2014. [Google Scholar]
- Dąbrowski, P.S.; Specht, C.; Felski, A.; Koc, W.; Wilk, A.; Czaplewski, K.; Karwowski, K.; Jaskólski, K.; Specht, M.; Chrostowski, P.; et al. The Accuracy of a Marine Satellite Compass under Terrestrial Urban Conditions. J. Mar. Sci. Eng. 2019, 8, 18. [Google Scholar] [CrossRef]
- Marchel, Ł.; Naus, K.; Specht, M. Optimisation of the Position of Navigational Aids for the Purposes of SLAM technology for Accuracy of Vessel Positioning. J. Navig. 2020, 73, 282–295. [Google Scholar] [CrossRef]
- Jaskólski, K. Zastosowanie łańcuchów Markowa w badaniu potencjalnych możliwości wykorzystania informacji automatycznego systemu identyfikacji (AIS) w aplikacjach antykolizyjnych. Zesz. Nauk. Akad. Mar. Wojennej 2013, 195, 51–72. [Google Scholar] [CrossRef]
- Sang, L.; Wall, A.; Mao, Z.; Yan, X.; Wang, J. A novel method for restoring the trajectory of the inland waterway ship by using AIS data. Ocean. Eng. 2015, 110, 183–194. [Google Scholar] [CrossRef]
- Jonker, R.; De Leve, G.; Van Der Velde, J.A.; Volgenant, A. Technical Note—Rounding Symmetric Traveling Salesman Problems with an Asymmetric Assignment Problem. Oper. Res. 1980, 28, 623–627. [Google Scholar] [CrossRef]
- Kearney, J.K.; Hansen, S. Stream Editing for Animation; Department of Computer Science, The University of Iowa: Iowa City, IA, USA, 1990. [Google Scholar]
- Sakoe, H.; Chiba, S. Dynamic programming algorithm optimization for spoken word recognition. IEEE Trans. Acoust. 1978, 26, 43–49. [Google Scholar] [CrossRef]
- Soong, F.K.; Rosenberg, A.E. On the use of instantaneous and transitional spectral information in speaker recognition. IEEE Trans. Acoust. 1988, 36, 871–879. [Google Scholar] [CrossRef]

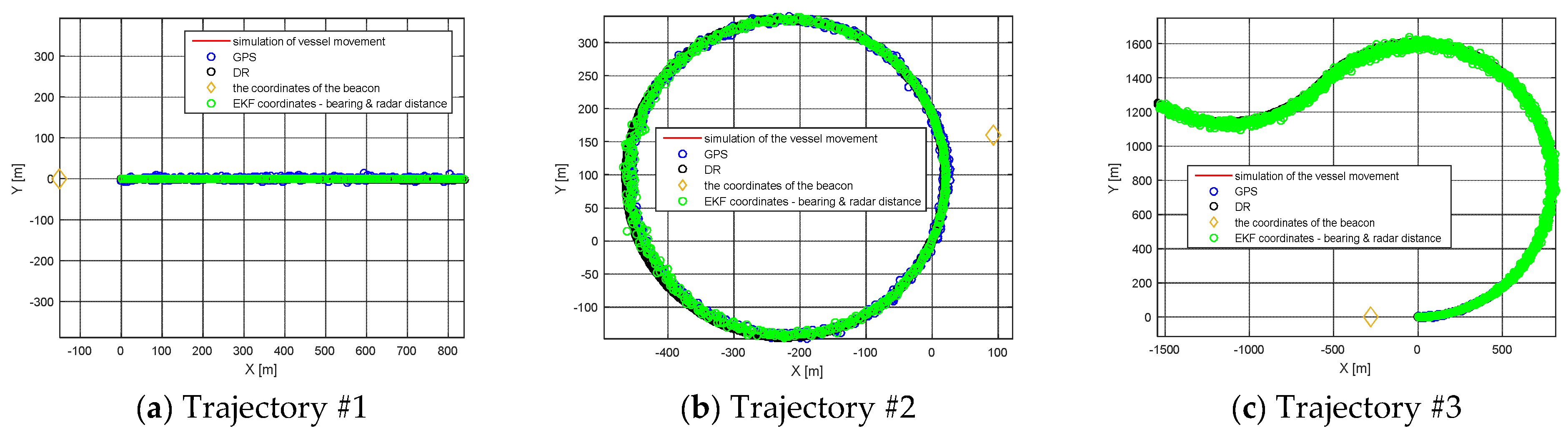

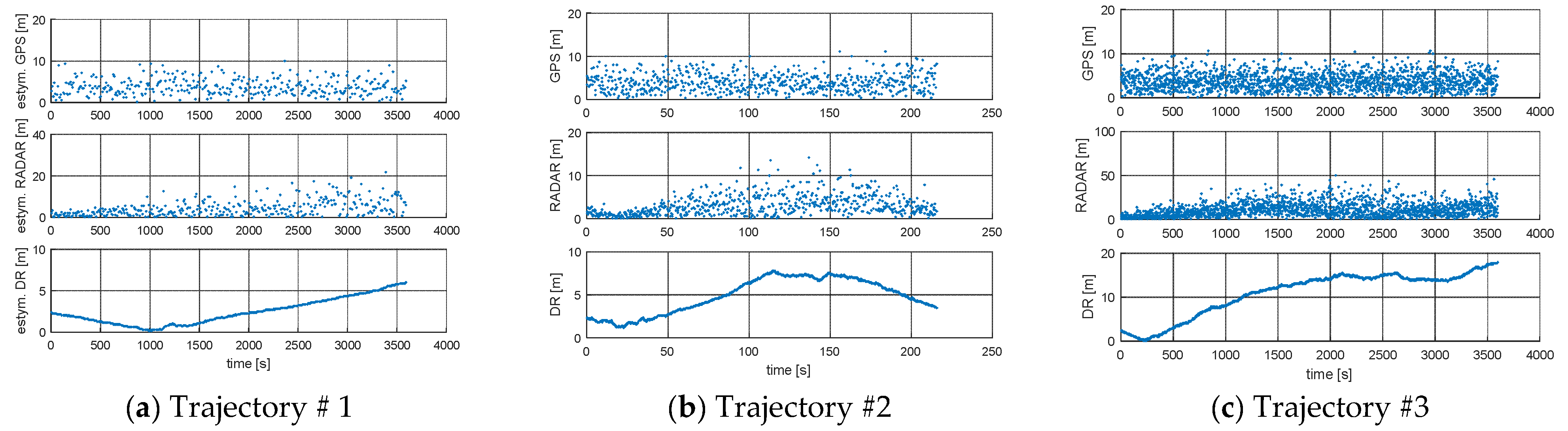
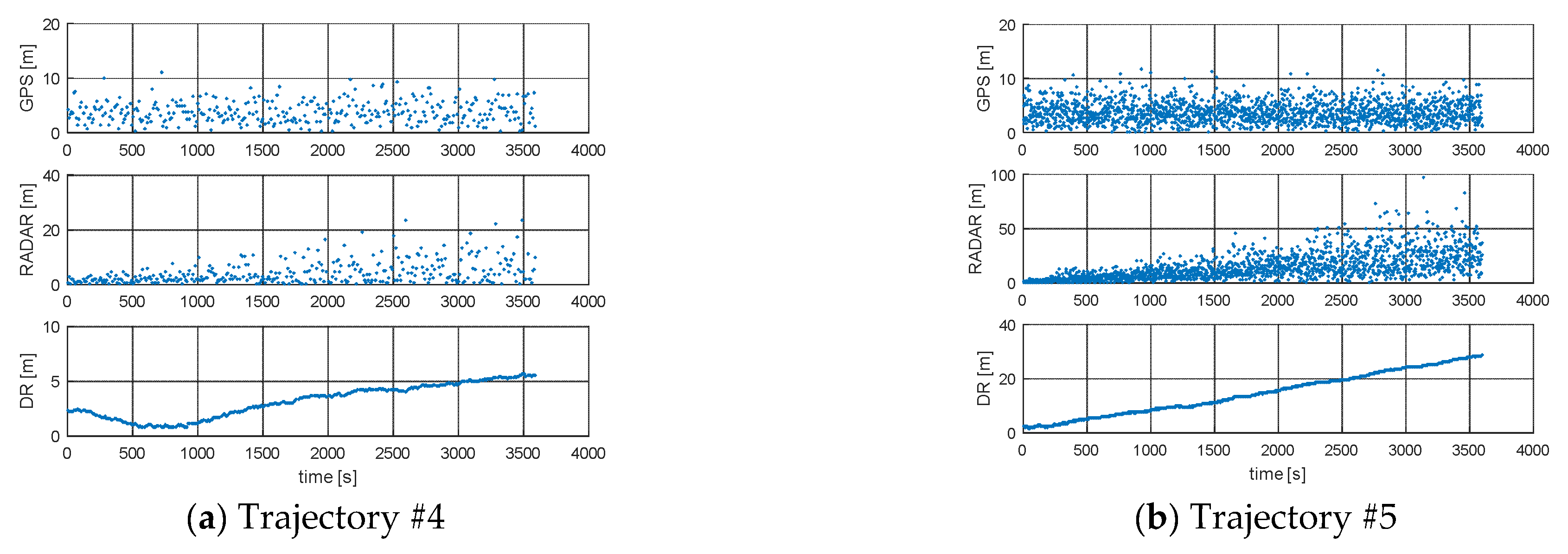
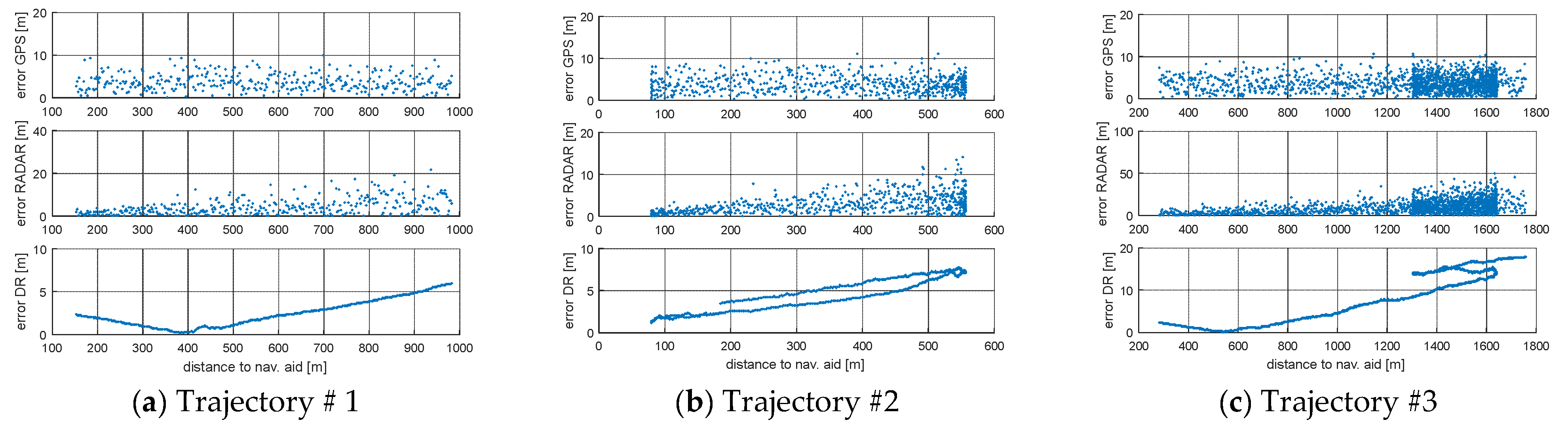
| Trajectory #1 | Trajectory #2 | Trajectory #3 | Trajectory #4 | Trajectory #5 | |
|---|---|---|---|---|---|
| initial COG [deg] | 000 | 066 | 000 | 315 | 315 |
| ROT [deg/min] | 000 | 010 | 005 | 003 | 015 |
| Turn after a time of [min] | 0 | 2 | 45 | 30 | 10 |
| SOG [knots] | 4.5 | 4.5 | 4.5 | 4.5 | 4.5 |
| Δt [s] | 10 | 3.33 | 2 | 10 | 2 |
| simulation time [s] | 3600 | 2160 | 3600 | 3600 | 3600 |
| σ(GPS) [m] | 3 | 3 | 3 | 3 | 3 |
| [deg] | 0.3 | 0.3 | 0.3 | 0.3 | 0.3 |
| [deg] | 1.5 | 1.5 | 1.5 | 1.5 | 1.5 |
| initial dist. to nav. aid [m] | 150 | 85 | 280 | 150 | 63 |
| Campaign Number | M(GPS) xy [m] | M(RADAR) xy [m] | M(DR) xy [m] |
|---|---|---|---|
| Trajectory #1 | 3.8 | 4.3 | 2.5 |
| Trajectory #2 | 3.9 | 3.1 | 4.9 |
| Trajectory #3 | 3.7 | 11.0 | 11.0 |
| Trajectory #4 | 3.9 | 4.3 | 3.2 |
| Trajectory #5 | 3.8 | 14.4 | 14.5 |
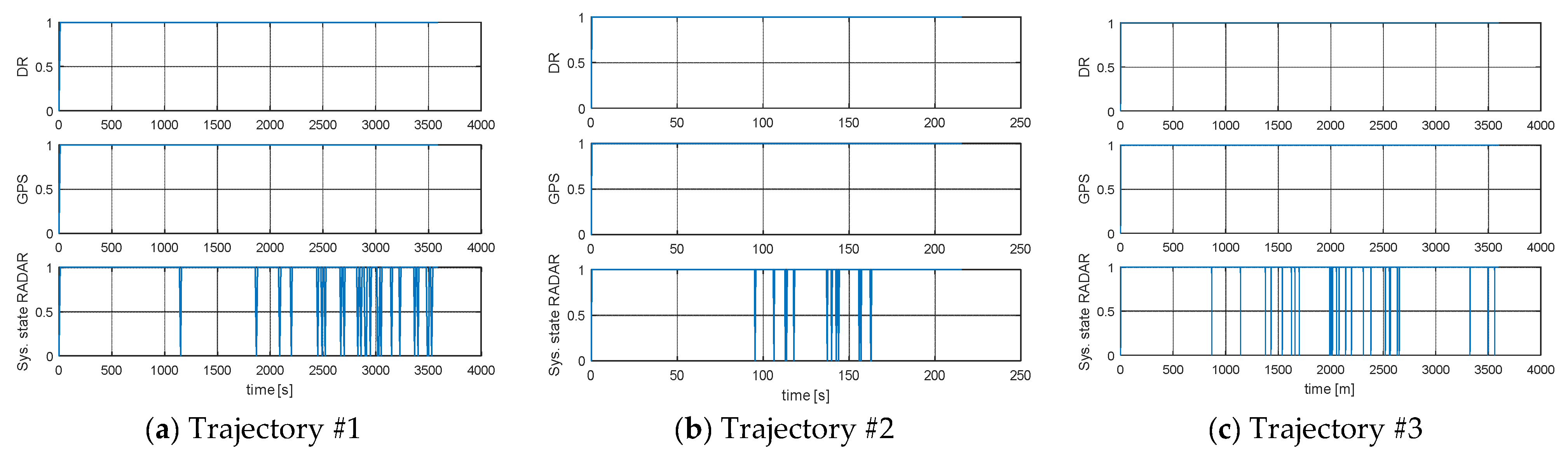
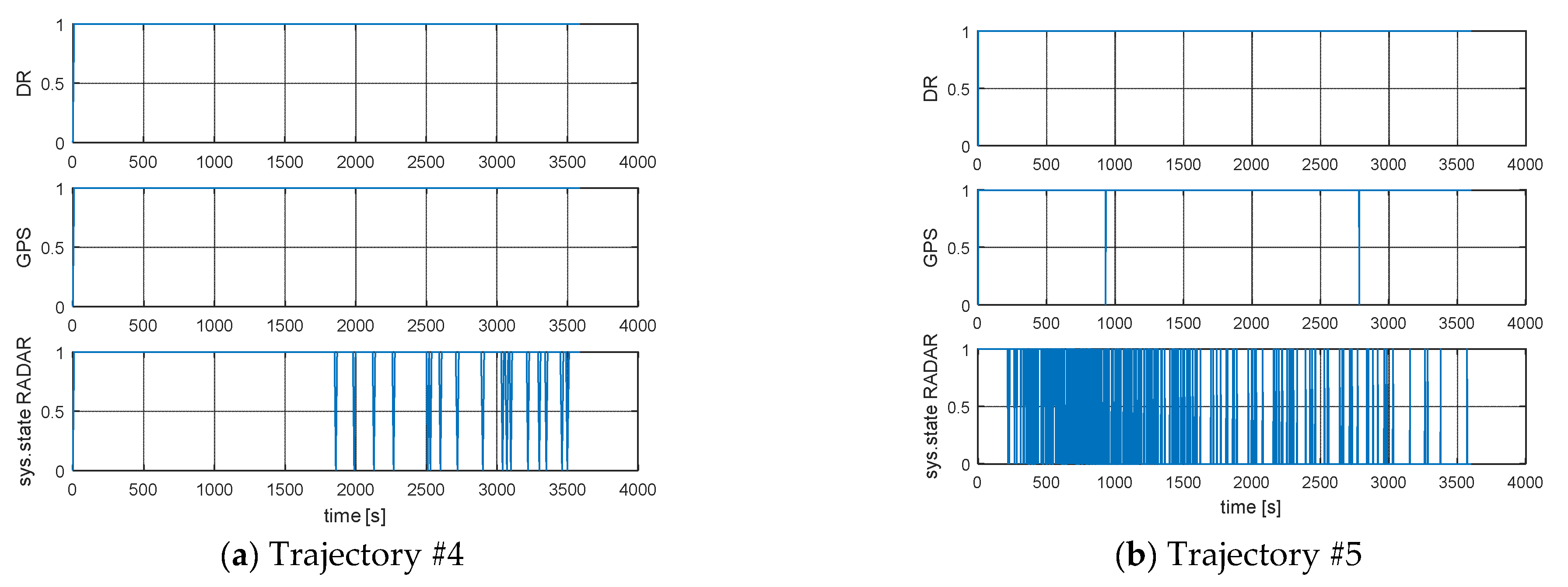
| Process Model | Trajectory No. | S(0)→S(0) | S(0)→S(1) | S(1)→S(0) | S(1)→S(1) | Number of States |
|---|---|---|---|---|---|---|
| DR | 1 | 0 | 1 | 0 | 359 | 360 |
| GPS | 1 | 0 | 1 | 0 | 359 | 360 |
| RADAR | 1 | 3 | 22 | 21 | 314 | 360 |
| DR | 2 | 0 | 1 | 0 | 647 | 648 |
| GPS | 2 | 0 | 1 | 0 | 647 | 648 |
| RADAR | 2 | 1 | 13 | 12 | 622 | 648 |
| DR | 3 | 0 | 1 | 0 | 1799 | 1800 |
| GPS | 3 | 0 | 1 | 0 | 1799 | 1800 |
| RADAR | 3 | 1 | 27 | 26 | 1746 | 1800 |
| DR | 4 | 0 | 1 | 0 | 359 | 360 |
| GPS | 4 | 0 | 1 | 0 | 359 | 360 |
| RADAR | 4 | 0 | 18 | 17 | 325 | 360 |
| DR | 5 | 0 | 1 | 0 | 1799 | 1800 |
| GPS | 5 | 0 | 3 | 2 | 1795 | 1800 |
| RADAR | 5 | 1140 | 191 | 191 | 278 | 1800 |
| Process Model | DR | GPS | RADAR |
|---|---|---|---|
| trajectory #1 | |||
| trajectory #2 | |||
| trajectory #3 | |||
| trajectory #4 | |||
| trajectory #5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jaskólski, K.; Marchel, Ł.; Felski, A.; Jaskólski, M.; Specht, M. Automatic Identification System (AIS) Dynamic Data Integrity Monitoring and Trajectory Tracking Based on the Simultaneous Localization and Mapping (SLAM) Process Model. Sensors 2021, 21, 8430. https://doi.org/10.3390/s21248430
Jaskólski K, Marchel Ł, Felski A, Jaskólski M, Specht M. Automatic Identification System (AIS) Dynamic Data Integrity Monitoring and Trajectory Tracking Based on the Simultaneous Localization and Mapping (SLAM) Process Model. Sensors. 2021; 21(24):8430. https://doi.org/10.3390/s21248430
Chicago/Turabian StyleJaskólski, Krzysztof, Łukasz Marchel, Andrzej Felski, Marcin Jaskólski, and Mariusz Specht. 2021. "Automatic Identification System (AIS) Dynamic Data Integrity Monitoring and Trajectory Tracking Based on the Simultaneous Localization and Mapping (SLAM) Process Model" Sensors 21, no. 24: 8430. https://doi.org/10.3390/s21248430
APA StyleJaskólski, K., Marchel, Ł., Felski, A., Jaskólski, M., & Specht, M. (2021). Automatic Identification System (AIS) Dynamic Data Integrity Monitoring and Trajectory Tracking Based on the Simultaneous Localization and Mapping (SLAM) Process Model. Sensors, 21(24), 8430. https://doi.org/10.3390/s21248430








