Reliability Analysis of the Proactive Transmission of Replicated Frames Mechanism over Time-Sensitive Networking
Abstract
:1. Introduction
2. Related Work
3. Overview of TSN Relevant Standards
4. Overview of the Proactive Transmission of Replicated Frames (PTRF) Mechanism
4.1. Fault and Failure Models for the Design of PTRF
4.2. PTRF Operation
4.2.1. Approach A: End-to-End Estimation and Replication
4.2.2. Approach B: End-to-End Estimation, Link-Based Replication
4.2.3. Approach C: Link-Based Estimation and Replication
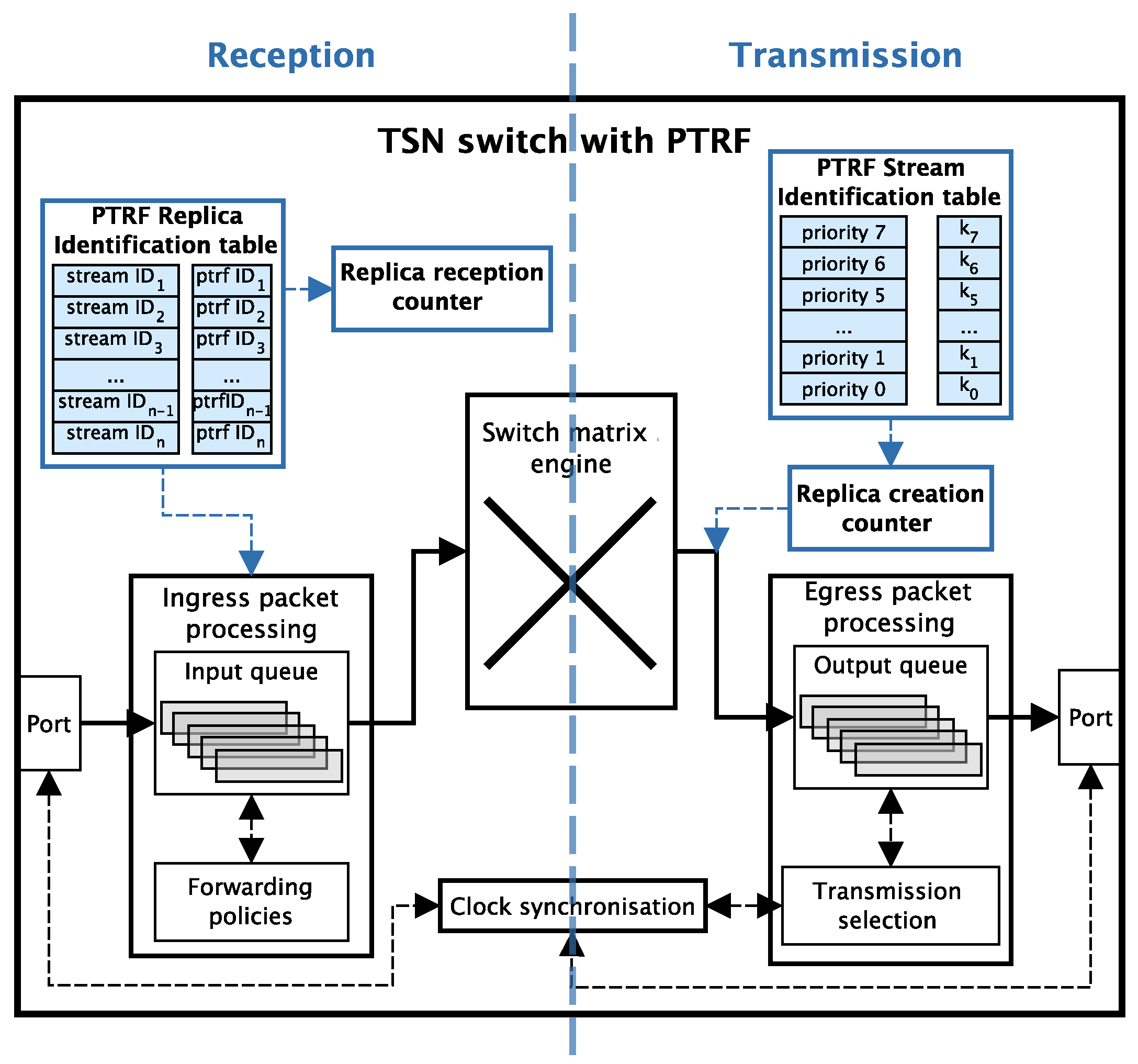
4.3. Basic Architecture of a PTRF-Enabled Device
5. Modelling Rationale
5.1. Reliability Metric
5.2. Fault Model of the Modelled System
5.3. Modelling Assumptions
5.3.1. Constituent Components and Failure Rates
5.3.2. Failure Model and Fault-Tolerance Coverages of the Modelled System
- Byzantine: lack of restrictions on the way the system can behave. It includes two-faced behaviours, i.e., a faulty device sending different information to different devices, and impersonations, i.e., a faulty device pretending to be a different device.
- Incorrect computation: the system delivers an incorrect result, either in the value or the time domain, but without showing two-faced behaviours nor impersonating other systems.
- Performance: the system delivers a correct result in the value domain, but fails to do it in the time domain.
- Omission: the system delays the delivery of a result forever.
5.3.3. Topology Assumptions
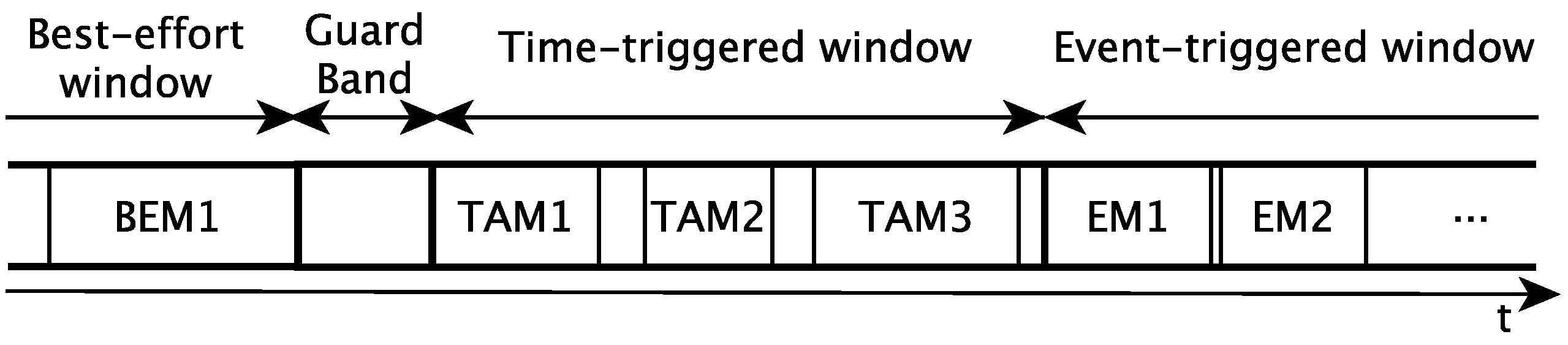
5.3.4. Traffic Scheduling Assumptions
5.4. Modelling Strategy
5.4.1. Link Model
- Number of replicas transmitted, k. In our model, the minimum value for k is 1 and the maximum value for k is 4.
- Number of replicas received correctly, n. The maximum value of n depends on the k we define, as we cannot receive more replicas than we transmit. Thus 0 ≤ n ≤ k.
- Frame size. Necessary to calculate the probability of a frame being affected by a fault, as depicted in Equation (2). We use the frame size values set for our sensitivity analyses: 64, 782 and 1500 bytes.
- BER. Necessary to calculate the probability of a frame being affected by a fault, as depicted in Equation (2). We evaluate the BER values set for our sensitivity analyses: from to .
| Parameter | Range | Reference | Meaning |
|---|---|---|---|
| Mission time | 10 h | 10 h | The time that the system is expected to operate in a continuous manner. We use 10 h in all the experiments as it is typically assumed for evaluating the reliability of critical applications such as throttle-by-wire [34]. |
| TAS window | 1.3 ms | 1.3 ms | The duration of the TAS window in milliseconds. Since we assume that frames are scheduled using CQF, each TAS window must last enough time for a frame to be transmitted, propagated, received and forwarded. Thus, to decide on the TAS window size we have taken into account the transmission and reception time, the propagation time and the forwarding time of a frame through a link and a bridge. These values have been mathematically estimated or measured using a real TSN bridge [35]. This parameter is fixed in all the experiments. |
| Period | 15 TAS windows | 15 | The number of TAS windows that elapse between the transmission of frames. This parameter is fix in all the experiments. |
| BER | {, ..., } | The bit error rate of the links. We consider values from considered in highly critical applications such as space missions, to considered for utility communications. We use as reference as it is the most pessimistic assumption while still considering critical applications such as automotive. | |
| Frame size | {64, 782, 1500}B | 782 | The size of the frames transmitted through the stream in bytes, being 64 the minimum size, 782 the medium size and 1500 the maximum size for Ethernet frames. We use 782 as reference to compare the impact when using smaller and larger frames. |
| # of replicas | {1, ..., 4} | 2 | The number of replicas transmitted by PTRF-enabled components. This value is always 1 in TSN and we consider up to 4 replicas as our results show that reliability converges with this number of replicas. Our case of reference is 1 replica for TSN and 2 replicas for PTRF as this is the lowest number of replicas that PTRF can transmit while still providing time redundancy. |
| # of bridges | {2, ..., 10} | 6 | The number of bridges in the path between the talker and the listener. We consider from 2 to 10 bridges. We select 6 bridges for our case of reference as this is the maximum number of bridges for which TSN ensures tight synchronisations. |
5.4.2. General Models
- Module system evaluation. This module decides whether the system has failed according to a set of predefined rules which are applied to the local variables of the path, phase and period modules. Specifically, the system fails if too many streams fail; a stream fails if too many paths fail, and a path fails if all the replicas of a message edition are lost in the path. The result of this module is shared with the path modules so that the affected path modules stop evolving (i.e., making calculations) when the system has already failed. Whenever the number of failures in any of these modules reaches the specified threshold, the whole model stops.
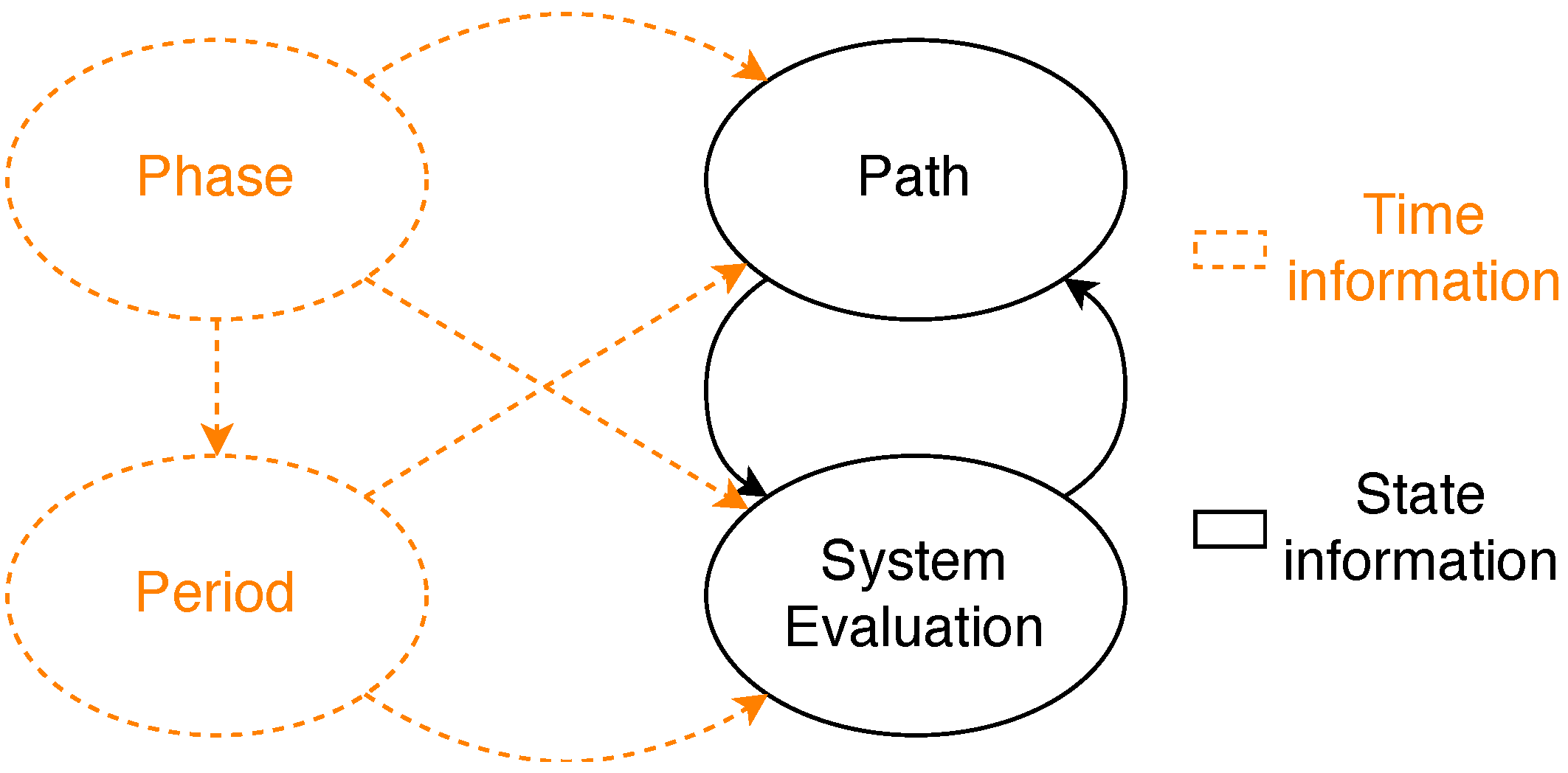
- Module path. This module models the transmission of frames through a given path of a stream. Specifically, for each message edition this module models whether the transmission, forwarding and reception of each replica are correct or not for all the hops of the path. If a stream has L intended listeners there must be L path modules for said stream. This module is further divided into three blocks, namely talker, bridge and listener. Figure 8 shows the different blocks that constitute the path module and their relationships.As we can see in Figure 8, the execution of the path module starts with the talker block, which transmits a frame or the specified number of replicas of a frame every period.The bridge block evaluates how many frames transmitted by the talker or the preceding bridge successfully reach the destination bridge of the current hop. Specifically, the bridge uses the loss probabilities calculated using the link model previously described to carry out this evaluation. Then it evaluates if the bridge correctly forwards the adequate number of frame replicas (or a single frame in TSN) following the corresponding approach depending on the model: TSN, PTRF approach A, or PTRF approach B. In case of deciding that the bridge fails in the forwarding, the bridge block models the specific way in which this failure manifests, e.g., by forwarding more replicas than expected. The bridge block is executed as many times as bridges are in the path.The listener block evaluates how many frames transmitted by the last bridge of the path successfully reach the listener. Then, it decides if the listener correctly eliminates the surplus replicas in the case of PTRF and if it correctly delivers the frame to the upper layer. Once the path is completed, the system evaluation module determines whether the stream is faulty or not and, if not, the path module is executed again when dictated by the period module.
- Module phase. We have just explained, the path module is divided intro three different blocks, namely the talker, the bridge and the listener block. Additionally, each block executes several steps, e.g., the bridge block receives, forwards and transmits frames. We must recall that we use CQF for the scheduling of frames, which means that all the steps of one block are executed within the same TAS window. The phase module dictates when the different steps of a block must be done within the TAS window.We must note that not all blocks execute the same number of steps. More concretely, the bridge is the block with the highest number of steps. Nonetheless, we have assumed that all the TAS windows have the same duration for a specific stream and, thus, the number of phases is the same for all the blocks of the stream. When the talker and the listener complete all the steps, they remain idle until all the phases pass, just like a real TSN device would do.
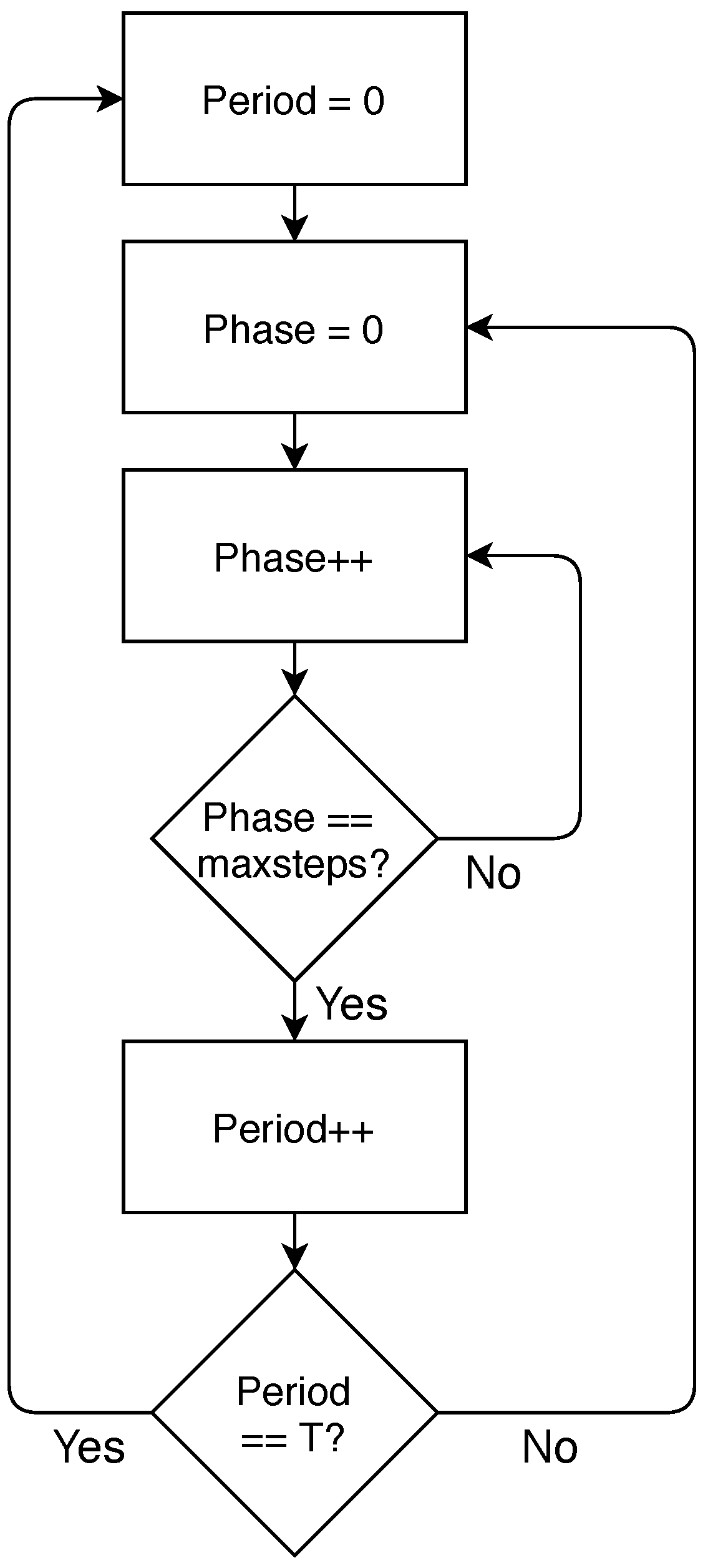
- Module period. This module dictates when each block of the path module is executed, i.e., it dictates the pass of time in a stream. Since we use CQF to schedule frames, each block of the path module is executed during one TAS window. The module period also counts the number of TAS windows in a period of a stream and triggers the transmission of a frame in the talker when required.Figure 9 shows the relationship between the phase and period modules. Specifically, the execution of the complete model starts initialising the period and phase modules to 0. The phase module is increased as many times as steps executed the bridge (as previously explained). Once all the steps of a block are executed, the period is increased and the phase module is reset.If the period is higher than the number of hops, the execution of the path module is completed before the period module reaches the specified period T. In that case, the path module remains idle until the period module reaches the value specified for the streaming period, then the period is reset and the talker creates a new frame.
5.5. Model Testing
6. Parameters of the Models
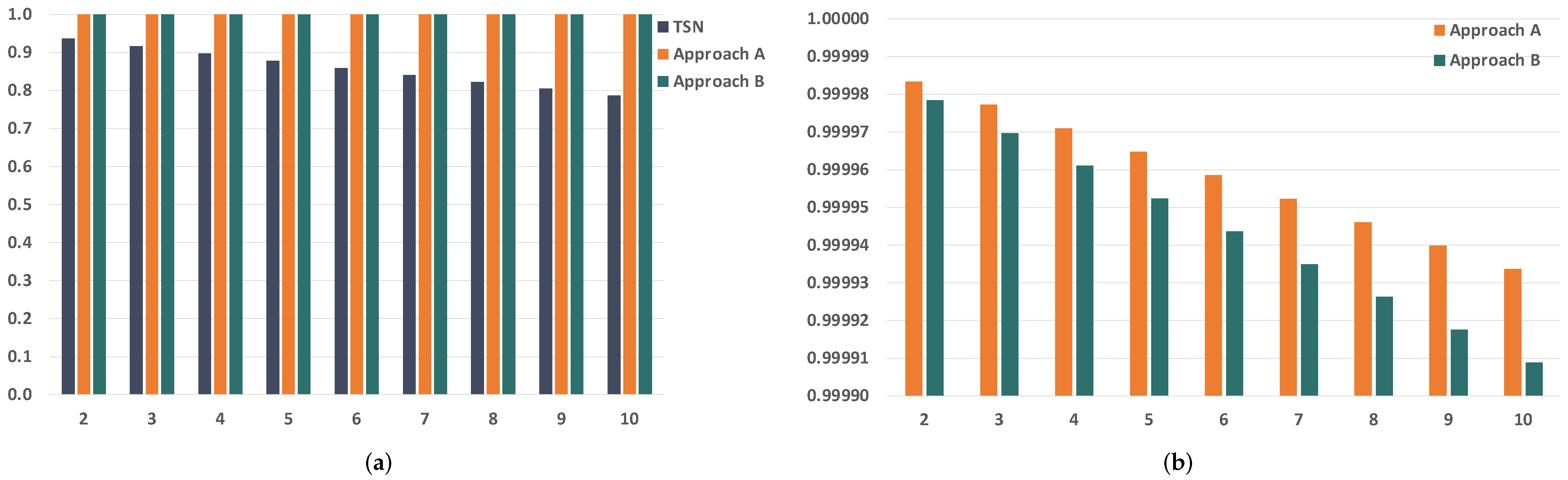
7. Results
7.1. Case of Reference
7.2. Bit Error Rate
7.3. Frame Size
7.4. Number of Replicas
7.5. Number of Bridges
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| BER | Bit Error Rate |
| CRC | Cyclic Redundancy Check |
| COTS | Commercial Off The Shelf |
| CQF | Cyclic Queuing and Forwarding |
| DTMC | Discrete-Time Markov chains |
| FT | Fault Tolerance |
| FRER | Frame Replication and Elimination for Reliability |
| PTRF | Proactive Transmission of Replicated Frames |
| RT | Real-Time |
| TAS | Time-Aware Shaper |
| TG | Task Group |
| TSN | Time-Sensitive Networking |
| TT | Time-Triggered |
References
- Time-Sensitive Networking (TSN) Task Group. Available online: https://1.ieee802.org/tsn/ (accessed on 9 December 2021).
- Wollschlaeger, M.; Sauter, T.; Jasperneite, J. The Future of Industrial Communication: Automation Networks in the Era of the Internet of Things and Industry 4.0. IEEE Ind. Electron. Mag. 2017, 11, 17–27. [Google Scholar] [CrossRef]
- P802.1DG—TSN Profile for Automotive In-Vehicle Ethernet Communications. Available online: https://1.ieee802.org/tsn/802-1dg/ (accessed on 9 December 2021).
- IEC/IEEE 60802 TSN Profile for Industrial Automation. Available online: https://1.ieee802.org/tsn/iec-ieee-60802/ (accessed on 9 December 2021).
- P802.1DP—TSN for Aerospace Onboard Ethernet Communications. Available online: https://1.ieee802.org/tsn/802-1dp/ (accessed on 9 December 2021).
- IEEE Standard for Local and Metropolitan Area Networks—Frame Replication and Elimination for Reliability. In IEEE Std 802.1CB-2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1–102. [CrossRef]
- IEEE Standard for Local and Metropolitan Area Networks—Bridges and Bridged Networks—Amendment 24: Path Control and Reservation. In IEEE Std 802.1Qca-2015 (Amendment to IEEE Std 802.1Q-2014 as amended by IEEE Std 802.1Qcd-2015 and IEEE Std 802.1Q-2014/Cor 1-2015); IEEE: Piscataway, NJ, USA, 2016; pp. 1–120. [CrossRef]
- IEEE Standard for Local and Metropolitan Area Networks—Bridges and Bridged Networks—Amendment 28: Per-Stream Filtering and Policing. In IEEE Std 802.1Qci-2017 (Amendment to IEEE Std 802.1Q-2014 as amended by IEEE Std 802.1Qca-2015, IEEE Std 802.1Qcd-2015, IEEE Std 802.1Q-2014/Cor 1-2015, IEEE Std 802.1Qbv-2015, IEEE Std 802.1Qbu-2016, and IEEE Std 802.1Qbz-2016); IEEE: Piscataway, NJ, USA, 2017. [CrossRef]
- Álvarez, I.; Proenza, J.; Barranco, M.; Knezic, M. Towards a time redundancy mechanism for critical frames in Time-Sensitive Networking. In Proceedings of the 22nd IEEE International Conference on Emerging Technologies and Factory Automation (ETFA), Limassol, Cyprus, 12–15 September 2017; pp. 1–4. [Google Scholar] [CrossRef]
- Álvarez, I.; Čavka, D.; Proenza, J.; Barranco, M. Simulation of the Proactive Transmission of Replicated Frames Mechanism over TSN. In Proceedings of the 2019 24th IEEE International Conference on Emerging Technologies and Factory Automation (ETFA), Zaragoza, Spain, 10–13 September 2019; pp. 1375–1378. [Google Scholar] [CrossRef]
- Álvarez, I.; Furió, I.; Proenza, J.; Barranco, M. Design and Experimental Evaluation of the Proactive Transmission of Replicated Frames Mechanism over Time-Sensitive Networking. Sensors 2021, 21, 756. [Google Scholar] [CrossRef] [PubMed]
- Álvarez, I.; Proenza, J.; Barranco, M. Mixing Time and Spatial Redundancy Over Time Sensitive Networking. In Proceedings of the 2018 48th Annual IEEE/IFIP International Conference on Dependable Systems and Networks Workshops (DSN-W), Luxembourg, 25–28 June 2018; pp. 63–64. [Google Scholar] [CrossRef]
- Lin, S.; Costello, D.J.; Miller, M.J. Automatic-repeat-request error-control schemes. IEEE Commun. Mag. 1984, 22, 5–17. [Google Scholar] [CrossRef]
- Ha, N.V.; Nguyen, T.T.T.; Tsuru, M. TCP with Network Coding Enhanced in Bi-directional Loss Tolerance. IEEE Commun. Lett. 2019, 24, 520–524. [Google Scholar] [CrossRef]
- Stallings, W. Data and Computer Communications, 10th ed.; Prentice Hall Press: New York, NY, USA, 2013. [Google Scholar]
- Hofmann, R.; Nikolić, B.; Ernst, R. Challenges and Limitations of IEEE 802.1CB-2017. IEEE Embed. Syst. Lett. 2020, 12, 105–108. [Google Scholar] [CrossRef]
- Atallah, A.A.; Hamad, G.B.; Mohamed, O.A. Reliability Analysis of TSN Networks Under SEU Induced Soft Error Using Model Checking. In Proceedings of the 2019 IEEE Latin American Test Symposium (LATS), Santiago, Chile, 11–13 March 2019. [Google Scholar]
- Pahlevan, M.; Obermaisser, R. Redundancy Management for Safety-Critical Applications with Time Sensitive Networking. In Proceedings of the 2018 28th International Telecommunication Networks and Applications Conference (ITNAC), Sydney, Australia, 21–23 November 2018; pp. 1–7. [Google Scholar] [CrossRef]
- Rosset, V.; Souto, P.F.; Portugal, P.; Vasques, F. Modeling the reliability of a group membership protocol for dual-scheduled time division multiple access networks. Comput. Stand. Interfaces 2012, 34, 281–291. [Google Scholar] [CrossRef]
- Barranco, M.; Derasevic, S.; Proenza, J. An Architecture for Highly Reliable Fault-Tolerant Adaptive Distributed Embedded Systems. Computer 2020, 53, 38–46. [Google Scholar] [CrossRef]
- IEEE Standard for Local and Metropolitan Area Networks—Timing and Synchronization for Time-Sensitive Applications. In IEEE Std 802.1AS-2020 (Revision of IEEE Std 802.1AS-2011); IEEE: Piscataway, NJ, USA, 2020; pp. 1–421. [CrossRef]
- IEEE Standard for Local and Metropolitan Area Networks—Bridges and Bridged Networks—Amendment 25: Enhancements for Scheduled Traffic. In IEEE Std 802.1Qbv-2015 (Amendment to IEEE Std 802.1Q—As amended by IEEE Std 802.1Qca-2015, IEEE Std 802.1Qcd-2015, and IEEE Std 802.1Q—/Cor 1-2015); IEEE: Piscataway, NJ, USA, 2016. [CrossRef]
- IEEE Standard for Local and metropolitan area networks–Bridges and Bridged Networks–Amendment 29: Cyclic Queuing and Forwarding. In IEEE 802.1Qch-2017 (Amendment to IEEE Std 802.1Q-2014 as amended by IEEE Std 802.1Qca-2015, IEEE Std 802.1Qcd(TM)-2015, IEEE Std 802.1Q-2014/Cor 1-2015, IEEE Std 802.1Qbv-2015, IEEE Std 802.1Qbu-2016, IEEE Std 802.1Qbz-2016, and IEEE Std 802.1Qci-2017); IEEE: Piscataway, NJ, USA, 2017; pp. 1–30. [CrossRef]
- Avižienis, A.; Laprie, J.C.; Randell, B.; Carl, L. Basic Concepts and Taxonomy of Dependable and Secure Computing. IEEE Trans. Dependable Secur. Comput. 2004, 1, 11–33. [Google Scholar] [CrossRef] [Green Version]
- Fujiwara, T.; Kasami, T.; Lin, S. Error detecting capabilities of the shortened Hamming codes adopted for error detection in IEEE Standard 802.3. IEEE Trans. Commun. 1989, 37, 986–989. [Google Scholar] [CrossRef]
- IEEE 802.3 Error Rates and Testability. Available online: https://www.ieee802.org/3/efm/public/may03/optics/dawe_optics_1_0503.pdf (accessed on 9 December 2021).
- IEEE 802.3ah BER Requirements. Available online: https://www.ieee802.org/3/efm/public/nov01/khermosh_3_1101.pdf (accessed on 9 December 2021).
- Smirnov, F.; Glaß, M.; Reimann, F.; Teich, J. Formal reliability analysis of switched Ethernet automotive networks under transient transmission errors. In Proceedings of the 2016 53nd ACM/EDAC/IEEE Design Automation Conference (DAC), Austin, TX, USA, 5–9 June 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Peti, P.; Obermaisser, R.; Ademaj, A.; Kopetz, H. A maintenance-oriented fault model for the DECOS integrated diagnostic architecture. In Proceedings of the 19th IEEE International Parallel and Distributed Processing Symposium, Denver, CO, USA, 4–8 April 2005; p. 8. [Google Scholar] [CrossRef] [Green Version]
- Proenza, J. RCMBnet: A Distributed Hardware and Firmware Support for Software Fault Tolerance. Ph.D. Thesis, Universitat de les Illes Balears, Palma, Spain, 2007. [Google Scholar]
- Poledna, S. Fault-Tolerant Real-Time Systems: The Problem of Replica Determinism; Kluwer Academic Publishers: Norwell, MA, USA, 1996. [Google Scholar]
- Gessner, D. Adding Fault Tolerance to a Flexible Real-Time Ethernet Network for Embedded Systems. Ph.D. Thesis, Universitat de les Illes Balears, Palma, Spain, 2017. [Google Scholar]
- Kwiatkowska, M.; Norman, G.; Parker, D. PRISM 4.0: Verification of Probabilistic Real-Time Systems. In Computer Aided Verification; Gopalakrishnan, G., Qadeer, S., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 585–591. [Google Scholar]
- Morris, J.; Koopman, P. Representing design tradeoffs in safety-critical systems. In ACM SIGSOFT Software Engineering Notes; ACM: New York, NY, USA, 2005; Volume 30, pp. 1–5. [Google Scholar]
- MTSN Kit: A Comprehensive Multiport TSN Setup. Available online: https://soc-e.com/mtsn-kit-a-comprehensive-multiport-tsn-setup/ (accessed on 9 December 2021).





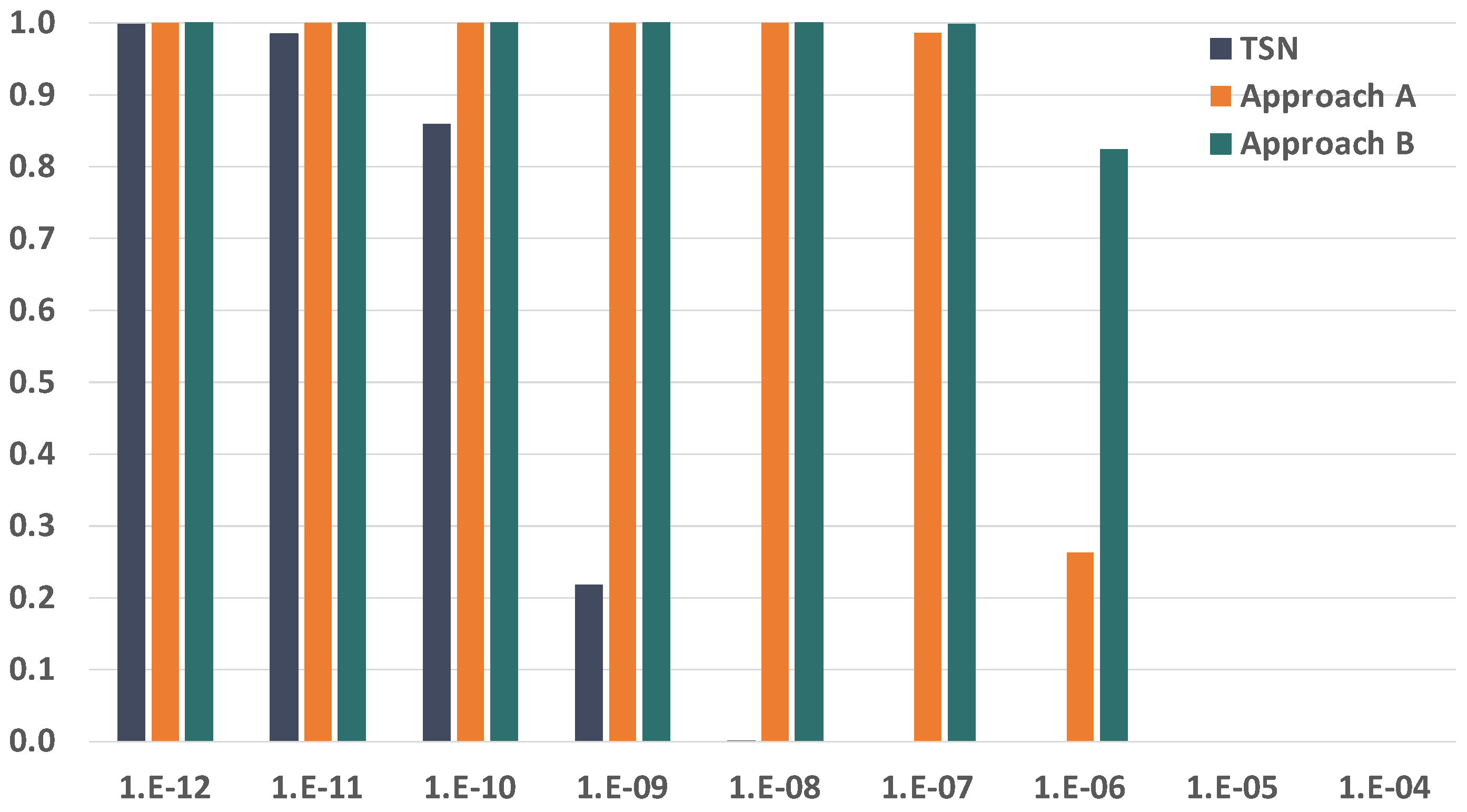
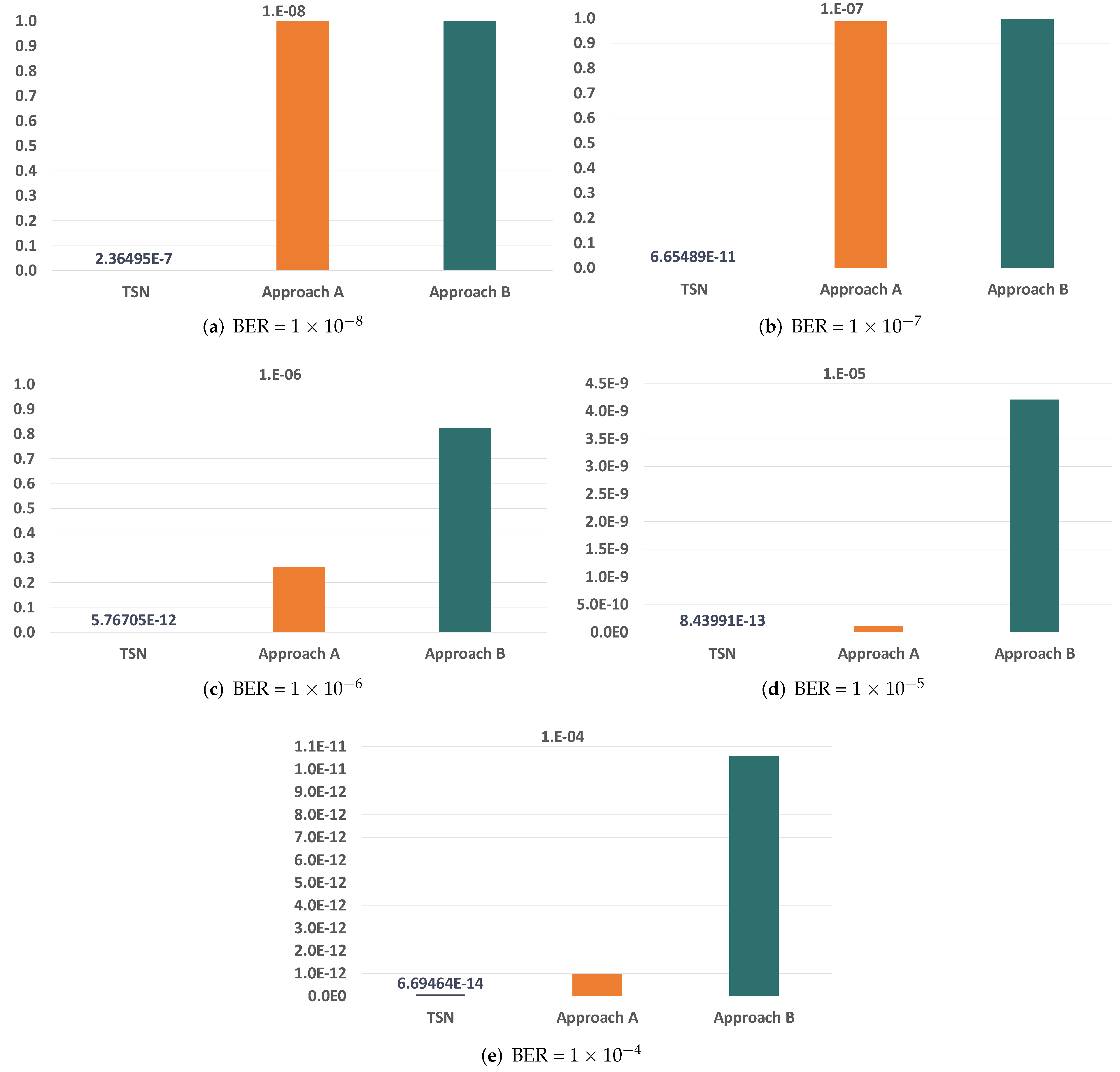
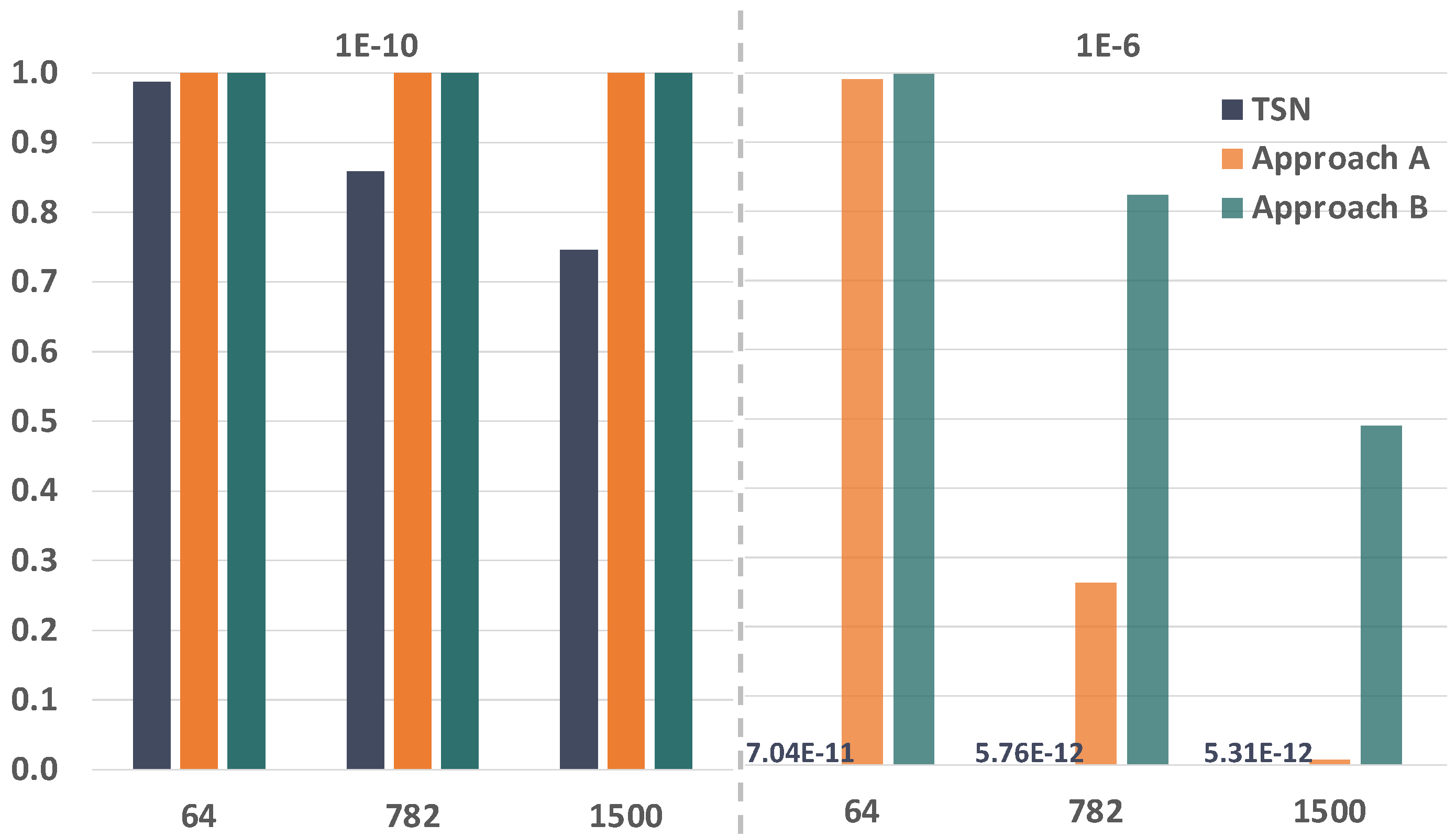
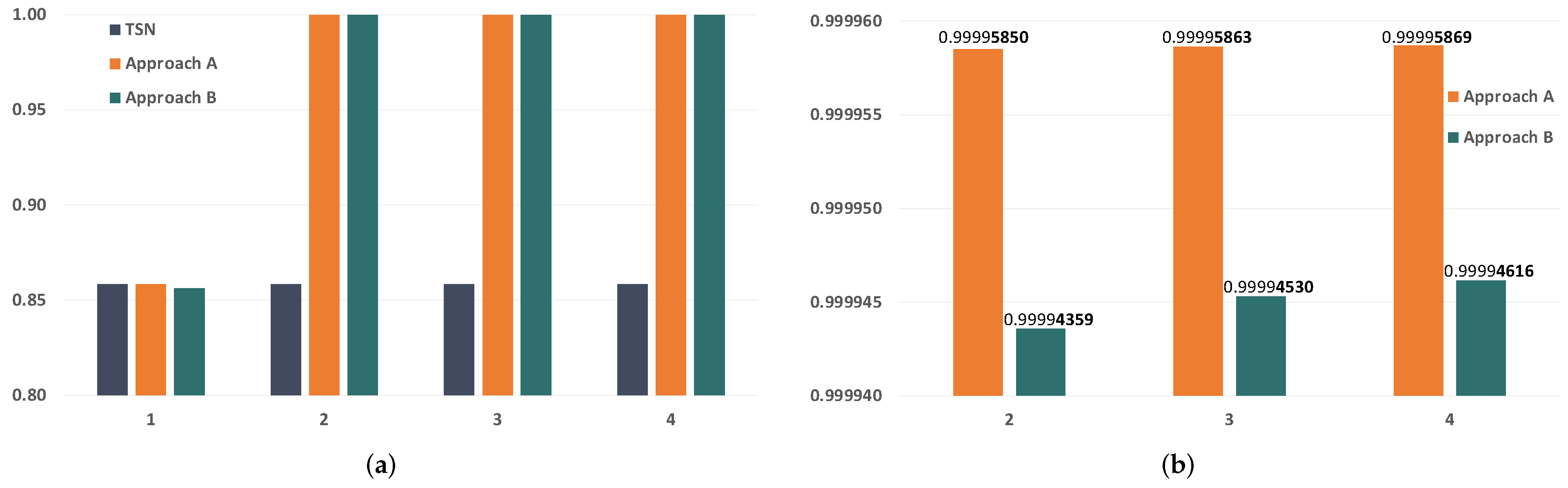
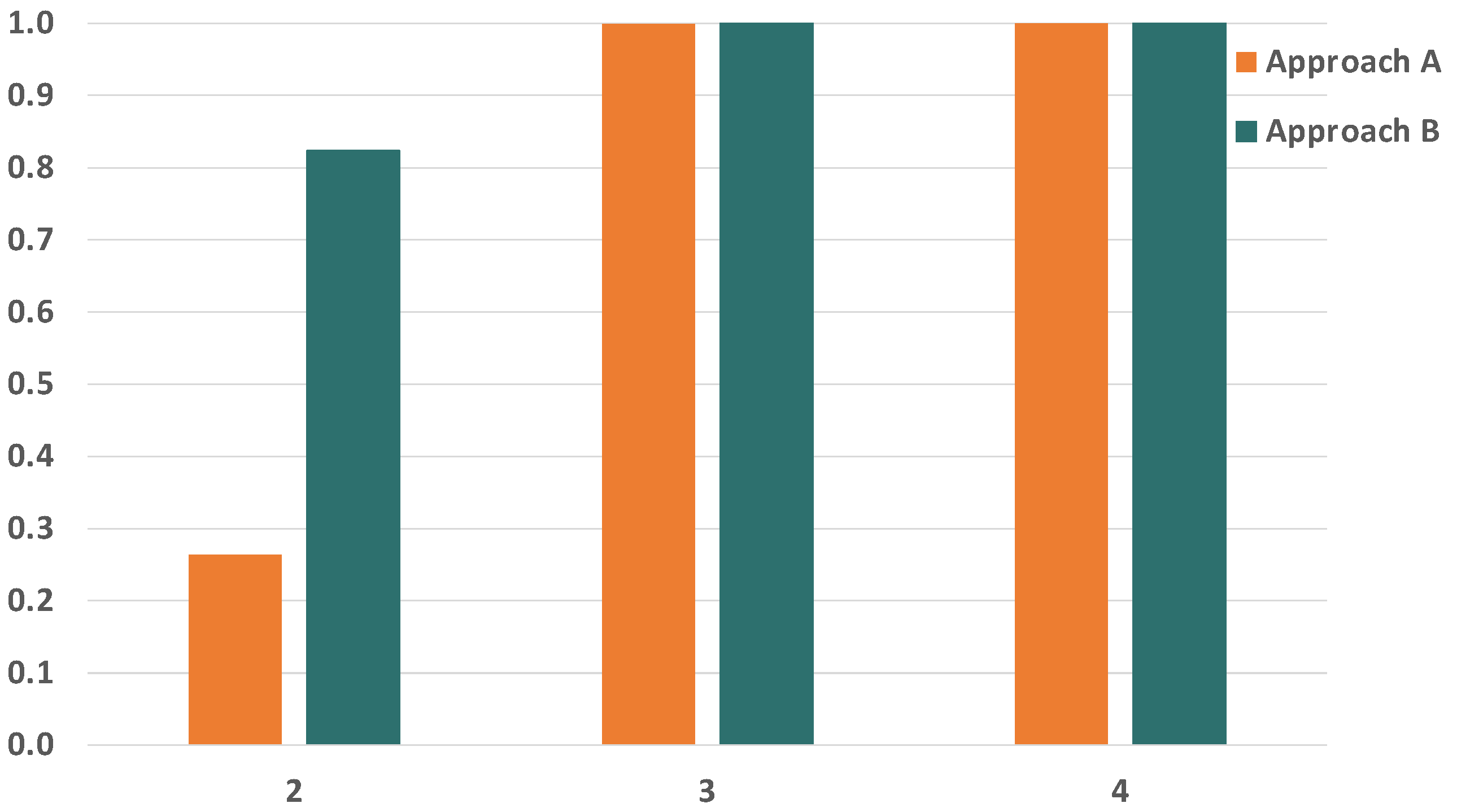
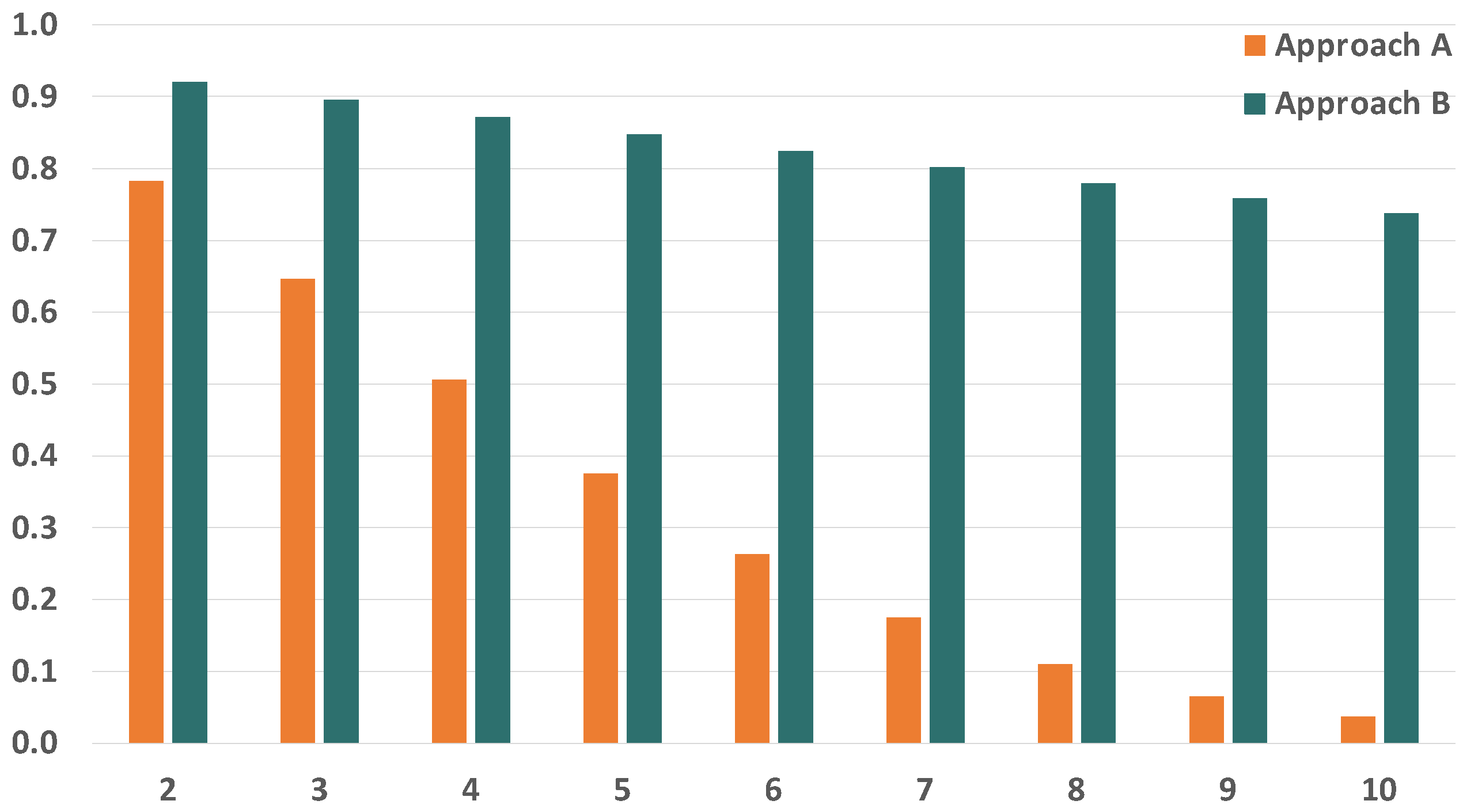
| Device | Unreliability | Faulty Port | Prop. | Faulty Component | Failure Mode | Prop. | Stream Failure |
|---|---|---|---|---|---|---|---|
| TSN Talker | 1 − | Output | 50% | Port/queue | Byzantine | 100% | Y |
| Input | 50% | - | - | - | N | ||
| TSN Bridge | 1 − | - | 100% | - | Byzantine | 100% | Y |
| TSN Listener | 1 − | Output | 50% | - | - | - | N |
| Input | 50% | Port/queue | - | 100% | Y | ||
| PTRF Talker | 1 − | Output | 50% | Port/queue | TSN + buffer | 83.33% | Y |
| PTRF transmission | counter > k | 8.33% | Y | ||||
| counter < k | 8.33% | ()N/()Y | |||||
| Input | 50% | - | - | - | N | ||
| PTRF Bridge | 1 − | Output | 50% | Port/queue | TSN + buffer | 83.33% | Y |
| PTRF transmission | counter > k | 8.33% | Y | ||||
| counter < k | 8.33% | ()N/()Y | |||||
| Input | 50% | PTRF reception | Fail to eliminate | 100% | Y | ||
| PTRF Listener | 1 − | Output | 50% | - | - | - | N |
| Input | 50% | PTRF reception | Fail to eliminate | 100% | Y |
| Component Failure | Description | Stream Failure |
|---|---|---|
| Frames corrupted in the replication buffer | Temporary faults can result in the corruption of frames before they are replicated, e.g., due to a bit flip. If the frame that is going to be replicated is corrupted, all the replicas will be corrupted too and the receiver will drop them when checking the CRC. If this happens the intended listeners do not receive the frame and, thus, they cannot carry out their operation properly. | Yes |
| Frame replication counter corrupted, creating n ≠ k replicas. | n > k. If a device creates more replicas than expected their transmission may affect the transmission of correct scheduled frames. | Yes |
| 0 < n < k. If the device creates fewer replicas than expected, then it provokes redundancy attrition, i.e., it reduces the number of forwarded frame replicas and thus the capacity of tolerating faults of the corresponding message edition in the hop, but does not provoke the failure of the stream. | No | |
| n = 0. If the device does not send any replicas of the frame, the intended listeners do not receive the frame and, thus, they cannot carry out their operation properly. | Yes | |
| Failing to eliminate surplus replicas upon reception | A PTRF device can fail to eliminate all surplus replicas upon reception. If this happens in a bridge, the surplus replica will be also forwarded and transmitted, violating the schedule. Let us illustrate this with an example. A PTRF bridge receives the first replica of a frame i , it correctly forwards replica and uses it to create a new set of replicas. Later on, the same bridge receives replica , and it fails to eliminate it. Thus, the bridge forwards replica and uses it to create a new set of replicas again, resulting in the transmission of twice the number of expected replicas and interfering in the transmission of correct frames. On the other hand, if this happens in the listener, PTRF passes the same frame several times to the application, causing the failure of the system. | Yes |
| Eliminating all replicas of a frame upon reception | Temporary faults may affect the identification of replicas upon reception in such a way that all the replicas of a specific frame are eliminated. If this happens the intended listeners do not receive the frame and, thus, they cannot carry out their operation properly. | Yes |
| TSN | Approach A | Approach B |
|---|---|---|
| 0.858467899141365 | 0.999958504043796 | 0.999943599679439 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Álvarez, I.; Barranco, M.; Proenza, J. Reliability Analysis of the Proactive Transmission of Replicated Frames Mechanism over Time-Sensitive Networking. Sensors 2021, 21, 8427. https://doi.org/10.3390/s21248427
Álvarez I, Barranco M, Proenza J. Reliability Analysis of the Proactive Transmission of Replicated Frames Mechanism over Time-Sensitive Networking. Sensors. 2021; 21(24):8427. https://doi.org/10.3390/s21248427
Chicago/Turabian StyleÁlvarez, Inés, Manuel Barranco, and Julián Proenza. 2021. "Reliability Analysis of the Proactive Transmission of Replicated Frames Mechanism over Time-Sensitive Networking" Sensors 21, no. 24: 8427. https://doi.org/10.3390/s21248427
APA StyleÁlvarez, I., Barranco, M., & Proenza, J. (2021). Reliability Analysis of the Proactive Transmission of Replicated Frames Mechanism over Time-Sensitive Networking. Sensors, 21(24), 8427. https://doi.org/10.3390/s21248427






