Data-Driven Analysis for Safe Ship Operation in Ports Using Quantile Regression Based on Generalized Additive Models and Deep Neural Network
Abstract
1. Introduction
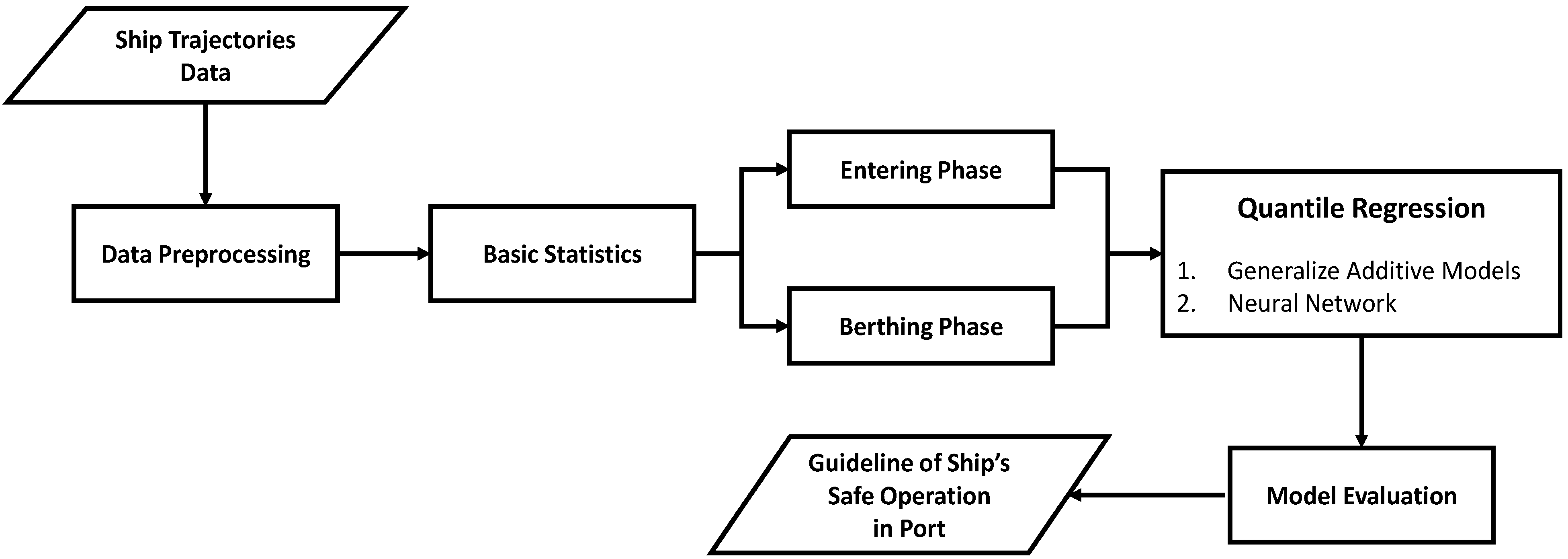
2. Materials and Methods
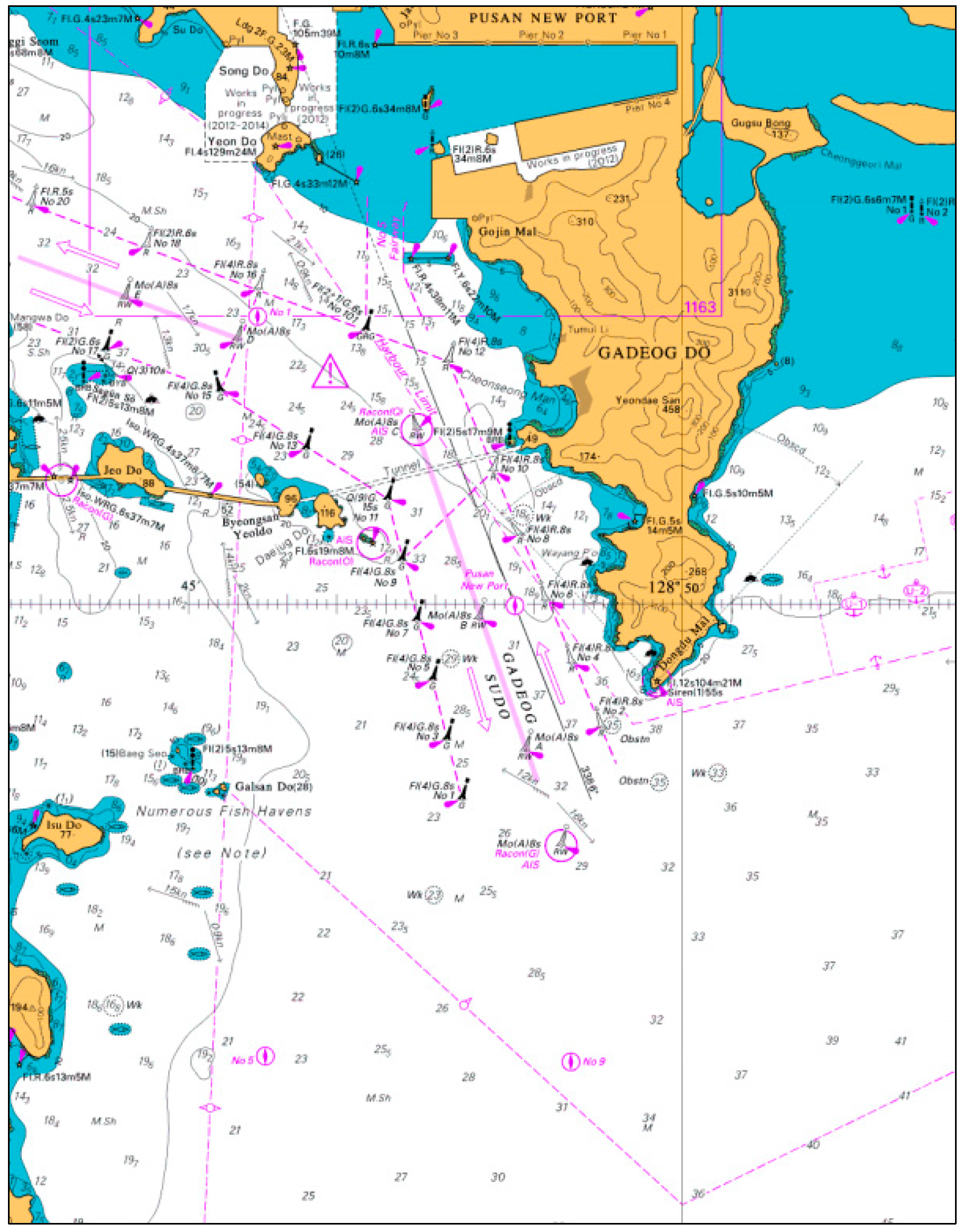
2.1. Ship Trajectory Data
2.2. Data Preprocessing and Statistics
2.3. Quantile Regression
2.4. Genealized Additive Models
2.5. Quantile Regression Newral Network
2.6. Model Evaluation
3. Experiments and Results
3.1. Data Preprocessing and Statistics
3.2. Modeling and Evaluation
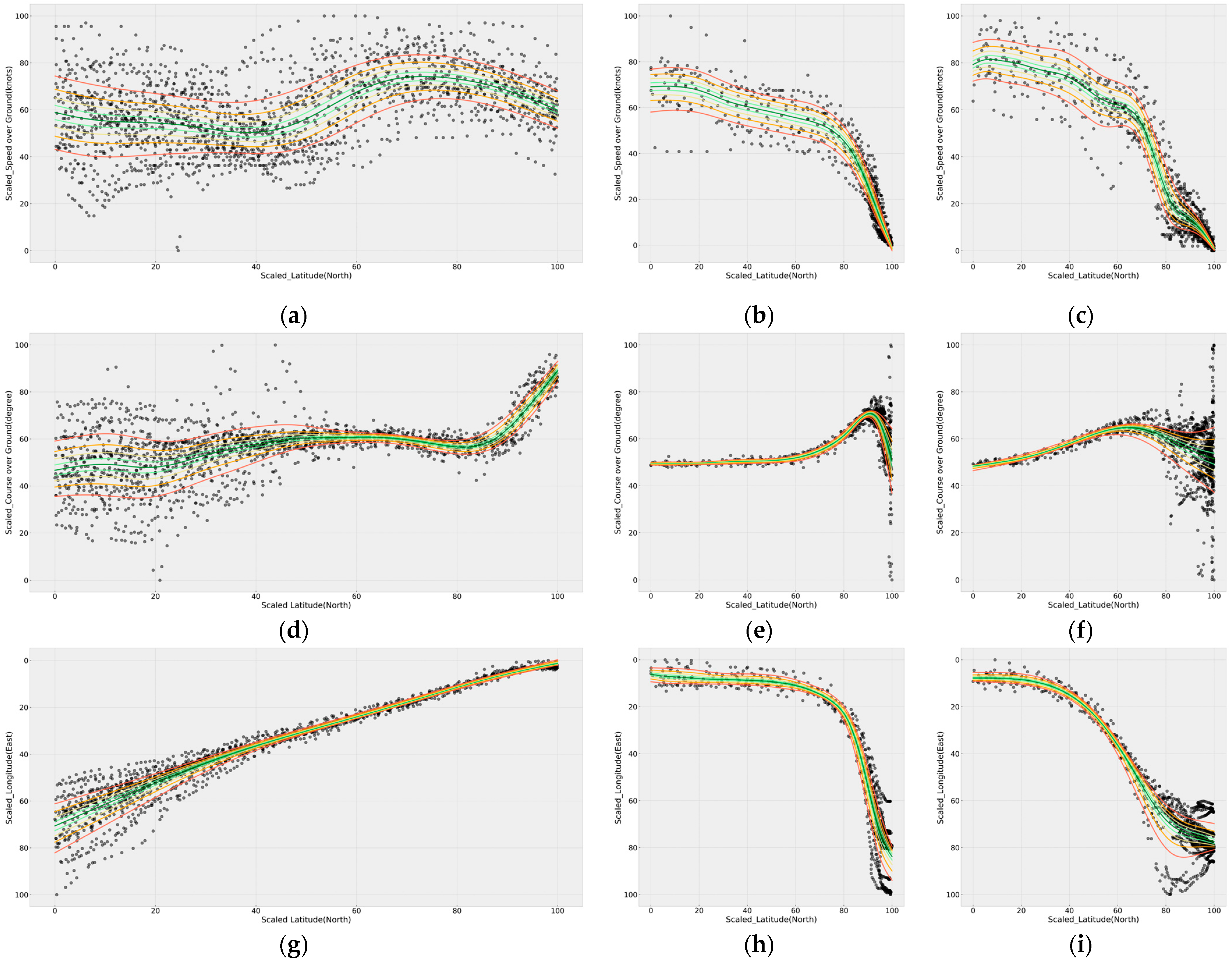
3.2.1. Modeling of Generalized Additive Models
3.2.2. Modeling of the Quantile Regression Neural Network
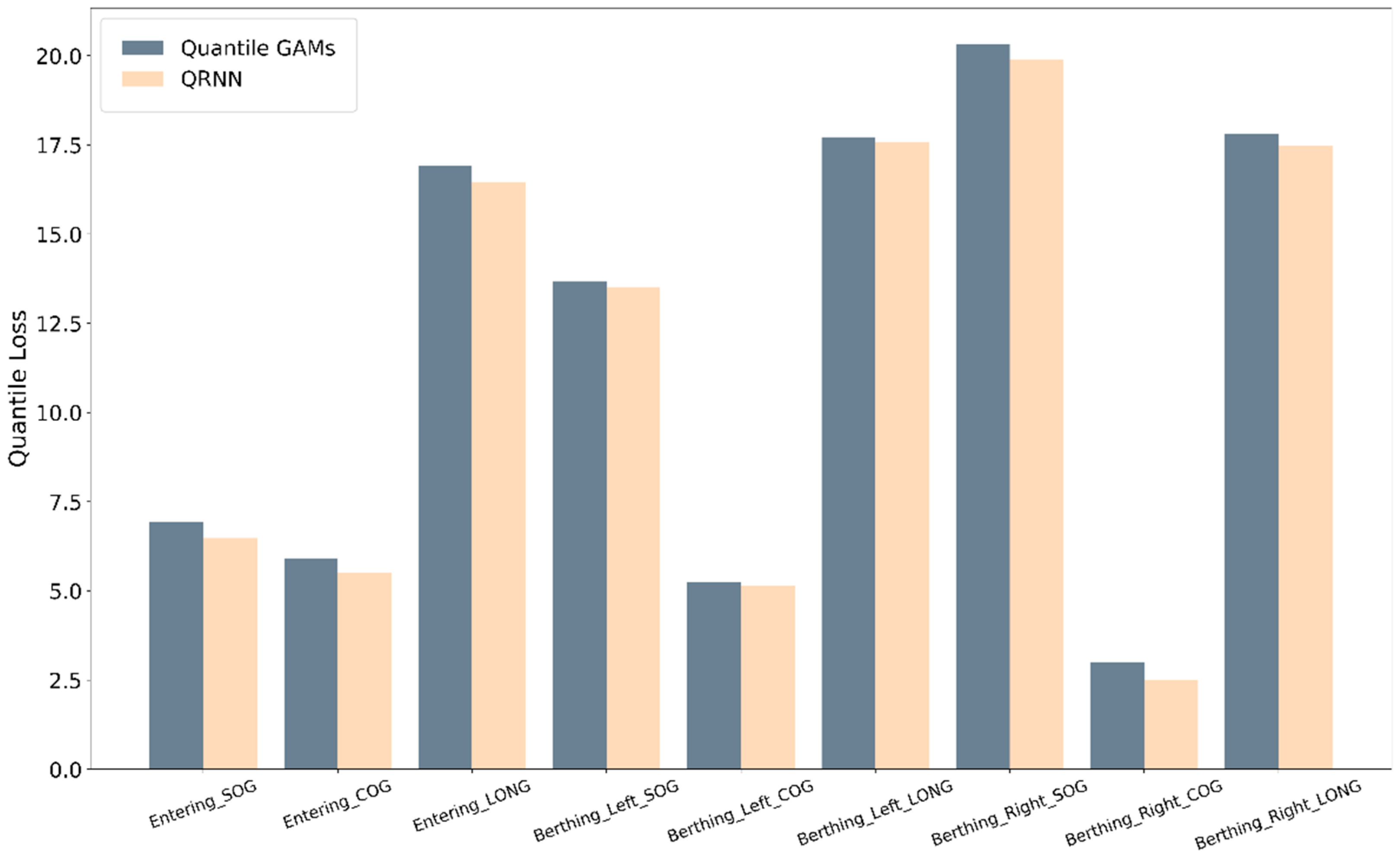
3.2.3. Evaluation
4. Discussion
5. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sur, J.M.; Kim, D.J. Comprehensive risk estimation of maritime accident using fuzzy evaluation method—Focusing on fishing vessel accident in Korean waters. Asian J. Shipp. Logist. 2020, 36, 127–135. [Google Scholar] [CrossRef]
- Kim, C.H.; Park, Y.S.; Kim, D.W. A Study on the safety measure for mega container Ship’s calling at Busan new port from the perspective of pilotage. J. Navig. Port Res. 2015, 44, 174–180. [Google Scholar]
- KMST. Maritime Accidents Special Investigation Report—Crane Collision Accident of Container Ship; Technical Report for Marine Accident Investigation; Marine Accident Investigation: Sejong, Korea, 2020. [Google Scholar]
- Perkovič, M.; Gucma, L.; Bilewski, M.; Muczynski, B.; Dimc, F.; Luin, B.; Vidmar, P.; Lorenčič, V.; Batista, M. Laser-based aid systems for berthing and docking. J. Mar. Sci. Eng. 2020, 8, 346. [Google Scholar] [CrossRef]
- Lee, H.T.; Lee, J.S.; Cho, J.W.; Yang, H.; Cho, I.S. A Study on the Pattern of Pilot’s Maneuvering using K-means Clustering of Ship’s Berthing Velocity. J. Coas.T Disaster Prev. 2020, 7, 221–232. [Google Scholar] [CrossRef]
- Ji, Y.; Wang, L.; Wu, W.; Shao, H.; Feng, Y. A method for LSTM-based trajectory modeling and abnormal trajectory detection. IEEE Access 2020, 8, 104063–104073. [Google Scholar] [CrossRef]
- Zhang, L.; Meng, Q.; Xiao, Z.; Fu, X. A novel ship trajectory reconstruction approach using AIS data. Ocean. Eng. 2018, 159, 165–174. [Google Scholar] [CrossRef]
- Lee, J.S.; Son, W.J.; Lee, H.T.; Cho, I.S. Verification of novel maritime route extraction using kernel density estimation analysis with automatic identification system data. J. Mar. Sci. Eng. 2020, 8, 375. [Google Scholar] [CrossRef]
- Son, W.J.; Lee, J.S.; Lee, H.T.; Cho, I.S. An investigation of the ship safety distance for bridges across waterways based on traffic distribution. J. Mar. Sci. Eng. 2020, 8, 331. [Google Scholar] [CrossRef]
- Huang, J.C.; Nieh, C.Y.; Kuo, H.C. Risk assessment of ships maneuvering in an approaching channel based on AIS data. Ocean. Eng. 2019, 173, 399–414. [Google Scholar] [CrossRef]
- Namgung, H.; Kim, J.S. Vessel trajectory analysis in designated harbor route considering the influence of external forces. J. Mar. Sci. Eng. 2020, 8, 860. [Google Scholar] [CrossRef]
- Suo, Y.; Chen, W.; Claramunt, C.; Yang, S.A. A Ship trajectory prediction framework based on a recurrent neural network. Sensors 2020, 20, 5133. [Google Scholar] [CrossRef] [PubMed]
- Gao, D.W.; Zhu, Y.S.; Zhang, J.F.; He, Y.K.; Yan, K.; Yan, B.R. A novel MP-LSTM method for ship trajectory prediction based on AIS data. Ocean. Eng. 2021, 228, 108956. [Google Scholar] [CrossRef]
- Zhang, D.; Zhang, Y.; Zhang, C. Data mining approach for automatic ship-route design for coastal seas using AIS trajectory clustering analysis. Ocean. Eng. 2021, 236, 109535. [Google Scholar] [CrossRef]
- Wang, L.; Chen, P.; Chen, L.; Mou, J. Ship AIS trajectory clustering: An HDBSCAN-based approach. J. Mar. Sci. Eng. 2021, 9, 566. [Google Scholar] [CrossRef]
- Lee, H.T.; Lee, J.S.; Yang, H.; Cho, I.S. An AIS data-driven approach to analyze the pattern of ship trajectories in ports using the DBSCAN algorithm. Appl. Sci. 2021, 11, 799. [Google Scholar] [CrossRef]
- Rong, H.; Teixeira, A.P.; Guedes Soares, C.G. Data mining approach to shipping route characterization and anomaly detection based on AIS data. Ocean. Eng. 2020, 198, 106936. [Google Scholar] [CrossRef]
- Choi, K.Y.; Lee, D.S.; Park, Y.S. A study on the analysis of present navigation method at the Ulsan waterways from the viewpoint of pilot. J. Navig. Port Res. 2011, 35, 469–475. [Google Scholar] [CrossRef][Green Version]
- DinparastDjadid, A.; Lee, J.D.; Domeyer, J.; Schwarz, C.; Brown, T.L.; Gunaratne, P. Designing for the extremes: Modeling drivers’ response time to take back control from automation using Bayesian quantile regression. Hum. Factors 2021, 63, 519–530. [Google Scholar] [CrossRef] [PubMed]
- Zou, Y.; Tang, J.; Wu, L.; Henrickson, K.; Wang, Y. Quantile analysis of factors influencing the time taken to clear road traffic incidents. Transp. 2017, 170, 296–304. [Google Scholar] [CrossRef]
- Murphy, R.R.; Perry, E.; Harcum, J.; Keisman, J. A generalized additive model approach to evaluating water quality: Chesapeake bay case study. Environ. Modell. Softw. 2019, 118, 1–13. [Google Scholar] [CrossRef]
- Dinga, R.; Fraza, C.J.; Bayer, J.M.; Kia, S.M.; Beckmann, C.F.; Marquand, A.F. Normative modeling of neuroimaging data using generalized additive models of location scale and shape. bioRxiv 2021. [Google Scholar] [CrossRef]
- Deng, Z.; Wang, B.; Guo, H.; Chai, C.; Wang, Y.; Zhu, Z. Unified quantile regression deep neural network with time-cognition for probabilistic residential load forecasting. Complexity 2020, 2020, 9147545. [Google Scholar] [CrossRef]
- Gan, D.; Wang, Y.; Yang, S.; Kang, C. Embedding based quantile regression neural network for probabilistic load forecasting. J. Mod. Power Syst. Clean Energy 2018, 6, 244–254. [Google Scholar] [CrossRef]
- Jia, Y.; Jeong, J.H. Deep learning for quantile regression under right censoring: DeepQuantreg. Comp. Stat. Data Anal. 2021, 107323. Available online: https://arxiv.org/abs/2007.07056 (accessed on 9 December 2021).
- Yoon, J.D.; Yun, J.H.; Lee, C.K. A study on the method of conducting a large container vessel safely to the newly built container pier to get alongside in Busan Harbour. J. Korean Soc. Mar. Environ. Saf. 2007, 13, 147–153. [Google Scholar]
- Han, J.; Pei, J.; Kamber, M. Data Preprocessing. In Data Mining: Concepts and Techniques, 3rd ed.; Elsevier: Waltham, MA, USA, 2011; pp. 83–124. [Google Scholar]
- Series, M. Technical characteristics for an automatic identification system using time-division multiple access in the VHF maritime mobile band. In Recommendation M.1371; International Telecommunication Union: Geneva, Switzerland, 2014; Available online: https://www.itu.int/dms_pubrec/itu-r/rec/m/R-REC-M.1371-5-201402-I!!PDF-E.pdf (accessed on 9 December 2021).
- Kim, D.Y.; Hong, T.H.; Jeong, J.S.; Lee, S.J. Building an algorithm for compensating AIS error data. J. Korean Inst. Intell Syst. 2014, 24, 310–315. [Google Scholar]
- Olinsky, A.; Chen, S.; Harlow, L. The comparative efficacy of imputation methods for missing data in structural equation modelling. Eur. J. Oper. Res. 2003, 151, 53–79. [Google Scholar] [CrossRef]
- Koenker, R.; Bassett, G. Regression quantiles. Econometrica 1978, 46, 33–50. [Google Scholar] [CrossRef]
- Cannon, A.J. Quantile regression neural networks: Implementation in R and application to precipitation downscaling. Comput. Geosci. 2011, 37, 1277–1284. [Google Scholar] [CrossRef]
- Koenker, R.; Park, B.J. An interior point algorithm for nonlinear quantile regression. J. Econ. 1996, 71, 265–283. [Google Scholar] [CrossRef]
- Saerens, M. Building cost functions minimizing to some summary statistics. IEEE Trans. Neural Netw. 2000, 11, 1263–1271. [Google Scholar] [CrossRef]
- Faraway, J.J. Extending the linear model with R: Generalized linear, mixed effects and nonparametric regression models. J. Am. Stat. Assoc. 2007, 102, 1477. [Google Scholar] [CrossRef]
- Yee, T.W.; Mitchell, N.D. Generalized additive models in plant ecology. J. Veg. Sci. 1991, 2, 587–602. [Google Scholar] [CrossRef]
- Lee, D.; Baldick, R. Short-term wind power ensemble prediction based on Gaussian processes and neural networks. IEEE Trans. Smart Grid 2013, 5, 501–510. [Google Scholar] [CrossRef]
- Jia, Y.; Jeong, J.H. Deep learning for quantile regression: DeepQuantreg. arXiv 2020, arXiv:2007.07056. Available online: https://ui.adsabs.harvard.edu/abs/2020arXiv200707056J/abstract (accessed on 9 December 2021).
- Clevert, D.A.; Unterthiner, T.; Hochreiter, S. Fast and accurate deep network learning by exponential linear units (ELUs). arXiv 2015, arXiv:1511.07289. [Google Scholar]
- Ruder, S. An overview of gradient descent optimization algorithms. arXiv 2016, arXiv:1609.04747. [Google Scholar]
- Xu, Q.; Zhang, J.; Jiang, C.; Huang, X.; He, Y. Weighted quantile regression via support vector machine. Expert Syst. Appl. 2015, 42, 5441–5451. [Google Scholar] [CrossRef]
- Lee, H.T.; Lee, J.S.; Son, W.J.; Cho, I.S. Development of machine learning strategy for predicting the risk range of Ship’s berthing velocity. J. Mar. Sci. Eng. 2020, 8, 376. [Google Scholar] [CrossRef]
- Lee, H.T.; Lee, S.W.; Cho, J.W.; Cho, I.S. Analysis of feature importance of ship’s berthing velocity using classification algorithms of machine learning. J. Korean Soc. Mar. Environ. Saf. 2020, 26, 139–148. [Google Scholar] [CrossRef]




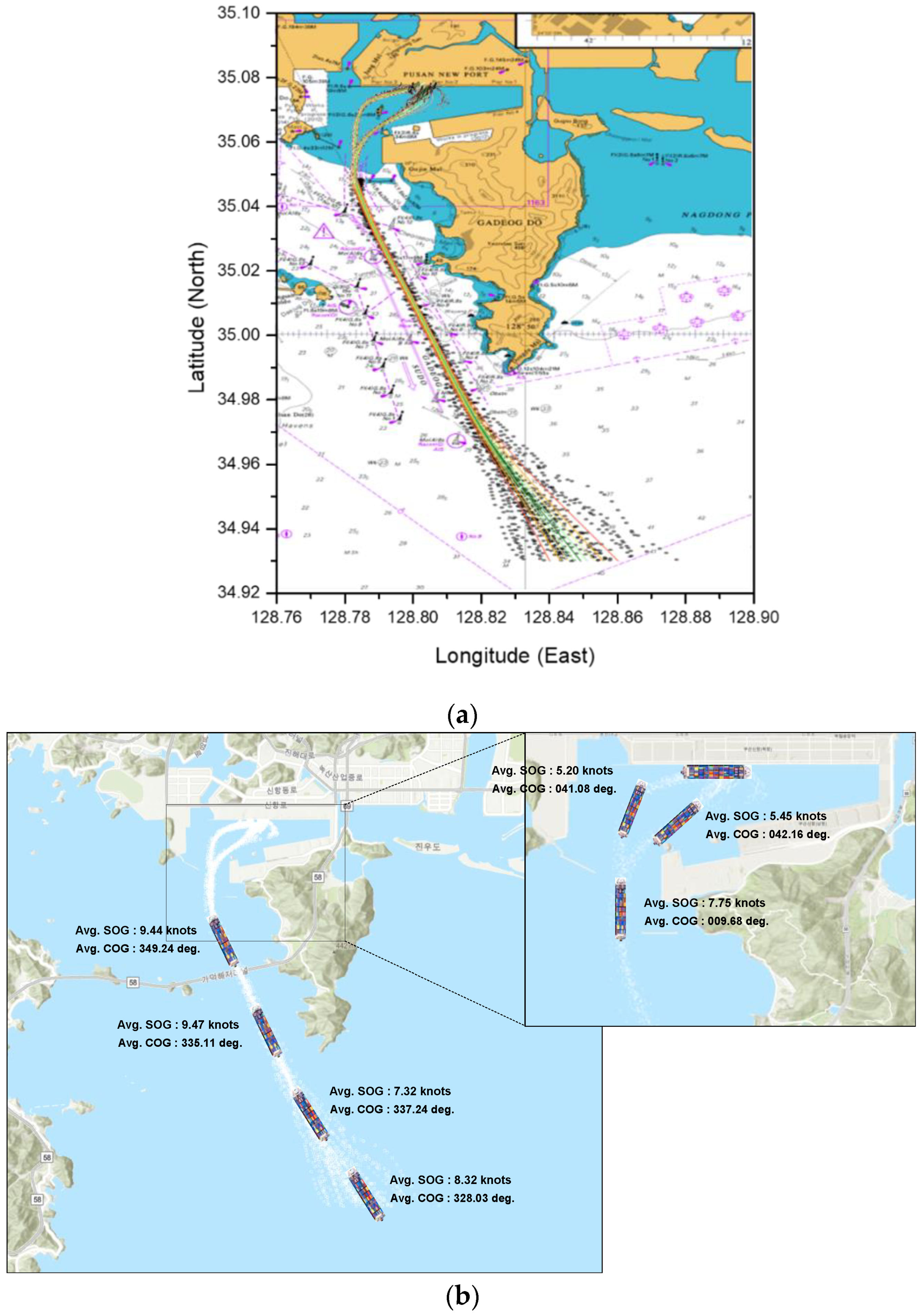
| Categorization | AIS Information |
|---|---|
| Period | 1 January 2020–30 April 2020 |
| Collection Area | Latitude 034.8 N–035.1 N Longitude 128.7 E–129.0 E (Around Busan New Port) |
| Pier | Pier 2 No. 4 Pier 2 No. 5 Pier 3 No. 1 |
| Ship Type | Container Ship |
| Size of ship | Gross tonnage 100–220k |
| Information | Ship’s position (latitude, longitude) Speed over Ground (knots) Course over Ground (degree) |
| Todo Passing | Pier | Total | ||
|---|---|---|---|---|
| Pier 2 No. 4 | Pier 2 No. 5 | Pier 3 No. 1 | ||
| Left | 5 | 17 | 1 | 23 |
| Right | 23 | 4 | - | 27 |
| Phase | Speed over Ground (Knots) | Course Over Ground (Degree) | Longitude (East) | Latitude (North) | |||||
|---|---|---|---|---|---|---|---|---|---|
| Min | Mas | Min | Max | Min | Max | Min | Max | ||
| Entering Phase | 0.9 | 14.4 | 293.5 | 007.8 (367.8) | 128.780 | 128.877 | 34.930 | 35.050 | |
| Berthing Phase | Left | 0.0 | 12.0 | 184.5 | 179.8 (539.8) | 128.781 | 128.805 | 35.050 | 35.078 |
| Right | 0.0 | 10.2 | 191.3 | 173.7 (533.7) | 128.781 | 128.811 | 35.050 | 35.078 | |
| Group 1 | SOG 2 | COG 3 | Longitude | |||
|---|---|---|---|---|---|---|
| Mean | Std. | Mean | Std. | Mean | Std. | |
| 34.930 | 9.07 | 2.28 | 329.03 | 10.40 | 128.85 | 0.01 |
| 34.935 | 8.45 | 2.44 | 328.95 | 10.23 | 128.85 | 0.01 |
| 34.940 | 8.29 | 2.53 | 330.16 | 11.00 | 128.84 | 0.01 |
| 34.945 | 8.44 | 2.13 | 330.19 | 11.70 | 128.84 | 0.01 |
| 34.950 | 8.30 | 1.92 | 329.10 | 10.90 | 128.83 | 0.01 |
| 34.955 | 8.24 | 1.94 | 328.82 | 10.83 | 128.83 | 0.01 |
| 34.960 | 8.11 | 2.19 | 330.97 | 8.15 | 128.83 | 0.01 |
| 34.965 | 8.11 | 1.78 | 332.45 | 7.59 | 128.82 | 0.01 |
| 34.970 | 7.76 | 1.49 | 334.94 | 9.22 | 128.82 | 0.01 |
| 34.975 | 7.69 | 1.65 | 334.95 | 6.53 | 128.82 | 0.01 |
| 34.980 | 7.78 | 1.92 | 336.18 | 4.86 | 128.81 | 0.01 |
| 34.985 | 7.79 | 1.88 | 338.68 | 7.14 | 128.81 | 0.01 |
| 34.990 | 8.42 | 2.08 | 338.17 | 3.23 | 128.81 | 0.01 |
| 34.995 | 9.27 | 2.36 | 338.42 | 2.60 | 128.81 | 0.01 |
| 35.000 | 9.80 | 1.85 | 338.19 | 2.35 | 128.80 | 0.01 |
| 35.005 | 10.53 | 1.79 | 338.59 | 1.68 | 128.80 | 0.01 |
| 35.010 | 10.73 | 1.67 | 338.54 | 1.76 | 128.80 | 0.01 |
| 35.015 | 10.97 | 1.42 | 337.68 | 1.57 | 128.80 | 0.01 |
| 35.020 | 10.87 | 1.48 | 336.63 | 2.16 | 128.79 | 0.01 |
| 35.025 | 10.66 | 1.34 | 336.27 | 2.47 | 128.79 | 0.01 |
| 35.030 | 10.60 | 1.31 | 335.80 | 2.77 | 128.79 | 0.01 |
| 35.035 | 10.43 | 1.43 | 337.06 | 2.76 | 128.79 | 0.01 |
| 35.040 | 10.06 | 1.28 | 343.79 | 5.73 | 128.78 | 0.01 |
| 35.045 | 9.38 | 1.36 | 353.08 | 4.86 | 128.78 | 0.01 |
| 35.050 | 8.62 | 1.26 | 359.07 | 3.30 | 128.78 | 0.01 |
| 35.055 | 8.16 | 1.16 | 363.07 | 4.79 | 128.78 | 0.01 |
| 35.060 | 7.48 | 1.15 | 014.97 | 12.56 | 128.78 | 0.01 |
| 35.065 | 6.65 | 1.19 | 032.51 | 21.38 | 128.79 | 0.01 |
| 35.070 | 4.77 | 1.86 | 042.87 | 18.27 | 128.79 | 0.01 |
| 35.075 | 1.17 | 1.20 | 031.33 | 46.24 | 128.80 | 0.01 |
| Hidden Layer | Neurons 1 | MAE 2 | Computation Time (s) |
|---|---|---|---|
| 2 | 4 | 16.528711 | 10 s |
| 8 | 16.545627 | 10 s | |
| 16 | 16.787603 | 11 s | |
| 32 | 16.524037 | 15 s | |
| 3 | 4 | 16.499576 | 12 s |
| 8 | 16.391850 | 12 s | |
| 16 | 16.671966 | 13 s | |
| 32 | 16.369946 | 17 s | |
| 4 | 4 | 16.201253 | 14 s |
| 8 | 16.292288 | 15 s | |
| 16 | 16.193952 | 15 s | |
| 32 | 16.668355 | 17 s | |
| 5 | 4 | 16.218435 | 15 s |
| 8 | 16.382307 | 15 s | |
| 16 | 16.237098 | 18 s | |
| 32 | 16.383952 | 20 s |
| Model | Phase | Information | Quantile | Total | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | |||||
| Quantile GAMs | Entering Phase | SOG | 5.465 | 7.046 | 7.877 | 8.267 | 8.283 | 7.960 | 7.261 | 6.093 | 4.174 | 6.936 | |
| COG | 6.238 | 6.807 | 6.998 | 6.944 | 6.686 | 6.221 | 5.516 | 4.521 | 3.203 | 5.904 | |||
| LONG | 14.398 | 15.429 | 16.162 | 16.752 | 17.249 | 17.666 | 17.997 | 18.220 | 18.262 | 16.904 | |||
| Berthing Phase | Left | SOG | 20.124 | 19.827 | 18.600 | 16.870 | 14.796 | 12.425 | 9.786 | 6.874 | 3.692 | 13.666 | |
| COG | 2.568 | 3.386 | 4.118 | 4.796 | 5.426 | 6.012 | 6.547 | 7.010 | 7.353 | 5.246 | |||
| LONG | 3.993 | 7.726 | 11.328 | 14.822 | 18.212 | 21.480 | 24.590 | 27.447 | 29.815 | 17.713 | |||
| Right | SOG | 28.796 | 28.128 | 26.381 | 24.119 | 21.501 | 18.604 | 15.441 | 11.963 | 8.040 | 20.330 | ||
| COG | 3.233 | 3.552 | 3.611 | 3.536 | 3.366 | 3.108 | 2.750 | 2.253 | 1.485 | 2.988 | |||
| LONG | 6.310 | 9.582 | 12.368 | 15.529 | 18.308 | 20.974 | 23.502 | 25.841 | 27.799 | 17.801 | |||
| QRNN | Entering Phase | SOG | 4.503 | 6.336 | 7.467 | 8.026 | 8.196 | 7.932 | 7.221 | 5.463 | 3.247 | 6.488 | |
| COG | 5.785 | 6.797 | 7.077 | 6.945 | 6.359 | 5.747 | 4.898 | 3.831 | 2.305 | 5.527 | |||
| LONG | 13.035 | 14.716 | 15.608 | 16.345 | 16.885 | 17.403 | 17.836 | 18.084 | 18.166 | 16.453 | |||
| Berthing Phase | Left | SOG | 17.964 | 18.230 | 17.706 | 16.726 | 15.561 | 13.531 | 10.633 | 7.359 | 3.978 | 13.521 | |
| COG | 2.431 | 3.309 | 4.123 | 4.840 | 5.446 | 5.878 | 6.168 | 6.712 | 7.418 | 5.147 | |||
| LONG | 4.224 | 8.098 | 11.491 | 14.836 | 18.253 | 21.472 | 24.216 | 26.734 | 28.745 | 17.563 | |||
| Right | SOG | 27.056 | 26.949 | 25.644 | 23.889 | 21.625 | 18.536 | 15.409 | 11.951 | 7.963 | 19.891 | ||
| COG | 2.179 | 2.815 | 3.001 | 2.990 | 3.093 | 2.846 | 2.438 | 1.935 | 1.166 | 2.496 | |||
| LONG | 5.829 | 9.398 | 12.511 | 15.381 | 18.121 | 20.724 | 23.185 | 25.339 | 26.972 | 17.496 | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, H.-T.; Yang, H.; Cho, I.-S. Data-Driven Analysis for Safe Ship Operation in Ports Using Quantile Regression Based on Generalized Additive Models and Deep Neural Network. Sensors 2021, 21, 8254. https://doi.org/10.3390/s21248254
Lee H-T, Yang H, Cho I-S. Data-Driven Analysis for Safe Ship Operation in Ports Using Quantile Regression Based on Generalized Additive Models and Deep Neural Network. Sensors. 2021; 21(24):8254. https://doi.org/10.3390/s21248254
Chicago/Turabian StyleLee, Hyeong-Tak, Hyun Yang, and Ik-Soon Cho. 2021. "Data-Driven Analysis for Safe Ship Operation in Ports Using Quantile Regression Based on Generalized Additive Models and Deep Neural Network" Sensors 21, no. 24: 8254. https://doi.org/10.3390/s21248254
APA StyleLee, H.-T., Yang, H., & Cho, I.-S. (2021). Data-Driven Analysis for Safe Ship Operation in Ports Using Quantile Regression Based on Generalized Additive Models and Deep Neural Network. Sensors, 21(24), 8254. https://doi.org/10.3390/s21248254








