Characterization of Supersonic Compressible Fluid Flow Using High-Speed Interferometry
Abstract
1. Introduction
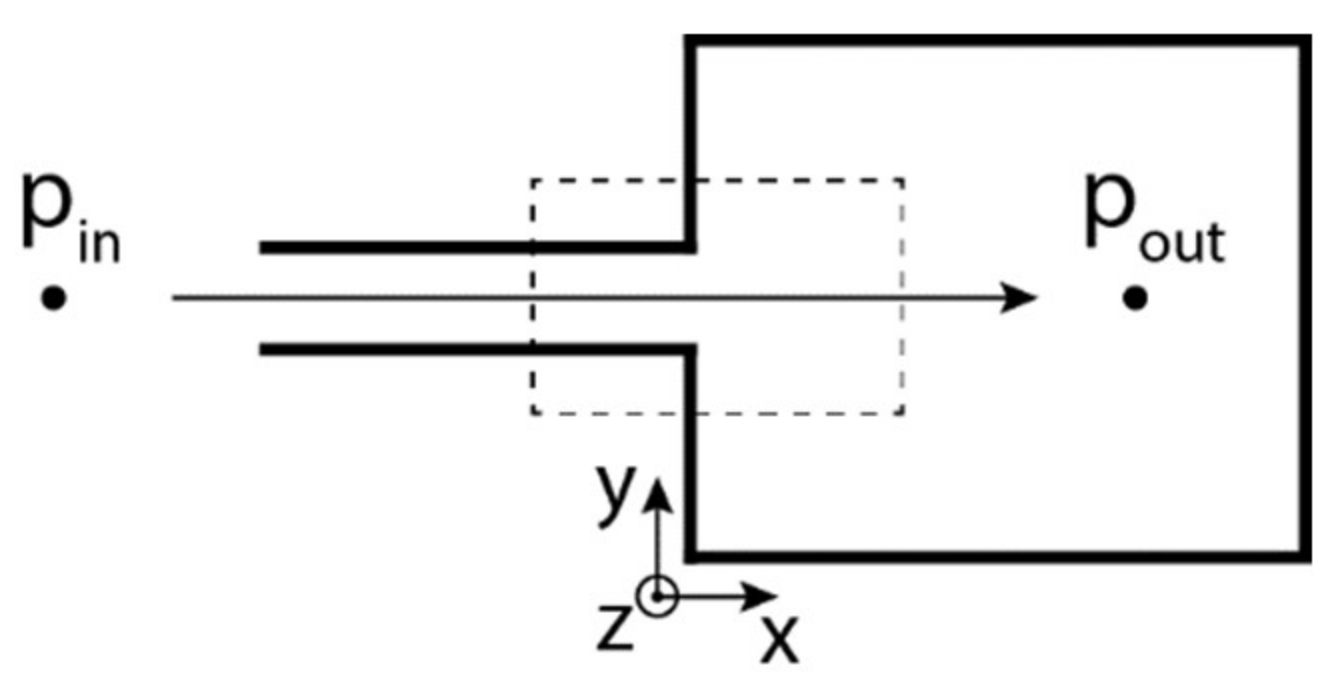
2. Method
2.1. Interferometry and Fluid Flow
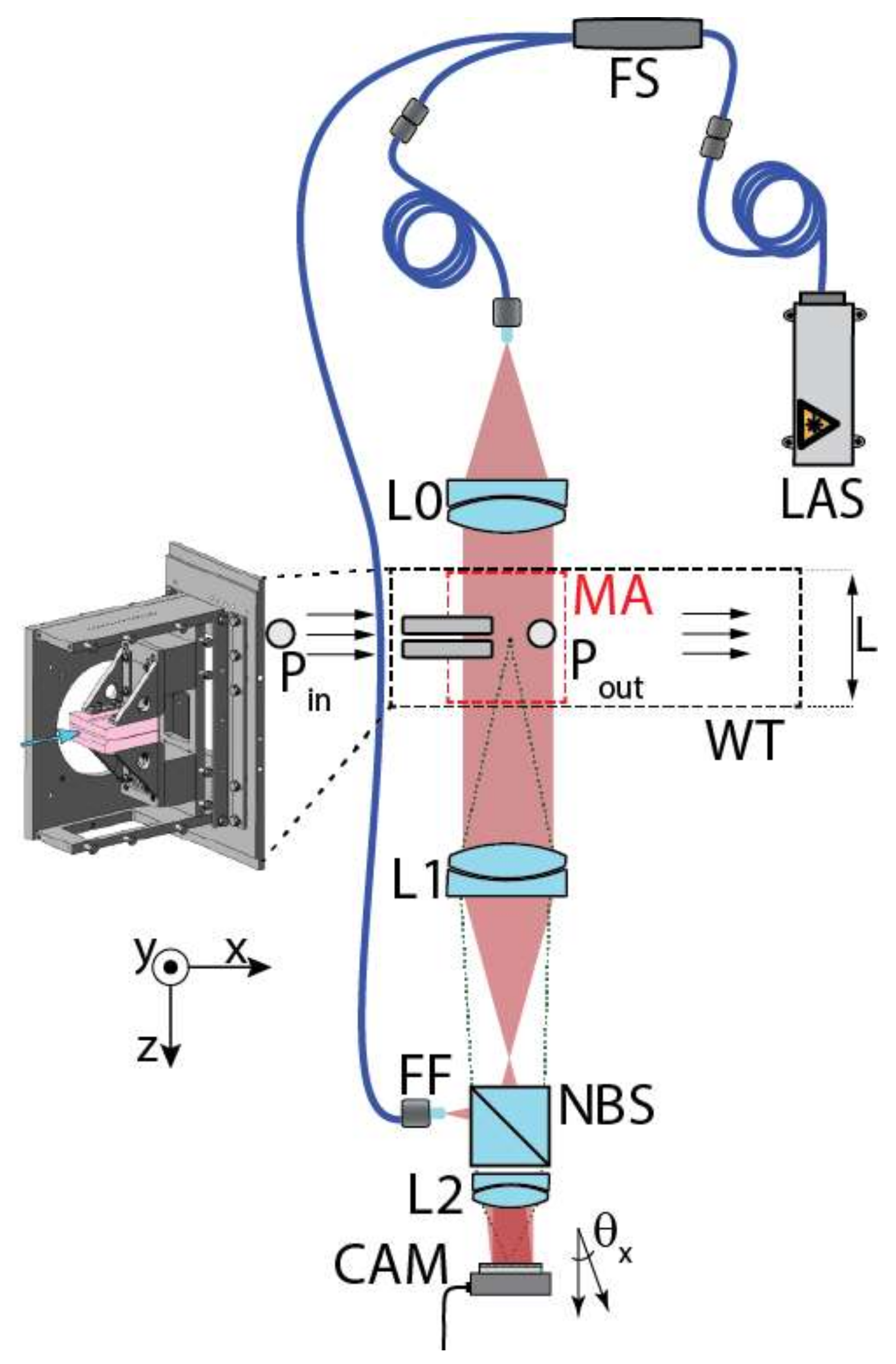
2.2. Spatial Carrier Interferometry
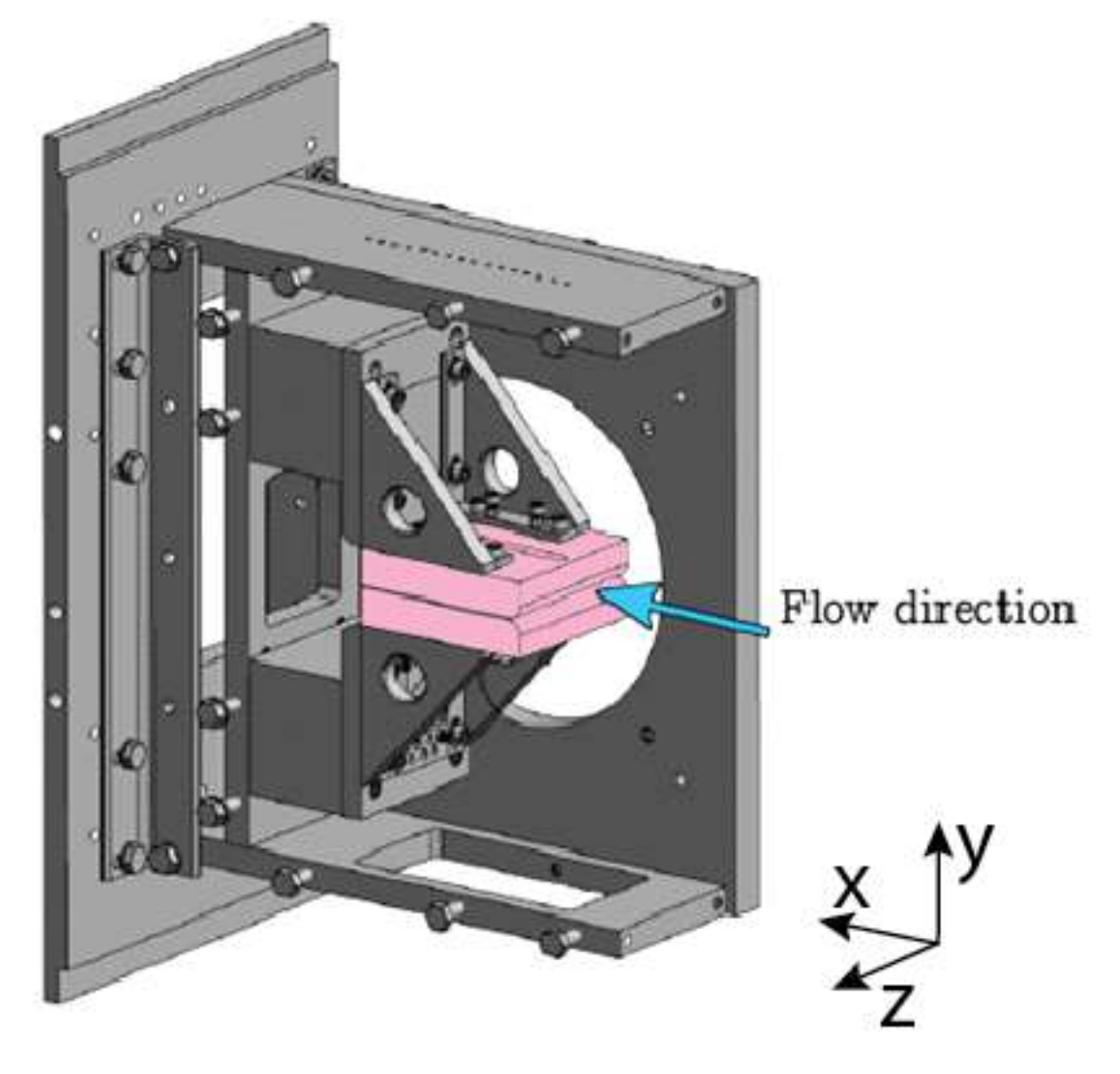
3. Materials and Methods
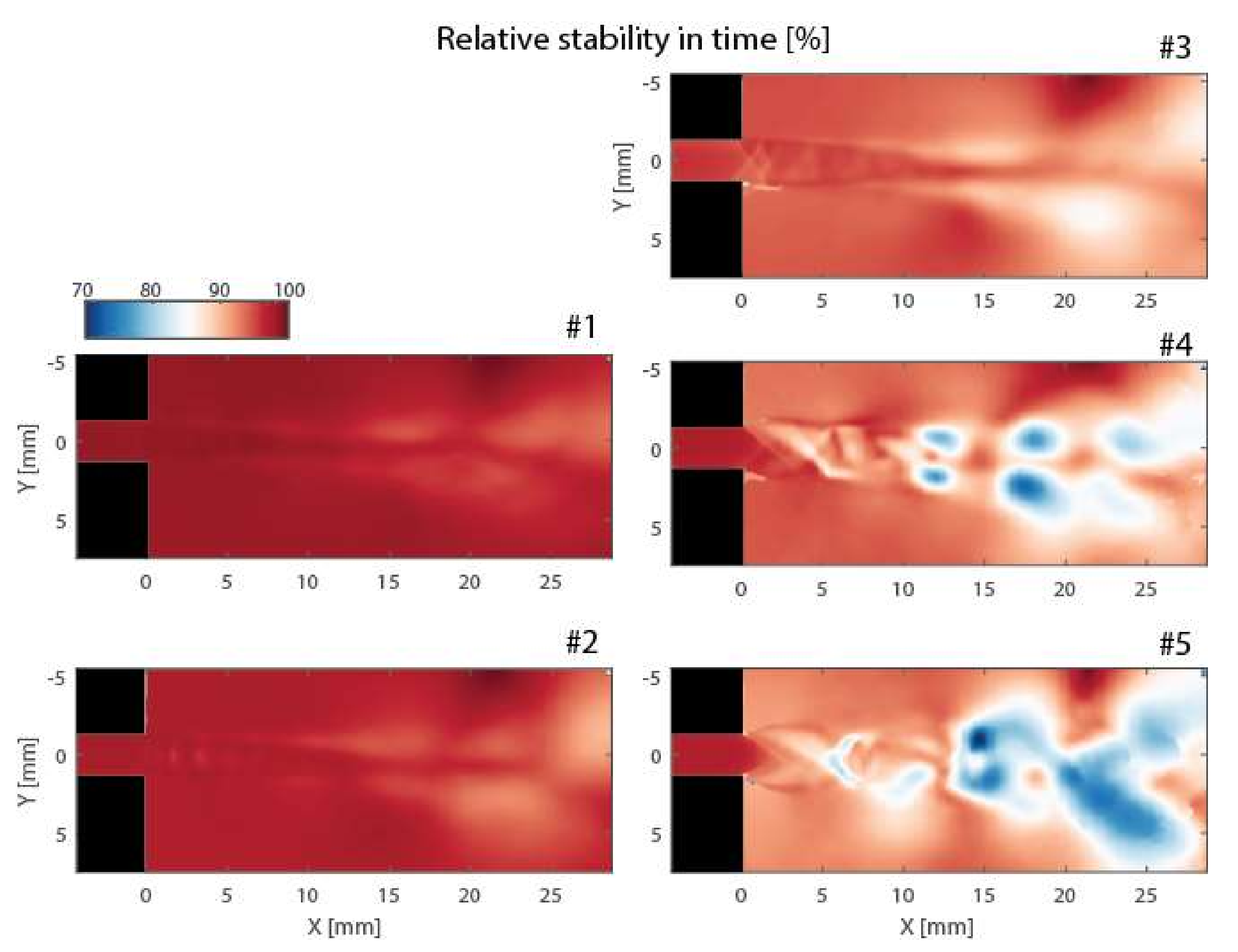
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Psota, P.; Dančová, P.; Cubreli, G.; Lédl, V.; Vít, T.; Doleček, R.; Matoušek, O. Development and application of spatial carrier interferometry for whole field real-time investigation of temperatures in liquid media. Int. J. Therm. Sci. 2019, 145, 106029. [Google Scholar] [CrossRef]
- Kim, K. Pneumatic Measurements for Pressure, Velocity, and Flow-direction. Appl. Fluid. Meas. Tech. 2016, 61–100. [Google Scholar] [CrossRef]
- Nour, M.A.; Hussain, M.M. A Review of the Real-Time Monitoring of Fluid-Properties in Tubular Architectures for Industrial Applications. Sensors 2020, 20, 3907. [Google Scholar] [CrossRef] [PubMed]
- Berthet, H.; Jundt, J.; Durivault, J.; Mercier, B.; Angelescu, D. Time-of-flight thermal flowrate sensor for lab-on-chip applications. Lab Chip 2011, 11, 215–223. [Google Scholar] [CrossRef] [PubMed]
- Meng, E.; Li, P.-Y.; Tai, Y.-C. A biocompatible Parylene thermal flow sensing array. Sens. Actuators A Phys. 2008, 144, 18–28. [Google Scholar] [CrossRef]
- Kuo, J.T.W.; Yu, L.; Meng, E. Micromachined Thermal Flow Sensors—A Review. Micromachines 2012, 3, 550–573. [Google Scholar] [CrossRef]
- Trolinger, J.D.; Buckner, B.; L’Esperance, D. Background-oriented schlieren for the study of large flow fields. Opt. Eng. Appl. 2015, 9576, 95760. [Google Scholar]
- Saravanan, S.; Nagashetty, K.; Hegde, G.M.; Jagadeesh, G.; Reddy, K.P.J. Schlieren Visualization of Shock Wave Phenomena over a Missile-Shaped Body at Hypersonic Mach Numbers. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2011, 225, 26–34. [Google Scholar] [CrossRef]
- Kleine, H.; Hiraki, K.; Maruyama, H.; Hayashida, T.; Yonai, J.; Kitamura, K.; Kondo, Y.; Etoh, T.G. High-speed time-resolved color schlieren visualization of shock wave phenomena. Shock Waves 2005, 14, 333–341. [Google Scholar] [CrossRef]
- Nel, L.; Skews, B.; Naidoo, K. Schlieren techniques for the visualization of an expansion fan/shock wave interaction. J. Vis. 2014, 18, 469–479. [Google Scholar] [CrossRef]
- Passmann, M.; Wiesche, S.A.D.A.D.; Joos, F. Focusing Schlieren Visualization of Transonic Turbine Tip-Leakage Flows. Int. J. Turbomach. Propuls. Power 2020, 5, 1. [Google Scholar] [CrossRef]
- Aftab, S.; Younis, O.; Al-Atabi, M. Four Decades of Utilizing Shadowgraph Techniques to study Natural Convection in Cavities: Literature Review. IOP Conf. Ser. Mater. Sci. Eng. 2012, 36, 012021. [Google Scholar] [CrossRef]
- Srivastava, A.; Phukan, A.; Panigrahi, P.; Muralidhar, K. Imaging of a convective field in a rectangular cavity using interferometry, schlieren and shadowgraph. Opt. Lasers Eng. 2004, 42, 469–485. [Google Scholar] [CrossRef]
- Hijikuro, M.; Anyoji, M. Application of Optical Flow Analysis to Shadowgraph Images of Impinging Jet. J. Flow Control. Meas. Vis. 2020, 8, 173–187. [Google Scholar] [CrossRef]
- Waynant, R.W.; Ediger, M.N. Electro-Optics Handbook; McGraw-Hill Education: New York, NY, USA, 2000. [Google Scholar]
- Xu, F.; Patterson, J.C.; Lei, C. Shadowgraph observations of the transition of the thermal boundary layer in a side-heated cavity. Exp. Fluids 2005, 38, 770–779. [Google Scholar] [CrossRef]
- Juste, G.L.; Benavides, E.M. Temperature Measurement in Small-Scale Flows with Digital Moiré Deflectometry. Exp. Heat Transf. 2011, 24, 201–214. [Google Scholar] [CrossRef]
- Juste, G.; Fajardo, P. Assessment of experimental optical techniques for characterizing heat transfer using numerical simulations. Eng. Appl. Comput. Fluid Mech. 2015, 9, 1–15. [Google Scholar] [CrossRef]
- Stricker, J.; Keren, E.; Kafri, O. Axisymmetric density field measurements by moire deflectometry. AIAA J. 1983, 21, 1767–1769. [Google Scholar] [CrossRef]
- Rasouli, S. Atmospheric Turbulence Characterization and Wavefront Sensing by Means of the Moiré Deflectometry. In Topics in Adaptive Optics; Intech: London, UK, 2012; p. 23. [Google Scholar] [CrossRef]
- Applications of 2-D Moiré Deflectometry to Atmospheric Turbulence. J. Appl. Fluid Mech. 2014, 7, 651–657. [CrossRef]
- Luxa, M.; Příhoda, J.; Šimurda, D.; Straka, P.; Synáč, J. Investigation of the compressible flow through the tip-section turbine blade cascade with supersonic inlet. J. Therm. Sci. 2016, 25, 138–144. [Google Scholar] [CrossRef]
- Borjian, E.; Yousefi, T.; Ashjaee, M. Optical interferometry to investigate the heat transfer from a vertical cone under air jet impingement. Opt. Lasers Eng. 2015, 67, 205–211. [Google Scholar] [CrossRef]
- Colombani, J.; Bert, J. Holographic interferometry for the study of liquids. J. Mol. Liq. 2007, 134, 8–14. [Google Scholar] [CrossRef][Green Version]
- Cubreli, G.; Psota, P.; Dančová, P.; Lédl, V.; Vít, T. Digital Holographic Interferometry for the Measurement of Symmetrical Temperature Fields in Liquids. Photonics 2021, 8, 200. [Google Scholar] [CrossRef]
- Psota, P.; Cubreli, G.; Kredba, J.; Stašík, M.; Ledl, V. Two Wavelength Digital Holographic Interferometry for Investigation of Dynamic Processes in Fluid Mechanics. Available online: https://dl.astfe.org/conferences/tfec2021,586fceb86446aa50,35eb4e3178980f3c.html (accessed on 1 August 2021).
- Agarwal, S.; Kumar, V.; Shakher, C. Temperature measurement of wick stabilized micro diffusion flame under the influence of magnetic field using digital holographic interferometry. Opt. Lasers Eng. 2018, 102, 161–169. [Google Scholar] [CrossRef]
- Li, C.; Liu, W.; Peng, X.; Shao, L.; Feng, S. Measurement of mass diffusion coefficients of O2 in aviation fuel through digital holographic interferometry. Chin. J. Aeronaut. 2019, 32, 1184–1189. [Google Scholar] [CrossRef]
- Xi, T.; Di, J.; Li, Y.; Dai, S.; Ma, C.; Zhao, J. Measurement of ultrafast combustion process of premixed ethylene/oxygen flames in narrow channel with digital holographic interferometry. Opt. Express 2018, 26, 28497–28504. [Google Scholar] [CrossRef]
- Meiners-Hagen, K.; Schödel, R.; Pollinger, F.; Abou-Zeid, A. Multi-Wavelength Interferometry for Length Measurements Using Diode Lasers. Meas. Sci. Rev. 2009, 9, 16–26. [Google Scholar] [CrossRef]
- Malacara, D. Optical Shop Testing; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2007. [Google Scholar]
- Guerrero-Mendez, C.; Anaya, T.S.; Araiza-Esquivel, M.; Balderas-Navarro, R.E.; Aranda-Espinoza, S.; López-Martínez, A.; Olvera, C.A.O. Real-time measurement of the average temperature profiles in liquid cooling using digital holographic interferometry. Opt. Eng. 2016, 55, 121730. [Google Scholar] [CrossRef]
- Anand, A.; Chhaniwal, V.K.; Narayanamurthy, C.S. Diffusivity studies of transparent liquid solutions by use of digital holographic interferometry. Appl. Opt. 2006, 45, 904–909. [Google Scholar] [CrossRef]
- Naylor, D. Recent developments in the measurement of convective heat transfer rates by laser interferometry. Int. J. Heat Fluid Flow 2003, 24, 345–355. [Google Scholar] [CrossRef]
- Narayan, S.; Singh, A.K.; Srivastava, A. Interferometric study of natural convection heat transfer phenomena around array of heated cylinders. Int. J. Heat Mass Transf. 2017, 109, 278–292. [Google Scholar] [CrossRef]
- Herman, C.; Kang, E. Experimental visualization of temperature fields and study of heat transfer enhancement in oscillatory flow in a grooved channel. Heat Mass Transf. 2001, 37, 87–99. [Google Scholar] [CrossRef]
- Picart, P. New Techniques in Digital Holography; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2015. [Google Scholar]
- Psota, P.; Tang, H.; Pooladvand, K.; Furlong, C.; Rosowski, J.J.; Cheng, J.T.; Ledl, V. Multiple angle digital holography for the shape measurement of the unpainted tympanic membrane. Opt. Express 2020, 28, 24614. [Google Scholar] [CrossRef] [PubMed]
- Bommareddi, R.R. Applications of Optical Interferometer Techniques for Precision Measurements of Changes in Temperature, Growth and Refractive Index of Materials. Technologies 2014, 2, 54–75. [Google Scholar] [CrossRef]
- Landsberg, G.S. Оптика/Optika, 5th ed.; Наука (Nauka): Moscow, Russia, 1976. [Google Scholar]
- Psota, P.; Mokrý, P.; Lédl, V.; Stašík, M.; Matoušek, O.; Kredba, J. Absolute and pixel-wise measurements of vibration amplitudes using time-averaged digital holography. Opt. Lasers Eng. 2019, 121, 236–245. [Google Scholar] [CrossRef]
- Blanche, P.A. Optical Holography: Materials, Theory and Applications; Elsevier: St. Louis, MO, USA, 2020. [Google Scholar]
- Šidlof, P.; Riss, Š.; Vlček, V. Evaluation of Interferograms of unsteady subsonic airflow past a fluttering airfoil. In Topical Problems of Fluid Mechanics 2016; Czech Technical University in Prague-Central Library: Prague, Czech Republic, 2016; pp. 223–228. [Google Scholar]
- Ristic, S.; Linić, S.L.; Samardzic, M. Turbulence investigation in the VTI’s experimental aerodynamics laboratory. Therm. Sci. 2017, 21, 629–647. [Google Scholar] [CrossRef]
- Kozic, M.; Ristic, S. Capability of two-dimensional Reynolds-averaged Navier—Stokes simulations for two-dimensional thrust vectoring nozzles. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2010, 224, 905–910. [Google Scholar] [CrossRef]
- Htun, Y.E.; Myint, Z.Y. Some Principles of Flow Visualization Techniques in Wind Tunnels. Int. J. Adv. Sci. Eng. Technol. 2016, 4, 2321–9009. Available online: http://iraj.in (accessed on 19 October 2021).
- Kleine, H.; Grönig, H.; Takayama, K. Simultaneous Shadow, Schlieren and Interferometric Visualization of Compressible Flows. Opt. Lasers Eng. 2005, 44, 170–189. [Google Scholar] [CrossRef]
- Emmert, T.; Lafon, P.; Bailly, C. Numerical study of self-induced transonic flow oscillations behind a sudden duct enlargement. Phys. Fluids 2009, 21, 106105. [Google Scholar] [CrossRef]
- Ristić, S. Optical Methods in Wind Tunnel Flow Visualization; FME Trans: Belgrade, Serbia, 2006; Volume 34, pp. 7–13. Available online: https://www.researchgate.net/publication/277183175_Optical_methods_in_wind_tunnel_flow_visualization (accessed on 8 November 2021).
- Ledl, V.; Psota, P.; Doleček, R. Digital holographic setups for phase object measurements in micro and macro scale. In Proceedings of the EPJ Web of Conferences, Dresden, Germany, 25–29 August 2015; EDP Sciences: Les Ulis, France, 2015; Volume 92, p. 01001. [Google Scholar]
- Doleček, R.; Psota, P.; Lédl, V.; Vít, T.; Václavík, J.; Kopecký, V. General temperature field measurement by digital holography. Appl. Opt. 2012, 52, A319–A325. [Google Scholar] [CrossRef]
- Malacara, Z.; Servín, M. Interferogram Analysis for Optical Testing; CRC Press, Taylor & Francis Group: Boca Raton, FL, USA, 2005. [Google Scholar]

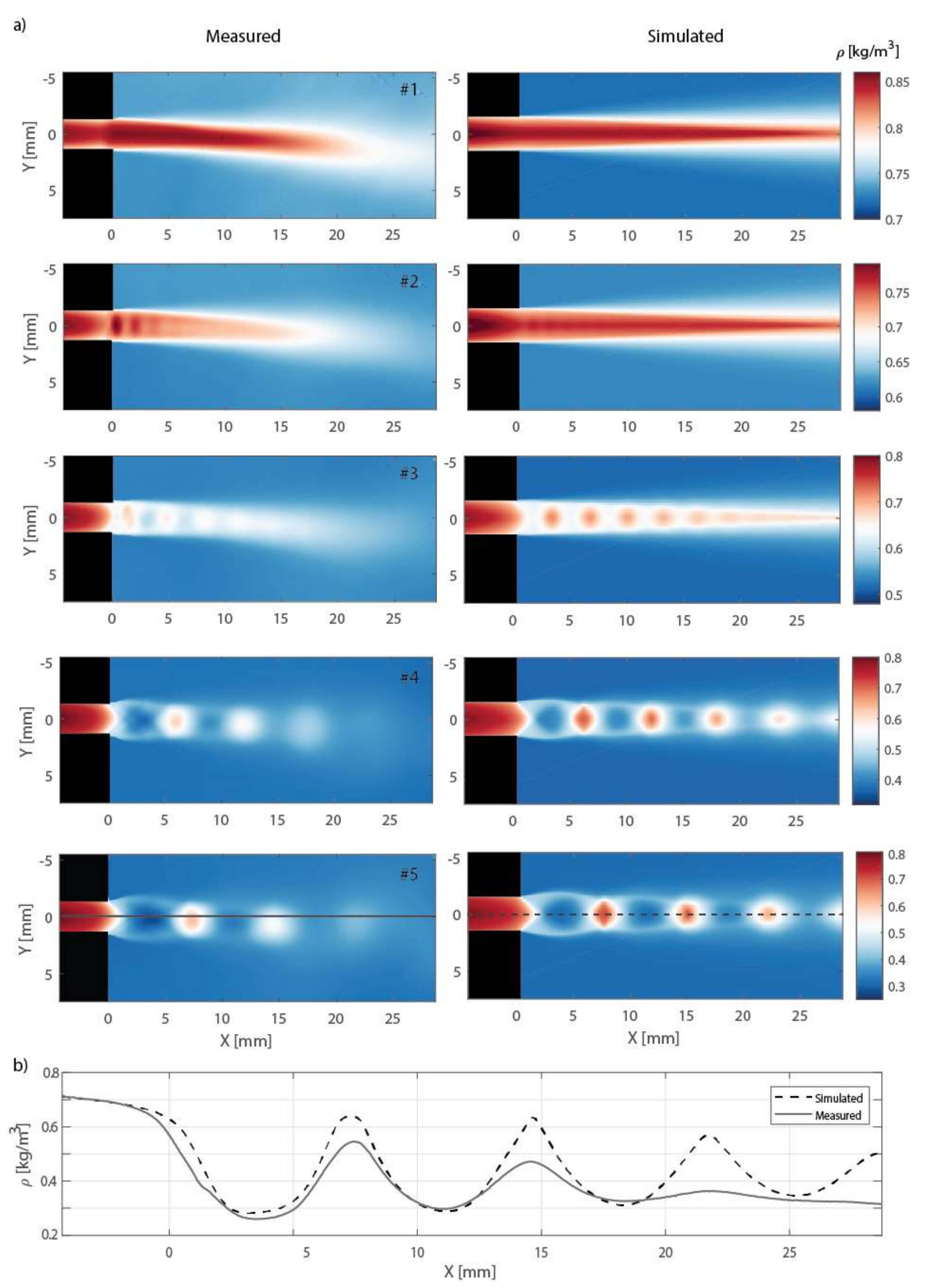

| Regime | #1 | #2 | #3 | #4 | #5 |
|---|---|---|---|---|---|
| Pout (kPa) | 54.923 | 47.140 | 39.236 | 28.114 | 23.871 |
| η [1] | 0.560 | 0.481 | 0.400 | 0.287 | 0.243 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Psota, P.; Çubreli, G.; Hála, J.; Šimurda, D.; Šidlof, P.; Kredba, J.; Stašík, M.; Lédl, V.; Jiránek, M.; Luxa, M.; et al. Characterization of Supersonic Compressible Fluid Flow Using High-Speed Interferometry. Sensors 2021, 21, 8158. https://doi.org/10.3390/s21238158
Psota P, Çubreli G, Hála J, Šimurda D, Šidlof P, Kredba J, Stašík M, Lédl V, Jiránek M, Luxa M, et al. Characterization of Supersonic Compressible Fluid Flow Using High-Speed Interferometry. Sensors. 2021; 21(23):8158. https://doi.org/10.3390/s21238158
Chicago/Turabian StylePsota, Pavel, Gramoz Çubreli, Jindřich Hála, David Šimurda, Petr Šidlof, Jan Kredba, Marek Stašík, Vít Lédl, Michal Jiránek, Martin Luxa, and et al. 2021. "Characterization of Supersonic Compressible Fluid Flow Using High-Speed Interferometry" Sensors 21, no. 23: 8158. https://doi.org/10.3390/s21238158
APA StylePsota, P., Çubreli, G., Hála, J., Šimurda, D., Šidlof, P., Kredba, J., Stašík, M., Lédl, V., Jiránek, M., Luxa, M., & Lepicovsky, J. (2021). Characterization of Supersonic Compressible Fluid Flow Using High-Speed Interferometry. Sensors, 21(23), 8158. https://doi.org/10.3390/s21238158






