A Model for Estimating Tactile Sensation by Machine Learning Based on Vibration Information Obtained while Touching an Object
Abstract
:1. Introduction
2. Materials and Methods
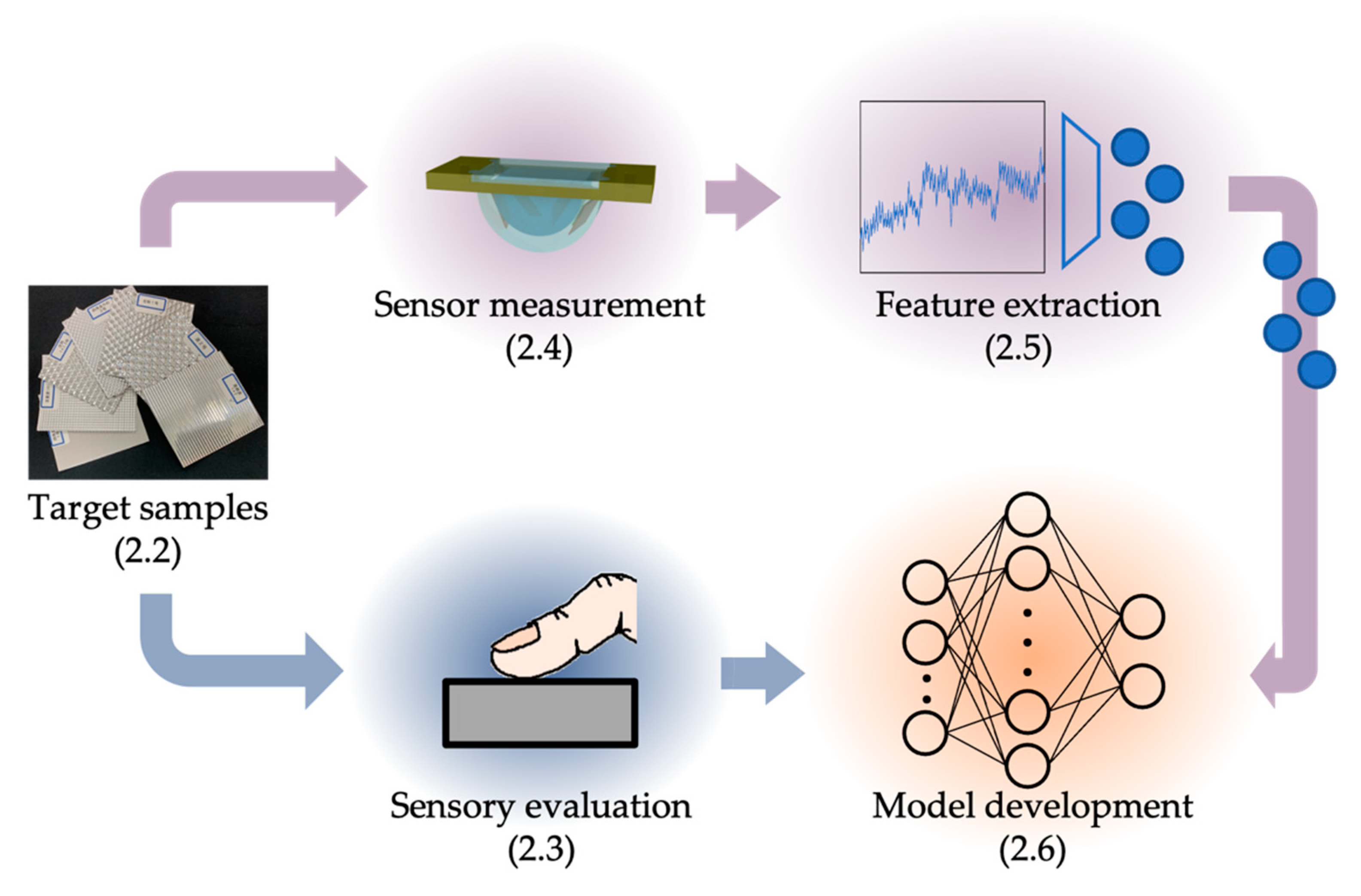
2.1. Strategy for Tactile Model Development
2.2. Target Samples
2.3. Sensory Evaluation of Samples
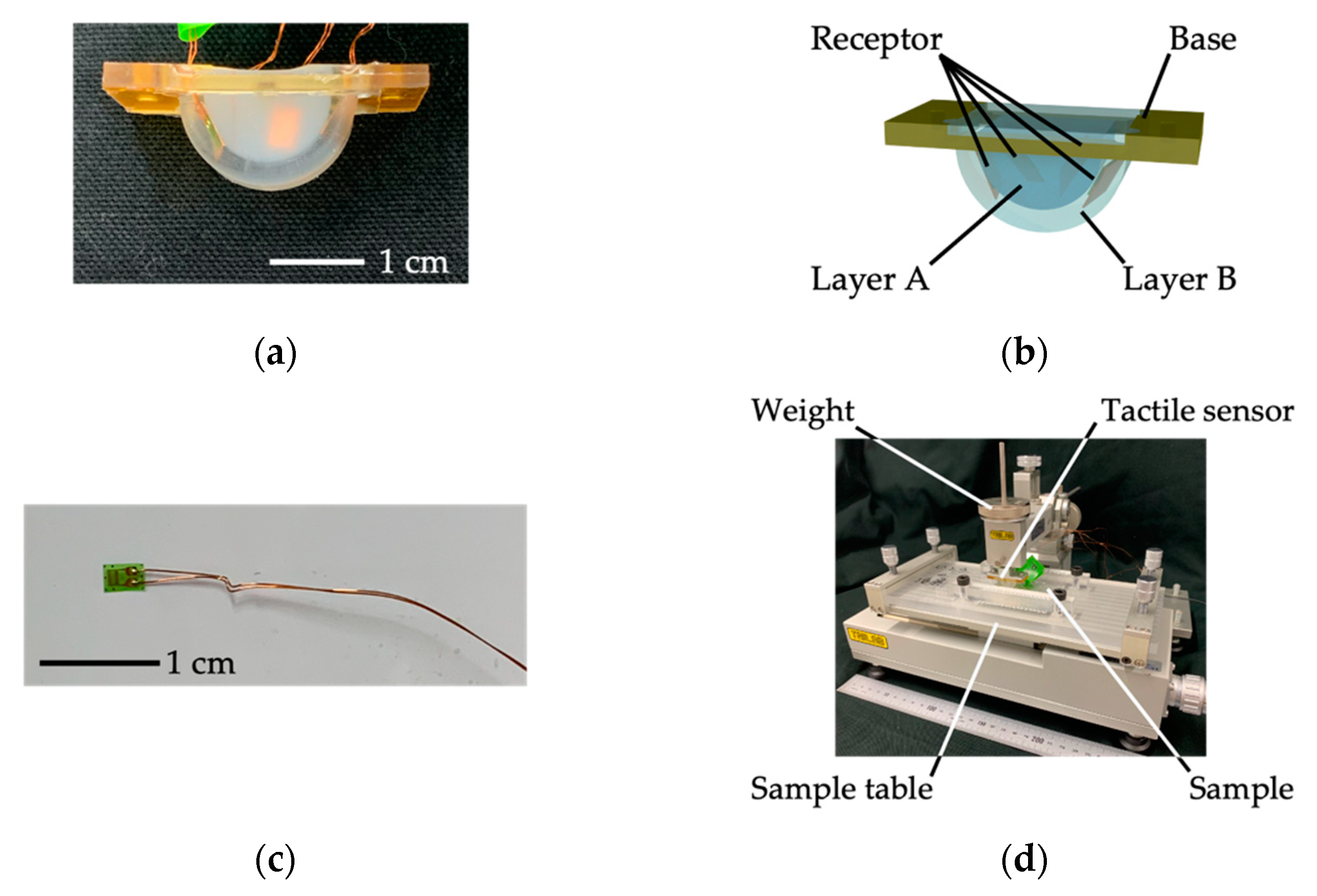
2.4. Tactile Sensing System and Experimental Conditions
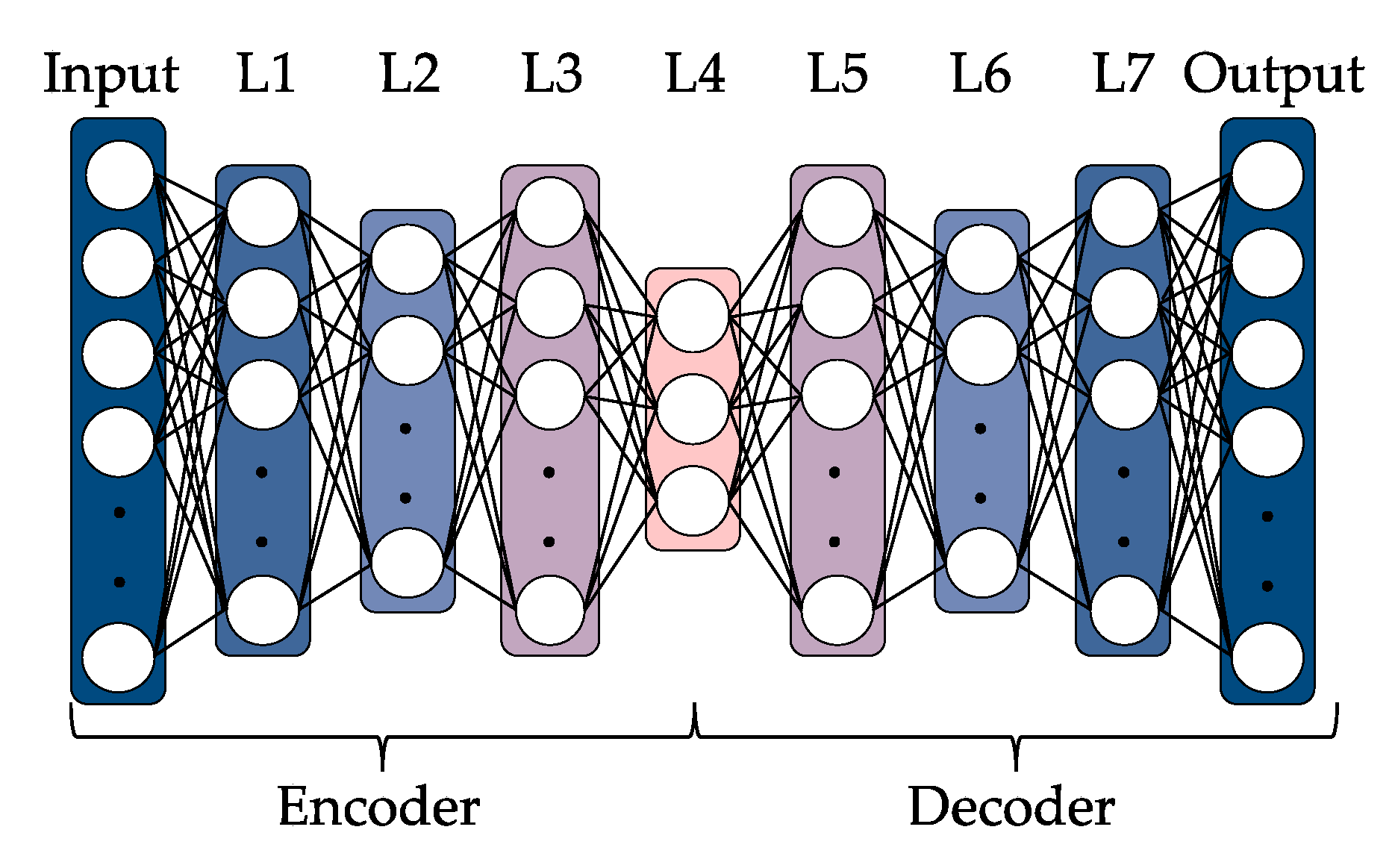
2.5. Feature Extraction for the Data Acquired by the Autoencoder
2.6. Establishment of a Tactile Estimation Model through Machine Learning
3. Results
3.1. Sensory Evaluation Results
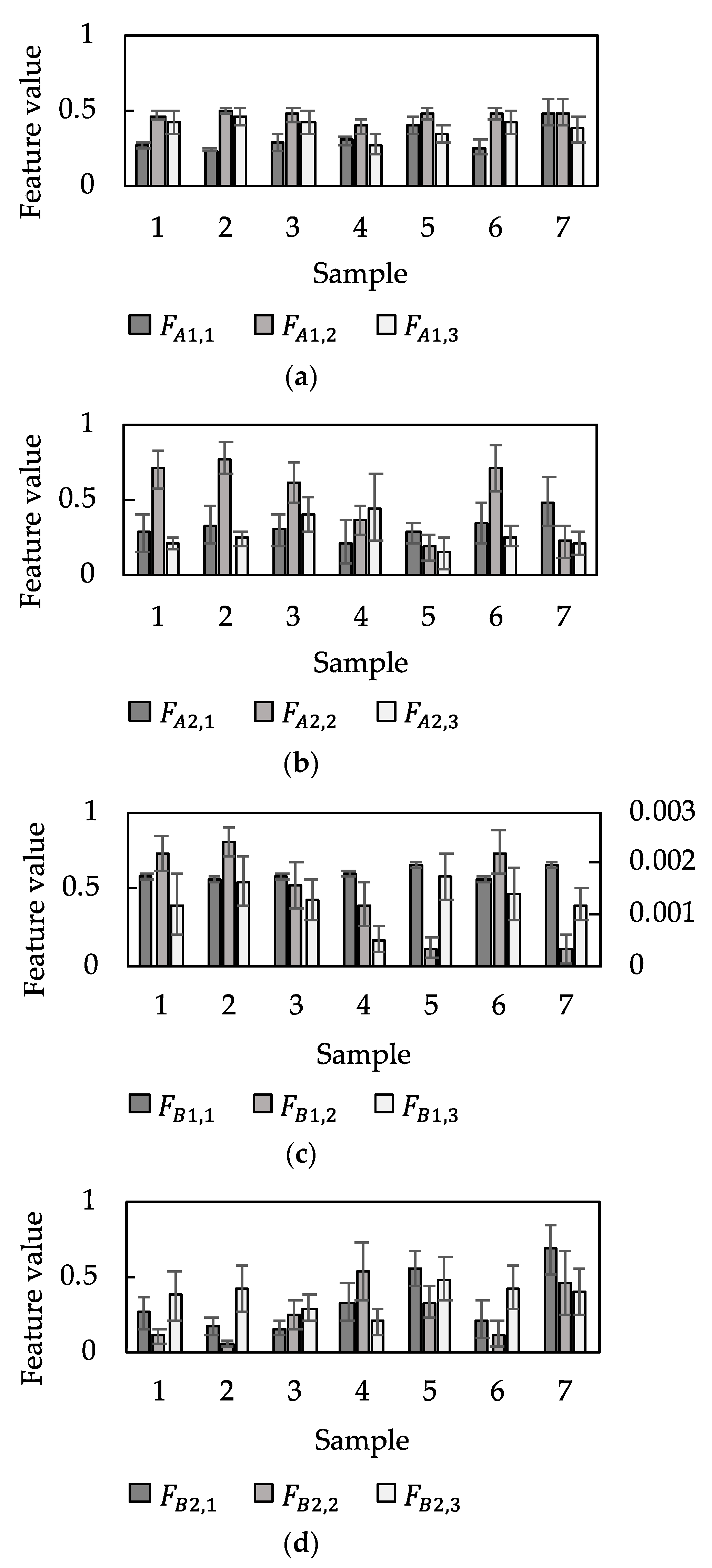
3.2. Feature Extraction from Acquired Vibration Data
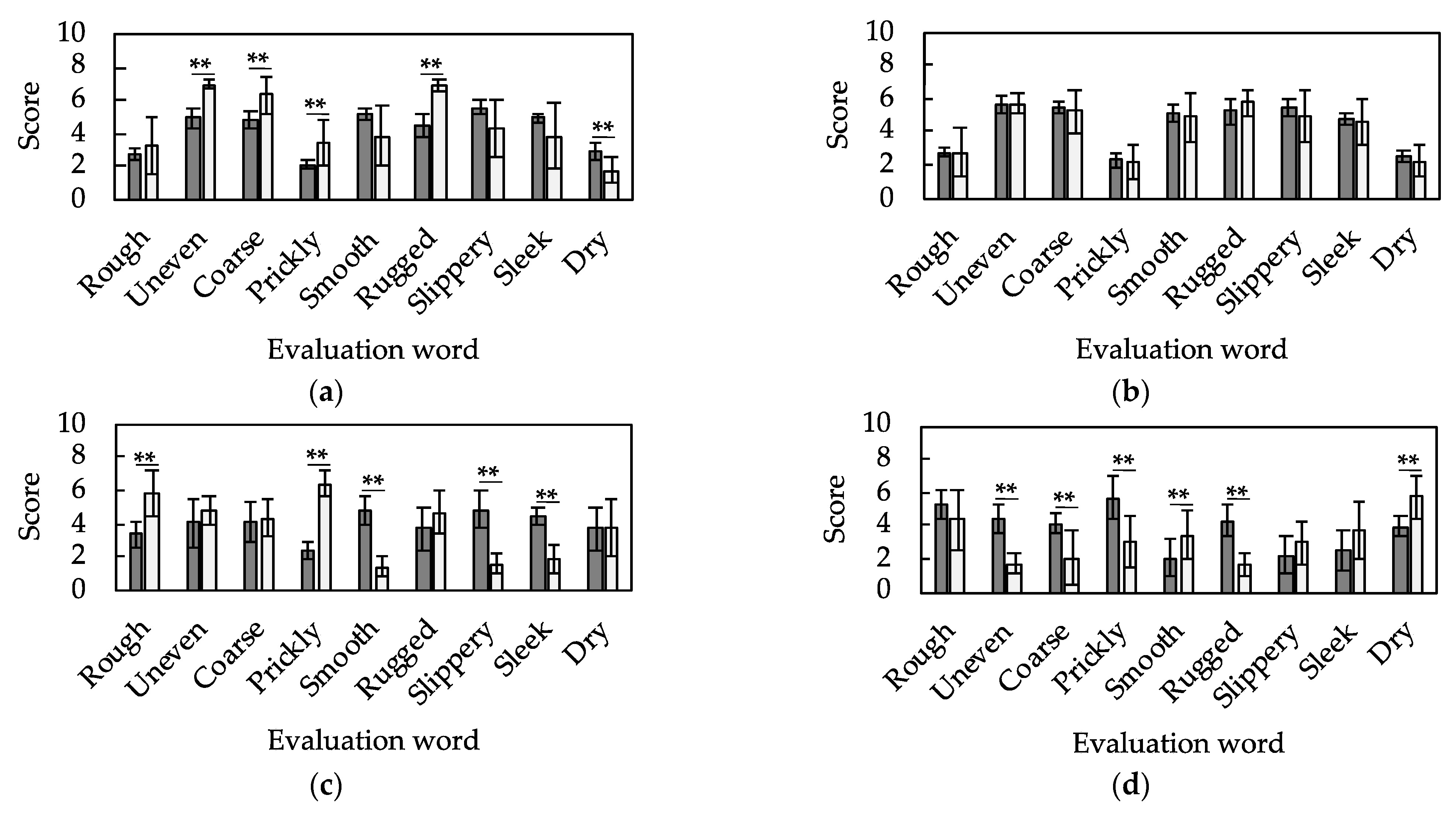
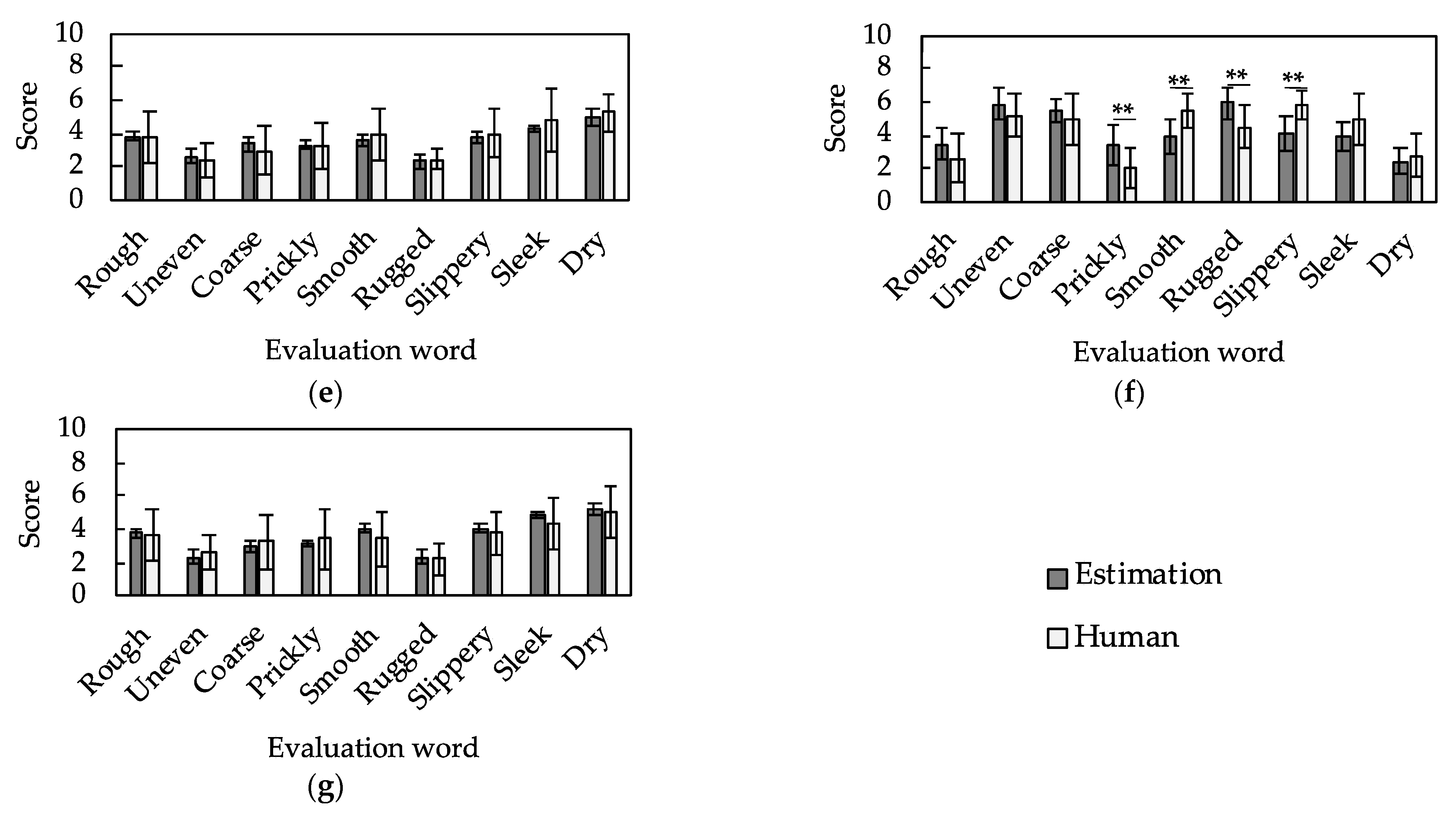
3.3. Tactile Estimation Models Developed through Machine Learning
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Grohmann, B.; Spangenberg, E.R.; Sprott, D.E. The influence of tactile input on the evaluation of retail product offerings. J. Retail. 2007, 83, 237–245. [Google Scholar] [CrossRef]
- Yanagisawa, H. Kansei Quality in Product Design. In Emotional Engineering Service Development; Fukuda, S., Ed.; Springer: London, UK, 2011; pp. 289–310. [Google Scholar]
- Jansson-Boyd, C.V. Touch matters: Exploring the relationship between consumption and tactile interaction. Soc. Semiot. 2011, 21, 531–546. [Google Scholar] [CrossRef]
- Atefeh, Y.; Nancy, S. Can consumers forgo the need to touch products? An investigation of nonhaptic situational factors in an online context. Psychol. Mark. 2013, 30, 46–61. [Google Scholar]
- Chen, S.; Ge, S.; Tang, W.; Zhang, J.; Chen, N. Tactile perception of fabrics with an artificial finger compared to human sensing. Text. Res. J. 2015, 85, 2177–2187. [Google Scholar] [CrossRef]
- Asaga, E.; Takemura, K.; Maeno, T.; Ban, A.; Toriumi, M. Tactile evaluation based on human tactile perception mechanism. Sens. Actuators A Phys. 2013, 203, 69–75. [Google Scholar] [CrossRef]
- Nobuyama, L.; Kurashina, Y.; Kawauchi, K.; Matsui, K.; Takemura, K. Tactile Estimation of Molded Plastic Plates Based on the Estimated Impulse Responses of Mechanoreceptive Units. Sensors 2018, 18, 1588. [Google Scholar] [CrossRef] [Green Version]
- Hashim, I.H.M.; Kumamoto, S.; Takemura, K.; Maeno, T.; Okuda, S.; Mori, Y. Tactile Evaluation Feedback System for Multi-Layered Structure Inspired by Human Tactile Perception Mechanism. Sensors 2017, 17, 2601. [Google Scholar] [CrossRef] [Green Version]
- Kerzel, M.; Ali, M.; Ng, H.G.; Wermter, S. Haptic material classification with a multi-channel neural network. In Proceedings of the 2017 International Joint Conference on Neural Networks (IJCNN), Anchorage, AK, USA, 14–19 May 2017; pp. 439–446. [Google Scholar] [CrossRef]
- Saga, S.; Agatsuma, S.; Vasilache, S.; Takahashi, S. Machine learning-based classification and generation of vibrotactile information. Int. J. Adv. Netw. Svcs. 2020, 13, 115–124. [Google Scholar]
- Li, G.; Liu, S.; Wang, L.; Zhu, R. Skin-inspired quadruple tactile sensors integrated on a robot hand enable object recognition. Sci. Robot. 2020, 5. [Google Scholar] [CrossRef]
- Gandarias, J.M.; Gómez-De-Gabriel, J.M.; García-Cerezo, A. Human and object recognition with a high-resolution tactile sensor. In Proceedings of the 2017 IEEE SENSORS, Glasgow, UK, 29 October–1 November 2017; pp. 981–983. [Google Scholar]
- Massari, L.; Schena, E.; Massaroni, C.; Saccomandi, P.; Menciassi, A.; Sinibaldi, E.; Oddo, C.M. A Machine-Learning-Based Approach to Solve Both Contact Location and Force in Soft Material Tactile Sensors. Soft Robot. 2020, 7, 409–420. [Google Scholar] [CrossRef] [PubMed]
- Huang, S.; Wu, H. Texture Recognition Based on Perception Data from a Bionic Tactile Sensor. Sensors 2021, 21, 5224. [Google Scholar] [CrossRef]
- Chun, S.; Hwang, I.; Son, W.; Chang, J.-H.; Park, W. Recognition, classification, and prediction of the tactile sense. Nanoscale 2018, 10, 10545–10553. [Google Scholar] [CrossRef] [PubMed]
- Qin, L.; Yi, Z.; Zhang, Y. Enhanced surface roughness discrimination with optimized features from bio-inspired tactile sensor. Sens. Actuators A Phys. 2017, 264, 133–140. [Google Scholar] [CrossRef]
- Hosoda, K.; Tada, Y.; Asada, M. Anthropomorphic robotic soft fingertip with randomly distributed receptors. Robot. Auton. Syst. 2006, 54, 104–109. [Google Scholar] [CrossRef]
- Johansson, R.S.; Landstrom, U.; Lundstrom, R. Responses of mechanoreceptive afferent units in the glabrous skin of the human hand to vibration. Brain Res. 1982, 244, 17–25. [Google Scholar] [CrossRef]
- Bolanowski, S.J.; Gescheider, G.A.; Verrillo, R.T.; Checkosky, C.M. Four channels mediate the mechanical aspects of touch. J. Acoust. Soc. Am. 1988, 84, 1680–1694. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, G. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Anitescu, C.; Atroshchenko, E.; Alajlan, N.; Rabczuk, T. Artificial Neural Network Methods for the Solution of Second Order Boundary Value Problems. Comput. Mater. Contin. 2019, 59, 345–359. [Google Scholar] [CrossRef] [Green Version]
- Weinan, E.; Han, J.; Jentzen, A. Deep Learning-Based Numerical Methods for High-Dimensional Parabolic Partial Differential Equations and Backward Stochastic Differential Equations. Commun. Math. Stat. 2017, 5, 349–380. [Google Scholar] [CrossRef] [Green Version]
- Zhuang, X.; Guo, H.; Alajlan, N.; Zhu, H.; Rabczuk, T. Deep autoencoder based energy method for the bending, vibration, and buckling analysis of Kirchhoff plates with transfer learning. Eur. J. Mech.-A/Solids 2021, 87, 104225. [Google Scholar] [CrossRef]
- Snoek, J.; Adams, R.P.; Larochelle, H. Nonparametric guidance of autoencoder representations using label information. J. Mach. Learn. Res. 2012, 13, 2567–2588. [Google Scholar]
- Qu, Y.; He, M.; Deutsch, J.; He, D. Detection of Pitting in Gears Using a Deep Sparse Autoencoder. Appl. Sci. 2017, 7, 515. [Google Scholar] [CrossRef]
- Shang, Z.; Sun, L.; Xia, Y.; Zhang, W. Vibration-based damage detection for bridges by deep convolutional denoising autoencoder. Struct. Health Monit. 2021, 20, 1880–1903. [Google Scholar] [CrossRef]
- Shao, H.; Jiang, H.; Zhao, H.; Wang, F. A novel deep autoencoder feature learning method for rotating machinery fault diagnosis. Mech. Syst. Signal Process. 2017, 95, 187–204. [Google Scholar] [CrossRef]
- Tuorila, H.; Huotilainen, A.; Lähteenmäki, L.; Ollila, S.; Tuomi-Nurmi, S.; Urala, N. Comparison of affective rating scales and their relationship to variables reflecting food consumption. Food Qual. Prefer. 2008, 19, 51–61. [Google Scholar] [CrossRef]
- Cantin, I.; Dubé, L.L. Attitudinal Moderation of Correlation between Food Liking and Consumption. Appetite 1999, 32, 367–381. [Google Scholar] [CrossRef] [PubMed]
- Liquid Silicone Rubber for Moldmaking. Available online: https://www.shinetsusilicone-global.com/catalog/pdf/mold_silicone_e.pdf (accessed on 1 September 2021).
- SYLGARD™ 184 Silicone Elastomer Kit Technical Data Sheet. Available online: https://www.dow.com/en-us/document-viewer.html?ramdomVar=6549482870393403912&docPath=/content/dam/dcc/documents/en-us/productdatasheet/11/11-31/11-3184-sylgard-184-elastomer.pdf (accessed on 1 September 2021).
- Johnson, K. Neural basis of haptic perception. In Steven’s Handbook of Experimental Psychology, 3rd ed.; Pashler, H., Yantis, S., Eds.; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2002; Volume 1, pp. 537–583. [Google Scholar]
- Greenspan, J.D.; Bolanowski, S.J. The Psychophysics of Tactile Perception and its Peripheral Physiological Basis. In Pain and Touch; Elsevier: Amsterdam, The Netherlands, 1996; pp. 25–103. ISBN 9780124269101. [Google Scholar]
- Gescheider, G.A.; Bolanowski, S.; Hardick, K. The frequency selectivity of information-processing channels in the tactile sensory system. Somatosens. Mot. Res. 2001, 18, 191–201. [Google Scholar] [CrossRef] [PubMed]
- Hinton, G.E.; Salakhutdinov, R.R. Reducing the Dimensionality of Data with Neural Networks. Science 2006, 313, 504–507. [Google Scholar] [CrossRef] [Green Version]
- Irie, B.; Miyake, S. Capabilities of Three-layered Perceptions. In Proceedings of the IEEE 1988 International Conference on Neural Networks, San Diego, CA, USA, 24–27 July 1988; pp. 641–648. [Google Scholar]
- Cybenko, G. Approximation by superpositions of a sigmoidal function. Math. Control. Signals Syst. 1989, 2, 303–314. [Google Scholar] [CrossRef]
- NumPy Reference. Available online: https://numpy.org/doc/stable/reference/ (accessed on 1 September 2021).
- Akiba, T.; Sano, S.; Yanase, T.; Ohta, T.; Koyama, M. A Next-generation Hyperparameter Optimization Framework. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Anchorage, AK, USA, 4–8 August 2019; pp. 2623–2631. [Google Scholar]
- Bergstra, J.; Bardnet, R.; Bengio, Y.; Kegi, B. Algorithms for Hyper-Parameter Optimization. In Proceedings of the Neural Information Processing Systems 2011, Granada, Spain, 12–17 December 2011; pp. 2546–2554. [Google Scholar]
- Keras Documentation. Available online: https://keras.io/ja/ (accessed on 1 September 2021).
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. In Proceedings of the International Conference on Learning Representations 2015, San Diego, CA, USA, 7–9 May 2015; pp. 1–15. [Google Scholar]
- Ward, J.R. Hierarchical grouping to optimize an objective function. J. Am. Stat. Assoc. 1963, 58, 236–244. [Google Scholar] [CrossRef]
- Wishart, D. An Algorithm for Hierarchical Classifications. Biometrics 1969, 25, 165–170. [Google Scholar] [CrossRef]
- SciPy User Guide. Available online: https://docs.scipy.org/doc/scipy/reference/tutorial/index.html#user-guide (accessed on 1 September 2021).




| Evaluation Words (Japanese) | ||
|---|---|---|
| Rough (Zarazara-suru) | Uneven (Dekoboko-suru) | Coarse (Kime-no-arai) |
| Prickle (Chikuchiku-suru) | Smooth (Namerakana) | Rugged (Gotsugotsu-suru) |
| Slippery (Tsurutsuru-suru) | Sleek (Subesube-suru) | Dry (Sarasara-suru) |
| The number of neurons of the input layer | 1000 |
| The number of neurons of the output layer | 1000 |
| The number of neurons of the feature extraction layer (L4) | 3 |
| The number of intermediate layers of encoder and decoder | 3 |
| Weight optimization algorithm | Adam [42] |
| Activation function | Encoder: sigmoid Decoder: ReLU |
| Loss function | Mean squared error |
| Batch size | 128 |
| Trial number of Optuna | 200 |
| Epochs | 200 |
| A1 | A2 | B1 | B2 | |
|---|---|---|---|---|
| L1 and L7 | 606 | 505 | 957 | 951 |
| L2 and L6 | 96 | 306 | 43 | 278 |
| L3 and L5 | 37 | 154 | 324 | 266 |
| The number of neurons of the input layer | 12 |
| The number of neurons of the output layer | 9 |
| The number of neurons of the feature extraction layer (L4) | 21,660 |
| Weight optimization algorithm | Adam |
| Activation function of the output layer | Linear |
| Activation function other than the output layer | sigmoid |
| The ration of train data and verification data | 4:1 |
| Loss function | Mean squared error |
| Batch size | 128 |
| Trial number of Optuna | 100 |
| Epochs | 200 |
| Model | L1 | L2 | L3 | L4 |
|---|---|---|---|---|
| Sample 1 | 449 | 442 | 155 | 150 |
| Sample 2 | 484 | 498 | 207 | 50 |
| Sample 3 | 399 | 412 | 408 | 402 |
| Sample 4 | 439 | 447 | 236 | 21 |
| Sample 5 | 474 | 446 | 157 | 411 |
| Sample 6 | 266 | 287 | 244 | 35 |
| Sample 7 | 492 | 481 | 320 | 116 |
| Receptor | |
|---|---|
| A1 | 2.20 |
| A2 | 2.93 |
| B1 | 4.09 |
| B2 | 3.11 |
| Model | Generalization Error [-] |
|---|---|
| Sample 1 | 4.05 |
| Sample 2 | 1.75 |
| Sample 3 | 8.33 |
| Sample 4 | 6.68 |
| Sample 5 | 2.08 |
| Sample 6 | 3.99 |
| Sample 7 | 2.38 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ito, F.; Takemura, K. A Model for Estimating Tactile Sensation by Machine Learning Based on Vibration Information Obtained while Touching an Object. Sensors 2021, 21, 7772. https://doi.org/10.3390/s21237772
Ito F, Takemura K. A Model for Estimating Tactile Sensation by Machine Learning Based on Vibration Information Obtained while Touching an Object. Sensors. 2021; 21(23):7772. https://doi.org/10.3390/s21237772
Chicago/Turabian StyleIto, Fumiya, and Kenjiro Takemura. 2021. "A Model for Estimating Tactile Sensation by Machine Learning Based on Vibration Information Obtained while Touching an Object" Sensors 21, no. 23: 7772. https://doi.org/10.3390/s21237772
APA StyleIto, F., & Takemura, K. (2021). A Model for Estimating Tactile Sensation by Machine Learning Based on Vibration Information Obtained while Touching an Object. Sensors, 21(23), 7772. https://doi.org/10.3390/s21237772






