The Vulnerability of the Power Grid Structure: A System Analysis Based on Complex Network Theory
Abstract
:1. Introduction
2. Related Works
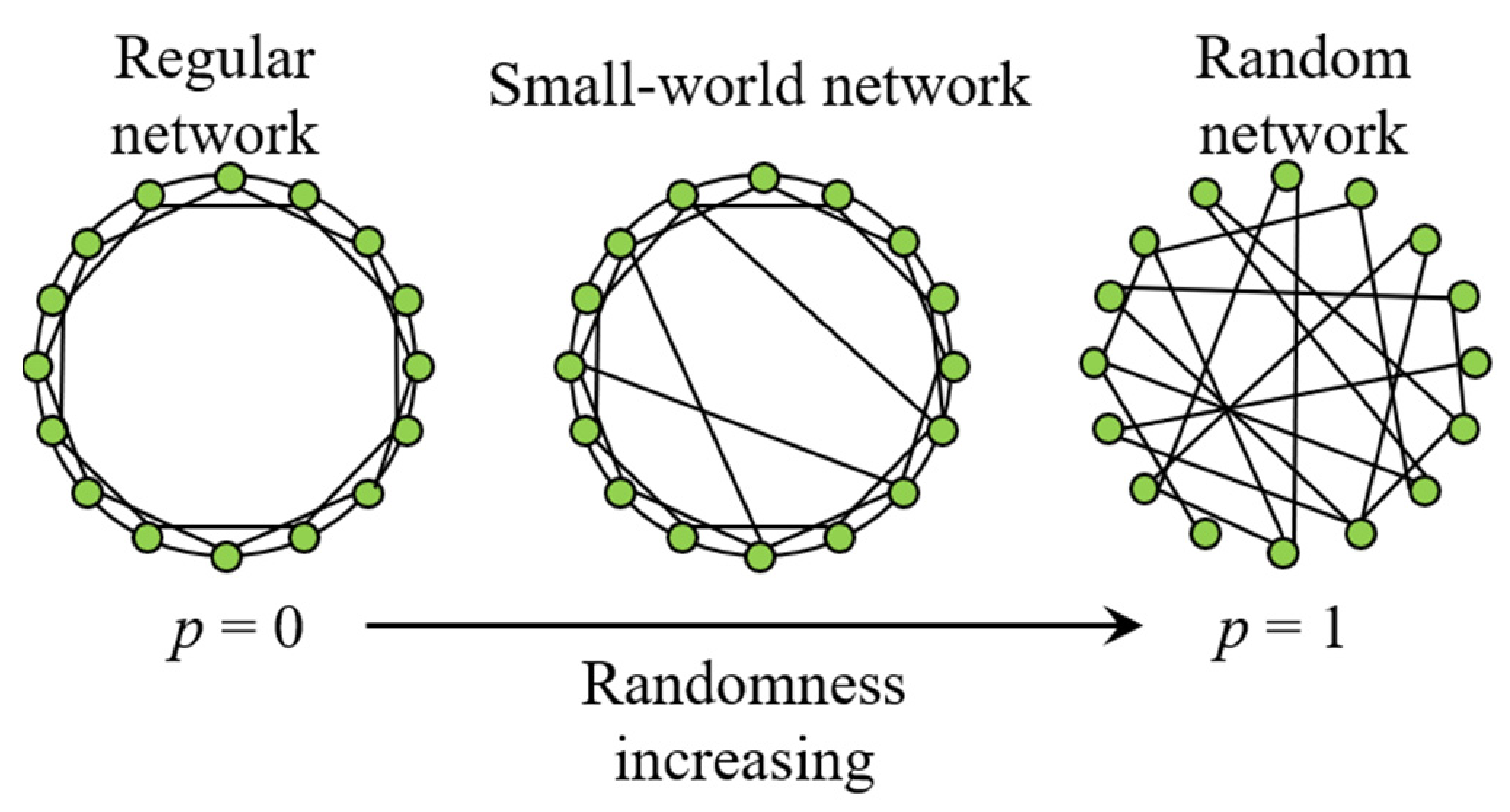
3. Background Knowledge
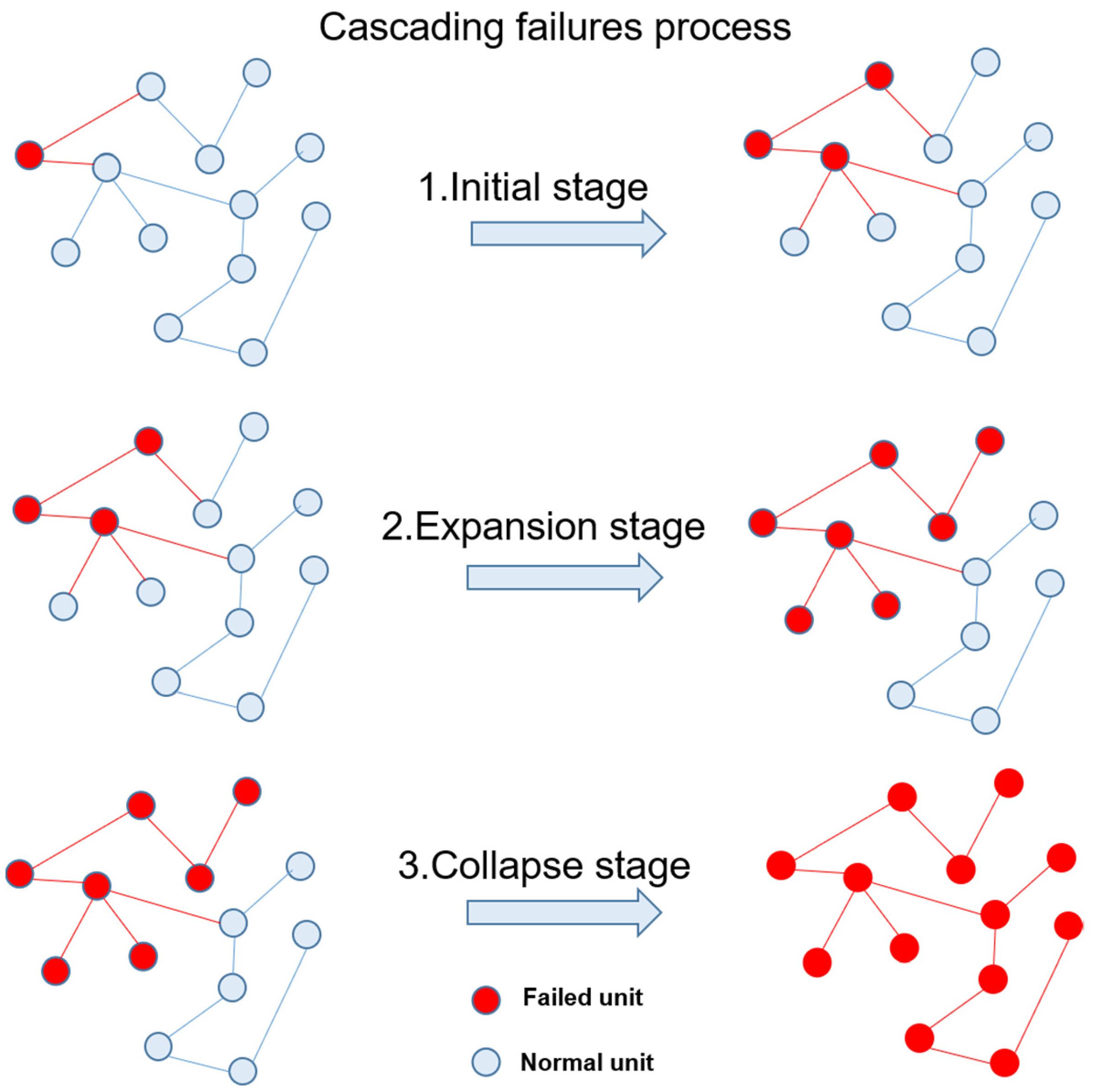
4. Vulnerability of Power Grid Structure Based on Cascading Failures
- Initial stage: due to external disturbance in extreme cases, individual disturbed units fail due to limited capacity. In the initial stage of the accident, the whole power grid is less affected at this stage. If the accident is found in time and the corresponding preventive measures are taken, the further deterioration of the accident can be controlled in time;
- Expansion stage: in the initial stage, the fault continues to spread and expand, which leads to the change of unit load related to the unit logic of the initial fault under the action of system structural vulnerability, so that it is easy for the fault to exit the operation system. The expansion stage of accident expansion is formed by concluding which time the fault range of the power grid is expanded. However, it is still a partially controllable stage.
- Collapse stage: when the faults continue to spread and expand in the expansion stage, the loads caused by many local unit faults will accumulate further, which makes the overall load distribution and initial distribution of the system change rapidly. Due to the influence of the power grid, larger-scale faults will eventually lead to the cracking of the power grid system and even the whole power grid.
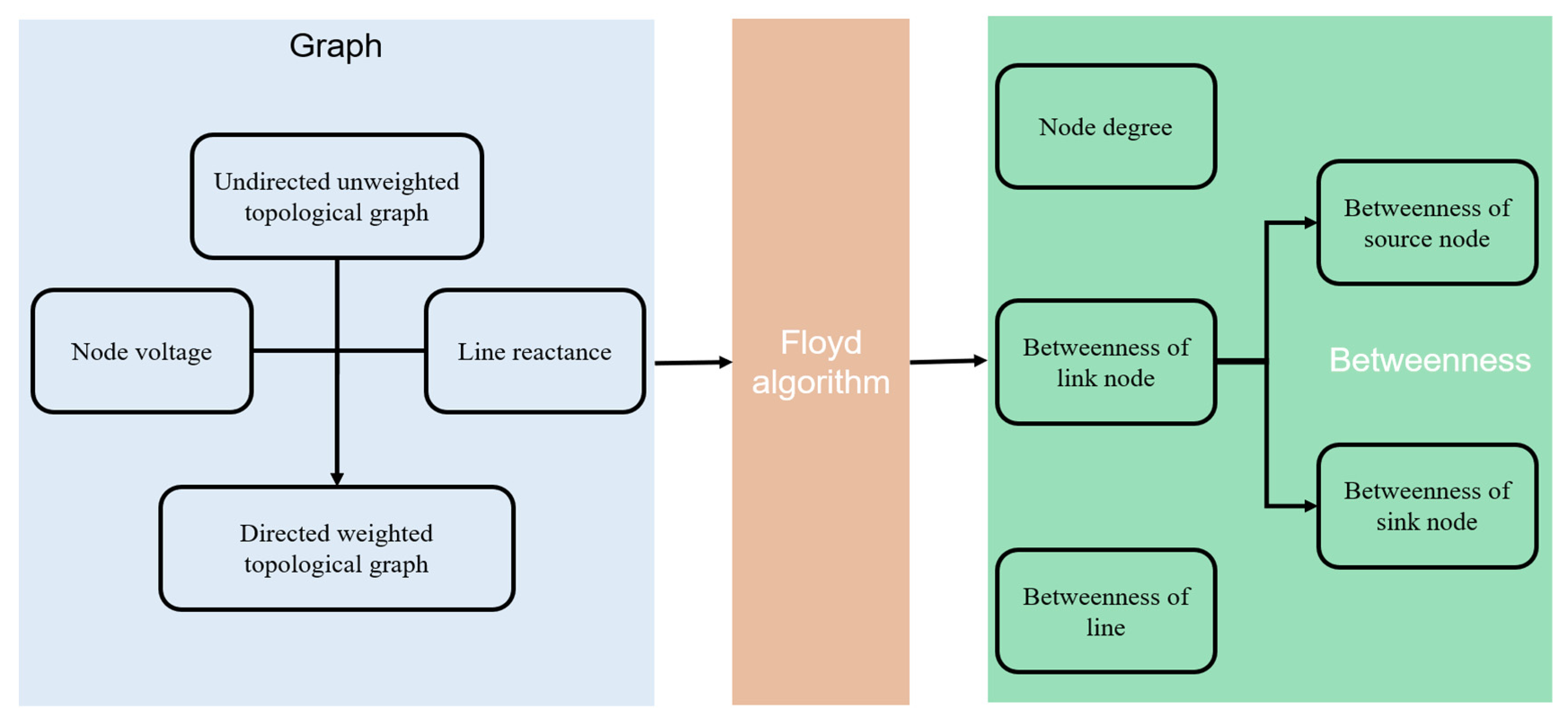
4.1. Evaluation Index of Power Grid Structural Vulnerability
4.1.1. Percentage of Load Loss
4.1.2. Network Transmission Efficiency
4.2. Vulnerability of Power Grid Structure
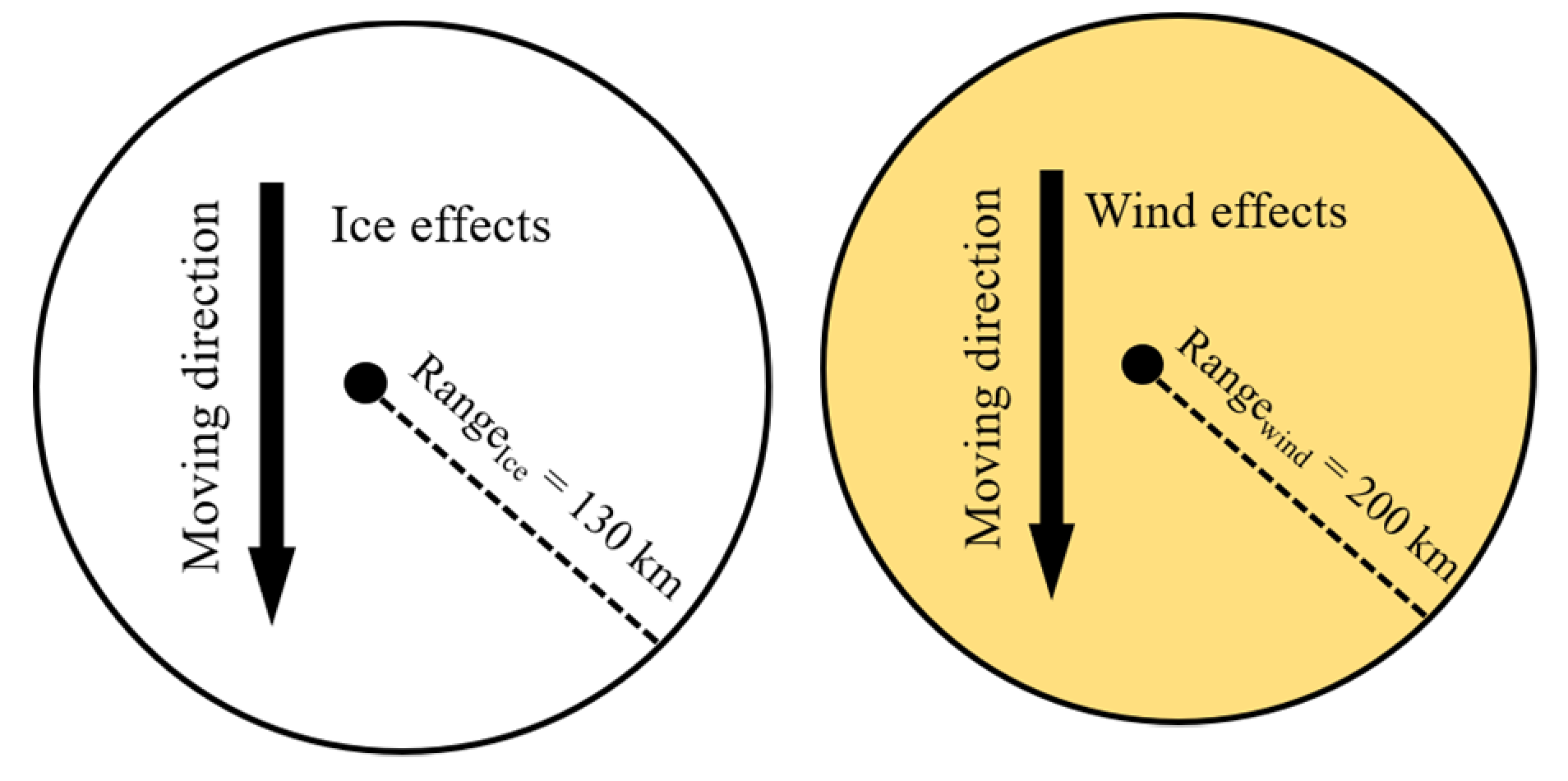
4.3. Extreme Weather Background
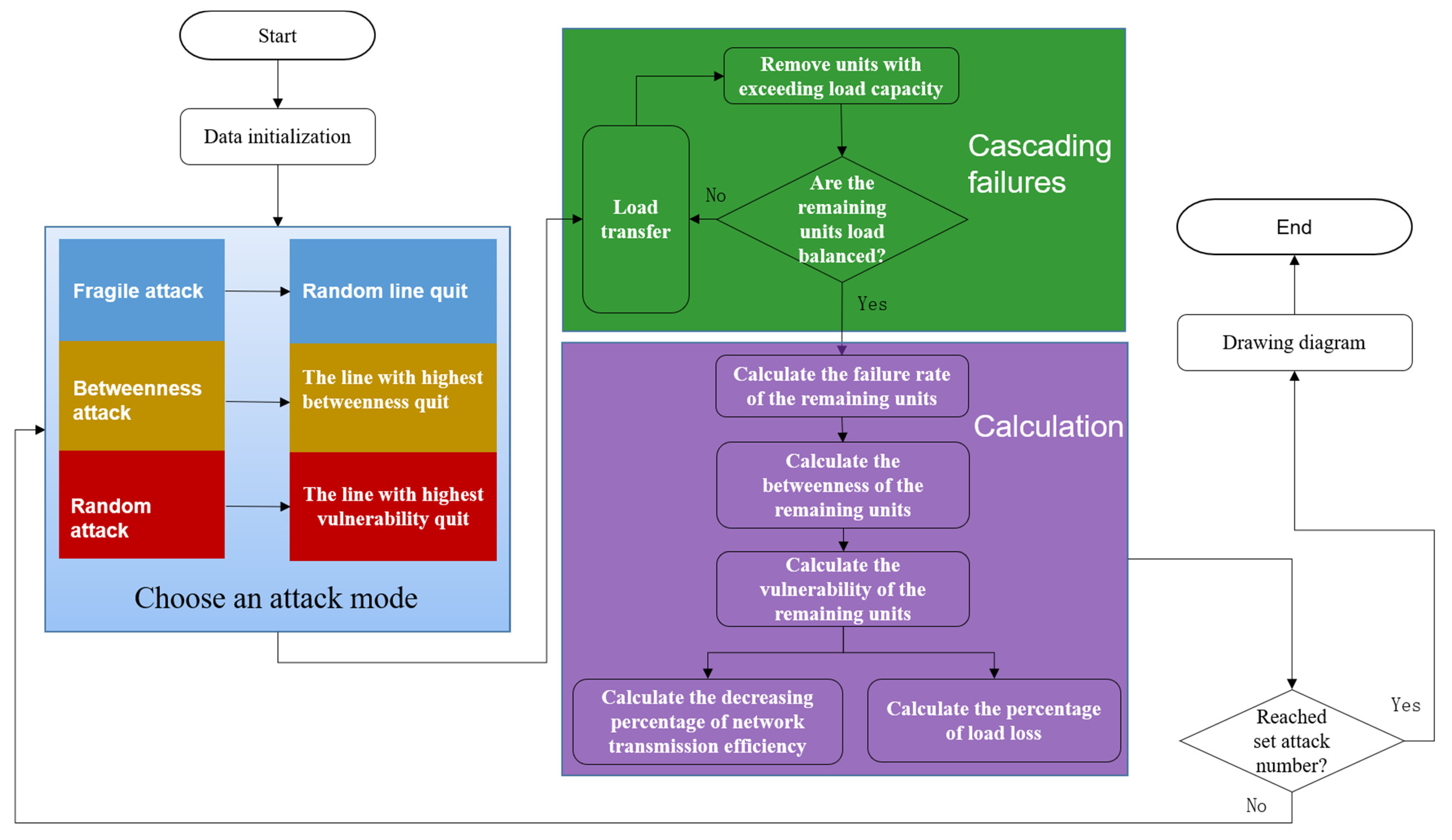
4.4. Vulnerability Analysis Process of Power Grid Structure
- (1)
- Line random attack: randomly attack a normal operation line according to the weight of line reliability and time is used to weigh the vulnerability of power grid function. This paper set the reliability as a time-based integration where is unit failure rate:
- (2)
- Line betweenness attack: attack the line with the largest specified betweenness in turn.
- (3)
- linear function vulnerability attack: attack the line with the highest specified vulnerability in turn. The vulnerability is calculated by using load of loss. The vulnerability is calculated by using betweenness times weigh the vulnerability of power grid:
5. Example Analysis
5.1. Topology Modeling and Analysis of Power Grid
5.1.1. IEEE 30 Topology Model
5.1.2. IEEE 118 Topology Model
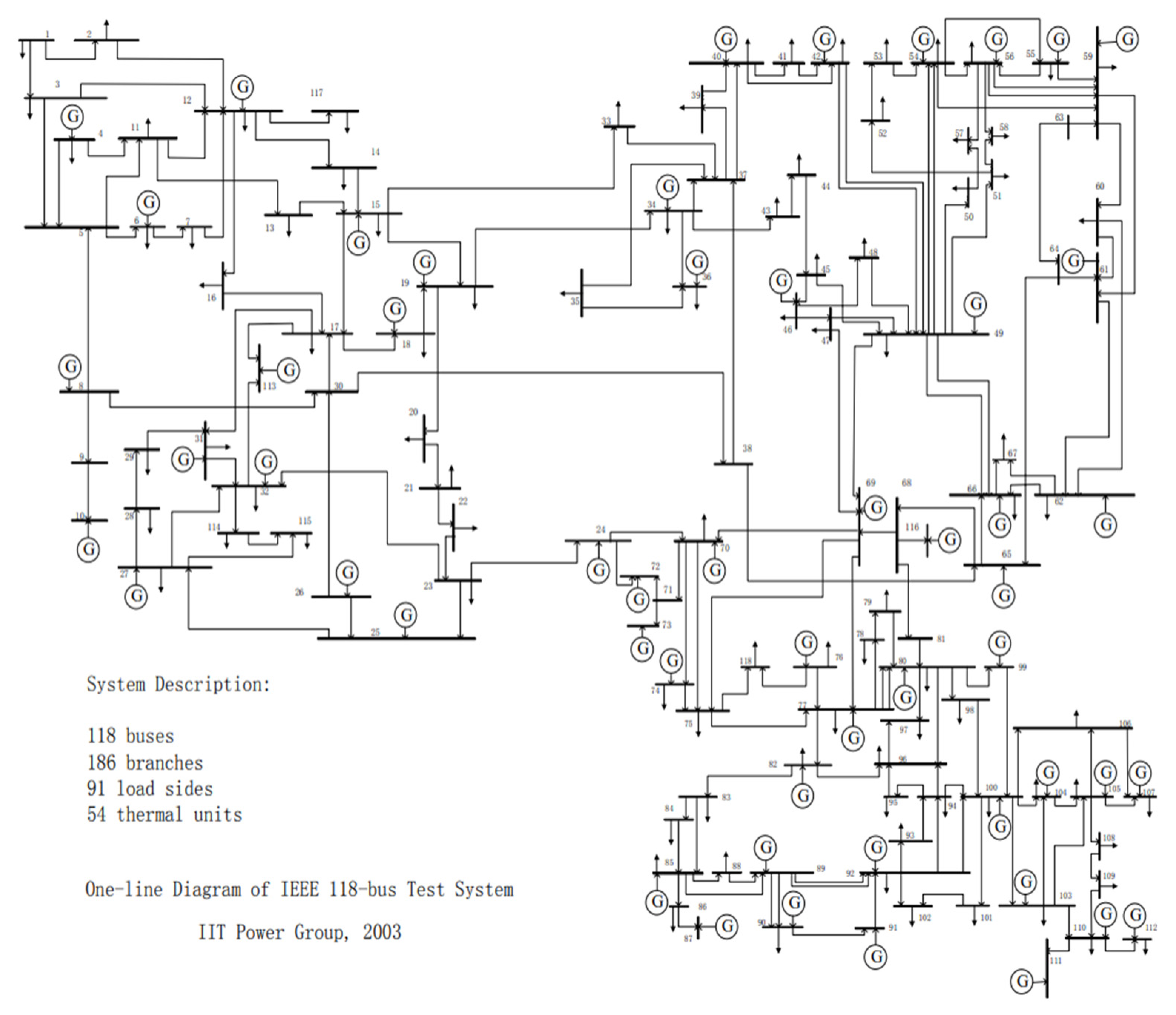
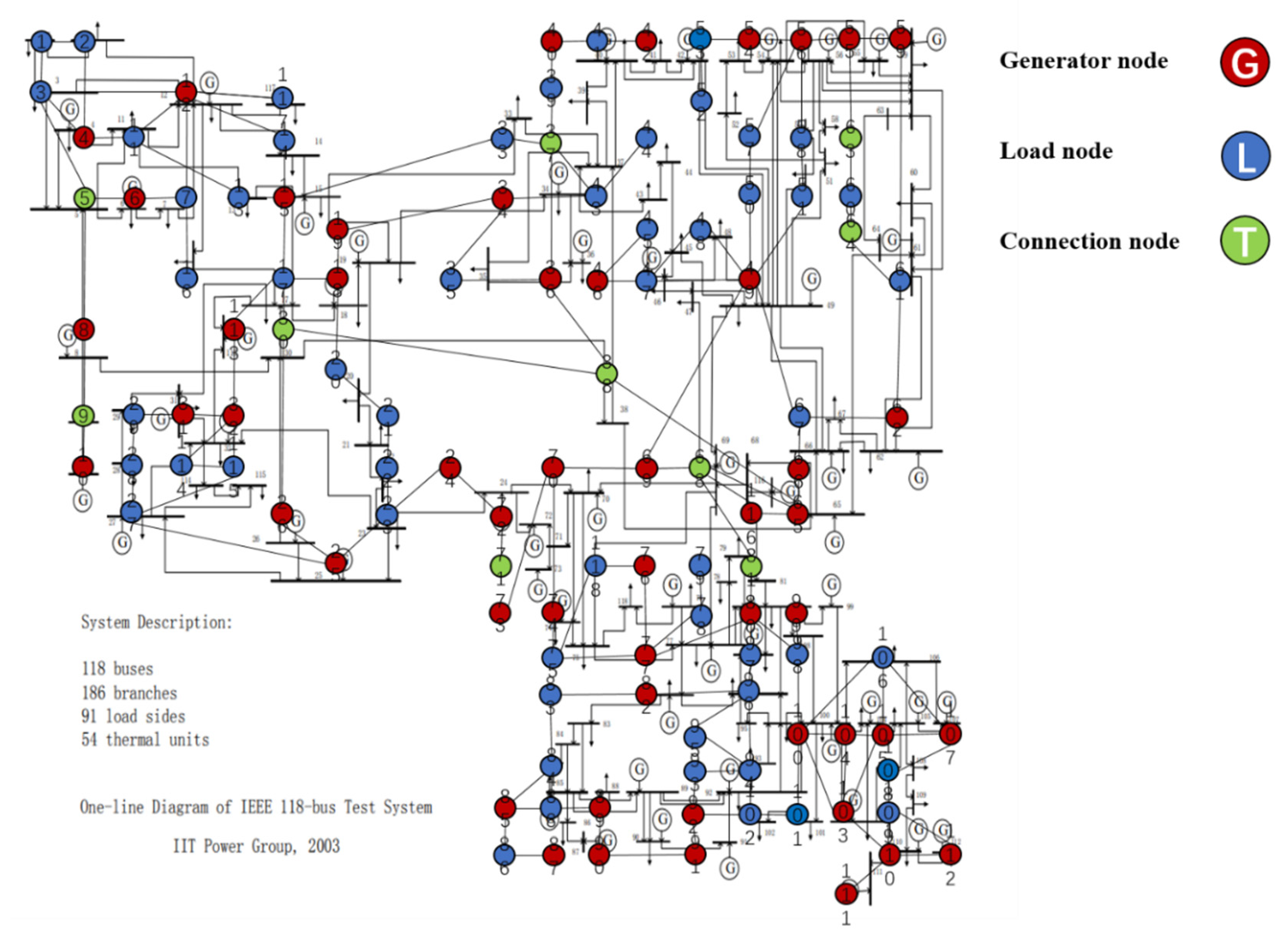

| Node Type | Node Number | Node ID |
|---|---|---|
| Source node | 15 | 10, 12, 25, 26, 31, 49, 61, 65, 66, 69, 80, 87, 89, 100, 103 |
| Sink node | 93 | 1, 2, 3, 4, 6, 7, 8, 11, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 27, 28, 29, 32, 33, 34, 35, 36, 39, 40, 41, 42, 43, 44, 45,46, 47, 48, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 62, 67, 70, 72, 73, 74, 75, 76, 77, 78, 79, 82, 83, 84, 85, 86, 88, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 101, 102, 104, 105, 106, 107, 108, 109, 110, 111, 112, 113, 114, 115, 116, 117, 118 |
| Link node | 10 | 5, 9, 30, 37, 38, 63, 64, 68, 71, 81 |
5.1.3. Extreme Weather Data
| LW | λW (Number/h, 50 km) | LI | λI (Number/h, 50 km) |
|---|---|---|---|
| LW ≤ 0.W | 1.2 × 10−5 | LI ≤ 0.3dlI | 0 |
| 0.9dlW < LW ≤ 1.0dlW | 8.0 × 10−4 | 0.3dlI < LI ≤ 0.5dlI | 4.5 × 10−3 |
| 1.0dlW < LW ≤ 1.1dlW | 0.048 | 0.5dlI < LI ≤ 0.9dlI | 0.010 |
| 1.1dlW < LW ≤ 1.2dlW | 0.060 | 0.9dlI < LI ≤ 1.0dlI | 0.015 |
| 1.2dlW < LW ≤ 1.5dlW | 0.028 | 1.0dlI < LI ≤ 1.1dlI | 0.033 |
| 1.5dlW < LW | 0.04 | 1.1dlI < LI ≤ 1.2dlI | 0.050 |
| / | / | 1.2dlI < LI ≤ 1.5dlI | 0.071 |
| / | / | 1.5dlI < LI | 0.10 |
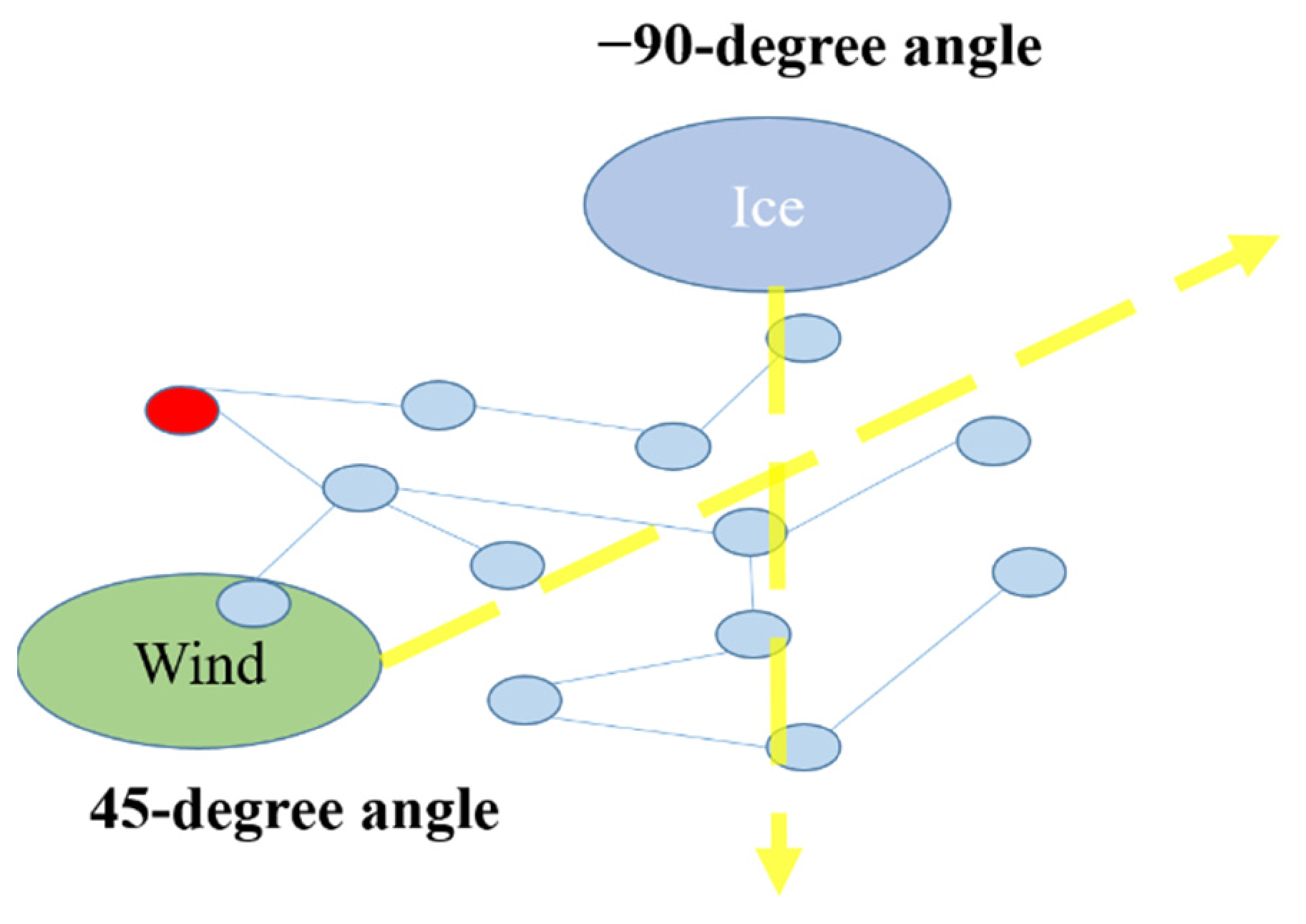
| Number of Lines (Wind) | Load of Wind | Number of Lines (Ice) | Load of Ice |
|---|---|---|---|
| 22 | 23.63285903 | 12 | 65.17233427 |
| 30 | 22.65910081 | 14 | 65.17233427 |
| 18 | 22.65449605 | 28 | 65.17233422 |
| 20 | 21.91749813 | 6 | 65.16670399 |
| 23 | 18.49225909 | 7 | 65.16670399 |
| 32 | 12.28254813 | 10 | 65.16670399 |
| 24 | 6.298664663 | 9 | 65.16577223 |
| 17 | 1.585745099 | 26 | 65.16028429 |
| Number of Lines (Wind) | Load of Wind | Number of Lines (Ice) | Load of Ice |
|---|---|---|---|
| 110 | 23.61433234 | 46 | 65.16670399 |
| 114 | 23.53946714 | 49 | 65.16670399 |
| 108 | 23.53265901 | 54 | 65.1241117 |
| 109 | 23.53114991 | 108 | 65.00203936 |
| 115 | 23.52855244 | 109 | 65.00203936 |
| 112 | 23.48828542 | 114 | 64.96905002 |
| 111 | 23.35066356 | 110 | 64.96862148 |
| 113 | 21.02053777 | 115 | 64.95683736 |
5.2. Simulation and Analysis of Power Grid Functional Vulnerability
5.2.1. Structural Vulnerability Calculation of Proposed Model without Extreme Weather
5.2.2. Structural Vulnerability Calculation of Proposed Model under Extreme Weather
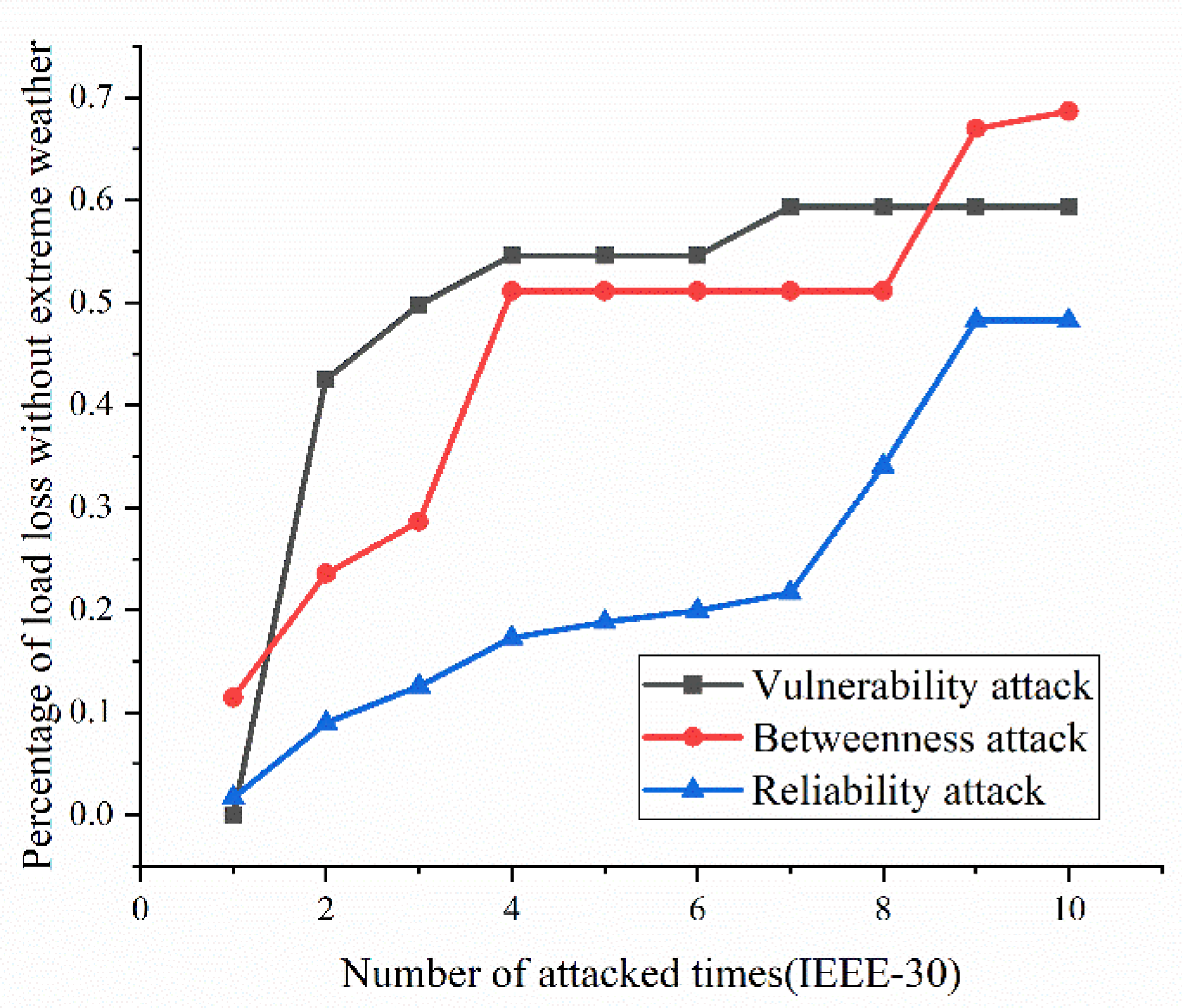
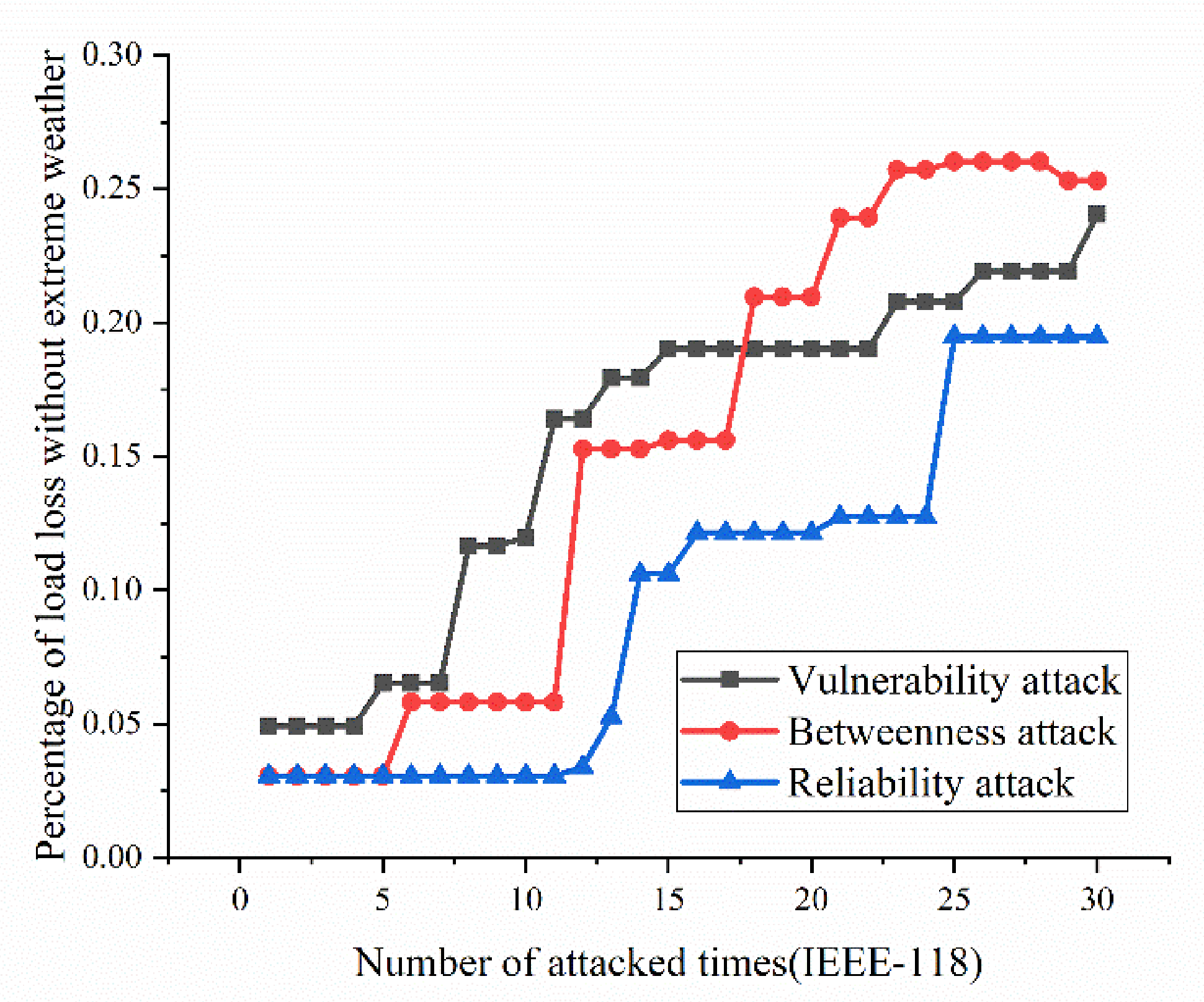
5.2.3. Structural Vulnerability Result Analysis by Comparing IEEE-30 with IEEE-118
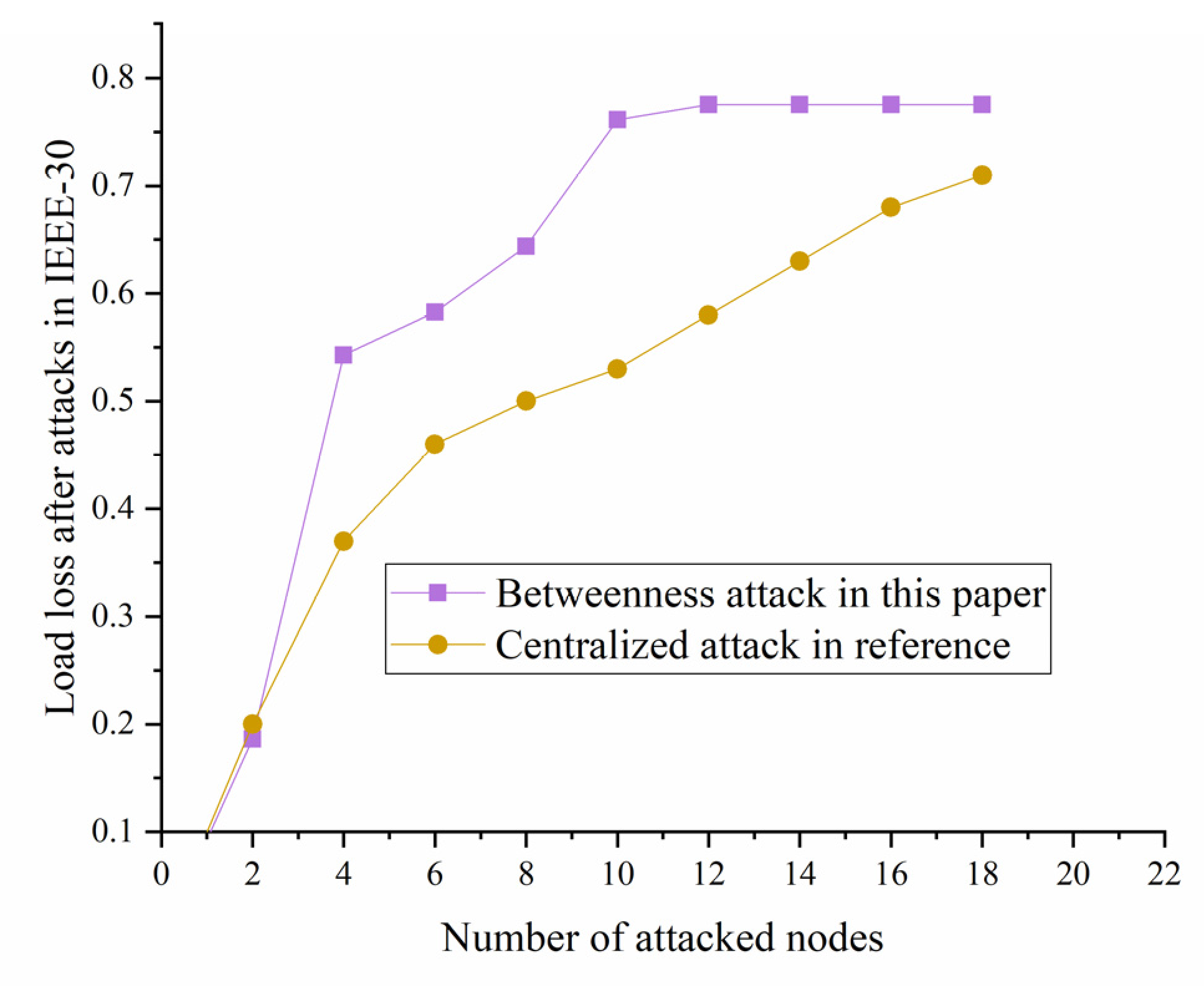
5.2.4. Comparation with Other Literatures
5.2.5. Cascading Failures of the Cases Study of IEEE-30 and IEEE-118
6. Discussion
7. Conclusions
- (1)
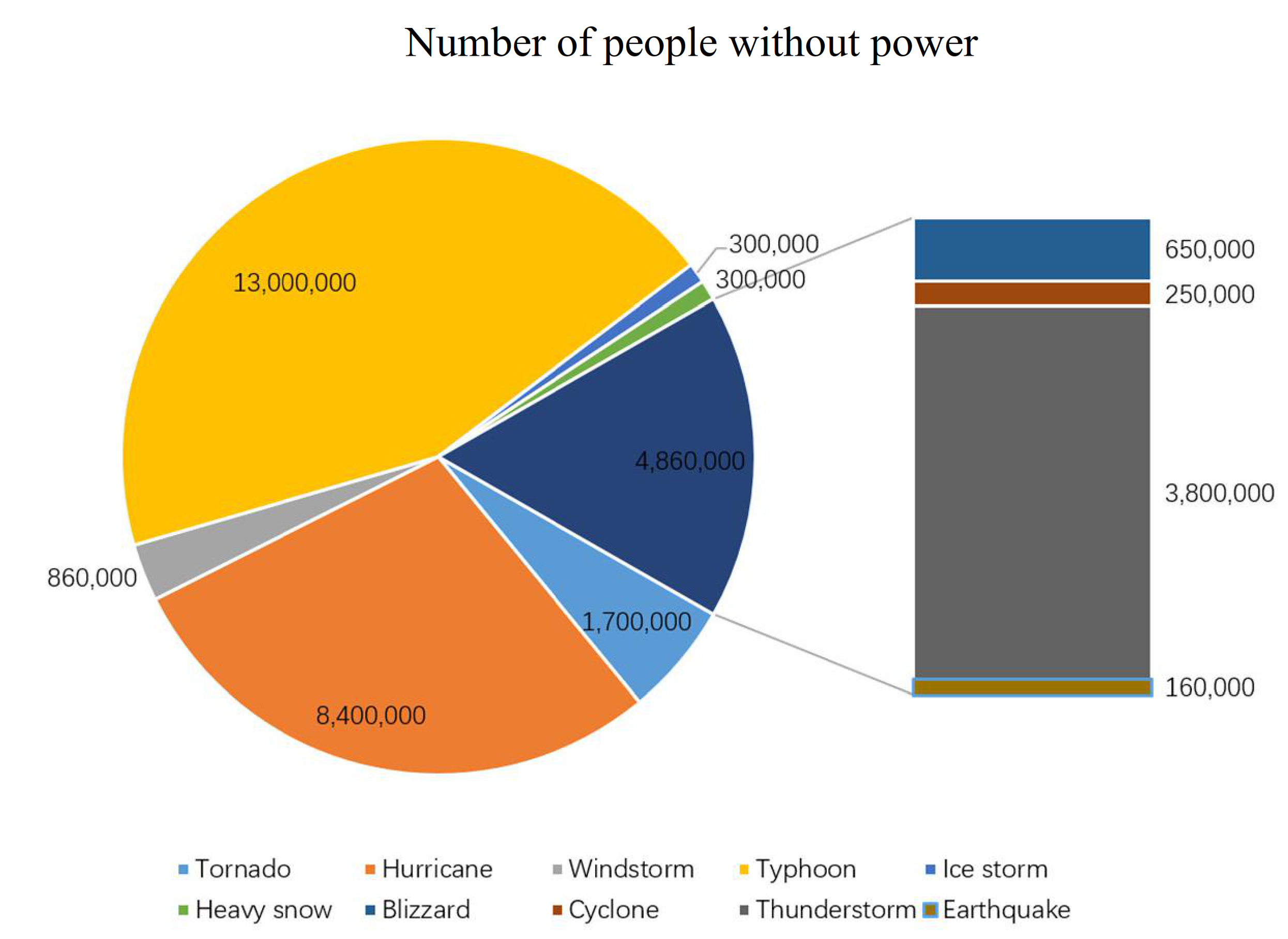
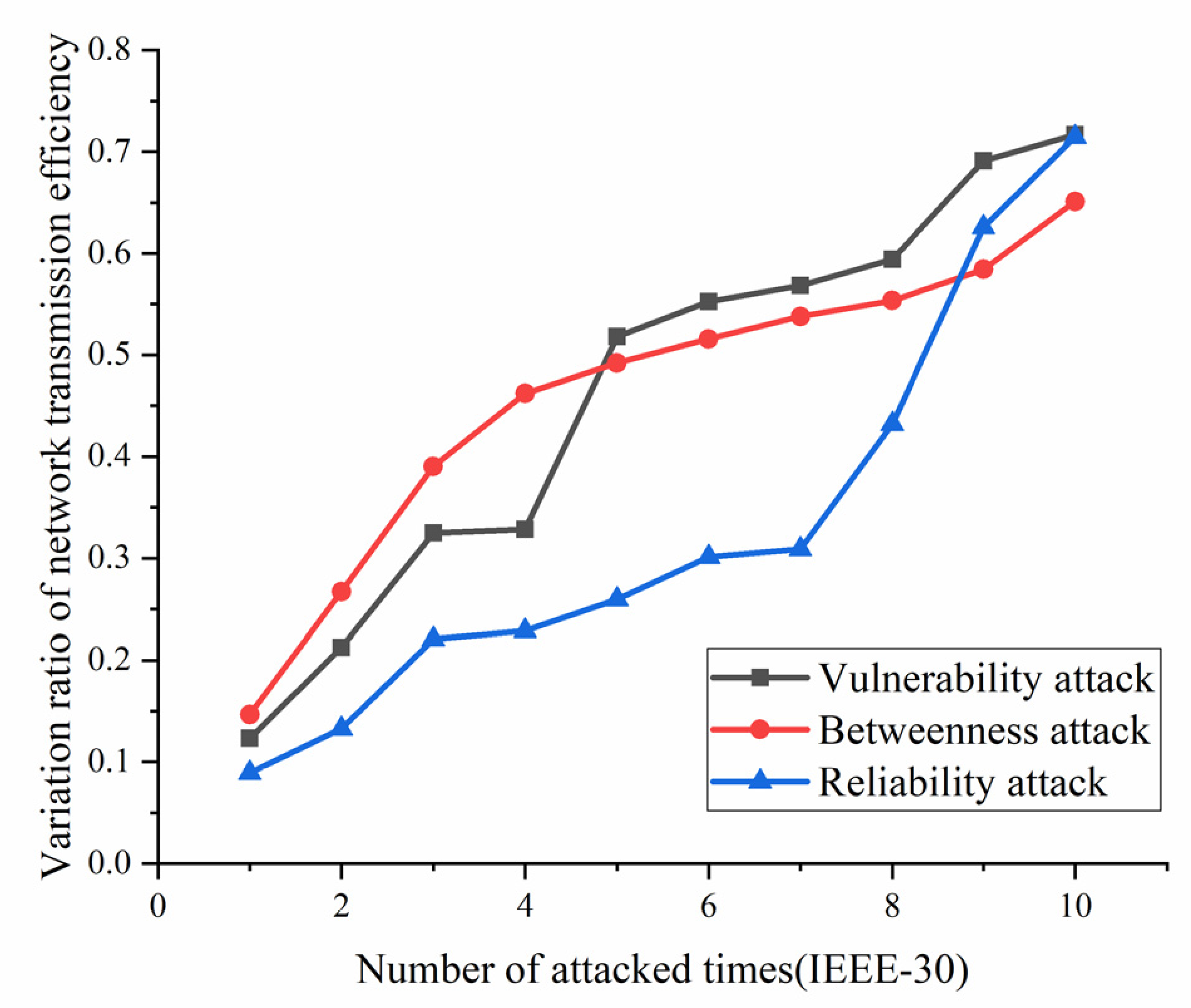
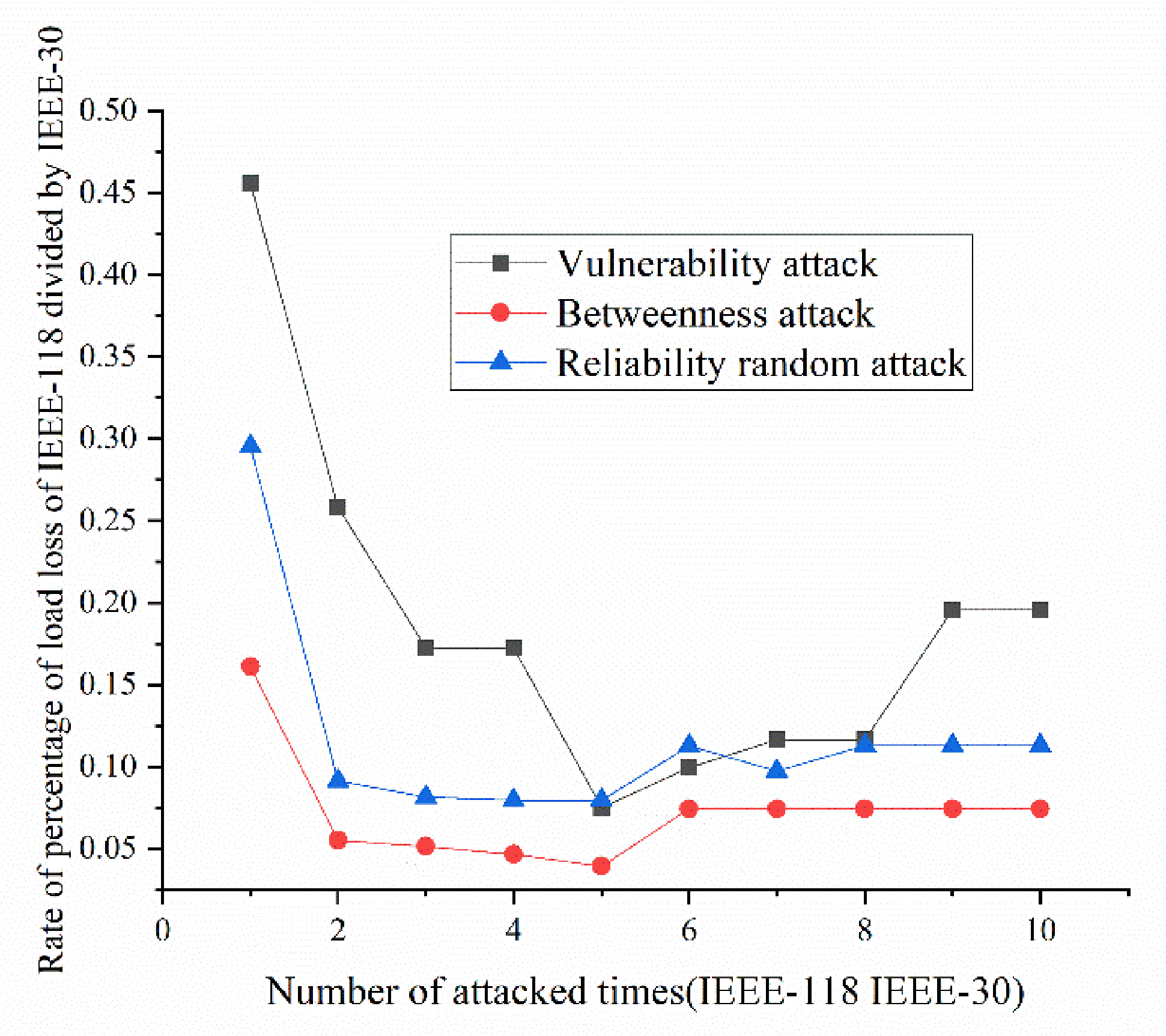
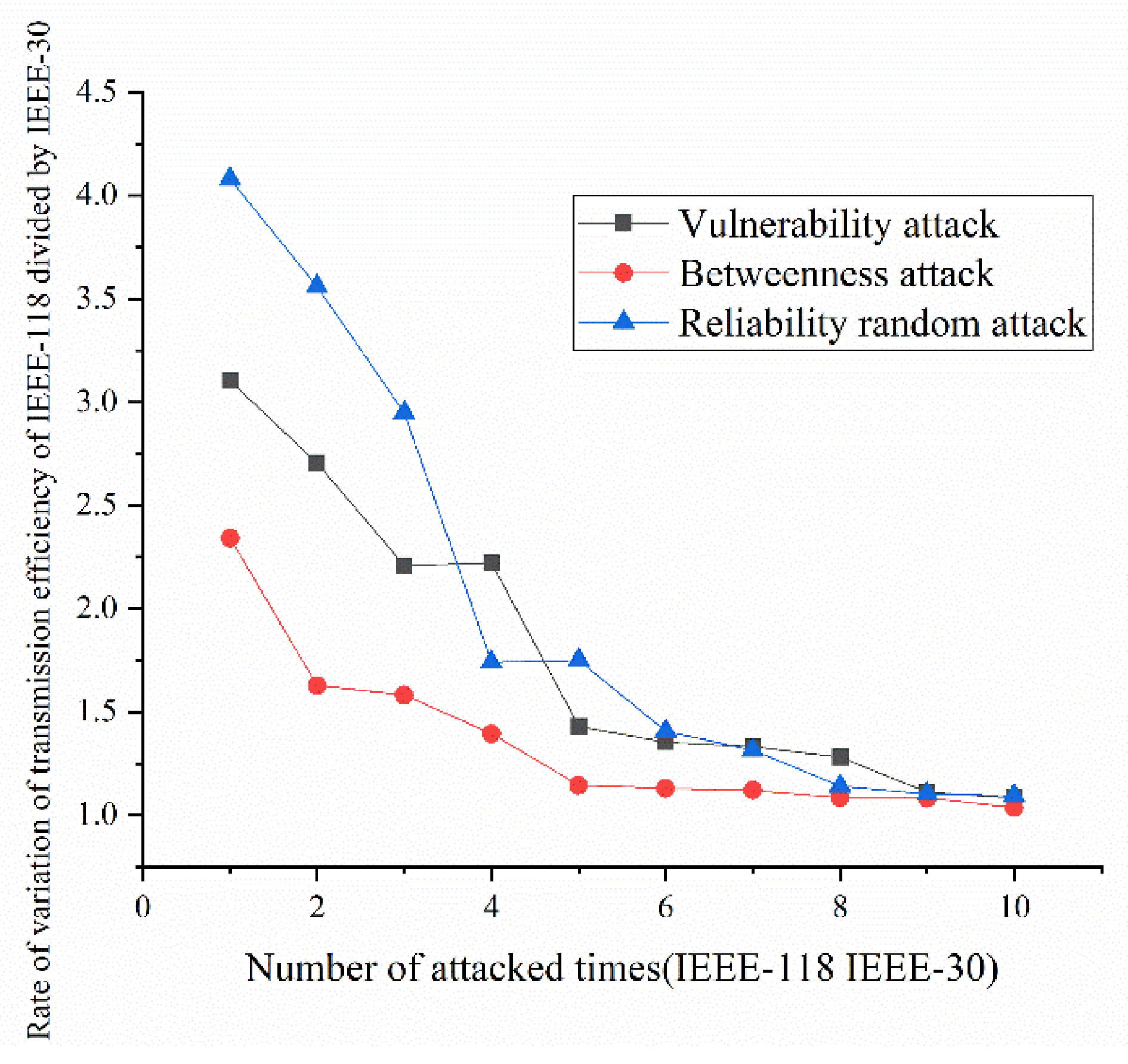
- Variation ratio of network transmission efficiency grows fast at the first 5 removed nodes both in IEEE-30 and IEEE-118. Vulnerability and betweenness attack caused load losses to shrink nearly 50% from IEEE-30 to IEEE-118, while the load loss caused by reliability attack only decreases 10%. It can be seen from Figure 18, Figure 19, Figure 20, Figure 21, Figure 22, Figure 23, Figure 24, Figure 25 and Figure 26 that the power grid has good robustness against line random attack in extreme cases, and the percentage of load loss and the percentage of network transmission efficiency de-cline increase slowly in line random attack mode.
- (2)
- The percentage of load loss and variation ratio of network transmission efficiency appear with higher values, considering extreme cases.
- (3)
- Bigger network IEEE-118 usually performs more stably and reliably than the IEEE-30, with regard to load loss. However, the variation ratio of transmission efficiency of IEEE-118 is obviously much higher than the ratio of IEEE-30; the influenced nodes and lines are more in IEEE-118.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Symbol | Description | SI (\ represents none) |
| Weight of edge ij | P.U. | |
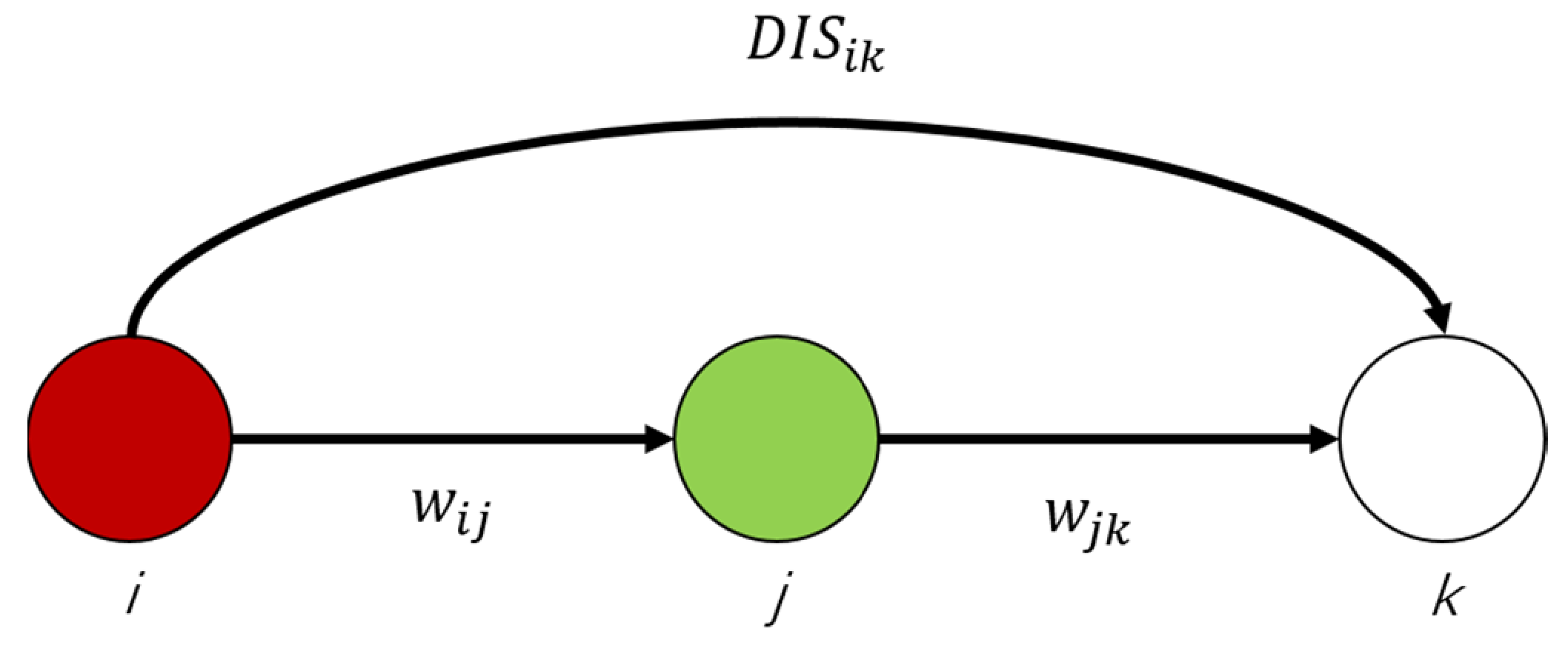
| The sum of the edge reactance included in the shortest path from node i to j. | P.U. | |
| Average distance of | P.U. | |
| Proportion of weighted shortest paths passing through a node in the network to all weighted shortest paths in the network | \ | |
| Proportion of weighted shortest paths passing through an edge in the network to all weighted shortest paths in the network | \ | |
| The number of shortest paths between node i and node j. | \ | |
| The number of shortest paths between node i and node j containing node v | \ | |
| the number of shortest paths between node i and node j containing edge e | \ | |
| The number of sink nodes | \ | |
| The number of source nodes | \ | |
| The degree of node i | ||
| The average degree of all node degree | \ | |
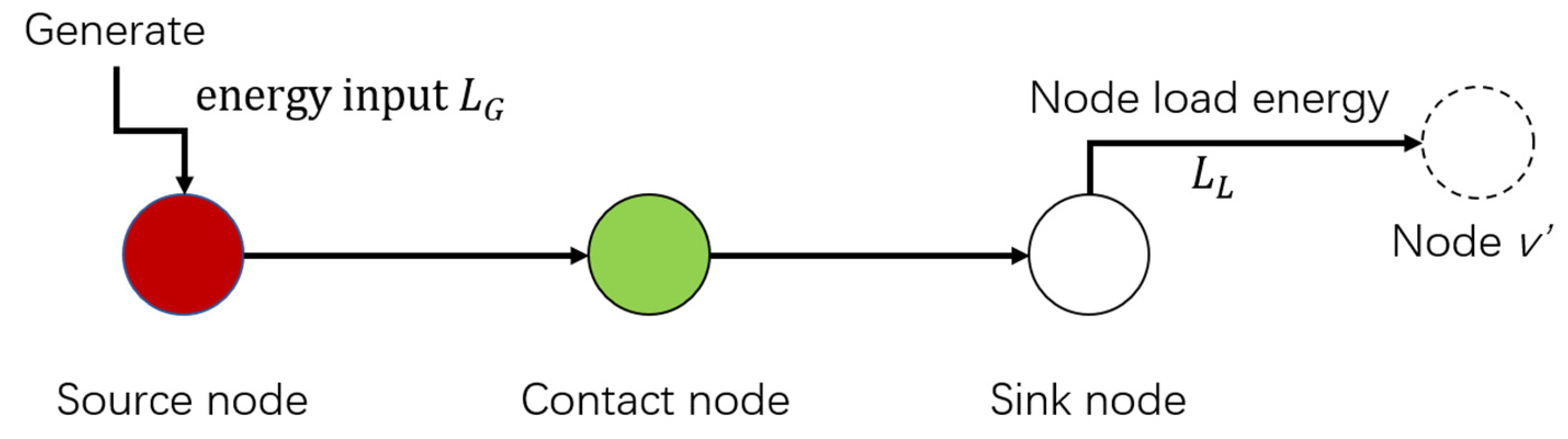
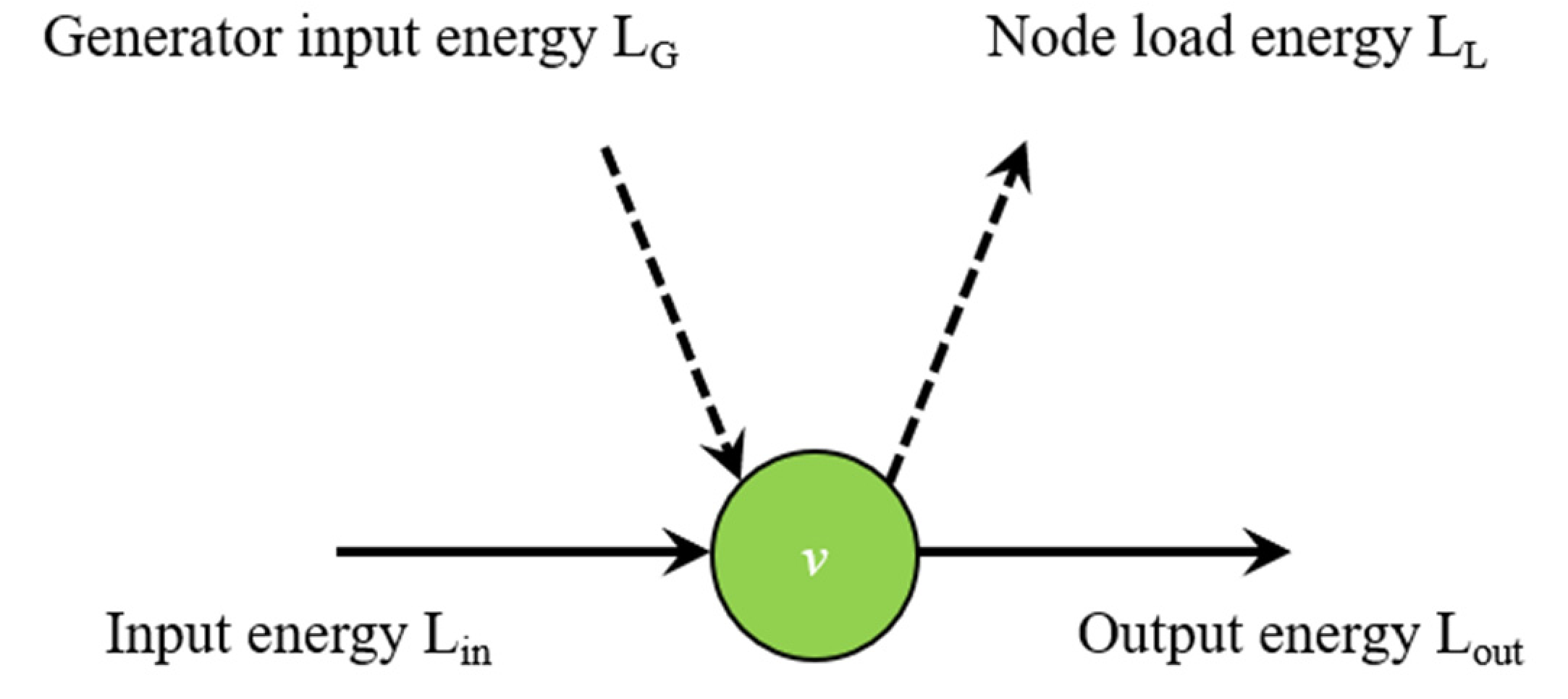
| the load of jth node | MV | |
| The ratio of the load of all normal operation sink nodes in the current power grid to the load of all nodes in the power grid in the initial state | \ | |
| the average of the reciprocal distance between the network nodes of all node pairs in the power grid | \ | |
| The ratio between the current network transmission efficiency E and the initial network transmission efficiency | \ | |
| Input energy | MV | |
| Output energy | MV | |
| Rated load capacity | MV | |
| Limited rated load capacity | MV | |
| Rated load capacity coefficient | \ | |
| Limited rated load capacity coefficient | \ | |
| Position of x-coordinate of line i in topological graph | KM | |
| Position of y-coordinate of line i in topological graph | KM | |
| Position of x-coordinate of the extreme case in topological graph | KM | |
| Position of y-coordinate of the extreme case in topological graph | KM | |
| Radius of impact range | KM | |
| Coefficient | \ | |
| Failure rate of extreme weather I | \ | |
| Coefficient of weather I | \ |
References
- Kezunovic, M.; Dobson, I.; Dong, Y. Impact of extreme weather on power system blackouts and forced outages: New challenges. In Proceedings of the 7th Balkan Power Conference, Šibenik, Croatia, 10–12 September 2008; pp. 1–5. [Google Scholar] [CrossRef]
- Panteli, M.; Mancarella, P. Influence of extreme weather and climate change on the resilience of power systems: Impacts and possible mitigation strategies. Electr. Power Syst. Res. 2015, 127, 259–270. [Google Scholar] [CrossRef]
- Li, T.; Luo, B.; Liu, L.; Wu, T. Wind accident analysis of transmission line in China Southern Power Grid’s Coastal Regions. In Proceedings of the 5th International Conference on Electric Utility Deregulation and Restructuring and Power Technologies (DRPT), Changsha, China, 26–29 November 2015; pp. 1700–1704. [Google Scholar] [CrossRef]
- Panteli, M.; Mancarella, P. Modeling and Evaluating the Resilience of Critical Electrical Power Infrastructure to Extreme Weather Events. IEEE Syst. J. 2015, 11, 1733–1742. [Google Scholar] [CrossRef]
- Cadini, F.; Agliardi, G.L.; Zio, E. A modeling and simulation framework for the reliability/availability assessment of a power transmission grid subject to cascading failures under extreme weather conditions. Appl. Energy 2017, 185, 267–279. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y. Short-term operational reliability evaluation for power systems under extreme weather conditions. In Proceedings of the 2015 IEEE Eindhoven PowerTech, Eindhoven, The Netherlands, 29 June–2 July 2015; pp. 1–5. [Google Scholar] [CrossRef]
- Anvari, M.; Lohmann, G.M.; Wächter, M.; Milan, P.; Lorenz, E.; Heinemann, D.; Tabar, M.R.R.; Peinke, J. Short term fluctuations of wind and solar power systems. New J. Phys. 2016, 18, 063027. [Google Scholar] [CrossRef]
- Pahwa, S.; Scoglio, C.M.; Scala, A. Abruptness of Cascade Failures in Power Grids. Sci. Rep. 2014, 4, 3694. [Google Scholar] [CrossRef] [Green Version]
- Gan, Y.; Hu, Y.; Ruan, J.; Du, Z.; Liu, C.; Du, W. Analysis and Prevention of Main Natural Disasters of 500kV Transmission Lines in Central China Power Grid. Electr. Power Constr. 2012, 6, 37–42. [Google Scholar]
- Kiel, E.S.; Kjølle, G.H. The impact of protection system failures and weather exposure on power system reliability. In Proceedings of the International Conference on Environment and Electrical Engineering and 2019 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Genova, Italy, 10–14 June 2019; pp. 1–6. [Google Scholar] [CrossRef] [Green Version]
- Jufri, F.H.; Widiputra, V.; Jung, J. State-of-the-art review on power grid resilience to extreme weather events: Definitions, frameworks, quantitative assessment methodologies, and enhancement strategies. Appl. Energy 2019, 239, 1049–1065. [Google Scholar] [CrossRef]
- Matko, M.; Golobič, M.; Kontić, B. Reducing risks to electric power infrastructure due to extreme weather events by means of spatial planning: Case studies from Slovenia. Utilities Policy 2017, 44, 12–24. [Google Scholar] [CrossRef]
- Albert, R.; Jeong, H.; Barabasi, A. Error and attack tolerance of complex networks. Nature 2000, 406, 378–382. [Google Scholar] [CrossRef] [Green Version]
- Chen, X.; Sun, K.; Cao, Y.; Wang, S. Identification of Vulnerable Lines in Power Grid Based on Complex Network Theory. In Proceedings of the 2007 IEEE Power Engineering Society General Meeting, Tampa, FL, USA, 23 July 2007; pp. 1–6. [Google Scholar] [CrossRef]
- Arianos, S.; Bompard, E.; Carbone, A.; Xue, F. Power grid vulnerability: A complex network approach. Chaos: Interdiscip. J. Nonlinear Sci. 2009, 19, 013119. [Google Scholar] [CrossRef]
- Pagani, G.A.; Aiello, M. The Power Grid as a complex network: A survey. Phys. A Stat. Mech. Its Appl. 2013, 392, 2688–2700. [Google Scholar] [CrossRef] [Green Version]
- Cuadra, L.; Salcedo-Sanz, S.; Del Ser, J.; Jiménez-Fernández, S.; Geem, Z.W.; Cuadra, L.; Salcedo-Sanz, S.; Del Ser, J.; Jiménez-Fernández, S.; Geem, Z.W. A Critical Review of Robustness in Power Grids Using Complex Networks Concepts. Energies 2015, 8, 9211–9265. [Google Scholar] [CrossRef] [Green Version]
- Li, Q.; Li, H.Q.; Huang, Z.M.; Li, Y.Q. Power system vulnerability assessment based on transient energy hybrid method. Power Syst. Protect. Control. 2013, 41, 1–6. [Google Scholar] [CrossRef]
- Li, X.; Qi, Z. Impact of cascading failure based on line vulnerability index on power grids. Energy Syst. 2021, 1–26. [Google Scholar] [CrossRef]
- Abedi, A.; Gaudard, L.; Romerio, F. Review of major approaches to analyze vulnerability in power system. Reliab. Eng. Syst. Saf. 2019, 183, 153–172. [Google Scholar] [CrossRef]
- Johansson, J.; Hassel, H.; Zio, E. Reliability and vulnerability analyses of critical infrastructures: Comparing two approaches in the context of power systems. Reliab. Eng. Syst. Saf. 2013, 120, 27–38. [Google Scholar] [CrossRef]
- Ouyang, M. Comparisons of purely topological model, betweenness based model and direct current power flow model to analyze power grid vulnerability. Chaos Interdiscip. J. Nonlinear Sci. 2013, 23, 023114. [Google Scholar] [CrossRef]
- Wei, X.; Gao, S.; Huang, T.; Bompard, E.; Pi, R.; Wang, T. Complex Network-Based Cascading Faults Graph for the Analysis of Transmission Network Vulnerability. IEEE Trans. Ind. Inform. 2018, 15, 1265–1276. [Google Scholar] [CrossRef]
- Wang, W.; Song, Y.; Li, Y.; Jia, Y. Research on Cascading Failures Model of Power Grid Based on Complex Network. In Proceedings of the 2020 Chinese Control and Decision Conference (CCDC), Hefei, China, 22–24 August 2020; pp. 1367–1372. [Google Scholar] [CrossRef]
- Carreras, B.A.; New Man, D.E.; Dobson, I.; Poole, A. Initial evidence for self-organized criticality in electric power blackouts. In Proceedings of the 33rd Hawaii International Conference on System Sciences, Maui, HI, USA, 7 January 2000; pp. 102–108. [Google Scholar] [CrossRef]
- Cao, Y.; Jiang, Q.; Ding, L. Self-organized criticality phenomenon for power system blackouts. Power Syst. Technol. 2005, 15, Available. Available online: https://en.cnki.com.cn/Article_en/CJFDTotal-DWJS200515000.htm (accessed on 11 August 2021).
- Dwivedi, A.; Yu, X. A Maximum-Flow-Based Complex Network Approach for Power System Vulnerability Analysis. IEEE Trans. Ind. Inform. 2011, 9, 81–88. [Google Scholar] [CrossRef]
- Ren, Z.; Zhang, J.; Zhang, J. Calculation of failure rate of power equipments based on partial least square method. Power Syst. Technol. 2005, 5. Available online: https://en.cnki.com.cn/Article_en/CJFDTotal-DWJS200505002.htm (accessed on 11 August 2021).
- Kim, C.J.; Obah, O.B. Vulnerability Assessment of Power Grid Using Graph Topological Indices. Int. J. Emerg. Electr. Power Syst. 2007, 8. [Google Scholar] [CrossRef]
- Zhongwei, M.; Zongxiang, L.; Jingyan, S. Comparison analysis of the small-world topological model of Chinese and American power grids. Autom. Electr. PowerSyst. 2004, 15, 004. [Google Scholar] [CrossRef]
- Chen, T.; Rong, J.; Yang, J.; Cong, G.; Li, G. Combining public opinion dissemination with polarization process considering individual heterogeneity. Healthcare 2021, 9, 176. [Google Scholar] [CrossRef]
- Chen, T.; Peng, L.; Yang, J.; Cong, G. Analysis of User Needs on Downloading Behavior of English Vocabulary APPs Based on Data Mining for Online Comments. Mathematics 2021, 9, 1341. [Google Scholar] [CrossRef]
- Chen, T.; Yin, X.; Peng, L.; Rong, J.; Yang, J.; Cong, G. Monitoring and Recognizing Enterprise Public Opinion from High-Risk Users Based on User Portrait and Random Forest Algorithm. Axioms 2021, 10, 106. [Google Scholar] [CrossRef]
- Busby, J.W.; Baker, K.; Bazilian, M.D.; Gilbert, A.Q.; Grubert, E.; Rai, V.; Rhodes, J.D.; Shidore, S.; Smith, C.A.; Webber, M.E. Cascading risks: Understanding the 2021 winter blackout in Texas. Energy Res. Soc. Sci. 2021, 77, 102106. [Google Scholar] [CrossRef]
- Dong, H.; Cui, L. System Reliability Under Cascading Failure Models. IEEE Trans. Reliab. 2015, 65, 929–940. [Google Scholar] [CrossRef]
- Liu, B.; Li, Z.; Chen, X.; Huang, Y.; Liu, X. Recognition and Vulnerability Analysis of Key Nodes in Power Grid Based on Complex Network Centrality. IEEE Trans. Circuits Syst. Ii Express Briefs 2017, 65, 346–350. [Google Scholar] [CrossRef]
- Li, K.; Liu, K.; Wang, M. Robustness of the Chinese power grid to cascading failures under attack and defense strategies. Int. J. Crit. Infrastruct. Prot. 2021, 33, 100432. [Google Scholar] [CrossRef]
- Wang, J.-W.; Rong, L.-L. Robustness of the western United States power grid under edge attack strategies due to cascading failures. Saf. Sci. 2011, 49, 807–812. [Google Scholar] [CrossRef]
- Ding, M.; Han, P. Vulnerability assessment to small-world power grid based on weighted topological model. Chin. Society of Electr. Eng. 2008, 28, 20. Available online: http://www.researchgate.net/publication/294297239_Vulnerability_assessment_to_small-world_power_grid_based_on_weighted_topological_model?ev=auth_pub (accessed on 11 August 2021).
- Amirioun, M.H.; Aminifar, F.; Lesani, H. Towards Proactive Scheduling of Microgrids Against Extreme Floods. IEEE Trans. Smart Grid 2018, 9, 3900–3902. [Google Scholar] [CrossRef]
- Gholami, A.; Aminifar, F. A hierarchical response-based approach to the load restoration problem. IEEE Trans. Smart Grid 2017, 8, 1700–1709. [Google Scholar] [CrossRef]
- Shao, C.; Shahidehpour, M.; Wang, X.; Wang, X.; Wang, B. Integrated Planning of Electricity and Natural Gas Transportation Systems for Enhancing the Power Grid Resilience. IEEE Trans. Power Syst. 2017, 32, 4418–4429. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, C.; Wang, J.; Baldick, R. Research on Resilience of Power Systems Under Natural Disasters—A Review. IEEE Trans. Power Syst. 2016, 31, 1604–1613. [Google Scholar] [CrossRef]
- Qi, N.; Cheng, L.; Jiang, Y.; Luo, J.; Sun, K.; Wang, D.; Wang, W.; Sun, W. Vulnerability Assessment Based on Operational Reliability Weighted and Preventive Planning. In Proceedings of the IEEE Sustainable Power and Energy Conference (iSPEC), Beijing, China, 21–23 November 2019; pp. 1749–1754. [Google Scholar] [CrossRef]
- Fang, J.; Su, C.; Chen, Z.; Haishun, S.; Lund, P. Power system structural vulnerability assessment based on an improved maximum flow approach. IEEE Trans. Smart Grid 2016, 9, 777–785. [Google Scholar] [CrossRef]
- Koc, Y.; Warnier, M.; Kooij, R.; Brazier, F. Structural vulnerability assessment of electric power grids. In Proceedings of the 11th IEEE International Conference on Networking, Sensing and Control, Miami, FL, USA, 7–9 April 2014; pp. 386–391. [Google Scholar] [CrossRef] [Green Version]
- Albert, R.; Albert, I.; Nakarado, G.L. Structural vulnerability of the North American power grid. Phys. Rev. E 2004, 69, 025103. [Google Scholar] [CrossRef] [Green Version]
- Bompard, E.; Pons, E.; Wu, D. Analysis of the structural vulnerability of the interconnected power grid of continental Europe with the Integrated Power System and Unified Power System based on extended topological approach. Int. Trans. Electr. Energy Syst. 2013, 23, 620–637. [Google Scholar] [CrossRef] [Green Version]
- Bender, J.; Farid, A. Seismic vulnerability of power transformer bushings. Eng. Struct. 2018, 162, 1–10. [Google Scholar] [CrossRef]
- Chang, L.; Wu, Z. Performance and reliability of electrical power grids under cascading failures. Int. J. Electr. Power Energy Syst. 2011, 33, 1410–1419. [Google Scholar] [CrossRef]
- Zhang, L.; Lu, J.; Fu, B.-B.; Li, S.-B. A cascading failures model of weighted bus transit route network under route failure perspective considering link prediction effect. Phys. A Stat. Mech. Its Appl. 2019, 523, 1315–1330. [Google Scholar] [CrossRef]
- Zscheischler, J.; Westra, S.; Hurk, B.J.J.M.V.D.; Seneviratne, S.I.; Ward, P.J.; Pitman, A.; AghaKouchak, A.; Bresch, D.N.; Leonard, M.; Wahl, T.; et al. Future climate risk from compound events. Nat. Clim. Chang. 2018, 8, 469–477. [Google Scholar] [CrossRef]
- Brenna, M.; Faranda, R.S.; Leva, S. Dynamic analysis of a new network topology for high power grid connected PV systems. In Proceedings of the IEEE PES General Meeting, Minneapolis, MN, USA, 25–29 July 2010; pp. 1–7. [Google Scholar] [CrossRef]
- Watts, D.J.; Strogatz, S. Collective dynamics of ‘small-world’ networks. Nature 1998, 393, 440–442. [Google Scholar] [CrossRef]
- Abbott, S.; Watts, D.J. Small-Worlds: The dynamics of between order and randomness. Am. Math. Mon. 2000, 107, 664–668. [Google Scholar] [CrossRef]
- Nima, A.; Masoud, E. Improving voltage security assessment and ranking vulnerable buses with consideration of power system limits. Electr. Power Energy Syst. 2003, 25, 705–715. [Google Scholar] [CrossRef]
- Ubeda, J.; Allan, R. Sequential simulation applied to composite system reliability evaluation. IEEE Trans. Power Syst. 1994, 9, 81–86. [Google Scholar] [CrossRef]
- Song, J.; Cotilla-Sanchez, E.; Ghanavati, G.; Hines, P.D.H. Dynamic Modeling of Cascading Failure in Power Systems. IEEE Trans. Power Syst. 2015, 31, 2085–2095. [Google Scholar] [CrossRef] [Green Version]
- Newman, D.E.; Carreras, B.; Lynch, V.; Dobson, I. Exploring Complex Systems Aspects of Blackout Risk and Mitigation. IEEE Trans. Reliab. 2011, 60, 134–143. [Google Scholar] [CrossRef]
- Alexandersson, H.; Tuomenvirta, H.; Schmith, T.; Iden, K. Trends of storms in NW Europe derived from an updated pressure data set. Clim. Research 2000, 14, 71–73. Available online: https://www.int-res.com/abstracts/cr/v14/n1/p71-73/ (accessed on 11 August 2021). [CrossRef] [Green Version]
- Brostrom, E.; Soder, L. Modeling of Ice Storms for Power Transmission reliabilit Calculations. In Proceedings of the 15th Power Systems Computation Conference, Liege, Belgium, 22–26 August 2005; Available online: https://www.researchgate.net/publication/228896987_Modelling_of_ice_storms_for_power_transmission_reliability_calculations (accessed on 11 August 2021).
- Chopade, P.; Bikdash, M. New centrality measures for assessing smart grid vulnerabilities and predicting brownouts and blackouts. Int. J. Crit. Infrastruct. Prot. 2016, 12, 29–45. [Google Scholar] [CrossRef] [Green Version]

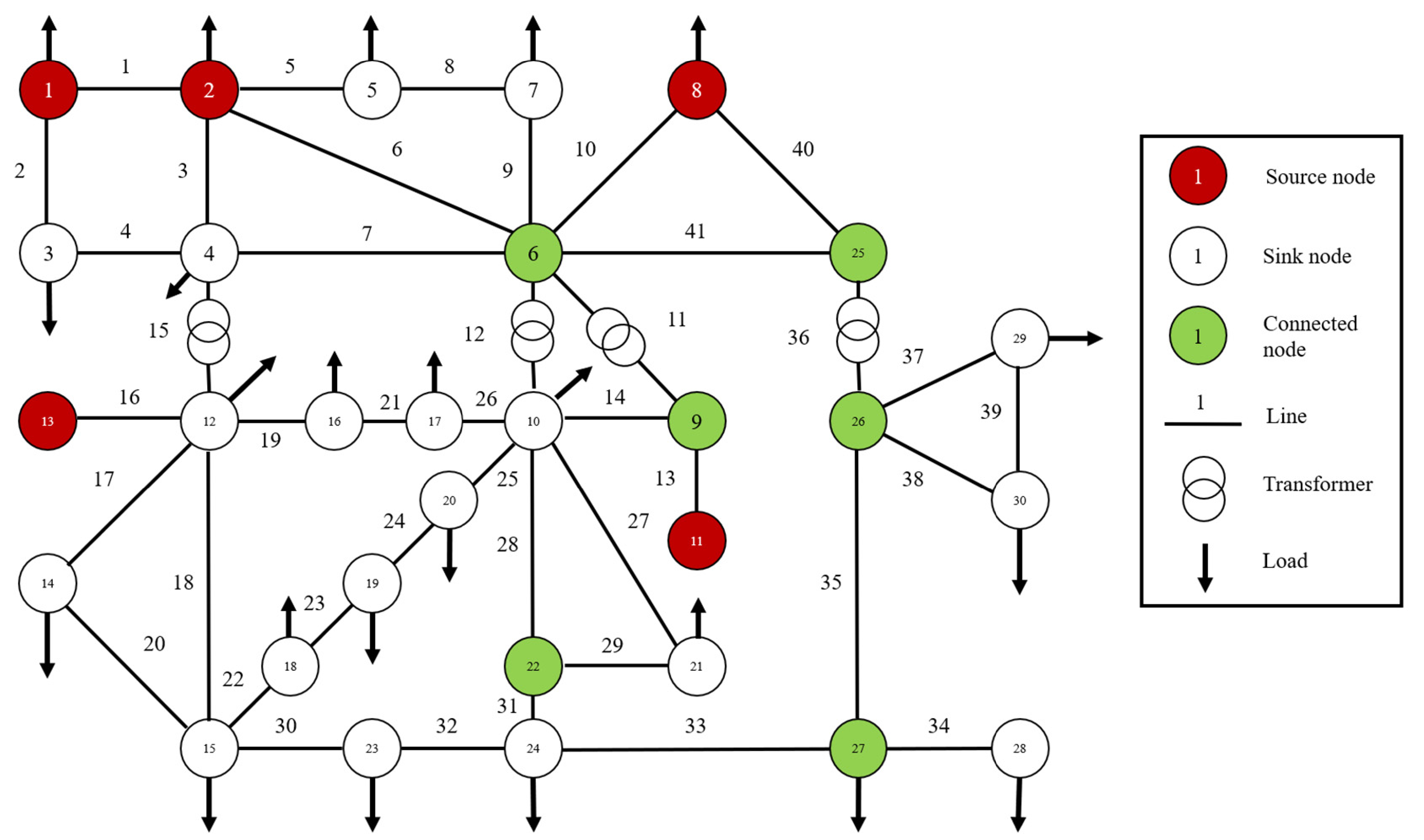






| Node Type | Node Number | Node ID |
|---|---|---|
| Source node | 5 | 1, 2, 8, 11, 13 |
| Sink node | 19 | 3, 4, 5, 7, 10, 12, 14, 15, 16, 17, 18, 19, 20, 21, 23, 24, 28, 29, 30 |
| Link node | 6 | 6, 9, 22, 25, 26, 27 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, B.; Tian, X.; Kong, L.; Chen, W. The Vulnerability of the Power Grid Structure: A System Analysis Based on Complex Network Theory. Sensors 2021, 21, 7097. https://doi.org/10.3390/s21217097
Xie B, Tian X, Kong L, Chen W. The Vulnerability of the Power Grid Structure: A System Analysis Based on Complex Network Theory. Sensors. 2021; 21(21):7097. https://doi.org/10.3390/s21217097
Chicago/Turabian StyleXie, Banghua, Xiaoge Tian, Liulin Kong, and Weiming Chen. 2021. "The Vulnerability of the Power Grid Structure: A System Analysis Based on Complex Network Theory" Sensors 21, no. 21: 7097. https://doi.org/10.3390/s21217097
APA StyleXie, B., Tian, X., Kong, L., & Chen, W. (2021). The Vulnerability of the Power Grid Structure: A System Analysis Based on Complex Network Theory. Sensors, 21(21), 7097. https://doi.org/10.3390/s21217097






