Abstract
The purpose of this paper is to explore a novel image encryption algorithm that is developed by combining the fractional-order Chua’s system and the 1D time-fractional diffusion system of order . To this end, we first discuss basic properties of the fractional-order Chua’s system and the 1D time-fractional diffusion system. After these, a new spatiotemporal chaos-based cryptosystem is proposed by designing the chaotic sequence of the fractional-order Chua’s system as the initial condition and the boundary conditions of the studied time-fractional diffusion system. It is shown that the proposed image encryption algorithm can gain excellent encryption performance with the properties of larger secret key space, higher sensitivity to initial-boundary conditions, better random-like sequence and faster encryption speed. Efficiency and reliability of the given encryption algorithm are finally illustrated by a computer experiment with detailed security analysis.
1. Introduction
Owing to the rapid development of internet and multimedia technologies, a great number of images have been used in various applications. Since images are usually required to be confidential between the sending side and the receiver end, the protection of images by encryption becomes more and more important. During the past several decades, different techniques have been introduced to design the image encryptions [1,2]. Among them, chaos-based encryption, which was first explored by Matthews in [3], is considered as one of the most excellent encryption methods in consequence of the good property of chaos, such as high sensitivity to initial value conditions, state ergodicity and nonconvergence [4,5,6]. Based on these advantages, some more complex encryption schemes consisting of chaos and other ways, such as information entropy [7], mixed linear–nonlinear coupled map lattice [8], a pseudo-random numbers generator [9] or the genetic algorithm [10] have been investigated. However, the control parameters for permutation in above-mentioned algorithms are all fixed and the key extracted from the chaotic signals depends only on the keys, which degrade the performance of the cryptosystems.
To deal with these drawbacks, in recent years, the spatiotemporal chaos-based encryption problems have been studied, due to the fact that they can pose many excellent properties, such as a large parameter space and a random-like sequence, thereby increasing the algorithm complexity and enhancing the security. For example, in [11], a spatiotemporal chaotic cryptosystem was developed by utilizing the impulsive synchronization of reaction–diffusion systems. Based on the permutation–diffusion architecture, more sensitive chaotic image encryption schemes were proposed in [12,13]. Considering that spatiotemporal chaos is often created by local nonlinearity dynamics and spatial diffusion governed by coupled map lattices (CML), the chaos-based multiple image encryption algorithms by using CML were developed in [14,15]. For more spatiotemporal chaos-based cryptosystems, we refer the reader to [16,17] via the cellular automata, to [18] by using the generalized heat equation associated with GVTSG, or to [19] based on the DNA operation.
It is worth noting that the last decade has witnessed a significant development in the study of fractional-order chaos-based image encryption strategies [20,21,22]. Due to the introduction of the fractional-order derivatives, fractional-order chaotic systems provide additional degrees of the freedom in optimization performance, hence exhibiting more complex characteristics and having a unique advantage in the secret key space extension [23]. These make the corresponding image encryption scheme more efficient, secure and reliable.
Further, nowadays, studies indicate that the canonical diffusion systems may be inadequate to describe those anomalous subdiffusion processes observed in a spatially inhomogeneous environment, such as reheating processes of the heterogeneous metal slabs [24,25] or the spread of contaminants in underground water [26]. To improve the modeling precision of these extremely complex transport processes, the authors in [27,28,29,30,31,32] have proven that time-fractional diffusion system with a time-fractional derivative of order can be regarded as a powerful alternative model. Most importantly, we see that the time-fractional diffusion system can recover the traditional diffusion system if the order [33,34]. Therefore, studies on proposing a novel spatiotemporal image encryption algorithm by integrating time-fractional diffusion system into the fractional-order chaos based image encryption should be both challenging and necessary.
Motivated by the above consideration, this paper aims to come up with a novel image encryption algorithm that is proposed by combining the fractional-order Chua’s system and the time-fractional diffusion systems of order . The reasons why we take the fractional-order Chua’s system into consideration are that (1) it is a well-known chaotic system, which generates three chaotic sequences; (2) the fractional-order Chua’s system is more simply than fractional-order Lorenz system because it requires only one nonlinear function of one variable, whereas the fractional-order Lorenz system requires two nonlinear functions of two variables; (3) most standard routes to chaos from the fractional-order Lorenz equation can be produced by the fractional-order Chua’s systems; (4) there exist some theoretical results for Chua’s system, which are absent for the Lorenz system [35]. More precisely, we first obtain the numerical solution of the fractional-order Chua’s system. Secondly, we present a novel spatiotemporal chaotic scheme by designing the chaotic sequence of fractional-order Chua’s system as the initial condition and the boundary conditions of the time-fractional diffusion system under consideration. It is revealed that the proposed image encryption algorithm, which has the properties of larger secret key space, higher sensitivity to initial boundary conditions, better random-like sequence and faster encryption speed, can gain excellent encryption performance in cryptography. To the best of our knowledge, no result is available on the topic that proposes a image encryption algorithm by integrating the time-fractional diffusion processes for fractional-order Chua’s system, which inspires this paper.
The structure of this paper is as follows. In Section 2, we provide some basic results to be used thereafter. Section 3 is devoted to giving the detailed image encryption algorithm. For the illustration, we perform a computer experiment in Section 4. The security analysis, including the histogram analysis, information entropy, adjacent pixel correlation and differential attack analysis to illustrate our results, are finally presented in Section 5.
2. Preliminaries
In this section, we aim to give some preliminary results to be used thereafter.
2.1. Fractional-Order Chua’s System
Let us consider the three-dimensional fractional-order Chua’s chaotic system [36] of the following form:
where is the state vector, is the parameter vector,
is the nonlinear function and , are two system parameters. Here, , , denote the order of the Caputo fractional-order derivative, is the Caputo time-fractional derivative given by [33]:
and represents the Riemann–Liouville fractional integral.
To illustrate the chaos property of above system (1), set , , , , , , and , we depict the evolution of the solution for fractional-order Chua’s system (1) in Figure 1.
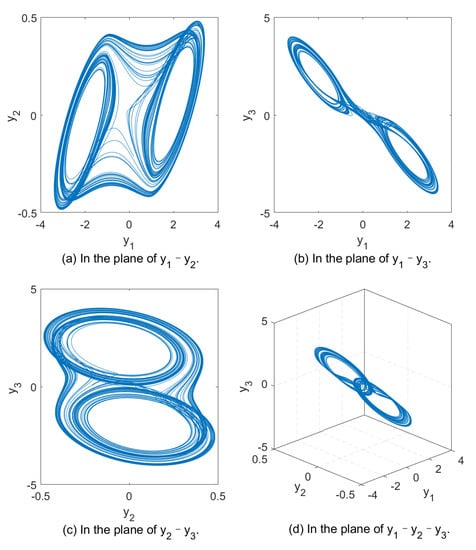
Figure 1.
Evolution of the chaotic and its projections.
2.2. Time-Fractional Diffusion System
Throughout this paper, we consider the following time fractional diffusion equation:
where denotes the system state, is a constant, K is the diffusion coefficient, V represents the reaction coefficient and are four constants. Moreover, , is the Caputo time-fractional derivative with respect to t defined as [33]:
and , are three given functions. Here, and are, respectively, the usual Hilbert spaces with the norms induced by corresponding inner products.
For the regularity results of this system (4), based on the eigenvalue theory of operator under the Robin boundary condition and the semigroup theory, we refer the reader to [37,38], where the detailed solution expression of time-fractional diffusion systems and its regularity results are obtained. Further, according to the high order approximation method on Caputo time-fractional derivative in [39], set
we extend to simulate above time-fractional diffusion system (4) and then have the Figure 2.
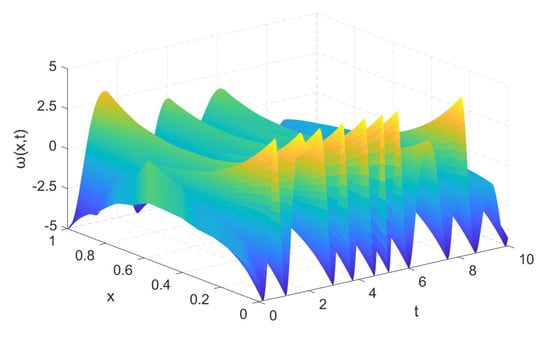
Figure 2.
The behaviors of time-fractional diffusion system (4).
Remark 1.
It is worth mentioning that the reason why we use the Caputo fractional-order derivative in both the fractional-order Chua’s system and time-fractional diffusion system, but not the Riemann–Liouville or the Grunwald–Letnikov formula is because of the physical significance of their initial conditions. We claim that it is okay to study the considered problems with the Riemann–Liouville or the Grunwald–Letnikov fractional-order derivatives in a mathematical sense.
3. Algorithm Description
This section aims to perform a detailed description of the proposed image cryptosystem.
By Figure 3, the proposed spatiotemporal chaos-based cryptosystem for digital images consists of the following three parts: key stream generation, image scrambling and image diffusion.
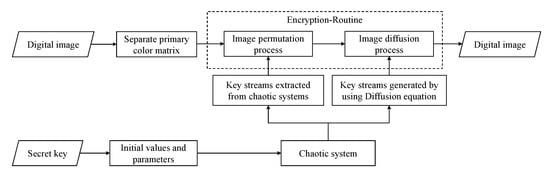
Figure 3.
Block diagram of the proposed image encryption algorithm.
- Part 1. Key stream generation: divide the three chaotic sequences generated by iterative chaotic system into nine sub-sequences;
- Part 2. Image scrambling: use six of the nine sub-sequences to respectively scramble the RGB primary color components of the image; design the other three sub-sequences as the initial-boundary conditions for studied time-fractional diffusion system;
- Part 3. Image diffusion: utilize the new sequence obtained by numerically solving the time-fractional diffusion system under consideration to diffuse the pixel values of scrambled image, thereby obtaining the encrypted image.
3.1. Sequence Generation and Processing
(1) Solve fractional-order Chua’s system (1) with given initial values , , to obtain the three chaotic sequences. This is , where denotes the number of iterations, , and M, N are two constants determined by the size of the image.
(2) To enhance the dependence of chaotic sequence on initial values and to avoid transient effects, we discard the first values of the chaotic sequence and have a new chaotic sequence as follows:
After these, we separate the new chaotic sequence into nine parts, according to the rules contained in Table 1.

Table 1.
The sub-sequences of three chaotic sequences.
(3) Let the sequence of Lside, Rside and Wside be the initial boundary conditions of the time-fractional diffusion system (4). More precisely, we rewrite the initial condition and the boundary conditions of the time-fractional diffusion system (4) as follows
where Lside, Rside, Wside.
(4) By extending the numerical method in [39], we here numerically solve the time-fractional diffusion system (4) and obtain a sequence W of size . Notice that each pixel value of the image is usually an integer number ranging from 0 to 255, while the obtained sequence W is a real matrix. The following optimization procedure is needed:
where denotes the absolute value of x, floor represents the maximum integer that is not greater than x, mod means x mod y and is an integer.
(5) Splitting the optimized sequence into three matrices , and with the size of , one has the following:
3.2. Specific Encryption Process
Suppose that M and N are, respectively, the width and height of the original digital image . The detailed encryption process is given as follows.
Step 1. Separate the three primary color matrices of R, G and B of image . We have the following:
Step 2. Sort the six sequences of , , , , and in ascending order of numerical value respectively to obtain new array sequences. After this, we replace the value of the new array sequences with the position index of the original sequence and then, have six new array sequences: , , , , and .
Step 3. Use the above six scrambled array sequences , , , , and to scramble the rows and columns of the primary color matrix , and , respectively, to obtain , and . Then, we transform the matrices , and and the matrices of primary color , and into the one-dimensional array of , and and primary color component arrays of , and in size of .
Step 4. Utilize the one-dimensional arrays , and to perform the ciphertext diffusion operation on the scrambled image . The details are as follows:
- S4-1 Process the first pixel values of the primary color component arrays , , and as the following:Here, ⊕ denotes the bitwise XOR operator, and , , are three arrays that have been diffused.
- S4-2 Encrypt the element value of each primary color component array according to the formula as follows:
- S4-3 Check i; if , go to step S4-2. Otherwise, stop the loop and go to Step 5.
Step 5. A second round of ciphertext diffusion is conducted on , and . The specific processes are:
- S5-1 Conduct the process on the primary color component arrays , and according to the following formula and obtain , , following:S5-2 Encrypt the element value of each primary color component array as follows:
- S5-3 Check j; if , go to process S5-2. Otherwise, stop the loop and then, complete the second round of ciphertext diffusion.
Step 6. Transform the three encrypted array , and with length into three matrices with size , named , , . Finally, we use , and to obtain the final ciphertext image C by:
It is worth pointing out that the encryption algorithm designed in this paper belongs to a symmetric cryptographic system and the original image can be decrypted by using the reverse encryption process.
4. Simulation Results
To illustrate the performance of proposed encryption strategy, we select the Lena digital image with a size of and use the Matlab 9.4 programming platform. The parameters of the fractional-order chaotic system are , , , , , , , and and the initial values read as , , and . The coefficient and fractional order of the time-fractional diffusion system are:
Following the encryption steps presented in Section 3.2, we show the effect of using proposed image encryption algorithm to encrypt the plaintext Lena image in Figure 4. Based on this, one can find that the encrypted image is messy and is impossible to distinguish any plaintext information. Most importantly, the original plaintext image can be decrypted accurately by using the correct key. Therefore, we conclude that the proposed image encryption algorithm is secure, efficient and reliable.

Figure 4.
Experimental results for Lena image. (a) Original image of Lena, (b) encrypted image of Lena, (c) decrypted image of Lena.
5. The Security Analysis
In this section, several security analyses, such as key analysis, statistical analysis and information entropy analysis are performed to illustrate the quality of our proposed image encryption algorithm.
5.1. Key Analysis
As stated in [40], the key space of the encryption algorithm should not be smaller than to ensure the security of the encryption algorithm. In our algorithm, the keys are divided into four parts: the initial values , , , the orders , , of the fractional-order Chua’s chaotic system, the coefficients K, V and the order in time-fractional diffusion system. Since the accuracy of the computer is and key space of the algorithm is , it is sufficient to resist exhaustive attack.
Moreover, an efficient encryption scheme must also be sensitive to the keys. To illustrate this, suppose the two key values are changed separately: and . By Figure 5, it implies that our proposed algorithm has a strong key sensitivity.

Figure 5.
Key sensitive test. (a) Decrypted image with original key, (b) decrypted image with , (c) decrypted image with .
5.2. Histogram Analysis
A histogram is mainly used to count the frequency of each pixel, which is an important feature of image analysis [41]. An image histogram reflects the statistical characteristics of the image, so a standard to measure the encryption effect is to make the histogram distribution of the ciphertext image as uniform as possible. To this end, we refer the reader to Figure 6, where the histogram of the plaintext image and the ciphertext image are displayed. We take into account that the pixel values of the ciphertext image on the three primary color matrices of R, G and B are more distributed than the plaintext image. Then, we obtain that the encryption algorithm proposed in this paper has a strong ability to resist statistical attacks.
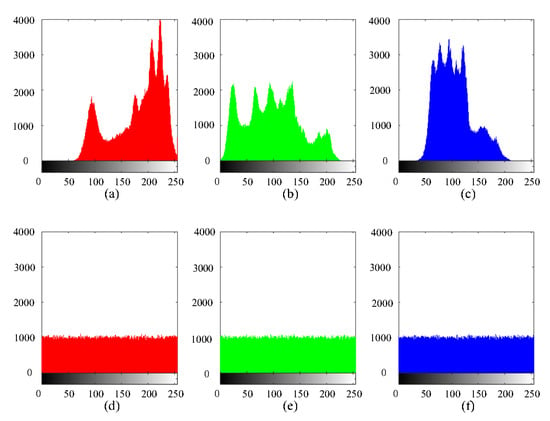
Figure 6.
Histograms of plaintext images ((a) red, (b) green, and (c) blue components) and ciphertext images ((d) red, (e) green, and (f) blue components).
5.3. Correlation Analysis
Notice that the correlation of adjacent pixels reflects the correlation degree of pixel values of adjacent positions in the image and a good image encryption algorithm can make adjacent pixels reach zero correlation as far as possible. More precisely, we see that the correlation of adjacent pixel points can be computed with the following formula:
where is the correlation coefficient, x and y represent pixel values, respectively, is the covariance of x and y, is the mean value of x, is the variance of x, and N is the total number of pixels selected from the image.
To this end, we randomly select 15,000 pairs of adjacent pixels from original images and encrypted image to test horizontal, vertical, and diagonal correlations and obtain Figure 7, which shows that high correlation between adjacent pixels of a plaintext image no longer exists in a ciphertext image. For more detailed values of correlation between the three color components of a plaintext image and ciphertext image in horizontal, vertical and diagonal directions, we refer the reader to Table 2. In addition, we perform a detailed comparison of correlation coefficients in horizontal, vertical and diagonal direction for several different image encryption algorithms in Table 3, which yields that the image encryption algorithm designed in this paper is more efficient and reliable.
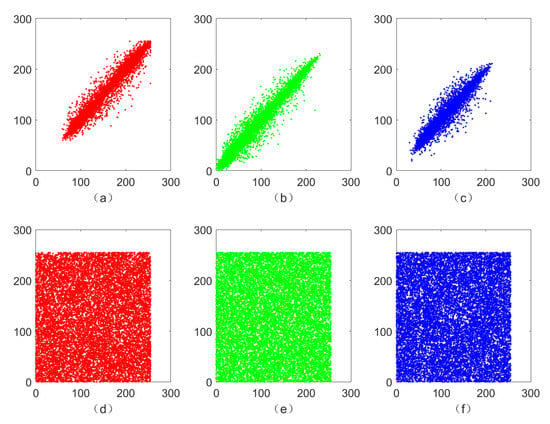
Figure 7.
Correlation of adjacent pixels in vertical direction in plaintext images ((a) red, (b) green, and (c) blue components) and ciphertext images ((d) red, (e) green, and (f) blue components).

Table 2.
The correlation coefficient of adjacent pixels.

Table 3.
Comparison of correlation coefficients for different encryptions.
5.4. Information Entropy Analysis
Image information entropy is an important indicator to measure the randomness of information in information theory. The distribution of image pixel values can be measured by information entropy as follows:
where s denotes the information source, N represents the bit number of the symbol, and is the probability that the symbol appears. For a 256-level grayscale image, each pixel has possible values, and the ideal information entropy is 8. In fact, the information source difficulty generates completely random information. Therefore, the entropy of information is usually lower than the ideal value and a good cryptographic system’s information entropy should be as close to the ideal value as possible.
According to Formula (22), we obtain that the information entropy values of the ciphertext image on the three color matrices of R, G and B are 7.9993, 7.9993 and 7.9992, which are very close to the ideal expectations 8. Moreover, we refer the reader to Table 4 for more comparisons of information entropy values between the proposed algorithm and other algorithms.

Table 4.
Comparison of ciphertext image information entropy for different encryptions.
5.5. Differential Attack Analysis
In general, the number of pixels change rate (NPCR) or the unified average changing intensity (UACI) are used to measure the encryption algorithm’s ability to resist differential attacks. So, if a slight change is made to the plaintext pixel value, a large change in the encrypted pixel value happens. This means that the encryption scheme is good. Consider that NPCR and UACI are usually given by:
where M and N are the number of rows and columns of the image matrix, respectively, and represent the pixels value of the ciphertext images at the coordinate when only one pixel value is different between two plaintext images, respectively.
As a illustration, for digital images with pixels, the expected values of and are and , respectively. For this purpose, we refer the reader to Table 5, which the average values of and obtained for different algorithms to encrypt Lena plaintext images are presented. Taking into account that the and encryptions based on the proposed algorithm exceed 99.96% and 36.36%, respectively, we conclude that the proposed encryption algorithm is very sensitive to small changes in the plaintext image and then, has a stronger ability to carry a differential attack.

Table 5.
Comparison of differential attack analysis for different encryptions.
5.6. Speed Performance Analysis
For an encryption algorithm, the speed of the algorithm directly affects its performance, especially in the era of the rapid development of the internet. To perform the comparisons, we validate the proposed image encryption algorithm by using Matlab 9.4. The Lena plaintext image with size 256 × 256 is tested in a personal computer with a Microsoft Windows 10 64-bit operating system, Intel Core i7-7700 CPU @3.60 GHz and 8.00 GB memory. As depicted in Table 6, it is shown that the speed of our designed encryption algorithm is faster than many available encryption algorithms.

Table 6.
Comparison of speed performance for different encryptions.
Remark 2.
According to the above security analyses for illustrating the quality of the proposed encryption algorithm, the best orders of the fractional derivative in systems (1) and (4) can be determined by optimizing the penalty function that consists of the correlation coefficient, the information entropy and the numbers of and . For this purpose, however, more constraints on both the studied systems and the encryption algorithms are required. This is beyond the scope of this paper. While interesting, we consider this question in our forthcoming papers.
6. Conclusions
In this paper, fractional-order Chau’s system and time-fractional diffusion system with Caputo fractional derivatives are combined to greatly improve the security, efficiency and reliability of the image encryption algorithm. Simulation results and the detailed security analysis are conducted to illustrate that the image encryption algorithm proposed in this paper can gain excellent encryption performance with the advantages of larger secret key space, higher sensitivity to initial-boundary conditions, better random-like sequence and faster encryption speed. Notice that there exist several different fractional-order systems that can drive into chaos, such as the fractional-order Lorenz system, the fractional-order van der Pol system, and these fractional-order chaotic system with Riemann–Liouville or Grunwald–Letnikov fractional derivatives. Then, investigation on proposing image encryption algorithms by combining different types of fractional-order chaotic systems with more complex nonlinear fractional partial differential equations (PDEs), such as time-fractional diffusion systems with space-time-varying coefficients, space-fractional systems or a hybrid diffusion–propagation system are also of great interest. Here, the considered fractional-order chaotic systems can also be of variable-order, distributed-order or even variable-distributed-order. Furthermore, we see that the problem of determining the optimal value of parameters and orders for fractional derivatives in the considered fractional-order chaotic system and nonlinear fractional-order PDEs, which yield the best encrypt performance, is also worth discussing.
Author Contributions
All authors contributed to this research. F.G. designed the research and wrote the paper. Z.Q. contributed in the numerical simulation and assisted in writing the paper. Y.C. contributed in designing the research and revised the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (Nos. 61907039 and 41801365) and the Fundamental Research Funds for the Central Universities, China University of Geosciences, Wuhan (No. CUGGC05).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Yang, Y.; Pan, Q.; Sun, S.; Xu, P. Novel image encryption based on quantum walks. Sci. Rep. 2015, 5, 1–9. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, J.; Li, J.S.; Pan, Y.Y.; Li, R. Compressive optical image encryption. Sci. Rep. 2015, 5, 10374. [Google Scholar] [CrossRef] [Green Version]
- Matthews, R. On the derivation of a chaotic encryption algorithm. Cryptologia 1989, 13, 29–42. [Google Scholar] [CrossRef]
- Uhl, A.; Pommer, A. Image and Video Encryption: From Digital Rights Management To Secured Personal Communication; Springer Science & Business Media: Boston, MA, USA, 2004. [Google Scholar]
- Abd El-Samie, F.E.; Ahmed, H.E.H.; Elashry, I.F.; Shahieen, M.H.; Faragallah, O.S.; El-Sayed, M.; Alshebeili, S.A. Image Encryption: A Communication Perspective; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Hua, Z.; Zhou, Y.; Huang, H. Cosine-transform-based chaotic system for image encryption. Inf. Sci. 2019, 480, 403–419. [Google Scholar] [CrossRef]
- Ye, G.; Pan, C.; Huang, X.; Zhao, Z.; He, J. A chaotic image encryption algorithm based on information entropy. Int. J. Bifurc. Chaos 2018, 28, 1850010. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, X. A symmetric image encryption algorithm based on mixed linear–nonlinear coupled map lattice. Inf. Sci. 2014, 273, 329–351. [Google Scholar] [CrossRef]
- Sahari, M.L.; Boukemara, I. A pseudo-random numbers generator based on a novel 3D chaotic map with an application to color image encryption. Nonlinear Dyn. 2018, 94, 723–744. [Google Scholar] [CrossRef]
- Kaur, M.; Kumar, V. Beta chaotic map based image encryption using genetic algorithm. Int. J. Bifurc. Chaos 2018, 28, 1850132. [Google Scholar] [CrossRef]
- Chen, W.; Luo, S.; Zheng, W.X. Impulsive synchronization of reaction–diffusion neural networks with mixed delays and its application to image encryption. IEEE Trans. Neural Networks Learn. Syst. 2016, 27, 2696–2710. [Google Scholar] [CrossRef] [PubMed]
- Yin, Q.; Wang, C. A new chaotic image encryption scheme using breadth-first search and dynamic diffusion. Int. J. Bifurc. Chaos 2018, 28, 1850047. [Google Scholar] [CrossRef]
- Cheng, G.; Wang, C.; Chen, H. A novel color image encryption algorithm based on hyperchaotic system and permutation-diffusion architecture. Int. J. Bifurc. Chaos 2019, 29, 1950115. [Google Scholar] [CrossRef]
- Wu, X.; Li, Y.; Kurths, J. A new color image encryption scheme using CML and a fractional-order chaotic system. PLoS ONE 2015, 10, e0119660. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, H.; Wang, X.; Wang, X.; Yan, P. Novel multiple images encryption algorithm using CML system and DNA encoding. IET Image Process. 2019, 14, 518–529. [Google Scholar] [CrossRef]
- Souyah, A.; Faraoun, K.M. An image encryption scheme combining chaos-memory cellular automata and weighted histogram. Nonlinear Dyn. 2016, 86, 639–653. [Google Scholar] [CrossRef]
- Niyat, A.Y.; Moattar, M.H.; Torshiz, M.N. Color image encryption based on hybrid hyper-chaotic system and cellular automata. Opt. Lasers Eng. 2017, 90, 225–237. [Google Scholar] [CrossRef]
- Kumar, M.; Sathish, G.; Alphonse, M.; Lahcen, R.A.M. A new RGB image encryption using generalized heat equation associated with generalized Vigenere-type table over symmetric group. Multimed. Tools Appl. 2019, 78, 28025–28061. [Google Scholar] [CrossRef]
- Kang, X.; Guo, Z. A new color image encryption scheme based on DNA encoding and spatiotemporal chaotic system. Signal Process. Image Commun. 2020, 80, 115670. [Google Scholar]
- Hou, J.; Xi, R.; Liu, P.; Liu, T. The switching fractional order chaotic system and its application to image encryption. IEEE/CAA J. Autom. Sin. 2016, 4, 381–388. [Google Scholar] [CrossRef]
- Wang, X.; Su, Y.; Luo, C.; Wang, C. A novel image encryption algorithm based on fractional order 5D cellular neural network and Fisher-Yates scrambling. PLoS ONE 2020, 15, e0236015. [Google Scholar] [CrossRef]
- Talhaoui, M.Z.; Wang, X. A new fractional one dimensional chaotic map and its application in high-speed image encryption. Inf. Sci. 2021, 550, 13–26. [Google Scholar] [CrossRef]
- Yang, Q.; Chen, D.; Zhao, T.; Chen, Y. Fractional calculus in image processing: A review. Fract. Calc. Appl. Anal. 2016, 19, 1222–1249. [Google Scholar] [CrossRef] [Green Version]
- Ge, F.; Chen, Y. Event-triggered boundary feedback control for networked reaction-subdiffusion processes with input uncertainties. Inf. Sci. 2019, 476, 239–255. [Google Scholar] [CrossRef]
- Ge, F.; Chen, Y. Observer-based event-triggered control for semilinear time-fractional diffusion systems with distributed feedback. Nonlinear Dyn. 2020, 99, 1089–1101. [Google Scholar] [CrossRef]
- Meerschaert, M.M.; Mortensen, J.; Wheatcraft, S.W. Fractional vector calculus for fractional advection—Dispersion. Phys. Stat. Mech. Its Appl. 2006, 367, 181–190. [Google Scholar] [CrossRef]
- Ge, F.; Chen, Y.; Kou, C. Regional Analysis of Time-Fractional Diffusion Processes; Springer: Cham, Switzerland, 2018. [Google Scholar]
- Hilfer, R. Applications of Fractional Calculus in Physics; World Scientific: Lodon, UK, 2000. [Google Scholar]
- Metzler, R.; Klafter, J. The random walk’s guide to anomalous diffusion: A fractional dynamics approach. Phys. Rep. 2000, 339, 1–77. [Google Scholar] [CrossRef]
- Ge, F.; Chen, Y.; Kou, C. Regional controllability analysis of fractional diffusion equations with Riemann–Liouville time fractional derivatives. Automatica 2017, 76, 193–199. [Google Scholar] [CrossRef] [Green Version]
- Ge, F.; Chen, Y. Optimal vaccination and treatment policies for regional approximate controllability of the time-fractional reaction-diffusion SIR epidemic systems. ISA Trans. 2021, 115, 143–152. [Google Scholar] [CrossRef]
- Song, W.; Ge, F.; Chen, Y. Subdiffusive Source Sensing by a Regional Detection Method. Sensors 2019, 19, 3504. [Google Scholar] [CrossRef] [Green Version]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier Science Limited: Lodon, UK, 2006. [Google Scholar]
- Ge, F.; Chen, Y.; Kou, C.; Podlubny, I. On the regional controllability of the sub-diffusion process with Caputo fractional derivative. Fract. Calc. Appl. Anal. 2016, 19, 1262–1281. [Google Scholar] [CrossRef]
- Pivka, L.; Wu, C.W.; Huang, A. Lorenz Equation and Chua’s Equation. Int. J. Bifurc. Chaos 1996, 6, 2443–2489. [Google Scholar] [CrossRef]
- Petráš, I. Fractional-Order Nonlinear Systems: Modeling, Analysis and Simulation; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Ge, F.; Chen, Y. Regional output feedback stabilization of semilinear time-fractional diffusion systems in a parallelepipedon with control constraints. Int. J. Robust Nonlinear Control. 2020, 30, 3639–3652. [Google Scholar] [CrossRef]
- Ge, F.; Chen, Y.; Kou, C. On the regional gradient observability of time fractional diffusion processes. Automatica 2016, 74, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Li, H.; Cao, J.; Li, C. High-order approximation to Caputo derivatives and Caputo-type advection–diffusion equations (III). J. Comput. Appl. Math. 2016, 299, 159–175. [Google Scholar] [CrossRef]
- Stinson, D.R.; Paterson, M. Cryptography: Theory and Practice; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Li, T.; Du, B.; Liang, X. Image Encryption Algorithm Based on Logistic and Two-Dimensional Lorenz. IEEE Access 2020, 8, 13792–13805. [Google Scholar] [CrossRef]
- Ye, G.; Wong, K. An efficient chaotic image encryption algorithm based on a generalized Arnold map. Nonlinear Dyn. 2012, 69, 2079–2087. [Google Scholar] [CrossRef]
- Wen, W.; Wei, K.; Zhang, Y.; Fang, Y.; Li, M. Colour light field image encryption based on DNA sequences and chaotic systems. Nonlinear Dyn. 2020, 99, 1587–1600. [Google Scholar] [CrossRef]
- Wu, X.; Wang, K.; Wang, X.; Kan, H.; Kurths, J. Color image DNA encryption using NCA map-based CML and one-time keys. Signal Process. 2018, 148, 272–287. [Google Scholar] [CrossRef]
- Wang, X.; Su, Y. Color image encryption based on chaotic compressed sensing and two-dimensional fractional Fourier transform. Sci. Rep. 2020, 10, 1–19. [Google Scholar] [CrossRef]
- Alawida, M.; Teh, J.S.; Samsudin, A.; Alshoura, W. An image encryption scheme based on hybridizing digital chaos and finite state machine. Signal Process. 2019, 164, 249–266. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).