Ocular Phantom-Based Feasibility Study of an Early Diagnosis Device for Glaucoma
Abstract
1. Introduction
- Ci is the concentration of this ion (i) in mol/m3;
- Ui is the ion (i) mobility in m²/s.V;
- F is 1 faraday or 96,500 C/mole;
- σ is conductivity in S.m−1 and ρ is resistivity in Ω.m.
- R is resistance (Ω);
- l is the height of the schematic column containing the solution (m);
- S is the surface of the schematic column containing the solution (m²);
- ρ is the resistivity of the liquid inside the column (Ω.m).
- -
- C (xc, yc) (centre of the Cole–Cole circle, r: radius of the Cole–Cole circle);
- -
- Rc, Xc and Fc characteristic data of the curve bend (characteristic resistance, characteristic reactance and characteristic frequency);
- -
- Ri (modelled resistance of the intracellular area in ohms);
- -
- Alpha α (phase angle in degrees at the characteristic frequency);
- -
- Tau τ (ionic relaxation time in µs);where Cm is the cell membrane’s capacitance in Farad, and therefore,
2. Materials and Methods
2.1. Phantoms
- n: number of moles in mole;
- m: sample mass in g;
- M: molar mass in g.mol−1 (i.e., 58.5 g.mol−1 for NaCl).
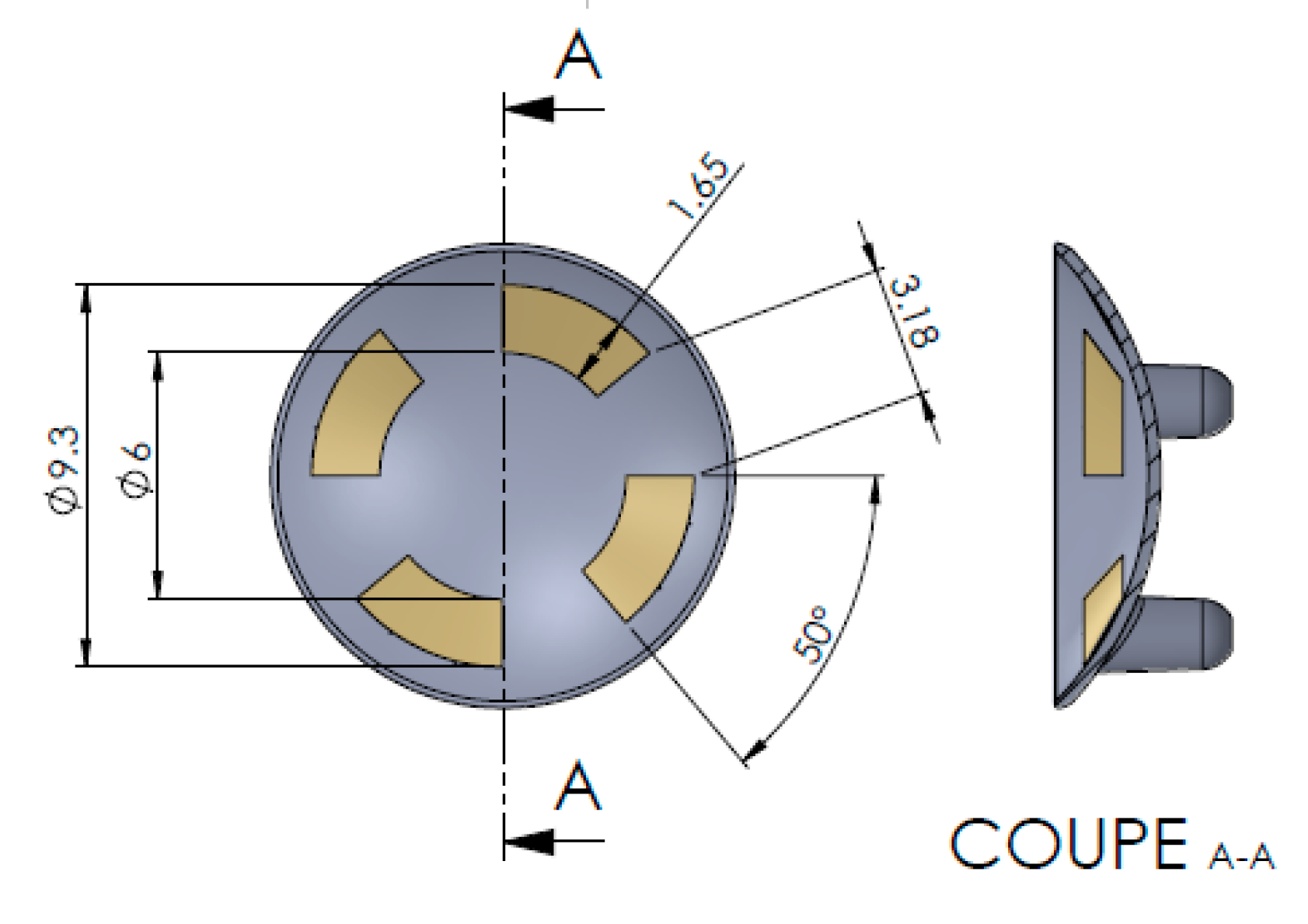
2.2. Materials
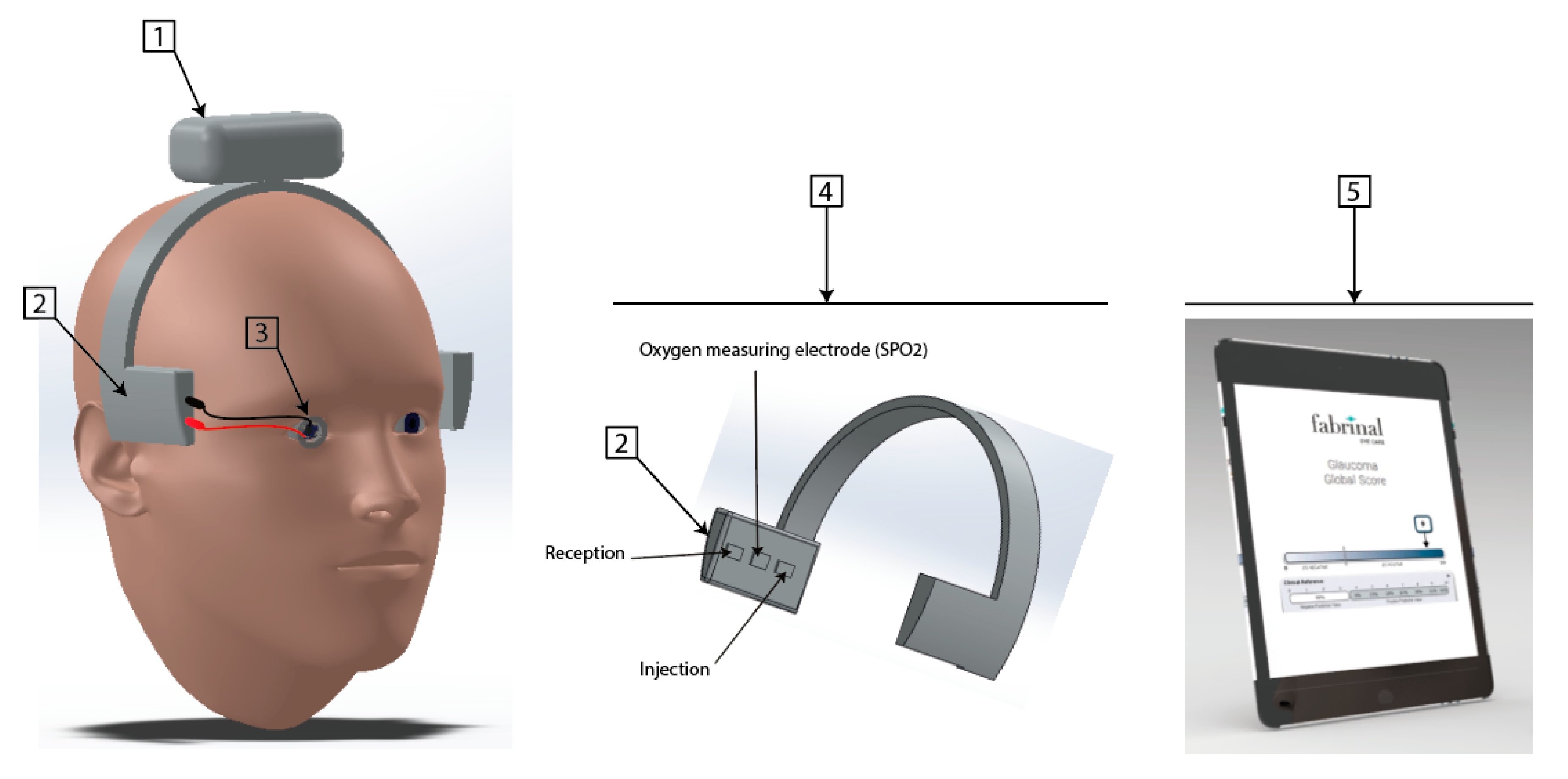
2.3. Final Prototype Description
- An electronic part composed of a battery, Bluetooth Low Energy;
- An electronic part composed of two types of sensors: a PPG (Photo Plethysmo Graph) sensor for SpO2 (oxygen saturation of the blood microcirculation of the ophthalmic artery based on optical analysis, based on three LEDs (536, 660 and 940 nm) and two photodiodes, sample rate 100 Hz, pulse width 115.2 ms) and a bioimpedance sensor analysing both chambers of the eye (anterior and posterior);
- An electrode (lens) allowing the bioimpedance of the anterior chamber when used with the bioimpedance sensors in part 2;
- A system allowing the temporal electrodes to be positioned;
- A user interface, under development, to be finalised with the clinical data.
2.4. The Algorithms
3. Results
3.1. Repeatability of the Phantom Measuring Chain
3.2. Inter-Lens Variability
3.3. Raw Data
3.4. Detection of the Presence of Glaucoma by the System
4. Discussion
5. Conclusions
6. Patents
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jürgens, I.; Rosellz, J.; RIu, P.J. Electrical impedance tomography of the eye: In vitro measurements of the cornea and the lens. Physiol. Meas. 1996, 17, A187–A195. [Google Scholar] [CrossRef] [PubMed]
- Grounauer, P.; Metraux, B. The Somnogen Visual Training: A new CBT to fight Insomnia through closed eyes and fNIRS Neuroimagin. J. Behav. Brain Sci. 2014, 4, 477–481. [Google Scholar] [CrossRef]
- Fukuda, M.; Sasaki, H. In vivo measurement of human corneal impedance value. Cornea J. 2016, 35, 10. [Google Scholar] [CrossRef] [PubMed]
- Bulpitt, C.J.; Hodes, C.; Everitt, M.G. Intraocular pressure and systemic blood pressure in the elderly. Br. J. Ophthalmol. 1975, 59, 717–720. [Google Scholar] [CrossRef]
- Nomura, H.; Ando, F.; Niino, N.; Shimokata, H.; Miyake, Y. The relationship between intraocular pressure and refractive error adjusting for age and central corneal thickness. Ophthalmic Physiol. Opt. 2004, 24, 41–45. [Google Scholar] [CrossRef] [PubMed]
- Ma, Z.; Cao, P.; Sun, P.; Li, L.; Lu, Y.; Yan, Y.; Chen, Y.; Chai, X. Optical imaging of visual cortical responses evoked by transcorneal electrical stimulation with different parameters. Invest. Ophthalmol. Vis. Sci. 2014, 55, 5320–5331. [Google Scholar] [CrossRef][Green Version]
- Bonomi, L.; Marchini, G.; Marraffa, M.; Bernardi, P.; De Franco, I.; Perfetti, S.; Varotto, A.; Tenna, V. Prevalence of glaucoma and intraocular pressure distribution in a defined population. Egna Neumarkt Study 1998, 105, 209–215. [Google Scholar] [CrossRef]
- Moreno, M.-V.; Coux, M.N.; Clarion, A.; Grounauer, P.A. Electrical evolution of aqueous humor with ageing. ICEBI 2016, 112, 16. [Google Scholar]
- Killer, H.E.; Pircher, A. Normal tension glaucoma: Review of current understanding and mechanisms of the pathogenesis. Eye 2018, 32, 924–930. [Google Scholar] [CrossRef]
- Esporcatte, B.L.B.; Tavares, I.M. Normal-tension glaucoma: An update. Arq. Bras. Oftalmol. 2016, 79, 4. [Google Scholar] [CrossRef][Green Version]
- Berdahl, J.P.; Fautsch, P.; Stinnett, S.S.; Allingham, R.R. Intracranial pressure in primary open angle glaucoma, normal tension glaucoma, and ocular hypertension: A case-control study. Investig. Ophthalmol. Vis. Sci. 2008, 49, 5412–5418. [Google Scholar] [CrossRef] [PubMed]
- Dou, Y.; Liu, L.; Cheng, X.; Cao, L.; Zuo, L. Comparison of bioimpedance methods for estimating total body water and intracellular water changes during hemodialysis. Nephrol. Dial. Transpl. 2011, 26, 3319–3324. [Google Scholar] [CrossRef] [PubMed]
- Grimnes, S.; Martisen, O.G. Wiley Encyclopedia of Biomedical Engineering; John Wiley and Sons: Hoboken, NJ, USA, 2006; p. 9. [Google Scholar]
- Kanai, H.; Sakamoto, K.; Haeno, M. Electrical measurement of fluid distribution in human legs: Estimation of extra- and intra-cellular fluid volume. J. Microw. Power 1983, 18, 233–243. [Google Scholar] [CrossRef]
- Meijer, J.H.; De Vries, P.M.; Goovaerts, H.G.; Oe, P.L.; Donker, A.J.; Schneider, H. Measurement of transcellular fluid shift during haemodialysis. Part 1. Method. Med Biol. Eng. Comput. 1989, 27, 147–151. [Google Scholar] [CrossRef] [PubMed]
- Bonnet, S.; Bourgerette, A.; Gharbi, S.; Rubeck, C.; Arkouche, W.; Massot, B.; McAdams, E.; Montalibet, A.; Jallon, P. Wearable impedance monitoring system for dialysis patients. Annu. Int. Conf. IEEE Eng. Med. Biol. Soc. 2016, 2016, 5196–5199. [Google Scholar]
- Roux, E. La Physiologie des Animaux de Laboratoire; UE Expérimentation animale; Université Bordeaux 2: Bordeaux, France, 1985. [Google Scholar]
- Moreno, M.-V.; Herrera, E. Evaluation on Phantoms of the Feasibility of a Smart Bra to Detect Breast Cancer in Young Adults. Sensors 2019, 19, 5491. [Google Scholar] [CrossRef]
- Claudel, J. Spectroscopie d’impédance électrique à micro-électrodes: Application à la cytométrie de flux de cellules sanguines. Ph.D. Thesis, University of Lorraine, Nancy, France, 29 March 2018. [Google Scholar]
- Chimarra, M.K.; Hansen, R.; Marvik, R.; Langot, T. Multimodal Phantom of Liver Tissue. PLoS ONE 2013, 5, 1373–1378. [Google Scholar]
- Kao, T.-J.; Saulnier, G.J.; Isaacson, D.; Szabo, T.-L.; Newell, J.C. A Versatile High-Permittivity Phantom for EIT. Biomed. Eng. IEEE Trans. 2008, 11, 2601–2607. [Google Scholar] [CrossRef]
- Onishi, T.; Uebayashi, S. Biological Tissue-Equivalent Phantoms Usable in Broadband Frequency Range. NTT DoCoMo Tech. J. 2006, 4, 61–65. [Google Scholar]
- Boscus, J. Transfert électro-osmotique en milieu poreux déformable. Application au gel d’agar-agar. Ph.D. Thesis, Université Montpellier, Montpellier, France, 30 June 2005. [Google Scholar]
- Tavernier, P.; Prache, P. Influence de la pression sur la résistivité d’une thermistance. J. Phys. Radium 1952, 13, 423–426. [Google Scholar] [CrossRef]
- Rabbani, K.S.; Sarker, M.; Akond, M.H.R.; Akter, T. Focused Impedance Measurement (FIM): A New Technique with Improved Zone Localization. Ann. N. Y. Acad. Sci. 1999, 873, 408–420. [Google Scholar] [CrossRef] [PubMed]
- Jaffrin, M.; Fenech, M.; Moreno, M.-V.; Kieffer, R. Total body water measurement by a modification of the bioimpedance spectroscopy method. Med Biol. Eng. Comput. 2006, 44, 873–882. [Google Scholar] [CrossRef] [PubMed]
- Moreno, M.-V.; Grounauer, P.-A. Dispositif Médical D’examen Oculaire. Patent FR2005831, 4 June 2020. [Google Scholar]






| ρHealthy (Ω.m) | |
|---|---|
| Saline Solution (NaCl 9g.l−1) | 0.625 |
| Aqueous Humour | 0.60–0.67 |
| Glass Humour | 0.63–0.66 |
| Cornea | 0.39–0.48 |
| Healthy Eye (Yellow Eye) | Glaucomatous Eye (Red Eye) | |
|---|---|---|
| Composition | 4 g/L Agarose 1l Demineralised Water 9 g/L NaCl | 4 g/L Agarose 1l Demineralised Water 10 g/L NaCl |
| “Glaucoma Phantom” | G1 | G2 | G3 | G4 | G5 | G6 | G7 | G8 |
| Zr (ohm) | 149.51 | 177.70 | 147.58 | 162.25 | 150.09 | 158.42 | 162.58 | 181.54 |
| Total Eye Water (mL) | 3.01 | 3.46 | 3.04 | 2.98 | 3.00 | 2.96 | 2.91 | 2.65 |
| “Healthy Phantom” | S1 | S2 | S3 | S4 | S5 | S6 | S7 | S8 |
| Zr (ohm) | 196.53 | 223.31 | 169.16 | 222.63 | 217.71 | 245.11 | 230.84 | 183.20 |
| Total Eye Water (mL) | 2.52 | 2.30 | 2.81 | 2.37 | 2.46 | 2.24 | 2.30 | 2.68 |
| Healthy Phantoms | Glaucoma Phantoms | Mann–Whitney Tests | |
|---|---|---|---|
| Average Zr ± SD (Ohms) | 211.9 ± 36.9 | 160.9 ± 24.3 | p < 0.01 |
| Average Difference ± SD (Ohms, %) | 51.0 − 24.1% (**) | ||
| Average Vt ± SD (ml) | 2.45 ± 0.28 | 3.02 ± 0.35 | p < 0.001 |
| Average Difference ± SD (ml, %) | 0.57 − 22.9 (***) |
| Phantom | Glaucoma Risk Score % |
|---|---|
| G1 | 78.8 |
| G2 | 83.4 |
| G7 | 96 |
| G8 | 100 |
| S2 | 26.5 |
| S3 | 0 |
| S7 | 0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moreno, M.-V.; Houriet, C.; Grounauer, P.-A. Ocular Phantom-Based Feasibility Study of an Early Diagnosis Device for Glaucoma. Sensors 2021, 21, 579. https://doi.org/10.3390/s21020579
Moreno M-V, Houriet C, Grounauer P-A. Ocular Phantom-Based Feasibility Study of an Early Diagnosis Device for Glaucoma. Sensors. 2021; 21(2):579. https://doi.org/10.3390/s21020579
Chicago/Turabian StyleMoreno, Marie-Valérie, Cloé Houriet, and Pierre-Alain Grounauer. 2021. "Ocular Phantom-Based Feasibility Study of an Early Diagnosis Device for Glaucoma" Sensors 21, no. 2: 579. https://doi.org/10.3390/s21020579
APA StyleMoreno, M.-V., Houriet, C., & Grounauer, P.-A. (2021). Ocular Phantom-Based Feasibility Study of an Early Diagnosis Device for Glaucoma. Sensors, 21(2), 579. https://doi.org/10.3390/s21020579





