Towards Providing Effective Data-Driven Responses to Predict the Covid-19 in São Paulo and Brazil
Abstract
1. Introduction
- The implementation of urgent responses, as listed below, to mitigate the progress of coronavirus in São Paulo state, which is the most populous and economically active state in Brazil, responsible for of the Brazilian GDP [35].
- A novel forecasting model that combines the simplicity of SIR-based formulation with the effectiveness of data-driven learning strategies for predicting Covid-19 cases, deaths, recoveries and the virus reproduction number. The designed method is also capable of addressing “the curse of delay”, as usually observed in the Brazilian reports of cases and deaths, determining whether or not a coronavirus-related time-series period is “well-posed”.
- Our predictive approach learns the epidemiological parameters as time-dependent functions, which are calibrated by a recursive training approach based on an Artificial Neural Network, therefore allowing the forecaster to fit and customize Covid-19 curves for each region of the state.
- The availability of a comprehensive Covid-19 data repository and a freely available online platform, which has been accessed by citizens, authorities and media agencies to track and inspect the Covid-19 progress in São Paulo state. New Covid-19 notifications are immediately available throughout the platform, by getting fresh data published daily by 92 city halls spread over the state (the so-called first-hand local sources), in an attempt to reduce the delay in reporting the new cases and deaths as often observed in the Brazilian government updates [36,37].
2. Materials and Methods
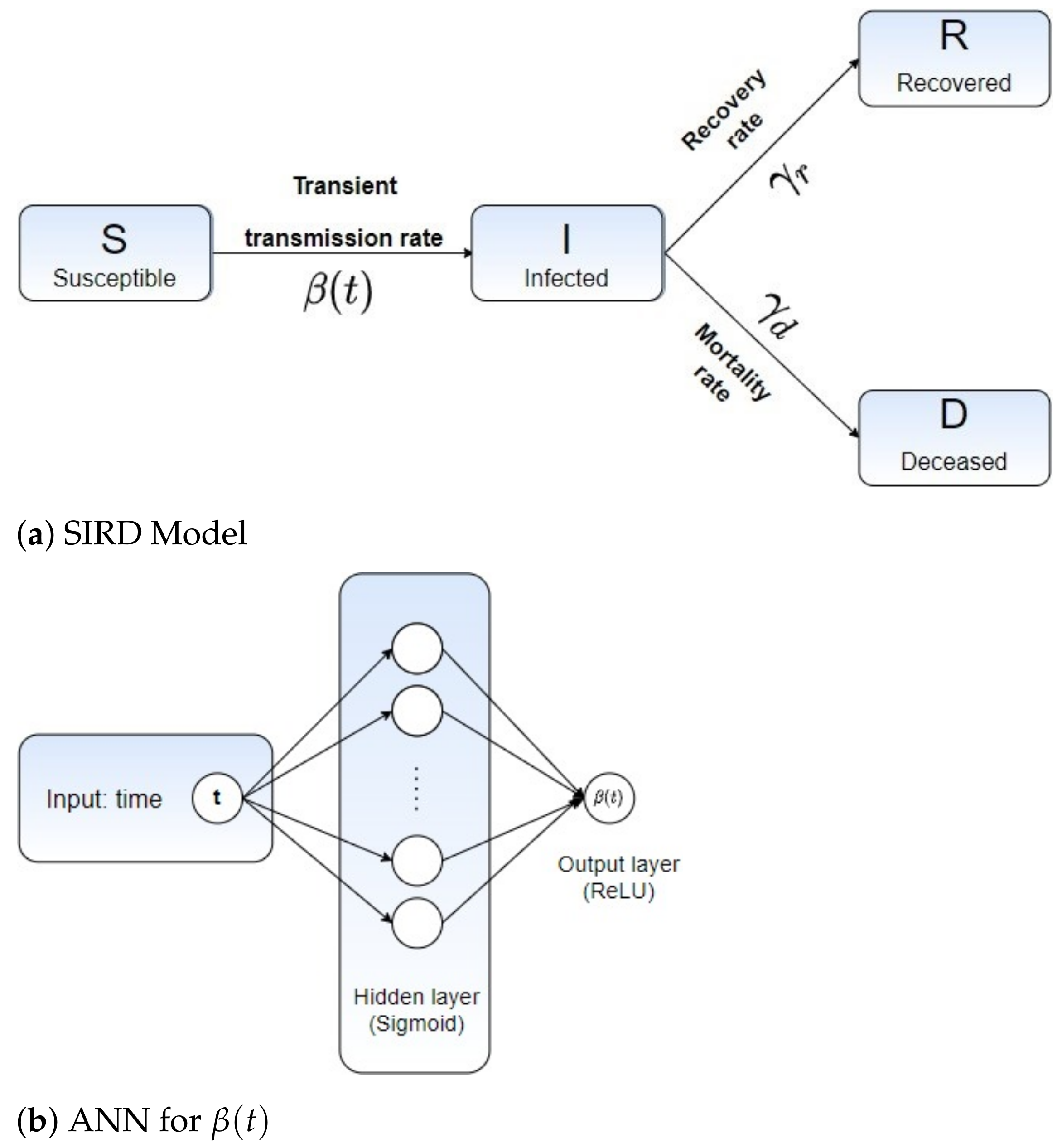
2.1. Mathematical Modeling: A Time-Dependent SIR-Based Model
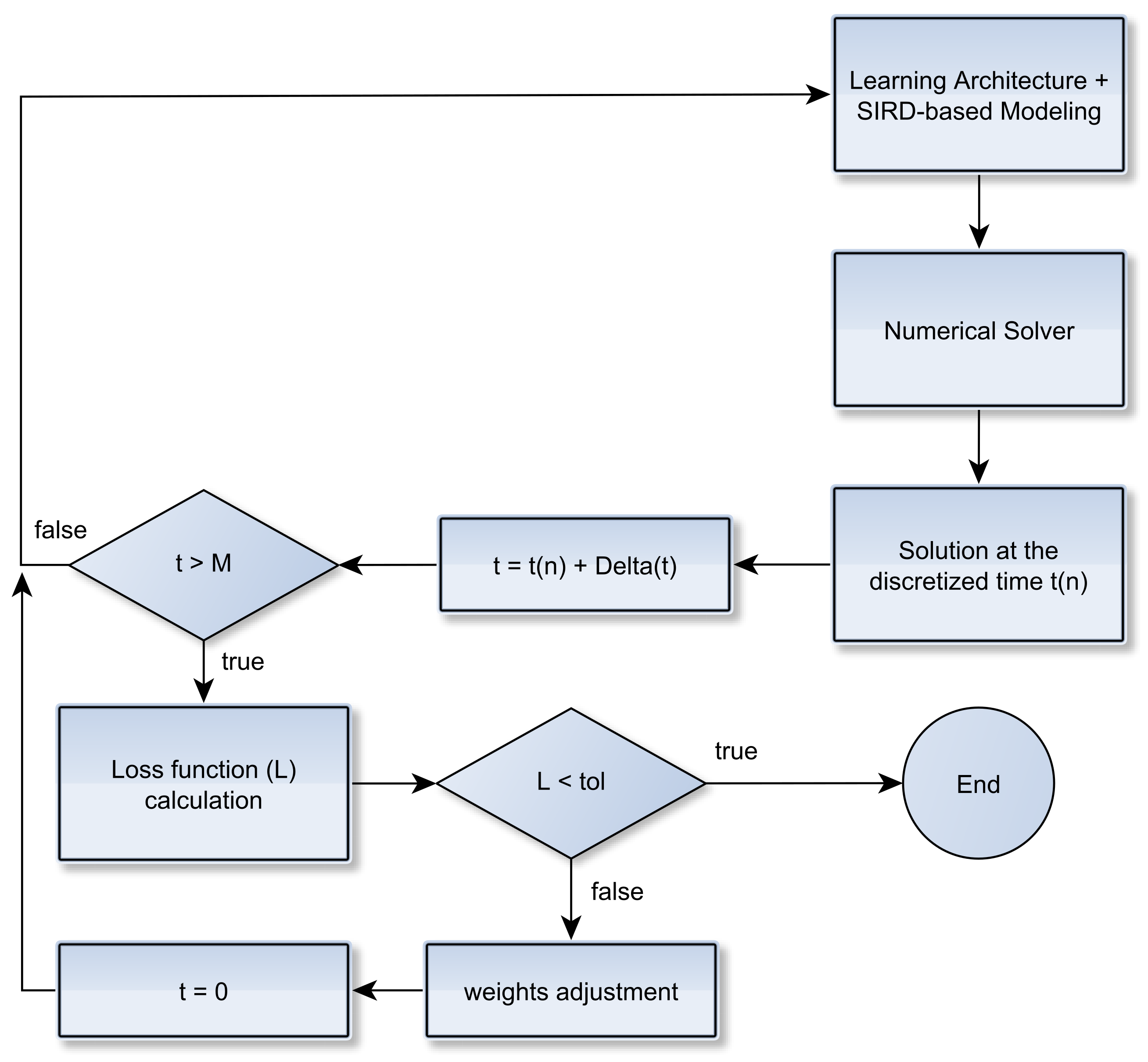
2.2. Learning Epidemiological Parameters: An Integrated Data-Driven Approach
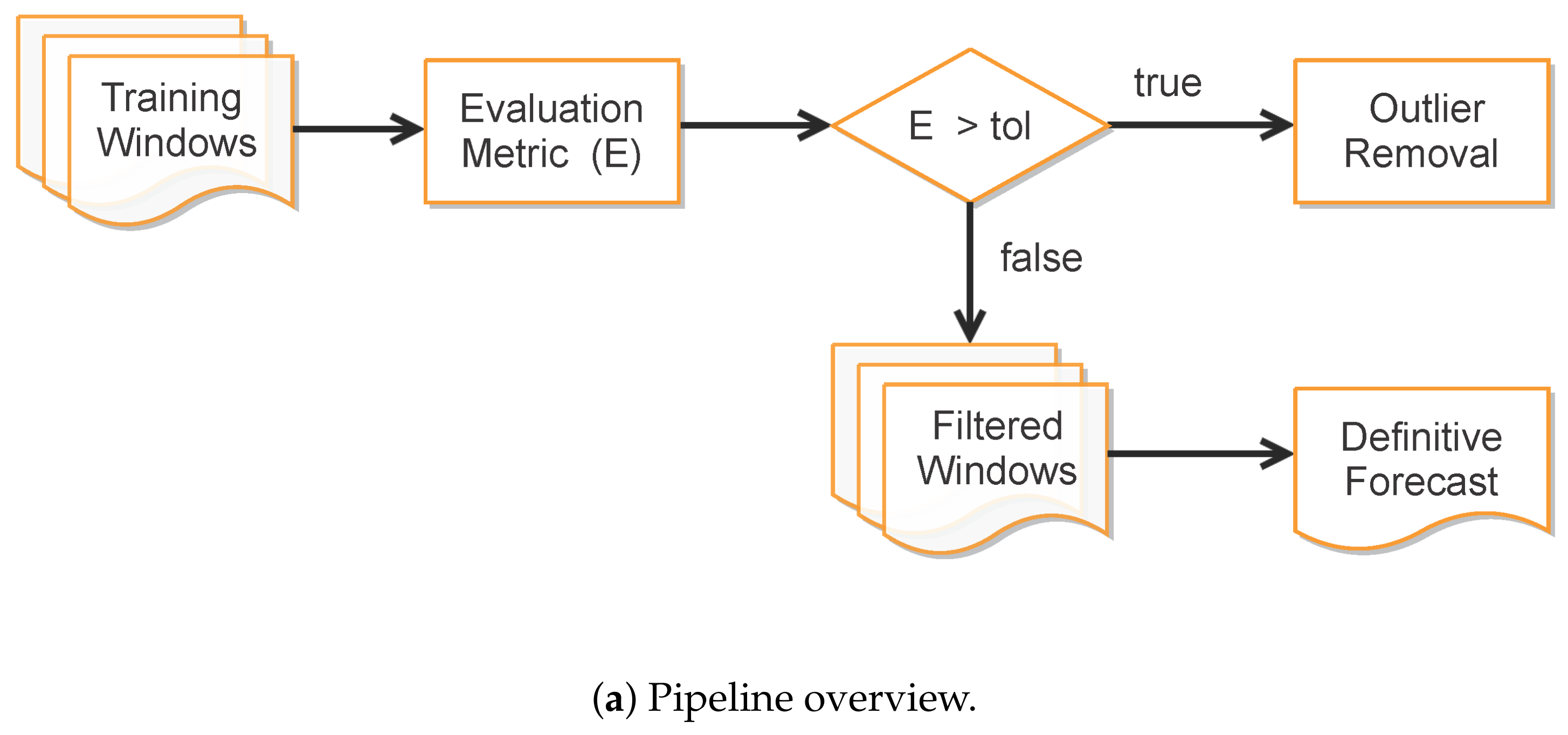
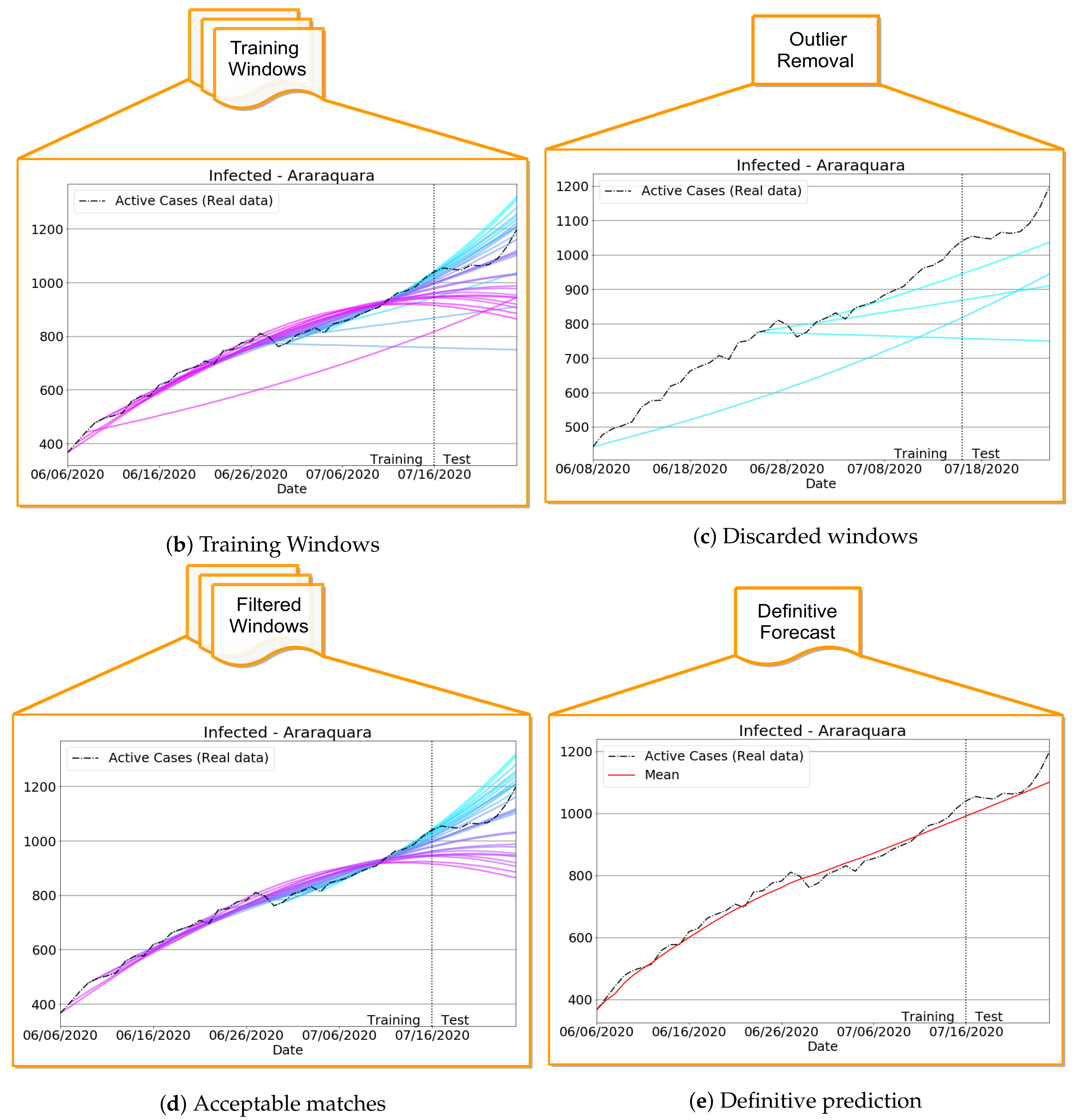
Improving Data Fitting Robustness and Accuracy
- 1.
- Compute training outputs for several time windows by repeatedly solving the ODE-SIRD system (2) for , where days, calibrating the net weights, bias, and parameters and for different simulation intervals.
- 2.
- Once the set of epidemiological curves is obtained, we compute the Mean Absolute Percentage Error (MAPE) (9), taken here as an error assessment metric, to decide whether or not a subset of from is classified as “outlier”, i.e., a badly conditioned time-series period whose epidemiological variables , , and highly diverge from other periods. In our tests, we discard the ill-behaved ’s whose MAPE errors are greater than for any of the variables , or .
- 3.
- Finally, the remaining trained curves are used to compute the definitive forecasts using the numerical solution of the SIRD system for , where p is the desirable forecast period. This is performed so as to balance the well-behaved contributions in the set of ODE solutions , taking the mean of these outputs to determine , , and .
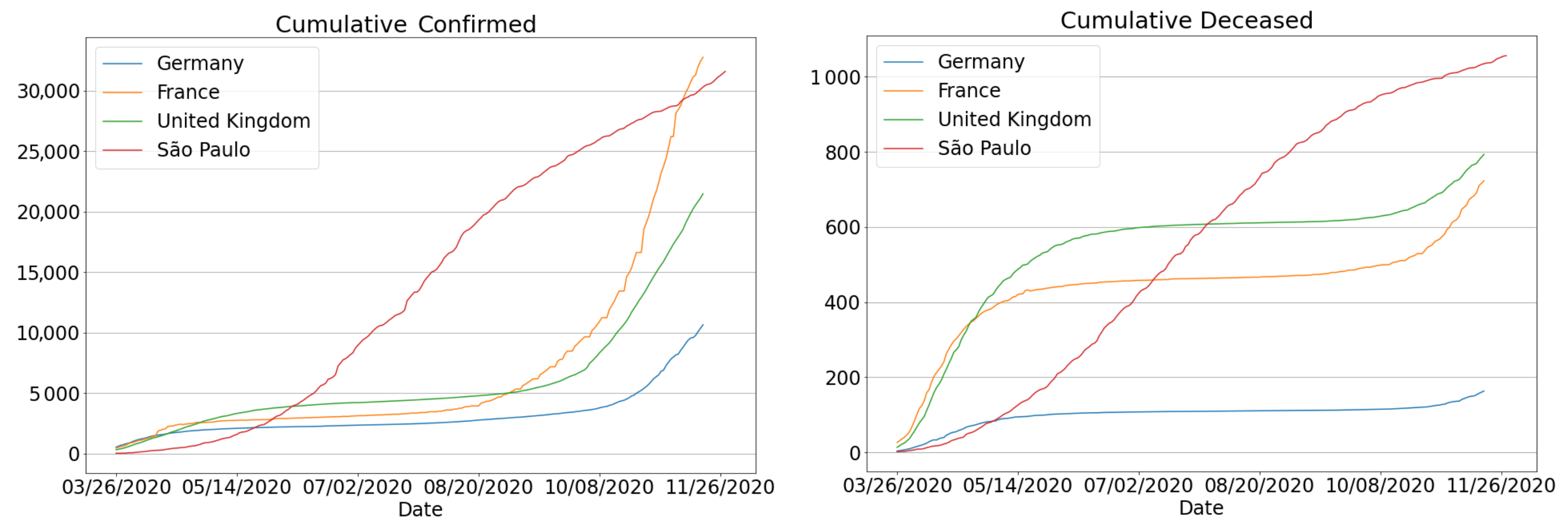
3. Results and Discussion
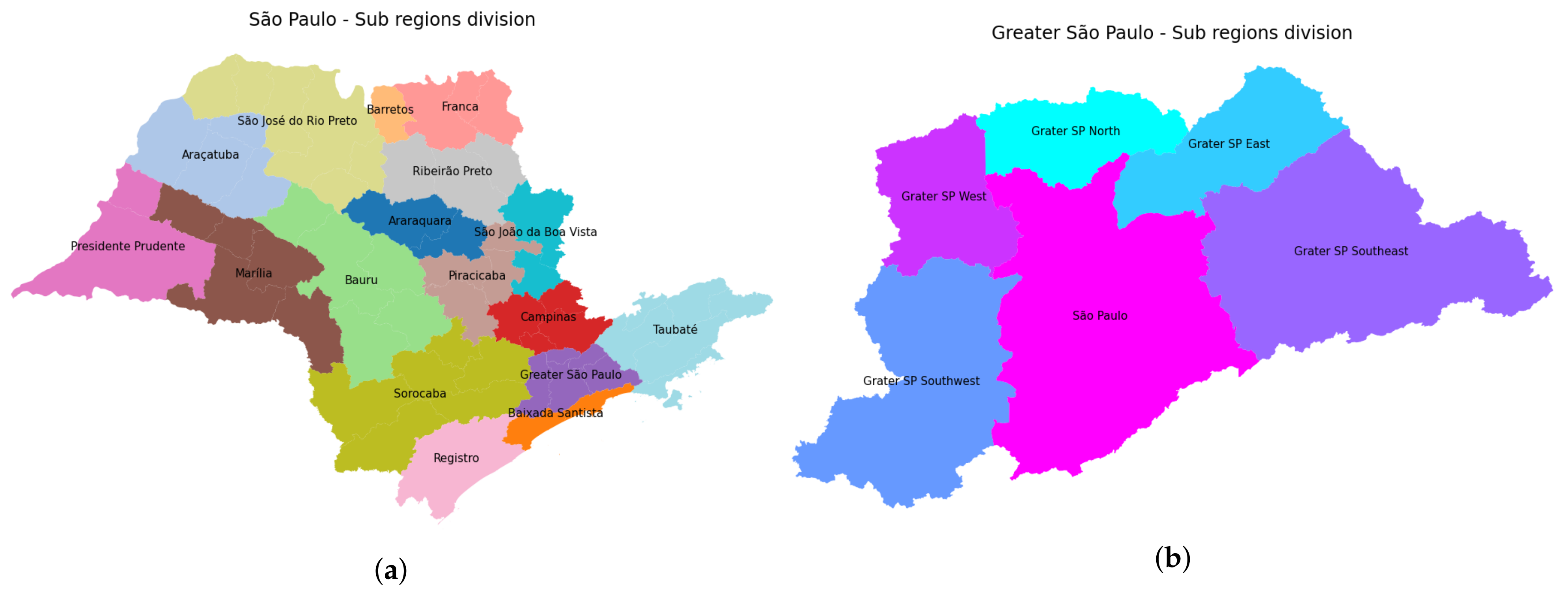
3.1. Data Organization
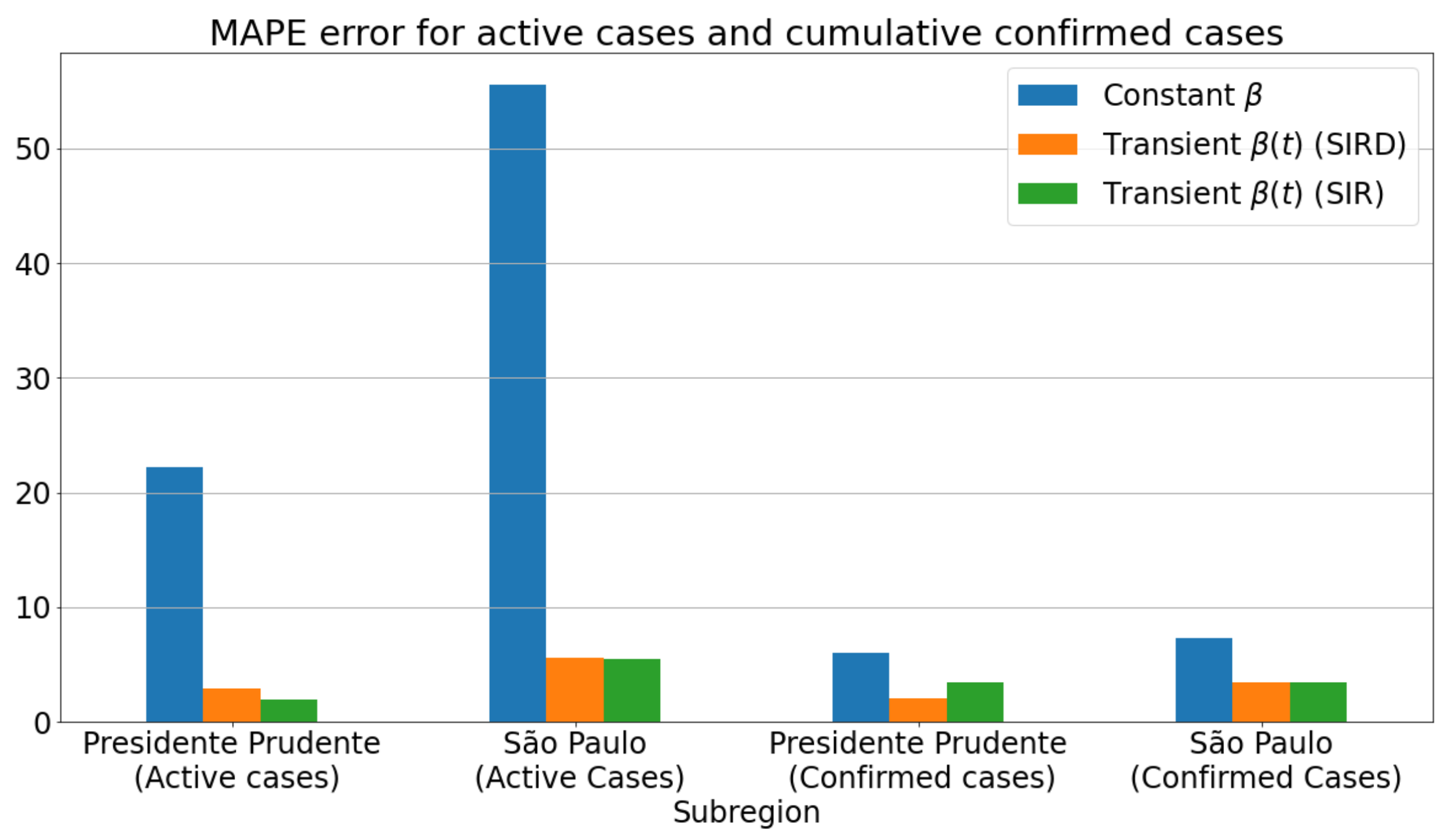
3.2. Metrics
3.3. The Proposed Forecasting Approach: Main Features and General Capabilities
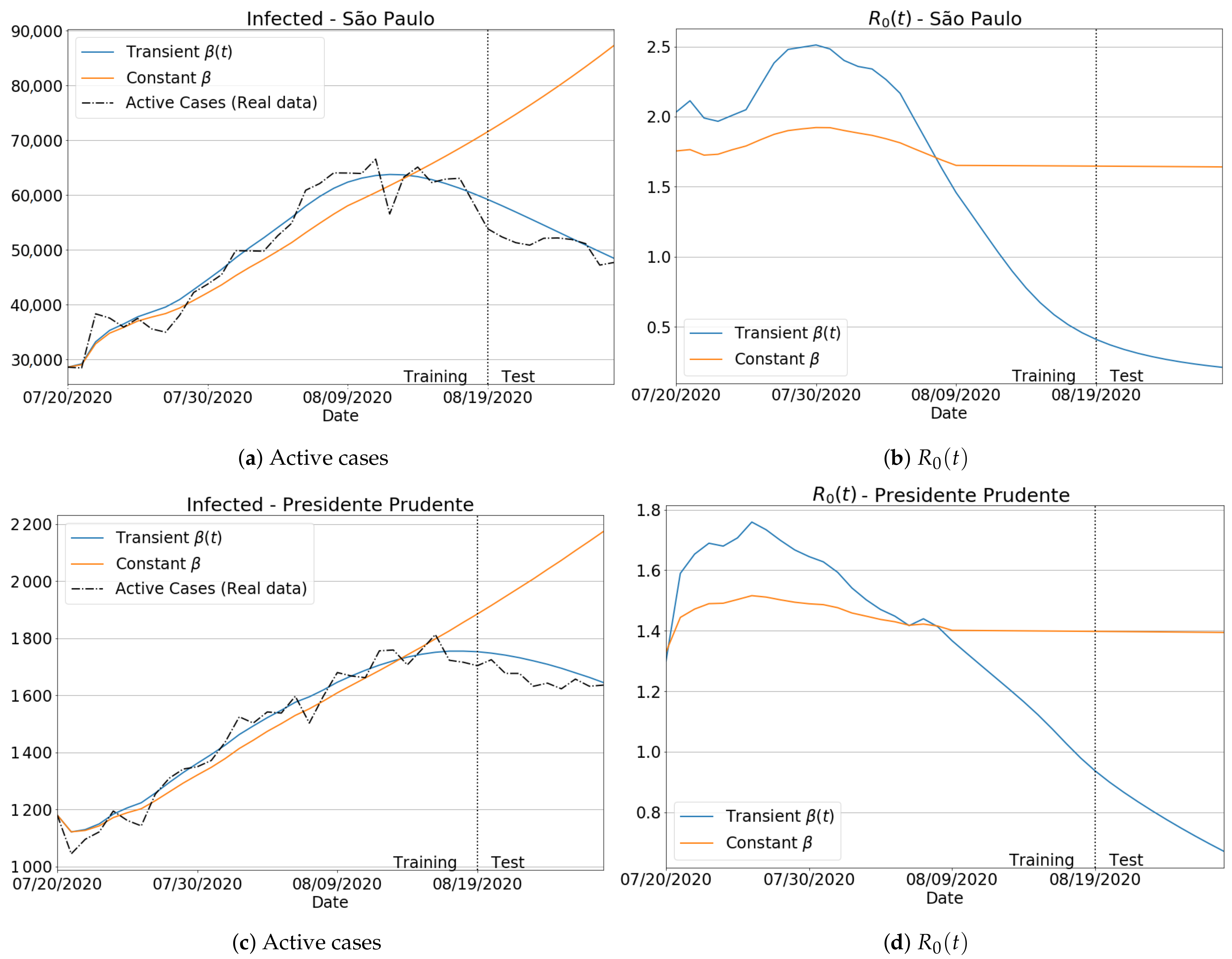
3.3.1. Badly Conditioned Samples × Data Fitting Robustness and Accuracy
3.3.2. The Transient Behavior of Transmission Rate
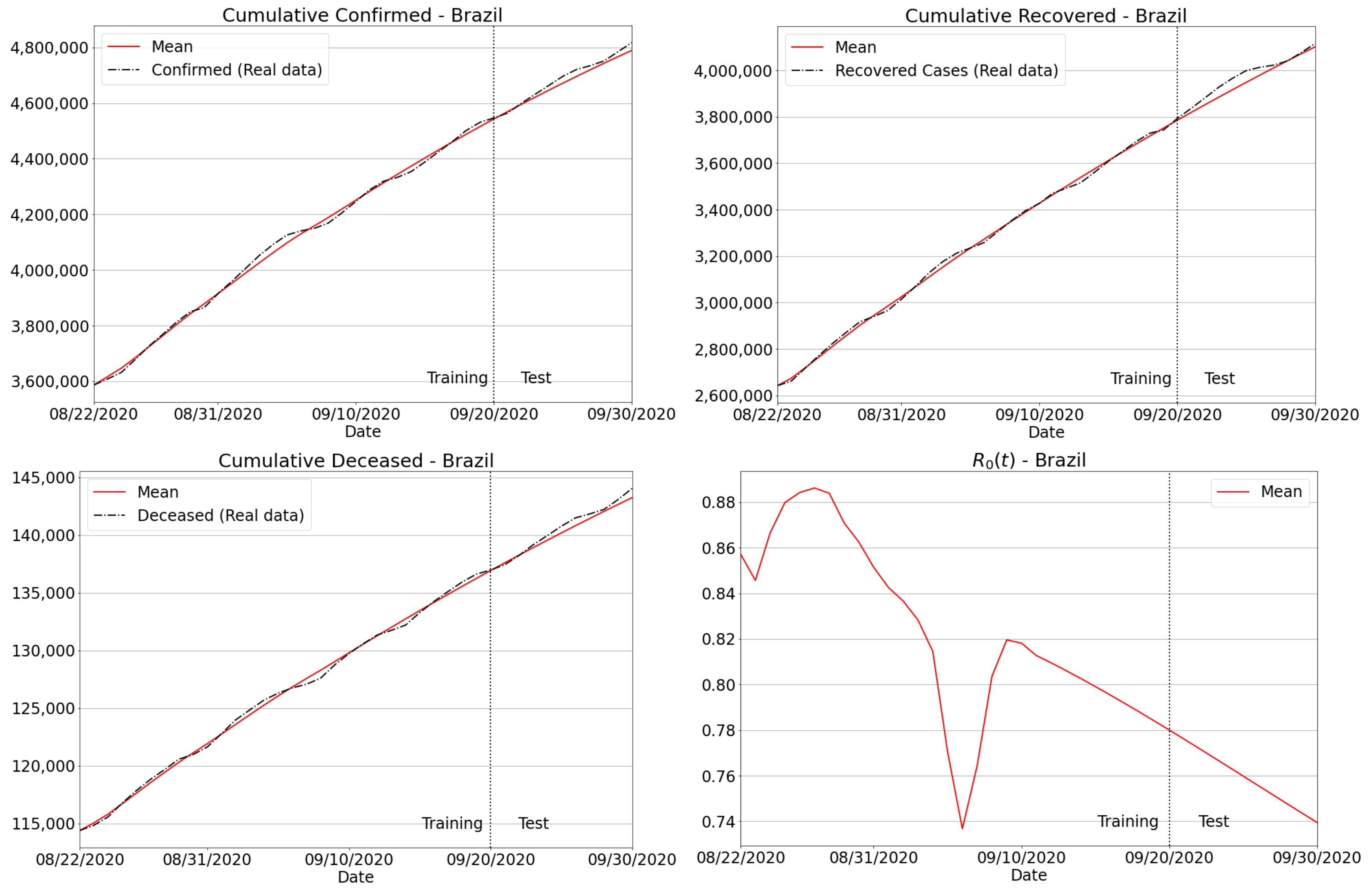
3.3.3. Invariance to Training Periods
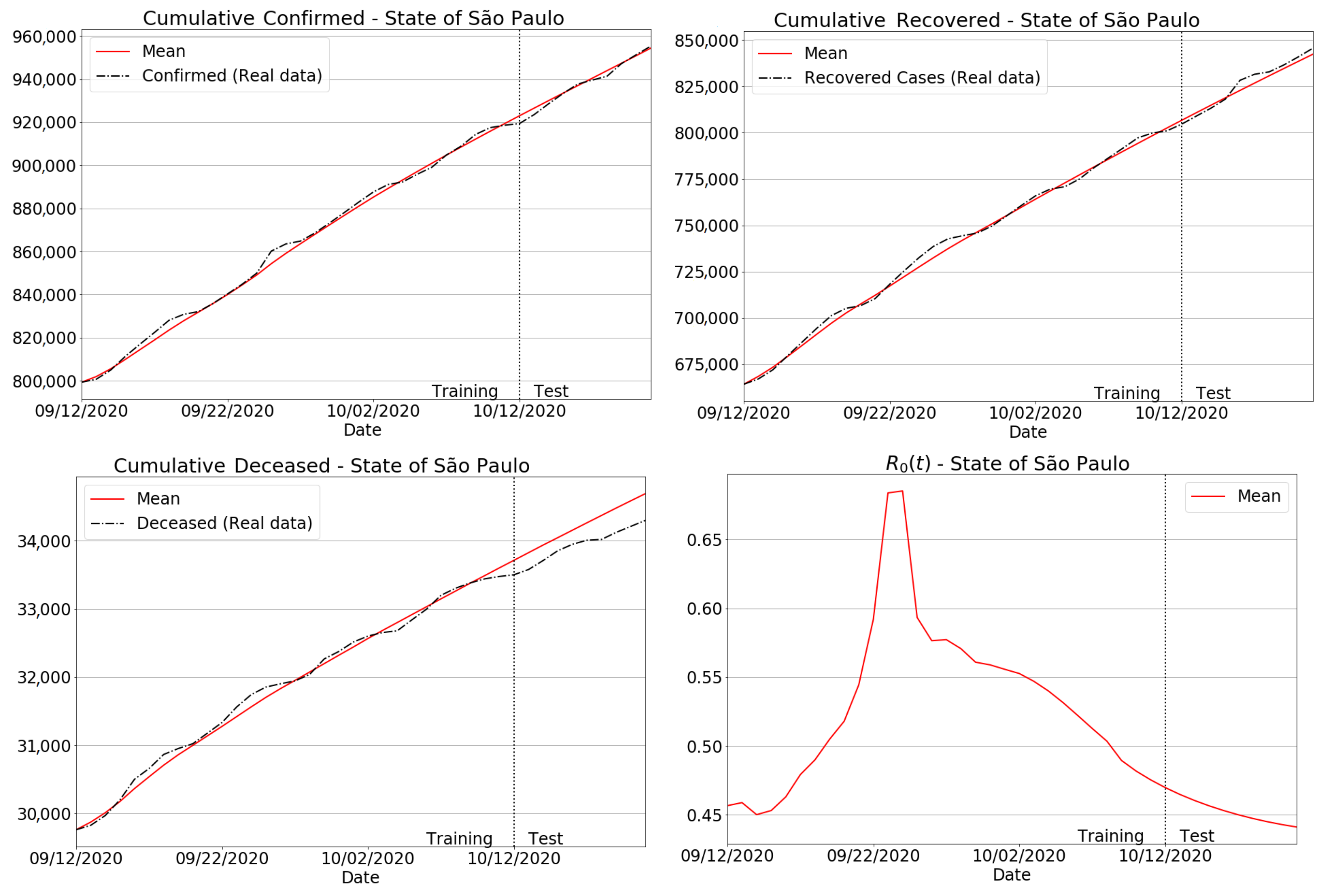
3.4. Quantitative and Qualitative Analyses
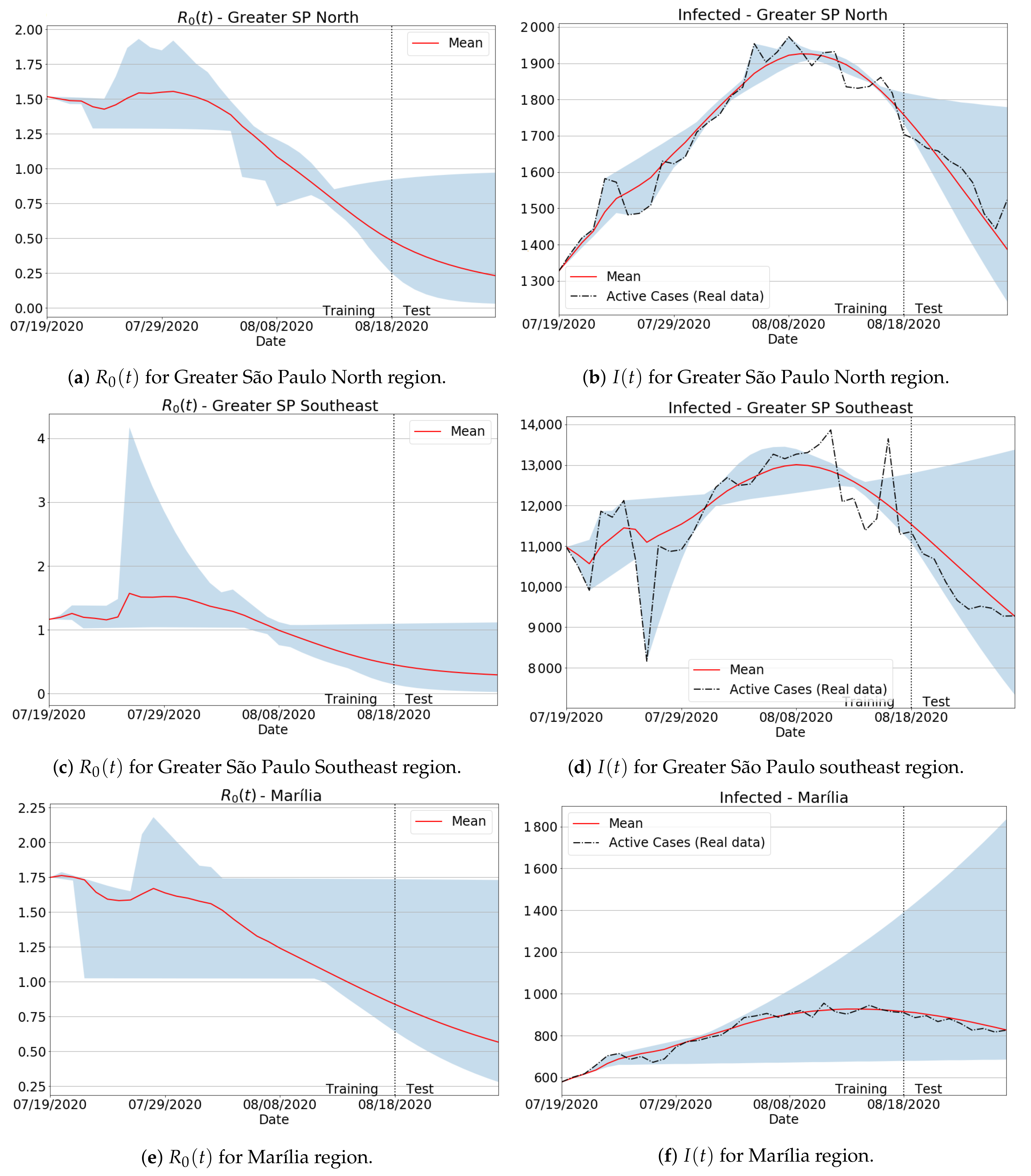
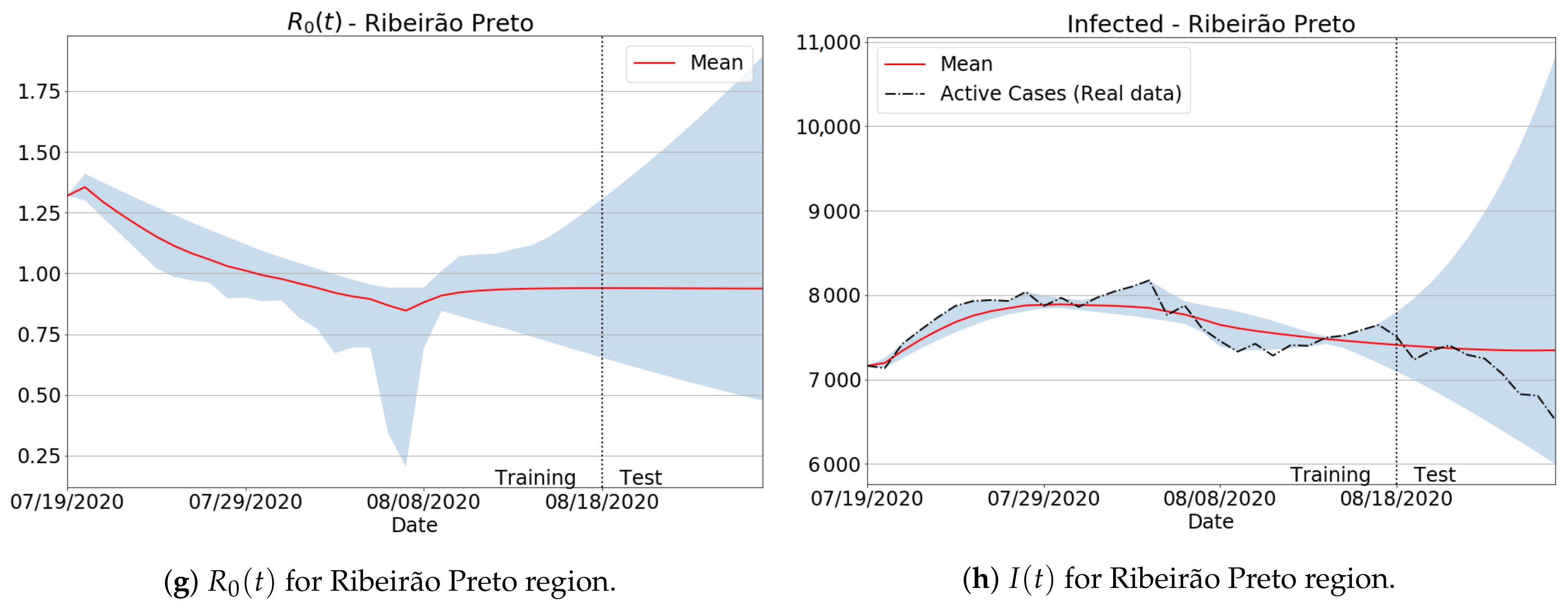
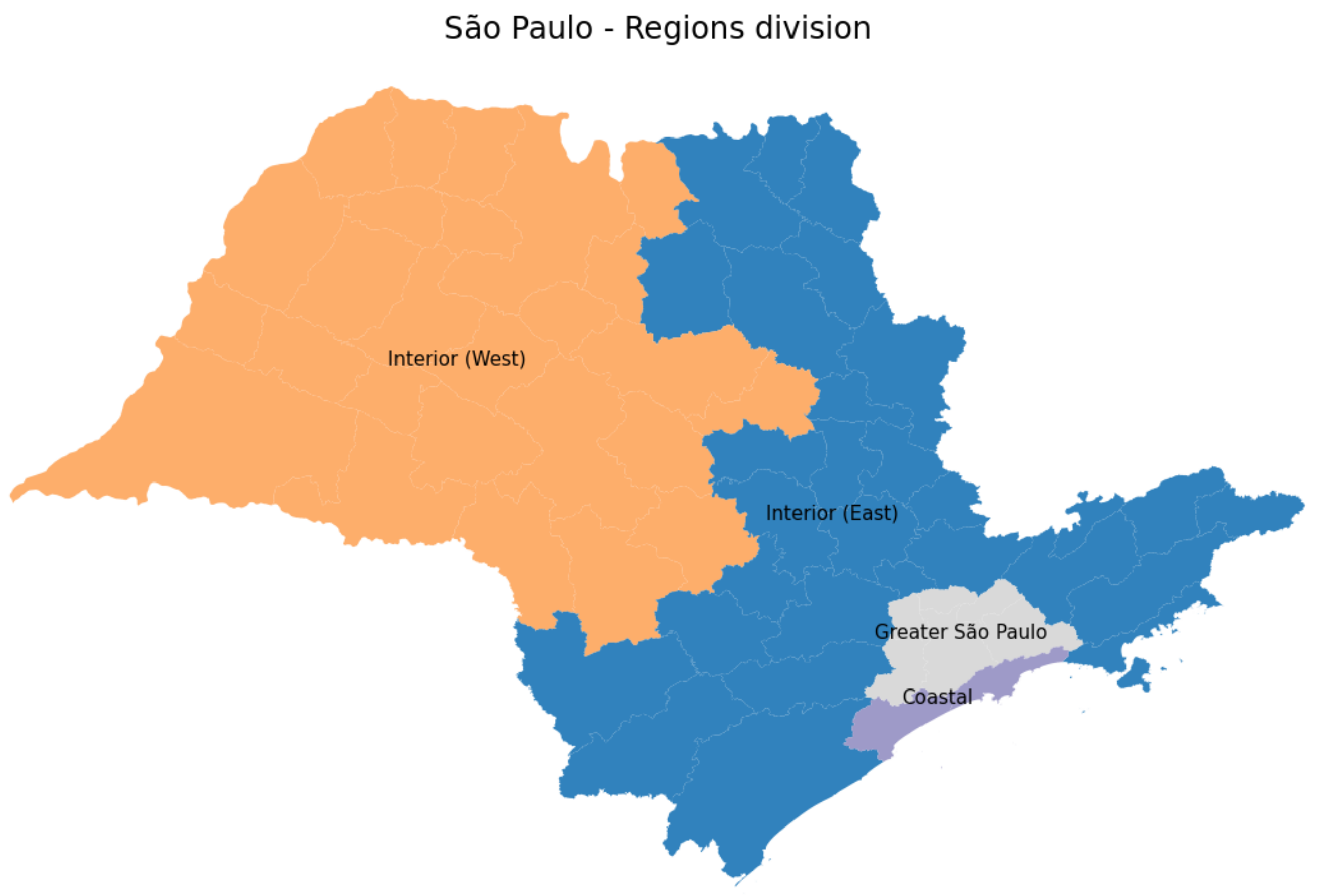
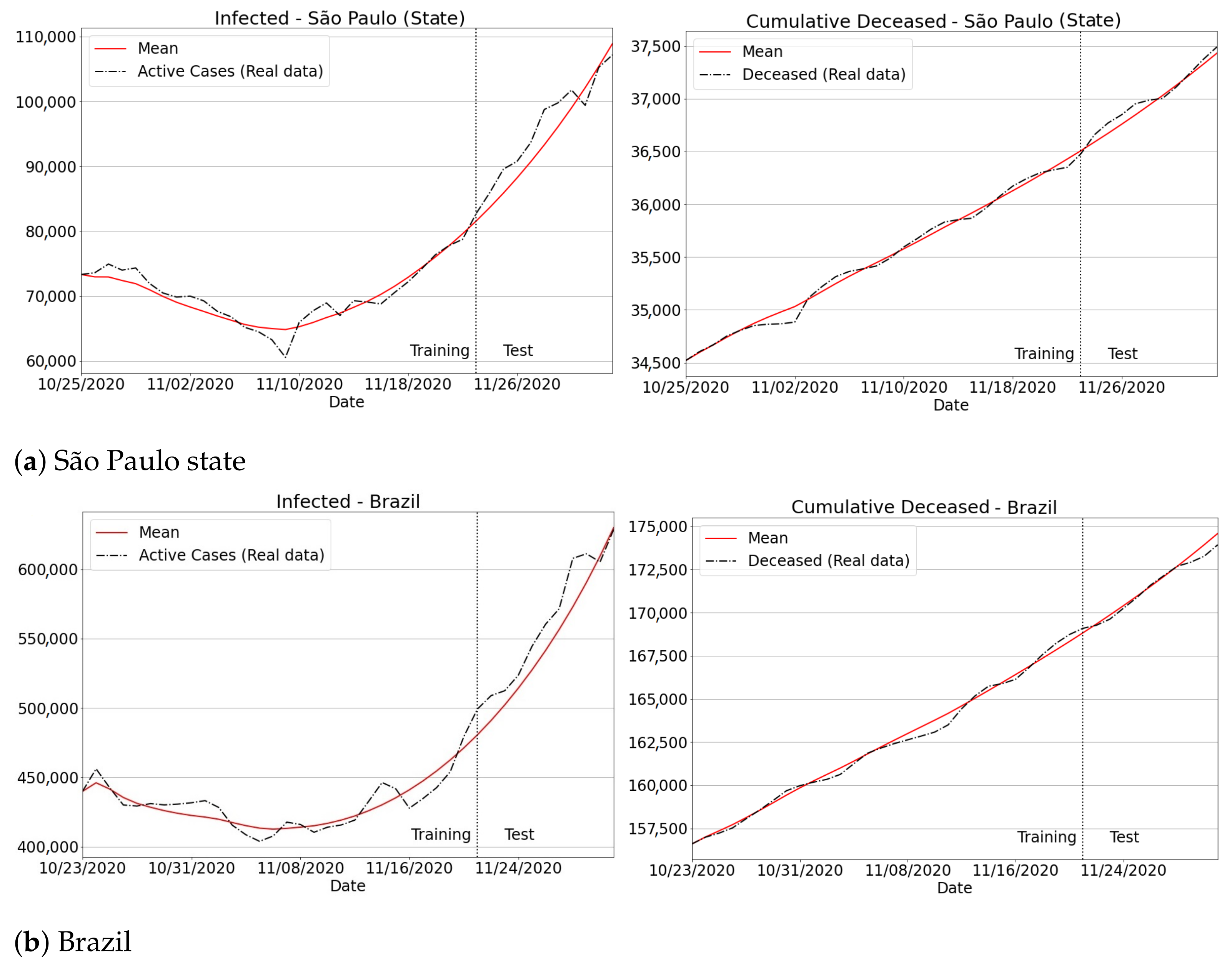
3.4.1. São Paulo State Regions
3.4.2. Brazilian Regions
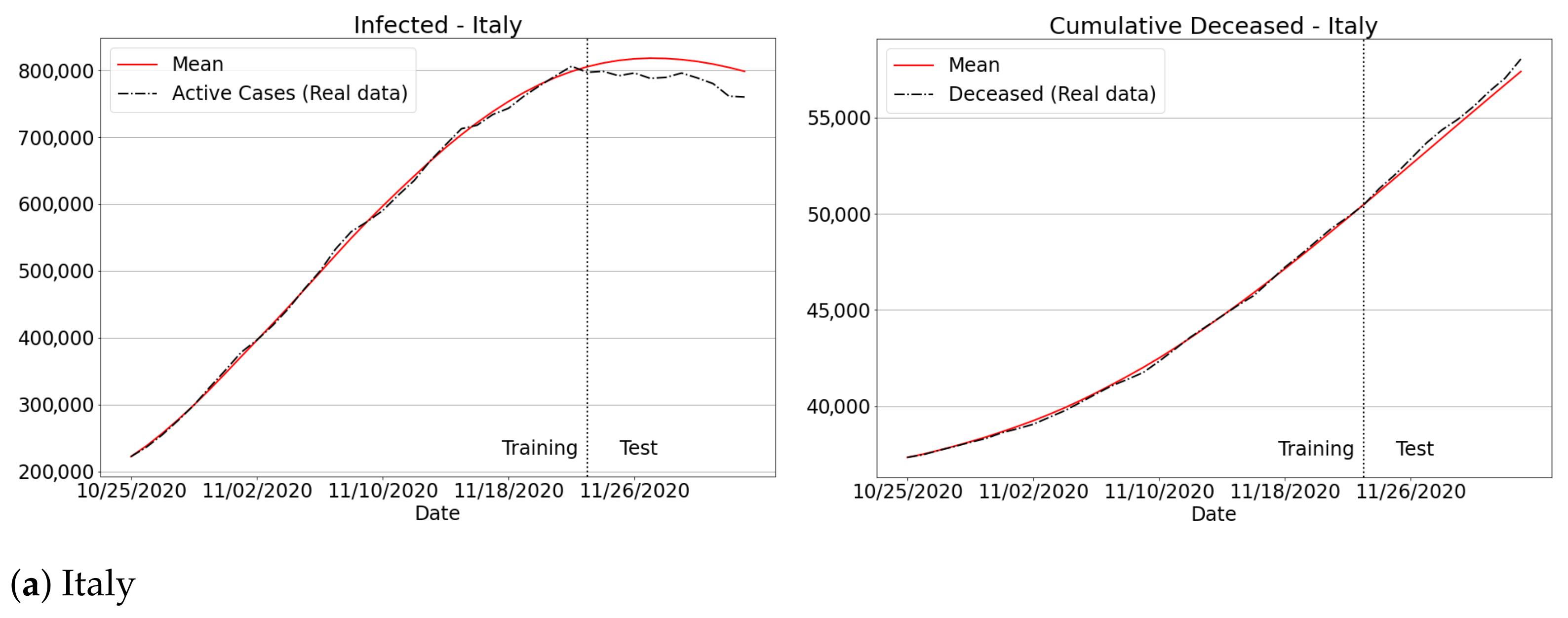
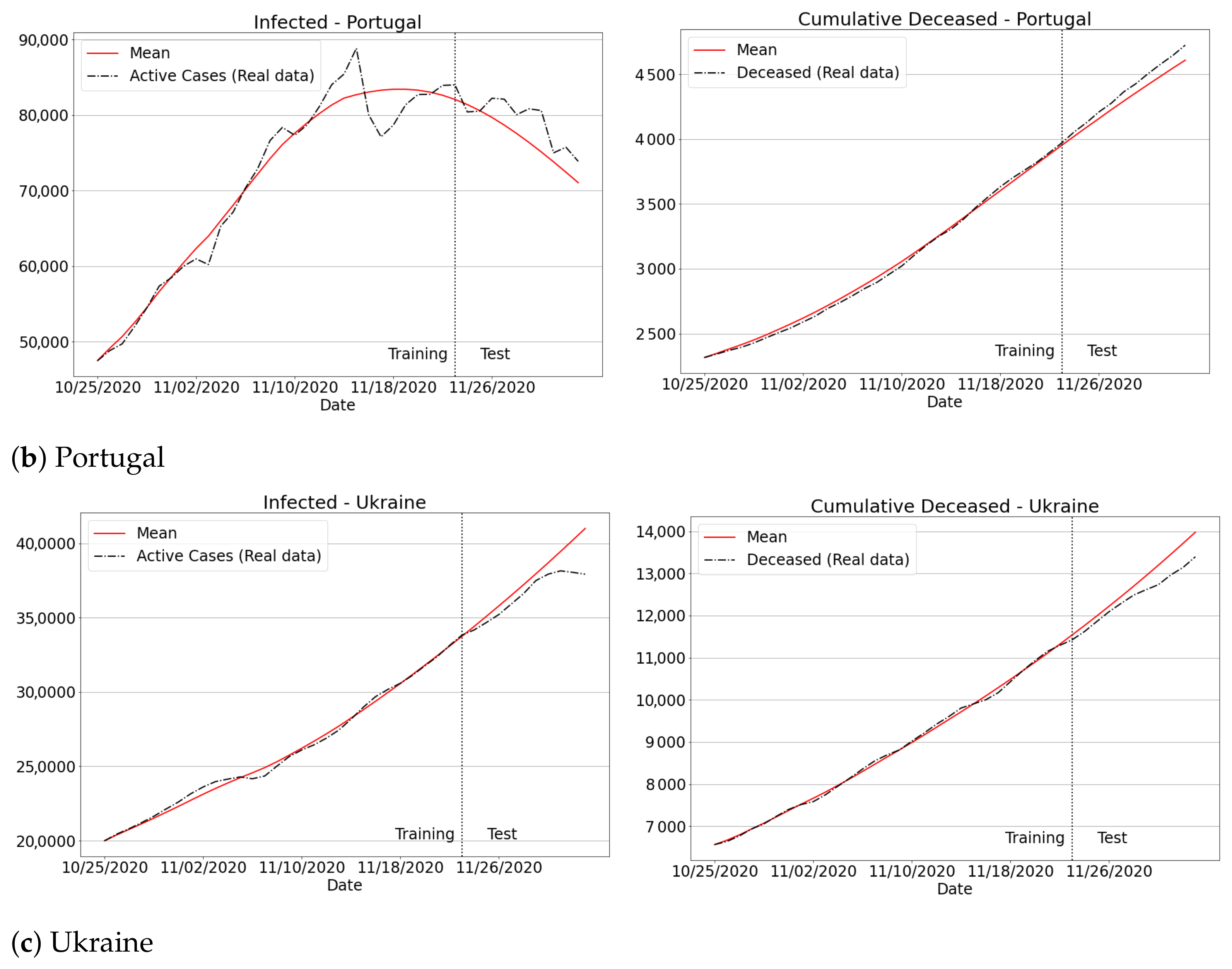
3.4.3. The Second Wave of Covid-19: Investigations in Brazil and Other Countries
4. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
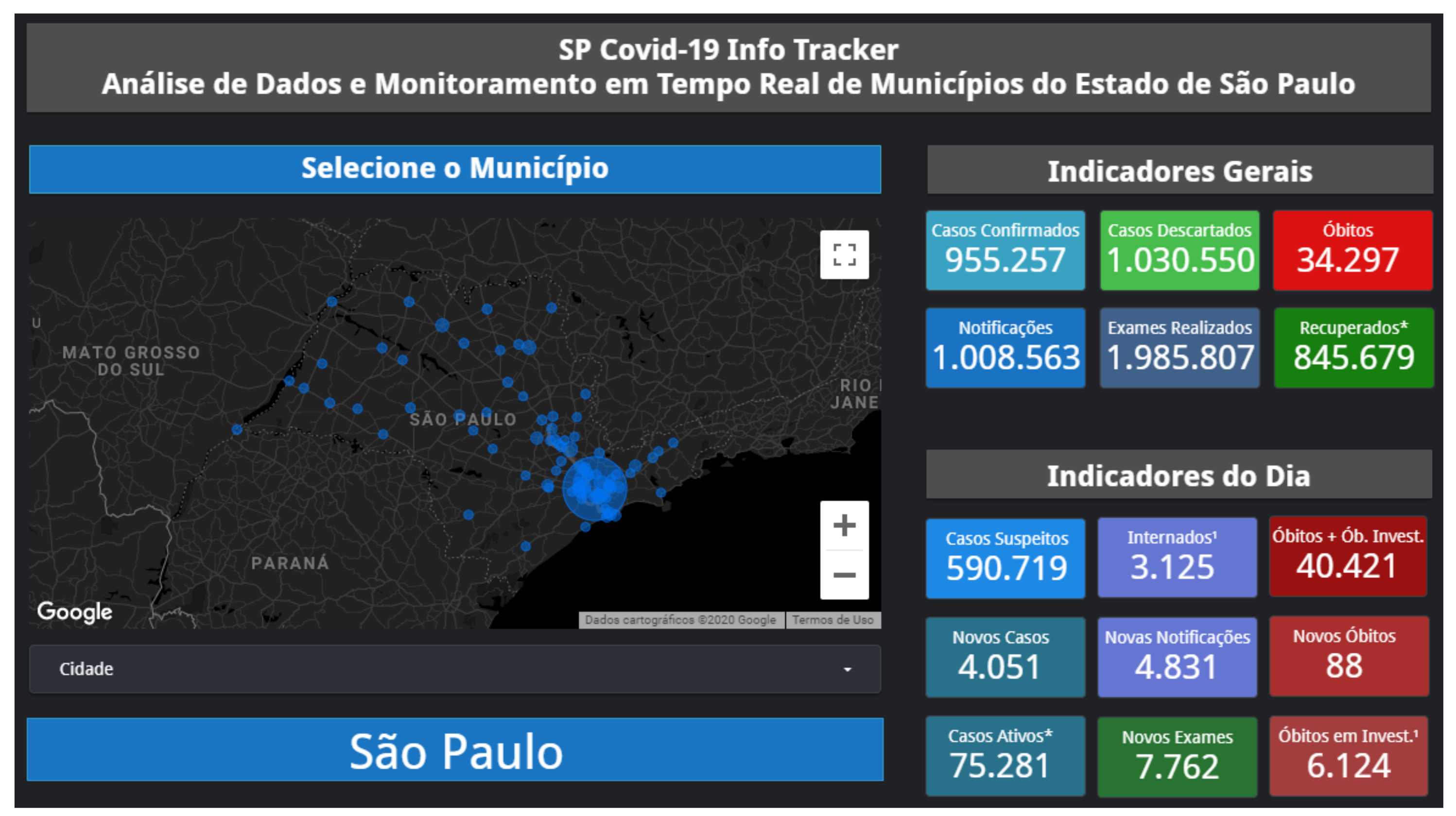
Appendix A. SP Covid-19 Info Tracker
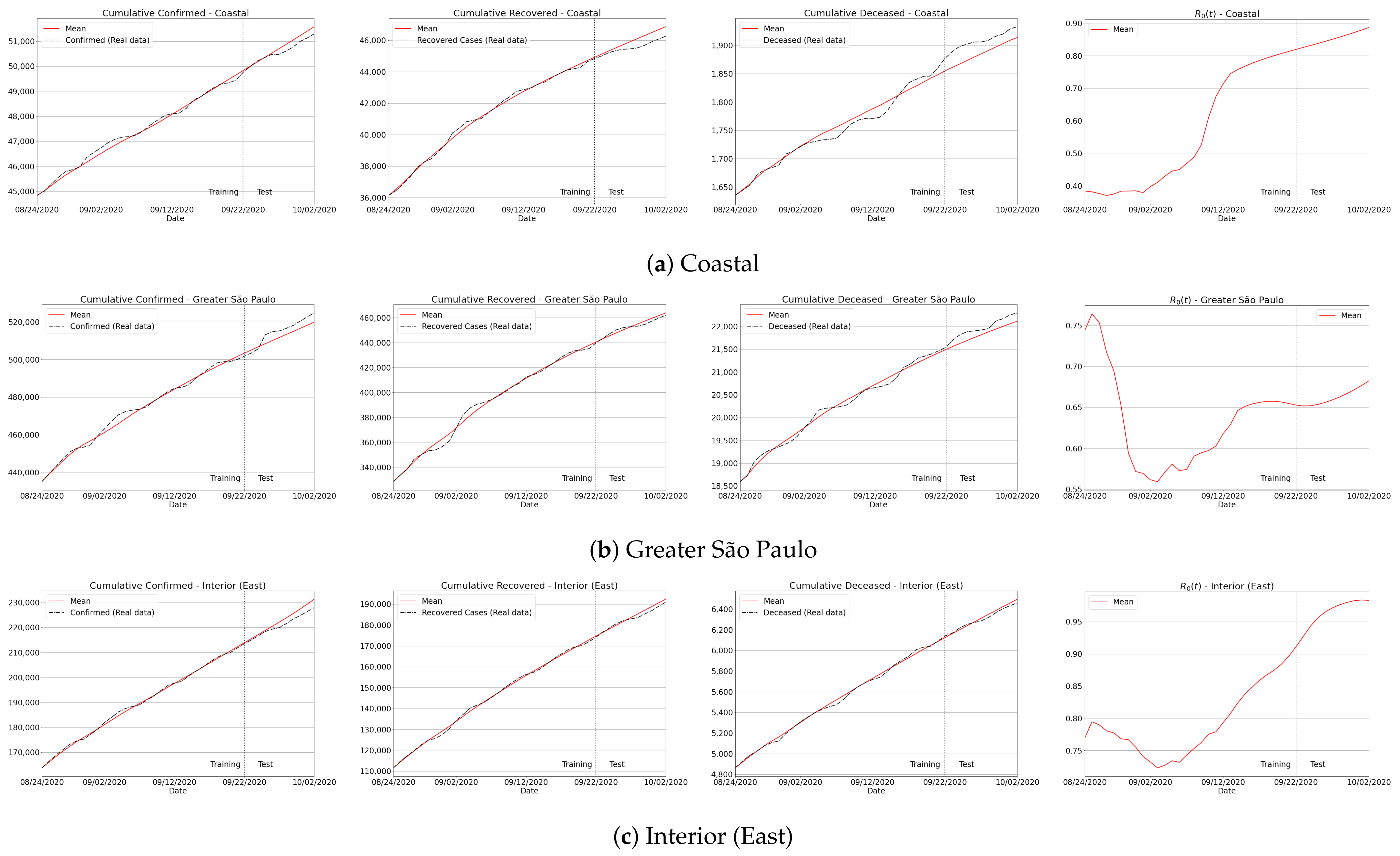
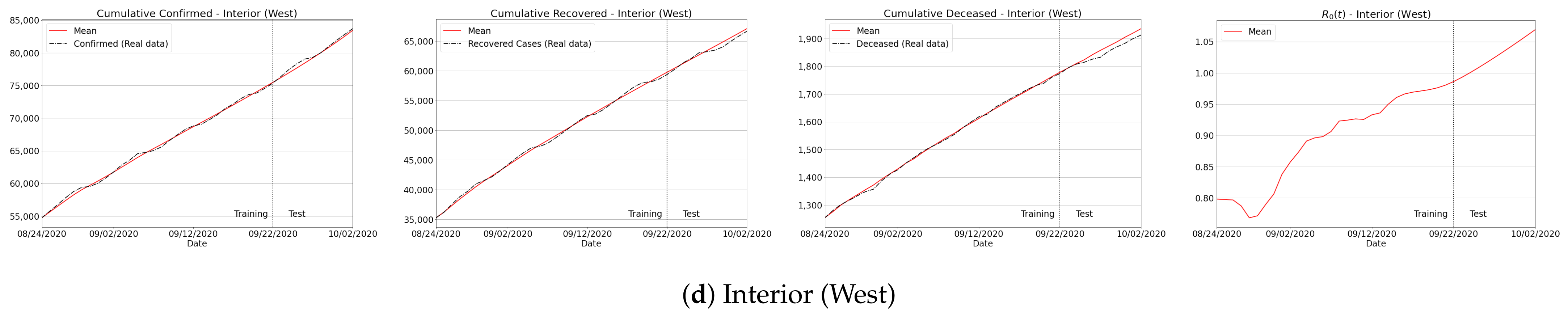
Appendix B. Qualitative Results for São Paulo State and Brazilian Regions
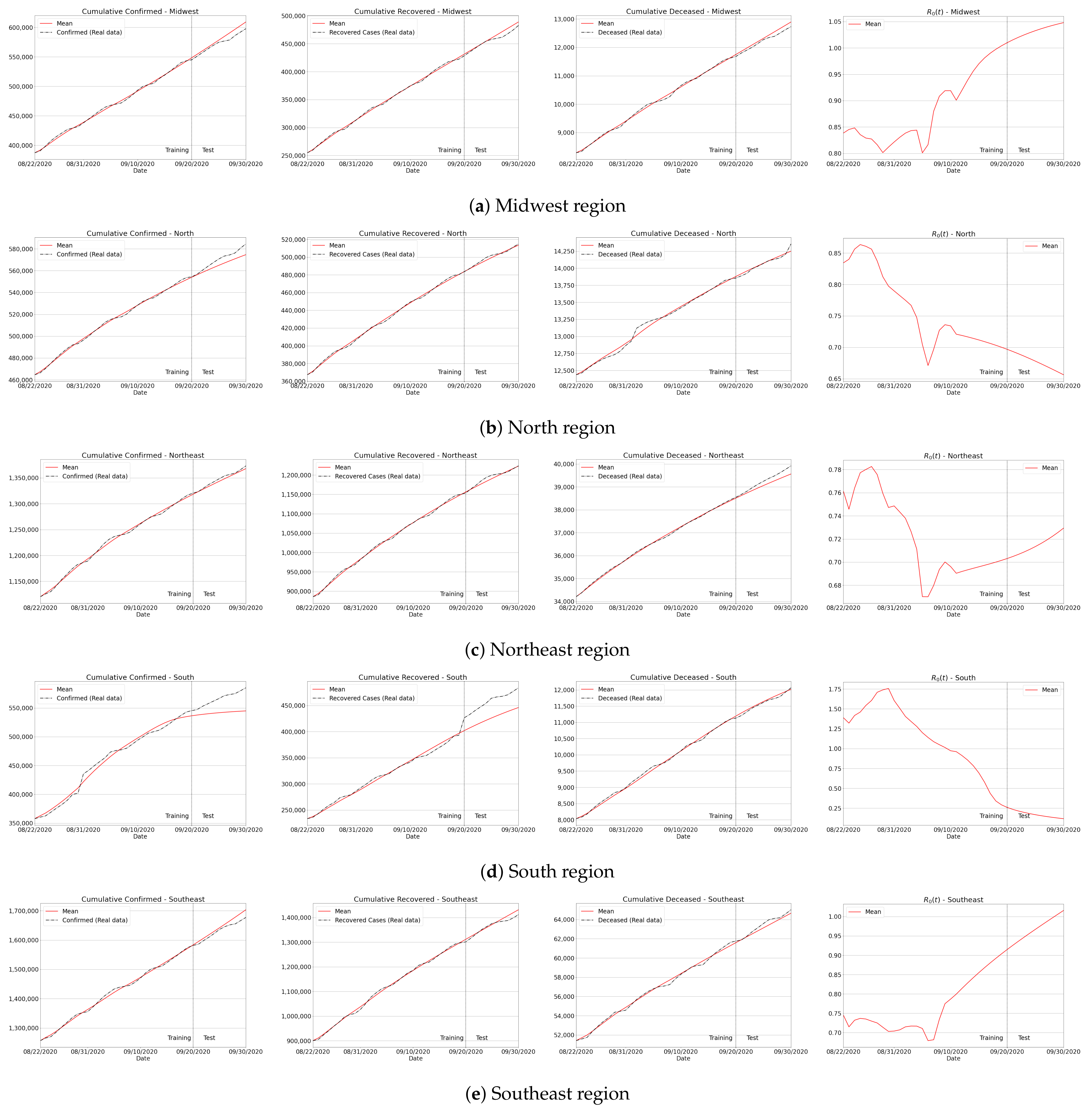
Appendix C. Algorithm
| Algorithm 1: Parameter Calibration and Forecast Process |
 |
References
- World Health Organization. WHO Coronavirus Disease (COVID-19) Dashboard. 2020. Available online: https://covid19.who.int/region/amro/country/br (accessed on 8 November 2020).
- Ministry of Health (Brazil). Brazilian Coronavirus Disease (COVID-19) Dashboard. 2020. Available online: https://covid.saude.gov.br (accessed on 8 October 2020).
- Worldometers. COVID-19 Coronavirus Pandemic. 2020. Available online: https://www.worldometers.info/coronavirus (accessed on 9 October 2020).
- Johns Hopkins University. COVID-19 Data Repository by the Center for Systems Science and Engineering (CSSE) at Johns Hopkins University. 2020. Available online: https://github.com/CSSEGISandData/COVID-19 (accessed on 20 November 2020).
- de Salles Neto, L.L.; Martins, C.B.; Chaves, A.A.; Konstantyner, T.C.R.D.O.K.; Yanasse, H.H.; Campos, C.B.L.D.; Bellini, A.J.A.D.O.; Butkeraites, R.B.; Correia, L.; Magro, I.L.; et al. Forecast UTI: Application for predicting intensive care unit beds in the context of the COVID-19 pandemic. Epidemiol. Serviços de Saúde 2020, 29, e2020391. [Google Scholar] [CrossRef]
- Ma, X.; Vervoort, D. Critical care capacity during the COVID-19 pandemic: Global availability of intensive care beds. J. Crit. Care 2020, 58, 96–97. [Google Scholar] [CrossRef] [PubMed]
- Lai, S.; Ruktanonchai, N.W.; Zhou, L.; Prosper, O.; Luo, W.; Floyd, J.R.; Wesolowski, A.; Santillana, M.; Zhang, C.; Du, X.; et al. Effect of non-pharmaceutical interventions to contain COVID-19 in China. Nature 2020, 585, 410–413. [Google Scholar] [CrossRef] [PubMed]
- Tian, H.; Liu, Y.; Li, Y.; Wu, C.H.; Chen, B.; Kraemer, M.U.G.; Li, B.; Cai, J.; Xu, B.; Yang, Q.; et al. An investigation of transmission control measures during the first 50 days of the COVID-19 epidemic in China. Science 2020, 368, 638–642. [Google Scholar] [CrossRef] [PubMed]
- Aquino, E.M.L.; Silveira, I.H.; Pescarini, J.M.; Aquino, R.; Souza-Filho, J.A.D.; Rocha, A.D.S.; Ferreira, A.; Victor, A.A.; Teixeira, C.; Machado, D.B.; et al. Social distancing measures to control the COVID-19 pandemic: Potential impacts and challenges in Brazil. Cienc. Saude Coletiva 2020, 25, 2423–2446. [Google Scholar] [CrossRef] [PubMed]
- Ebrahim, S.H.; Ahmed, Q.A.; Gozzer, E.; Schlagenhauf, P.; Memish, Z.A. Covid-19 and community mitigation strategies in a pandemic. BMJ 2020, 368, m1066. [Google Scholar] [CrossRef]
- Bruinen de Bruin, Y.; Lequarre, A.S.; McCourt, J.; Clevestig, P.; Pigazzani, F.; Zare Jeddi, M.; Colosio, C.; Goulart, M. Initial impacts of global risk mitigation measures taken during the combatting of the COVID-19 pandemic. Saf. Sci. 2020, 128, 104773. [Google Scholar] [CrossRef]
- Anastassopoulou, C.; Russo, L.; Tsakris, A.; Siettos, C. Data-based analysis, modelling and forecasting of the COVID-19 outbreak. PLoS ONE 2020, 15, e0230405. [Google Scholar] [CrossRef]
- Wu, P.; Hao, X.; Lau, E.H.Y.; Wong, J.Y.; Leung, K.S.M.; Wu, J.T.; Cowling, B.J.; Leung, G.M. Real-time tentative assessment of the epidemiological characteristics of novel coronavirus infections in Wuhan, China. Eurosurveillance 2020, 25, 2000044. [Google Scholar] [CrossRef]
- Battegay, M.; Kuehl, R.; Tschudin-Sutter, S.; Hirsch, H.H.; Widmer, A.F.; Neher, R.A. 2019-Novel Coronavirus (2019-nCoV): Estimating the case fatality rate—A word of caution. Swiss Med. Wkly. 2020, 150, w20203. [Google Scholar] [CrossRef]
- Wang, N.; Fu, Y.; Zhang, H.; Shi, H. An evaluation of mathematical models for the outbreak of COVID-19. Precis. Clin. Med. 2020, 3, 85–93. [Google Scholar] [CrossRef]
- Bastos, S.B.; Cajueiro, D.O. Modeling and Forecasting the Early Evolution of the Covid-19 Pandemic in Brazil. arXiv 2020, arXiv:q-bio.PE/2003.14288. [Google Scholar]
- Anderez, D.O.; Kanjo, E.; Pogrebna, G.; Kaiwartya, O.; Johnson, S.D.; Hunt, J.A. A COVID-19-Based Modified Epidemiological Model and Technological Approaches to Help Vulnerable Individuals Emerge from the Lockdown in the UK. Sensors 2020, 20, 4967. [Google Scholar] [CrossRef] [PubMed]
- Jo, H.; Son, H.; Jung, S.Y.; Hwang, H.J. Analysis of COVID-19 spread in South Korea using the SIR model with time-dependent parameters and deep learning. medRxiv 2020. [Google Scholar] [CrossRef]
- Chen, Y.C.; Lu, P.E.; Chang, C.S.; Liu, T.H. A Time-dependent SIR model for COVID-19 with Undetectable Infected Persons. IEEE Trans. Netw. Sci. Eng. 2020, 7, 3279–3294. [Google Scholar] [CrossRef]
- Yang, H.C.; Xue, Y.; Pan, Y.; Liu, Q.; Hu, G. Time Fused Coefficient SIR Model with Application to COVID-19 Epidemic in the United States. arXiv 2020, arXiv:stat.AP/2008.04284. [Google Scholar]
- Sun, H.; Qiu, Y.; Yan, H.; Huang, Y.; Zhu, Y.; Gu, J.; Chen, S.X. Tracking Reproductivity of COVID-19 Epidemic in China with Varying Coefficient SIR Model. J. Data Sci. 2020, 18, 455–472. [Google Scholar]
- Kiamari, M.; Ramachandran, G.; Nguyen, Q.; Pereira, E.; Holm, J.; Krishnamachari, B. COVID-19 Risk Estimation using a Time-varying SIR-model. arXiv 2020, arXiv:physics.soc-ph/2008.08140. [Google Scholar]
- Jia, W.; Han, K.; Song, Y.; Gao, W.; Wang, S.; Yang, S.; Wang, J.; Kou, F.; Tai, P.; Li, J.; et al. Extended SIR Prediction of the Epidemics Trend of COVID-19 in Italy and Compared With Hunan, China. medRxiv 2020. [Google Scholar] [CrossRef]
- Wang, L.; Zhou, Y.; He, J.; Zhu, B.; Wang, F.; Tang, L.; Kleinsasser, M.; Barker, D.; Eisenberg, M.C.; Song, P.X. Rejoinder: An epidemiological forecast model and software assessing interventions on COVID-19 epidemic in China. J. Data Sci. 2020, 18, 446–454. [Google Scholar]
- Atkeson, A.G. On Using SIR Models to Model Disease Scenarios for COVID-19. Q. Rev. 2020, 41, 1–33. [Google Scholar] [CrossRef]
- Atkeson, A.; Kopecky, K.; Zha, T. Estimating and Forecasting Disease Scenarios for COVID-19 with an SIR Model; NBER Working Paper; NBER: Cambridge, MA, USA, 2020. [Google Scholar]
- Wang, Z.; Zhang, X.; Teichert, G.; Carrasco-Teja, M.; Garikipati, K. System inference for the spatio-temporal evolution of infectious diseases: Michigan in the time of COVID-19. Comput. Mech. 2020, 1, 1153–1176. [Google Scholar] [CrossRef]
- Hong, H.G.; Li, Y. Estimation of time-varying reproduction numbers underlying epidemiological processes: A new statistical tool for the COVID-19 pandemic. PLoS ONE 2020, 15, e0236464. [Google Scholar] [CrossRef]
- Ndiaye, B.M.; Tendeng, L.; Seck, D. Analysis of the COVID-19 pandemic by SIR model and machine learning technics for forecasting. arXiv 2020, arXiv:q-bio.PE/2004.01574. [Google Scholar]
- Dandekar, R.; Barbastathis, G. Neural Network aided quarantine control model estimation of COVID spread in Wuhan, China. arXiv 2020, arXiv:q-bio.PE/2003.09403. [Google Scholar]
- Biswas, K.; Khaleque, A.; Sen, P. Covid-19 spread: Reproduction of data and prediction using a SIR model on Euclidean network. arXiv 2020, arXiv:physics.soc-ph/2003.07063. [Google Scholar]
- Mohamadou, Y.; Halidou, A.; Kapen, P.T. A review of mathematical modeling, artificial intelligence and datasets used in the study, prediction and management of COVID-19. Appl. Intell. 2020, 50, 3913–3925. [Google Scholar] [CrossRef]
- Pham, Q.; Nguyen, D.C.; Huynh-The, T.; Hwang, W.; Pathirana, P.N. Artificial Intelligence (AI) and Big Data for Coronavirus (COVID-19) Pandemic: A Survey on the State-of-the-Arts. IEEE Access 2020, 8, 130820–130839. [Google Scholar] [CrossRef]
- Kermack, W.O.; McKendrick, A.G. A contribution to the mathematical theory of epidemics. Proc. R. Soc. A 1927, 115, 700–721. [Google Scholar]
- Wikipedia. São Paulo (State). 2020. Available online: https://en.wikipedia.org/wiki/S%C3%A3o_Paulo_(state) (accessed on 8 November 2020).
- Reuters. Brazil Takes down COVID-19 Data, Hiding Soaring Death Toll. 2020. Available online: https://www.reuters.com/article/us-health-coronavirus-brazil-idUSKBN23D0PW (accessed on 25 September 2020).
- França, E.B.; Ishitani, L.H.; Teixeira, R.A.; Abreu, D.M.X.D.; Corrêa, P.R.L.; Marinho, F.; Vasconcelos, A.M.N. Deaths due to COVID-19 in Brazil: How many are there and which are being identified? Rev. Bras. Epidemiol. 2020, 23, 1–7. [Google Scholar]
- Hethcote, H.W. The Mathematics of Infectious Diseases. SIAM Rev. 2000, 42, 599–653. [Google Scholar] [CrossRef]
- Okabe, Y.; Shudo, A. A Mathematical Model of Epidemics—A Tutorial for Students. Mathematics 2020, 8, 1174. [Google Scholar] [CrossRef]
- Cohen, J.; Powderly, W.G.; Opal, S.M. Infectious Diseases, 4th ed.; Elsevier: Amsterdam, The Netherlands, 2017. [Google Scholar]
- Petzold, L. Automatic Selection of Methods for Solving Stiff and Nonstiff Systems of Ordinary Differential Equations. SIAM J. Sci. Stat. Comput. 1983, 4, 136–148. [Google Scholar] [CrossRef]
- Byrd, R.H.; Hansen, S.L.; Nocedal, J.; Singer, Y. A Stochastic Quasi-Newton Method for Large-Scale Optimization. SIAM J. Optim. 2016, 26, 1008–1031. [Google Scholar] [CrossRef]
- Istaiteh, O.; Owais, T.; Al-Madi, N.; Abu-Soud, S. Machine Learning Approaches for COVID-19 Forecasting. In Proceedings of the International Conference on Intelligent Data Science Technologies and Applications (IDSTA), Valencia, Spain, 19–22 October 2020; pp. 50–57. [Google Scholar]
- Alsayed, A.; Sadir, H.; Kamil, R.; Sari, H. Prediction of Epidemic Peak and Infected Cases for COVID-19 Disease in Malaysia, 2020. Int. J. Environ. Res. Public Health 2020, 17, 4076. [Google Scholar] [CrossRef]
- Leme, J.V.; Casaca, W.; Colnago, M.; Dias, M.A. Towards Assessing the Electricity Demand in Brazil: Data-Driven Analysis and Ensemble Learning Models. Energies 2020, 13, 1407. [Google Scholar] [CrossRef]
- Liu, L.; Chen, Y.; Wu, L. Forecasting Confirmed Cases, Deaths, and Recoveries from COVID-19 in China during the Early Stage. Math. Probl. Eng. 2020, 2020, 1405764. [Google Scholar] [CrossRef]
- Rajagopal, K.; Hasanzadeh, N.; Parastesh, F.; Hamarash, I.I.; Jafari, S.; Hussain, I. A Fractional-order Model for the Novel Coronavirus (COVID-19) Outbreak. Nonlinear Dyn. 2020, 101, 711–718. [Google Scholar] [CrossRef]
- Folha de S. Paulo (The Second Largest Brazilian Media Conglomerate). Problems in the Ministry of Health’s System Hamper Analysis of Covid-19 Data. 2020. Available online: https://www1.folha.uol.com.br/equilibrioesaude/2020/08/problemas-em-sistema-do-ministerio-da-saude-prejudicam-analise-de-dados-da-covid-19.shtml (accessed on 6 August 2020). (In Portuguese).
- BBC News Brazil. Hospital Doctors in SP Raise the Alarm for New Wave of Covid-19. 2020. Available online: https://newsbeezer.com/brazileng/hospital-doctors-in-sp-raise-the-alarm-for-new-wave-of-covid-19/ (accessed on 16 November 2020).
- CanalTech Press Agency (Translated by Time 24 News). Public Hospitals Face Increase in Admissions for COVID-19 in SP. 2020. Available online: https://www.time24.news/2020/11/public-hospitals-face-increase-in-admissions-for-covid-19-in-sp.html (accessed on 17 November 2020).
- RecordTV (R7) Television Network (Translated by Time 24 News). State of SP Has 15 Regions with Accelerated Transmission of COVID-19. 2020. Available online: https://www.time24.news/2020/12/state-of-sp-has-15-regions-with-accelerated-transmission-of-covid-19-news.html (accessed on 1 December 2020).
- Cacciapaglia, G.; Cot, C.; Sannino, F. Second wave COVID-19 pandemics in Europe: A temporal playbook. Sci. Rep. 2020, 10, 15514. [Google Scholar] [CrossRef]
- Ghanbari, B. On forecasting the spread of the COVID-19 in Iran: The second wave. Chaos Solitons Fractals 2020, 140, 110176. [Google Scholar] [CrossRef]
- Renardy, M.; Eisenberg, M.; Kirschner, D. Predicting the second wave of COVID-19 in Washtenaw County, MI. J. Theor. Biol. 2020, 507, 110461. [Google Scholar] [CrossRef] [PubMed]
- Faranda, D.; Alberti, T. Modeling the second wave of COVID-19 infections in France and Italy via a stochastic SEIR model. Chaos Interdiscip. J. Nonlinear Sci. 2020, 30, 111101. [Google Scholar] [CrossRef] [PubMed]
- Lin, C.B.; Hung, R.W.; Hsu, C.Y.; Chen, J.S. A GNSS-Based Crowd-Sensing Strategy for Specific Geographical Areas. Sensors 2020, 20, 4171. [Google Scholar] [CrossRef] [PubMed]
- Olha Digital. Platform Publishes Real-Time Data on Covid-19’s Progress in SP. 2020. Available online: https://olhardigital.com.br/en/2020/06/22/news/platform-publishes-real-time-data-on-covid-19-progress-in-sp/amp/ (accessed on 22 June 2020).
- FAPESP—São Paulo Research Foundation. A Dimensão da Pandemia. 2020. Available online: https://revistapesquisa.fapesp.br/a-dimensao-da-pandemia (accessed on 20 October 2020). (In Portuguese).
- Cornide-Reyes, H.; Riquelme, F.; Monsalves, D.; Noel, R.; Cechinel, C.; Villarroel, R.; Ponce, F.; Munoz, R. A Multimodal Real-Time Feedback Platform Based on Spoken Interactions for Remote Active Learning Support. Sensors 2020, 20, 6337. [Google Scholar] [CrossRef] [PubMed]
- Martinez, M.; Yang, K.; Constantinescu, A.; Stiefelhagen, R. Helping the Blind to Get through COVID-19: Social Distancing Assistant Using Real-Time Semantic Segmentation on RGB-D Video. Sensors 2020, 20, 5202. [Google Scholar] [CrossRef] [PubMed]

| Notation | Description |
|---|---|
| number of susceptible at time t | |
| number of infected at time t | |
| number of recovered at time t | |
| number of deaths at time t | |
| transmission rate | |
| transient transmission rate | |
| rate of recovered | |
| rate of mortality | |
| or | time-dependent reproduction number |
| prediction for the transmission rate at time t | |
| M | pre-specified training period |
| p | desirable forecast period |
| and | real and predicted daily values with respect to a given target variable |
| Region | Variance Norm | MAPE for Active Cases (%) |
|---|---|---|
| Greater São Paulo North | 0.098 | 2.658 |
| Greater São Paulo Southeast | 1.478 | 4.414 |
| Marília | 0.378 | 1.928 |
| Ribeirão Preto | 0.063 | 3.894 |
| Region | MAPE Error for Cumulative Cases (%) | MAPE Error for Cumulative Recovered Cases (%) | MAPE Error for Cumulative Deceased Cases (%) |
|---|---|---|---|
| 15 August 2020–24 August 2020 | |||
| Coastal | 1.513 | 0.951 | 1.046 |
| Greater São Paulo | 0.753 | 3.731 | 1.394 |
| Interior (East) | 0.454 | 1.491 | 3.465 |
| Interior (West) | 1.085 | 1.826 | 2.618 |
| 15 September 2020–24 September 2020 | |||
| Coastal | 1.536 | 0.347 | 2.503 |
| Greater São Paulo | 0.598 | 0.344 | 0.926 |
| Interior (East) | 0.937 | 0.461 | 1.157 |
| Interior (West) | 1.277 | 0.753 | 0.603 |
| 15 October 2020–24 October 2020 | |||
| Coastal | 0.533 | 0.249 | 0.268 |
| Greater São Paulo | 0.105 | 0.438 | 0.776 |
| Interior (East) | 1.413 | 0.886 | 0.236 |
| Interior (West) | 0.832 | 1.097 | 0.881 |
| Training Windows | MAPE Error for Cumulative Cases (%) | MAPE Error for Cumulative Deceases (%) | MAPE Error for Cumulative Recovereies (%) |
|---|---|---|---|
| 10-30 days | 0.285 | 0.753 | 0.293 |
| 10-40 days | 0.762 | 0.928 | 0.321 |
| 10-50 days | 1.179 | 0.894 | 0.592 |
| Region | Cases | Recoveries | Deaths | |||
|---|---|---|---|---|---|---|
| MAPE | NRMSE | MAPE | NRMSE | MAPE | NRMSE | |
| Costal | 0.325 | 0.004 | 0.907 | 0.010 | 1.200 | 0.012 |
| Greater São Paulo | 0.680 | 0.007 | 0.371 | 0.004 | 0.714 | 0.007 |
| Interior (East) | 0.818 | 0.010 | 0.592 | 0.007 | 0.312 | 0.004 |
| Interior (West) | 0.376 | 0.005 | 0.626 | 0.007 | 0.826 | 0.009 |
| State of São Paulo | 0.219 | 0.003 | 0.455 | 0.005 | 0.475 | 0.005 |
| Region | Cases | Recoveries | Deaths | |||
|---|---|---|---|---|---|---|
| MAPE | NRMSE | MAPE | NRMSE | MAPE | NRMSE | |
| Midwest | 1.169 | 0.014 | 0.989 | 0.013 | 0.856 | 0.009 |
| North | 0.889 | 0.010 | 0.282 | 0.003 | 0.173 | 0.003 |
| Northeast | 0.244 | 0.003 | 0.342 | 0.005 | 0.487 | 0.005 |
| South | 4.413 | 0.047 | 7.111 | 0.072 | 0.397 | 0.004 |
| Southeast | 0.815 | 0.009 | 0.675 | 0.009 | 0.427 | 0.005 |
| Brazil | 0.323 | 0.004 | 0.638 | 0.008 | 0.273 | 0.003 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amaral, F.; Casaca, W.; Oishi, C.M.; Cuminato, J.A. Towards Providing Effective Data-Driven Responses to Predict the Covid-19 in São Paulo and Brazil. Sensors 2021, 21, 540. https://doi.org/10.3390/s21020540
Amaral F, Casaca W, Oishi CM, Cuminato JA. Towards Providing Effective Data-Driven Responses to Predict the Covid-19 in São Paulo and Brazil. Sensors. 2021; 21(2):540. https://doi.org/10.3390/s21020540
Chicago/Turabian StyleAmaral, Fabio, Wallace Casaca, Cassio M. Oishi, and José A. Cuminato. 2021. "Towards Providing Effective Data-Driven Responses to Predict the Covid-19 in São Paulo and Brazil" Sensors 21, no. 2: 540. https://doi.org/10.3390/s21020540
APA StyleAmaral, F., Casaca, W., Oishi, C. M., & Cuminato, J. A. (2021). Towards Providing Effective Data-Driven Responses to Predict the Covid-19 in São Paulo and Brazil. Sensors, 21(2), 540. https://doi.org/10.3390/s21020540






