Investigation and Mitigation of Noise Contributions in a Compact Heterodyne Interferometer
Abstract
1. Introduction
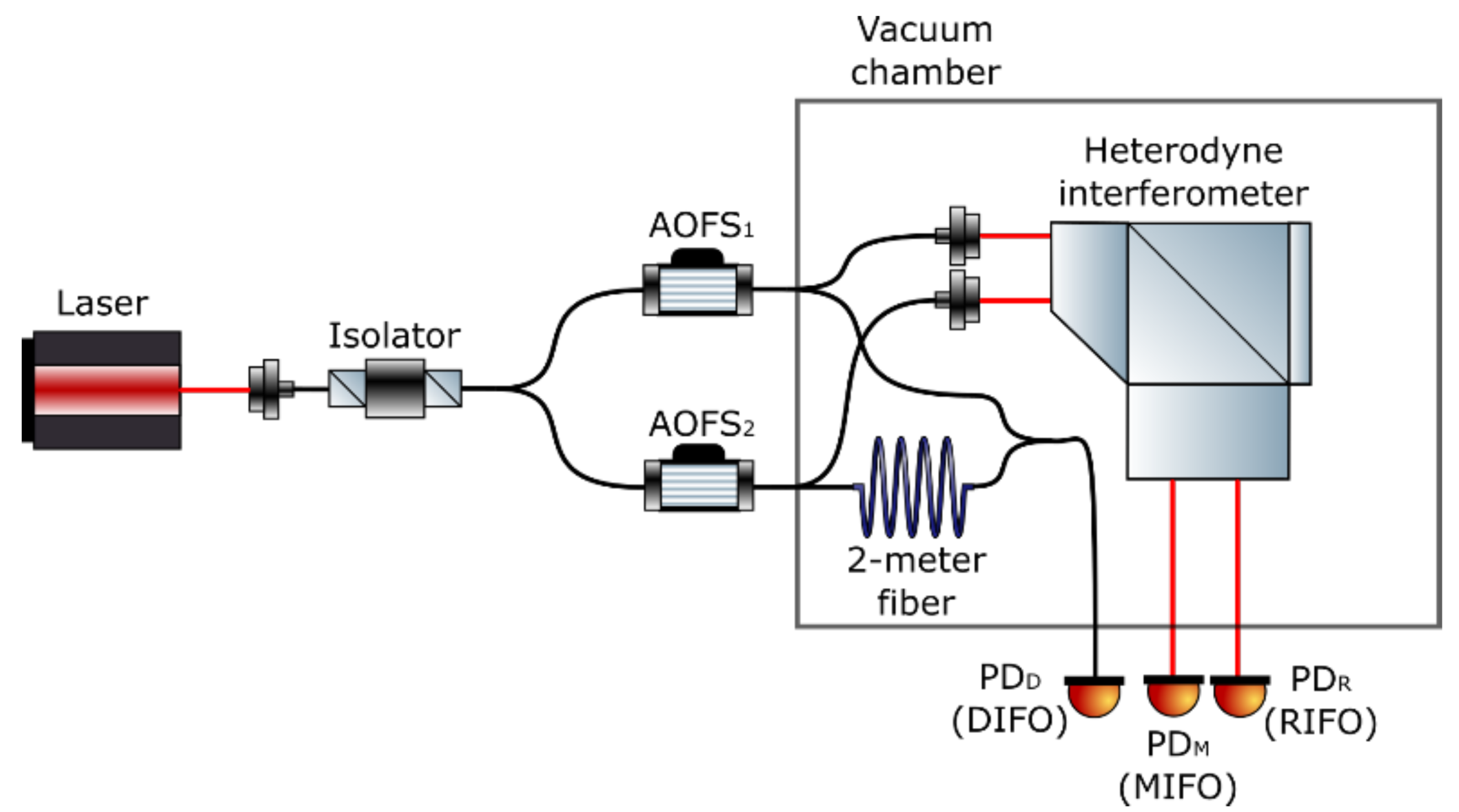
2. Compact Heterodyne Laser Interferometer
2.1. Design and Benchtop Prototype
2.2. Operation Environments
2.3. Preliminary Test
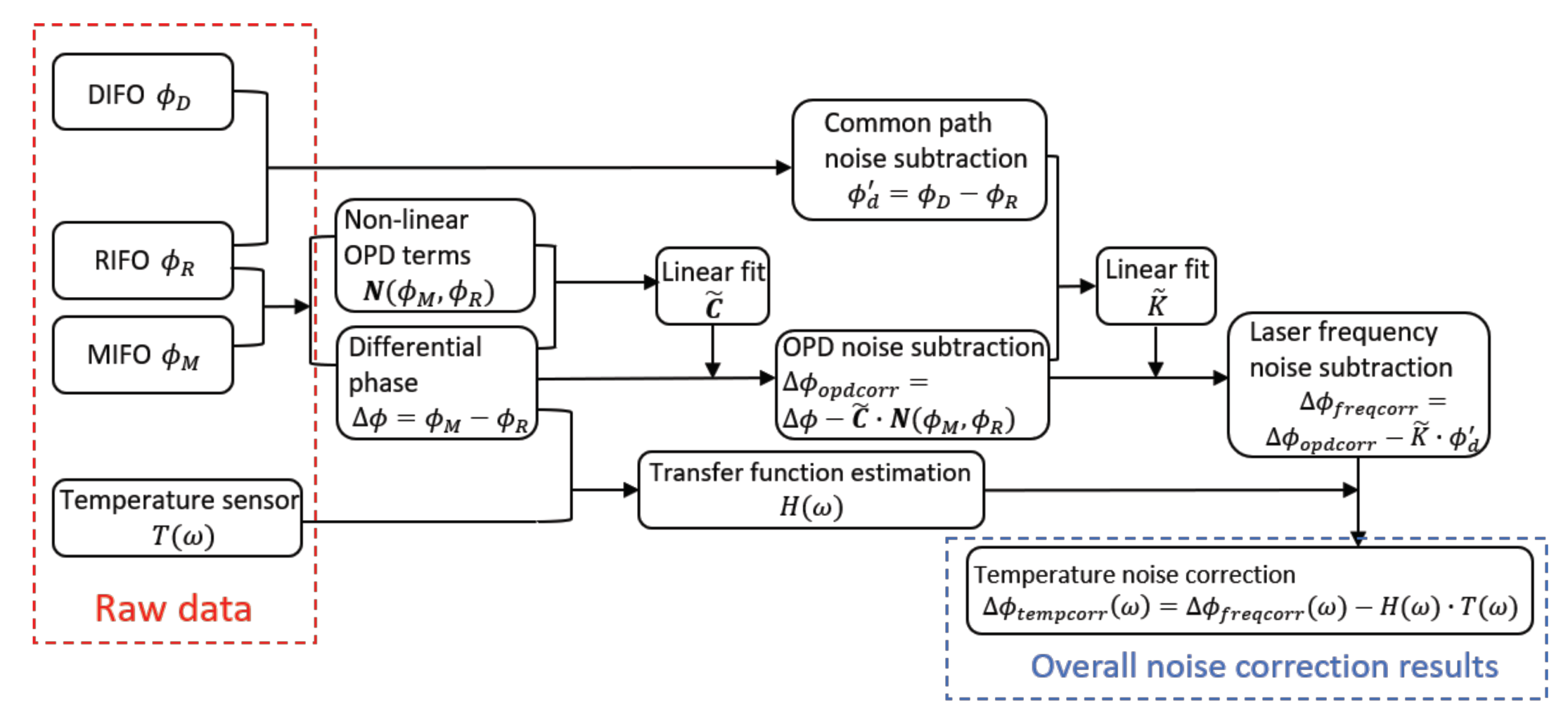
3. Noise Source Characterization and Suppression
3.1. Non-Linear OPD Noise
3.2. Laser Frequency Noise
3.3. Temperature Fluctuation Noise
3.4. Detection System Noise Limit
3.5. Discussions
4. Conclusions and Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Heinzel, G. The LTP interferometer and phasemeter. Class. Quant. Grav. 2004, 21, S581–S587. [Google Scholar] [CrossRef][Green Version]
- Wand, V.; Guzmán, F.; Heinzel, G.; Danzmann, K. LISA Phasemeter development. In Laser Interferometer Space Antenna: 6th International LISA Symposium; American Institute of Physics Conference Series; Merkovitz, S.M., Livas, J.C., Eds.; American Institute of Physics: Melville, NY, USA, 2006; Volume 873, pp. 689–696. [Google Scholar]
- Aston, S.M.; Speake, C.C. An Interferometric Based Optical Read-Out Scheme For The LISA Proof-Mass. In Laser Interferometer Space Antenna: 6th International LISA Symposium; American Institute of Physics Conference Series; Merkovitz, S.M., Livas, J.C., Eds.; American Institute of Physics: Melville, NY, USA, 2006; Volume 873, pp. 326–333. [Google Scholar]
- Schuldt, T.; Kraus, H.J.; Weise, D.; Braxmaier, C.; Peters, A.; Johann, U. A high sensitivity heterodyne interferometer as optical readout for the LISA inertial sensor. In Proceedings of the Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series, San Diego, CA, USA, 13 August 2006; Volume 6293, p. 62930Z. [Google Scholar]
- Armano, M. LISA Pathfinder: The experiment and the route to LISA. Class. Quant. Grav. 2009, 26, 094001. [Google Scholar] [CrossRef]
- Abich, K.; Abramovici, A.; Amparan, B.; Baatzsch, A.; Okihiro, B.B.; Barr, D.C.; Bize, M.P.; Bogan, C.; Braxmaier, C.; Burke, M.J.; et al. In-Orbit Performance of the GRACE Follow-on Laser Ranging Interferometer. Phys. Rev. Lett. 2019, 123, 031101. [Google Scholar] [CrossRef] [PubMed]
- Hines, A.; Richardson, L.; Wisniewski, H.; Guzman, F. Optomechanical Inertial Sensors. Appl. Opt. 2020, 59, G167–G174. [Google Scholar] [CrossRef] [PubMed]
- Robertson, N.; Drever, R.; Kerr, I.; Hough, J. Passive and active seismic isolation for gravitational radiation detectors and other instruments. J. Phys. E Sci. Instruments 1982, 15, 1101–1105. [Google Scholar] [CrossRef]
- Joo, K.N.; Clark, E.; Zhang, Y.; Ellis, J.D.; Guzmán, F. A compact high-precision periodic-error-free heterodyne interferometer. J. Opt. Soc. Am. A 2020, 37, B11–B18. [Google Scholar] [CrossRef]
- Wu, C.M.; Deslattes, R. Analytical Modeling of the Periodic Nonlinearity in Heterodyne Interferometry. Appl. Opt. 1998, 37, 6696–6700. [Google Scholar] [CrossRef] [PubMed]
- Joo, K.N.; Ellis, J.D.; Spronck, J.W.; van Kan, P.J.; Schmidt, R.H. Simple heterodyne laser interferometer with subnanometer periodic errors. Opt. Lett. 2009, 34, 386–388. [Google Scholar] [CrossRef]
- Wand, V.; Bogenstahl, J.; Braxmaier, C.; Danzmann, K.; Garcia, A.; Guzmán, F.; Heinzel, G.; Hough, J.; Jennrich, O.; Killow, C.; et al. Noise sources in the LTP heterodyne interferometer. Class. Quant. Grav. 2006, 23, S159–S167. [Google Scholar] [CrossRef]
- Heinzel, G.; Wand, V.; Garcia, A.; Guzman, F.; Steier, F.; Killow, C.; Robertson, D.L.; Ward, H. Investigation of Noise Sources in the LTP Interferometer S2-AEI-TN-3028. 2008. Available online: http://hdl.handle.net/11858/00-001M-0000-0013-4724-5 (accessed on 7 April 2021).
- Salvadé, Y.; Dändliker, R. Limitations of interferometry due to the flicker noise of laser diodes. J. Opt. Soc. Am. A 2000, 17, 927–932. [Google Scholar] [CrossRef]
- Drever, R.W.P.; Hall, J.L.; Kowalski, F.V.; Hough, J.; Ford, G.M.; Munley, A.J.; Ward, H. Laser phase and frequency stabilization using an optical resonator. Appl. Phys. B 1983, 31, 97–105. [Google Scholar] [CrossRef]
- Supplee, J.M.; Whittaker, E.A.; Lenth, W. Theoretical description of frequency modulation and wavelength modulation spectroscopy. Appl. Opt. 1994, 33, 6294–6302. [Google Scholar] [CrossRef]
- Numata, K.; Yu, A.W.; Jiao, H.; Merritt, S.A.; Micalizzi, F.; Fahey, M.E.; Camp, J.B.; Krainak, M.A. Laser system development for the LISA (Laser Interferometer Space Antenna) mission. In Solid State Lasers XXVIII: Technology and Devices; Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series; SPIE: Bellingham, WA, USA, 2019; Volume 10896, p. 108961H. [Google Scholar]
- Ellis, J.D.; Joo, K.N.; Buice, E.S.; Spronck, J.W. Frequency stabilized three mode HeNe laser using nonlinear optical phenomena. Opt. Express 2010, 18, 1373–1379. [Google Scholar] [CrossRef] [PubMed]
- Guzman Cervantes, F.; Livas, J.; Silverberg, R.; Buchanan, E.; Stebbins, R. Characterization of photoreceivers for LISA. Class. Quant. Grav. 2011, 28, 094010. [Google Scholar] [CrossRef]
- Nofrarias, M.; Gibert, F.; Karnesis, N.; Garcia, A.F.; Hewitson, M.; Heinzel, G.; Danzmann, K. Subtraction of temperature induced phase noise in the LISA frequency band. Phys. Rev. D 2013, 87, 102003. [Google Scholar] [CrossRef]
- Gibert, F.; Nofrarias, M.; Karnesis, N.; Gesa, L.; Martin, V.; Mateos, I.; Lobo, A.; Flatscher, R.; Gerardi, D.; Burkhardt, J. Thermo-elastic induced phase noise in the LISA Pathfinder spacecraft. Class. Quant. Grav. 2015, 32, 045014. [Google Scholar] [CrossRef]
- Badami, V.; de Groot, P. Displacement Measuring Interferometry. In Handbook of Optical Dimensional Metrology, 3rd ed.; Taylor & Francis: Boca Raton, FL, USA, 2013; pp. 178–198. [Google Scholar]
- Gerberding, O.; Diekmann, C.; Kullmann, J.; Tröbs, M.; Bykov, I.; Barke, S.; Brause, N.C.; Esteban Delgado, J.J.; Schwarze, T.S.; Reiche, J.; et al. Readout for intersatellite laser interferometry: Measuring low frequency phase fluctuations of high-frequency signals with microradian precision. Rev. Sci. Instruments 2015, 86, 074501. [Google Scholar] [CrossRef] [PubMed]
- Ellis, J.D. Field Guide to Displacement Measuring Interferometry; Greivenkamp, J.E., Ed.; SPIE Press: Bellingham, WA, USA, 2014; Volume FG30. [Google Scholar]
- Gardner, F.M. Phaselock Techniques, 3rd ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2005. [Google Scholar]
- Cervantes, F.G.; Steier, F.; Wanner, G.; Heinzel, G.; Danzmann, K. Subtraction of test mass angular noise in the LISA Technology Package interferometer. Appl. Phys. B 2008, 90, 395–400. [Google Scholar] [CrossRef]
- Marquardt, D.W. An Algorithm for Least-Squares Estimation of Nonlinear Parameters. J. Soc. Ind. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]
- Guzman, F. Gravitational Wave Observation from Space: Optical Measurement Techniques for LISA and LISA Pathfinder. Ph.D. Thesis, Max Planck Institute for Gravitational Physics & Gottfried Wilhelm Leibniz Universität Hannover, Hannover, Germany, 2009. Available online: https://edocs.tib.eu/files/e01dh09/606793232.pdf (accessed on 7 April 2021).
- Watchi, J.; Cooper, S.; Ding, B.; Mow-Lowry, C.M.; Collette, C. Contributed Review: A review of compact interferometers. Rev. Sci. Instruments 2018, 89, 121501. [Google Scholar] [CrossRef]
- Dehne, M.; Tröbs, M.; Heinzel, G.; Danzmann, K. Verification of polarising optics for the LISA optical bench. Opt. Express 2012, 20, 27273–27287. [Google Scholar] [CrossRef] [PubMed]









| i | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Hines, A.S.; Valdes, G.; Guzman, F. Investigation and Mitigation of Noise Contributions in a Compact Heterodyne Interferometer. Sensors 2021, 21, 5788. https://doi.org/10.3390/s21175788
Zhang Y, Hines AS, Valdes G, Guzman F. Investigation and Mitigation of Noise Contributions in a Compact Heterodyne Interferometer. Sensors. 2021; 21(17):5788. https://doi.org/10.3390/s21175788
Chicago/Turabian StyleZhang, Yanqi, Adam S. Hines, Guillermo Valdes, and Felipe Guzman. 2021. "Investigation and Mitigation of Noise Contributions in a Compact Heterodyne Interferometer" Sensors 21, no. 17: 5788. https://doi.org/10.3390/s21175788
APA StyleZhang, Y., Hines, A. S., Valdes, G., & Guzman, F. (2021). Investigation and Mitigation of Noise Contributions in a Compact Heterodyne Interferometer. Sensors, 21(17), 5788. https://doi.org/10.3390/s21175788







