The Adaptive Dynamic Programming Toolbox
Abstract
:1. Introduction
2. Review of Adaptive Dynamic Programming
| Algorithm 1. Policy iteration |
| Input: An initial admissible control , and a threshold . |
| Output: The approximate optimal control and the approximate optimal cost function . |
| 1: Set . |
| 2: while do |
| 3: Policy evaluation: solve for the continuously differentiable cost function with using |
| 4: Policy improvement: update the control policy by
|
| 5: if for all x then |
| 6: break |
| 7: end if |
| 8: Set . |
| 9: end while |
3. Implementation Details and Software Features
3.1. Implementation of Computational Adaptive Dynamic Programming
| Algorithm 2. Computational adaptive dynamic programming |
| Input: An approximation degree , an initial admissible control , an exploration signal , and a threshold . |
| Output: The approximate optimal control and the approximate optimal cost function . |
| 1: Apply as the input during a sufficiently long period and collect necessary data. |
| 2: Set . |
| 3: while do |
| 4: Generate and . |
| 5: Obtain and by solving the minimization problem
|
| 6: if and then |
| 7: break |
| 8: end if |
| 9: Set . |
| 10: end while |
| 11: return and |
3.2. Software Features
3.2.1. Symbolic Expressions
3.2.2. Working Modes
3.2.3. Options
4. Applications to the Satellite Attitude Stabilizing Problem
4.1. Model-Based Case
4.2. Model-Free Case
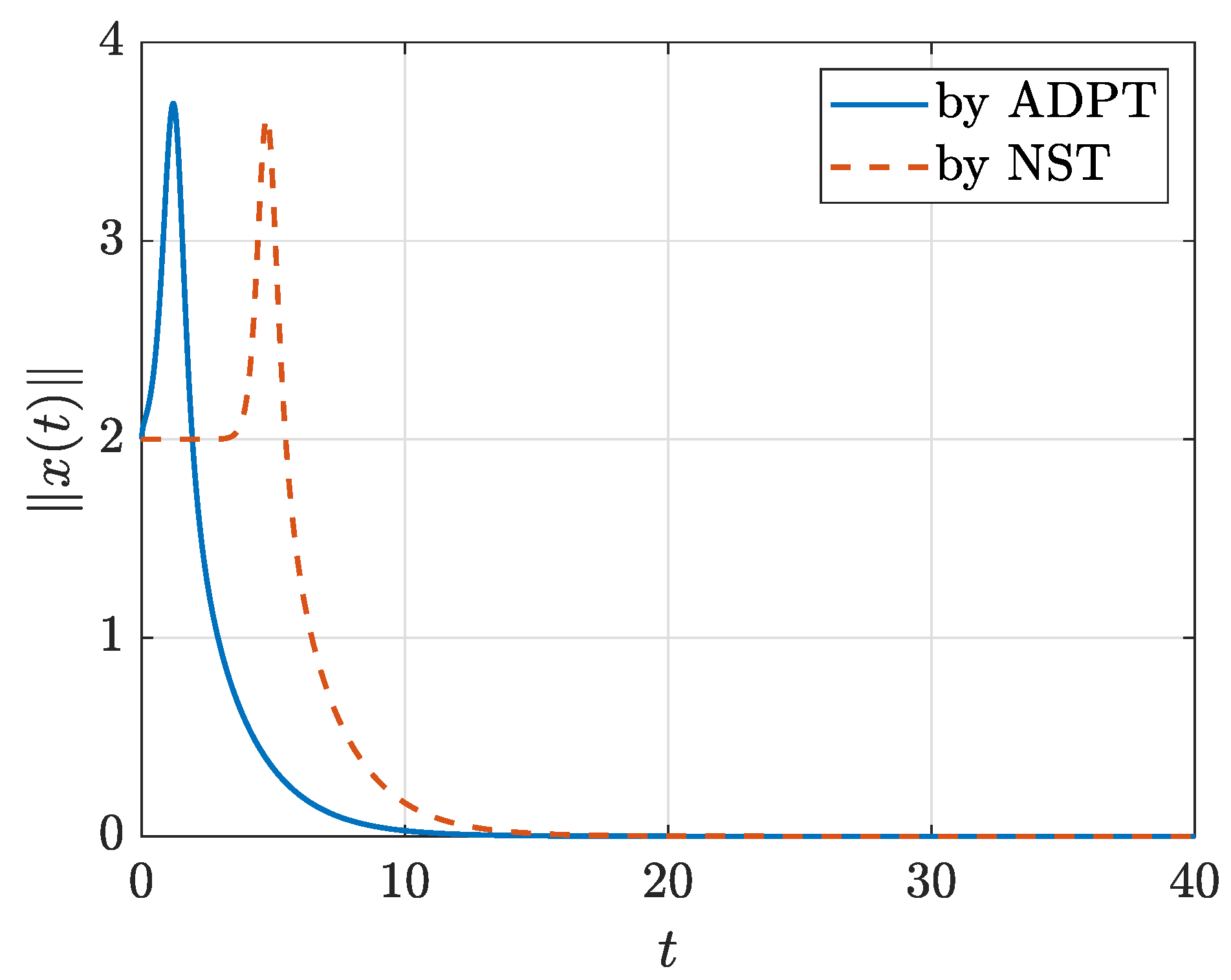
4.3. Discussion
5. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Appendix A
| 1 | n = 2; % state dimension |
| 2 | m = 1; % control dimension |
| 3 | %% Symbolic variables. |
| 4 | syms x [n,1] real |
| 5 | syms u [m,1] real |
| 6 | syms t real |
| 7 | |
| 8 | %% Define the system. |
| 9 | k1 = 3; k2 = 2; k3 = 2; k4 = 5; |
| 10 | f = [x2; |
| 11 | (-k1*x1-k2*x1^3-k3*x2)/k4]; |
| 12 | g = [0; |
| 13 | 1/k4]; |
| 14 | |
| 15 | %% Define the cost function. |
| 16 | q = 5*x1^2 + 3*x2^2; |
| 17 | R = 2; |
| 18 | |
| 19 | %% Execute ADP iterations. |
| 20 | d = 3; % approximation degree |
| 21 | [w,c] = adpModelBased(f,g,x,n,u,m,q,R,t,d); |
| 1 | n = 2; % state dimension |
| 2 | m = 1; % control dimension |
| 3 | |
| 4 | %% Define the cost function. |
| 5 | q = @(x) 5*x(1)^2 + 3*x(2)^2; |
| 6 | R = 2; |
| 7 | |
| 8 | %% Generate data. |
| 9 | syms x [n,1] real |
| 10 | syms t real |
| 11 | k1 = 3; k2 = 2; k3 = 2; k4 = 5; |
| 12 | % System dynamics. |
| 13 | f = [x2; |
| 14 | (-k1*x1-k2*x1^3-k3*x2)/k4]; |
| 15 | g = [0; |
| 16 | 1/k4]; |
| 17 | |
| 18 | F = [1, 1] % feedback gain |
| 19 | |
| 20 | % Exploration signal. |
| 21 | eta = 0.8*(sin(7*t)+sin(1.1*t)+sin(sqrt(3)*t)+... |
| 22 | sin(sqrt(6)*t)); |
| 23 | e = matlabFunction(eta,’Vars’,t); |
| 24 | |
| 25 | % To be used in the function ode45. |
| 26 | dx = matlabFunction(f+g*(-F*x+eta),’Vars’,{t,x}); |
| 27 | |
| 28 | xInit = [-3, 2; |
| 29 | 2.2, 3]; |
| 30 | tSpan = [0:0.002:6; |
| 31 | 0:0.002:6]; |
| 32 | odeOpts = odeSet(’RelTol’,1e-6,’AbsTol’,1e-6); |
| 33 | |
| 34 | t_save = []; |
| 35 | x_save = []; |
| 36 | for i = 1:size(xInit,1) |
| 37 | [time, states] = ode45(@(t,x)dx(t,x),tSpan(i,:),... |
| 38 | xInit(i,:),odeOpts); |
| 39 | t_save = [t_save; time]; |
| 40 | x_save = [x_save; states]; |
| 41 | end |
| 42 | |
| 43 | u0_save = -x_save * F; |
| 44 | eta_save = e(t_save); |
| 45 | |
| 46 | %% Execute ADP iterations. |
| 47 | d = 3; % approximation degree |
| 48 | [w,c] = adpModelFree(t_save,x_save,n,u0_save,m,... |
| 49 | eta_save,d,q,R); |
| 1 | %% The user may specify settings. |
| 2 | xInit = [-3, 2; |
| 3 | 2.2, 3]; |
| 4 | tSpan = [0, 10; |
| 5 | 0, 8]; |
| 6 | |
| 7 | syms t real |
| 8 | eta = [0.8*sin(7*t)+sin(3*t); |
| 9 | sin(1.1*t)+sin(pi*t)]; |
| 10 | |
| 11 | adpOpt = adpSetModelBased(’xInit’,xInit,’tSpan’,tSpan,... |
| 12 | ’explSymb’,eta); |
| 13 | |
| 14 | %% Execute ADP iterations. |
| 15 | [w,c] = adpModelBased(f,g,x,n,u,m,q,R,t,d,adpOpt); |
| 1 %% The user may specify settings. |
| 2 adpOpt = adpSetModelFree(’stride’,2); |
| 3 |
| 4 %% Execute ADP iterations. |
| 5 [w,c] = adpModelFree(t_save,x_save,n,u0_save,m,... |
| 6 eta_save,d,q,R,adpOpt); |
References
- Kirk, D.E. Optimal Control Theory: An Introduction; Prentice-Hall: Englewood Cliffs, NJ, USA, 1970. [Google Scholar]
- Lewis, F.L.; Vrabie, D.L.; Syrmos, V.L. Optimal Control; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2012. [Google Scholar]
- Al’brekht, E.G. On the optimal stabilization of nonlinear systems. J. Appl. Math. Mech. 1961, 25, 1254–1266. [Google Scholar] [CrossRef]
- Garrard, W.L.; Jordan, J.M. Design of nonlinear automatic flight control systems. Automatica 1977, 13, 497–505. [Google Scholar] [CrossRef]
- Nishikawa, Y.; Sannomiya, N.; Itakura, H. A method for suboptimal design of nonlinear feedback systems. Automatica 1971, 7, 703–712. [Google Scholar] [CrossRef]
- Saridis, G.N.; Lee, C.-S.G. An approximation theory of optimal control for trainable manipulators. IEEE Trans. Syst. Man Cybern. 1979, SMC-9, 152–159. [Google Scholar] [CrossRef]
- Beard, R.W.; Saridis, G.N.; Wen, J.T. Galerkin approximations of the generalized Hamilton-Jacobi-Bellman equation. Automatica 1997, 33, 2159–2177. [Google Scholar] [CrossRef]
- Beard, R.W.; Saridis, G.N.; Wen, J.T. Approximate solutions to the time-invariant Hamilton-Jacobi-Bellman equation. J. Optim. Theory Appl. 1998, 96, 589–626. [Google Scholar] [CrossRef]
- Abu-Khalaf, M.; Lewis, F.L. Nearly optimal control laws for nonlinear systems with saturating actuators using a neural network HJB approach. Automatica 2005, 41, 779–791. [Google Scholar] [CrossRef]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction; MIT Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Jiang, Y.; Jiang, Z.-P. Computational adaptive optimal control for continuous-time linear systems with completely unknown dynamics. Automatica 2012, 48, 2699–2704. [Google Scholar] [CrossRef]
- Vrabie, D.L.; Lewis, F.L. Neural network approach to continuous-time direct adaptive optimal control for partially unknown nonlinear systems. Neural Netw. 2009, 22, 237–246. [Google Scholar] [CrossRef] [PubMed]
- Jiang, Y.; Jiang, Z.-P. Robust adaptive dynamic programming and feedback stabilization of nonlinear systems. IEEE Trans. Neural Netw. Learn. Syst. 2014, 25, 882–893. [Google Scholar] [CrossRef] [PubMed]
- Jiang, Y.; Jiang, Z.-P. Robust Adaptive Dynamic Programming; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2014. [Google Scholar]
- Lee, J.Y.; Park, J.B.; Choi, Y.H. Integral reinforcement learning for continuous-time input-affine nonlinear systems with simultaneous invariant explorations. IEEE Trans. Neural Netw. Learn. Syst. 2015, 26, 916–932. [Google Scholar] [PubMed]
- Krener, A.J. Nonlinear Systems Toolbox. MATLAB Toolbox Available upon Request from ajkrener@ucdavis.edu.
- Giftthaler, M.; Neunert, M.; Stäuble, M.; Buchli, J. The Control Toolbox—An open-source C++ library for robotics, optimal and model predictive control. In Proceedings of the IEEE 2018 IEEE International Conference on Simulation, Modeling, and Programming for Autonomous Robots (SIMPAR), Brisbane, Australia, 16–19 May 2018; pp. 123–129. [Google Scholar]
- Houska, B.; Ferreau, H.J.; Diehl, M. ACADO Toolkit—An open source framework for automatic control and dynamic optimization. Optim. Control Appl. Meth. 2011, 32, 298–312. [Google Scholar] [CrossRef]
- Verschueren, R.; Frison, G.; Kouzoupis, D.; Frey, J.; van Duijkeren, N.; Zanelli, A.; Novoselnik, B.; Albin, T.; Quirynen, R.; Diehl, M. ACADOS: A modular open-source framework for fast embedded optimal control. arXiv 2019, arXiv:1910.13753. [Google Scholar]
- Patterson, M.A.; Rao, A.V. GPOPS-II: A MATLAB software for solving multiple-phase optimal control problems using hp-adaptive Gaussian quadrature collocation methods and sparse nonlinear programming. ACM Trans. Math. Softw. 2014, 41, 1–37. [Google Scholar] [CrossRef] [Green Version]
- Cox, D.A.; Little, J.; O’Shea, D. Ideals, Varieties, and Algorithms: An Introduction to Computational Algebraic Geometry and Commutative Algebra; Springer: New York, NY, USA, 2015. [Google Scholar]
- Chang, D.E. On controller design for systems on manifolds in Euclidean space. Int. J. Robust Nonlinear Control 2018, 28, 4981–4998. [Google Scholar] [CrossRef]
- Ko, W. A Stable Embedding Technique for Control of Satellite Attitude Represented in Unit Quaternions. Master’s Thesis, Korea Advanced Institute of Science & Technology, Daejeon, Korea, 2020. [Google Scholar]
- Ko, W.; Phogat, K.S.; Petit, N.; Chang, D.E. Tracking controller design for satellite attitude under unknown constant disturbance using stable embedding. J. Electr. Eng. Technol. 2021, 16, 1089–1097. [Google Scholar] [CrossRef]
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous control with deep reinforcement learning. arXiv 2015, arXiv:509.02971. [Google Scholar]
- Gurney, K. An Introduction to Neural Networks; UCL Press: London, UK, 1997. [Google Scholar]
- Caterini, A.L.; Chang, D.E. Deep Neural Networks in a Mathematical Framework; Springer: New York, NY, USA, 2018. [Google Scholar]
| Time [s] | |||
|---|---|---|---|
| ADPT (model-based) | 37.8259 | 1.5994 | |
| 33.6035 | 3.2586 | ||
| 33.4986 | 13.1021 | ||
| ADPT (model-free) | 43.8308 | 0.9707 | |
| 36.8319 | 3.3120 | ||
| 37.4111 | 64.8562 | ||
| NST | 208.9259 | 0.2702 | |
| 94.6868 | 0.6211 | ||
| 64.0721 | 3.6201 | ||
| ACADO | - | 32.6000 | 2359.67 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xing, X.; Chang, D.E. The Adaptive Dynamic Programming Toolbox. Sensors 2021, 21, 5609. https://doi.org/10.3390/s21165609
Xing X, Chang DE. The Adaptive Dynamic Programming Toolbox. Sensors. 2021; 21(16):5609. https://doi.org/10.3390/s21165609
Chicago/Turabian StyleXing, Xiaowei, and Dong Eui Chang. 2021. "The Adaptive Dynamic Programming Toolbox" Sensors 21, no. 16: 5609. https://doi.org/10.3390/s21165609
APA StyleXing, X., & Chang, D. E. (2021). The Adaptive Dynamic Programming Toolbox. Sensors, 21(16), 5609. https://doi.org/10.3390/s21165609






