Opportunistic DF-AF Selection Relaying in Hybrid Wireless and Power Line Communication for Indoor IoT Networks
Abstract
:1. Introduction
- The for the direct link and ODF-AF relay-aided links of the dual-hop HD EH HWP over log-normal fading channels is analytically expressed.
- The and throughput performance of the ODF-AF selection relaying scheme in the HWP are analyzed and validated with Monte Carlo simulation results.
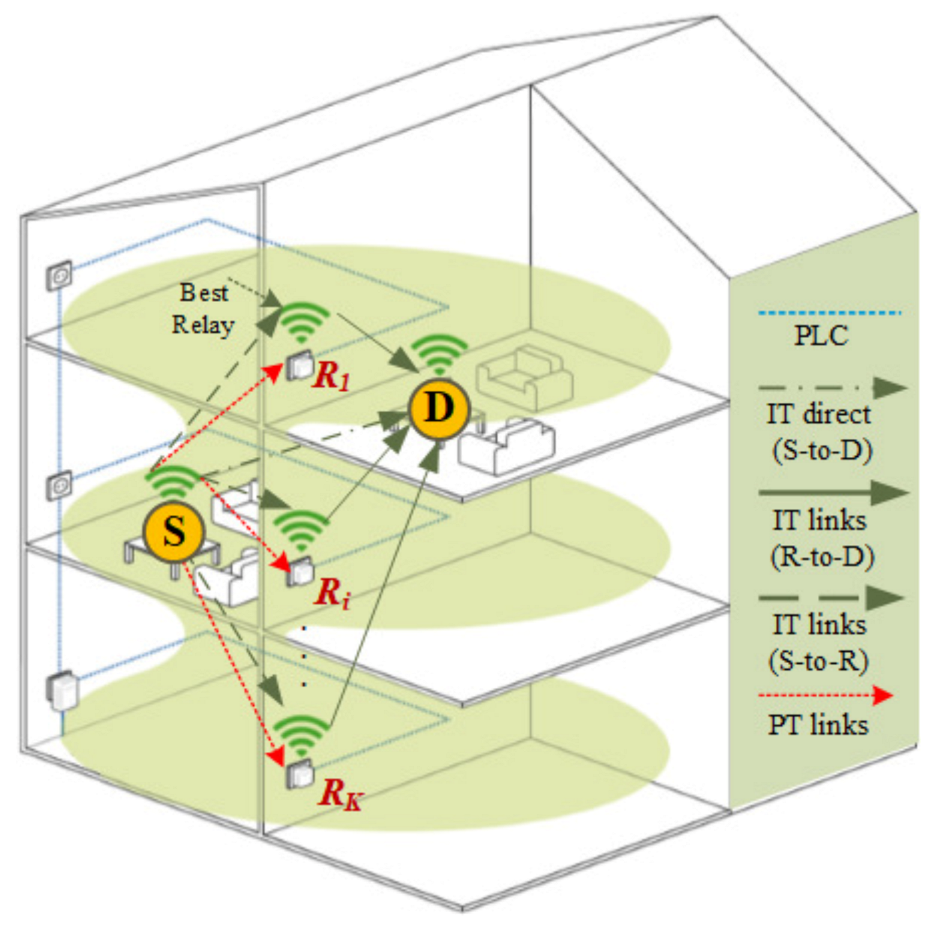
2. System Model
3. Performance Analysis
3.1. Opportunistic Decode-and-Forward (ODF) Relaying Scheme
3.2. Opportunistic Amplify-and-Forward (OAF) Relaying Scheme
3.3. Opportunistic Decode-and-Forward and Amplify-and-Forward (ODF-AF) Relaying Scheme
3.4. Throughput Performance
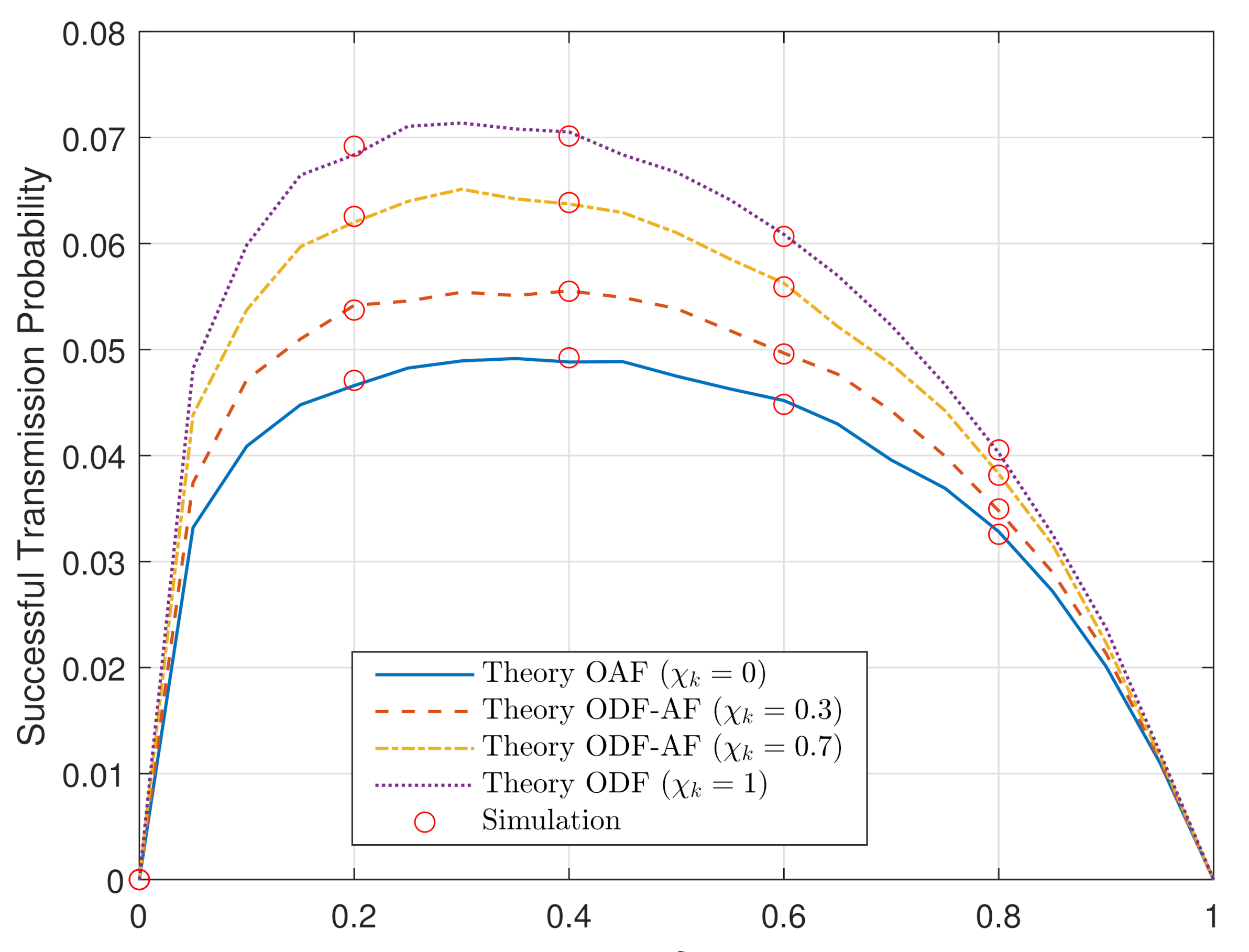
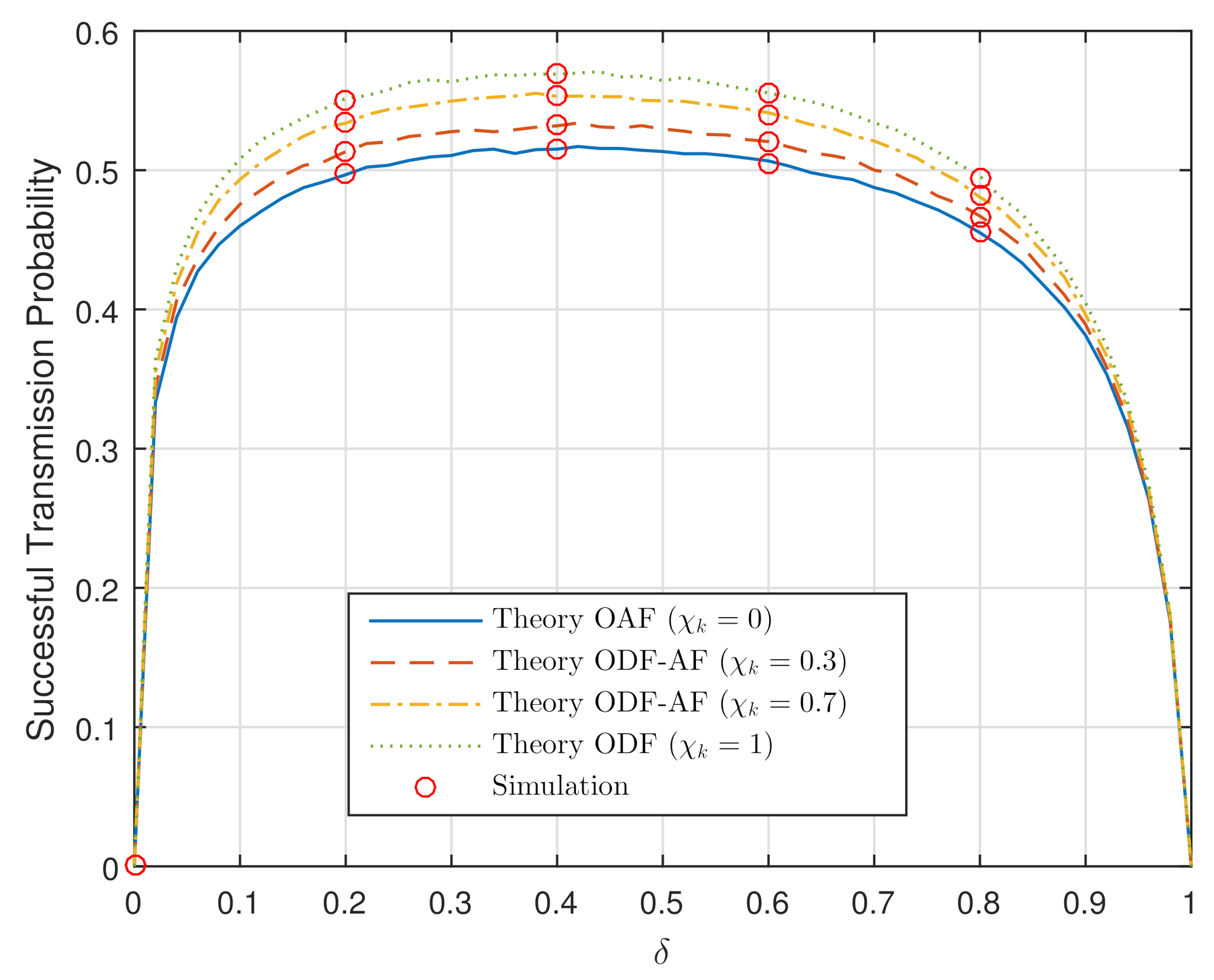
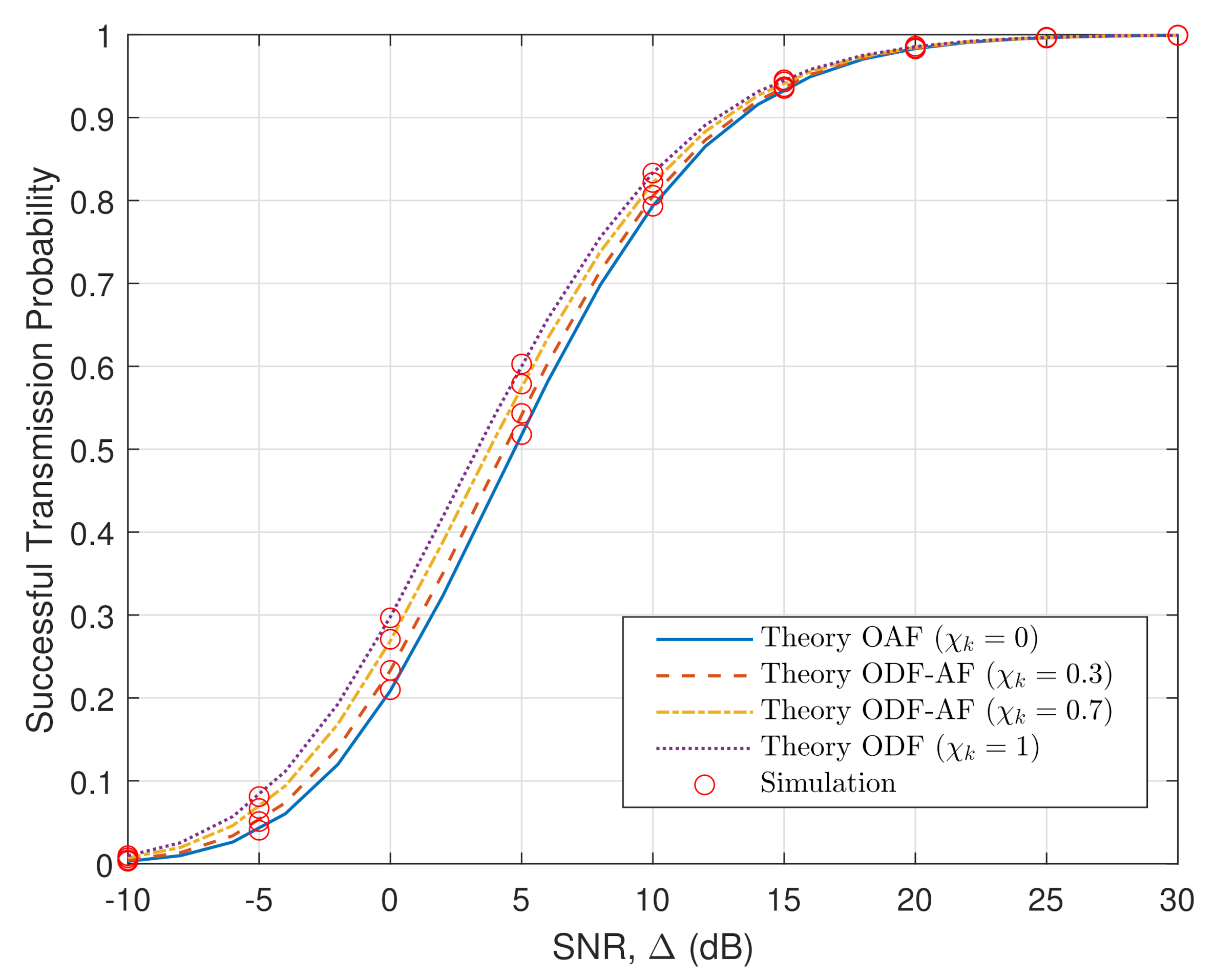
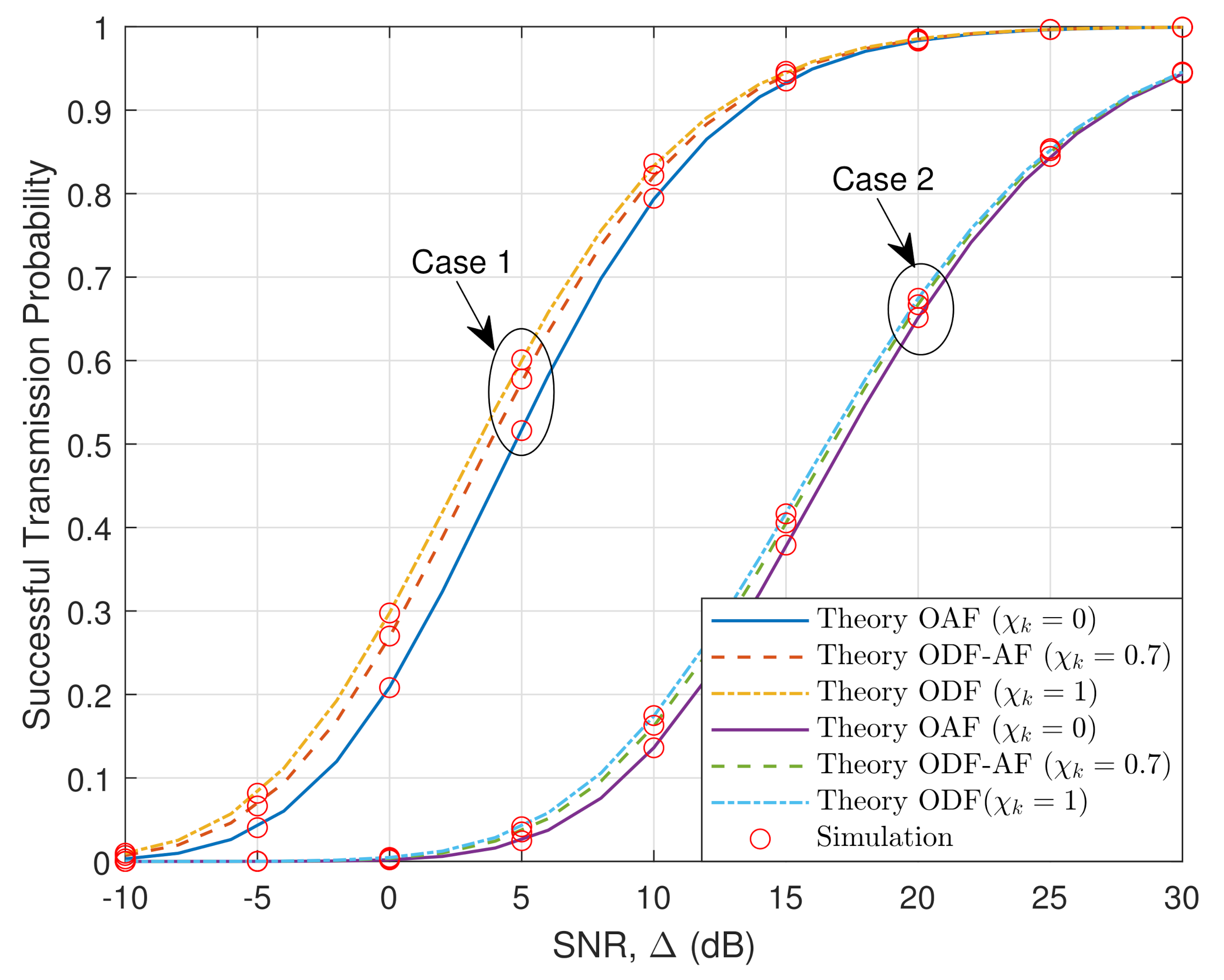
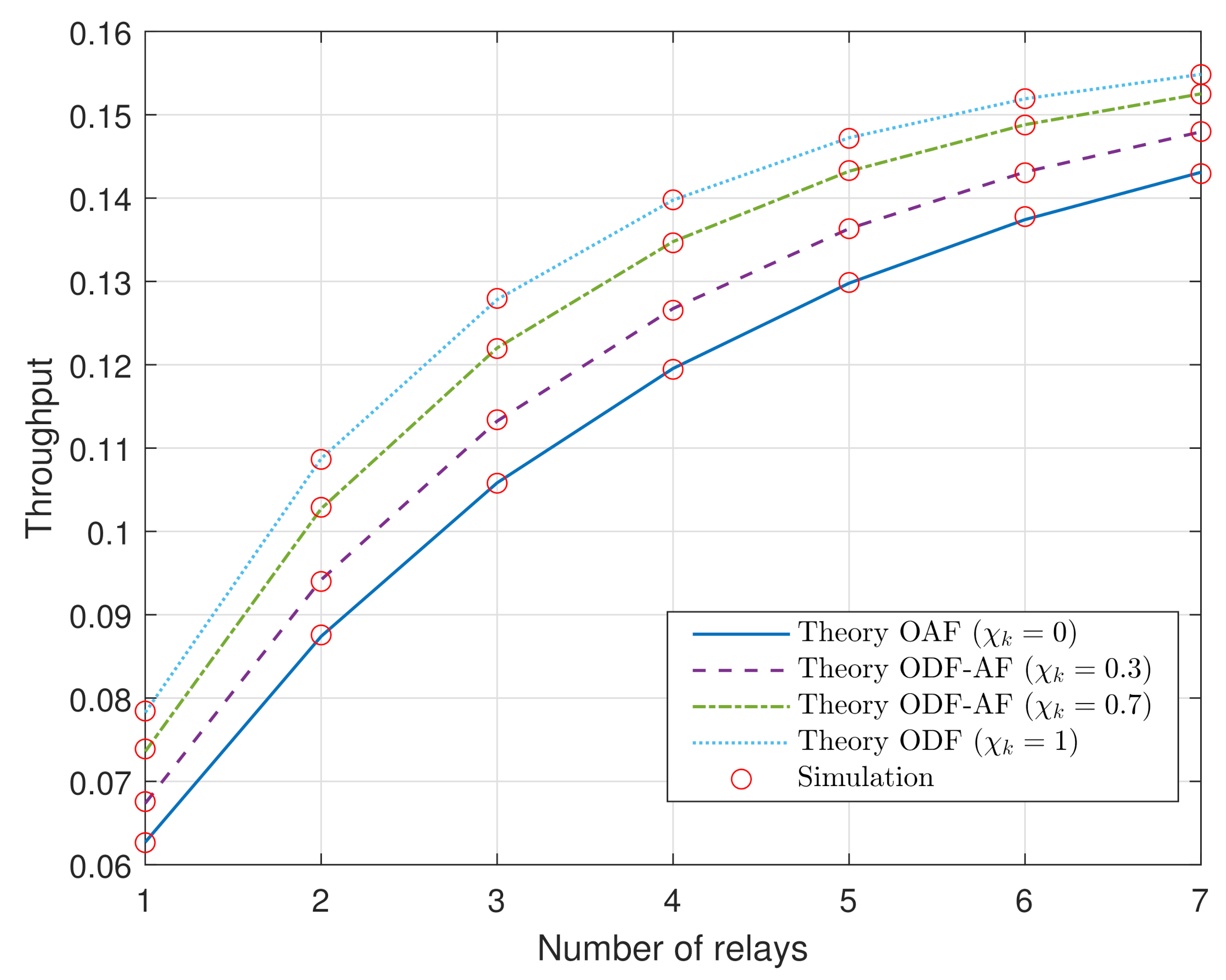
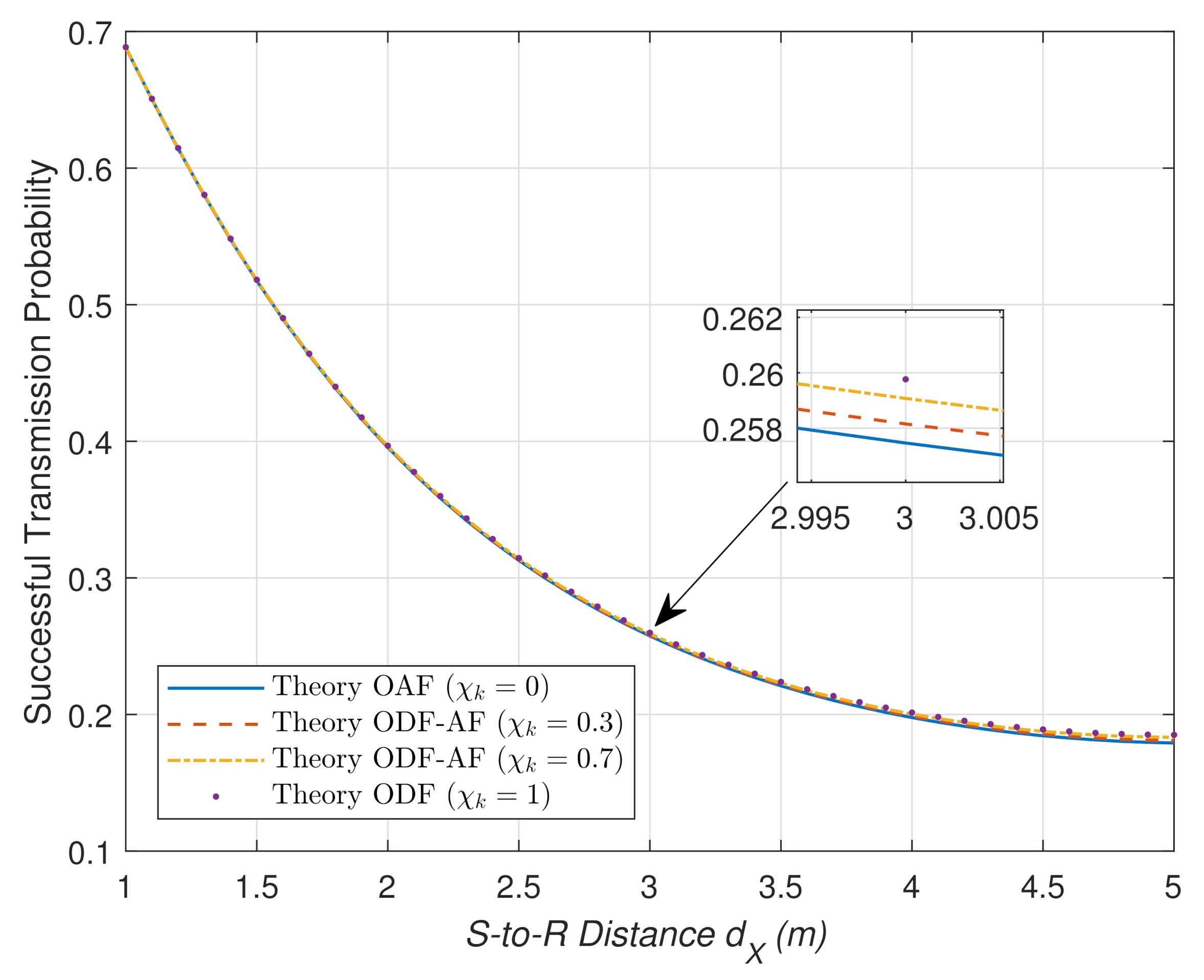
4. Numerical Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| 5G | Fifth generation of cellular networks |
| EH | Energy harvesting |
| RF | Radio frequency |
| SWIPT | Simultaneous wireless information and power transfer |
| PLC | Power line communication |
| SG | Smart grids |
| IoT | Internet of Things |
| HWP | Hybrid wireless and power line communication |
| EE | Energy efficiency |
| SE | Spectrum efficiency |
| PT | Power transmission |
| PS | Power splitting |
| PSR | Power splitting-based relaying |
| TSR | Time splitting-based relaying |
| (O)DF | (Opportunistic) decode-and-forward |
| (O)AF | (Opportunistic) amplify-and-forward |
| ODF-AF | Opportunistic DF-AF |
| HD | Half-duplex |
| FD | Full-duplex |
| RS | Relay selection |
| SDP | Signal decision processor |
| SNR | Signal-to-noise ratio |
| CSI | Channel state information |
| AWGN | Additive white Gaussian noise |
| i.i.d. | independently and identically distributed |
| Probability density function | |
| CDF | Cumulative distribution function |
| Outage probability | |
| Successful transmission probability | |
| ACK | Acknowledgement signal |
| RV | Random variable |
| TDMA | Time division multiple access |
| SC | Selection combining |
| S | The source node |
| D | The destination node |
| The i-th relay of K relays, () | |
| X, Y, Z | The channel coefficients of S–, –D, S–D links |
| , and | The i.i.d. log-normal RVs with , and |
| , | The mean and the standard deviation of |
| , , | The S–, –D, S–D distances |
| The power of S | |
| The energy of i-th R | |
| Additive white Gaussian noise (AWGN), () | |
| The zero mean and variance at the i-th R and D | |
| The decoding state of ODF-AF , |
References
- Andrews, J.G.; Buzzi, S.; Choi, W.; Hanly, S.V.; Lozano, A.; Soong, A.C.K.; Zhang, J.C. What will 5G be? IEEE J. Sel. Areas Commun. 2014, 32, 1065–1082. [Google Scholar] [CrossRef]
- Osseiran, A.; Boccardi, F.; Braun, V.; Kusume, K.; Marsch, P.; Maternia, M.; Queseth, O.; Schellmann, M.; Schotten, H.; Taoka, H.; et al. Scenarios for 5G mobile and wireless communications: The vision of the METIS project. IEEE Commun. Mag. 2014, 52, 26–35. [Google Scholar] [CrossRef]
- Agiwal, M.; Roy, A.; Saxena, N. Next generation 5G wireless networks: A comprehensive survey. IEEE Commun. Surv. Tutor. 2016, 18, 1617–1655. [Google Scholar] [CrossRef]
- Palattella, M.R.; Dohler, M.; Grieco, A.; Rizzo, G.; Torsner, J.; Engel, T.; Ladid, L. Internet of Things in the 5G era: Enablers architecture and business models. IEEE J. Sel. Areas Commun. 2016, 34, 510–527. [Google Scholar] [CrossRef] [Green Version]
- Lin, J.; Yu, W.; Zhang, N.; Yang, X.; Zhang, H.; Zhao, W. A survey on Internet of Things: Architecture enabling technologies security privacy and applications. IEEE Internet Things J. 2017, 4, 1125–1142. [Google Scholar] [CrossRef]
- Nguyen, H.-S.; Voznak, M.; Nguyen, M.-T.; Sevcik, L. Performance Analysis with Wireless Power Transfer Constraint Policies in Full-Duplex Relaying Networks. Elektronika ir Elektrotechnika 2017, 23, 70–76. [Google Scholar] [CrossRef] [Green Version]
- Lu, X.; Wang, P.; Niyato, D.; Kim, D.I.; Han, Z. Wireless networks with RF energy harvesting: A contemporary survey. IEEE Commun. Surv. Tutor. 2015, 17, 757–789. [Google Scholar] [CrossRef] [Green Version]
- Huang, K.; Zhou, X. Cutting the last wires for mobile communications by microwave power transfer. IEEE Commun. Mag. 2015, 53, 86–93. [Google Scholar] [CrossRef] [Green Version]
- Ponnimbaduge Perera, T.D.; Jayakody, D.N.K.; Sharma, S.K.; Chatzinotas, S.; Li, J. Simultaneous Wireless Information and Power Transfer (SWIPT): Recent Advances and Future Challenges. IEEE Commun. Surv. Tutor. 2018, 20, 264–302. [Google Scholar] [CrossRef] [Green Version]
- Zhang, R.; Ho, C. MIMO broadcasting for simultaneous wireless information and power transfer. IEEE Trans. Wirel. Commun. 2013, 12, 1989–2001. [Google Scholar] [CrossRef] [Green Version]
- Zhou, X.; Zhang, R.; Ho, C. Wireless information and power transfer: Architecture design and rate-energy tradeoff. IEEE Trans. Commun. 2013, 61, 4754–4767. [Google Scholar] [CrossRef] [Green Version]
- Liu, L.; Zhang, R.; Chua, K. Wireless Information Transfer with Opportunistic Energy Harvesting. IEEE Trans. Wirel. Commun. 2013, 12, 288–300. [Google Scholar] [CrossRef] [Green Version]
- Ng, D.W.K.; Lo, E.S.; Schober, R. Wireless Information and Power Transfer: Energy Efficiency Optimization in OFDMA Systems. IEEE Trans. Wirel. Commun. 2013, 12, 6352–6370. [Google Scholar] [CrossRef] [Green Version]
- Chang, Z.; Wang, Z.; Guo, X.; Yang, C.; Han, Z.; Ristaniemi, T. Distributed Resource Allocation for Energy Efficiency in OFDMA Multicell Networks With Wireless Power Transfer. IEEE J. Sel. Areas Commun. 2019, 37, 345–356. [Google Scholar] [CrossRef] [Green Version]
- Ng, D.W.K.; Schober, R. Dynamic resource allocation in OFDMA systems with full-duplex and hybrid relaying. In Proceedings of the 2011 IEEE International Conference on Communications (ICC), Kyoto, Japan, 5–9 June 2011; pp. 1–6. [Google Scholar]
- Zhang, M.; Liu, Y. Energy Harvesting for Physical-Layer Security in OFDMA Networks. IEEE Trans. Inf. Forens. Secur. 2016, 11, 154–162. [Google Scholar] [CrossRef] [Green Version]
- Yu, H.; Guo, S.; Yang, Y.; Ji, L.; Yang, Y. Secrecy Energy Efficiency Optimization for Downlink Two-User OFDMA Networks with SWIPT. IEEE Syst. J. 2019, 13, 324–335. [Google Scholar] [CrossRef]
- Nasir, A.A.; Zhou, X.; Durrani, S.; Kennedy, R.A. Relaying protocols for wireless energy harvesting and information processing. IEEE Trans. Wirel. Commun. 2013, 12, 3622–3636. [Google Scholar] [CrossRef] [Green Version]
- Nguyen, H.-S.; Nguyen, T.-S.; Voznak, M. Wireless powered D2D communications underlying cellular networks: Design and performance of the extended coverage. Automatika 2017, 58, 391–399. [Google Scholar] [CrossRef] [Green Version]
- Xia, M.; Assa, S. Modeling and analysis of cooperative relaying in spectrum-sharing cellular systems. IEEE Trans. Veh. Technol. 2016, 65, 9112–9122. [Google Scholar] [CrossRef]
- Chen, E.; Xia, M.; da Costa, D.B.; Assa, S. Multi-hop cooperative relaying with energy harvesting from cochannel interferences. IET Commun. 2017, 21, 1089–7798. [Google Scholar] [CrossRef]
- Laneman, J.N.; Tse, D.N.C.; Wornell, G.W. Cooperative diversity in wireless networks: Efficient protocols and outage behavior. IEEE Trans. Inf. Theor. 2004, 50, 3062–3080. [Google Scholar] [CrossRef]
- Bhatnagar, M.R.; Hjorungnes, A. ML decoder for decode-and-forward based cooperative communication system. IEEE Trans. Wirel. Commun. 2011, 10, 4080–4090. [Google Scholar] [CrossRef]
- Li, Y.; Vucetic, B. On the performance of a simple adaptive relaying protocol for wireless relay networks. In Proceedings of the VTC Spring 2008—IEEE Vehicular Technology Conference, Marina Bay, Singapore, 11–14 May 2008. [Google Scholar]
- Su, W.; Liu, X. On optimum selection relaying protocols in cooperative wireless networks. IEEE Trans. Commun. 2010, 58, 52–57. [Google Scholar] [CrossRef]
- Zhang, T.; Chen, W.; Cao, Z. Opportunistic DF-AF selection relaying with optimal relay selection in Nakagami-m fading environments. In Proceedings of the 2012 1st IEEE International Conference on Communications in China (ICCC), Beijing, China, 15–17 August 2012; pp. 619–624. [Google Scholar]
- Li, D. Opportunistic DF-AF Selection for Cognitive Relay Networks. IEEE Trans. Veh. Technol. 2016, 65, 2790–2796. [Google Scholar] [CrossRef]
- Xiuping, W.; Feng, Y.; Tian, Z. The DF-AF Selection Relay Transmission Based on Energy Harvesting. In Proceedings of the 10th International Conference on Measuring Technology and Mechatronics Automation (ICMTMA), Changsha, China, 10–11 February 2018; pp. 174–177. [Google Scholar]
- Nguyen, H.-S.; Bui, A.; Do, D.; Voznak, M. Imperfect channel state information of AF and DF energy harvesting cooperative networks. China Commun. 2016, 13, 11–19. [Google Scholar] [CrossRef]
- Riihonen, T.; Werner, S.; Wichman, R. Hybrid Full-Duplex/Half-Duplex Relaying with Transmit Power Adaptation. IEEE Trans. Wirel. Commun. 2011, 10, 3074–3085. [Google Scholar] [CrossRef]
- Nguyen, H.-S.; Nguyen, T.-S.; Vo, V.-T.; Voznak, M. Hybrid full-duplex/half-duplex relay selection scheme with optimal power under individual power constraints and energy harvesting. Comput. Commun. 2018, 124, 31–44. [Google Scholar] [CrossRef]
- Zhang, Z.; Chai, X.; Long, K.; Vasilakos, A.V.; Hanzo, L. Full duplex techniques for 5G networks: Self-interference cancellation, protocol design, and relay selection. IEEE Commun. Mag. 2015, 53, 128–137. [Google Scholar] [CrossRef] [Green Version]
- Foschini, G.J. Layered space-time architecture for wireless communication in a fading environment when using multi-element antennas. Bell Syst. Technol. J. 1996, 1, 41–59. [Google Scholar] [CrossRef]
- Krikidis, I.; Suraweera, H.A.; Smith, P.J.; Yuen, C. Full-Duplex Relay Selection for Amplify-and-Forward Cooperative Networks. IEEE Trans. Wirel. Commun. 2012, 11, 4381–4393. [Google Scholar] [CrossRef]
- Luo, S.; Teh, K.C. Buffer State Based Relay Selection for Buffer-Aided Cooperative Relaying Systems. IEEE Trans. Wirel. Commun. 2015, 14, 5430–5439. [Google Scholar] [CrossRef]
- Zou, Y.; Champagne, B.; Zhu, W.; Hanzo, L. Relay-Selection Improves the Security-Reliability Trade-Off in Cognitive Radio Systems. IEEE Trans. Commun. 2015, 63, 215–228. [Google Scholar] [CrossRef] [Green Version]
- Wang, W.; Teh, K.C.; Li, K.H. Generalized Relay Selection for Improved Security in Cooperative DF Relay Networks. IEEE Wirel. Commun. Lett. 2016, 5, 28–31. [Google Scholar] [CrossRef]
- Oestges, C.; Czink, N.; Bandemer, B.; Paulraj, A. Capacity performance of outdoor-to-indoor relay schemes in measured radio channels. In Proceedings of the IEEE 20th International Symposium on Personal, Indoor and Mobile Radio Communications, Tokyo, Japan, 13–16 September 2009; pp. 1113–1117. [Google Scholar]
- Renzo, M.D.; Graziosi, F.; Santucci, F. A comprehensive framework for performance analysis of cooperative multi-hop wireless systems over log-normal fading channels. IEEE Trans. Commun. 2010, 58, 531–544. [Google Scholar] [CrossRef] [Green Version]
- Nouri, H.; Touati, F.; Uysal, M. Diversity-Multiplexing Tradeoff for Log-Normal Fading Channels. IEEE Trans. Commun. 2016, 64, 3119–3129. [Google Scholar] [CrossRef]
- Zhu, B.; Cheng, J.; Yan, J.; Wang, J.; Wu, L.; Wang, Y. A new technique for analyzing asymptotic outage performance of diversity over log-normal fading channels. In Proceedings of the 15th Canadian Workshop on Information Theory (CWIT), Quebec City, QC, Canada, 11–14 June 2017; pp. 1–5. [Google Scholar]
- Cammin, C.; Krush, D.; Heynicke, R.; Scholl, G. Test method for narrowband F/TDMA-based wireless sensor/actuator networks including radio channel emulation in severe multipath environments. J. Sens. Sens. Syst. 2018, 7, 183–192. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Xiao, R.; Shen, J.; Yang, H.; Yan, C. Hybrid protocol for wireless energy harvesting network over log-normal fading channel. J. Eng. 2018, 6, 339–341. [Google Scholar] [CrossRef]
- Liu, Y.; Shen, J.; Pan, Z.; Xiao, R.; Yang, H.; Yan, C. Performance analysis of dual-hop AF relaying networks over log-normal fading channels with interferences. In Proceedings of the IEEE/CIC International Conference on Communications Workshops in China (ICCC Workshops), Changchun, China, 1–13 August 2019; pp. 130–135. [Google Scholar]
- Rabie, K.; Tonello, A.M.; Al-Dhahir, N.; Song, J.; Sendin, A. IEEE Access Special Section Editorial: Advances in Power Line Communication and its Applications. IEEE Access 2019, 7, 133371–133374. [Google Scholar] [CrossRef]
- Rubin, I.; Lin, Y.; Kofman, D. Relay-aided networking for power line communications. In Proceedings of the 2014 Information Theory and Applications Workshop (ITA), San Diego, CA, USA, 9–14 February 2014; pp. 1–6. [Google Scholar]
- Qian, Y.; Yan, J.; Guan, H.; Li, J.; Zhou, X.; Guo, S.; Jayakody, D.N.K. Design of Hybrid Wireless and Power Line Sensor Networks With Dual-Interface Relay in IoT. IEEE Internet Things J. 2019, 6, 239–249. [Google Scholar] [CrossRef]
- Lee, J.; Kim, Y. Diversity Relaying for Parallel Use of Power-Line and Wireless Communication Networks. IEEE Trans. Power Deliv. 2014, 29, 1301–1310. [Google Scholar] [CrossRef]
- Dib, L.d.M.B.A.; Fernandes, V.; Filomeno, M.d.L.; Ribeiro, M.V. Hybrid PLC/Wireless Communication for Smart Grids and Internet of Things Applications. IEEE Internet Things J. 2018, 5, 655–667. [Google Scholar] [CrossRef]
- Rabie, K.M.; Adebisi, B.; Yousif, E.H.G.; Gacanin, H.; Tonello, A.M. A comparison between orthogonal and non-orthogonal multiple access in cooperative relaying power line communication systems. IEEE Access 2017, 5, 10118–10129. [Google Scholar] [CrossRef]
- Pu, H.; Liu, X.; Zhang, S.; Xu, D. Adaptive cooperative non-orthogonal multiple access-based power line communication. IEEE Access 2019, 7, 73856–73869. [Google Scholar] [CrossRef]
- Ahiadormey, R.K.; Anokye, P.; Lee, K.-J. Cooperative non-orthogonal multiple access over log-normal power line communication channels. Electronics 2019, 8, 1254. [Google Scholar] [CrossRef] [Green Version]
- Ahiadormey, R.K.; Anokye, P.; Park, S.-H.; Lee, K.-J. Two-Way Relaying Non-Orthogonal Multiple Access with Imperfect Successive Interference Cancellation in Power Line Communications. IEEE Open J. Commun. Soc. 2020, 1, 1872–1885. [Google Scholar] [CrossRef]
- Bletsas, A.; Khisti, A.; Reed, D.; Lippman, A. A simple cooperative diversity method based on network path selection. IEEE J. Sel. Areas Commun. 2006, 24, 659–672. [Google Scholar] [CrossRef] [Green Version]
- Wang, H.; Ma, S.; Ng, T.-S.; Poor, H.V. A general analytical approach for opportunistic cooperative systems with spatially random relays. IEEE Trans. Wirel. Commun. 2011, 10, 4122–4129. [Google Scholar] [CrossRef] [Green Version]
- Nasir, A.A.; Zhou, X.; Durrani, S.; Kennedy, R.A. Wireless-Powered Relays in Cooperative Communications: Time-Switching Relaying Protocols and Throughput Analysis. IEEE Trans. Commun. 2015, 63, 1607–1622. [Google Scholar] [CrossRef] [Green Version]

| Primary Parameters | Description | Values |
|---|---|---|
| W | frequency bandwidth | 5 (W) |
| transmission rate threshold | 1 (bps/Hz) | |
| traditional stabilized power source | −10 (dB) | |
| overall AWGNs | 1 | |
| energy harvesting efficiency | 1 | |
| power splitting fraction | 0.2 | |
| m | path-loss | 2.7 |
| S to R distance | 1 (m) | |
| R to D distance | 1 (m) | |
| S to D distance | 2 (m) | |
| S to R channel mean, log-normally distributed | 4 (dB) | |
| Rto D channel mean, log-normally distributed | 4 (dB) | |
| S to D channel mean, log-normally distributed | 4 (dB) | |
| S to R channel variance, log-normally distributed | 3 (dB) | |
| R to D channel variance, log-normally distributed | 3 (dB) | |
| S to D channel variance, log-normally distributed | 3 (dB) | |
| K | Number of relays | 3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Van, H.T.; Van, Q.-N.; Le, D.H.; Van, H.-P.; Jalowiczor, J.; Nguyen, H.-S.; Voznak, M. Opportunistic DF-AF Selection Relaying in Hybrid Wireless and Power Line Communication for Indoor IoT Networks. Sensors 2021, 21, 5469. https://doi.org/10.3390/s21165469
Van HT, Van Q-N, Le DH, Van H-P, Jalowiczor J, Nguyen H-S, Voznak M. Opportunistic DF-AF Selection Relaying in Hybrid Wireless and Power Line Communication for Indoor IoT Networks. Sensors. 2021; 21(16):5469. https://doi.org/10.3390/s21165469
Chicago/Turabian StyleVan, Hoang Thien, Quyet-Nguyen Van, Danh Hong Le, Hoang-Phuong Van, Jakub Jalowiczor, Hoang-Sy Nguyen, and Miroslav Voznak. 2021. "Opportunistic DF-AF Selection Relaying in Hybrid Wireless and Power Line Communication for Indoor IoT Networks" Sensors 21, no. 16: 5469. https://doi.org/10.3390/s21165469
APA StyleVan, H. T., Van, Q.-N., Le, D. H., Van, H.-P., Jalowiczor, J., Nguyen, H.-S., & Voznak, M. (2021). Opportunistic DF-AF Selection Relaying in Hybrid Wireless and Power Line Communication for Indoor IoT Networks. Sensors, 21(16), 5469. https://doi.org/10.3390/s21165469









