The Quadrature Method: A Novel Dipole Localisation Algorithm for Artificial Lateral Lines Compared to State of the Art
Abstract
:1. Introduction
2. Materials and Methods
2.1. The Dipole Flow Field
2.2. Simulation Environment
2.3. Performance Analyses
2.4. Parameter Optimisation Approach
2.5. Dipole Localisation Algorithms
2.5.1. The Random Predictor (RND)
2.5.2. Linear Constraint Minimum Variance (LCMV) Beamforming
2.5.3. K-Nearest Neighbours (KNN)
2.5.4. The Continuous Wavelet Transform (CWT)
2.5.5. The Extreme Learning Machine (ELM)
2.5.6. The Multi-Layer Perceptron (MLP)
2.5.7. The Gauss–Newton (GN) Algorithm
2.5.8. The Newton–Raphson (NR) Algorithm
2.5.9. The Least Square Curve Fit (LSQ) Algorithm
2.5.10. The Quadrature Method (QM) Algorithm
3. Results
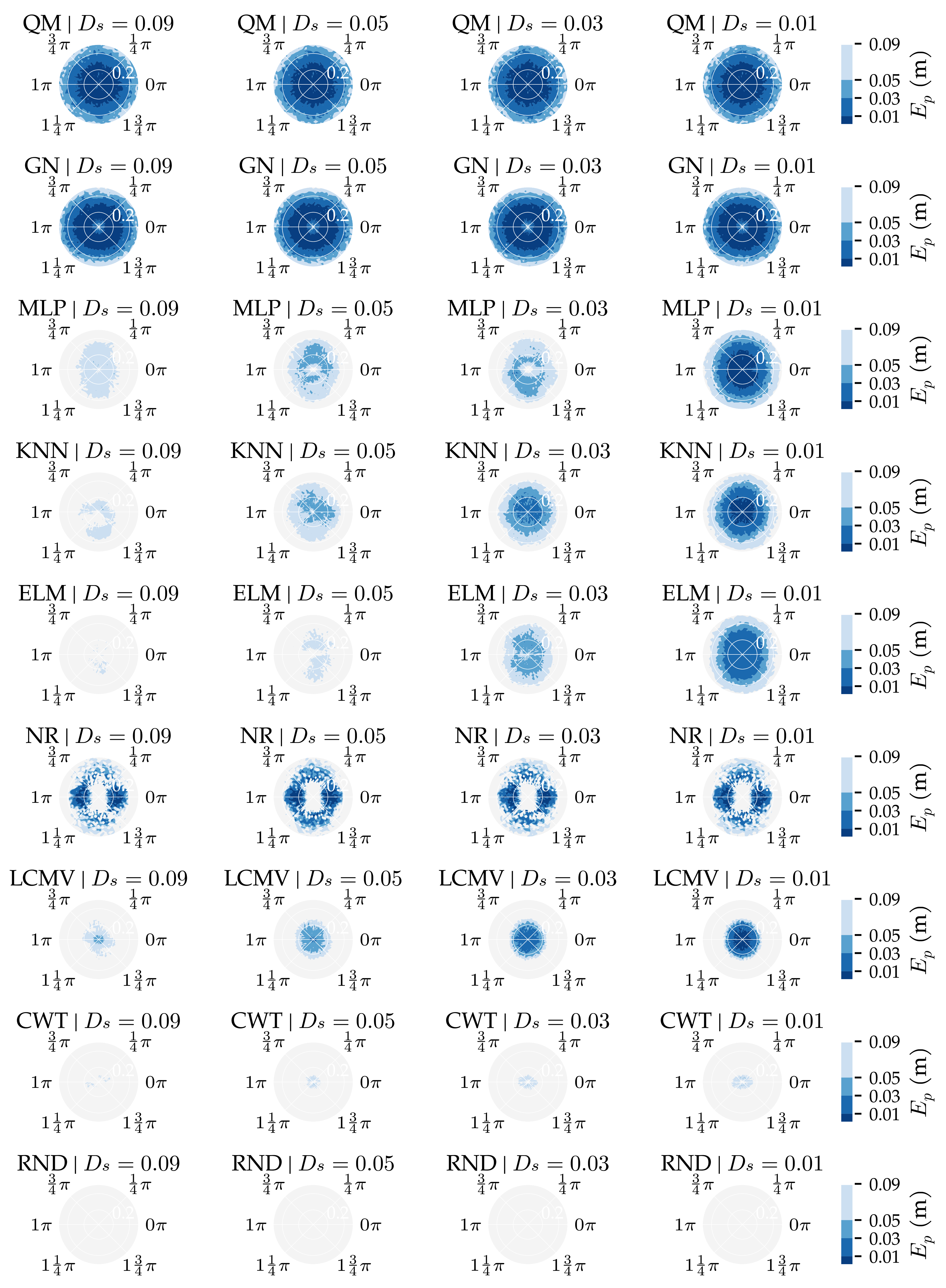
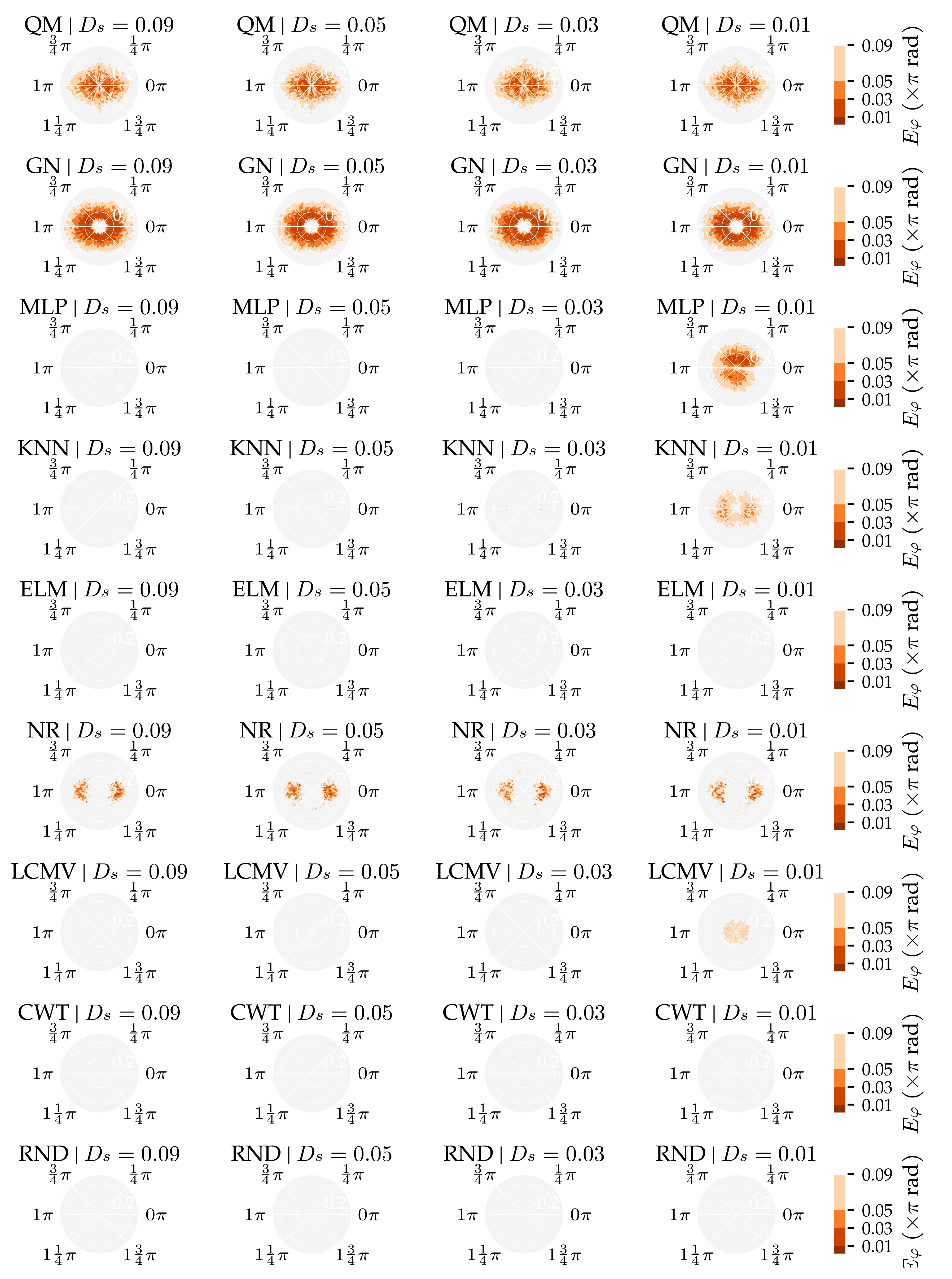
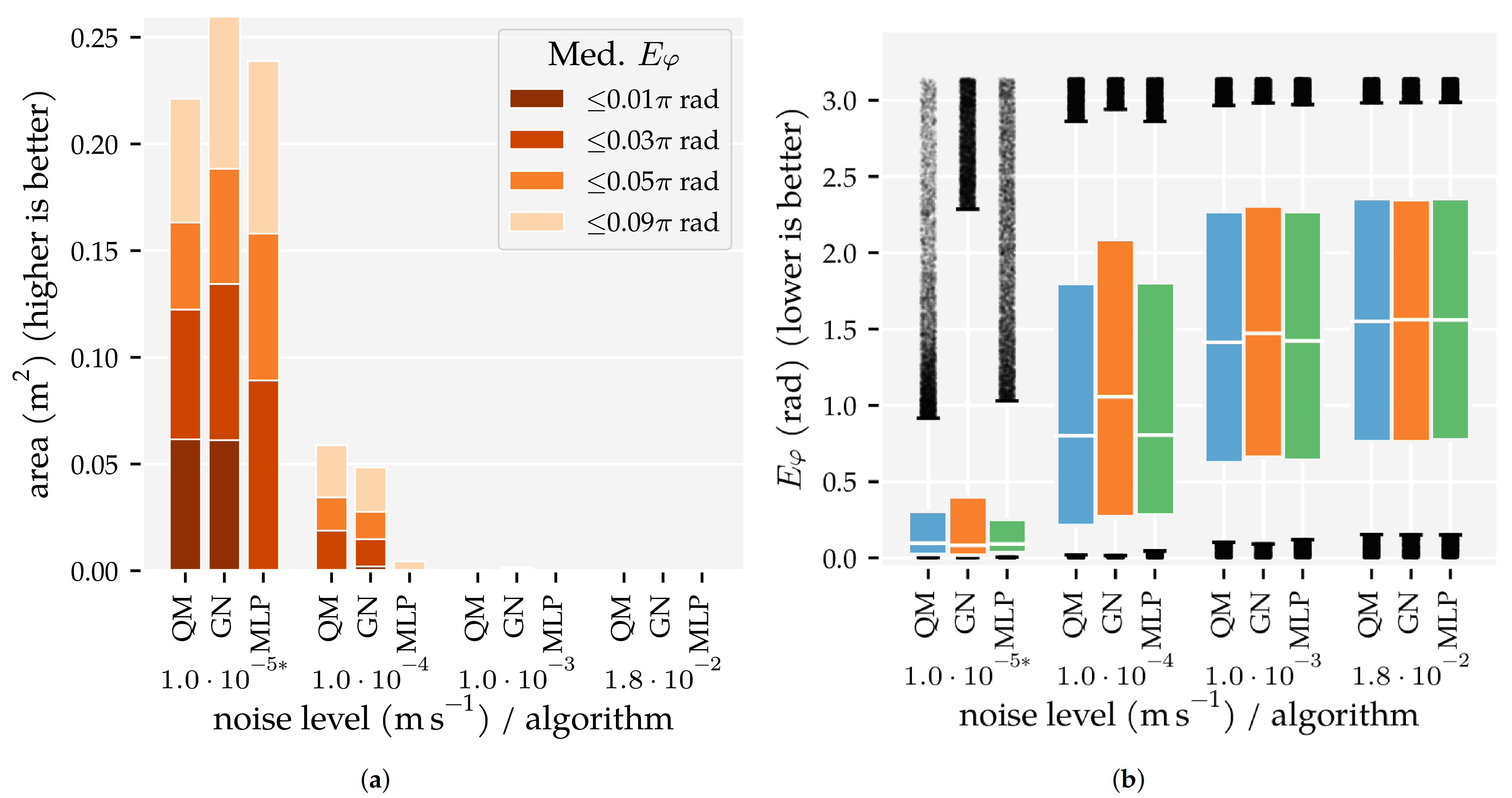
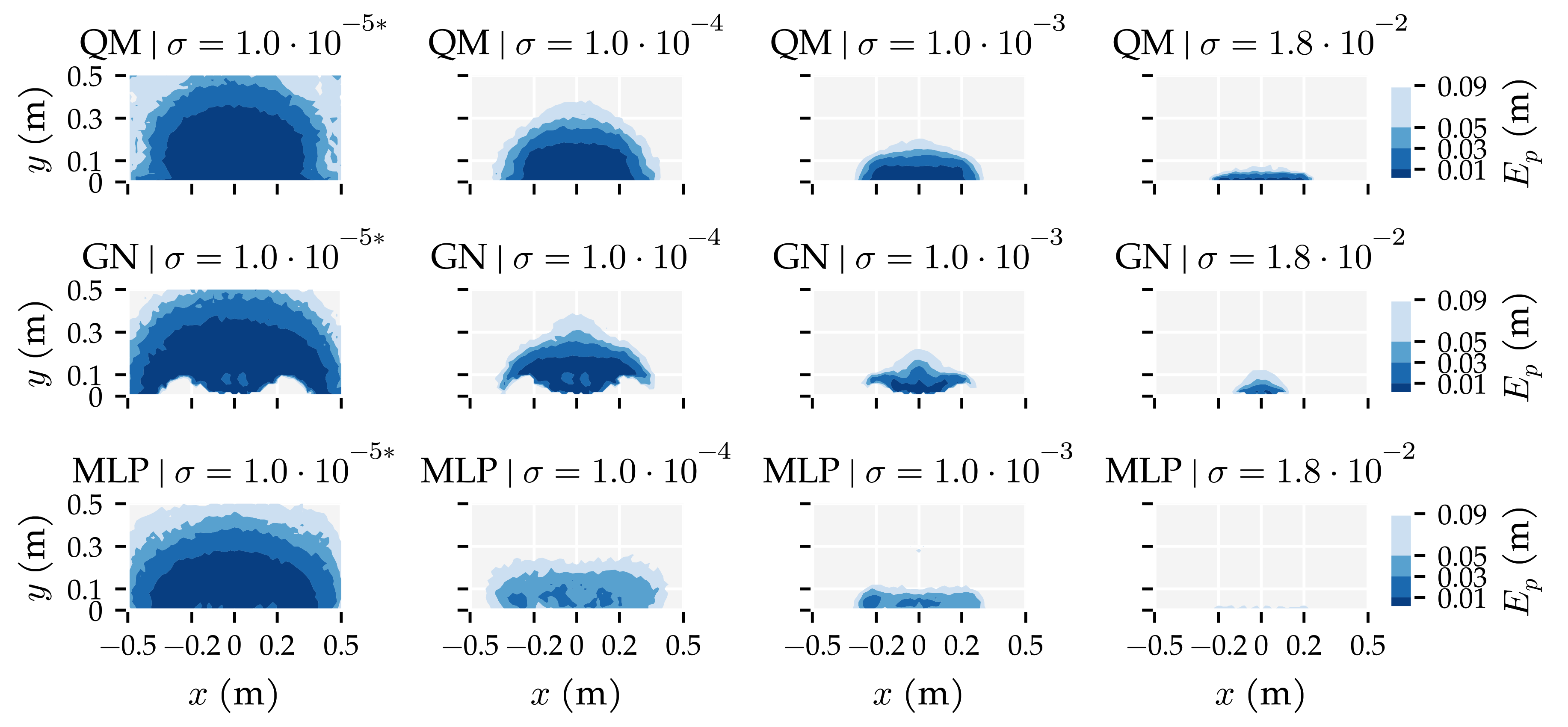
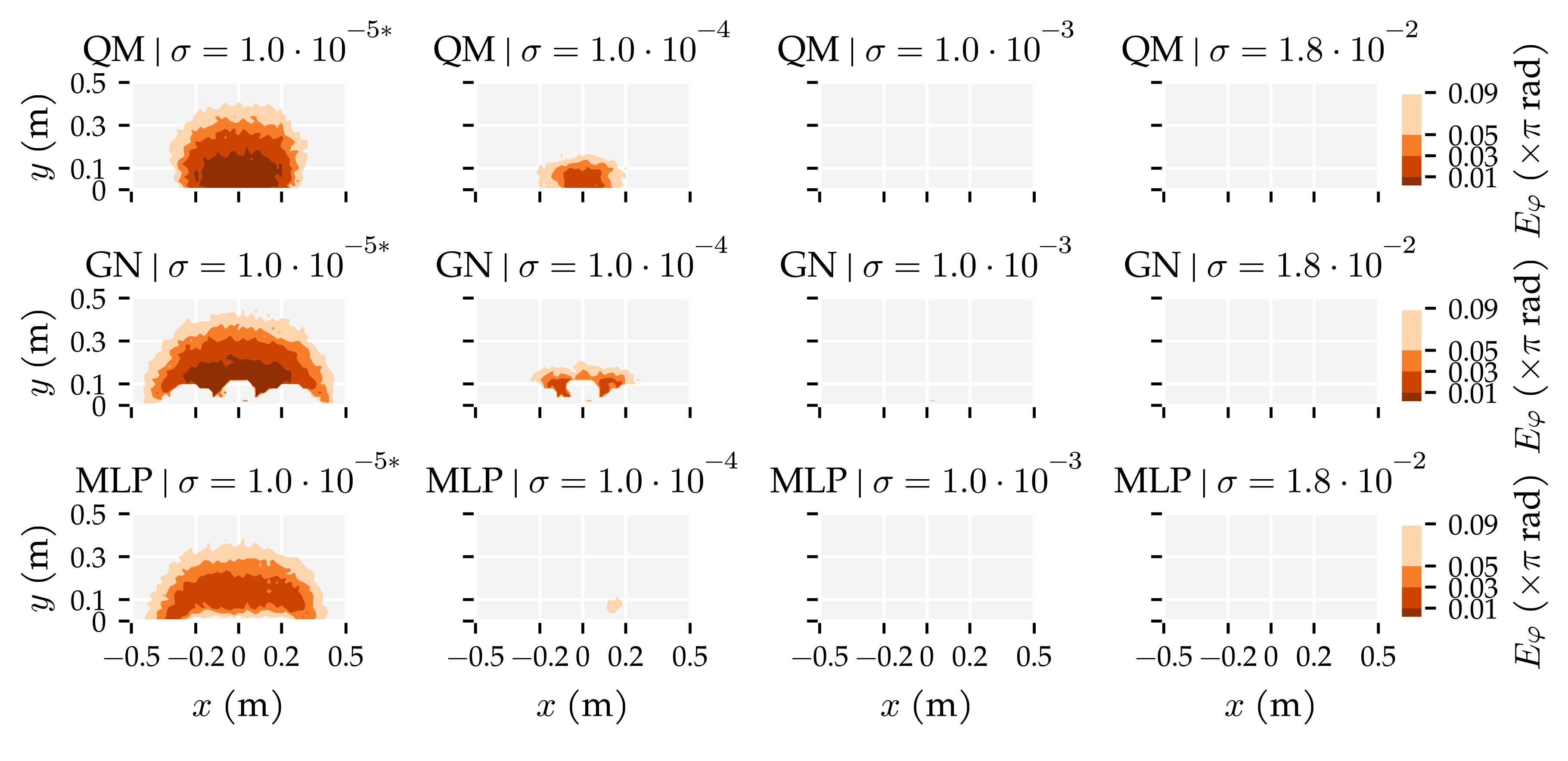
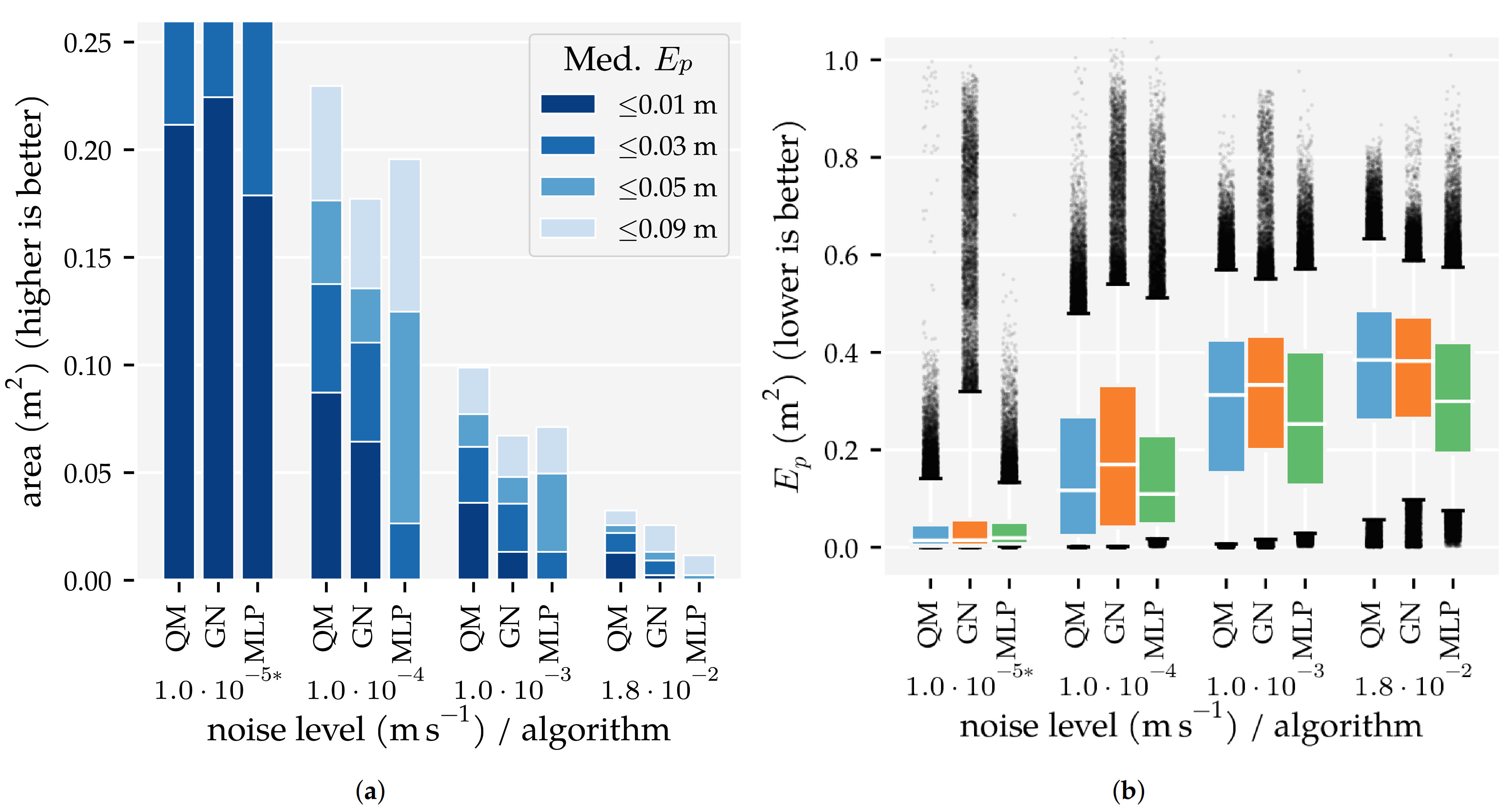
3.1. Analysis Method 1: Amount of Training and Optimisation Data
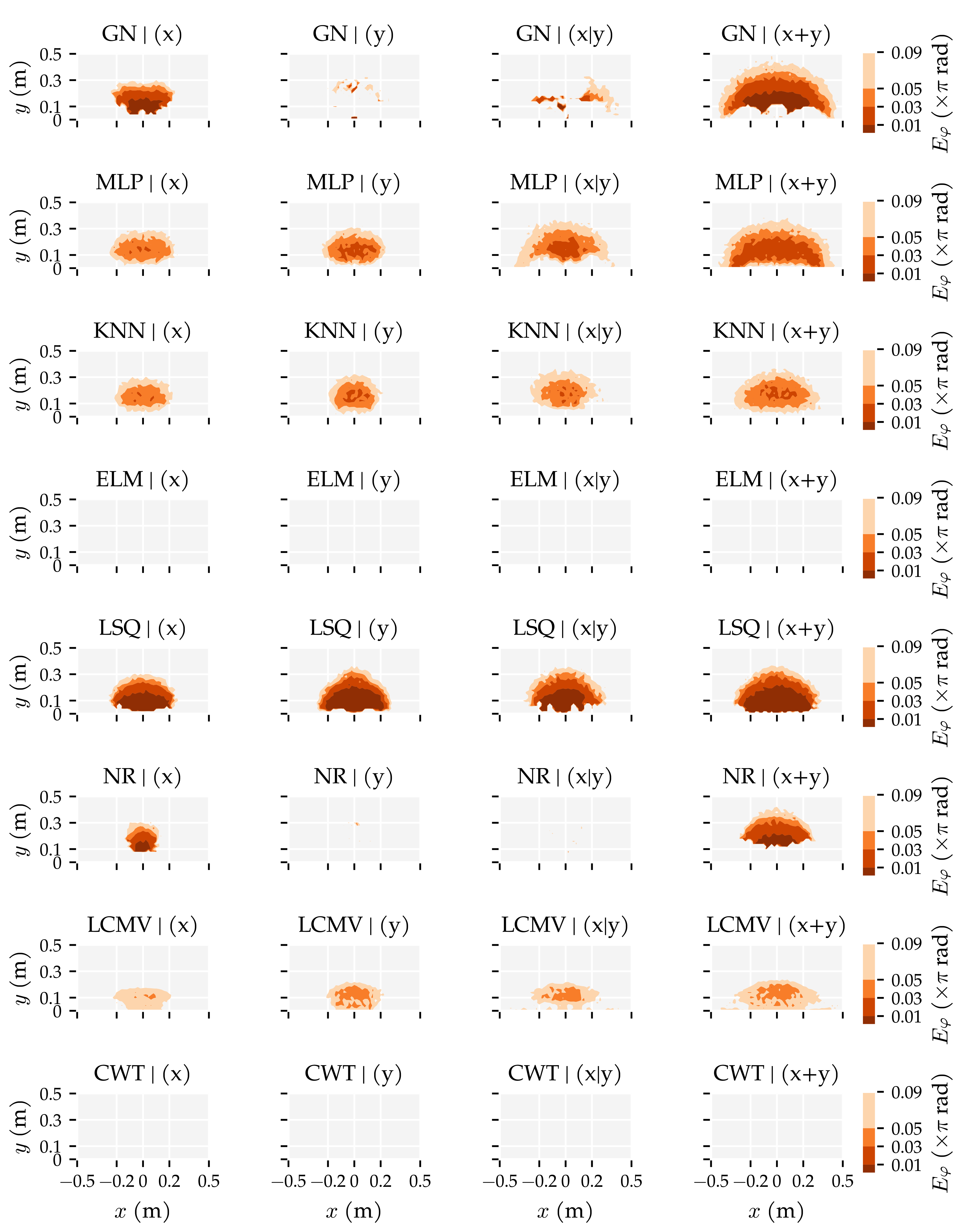
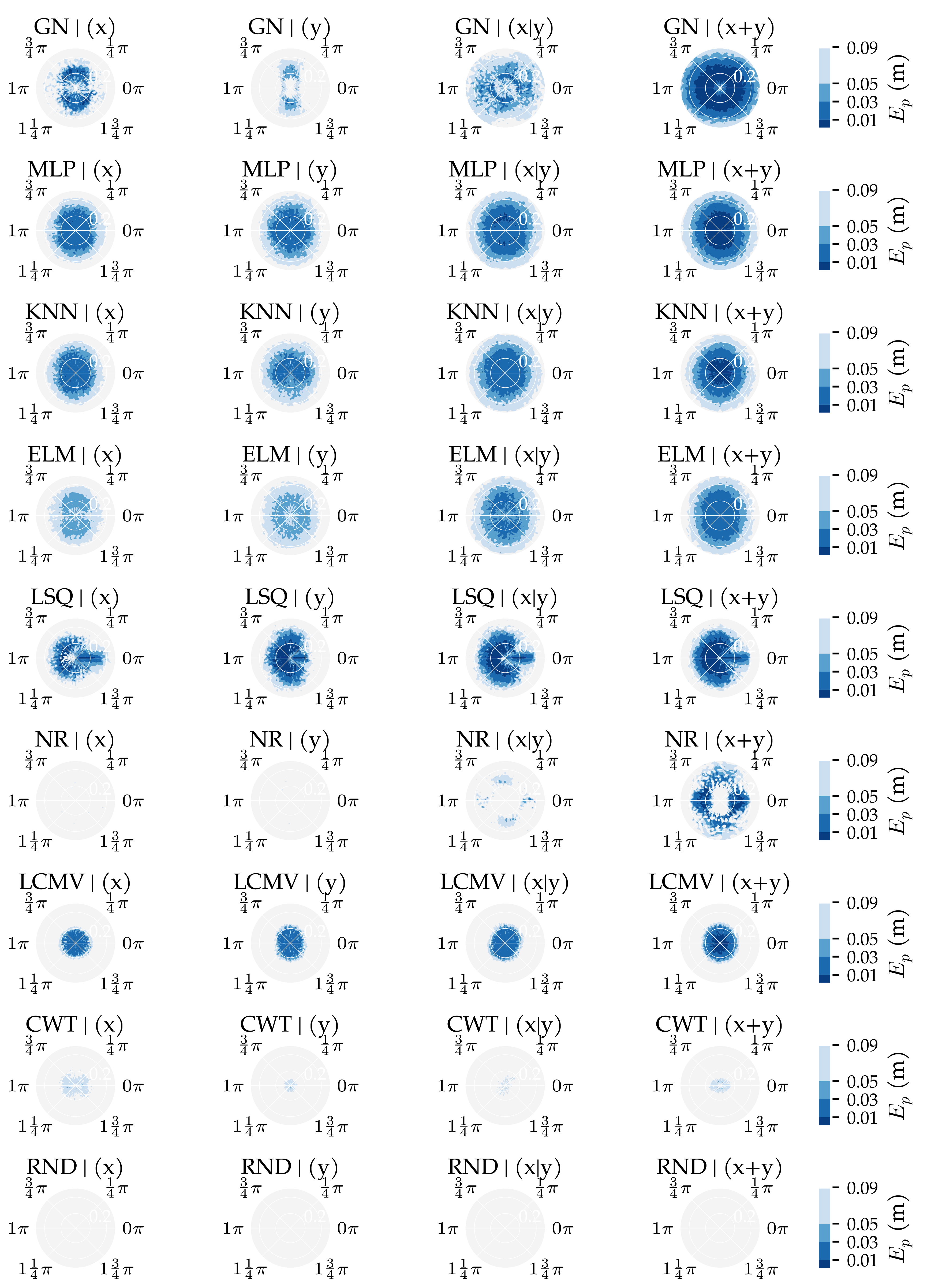
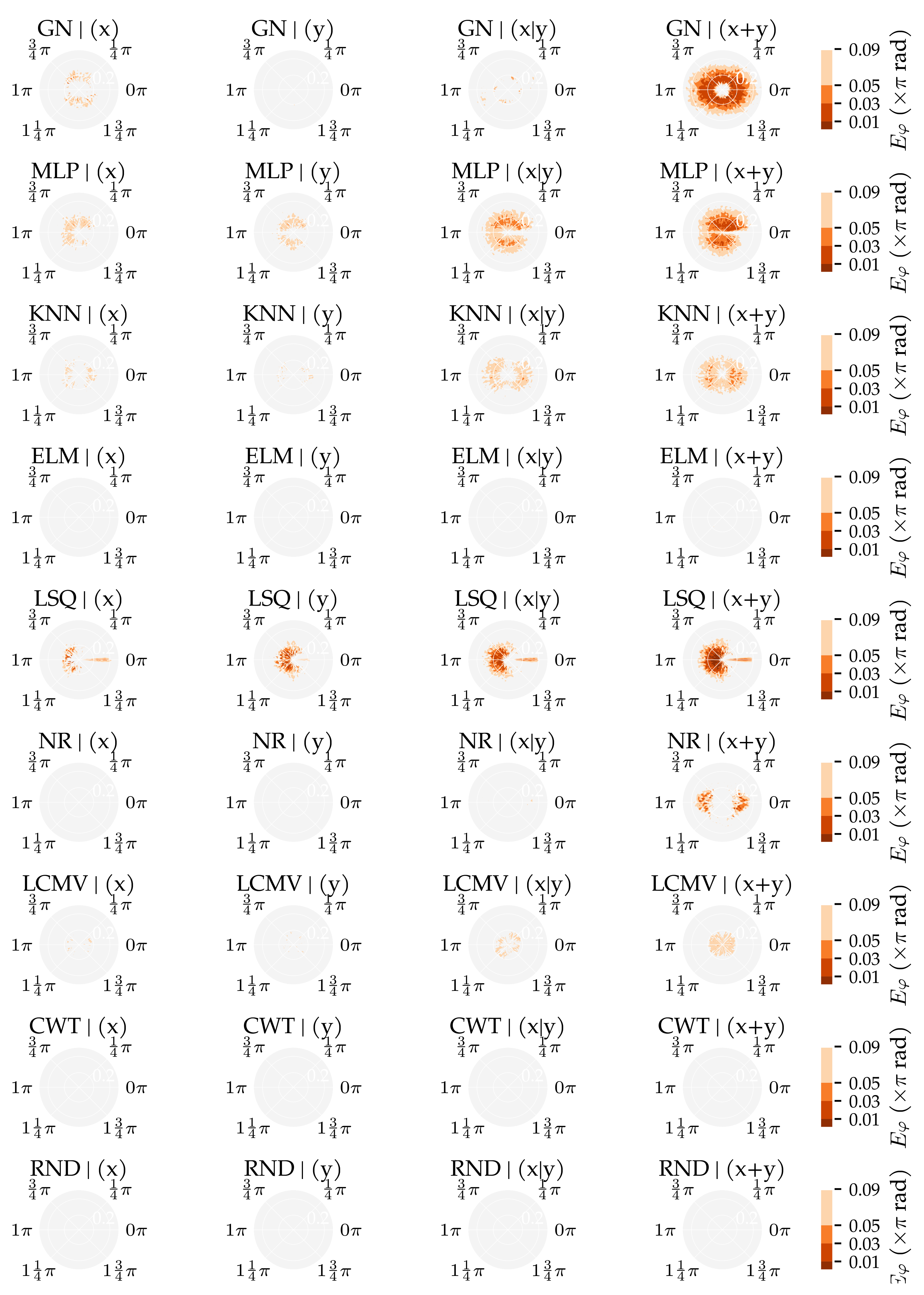
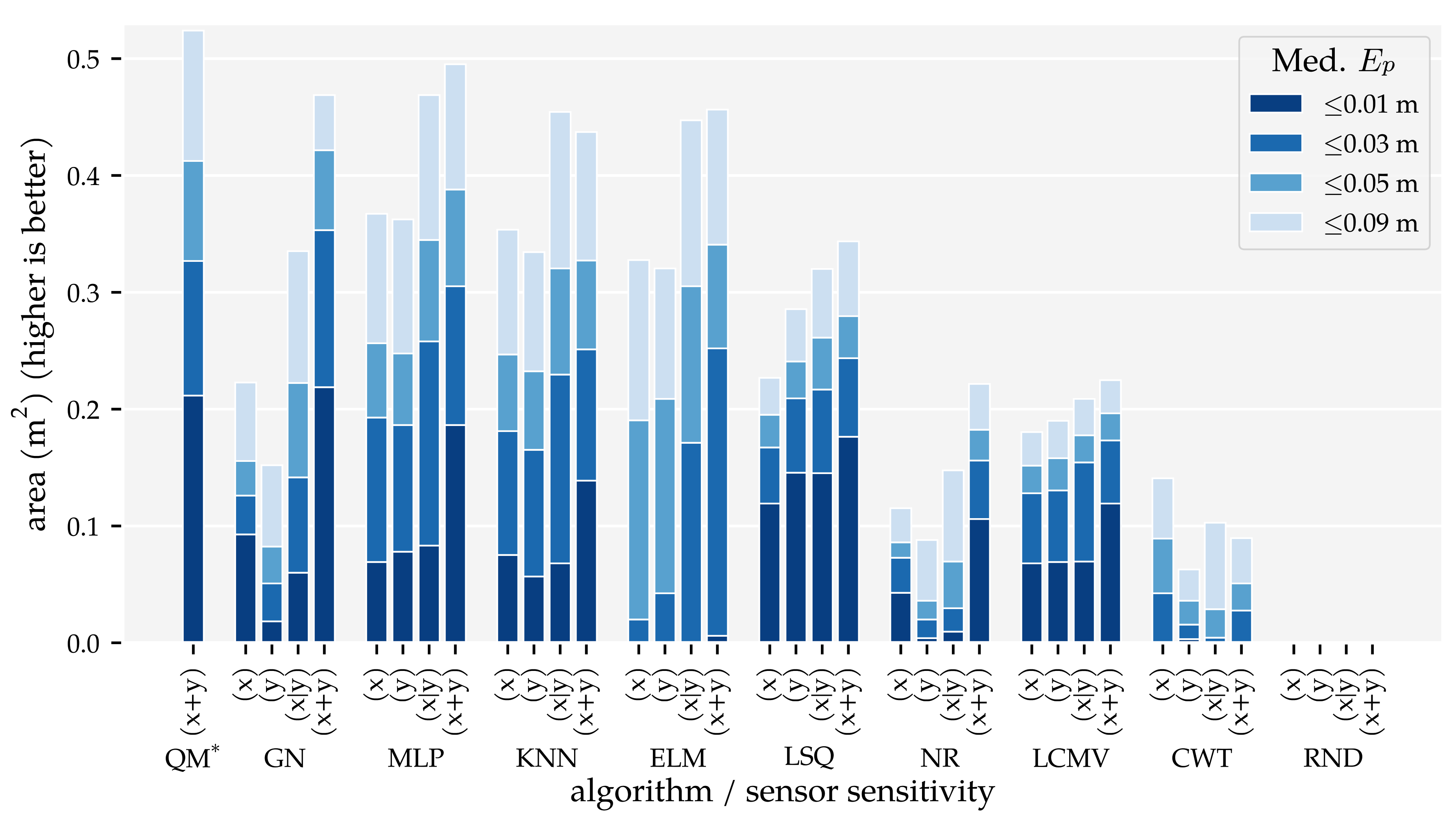
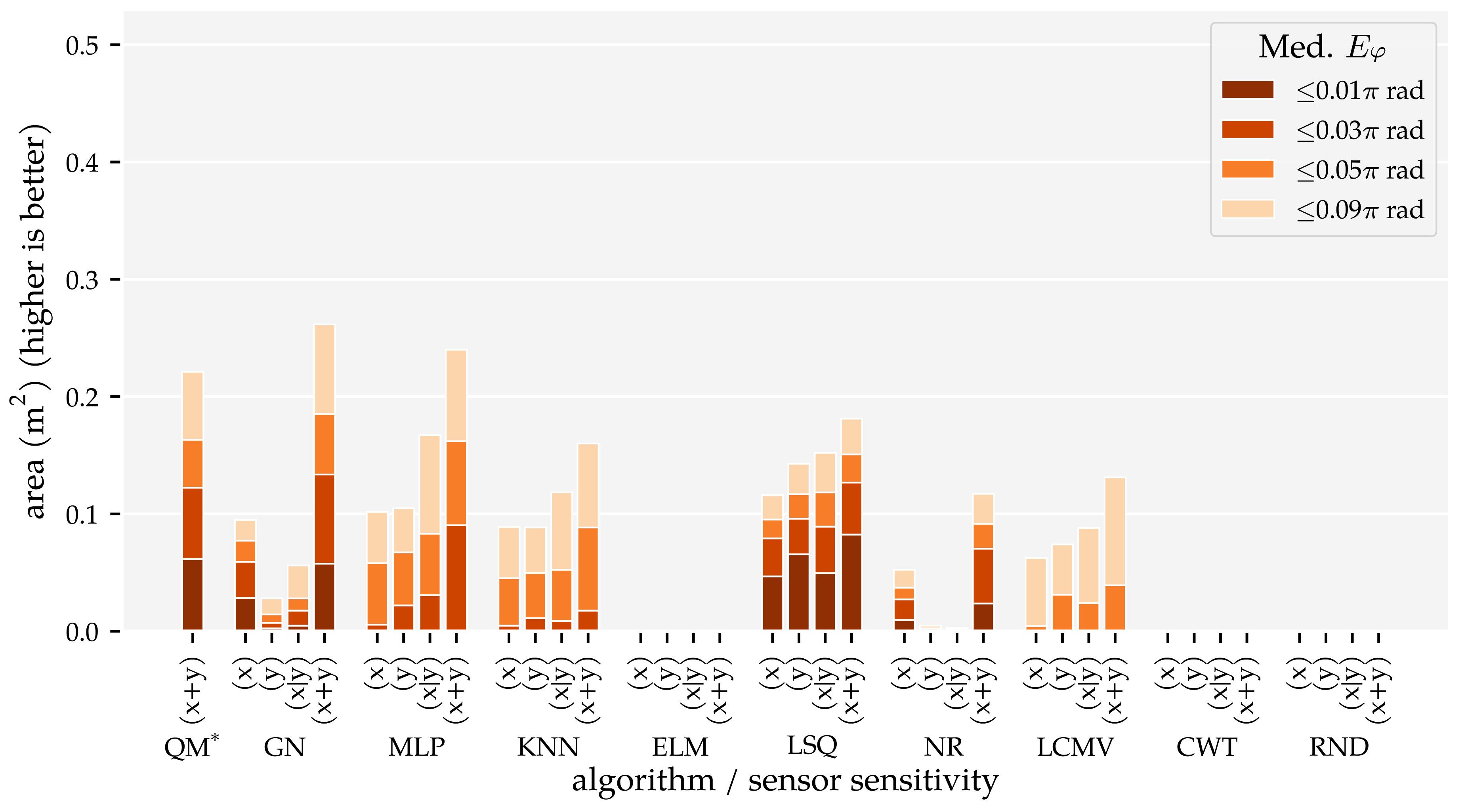
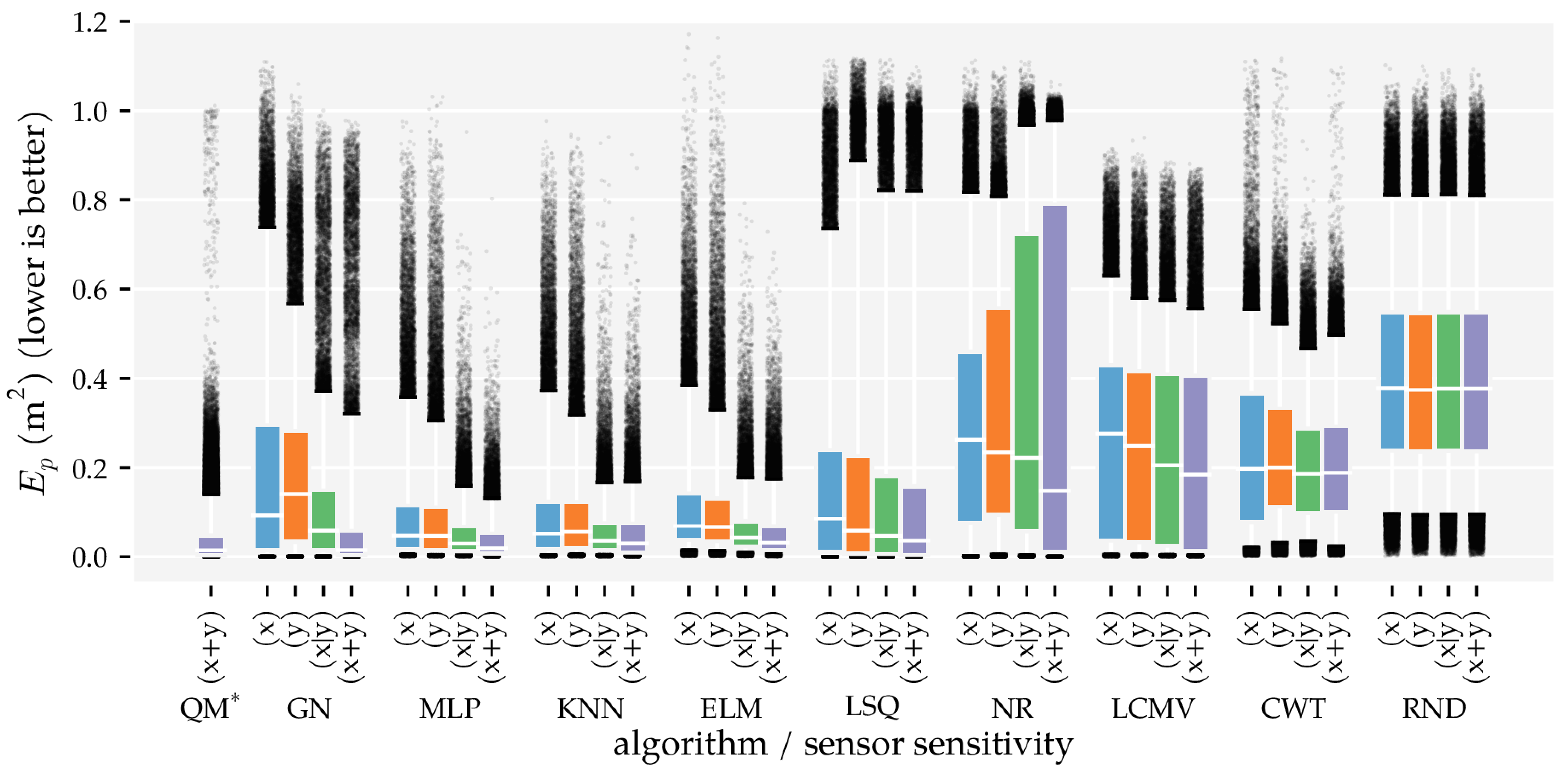
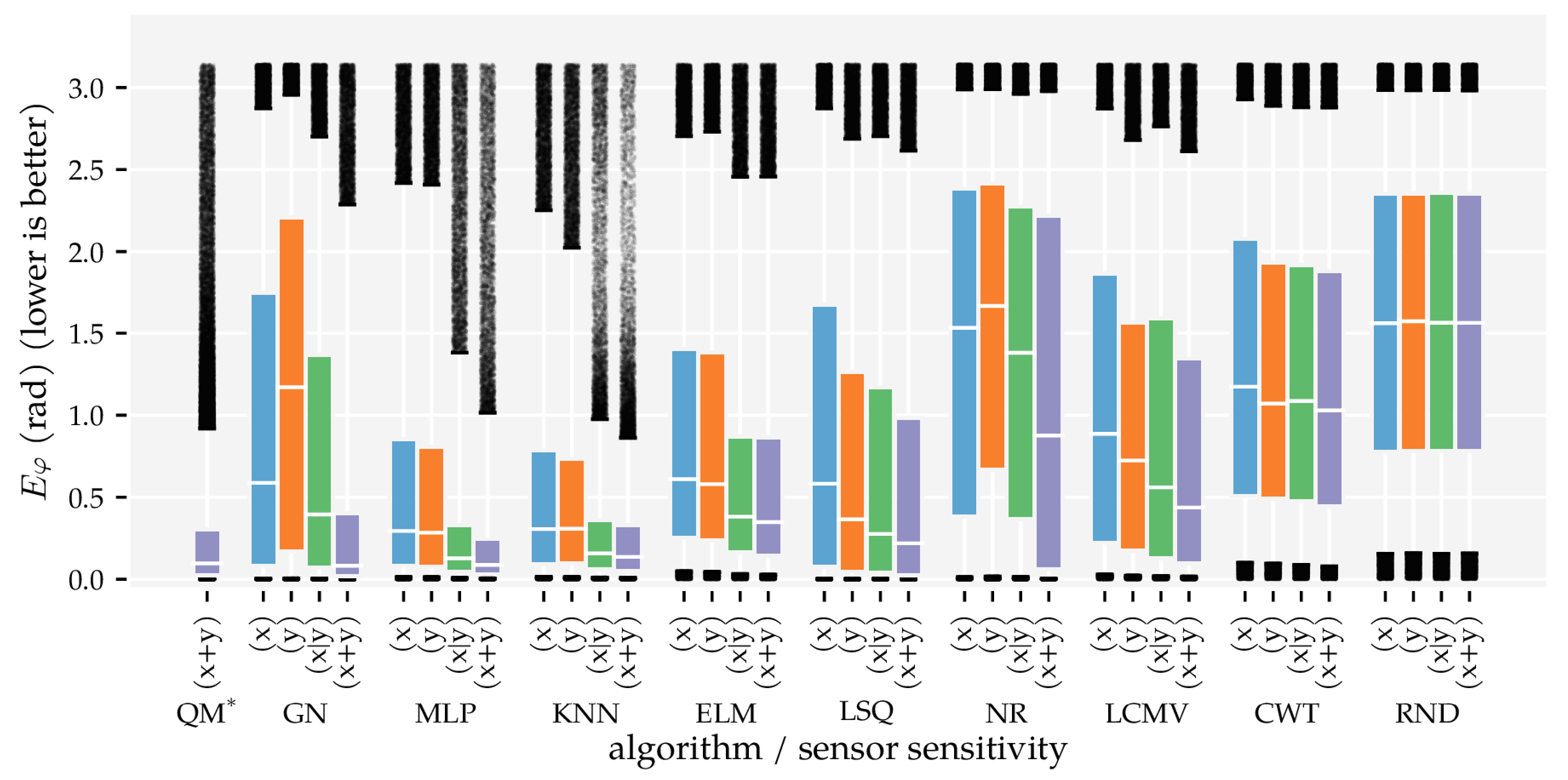
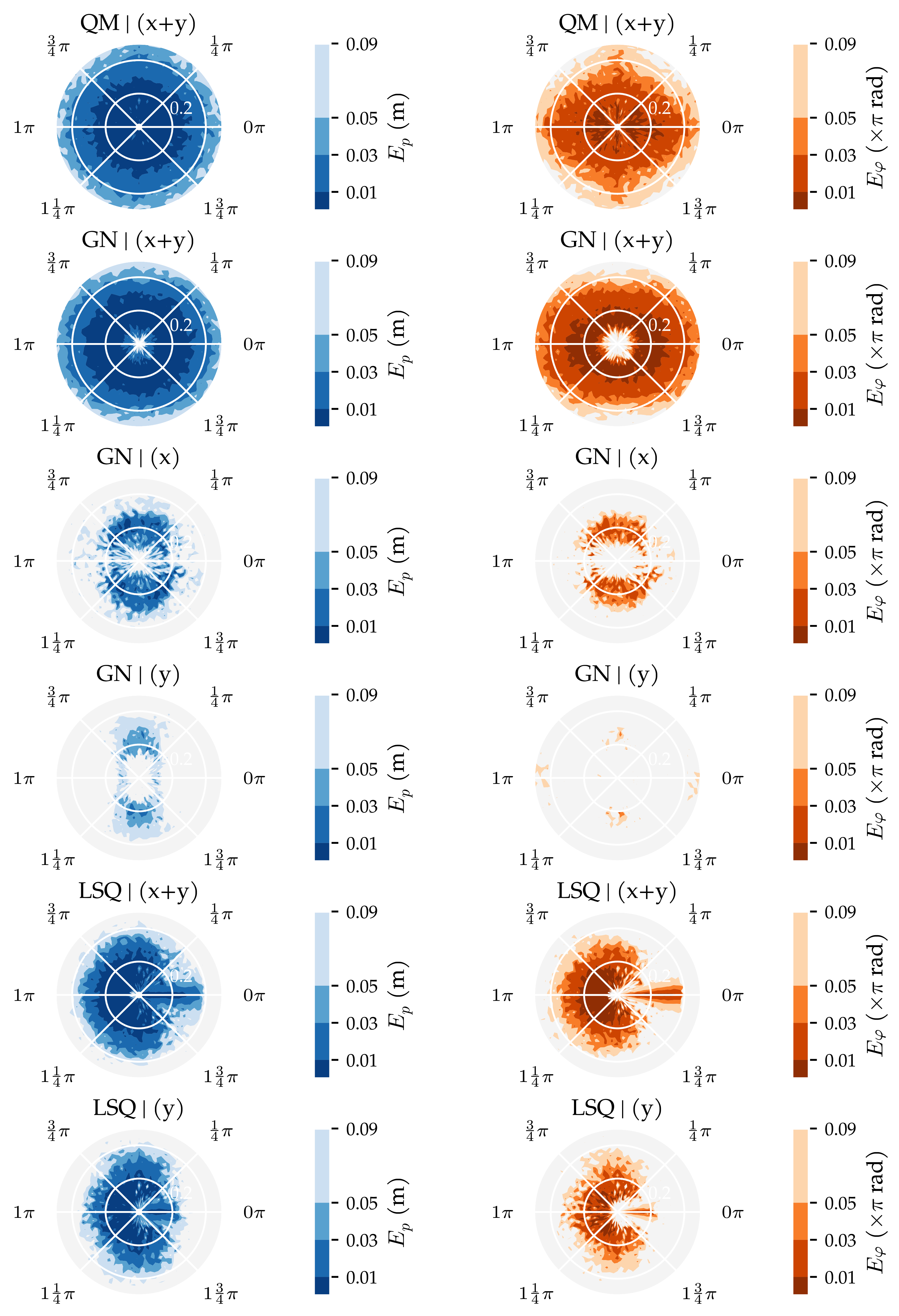
3.2. Analysis Method 2: Sensor Sensitivity Axes
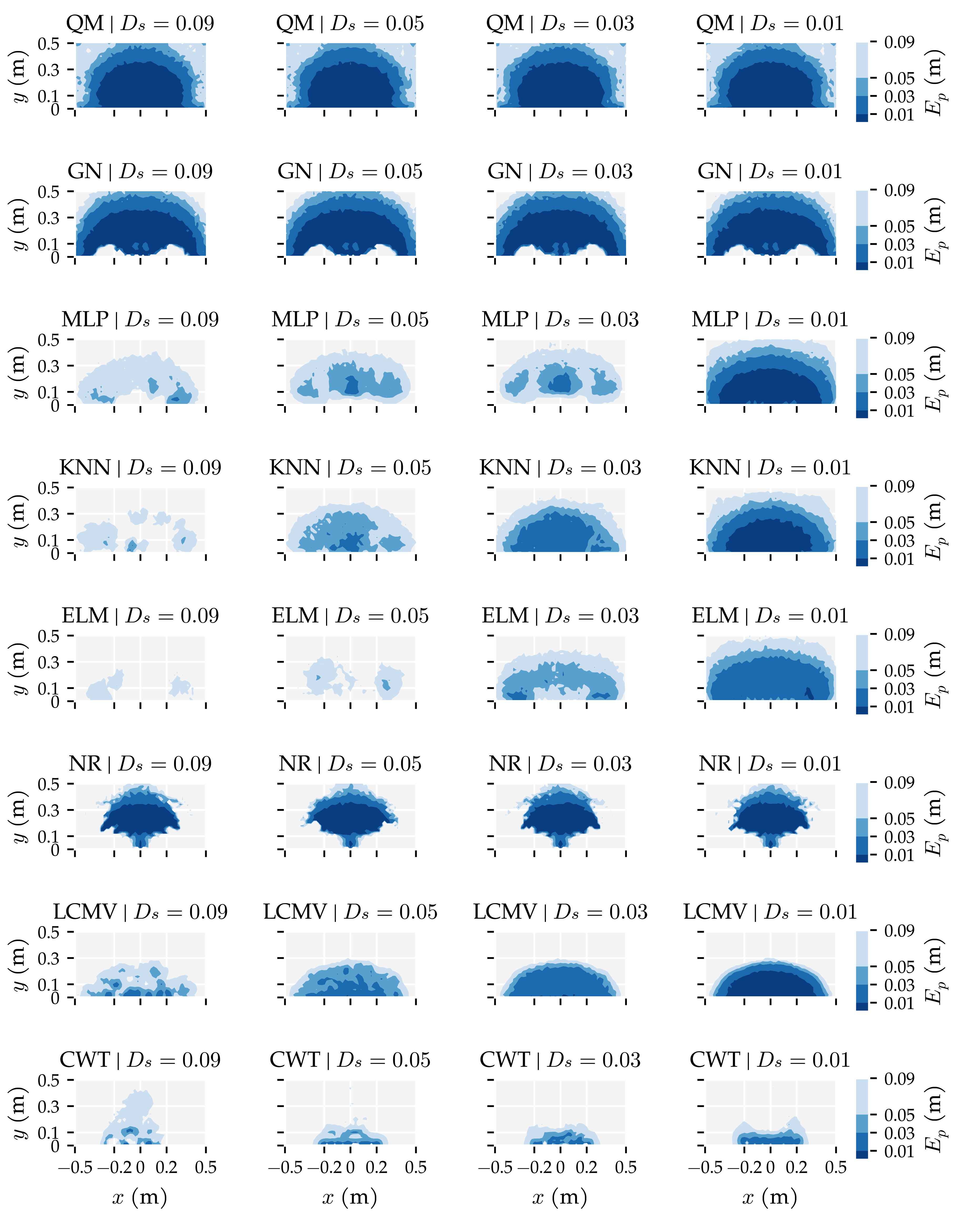
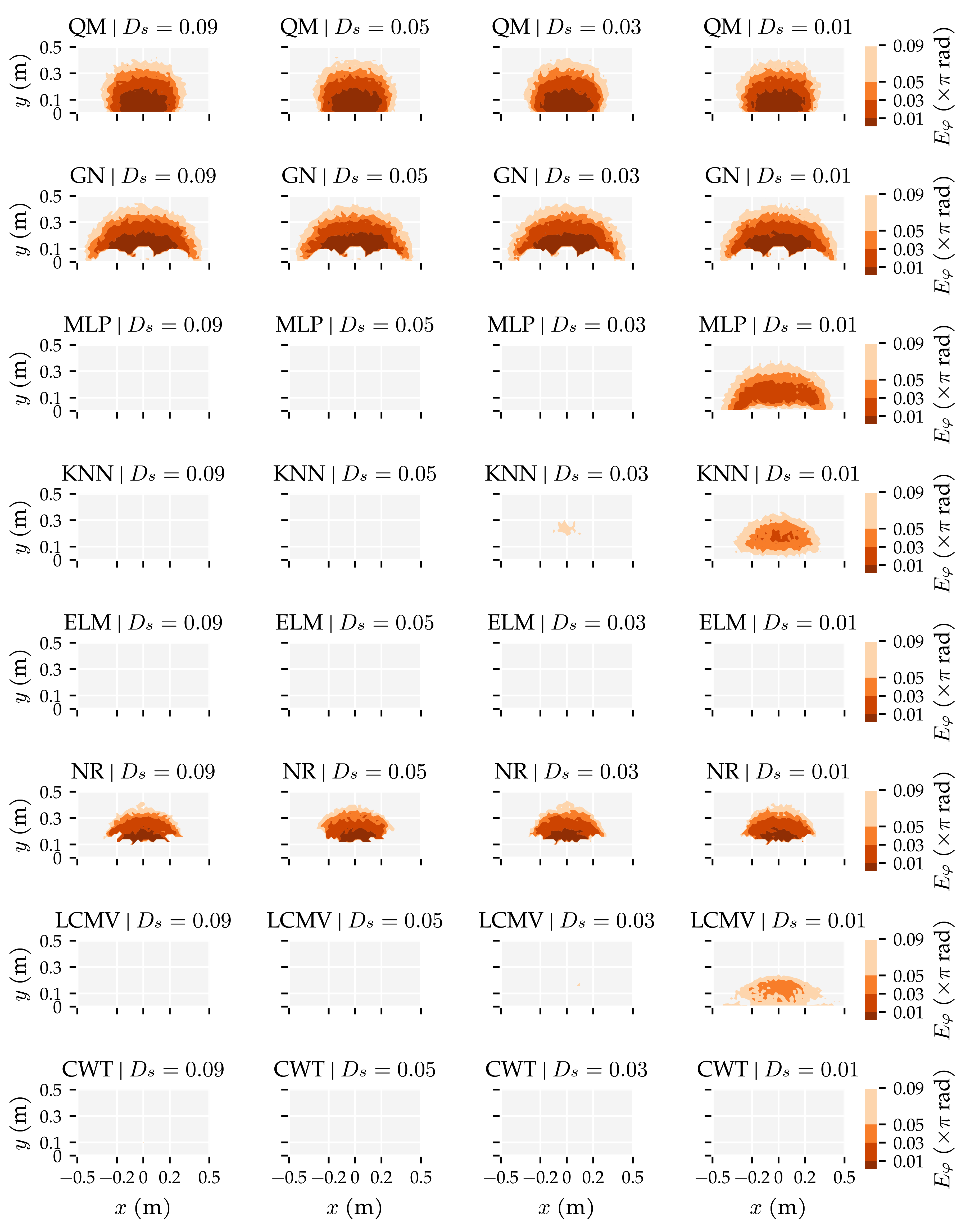
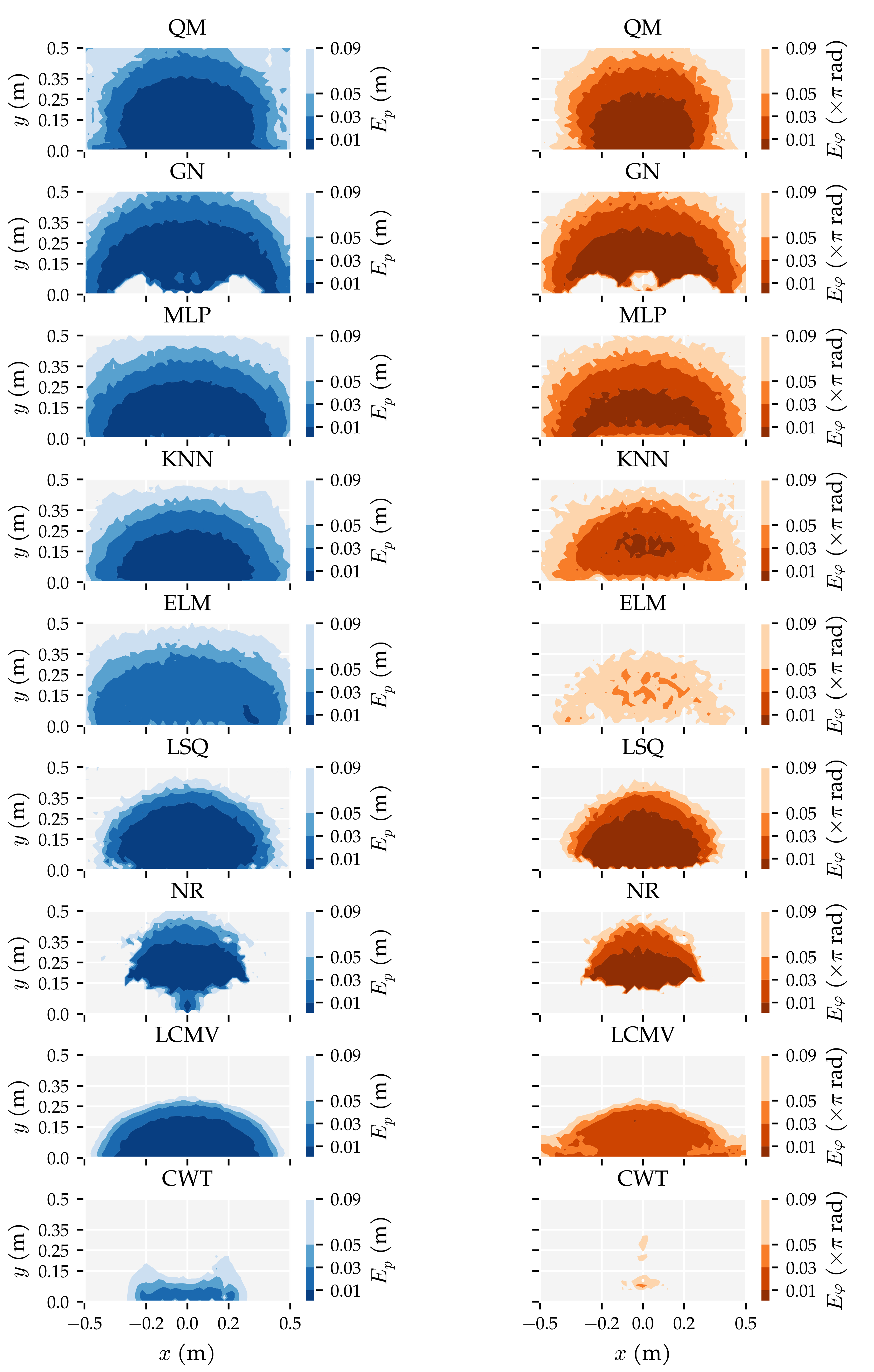
3.3. Additional Results
4. Discussion
4.1. The Gauss–Newton (GN) Algorithm
4.2. The Newton–Raphson (NR) Algorithm
4.3. The Multi-Layer Perceptron (MLP) and Extreme Learning Machine (ELM)
4.4. The Quadrature Method (QM) Algorithm
4.5. Future Research Directions and Possible Applications
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ALL | artificial lateral line |
| AUV | autonomous underwater vehicle |
| CNN | convolutional neural network |
| CWT | continuous wavelet transform |
| DFT | discrete Fourier transform |
| ELM | extreme learning machine |
| ESN | echo state network |
| GN | Gauss–Newton |
| KNN | k-nearest neighbours |
| LCMV | linear constraint minimum variance |
| LSQ | least square curve fit |
| MAE | mean absolute error |
| MSE | mean squared error |
| MLP | multi-layer perceptron |
| NR | Newton–Raphson |
| OS-ELM | online sequential extreme learning machine |
| QM | quadrature method |
| RND | random |
| SLFN | single layer feed-forward network |
| SNR | signal to noise ratio |
Appendix A. Final Hyperparameter Values
| KNN | k neighbours | ||||
| 0.09 | 3 | ||||
| 0.05 | 3 | ||||
| 0.03 | 3 | ||||
| 0.01 | 5 | ||||
| CWT | threshold | threshold | factor | factor | |
| 0.09 | 0.36 | 1.0 | 1.0 | 0.30 | |
| 0.05 | 0.18 | 0.92 | 0.89 | 0.89 | |
| 0.03 | 0.21 | 0.74 | 0.98 | 0.35 | |
| 0.01 | 0.26 | 0.57 | 0.82 | 0.38 | |
| ELM | nodes | Analytical (higher value tunes | |||
| 0.09 | 120 | estimation for longer distances) | |||
| 0.05 | 75 | Analytical (lower value tunes | |||
| 0.03 | 1383 | estimation for longer distances) | |||
| 0.01 | 11,169 | ||||
| MLP | learning rate | n layers | nodes per layer | ||
| 0.09 | 1 | 990 | |||
| 0.05 | 1 | 798 | |||
| 0.03 | 1 | 1015 | |||
| 0.01 | 4 | 993 | |||
| GN | initial distance () | ||||
| 0.09 | 5.0 | ||||
| 0.05 | 5.0 | ||||
| 0.03 | 2.5 | ||||
| 0.01 | 5.0 | ||||
| NR | initial distance () | norm limit l | |||
| 0.09 | 2.5 | 0.14 | |||
| 0.05 | 2.9 | 0.10 | |||
| 0.03 | 2.5 | 0.10 | |||
| 0.01 | 2.5 | 0.10 | |||
| KNN | sensor | k neighbours | |||
| (x + y) | 5 | ||||
| (x|y) | 5 | ||||
| (x) | 6 | ||||
| (y) | 6 | ||||
| CWT | sensor | threshold | threshold | factor | factor |
| (x + y) | 0.23 | 0.60 | 0.71 | 0.33 | |
| (x|y) | 0.22 | 0.40 | 0.76 | 0.64 | |
| (x) | 0.21 | 0.53 | 0.61 | 0.40 | |
| (y) | 0.12 | 0.79 | 0.58 | 0.87 | |
| ELM | sensor | nodes | Analytical (higher value tunes | ||
| (x + y) | 11,169 | estimation for longer distances) | |||
| (x|y) | 5165 | Analytical (lower value tunes | |||
| (x) | 5579 | estimation for longer distances) | |||
| (y) | 5579 | ||||
| MLP | sensor | learning rate | n layers | nodes per layer | |
| (x + y) | 4 | 1014 | |||
| (x|y) | 4 | 982 | |||
| (x) | 4 | 1024 | |||
| (y) | 4 | 1016 | |||
| GN | sensor | initial distance () | |||
| (x + y) | 5.0 | ||||
| (x|y) | 2.5 | ||||
| (x) | 7.5 | ||||
| (y) | 2.5 | ||||
| NR | sensor | initial distance () | norm limit l | ||
| (x + y) | 2.5 | 0.10 | |||
| (x|y) | 7.8 | 0.13 | |||
| (x) | 9.3 | 0.10 | |||
| (y) | 2.5 | 0.10 | |||
Appendix B. Potential Flow Wavelets
Appendix B.1. The Even Wavelet
Appendix B.2. The Odd Wavelet
Appendix C. Movement Direction Estimation with the Continuous Wavelet Transform (CWT)CWT
Appendix C.1. Movement Direction Estimation with the Parallel Velocity Component
Appendix C.2. Movement Direction Estimation with the Perpendicular Velocity Component
Appendix D. The Quadrature Method (QM)
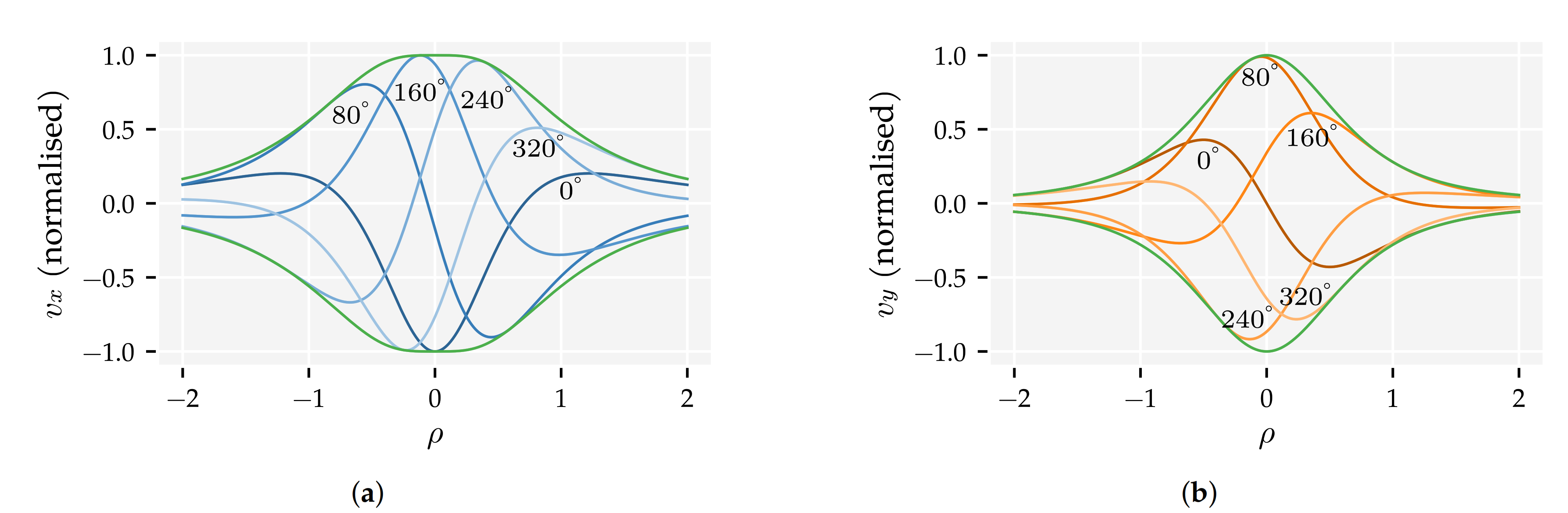

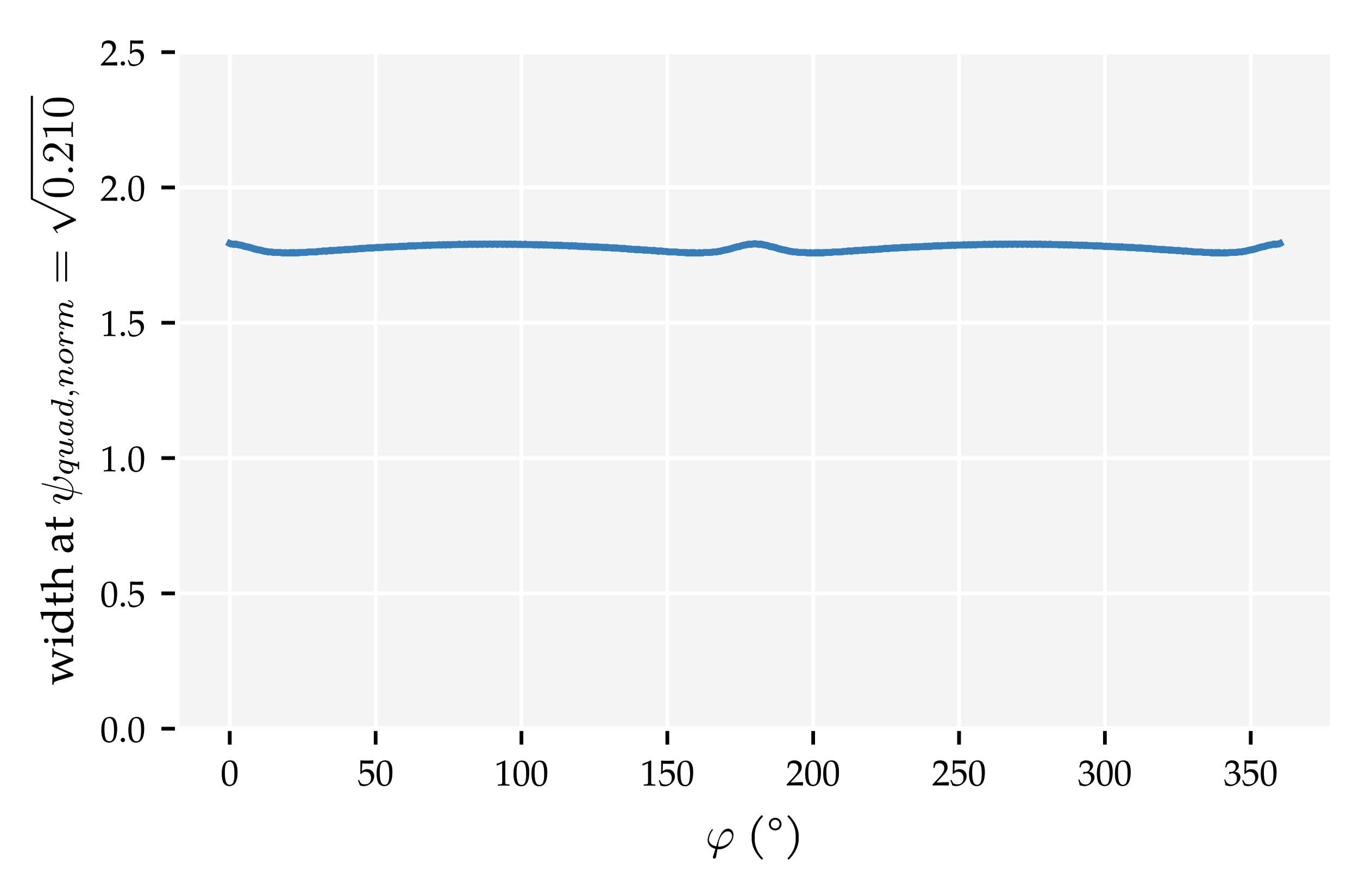
Appendix E. Additional Figures



References
- Dijkgraaf, S. The Functioning and Significance of the Lateral-Line Organs. Biol. Rev. 1963, 38, 51–105. [Google Scholar] [CrossRef] [PubMed]
- Coombs, S.; van Netten, S. The Hydrodynamics and Structural Mechanics of the Lateral Line System. In Fish Physiology; Elsevier: Amsterdam, The Netherlands, 2005; Volume 23, pp. 103–139. [Google Scholar] [CrossRef]
- Yang, Y.; Chen, J.; Engel, J.; Pandya, S.; Chen, N.; Tucker, C.; Coombs, S.; Jones, D.L.; Liu, C. Distant touch hydrodynamic imaging with an artificial lateral line. Proc. Natl. Acad. Sci. USA 2006, 103, 18891–18895. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vollmayr, A.N.; Sosnowski, S.; Urban, S.; Hirche, S.; van Hemmen, J.L. Snookie: An Autonomous Underwater Vehicle with Artificial Lateral-Line System. In Flow Sensing in Air and Water; Springer: Berlin/Heidelberg, Germany, 2014; pp. 521–562. [Google Scholar] [CrossRef]
- Ćurčić-Blake, B.; van Netten, S.M. Source location encoding in the fish lateral line canal. J. Exp. Biol. 2006, 209, 1548–1559. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pandya, S.; Yang, Y.; Jones, D.L.; Engel, J.; Liu, C. Multisensor Processing Algorithms for Underwater Dipole Localization and Tracking Using MEMS Artificial Lateral-Line Sensors. EURASIP J. Adv. Signal Process. 2006, 2006, 076593. [Google Scholar] [CrossRef] [Green Version]
- Abdulsadda, A.T.; Tan, X. An artificial lateral line system using IPMC sensor arrays. Int. J. Smart Nano Mater. 2012, 3, 226–242. [Google Scholar] [CrossRef] [Green Version]
- Abdulsadda, A.T.; Tan, X. Nonlinear estimation-based dipole source localization for artificial lateral line systems. Bioinspir. Biomim. 2013, 8, 026005. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Boulogne, L.H.; Wolf, B.J.; Wiering, M.A.; van Netten, S.M. Performance of neural networks for localizing moving objects with an artificial lateral line. Bioinspir. Biomim. 2017, 12, 56009. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wolf, B.J.; Warmelink, S.; van Netten, S.M. Recurrent neural networks for hydrodynamic imaging using a 2D-sensitive artificial lateral line. Bioinspir. Biomim. 2019, 14, 055001. [Google Scholar] [CrossRef]
- Nguyen, N.; Jones, D.; Pandya, S.; Yang, Y.; Chen, N.; Tucker, C.; Liu, C. Biomimetic Flow Imaging with an Artificial Fish Lateral Line. In Proceedings of the International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSIGNALS), Madeira, Portugal, 19–21 January 2018; pp. 269–276. [Google Scholar] [CrossRef] [Green Version]
- Yang, Y.; Nguyen, N.; Chen, N.; Lockwood, M.; Tucker, C.; Hu, H.; Bleckmann, H.; Liu, C.; Jones, D.L. Artificial lateral line with biomimetic neuromasts to emulate fish sensing. Bioinspir. Biomim. 2010, 5, 016001. [Google Scholar] [CrossRef] [Green Version]
- Nguyen, N.; Jones, D.L.; Yang, Y.; Liu, C. Flow Vision for Autonomous Underwater Vehicles via an Artificial Lateral Line. EURASIP J. Adv. Signal Process. 2011, 2011, 806406. [Google Scholar] [CrossRef] [Green Version]
- Wolf, B.J.; van Netten, S.M. Hydrodynamic Imaging using an all-optical 2D Artificial Lateral Line. In Proceedings of the 2019 IEEE Sensors Applications Symposium, Sophia Antipolis, France, 11–13 March 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Wolf, B.J.; van de Wolfshaar, J.; van Netten, S.M. Three-dimensional multi-source localization of underwater objects using convolutional neural networks for artificial lateral lines. J. R. Soc. Interface 2020, 17, 20190616. [Google Scholar] [CrossRef]
- Lamb, H. Hydrodynamics. Cambridge University Press: Cambridge, UK, 1924; p. 687. [Google Scholar]
- Que, R.; Zhu, R. A Two-Dimensional Flow Sensor with Integrated Micro Thermal Sensing Elements and a Back Propagation Neural Network. Sensors 2013, 14, 564–574. [Google Scholar] [CrossRef]
- Pjetri, O.; Wiegerink, R.J.; Krijnen, G.J.M. A 2D particle velocity sensor with minimal flow-disturbance. IEEE Sens. J. 2015, 16, 8706–8714. [Google Scholar] [CrossRef]
- Lei, H.; Sharif, M.A.; Tan, X. Dynamics of Omnidirectional IPMC Sensor: Experimental Characterization and Physical Modeling. IEEE/ASME Trans. Mechatron. 2016, 21, 601–612. [Google Scholar] [CrossRef]
- Wolf, B.J.; Morton, J.A.S.; MacPherson, W.N.; van Netten, S.M. Bio-inspired all-optical artificial neuromast for 2D flow sensing. Bioinspir. Biomim. 2018, 13, 026013. [Google Scholar] [CrossRef]
- Lu, Z.; Popper, A. Neural response directionality correlates of hair cell orientation in a teleost fish. J. Comp. Physiol. A Sens. Neural Behav. Physiol. 2001, 187, 453–465. [Google Scholar] [CrossRef]
- Kalmijn, A.J. Hydrodynamic and Acoustic Field Detection. In Sensory Biology of Aquatic Animals; Springer: New York, NY, USA, 1988; pp. 83–130. [Google Scholar] [CrossRef]
- Abdulsadda, A.T.; Tan, X. Underwater Tracking and Size-Estimation of a Moving Object Using an IPMC Artificial Lateral Line. In Smart Materials, Adaptive Structures and Intelligent Systems; American Society of Mechanical Engineers: New York, NY, USA, 2012; pp. 657–665. [Google Scholar] [CrossRef]
- Abdulsadda, A.T.; Tan, X. Underwater tracking of a moving dipole source using an artificial lateral line: Algorithm and experimental validation with ionic polymer–metal composite flow sensors. Smart Mater. Struct. 2013, 22, 045010. [Google Scholar] [CrossRef]
- Franosch, J.M.P.; Sichert, A.B.; Suttner, M.D.; Van Hemmen, J.L. Estimating position and velocity of a submerged moving object by the clawed frog Xenopus and by fish—A cybernetic approach. Biol. Cybern. 2005, 93, 231–238. [Google Scholar] [CrossRef]
- Goulet, J.; Engelmann, J.; Chagnaud, B.P.; Franosch, J.M.P.; Suttner, M.D.; van Hemmen, J.L. Object localization through the lateral line system of fish: Theory and experiment. J. Comp. Physiol. A 2008, 194, 1–17. [Google Scholar] [CrossRef]
- Pandya, S.; Yang, Y.; Liu, C.; Jones, D.L. Biomimetic Imaging of Flow Phenomena. In Proceedings of the 2007 IEEE International Conference on Acoustics, Speech and Signal Processing—ICASSP ’07, Honolulu, HI, USA, 15–20 April 2007; Volume 2, pp. II-933–II-936. [Google Scholar] [CrossRef]
- Sichert, A.B.; Bamler, R.; van Hemmen, J.L. Hydrodynamic Object Recognition: When Multipoles Count. Phys. Rev. Lett. 2009, 102, 058104. [Google Scholar] [CrossRef] [Green Version]
- Coombs, S.; Hastings, M.; Finneran, J. Modeling and measuring lateral line excitation patterns to changing dipole source locations. J. Comp. Physiol. A 1996, 178, 359–371. [Google Scholar] [CrossRef]
- Jiang, Y.; Ma, Z.; Zhang, D. Flow field perception based on the fish lateral line system. Bioinspir. Biomim. 2019, 14, 041001. [Google Scholar] [CrossRef]
- McConney, M.E.; Chen, N.; Lu, D.; Hu, H.A.; Coombs, S.; Liu, C.; Tsukruk, V.V. Biologically inspired design of hydrogel-capped hair sensors for enhanced underwater flow detection. Soft Matter 2009, 5, 292–295. [Google Scholar] [CrossRef]
- Asadnia, M.; Kottapalli, A.G.P.; Karavitaki, K.D.; Warkiani, M.E.; Miao, J.; Corey, D.P.; Triantafyllou, M. From Biological Cilia to Artificial Flow Sensors: Biomimetic Soft Polymer Nanosensors with High Sensing Performance. Sci. Rep. 2016, 6, 32955. [Google Scholar] [CrossRef] [PubMed]
- Asadnia, M.; Kottapalli, A.G.P.; Miao, J.; Warkiani, M.E.; Triantafyllou, M.S. Artificial fish skin of self-powered micro-electromechanical systems hair cells for sensing hydrodynamic flow phenomena. J. R. Soc. Interface 2015, 12, 20150322. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yang, Y.; Pandya, S.; Chen, J.; Engel, J.; Chen, N.; Liu, C. Micromachined Hot-Wire Boundary Layer Flow Imaging Array. In CANEUS: MNT for Aerospace Applications; American Society of Mechanical Engineers Digital Collection (ASMEDC): New York City, NY, USA, 2006; pp. 213–218. [Google Scholar] [CrossRef]
- Abdulsadda, A.T.; Tan, X. Underwater source localization using an IPMC-based artificial lateral line. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 2719–2724. [Google Scholar] [CrossRef]
- Kottapalli, A.G.P.; Bora, M.; Asadnia, M.; Miao, J.; Venkatraman, S.S.; Triantafyllou, M. Nanofibril scaffold assisted MEMS artificial hydrogel neuromasts for enhanced sensitivity flow sensing. Sci. Rep. 2016, 6, 19336. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dunbar, D.; Humphreys, G. A spatial data structure for fast Poisson-disk sample generation. ACM Trans. Graph. 2006, 25, 503–508. [Google Scholar] [CrossRef]
- MATLAB. Version 9.4.0.813654 (R2018a); The MathWorks Inc.: Natick, MA, USA, 2018. [Google Scholar]
- Huang, G.-B.; Zhu, Q.-Y.; Siew, C.-K. Extreme learning machine: A new learning scheme of feedforward neural networks. In Proceedings of the 2004 IEEE International Joint Conference on Neural Networks (IEEE Cat. No.04CH37541), Budapest, Hungary, 25–29 July 2004; Volume 2, pp. 985–990. [Google Scholar] [CrossRef]
- Liang, N.-Y.; Huang, G.-B.; Saratchandran, P.; Sundararajan, N. A Fast and Accurate Online Sequential Learning Algorithm for Feedforward Networks. IEEE Trans. Neural Netw. 2006, 17, 1411–1423. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Glorot, X.; Bengio, Y. Understanding the difficulty of training deep feedforward neural networks. In Proceedings of the Thirteenth International Conference on Artificial Intelligence and Statistics, Sardinia, Italy, 13–15 May 2010; Volume 9, pp. 249–256. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Constrained Nonlinear Optimization Algorithms—MATLAB & Simulink. Available online: https://www.mathworks.com/help/optim/ug/constrained-nonlinear-optimization-algorithms.html (accessed on 13 April 2020).
- Wolf, B.J.; van Netten, S.M. Training submerged source detection for a 2D fluid flow sensor array with extreme learning machines. In Proceedings of the Eleventh International Conference on Machine Vision (ICMV 2018), Munich, Germany, 1–3 November 2018; Nikolaev, D.P., Radeva, P., Verikas, A., Zhou, J., Eds.; International Society for Optics and Photonics (SPIE): Bellingham, WA, USA, 2019; Volume 11041, p. 2. [Google Scholar] [CrossRef]
- Windsor, S.P.; Norris, S.E.; Cameron, S.M.; Mallinson, G.D.; Montgomery, J.C. The flow fields involved in hydrodynamic imaging by blind Mexican cave fish (Astyanax fasciatus ). Part I: Open water and heading towards a wall. J. Exp. Biol. 2010, 213, 3819–3831. [Google Scholar] [CrossRef] [Green Version]
- Lin, X.; Wu, J.; Qin, Q. A novel obstacle localization method for an underwater robot based on the flow field. J. Mar. Sci. Eng. 2019, 7, 437. [Google Scholar] [CrossRef] [Green Version]
- Bot, D.; Wolf, B.; van Netten, S. Dipole Localisation Predictions Data Set. 2021. Available online: https://doi.org/10.5281/zenodo.4973492 (accessed on 30 June 2021).
- Bot, D.; Wolf, B.; van Netten, S. Dipole Localisation Algorithms for Simulated Artificial Lateral Line. 2021. Available online: https://doi.org/10.5281/zenodo.4973515 (accessed on 30 June 2021).
- Mallat, S. A Wavelet Tour of Signal Processing; Elsevier: Amsterdam, The Netherlands, 1999. [Google Scholar]
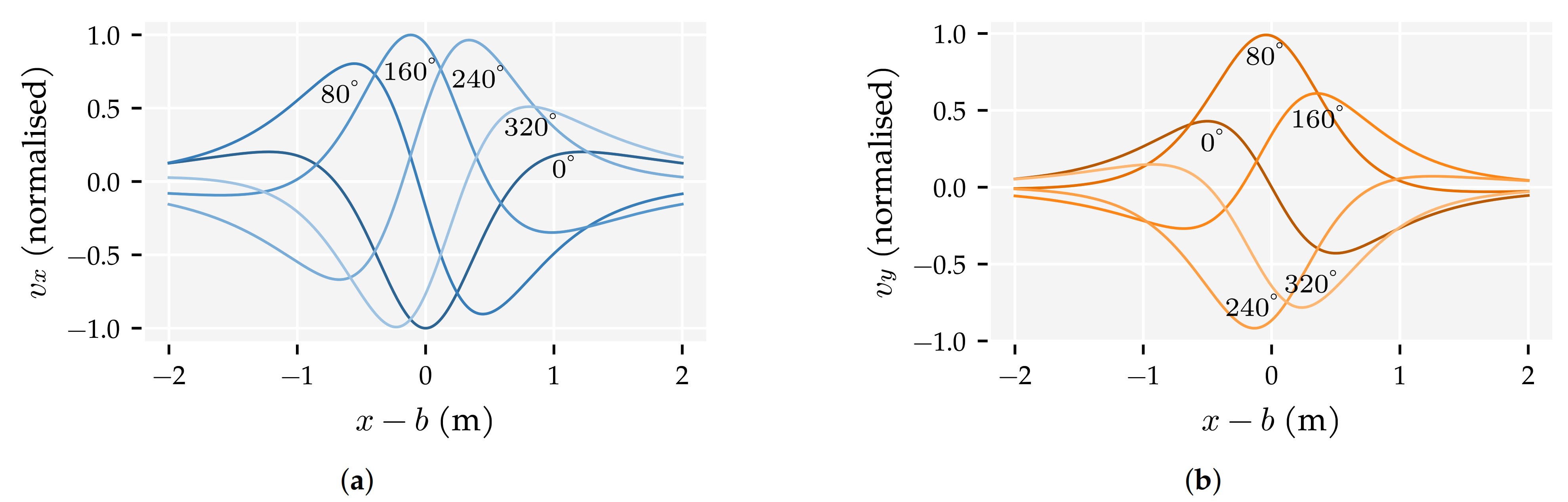
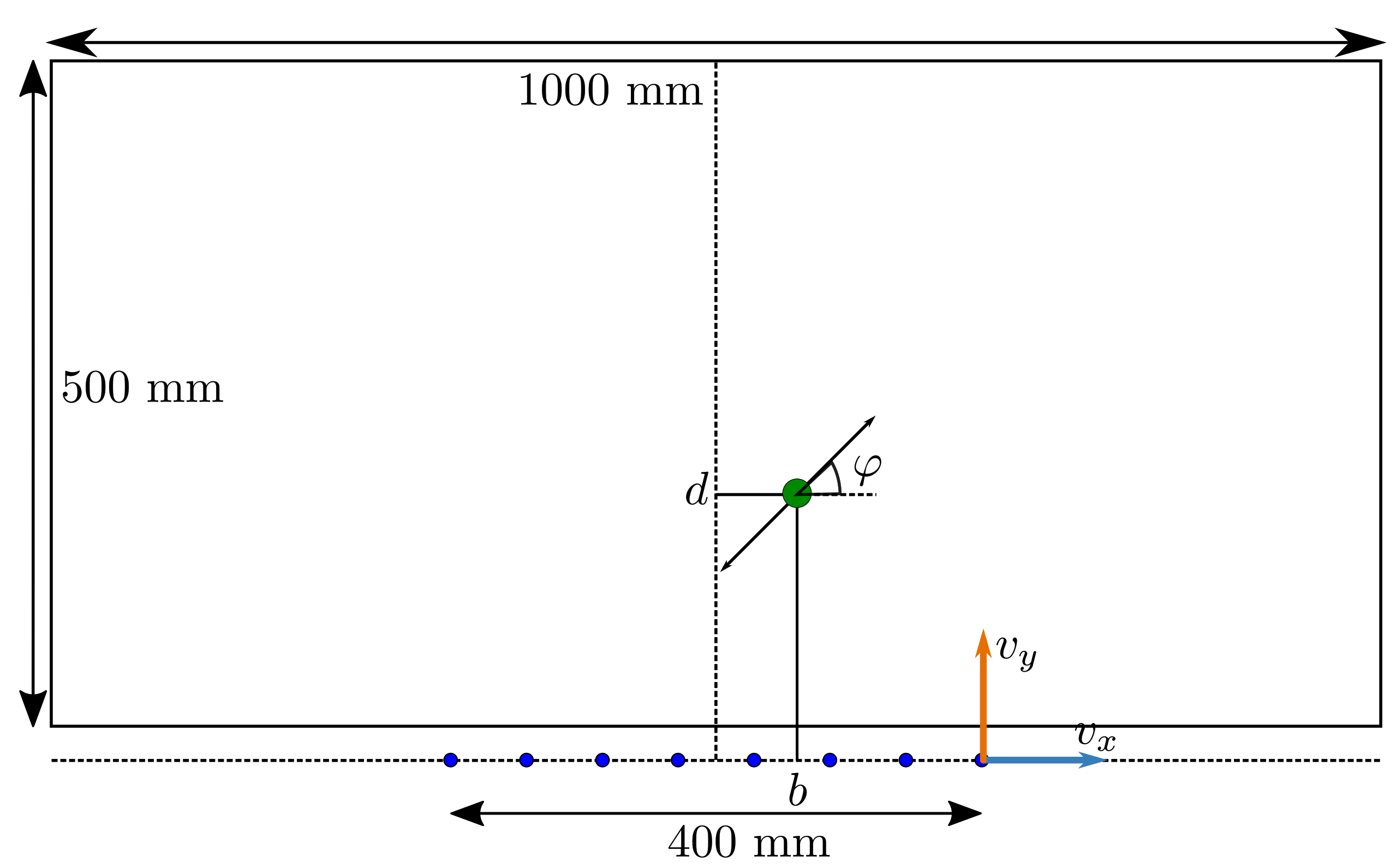
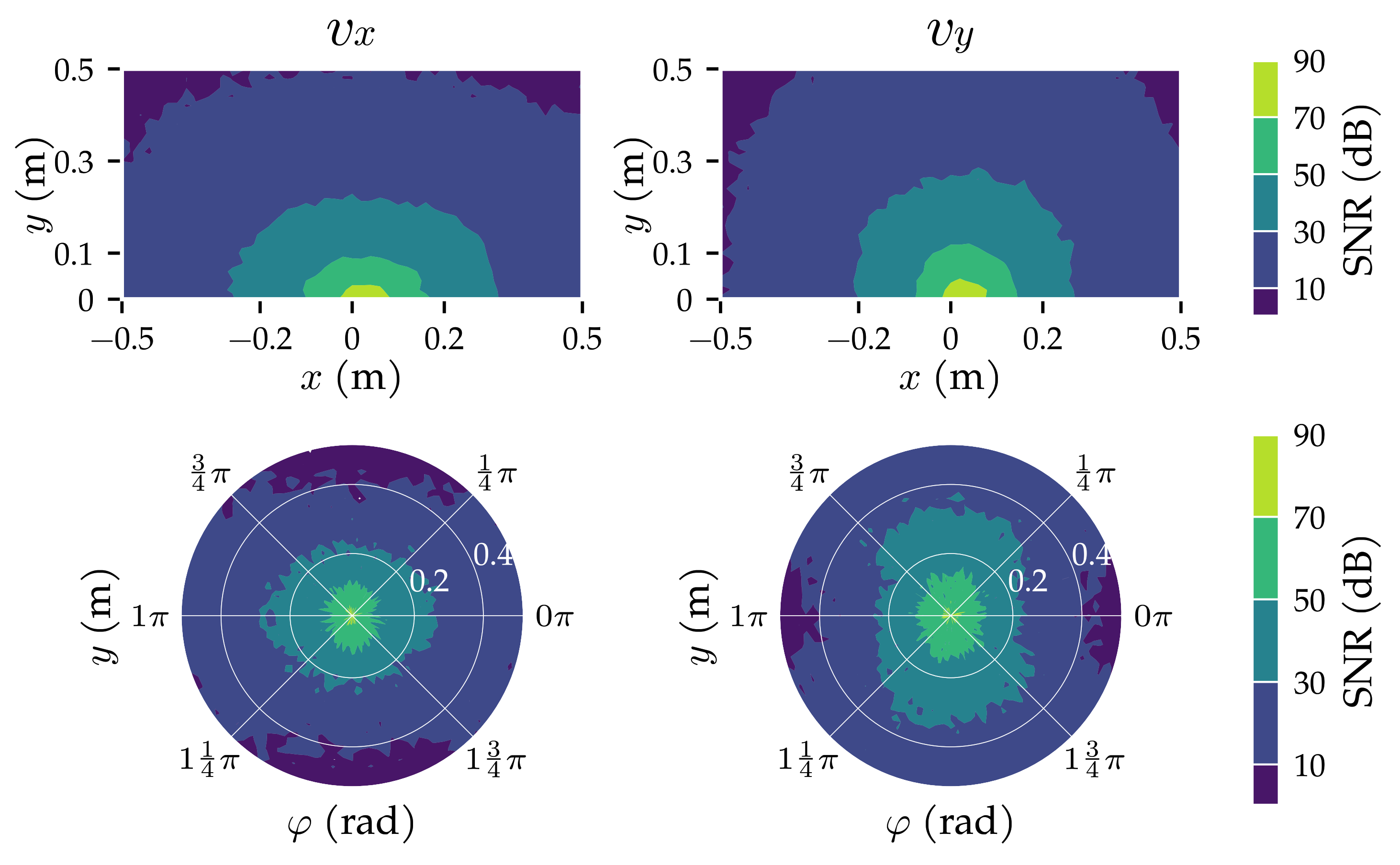
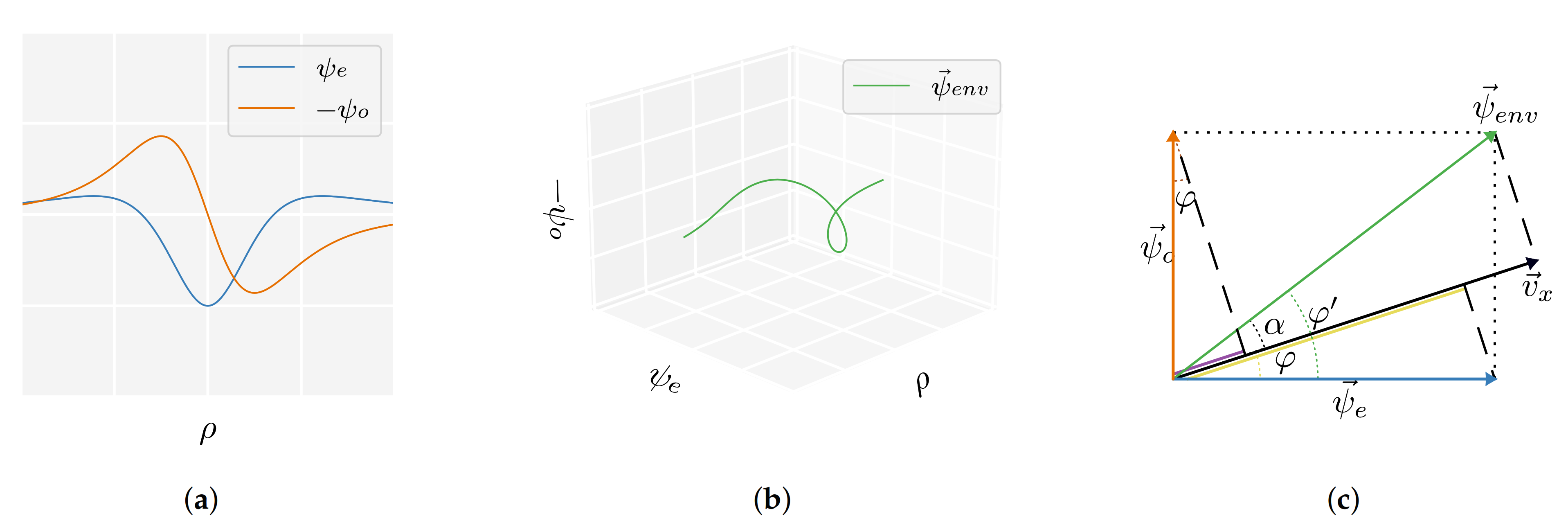
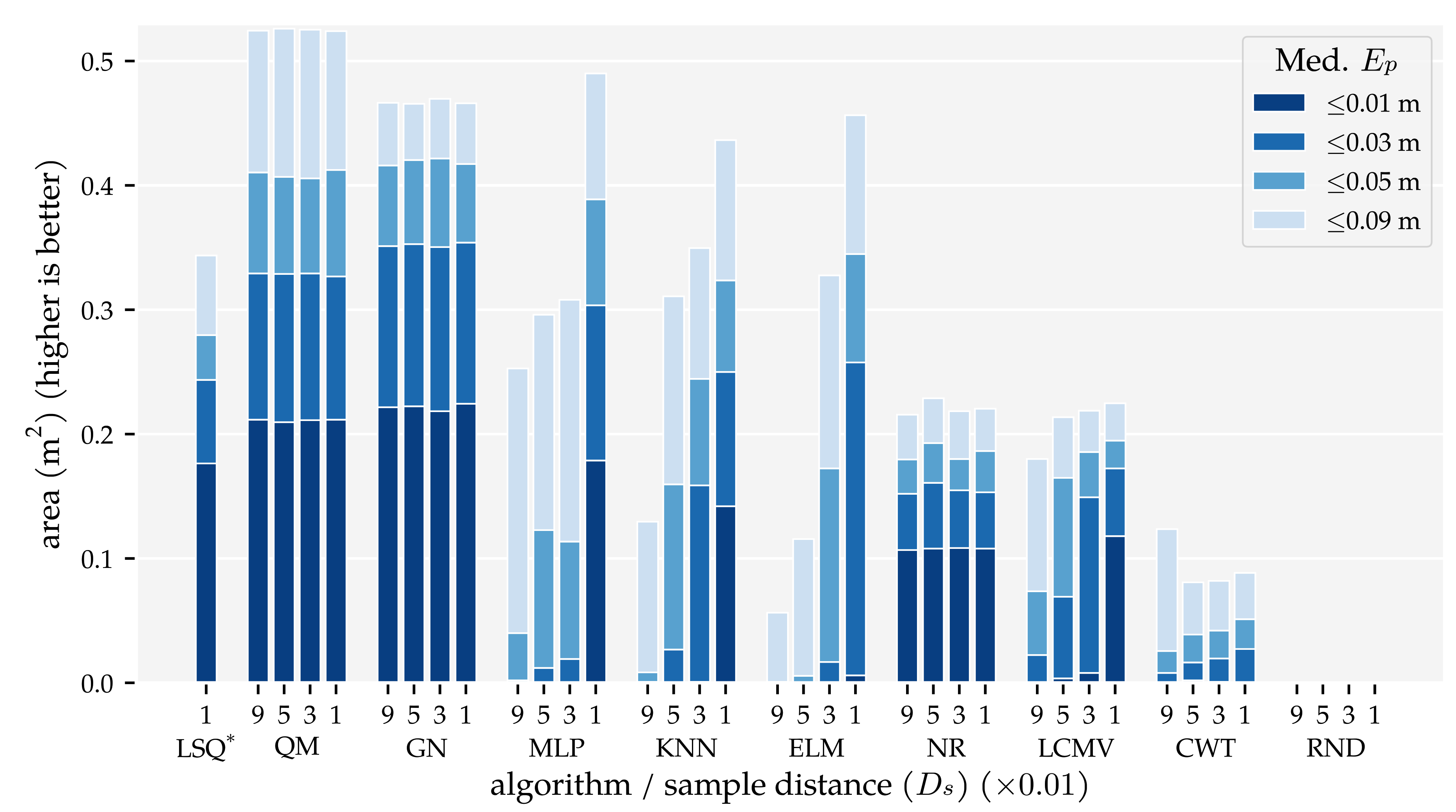
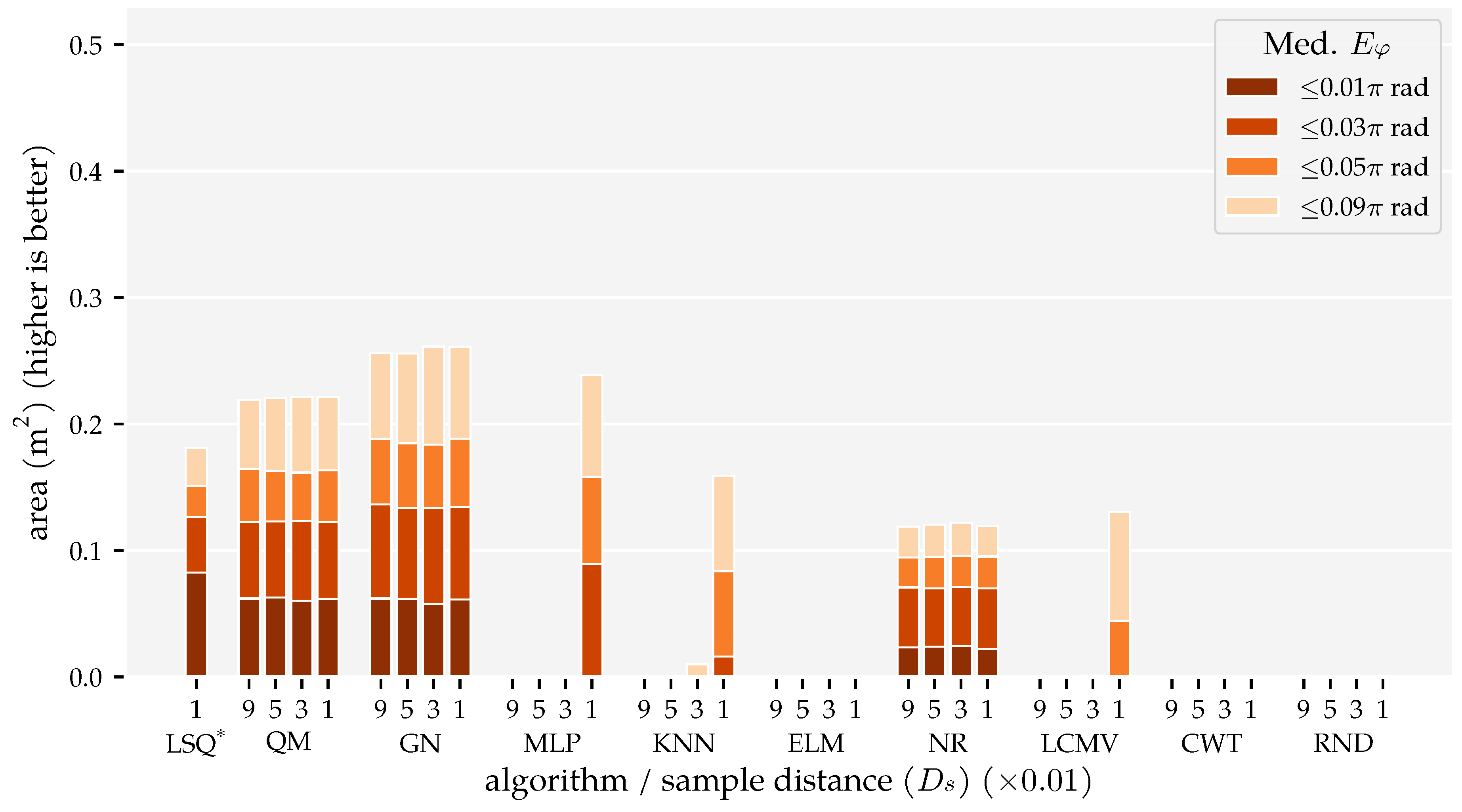
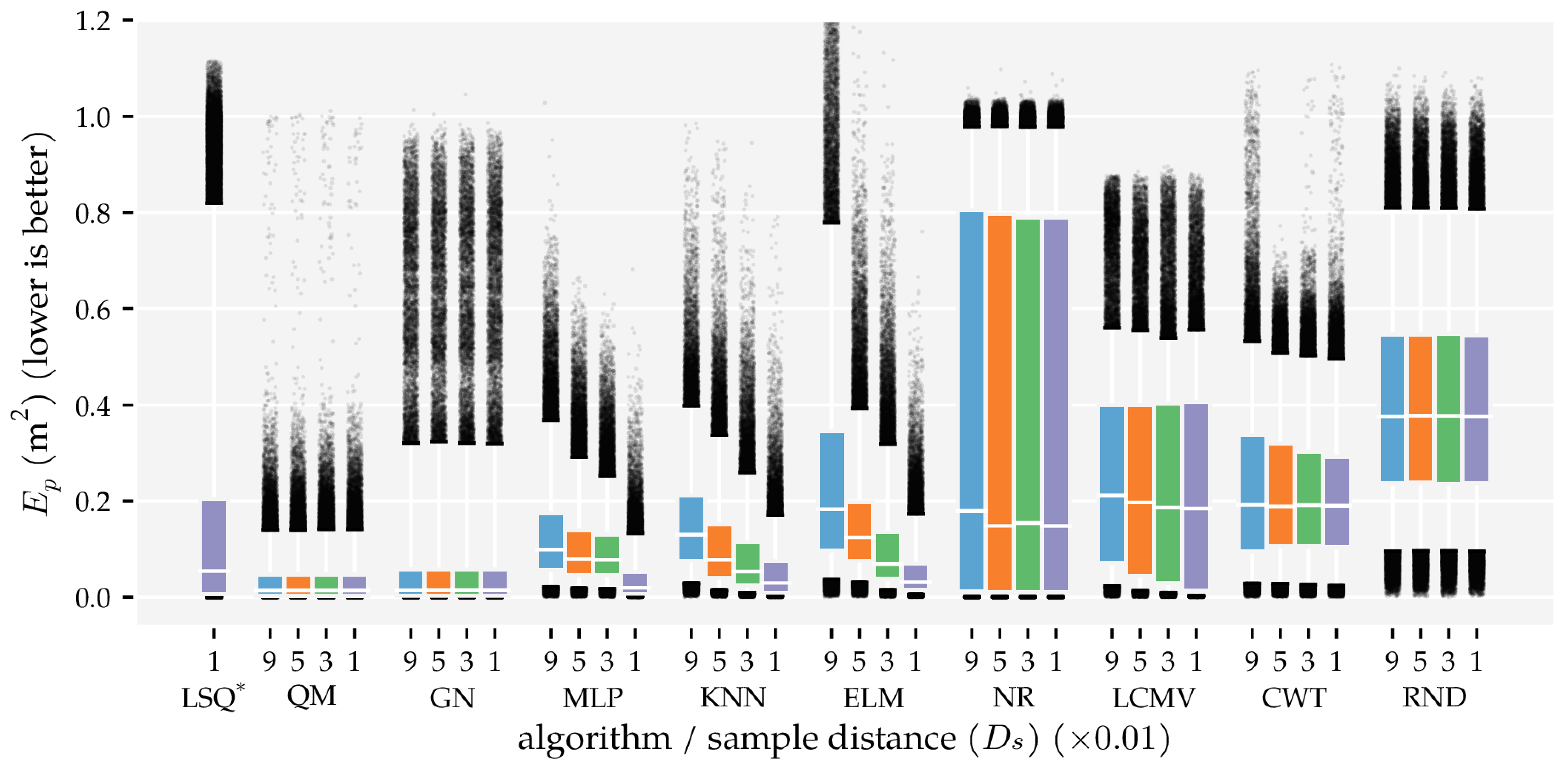
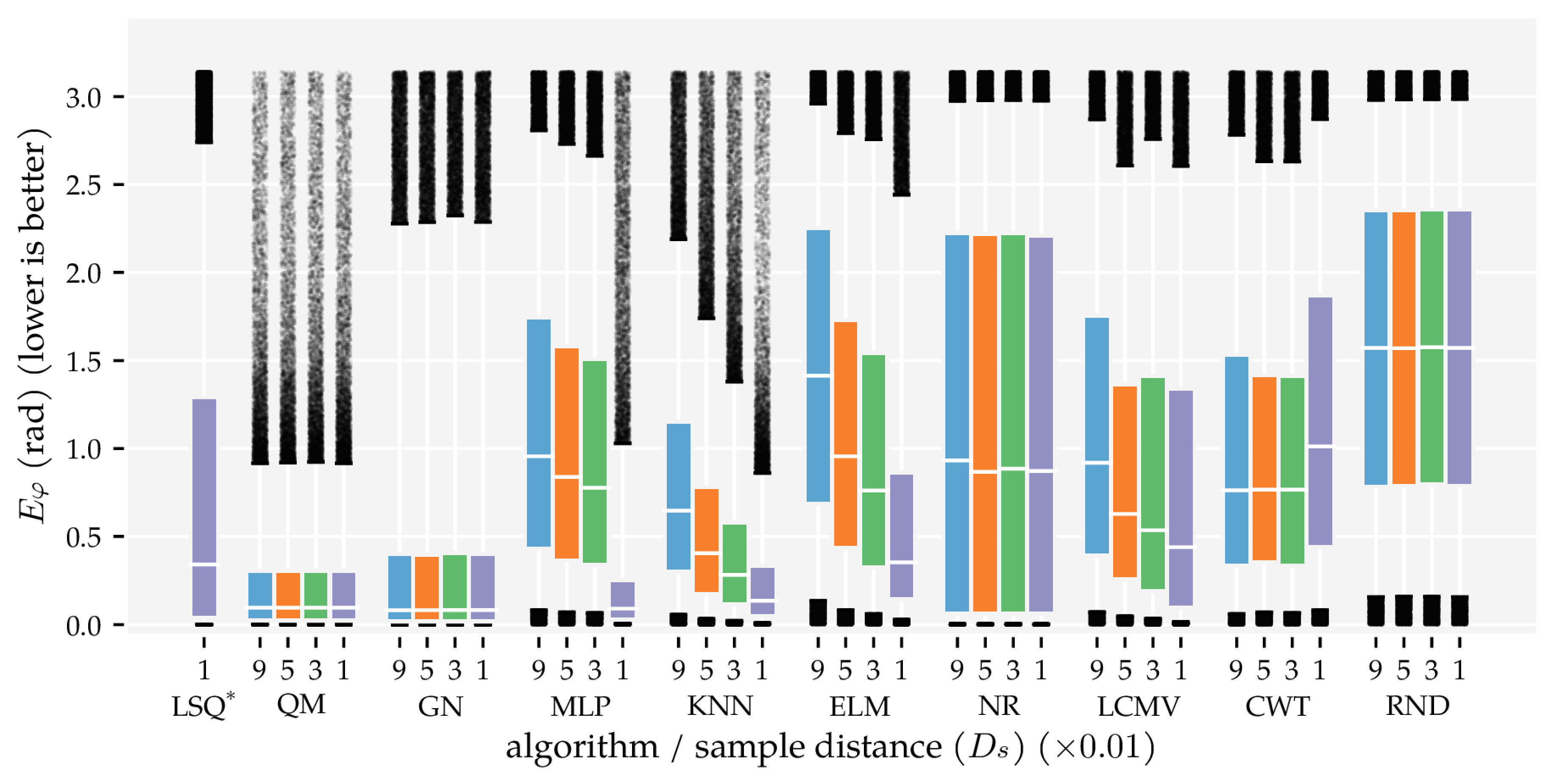
| Type | Min. Sample Distance () | Num. States | Avg. Min (m) | Avg. Min () |
|---|---|---|---|---|
| training | 0.09 | 169 | ||
| training | 0.05 | 874 | ||
| training | 0.03 | 3796 | ||
| training | 0.01 | 90,435 | ||
| testing | 0.01 | 90,502 |
| Algorithm | Type | Training | Hyperparameters | Limited to Domain | Limited to Sample |
|---|---|---|---|---|---|
| RND | — | no | no | yes | no |
| LCMV [12,13] | template-based | yes | no | yes | yes |
| KNN | template-based | yes | yes | yes | no |
| CWT [5] | template-based | yes | yes | yes | no |
| ELM [9,10] | neural network | yes | no | no | no |
| MLP [7,9] | neural network | yes | no | no | no |
| GN [8] | model-based | no | yes | yes | no |
| NR [8] | model-based | no | yes | yes | no |
| LSQ | model-based | no | yes | yes | no |
| QM | model-based | no | yes | yes | no |
| Algorithm | Avg. Prediction Time | Relative to MLP | Total Training Time |
|---|---|---|---|
| RND | 0.9 | ||
| MLP | 1.0 | 12 0 | |
| ELM | 1.2 | 1 52 | |
| KNN | 2.7 | ||
| GN | 3.9 | ||
| LSQ | 7.8 | ||
| QM | 9.6 | ||
| LCMV | 37.1 | ||
| NR | 176.3 | ||
| CWT | 311.1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bot, D.M.; Wolf, B.J.; van Netten, S.M. The Quadrature Method: A Novel Dipole Localisation Algorithm for Artificial Lateral Lines Compared to State of the Art. Sensors 2021, 21, 4558. https://doi.org/10.3390/s21134558
Bot DM, Wolf BJ, van Netten SM. The Quadrature Method: A Novel Dipole Localisation Algorithm for Artificial Lateral Lines Compared to State of the Art. Sensors. 2021; 21(13):4558. https://doi.org/10.3390/s21134558
Chicago/Turabian StyleBot, Daniël M., Ben J. Wolf, and Sietse M. van Netten. 2021. "The Quadrature Method: A Novel Dipole Localisation Algorithm for Artificial Lateral Lines Compared to State of the Art" Sensors 21, no. 13: 4558. https://doi.org/10.3390/s21134558
APA StyleBot, D. M., Wolf, B. J., & van Netten, S. M. (2021). The Quadrature Method: A Novel Dipole Localisation Algorithm for Artificial Lateral Lines Compared to State of the Art. Sensors, 21(13), 4558. https://doi.org/10.3390/s21134558






