ATARI: A Graph Convolutional Neural Network Approach for Performance Prediction in Next-Generation WLANs
Abstract
:1. Introduction
- We propose a GNN model that predicts the achieved throughput in highly dense IEEE 802.11 WLANs using CB. To the best of our knowledge, this is the first time GNNs are applied to this problem.
- We compare our approach with recent state-of-the-art DL and ML approaches and discuss how different features impact the prediction accuracy. Based on the available features, a given model can be optimally selected.
- Our proposal accurately predicts the throughput generating a model that can be employed in future intelligent decision frameworks for CB, similar to [9].
2. Related Work
- Instead of defining an analytical model that does not scale when the number of nodes in the environment increases, we propose several ML approaches that learn from data. The proposed approaches take care of the complex task of defining wireless interactions.
- Unlike [15], our approach does not define the best CB policy that a WLAN needs to apply to maximize its reward. Our goal is that the ML model learns how the wireless interactions affect the throughput of a given WLAN without any explicit assumptions, such as user demand or user mobility patterns. This approach can later be used as a function approximator in such RL approaches.
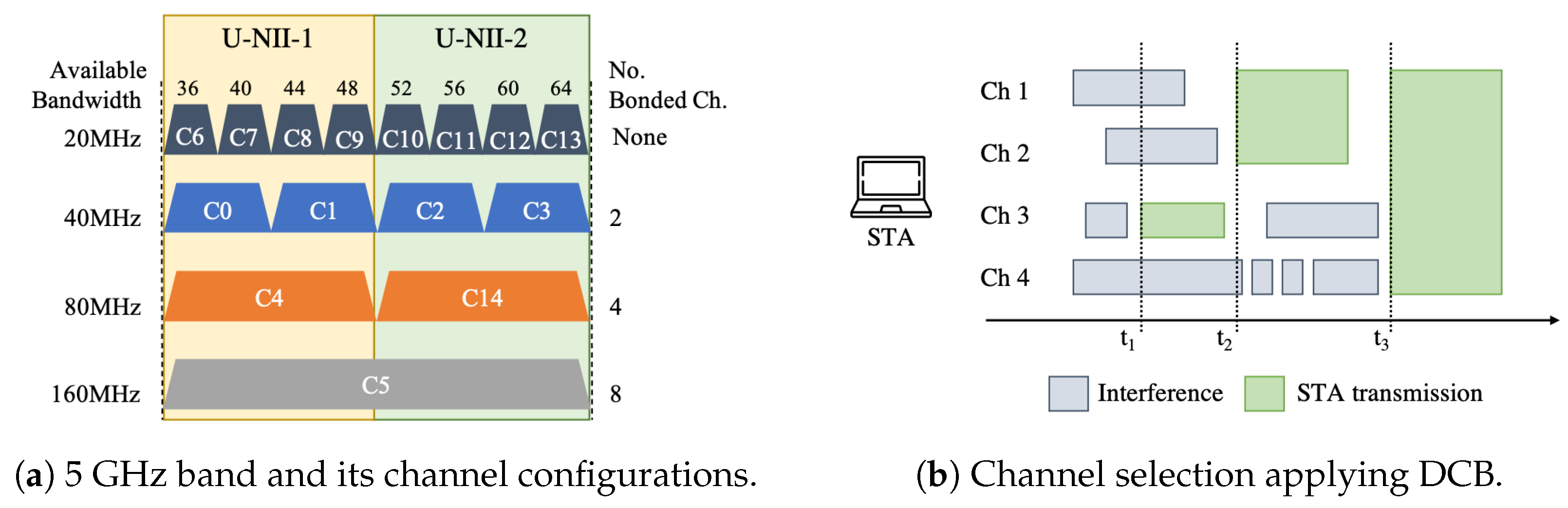
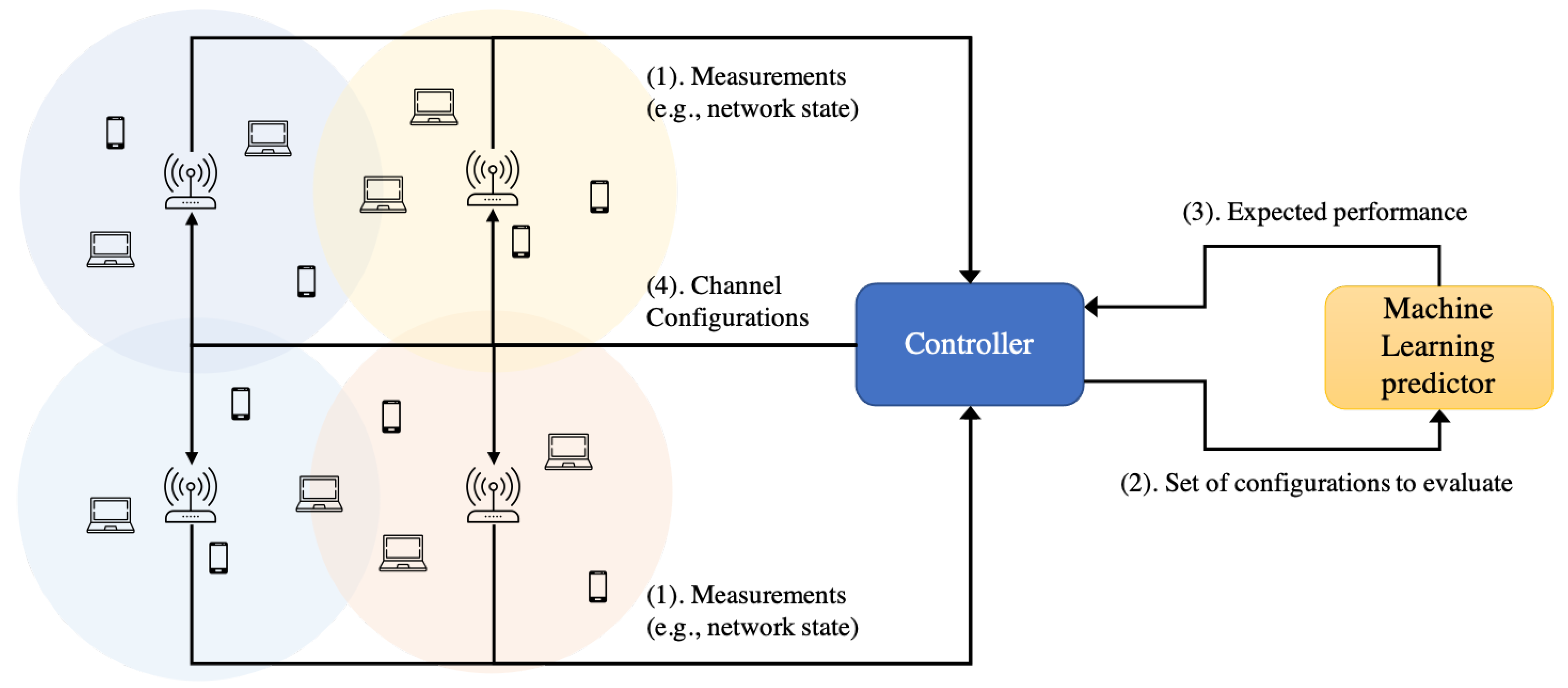
3. Motivation for Learning Models in Next-Generation WLANs
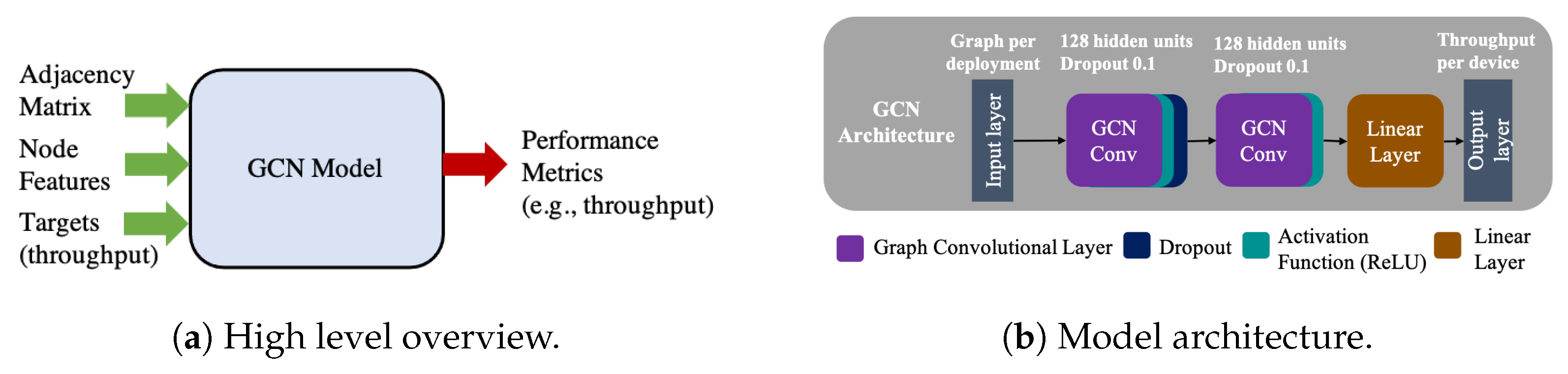
4. A GNN Model for Performance Prediction in Next-Generation WLANs
- CB is a problem with a combinatorial action space in dense deployments, where the complexity increases exponentially with the size of the deployment and the number of possible channel configurations.
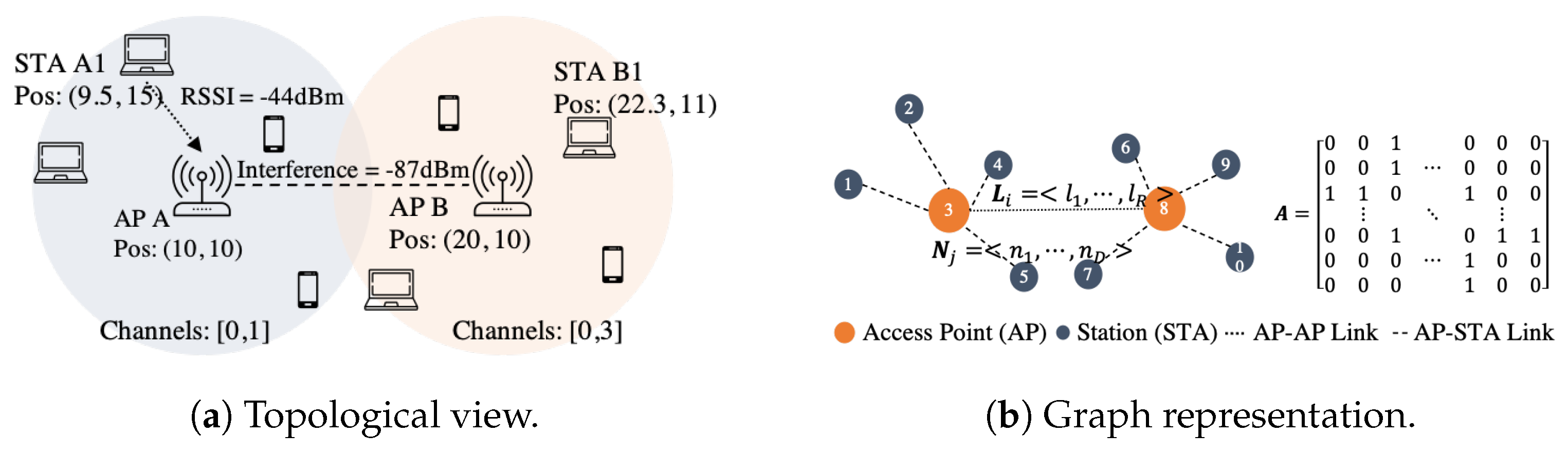
- The relationships between STAs and APs (connectivity, interference, among others) can be captured via a graph representation, i.e., there is one-to-one mapping between the network topology and the graph representation.
- GNNs are also proposed to solve multiple network optimization processes [23], given their ability to generalize to large-scale problems.
- GNNs can easily operate and generalize over environments with a changing topology and a variable number of nodes.
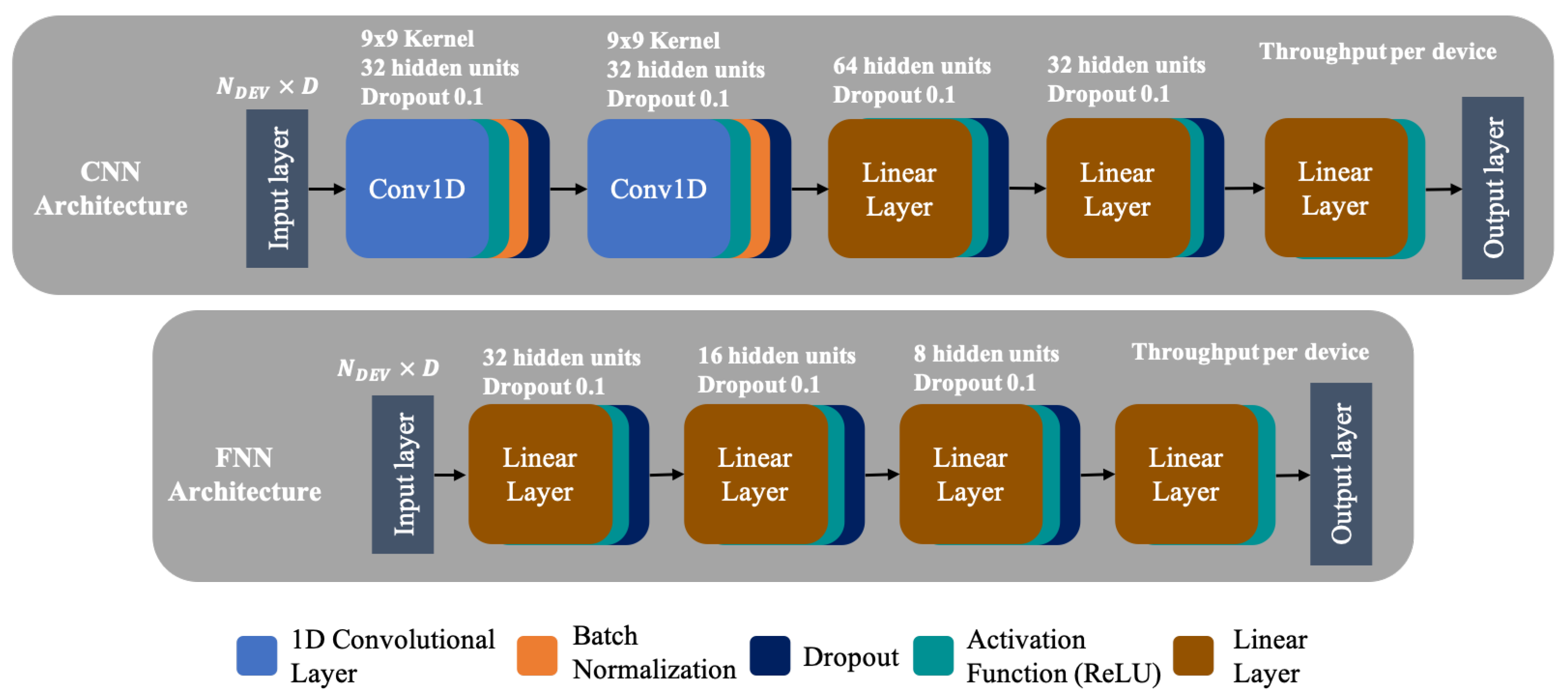
5. State-of-the-Art ML Models
6. Data Set
6.1. Simulated Data Sets for Training Ml-Based Networking Solutions
6.2. Data Set Generation
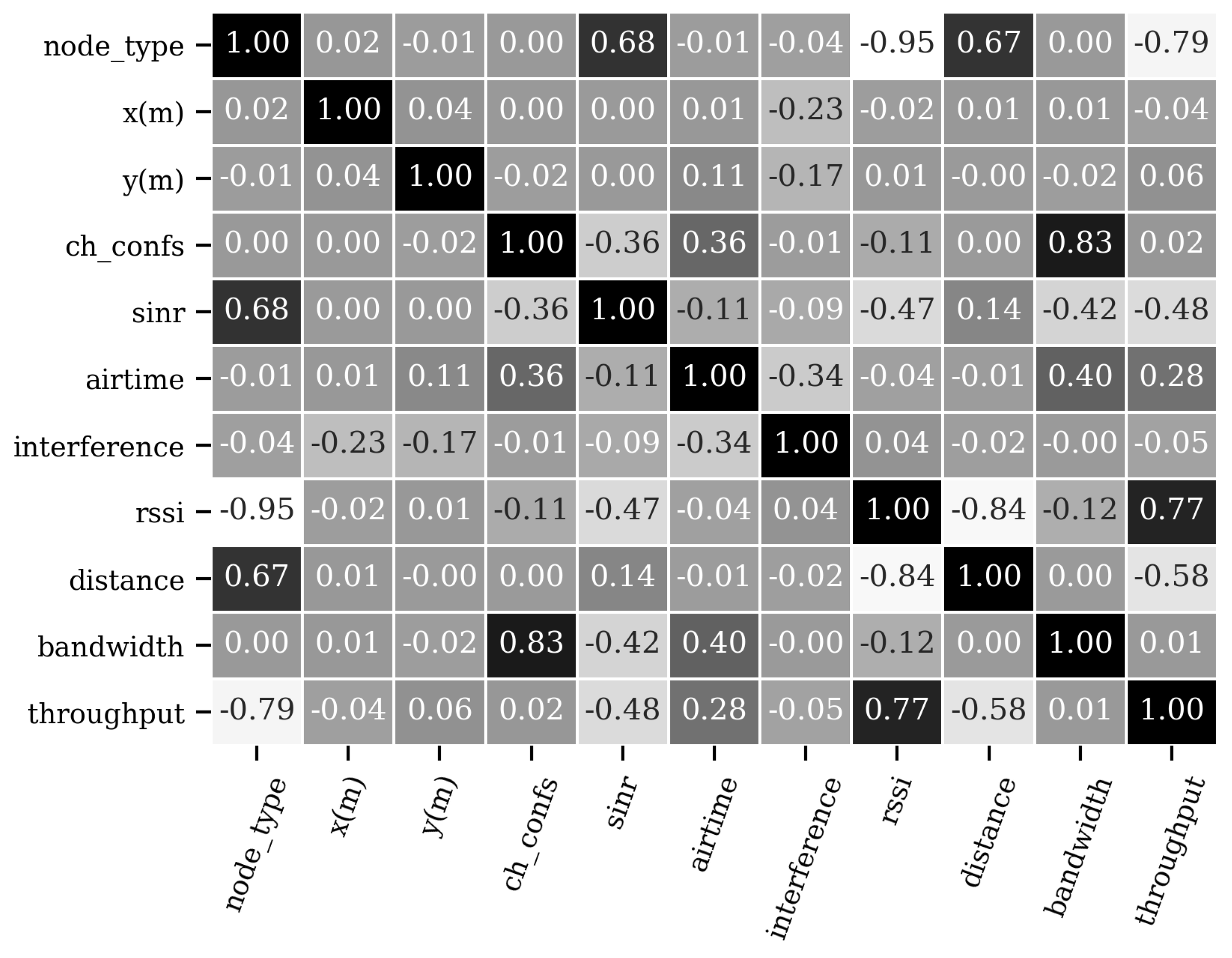
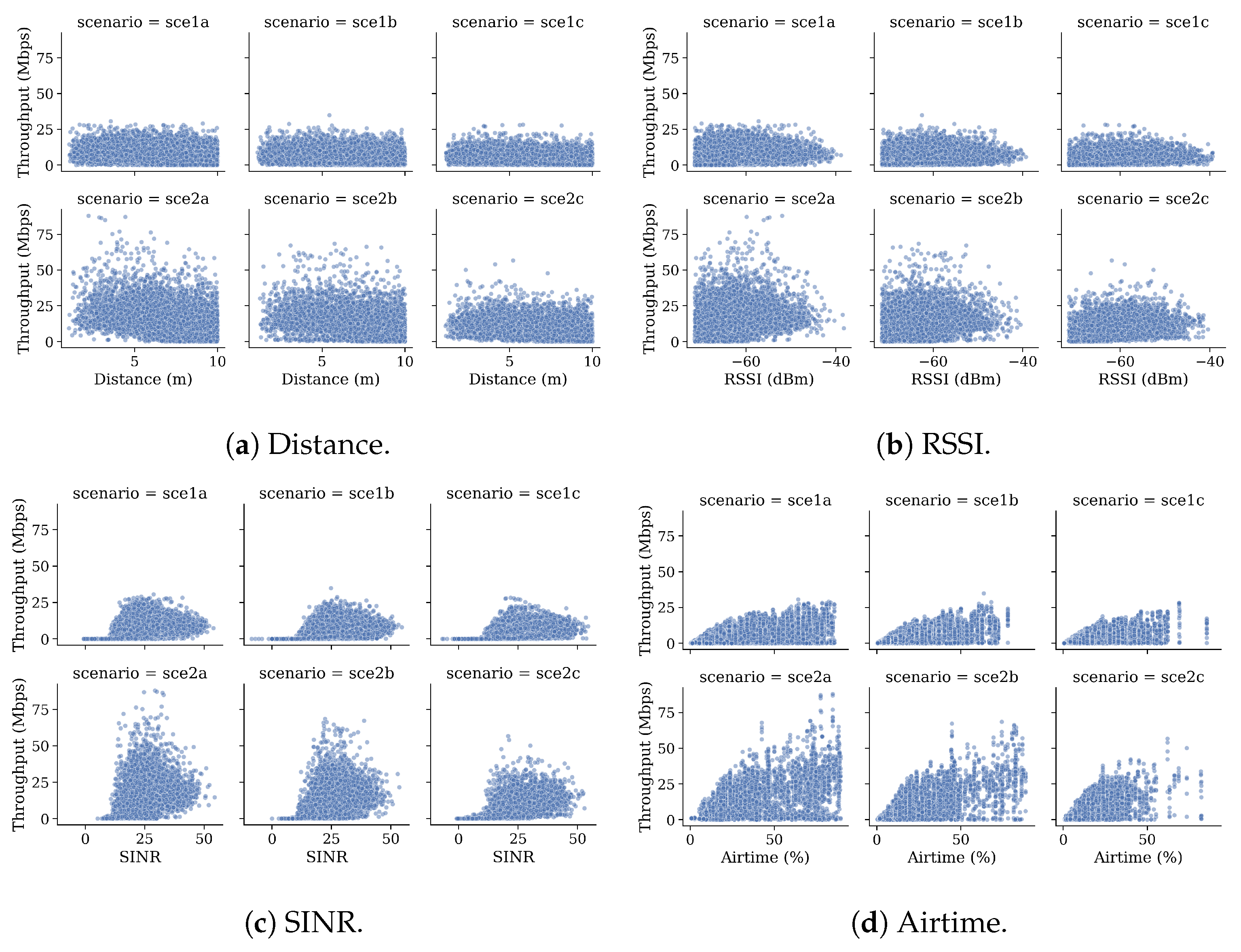
6.3. Data Set Analysis
7. Results
7.1. Training and Validation
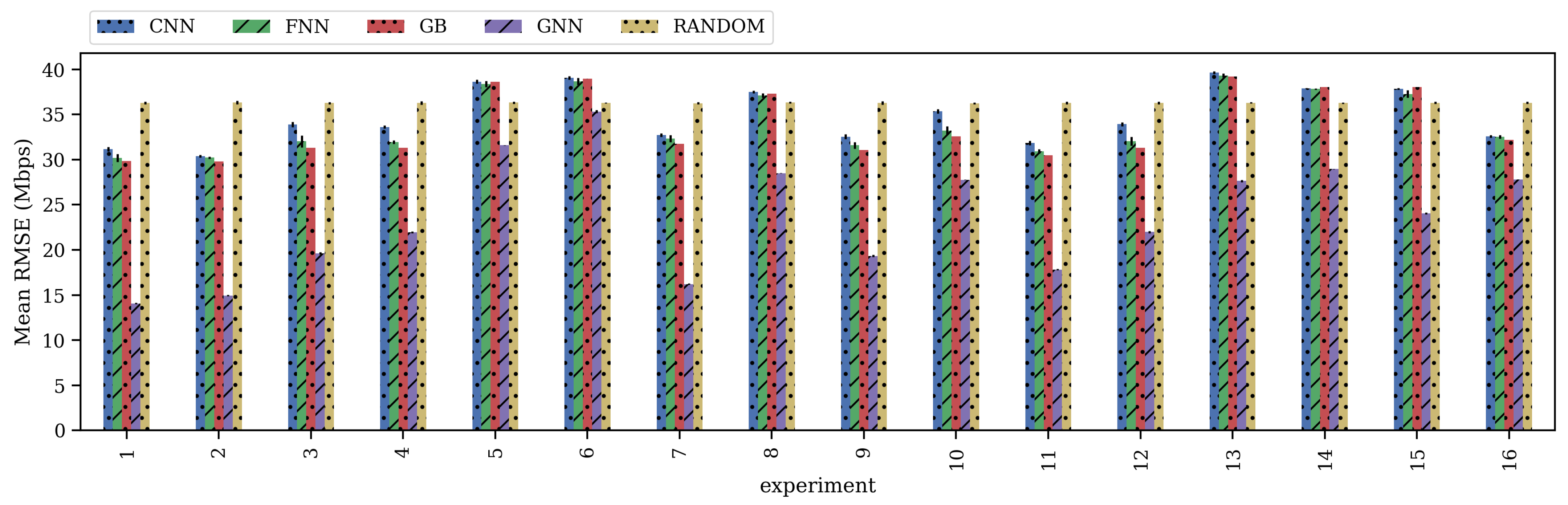
7.2. Performance Evaluation of the Proposed Models
8. Discussion
9. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- CISCO. CISCO Annual Internet Report (2018–2023) White Paper; CISCO: San Jose, CA, USA, 2020. [Google Scholar]
- IEEE. IEEE 802.11ax-2021—IEEE Standard for Information Technology—Telecommunications and Information Exchange between Systems Local and Metropolitan Area Networks—Specific Requirements Part 11: Wireless LAN Medium Access Control (MAC) and Physical Layer (PHY) Specifications Amendment 1: Enhancements for High-Efficiency WLAN; Draft; IEEE: Piscataway, NJ, USA, 2021. [Google Scholar]
- Deek, L.; Garcia-Villegas, E.; Belding, E.; Lee, S.J.; Almeroth, K. Intelligent channel bonding in 802.11 n WLANs. IEEE Trans. Mob. Comput. 2013, 13, 1242–1255. [Google Scholar] [CrossRef]
- Park, M. IEEE 802.11 ac: Dynamic bandwidth channel access. In Proceedings of the 2011 IEEE International Conference on Communications (ICC), Kyoto, Japan, 5–9 June 2011; pp. 1–5. [Google Scholar]
- Qiu, L.; Zhang, Y.; Wang, F.; Han, M.K.; Mahajan, R. A general model of wireless interference. In Proceedings of the 13th Annual ACM International Conference on Mobile Computing and Networking, Montreal, QC, Canada, 9–14 September 2007; pp. 171–182. [Google Scholar]
- Bianchi, G. Performance analysis of the IEEE 802.11 distributed coordination function. IEEE J. Sel. Areas Commun. 2000, 18, 535–547. [Google Scholar] [CrossRef]
- Wilhelmi, F.; Carrascosa, M.; Cano, C.; Jonsson, A.; Ram, V.; Bellalta, B. Usage of Network Simulators in Machine-Learning-Assisted 5G/6G Networks. IEEE Wirel. Commun. 2021, 28, 160–166. [Google Scholar] [CrossRef]
- Barrachina-Munoz, S.; Wilhelmi, F.; Selinis, I.; Bellalta, B. Komondor: A wireless network simulator for next-generation high-density WLANs. In Proceedings of the 2019 Wireless Days (WD), Manchester, UK, 24–26 April 2019; pp. 1–8. [Google Scholar]
- Karmakar, R.; Chattopadhyay, S.; Chakraborty, S. A Deep Probabilistic Control Machinery for Auto-Configuration of WiFi Link Parameters. IEEE Trans. Wirel. Commun. 2020, 19, 8330–8340. [Google Scholar] [CrossRef]
- Daldoul, Y.; Meddour, D.E.; Ksentini, A. IEEE 802.11 ac: Effect of channel bonding on spectrum utilization in dense environments. In Proceedings of the 2017 IEEE International Conference on Communications (ICC), Paris, France, 21–25 May 2017; pp. 1–6. [Google Scholar]
- Faridi, A.; Bellalta, B.; Checco, A. Analysis of dynamic channel bonding in dense networks of WLANs. IEEE Trans. Mob. Comput. 2016, 16, 2118–2131. [Google Scholar] [CrossRef] [Green Version]
- Barrachina-Muñoz, S.; Wilhelmi, F.; Bellalta, B. Dynamic Channel Bonding in Spatially Distributed High-Density WLANs. IEEE Trans. Mob. Comput. 2020, 19, 821–835. [Google Scholar] [CrossRef] [Green Version]
- Khan, M.A.; Hamila, R.; Al-Emadi, N.A.; Kiranyaz, S.; Gabbouj, M. Real-time throughput prediction for cognitive Wi-Fi networks. J. Netw. Comput. Appl. 2020, 150, 102499. [Google Scholar] [CrossRef]
- Herzen, J.; Lundgren, H.; Hegde, N. Learning wi-fi performance. In Proceedings of the 2015 12th Annual IEEE International Conference on Sensing, Communication, and Networking (SECON), Seattle, WA, USA, 22–25 June 2015; pp. 118–126. [Google Scholar]
- Luo, Y.; Chin, K.W. Learning to Bond in Dense WLANs With Random Traffic Demands. IEEE Trans. Veh. Technol. 2020, 69, 11868–11879. [Google Scholar] [CrossRef]
- Bellalta, B. IEEE 802.11 ax: High-efficiency WLANs. IEEE Wirel. Commun. 2016, 23, 38–46. [Google Scholar] [CrossRef] [Green Version]
- López-Pérez, D.; Garcia-Rodriguez, A.; Galati-Giordano, L.; Kasslin, M.; Doppler, K. IEEE 802.11 be extremely high throughput: The next generation of Wi-Fi technology beyond 802.11 ax. IEEE Commun. Mag. 2019, 57, 113–119. [Google Scholar] [CrossRef] [Green Version]
- ITU-T. ITU-T Y.3172-Series—Architectural Framework for Machine Learning in Future Networks Including IMT-2020; Recommendation; ITU-T: Geneva, Switzerland, 2019. [Google Scholar]
- Scarselli, F.; Gori, M.; Tsoi, A.C.; Hagenbuchner, M.; Monfardini, G. The graph neural network model. IEEE Trans. Neural Netw. 2008, 20, 61–80. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fey, M.; Lenssen, J.E. Fast Graph Representation Learning with PyTorch Geometric. arXiv 2019, arXiv:1903.02428. [Google Scholar]
- Bello, I.; Pham, H.; Le, Q.V.; Norouzi, M.; Bengio, S. Neural combinatorial optimization with reinforcement learning. arXiv 2016, arXiv:1611.09940. [Google Scholar]
- Battaglia, P.W.; Hamrick, J.B.; Bapst, V.; Sanchez-Gonzalez, A.; Zambaldi, V.; Malinowski, M.; Tacchetti, A.; Raposo, D.; Santoro, A.; Faulkner, R.; et al. Relational inductive biases, deep learning, and graph networks. arXiv 2018, arXiv:1806.01261. [Google Scholar]
- Rusek, K.; Suárez-Varela, J.; Mestres, A.; Barlet-Ros, P.; Cabellos-Aparicio, A. Unveiling the potential of Graph Neural Networks for network modeling and optimization in SDN. In Proceedings of the 2019 ACM Symposium on SDN Research, San Jose, CA, USA, 3 April 2019; pp. 140–151. [Google Scholar]
- Kipf, T.N.; Welling, M. Semi-supervised classification with graph convolutional networks. arXiv 2016, arXiv:1609.02907. [Google Scholar]
- Wilhelmi, F. [ITU-T AI Challenge] Input/Output of Project “Improving the Capacity of IEEE 802.11 WLANs through Machine Learning. 2020. Available online: https://zenodo.org/record/4106127#.YNBwAJMzZB0 (accessed on 6 December 2020).
- Barrachina-Muñoz, S.; Wilhelmi, F. Komondor: An IEEE 802.11ax Simulator. 2019. Commit: d330ed9. Available online: https://github.com/wn-upf/Komondor (accessed on 21 June 2021).
- Henderson, T.R.; Lacage, M.; Riley, G.F.; Dowell, C.; Kopena, J. Network simulations with the ns-3 simulator. SIGCOMM Demonstr. 2008, 14, 527. [Google Scholar]
- Bellalta, B.; Zocca, A.; Cano, C.; Checco, A.; Barcelo, J.; Vinel, A. Throughput analysis in CSMA/CA networks using continuous time Markov networks: A tutorial. Wirel. Netw. Mov. Obj. 2014, 115–133. [Google Scholar] [CrossRef] [Green Version]
- Barrachina-Muñoz, S.; Bellalta, B.; Knightly, E. Wi-Fi All-Channel Analyzer. In Proceedings of the 14th International Workshop on Wireless Network Testbeds, Experimental Evaluation & Characterization (WiNTECH), London, UK, 21 September 2020; pp. 72–79. [Google Scholar]
- IEEE. TGax Simulation Scenarios. Doc.: IEEE 802.11-14/0980r16. 2015. Available online: https://mentor.ieee.org/802.11/dcn/14/11-14-0980-16-00ax-simulation-scenarios.docx (accessed on 15 June 2021).
- Adame, T.; Carrascosa, M.; Bellalta, B. The TMB path loss model for 5 GHz indoor WiFi scenarios: On the empirical relationship between RSSI, MCS, and spatial streams. In Proceedings of the 2019 Wireless Days (WD), Manchester, UK, 24–26 April 2019; pp. 1–8. [Google Scholar]
- Deek, L.; Garcia-Villegas, E.; Belding, E.; Lee, S.J.; Almeroth, K. The impact of channel bonding on 802.11 n network management. In Proceedings of the 7th Conference on emerging Networking Experiments and Technologies, Tokyo, Japan, 6–9 December 2011; pp. 1–12. [Google Scholar]
- IETF. Intent-Based Networking–Concepts and Overview; IETF: Wilmington, NC, USA, 2019. [Google Scholar]
- ETSI. Zero-Touch Network and Service Management (ZSM): Means of Automation; ETSI: Valbonne, France, 2020. [Google Scholar]
- Hornik, K.; Stinchcombe, M.; White, H. Multilayer feedforward networks are universal approximators. Neural Netw. 1989, 2, 359–366. [Google Scholar] [CrossRef]
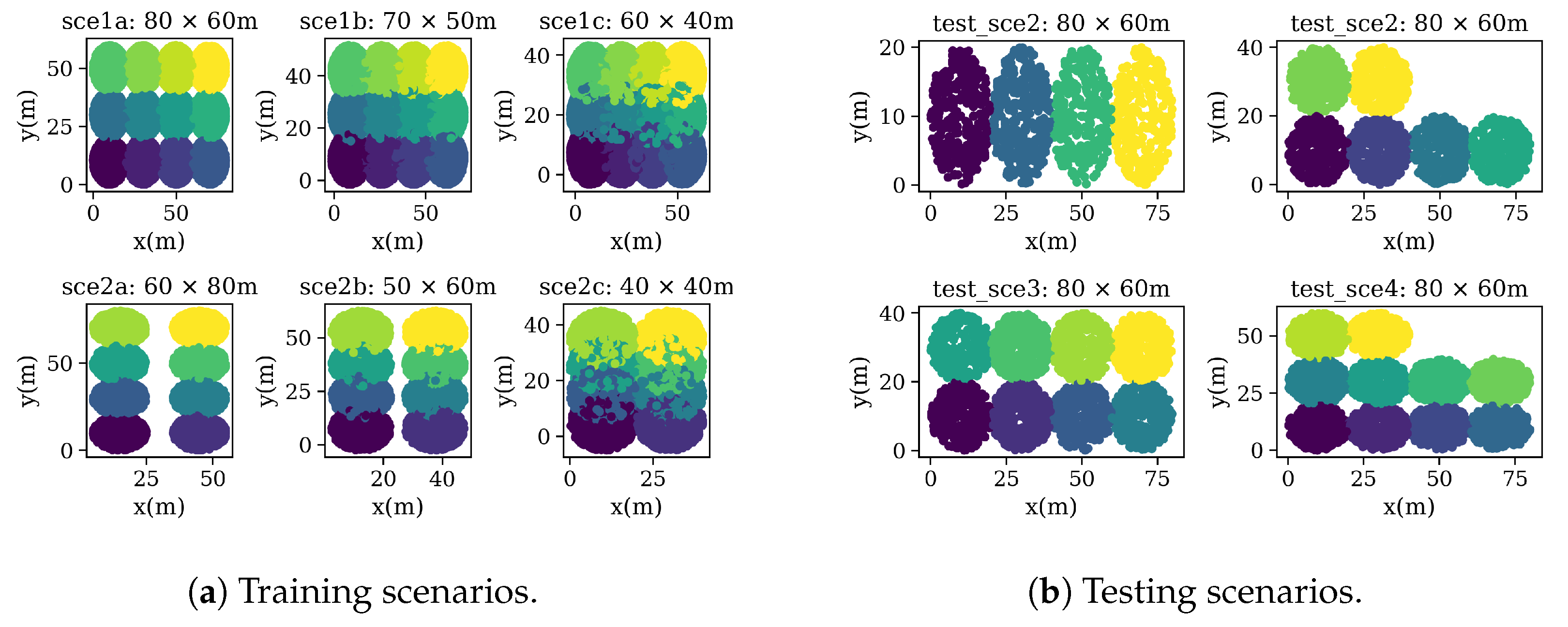
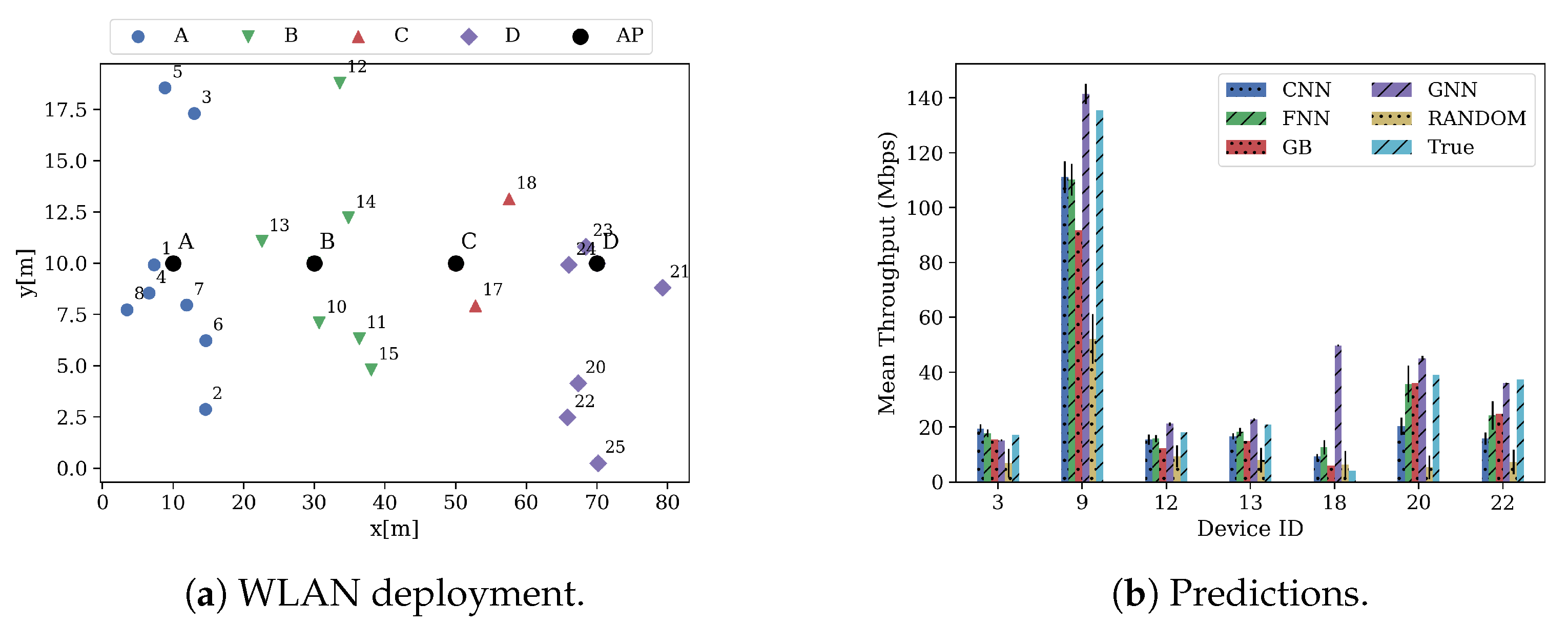
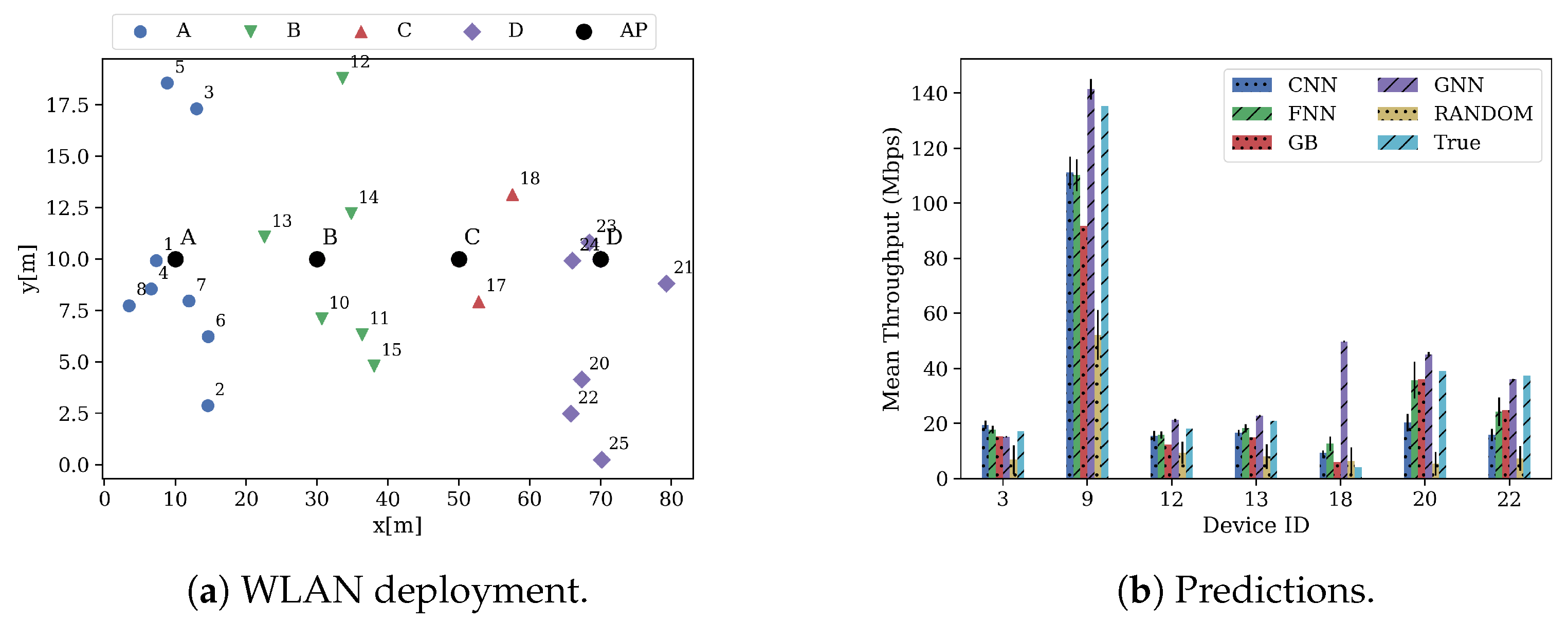
| Data Set | Scenarios | Map Size | № Deployments | Total Devices | APs Per Deployment | STAs Per Deployment | Mean–Std–Min–Max STA Throughput | Mean–Std–Min–Max AP Throughput |
|---|---|---|---|---|---|---|---|---|
| Training and Validation | 1a | 80 × 60 m | 100 | 78,078: 6000 APs 72,078 STAs | 12 | [10–20] | [6.93–6.99–0–88] Mbps | [83.29–52.24–0–400] Mbps |
| 1b | 70 × 50 m | 100 | 12 | [10–20] | ||||
| 1c | 60 × 40 m | 100 | 12 | [10–20] | ||||
| 2a | 60 × 40 m | 100 | 8 | [5–10] | ||||
| 2b | 50 × 30 m | 100 | 8 | [5–10] | ||||
| 2c | 40 × 20 m | 100 | 8 | [5–10] | ||||
| Testing | 1 | 80 × 60 m | 50 | 9831: 1400 APs 8431 STAs | 4 | Random | N/A | N/A |
| 2 | 80 × 60 m | 50 | 6 | Random | ||||
| 3 | 80 × 60 m | 50 | 8 | Random | ||||
| 4 | 80 × 60 m | 50 | 10 | Random |
| Parameter | Value | ||
|---|---|---|---|
| Training | Test | ||
| Depl. | # APs | {8, 12} | {4, 6, 8, 10} |
| APs location | Fixed to the center of the cell | ||
| # STAs | {5–10, 10–20} | 5–10 | |
| STAs location | Uniform at random | ||
| Traffic profile | Downlink UDP | ||
| Traffic load | Full buffer mode | ||
| Channel allocation | Uniform at random | ||
| PHY | Central freq. | 5 GHz | |
| Path-loss model | See [31] | ||
| Bandwidth | {20, 40, 80, 160} MHz | ||
| # spatial streams | 1 | ||
| Allowed MCS indexes | 1–12 | ||
| MAC | Contention window | 32 (fixed) | |
| Data and ACK length | 12,000/32 bits | ||
| RTS and CTC length | 160/112 bits | ||
| Max. A-MPDU | 1 | ||
| DCB policy | Dynamic (see [12]) | ||
| Feature | Definition | E1 | E2 | E3 | E4 | E5 | E6 | E7 | E8 | E9 | E10 | E11 | E12 | E13 | E14 | E15 | E16 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Node Type | Wireless node type, AP = 0, STA = 1 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||||
| x(m) | x-coordinate of the wireless node | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||||
| y(m) | y-coordinate of the wireless node | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||||
| Channel Configuration | Combination of Primary, minimum and maximum channel | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||||
| SINR | Signal to Interference plus Noise Ratio | ✓ | ✓ | ✓ | ✓ | ||||||||||||
| Airtime | Percentage of time each AP occupies each of the assigned channels (mean) | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||
| Interference | Inter-AP interference sensed from every AP (mean) | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |||||
| RSSI | Received Signal Strength Indicator | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||||||
| Distance | Euclidean distance between AP and STAs | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||||||
| Bandwidth | Maximum channel bandwidth | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Soto, P.; Camelo, M.; Mets, K.; Wilhelmi, F.; Góez, D.; Fletscher, L.A.; Gaviria, N.; Hellinckx, P.; Botero, J.F.; Latré, S. ATARI: A Graph Convolutional Neural Network Approach for Performance Prediction in Next-Generation WLANs. Sensors 2021, 21, 4321. https://doi.org/10.3390/s21134321
Soto P, Camelo M, Mets K, Wilhelmi F, Góez D, Fletscher LA, Gaviria N, Hellinckx P, Botero JF, Latré S. ATARI: A Graph Convolutional Neural Network Approach for Performance Prediction in Next-Generation WLANs. Sensors. 2021; 21(13):4321. https://doi.org/10.3390/s21134321
Chicago/Turabian StyleSoto, Paola, Miguel Camelo, Kevin Mets, Francesc Wilhelmi, David Góez, Luis A. Fletscher, Natalia Gaviria, Peter Hellinckx, Juan F. Botero, and Steven Latré. 2021. "ATARI: A Graph Convolutional Neural Network Approach for Performance Prediction in Next-Generation WLANs" Sensors 21, no. 13: 4321. https://doi.org/10.3390/s21134321
APA StyleSoto, P., Camelo, M., Mets, K., Wilhelmi, F., Góez, D., Fletscher, L. A., Gaviria, N., Hellinckx, P., Botero, J. F., & Latré, S. (2021). ATARI: A Graph Convolutional Neural Network Approach for Performance Prediction in Next-Generation WLANs. Sensors, 21(13), 4321. https://doi.org/10.3390/s21134321







