ECG Localization Method Based on Volume Conductor Model and Kalman Filtering
Abstract
1. Introduction
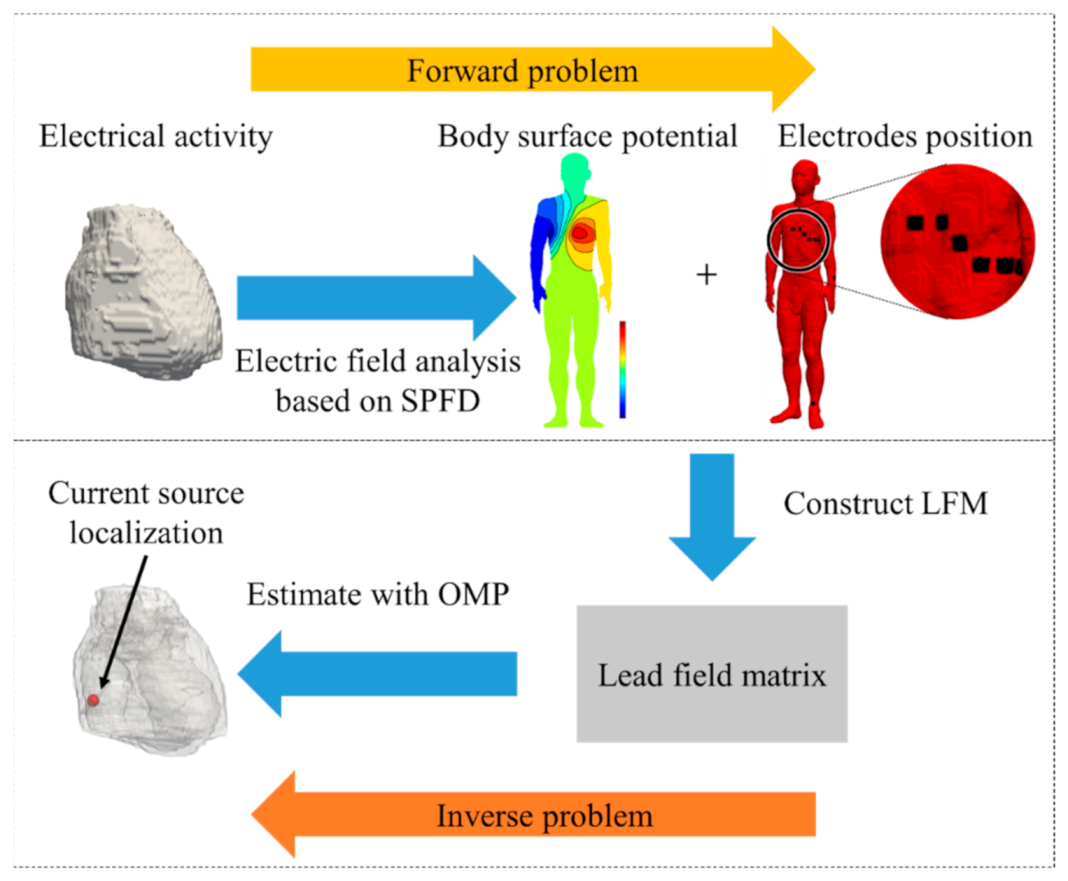
2. Materials and Methods
2.1. Whole-body Models
2.2. Solving the Forward Problem
2.3. Location of Cardiac Source
2.4. Simulation Protocol
2.5. Kalman Filtering
3. Results
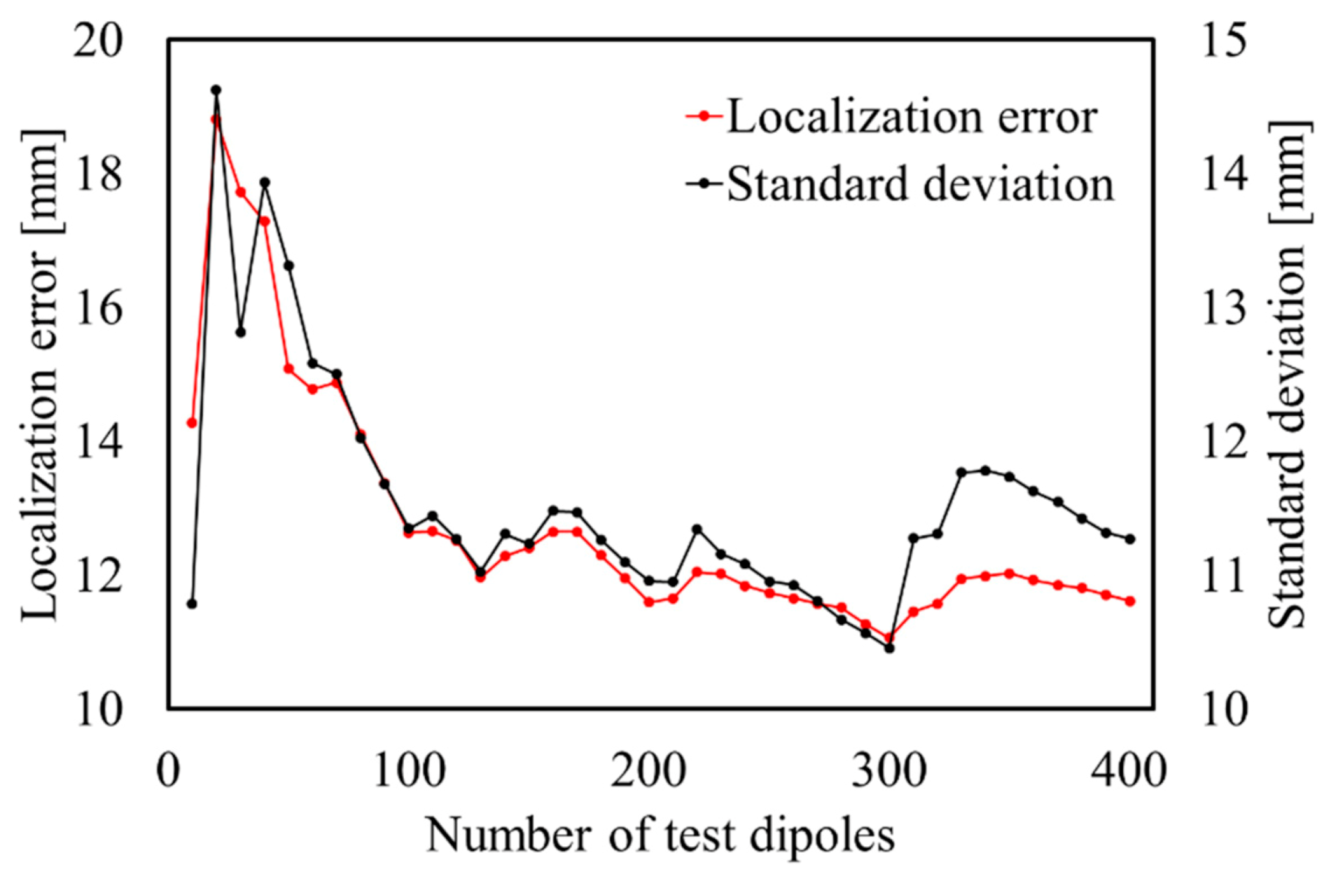
3.1. Determining Criteria for the Number of Test Dipoles
3.2. Evaluation of Estimation Performance
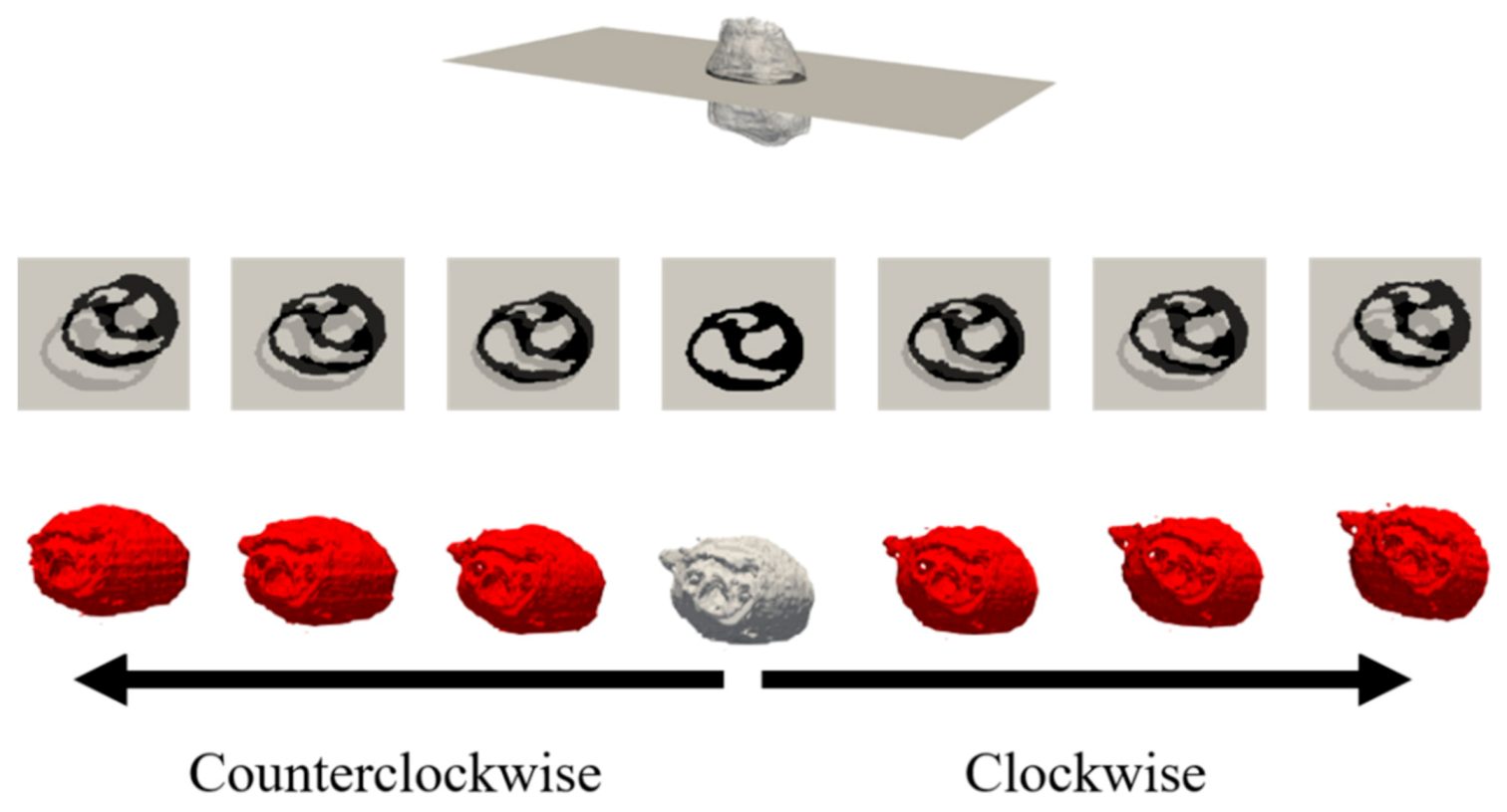
3.3. Sensitivity Due to Cardiac Modeling
3.4. Demonstration of Source Localization Using Pseudo-ECG
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Malmivuo, J.; Plonsey, R. Bioelectromagnetism: Principles and Applications of Bioelectric and Biomagnetic Fields; Oxford University Press: New York, NY, USA, 1995. [Google Scholar]
- Yildirim, O.; Talo, M.; Ciaccio, E.J.; Tan, R.S.; Acharya, U.R. Accurate deep neural network model to detect cardiac arrhythmia on more than 10,000 individual subject ECG records. Comput. Methods Programs Biomed. 2020, 197, 105740. [Google Scholar] [CrossRef] [PubMed]
- Le, T.Q.; Chandra, V.; Afrin, K.; Srivatsa, S.; Bukkapatnam, S. A Dynamic Systems Approach for Detecting and Localizing of Infarct-Related Artery in Acute Myocardial Infarction Using Compressed Paper-Based Electrocardiogram (ECG). Sensors 2020, 20, 3975. [Google Scholar] [CrossRef] [PubMed]
- Elhaj, F.A.; Salim, N.; Harris, A.R.; Swee, T.T.; Ahmed, T. Arrhythmia recognition and classification using combined linear and nonlinear features of ECG signals. Comput. Methods Programs Biomed. 2016, 127, 52–63. [Google Scholar] [CrossRef] [PubMed]
- Fu, L.; Lu, B.; Nie, B.; Peng, Z.; Liu, H.; Pi, X. Hybrid Network with Attention Mechanism for Detection and Location of Myocardial Infarction Based on 12-Lead Electrocardiogram Signals. Sensors 2020, 20, 1020. [Google Scholar] [CrossRef] [PubMed]
- Li, G.; He, B. Localization of the site of origin of cardiac activation by means of a heart-model-based electrocardiographic imaging approach. IEEE Trans. Biomed. Eng. 2001, 48, 660–669. [Google Scholar] [CrossRef] [PubMed]
- Boulakia, M.; Cazeau, S.; Fernández, M.A.; Gerbeau, J.F.; Zemzemi, N. Mathematical modeling of electrocardiograms: A numerical study. Ann. Biomed. Eng. 2010, 38, 1071–1097. [Google Scholar] [CrossRef] [PubMed]
- He, B.; Li, G.; Zhang, X. Noninvasive imaging of cardiac transmembrane potentials within three-dimensional myocardium by means of a realistic geometry anisotropic heart model. IEEE Trans. Biomed. Eng. 2003, 50, 1190–1202. [Google Scholar] [PubMed]
- He, B.; Li, G.; Zhang, X. Noninvasive three-dimensional activation time imaging of ventricular excitation by means of a heart-excitation model. Phys. Med. Biol. 2002, 47, 4063–4078. [Google Scholar] [CrossRef]
- Kligfield, P.; Gettes, L.S.; Bailey, J.J.; Childers, R.; Deal, B.J.; Hancock, E.W.; Herpen, G.V.; Kors, J.A.; Macfarlane, P.; Mirvis, D.M.; et al. Recommendations for the standardization and interpretation of the electrocardiogram: Part I: The electrocardiogram and its technology. A scientific statement from the American Heart Association Electrocardiography and Arrhythmias Committee, Council on Clinical Cardiology; the American College of Cardiology Foundation; and the Heart Rhythm Society. J. Am. Coll. Cardiol. 2007, 49, 1109–1127. [Google Scholar]
- Rautaharju, P.M.; Prineas, R.J.; Crow, R.S.; Seale, D.; Furberg, C. The effect of modified limb electrode positions on electrocardiographic wave amplitudes. J. Electrocardiol. 1980, 13, 109–113. [Google Scholar] [CrossRef]
- Schenone, E.; Collin, A.; Gerbeau, J.F. Numerical simulation of electrocardiograms for full cardiac cycles in healthy and pathological conditions. Int. J. Numer. Methods Biomed. Eng. 2016, 32, 2744. [Google Scholar] [CrossRef]
- Zemzemi, N.; Bernabeu, M.O.; Saiz, J.; Cooper, J.; Pathmanathan, P.; Mirams, G.R.; Pitt-Francis, J.; Rodriguez, B. Computational assessment of drug-induced effects on the electrocardiogram: From ion channel to body surface potentials. Br. J. Pharmacol. 2013, 168, 718–733. [Google Scholar] [CrossRef]
- Houari, K.E.; Kachenoura, A.; Albera, L.; Bensaid, S.; Karfoul, A.; Boichon-Grivot, C.; Rochette, M.; Hernández, A. A fast model for solving the ECG forward problem based on an evolutionary algorithm. In Proceedings of the IEEE 7th Int’l Workshop Computational Advances in Multi-Sensor Adaptive Processing, Curacao, 10–13 December 2017. [Google Scholar]
- Saleheen, H.I.; Ng, K.T. New finite difference formulations for general inhomogeneous anisotropic bioelectric problems. IEEE Trans. Biomed. Eng. 1997, 44, 800–809. [Google Scholar] [CrossRef]
- Vanrumste, B.; Hoey, G.V.; Walle, R.V.D.; D’Havè, M.R.P.; Lemahieu, I.A.; Boon, P.A.J.M. The validation of the finite difference method and reciprocity for solving the inverse problem in EEG dipole source analysis. Brain Topogr. 2001, 14, 83–92. [Google Scholar] [CrossRef]
- Nakane, T.; Ito, T.; Matsuura, N.; Togo, H.; Hirata, A. Forward Electrocardiogram Modeling by Small Dipoles Based on Whole-Body Electric Field Analysis. IEEE Access 2019, 7, 123463–123472. [Google Scholar] [CrossRef]
- Seger, M.; Fischer, G.; Modre, R.; Messnarz, B.; Hanser, F.; Tilg, B. Lead field computation for the electrocardiographic inverse problem - Finite elements versus boundary elements. Comput. Methods Programs Biomed. 2005, 77, 241–252. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Liu, C.; He, B. Noninvasive reconstruction of three-dimensional ventricular activation sequence from the inverse solution of distributed equivalent current density. IEEE Trans. Med. Imaging. 2006, 25, 1307–1318. [Google Scholar] [PubMed]
- Potyagaylo, D.; Cortés, E.G.; Schulze, W.H.W.; Dössel, O. Binary optimization for source localization in the inverse problem of ECG. Med. Biol. Eng. Comput. 2014, 52, 717–728. [Google Scholar] [CrossRef]
- Farina, D.; Jiang, Y.; Skipa, O.; Dossel, O.; Kaltwasser, C.; Bauer, W.R. The use of the simulation results as a priori information to solve the inverse problem of electrocardiography for a patient. Comput. Cardiol. 2005, 32, 571–574. [Google Scholar]
- Wang, J.Z.; Williamson, S.J.; Kaufman, L. Magnetic Source Images Determined by a Lead-Field Analysis: The Unique Minimum-Norm Least-Squares Estimation. IEEE Trans. Biomed. Eng. 1992, 39, 665–675. [Google Scholar] [CrossRef]
- Nenonen, J.T.; Hämäläinen, M.S.; Iimoniemi, R.J. Minimum-norm estimation in a boundary-element torso model. Med. Biol. Eng. Comput. 1994, 32, 43–48. [Google Scholar] [CrossRef]
- Greensite, F.; Huiskamp, G.; Oosterom, A.V. New quantitative and qualitative approaches to the inverse problem of electrocardiology: Their theoretical relationship and experimental consistency. Med. Phys. 1990, 17, 369–379. [Google Scholar] [CrossRef]
- Wu, S.C.; Swindlehurst, A.L. Matching Pursuit and Source Deflation for Sparse EEG/MEG Dipole Moment Estimation. IEEE Trans. Biomed. Eng. 2013, 60, 2280–2288. [Google Scholar] [PubMed]
- Konttila, T.; Mäntynen, V.; Stenroos, M. Comparison of minimum-norm estimation and beamforming in electrocardiography with acute ischemia. Physiol. Meas. 2014, 35, 623–638. [Google Scholar] [CrossRef] [PubMed]
- Modre, R.; Tilg, B.; Fischer, G.; Wach, P. Noninvasive myocardial activation time imaging: A novel inverse algorithm applied to clinical ECG mapping data. IEEE Trans. Biomed. Eng. 2002, 49, 1153–1161. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Z.; Han, C.; Yang, T.; He, B. Noninvasive imaging of 3-dimensional myocardial infarction from the inverse solution of equivalent current density in pathological hearts. IEEE Trans. Biomed. Eng. 2015, 62, 468–476. [Google Scholar] [CrossRef] [PubMed]
- Cotter, S.F.; Rao, B.D.; Engan, K.; Kreutz-Delgado, K. Sparse solutions to linear inverse problems with multiple measurement vectors. IEEE Trans. Signal. Process. 2005, 53, 2477–2488. [Google Scholar] [CrossRef]
- Xu, P.; Tian, Y.; Chen, H.; Yao, D. Lp norm iterative sparse solution for EEG source localization. IEEE Trans. Biomed. Eng. 2007, 54, 400–409. [Google Scholar] [CrossRef]
- Hayashi, K.; Nagahara, M.; Tanaka, T. A User’s Guide to Compressed Sensing for Communications Systems. IEICE Trans. Commun. 2013, E96-B, 685–712. [Google Scholar] [CrossRef]
- Brown, R.A.; Schlegel, T. Diagnostic utility of the spatial versus individual planar QRS-T angles in cardiac disease detection. J. Electrocardio. 2011, 44, 404–409. [Google Scholar] [CrossRef]
- Nagaoka, T.; Watanabe, S.; Sakurai, K.; Kunieda, E.; Watanabe, S.; Taki, M.; Yamanaka, Y. Development of realistic high-resolution whole-body voxel models of Japanese adult males and females of average height and weight, and application of models to radio-frequency electromagnetic-field dosimetry. Phys. Med. Biol. 2004, 49, 1–15. [Google Scholar] [CrossRef]
- Gabriel, S.; Lau, R.W.; Gabriel, C. The dielectric properties of biological tissues: III. Parametric models for the dielectric spectrum of tissues. Phys. Med. Biol. 1996, 41, 2271–2293. [Google Scholar] [CrossRef]
- Kavet, R.; Dovan, T.; Reilly, J.P. The relationship between anatomically correct electric and magnetic field dosimetry and published electric and magnetic field exposure limits. Radiat. Prot. Dosimetry 2012, 152, 279–295. [Google Scholar] [CrossRef][Green Version]
- Keller, D.U.J.; Weber, F.M.; Seemann, G.; Dössel, O. Ranking the influence of tissue conductivities on forward-calculated ecgs. IEEE Trans. Biomed. Eng. 2010, 57, 1568–1576. [Google Scholar] [CrossRef]
- Motogi, J.; Sugiyama, Y.; Laakso, I.; Hirata, A.; Inui, K.; Tamura, M.; Muragaki, Y. Why intra-epidermal electrical stimulation achieves stimulation of small fibres selectively: A simulation study. Phys. Med. Biol. 2016, 61, 4479–4490. [Google Scholar] [CrossRef]
- Klabunde, R.E. Cardiovascular Physiology Concepts, 2nd ed.; Lippincott Williams & Wilkins/Wolters Kluwer: Philadelphia, PA, USA, 2012. [Google Scholar]
- Nemati, E.; Deen, M.J.; Mondal, T. A wireless wearable ECG sensor for long-term applications. IEEE Commun. Mag. 2012, 50, 36–43. [Google Scholar] [CrossRef]
- Dawson, T.W.; Stuchly, M.A. Analytic validation of a three-dimensional scalar-potential finite-difference code for low-frequency magnetic induction. J. Appl. Comput. Electromagn. Soc. 1996, 11, 72–81. [Google Scholar]
- Dimbylow, P.J. Induced current densities from low-frequency magnetic fields in a 2 mm resolution, anatomically realistic model of the body. Phys. Med. Biol. 1998, 43, 22. [Google Scholar] [CrossRef] [PubMed]
- Hirata, A.; Ito, F.; Laakso, I. Confirmation of quasi-static approximation in SAR evaluation for a wireless power transfer system. Phys. Med. Biol. 2013, 58, N241–N249. [Google Scholar] [CrossRef]
- Laakso, I.; Hirata, A. Fast multigrid-based computation of the induced electric field for transcranial magnetic stimulation. Phys. Med. Biol. 2012, 57, 7753–7765. [Google Scholar] [CrossRef]
- Ghimire, S.; Sapp, J.L.; Horacek, M.; Wang, L. A variational approach to sparse model error estimation in cardiac electrophysiological imaging. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Quebec City, QC, Canada, 11–13 September 2017; Springer: Berlin/Heidelberg, Germany, 2017; pp. 745–753. [Google Scholar]
- Yang, T.; Pogwizd, S.M.; Walcott, G.P.; Yu, L.; He, B. Noninvasive activation imaging of ventricular arrhythmias by spatial gradient sparse in frequency domain—application to mapping reentrant ventricular tachycardia. IEEE Trans. Med. Imaging 2019, 38, 525–539. [Google Scholar] [CrossRef]
- Yu, L.; Zhou, Z.; He, B. Temporal sparse promoting three dimensional imaging of cardiac activation. IEEE Trans. Med. Imaging 2015, 34, 2309–2319. [Google Scholar] [CrossRef] [PubMed]
- Harville, D.A. Linear Spaces: Row and Column Spaces. In Matrix Algebra From a Statistician’s Perspective; Springer: Berlin/Heidelberg, Germany, 1997. [Google Scholar]
- Carlsson, M.; Cain, P.; Holmqvist, C.; Stahlberg, F.; Lundback, S.; Arheden, H. Total heart volume variation throughout the cardiac cycle in humans. Am. J. Physiol. Circ. Physiol. 2004, 287, H243–H250. [Google Scholar] [CrossRef]
- Chang, K.M.; Liu, S.H. Gaussian noise filtering from ECG by Wiener filter and ensemble empirical mode decomposition. J. Signal. Process. Syst. 2011, 64, 249–264. [Google Scholar] [CrossRef]
- Segar, W.P.; Sturgeon, G.; Mendonca, S.; Grimes, J.; Tsui, B.M.W. 4D XCAT phantom for multimodality imaging research. Med. Phys. 2010, 37, 4902–4915. [Google Scholar] [CrossRef] [PubMed]
- Rodrigo, M.; Climent, A.M.; Liberos, A.; Hernández-Romero, I.; Arenal, Á.; Bermejo, J.; Fernández-Avilés, F.; Atienza, F.; Guillem, M.S. Solving Inaccuracies in Anatomical Models for Electrocardiographic Inverse Problem Resolution by Maximizing Reconstruction Quality. IEEE Trans. Med. Imaging 2018, 37, 733–740. [Google Scholar] [CrossRef]
- Frangi, A.F.; Rueckert, D.; Schnabel, J.A.; Niessen, W.J. Automatic construction of multiple-object three-dimensional statistical shape models: Application to cardiac modeling. IEEE Trans. Med. Imaging 2002, 21, 1151–1166. [Google Scholar] [CrossRef]
- Svehlikova, J.; Teplan, M.; Tysler, M. Geometrical constraint of sources in noninvasive localization of premature ventricular contractions. J. Electrocardiol. 2018, 51, 370–377. [Google Scholar] [CrossRef]
- Potyagaylo, D.; Dossel, O.; Dam, P.V. Influence of Modeling Errors on the Initial Estimate for Nonlinear Myocardial Activation Times Imaging Calculated with Fastest Route Algorithm. IEEE Trans. Biomed. Eng. 2016, 63, 2576–2584. [Google Scholar] [CrossRef]
- Song, J.; Davey, C.; Poulsen, C.; Luu, P.; Turovets, S.; Anderson, E.; Li, K.; Tucker, D. EEG source localization: Sensor density and head surface coverage. J. Neurosci. Methods 2015, 256, 9–21. [Google Scholar] [CrossRef]
- Moridera, T.; Rashed, E.A.; Mizutani, S.; Hirata, A. High-resolution EEG source localization in segmentation-free head models based on finite-difference method and matching pursuit algorithm. Front. Neurosci. 2021, 15, 789. [Google Scholar]
- Gu, L.; Istook, C.; Ruan, Y.; Gert, G.; Liu, X. Customized 3D digital human model rebuilding by orthographic images-based modelling method through open-source software. J. Text. Inst. 2019, 110, 740–755. [Google Scholar] [CrossRef]
- Zhou, S.; Fu, H.; Liu, L.; Cohen-Or, D.; Han, X. Parametric Reshaping of Human Bodies in Images. ACM. Trans. 2010, 29, 1–10. [Google Scholar] [CrossRef]











| Tissues | Conductivity (S/m) | Tissues | Conductivity (S/m) |
|---|---|---|---|
| Adrenal | 0.20 | Hypothalamus | 0.02 |
| Air | 0.00 | Internal air | 0.00 |
| Bile | 1.40 | Kidneys | 0.05 |
| Bladder | 0.20 | Lens | 0.30 |
| Blood | 0.70 | Ligaments | 0.25 |
| Bone (cancellous) | 0.07 | Liver | 0.02 |
| Bone (cortical) | 0.02 | Lung | 0.20 |
| Cartilage | 0.15 | Muscle | 0.20 |
| Cerebellum | 0.04 | Nerve | 0.01 |
| Cerebrospinal fluid | 2.00 | Pancreas | 0.50 |
| Colon | 0.01 | Seminal capsule | 0.20 |
| Content of the large intestine | 0.20 | Skin | 0.10 |
| Content of the small intestine | 0.20 | Small intestine | 0.50 |
| Content of the stomach | 0.20 | Spleen | 0.03 |
| Cornea | 0.40 | Stomach | 0.50 |
| Corpus spongiosum | 0.20 | Tendon | 0.25 |
| Diaphragma sellae | 0.20 | Testicle | 0.20 |
| Duodenum | 0.50 | Testis prostate | 0.40 |
| Esophagus | 0.50 | Thalamus | 0.02 |
| Fat | 0.04 | Thyroid thymus | 0.50 |
| Gall bladder | 0.90 | Tongue | 0.25 |
| Glandula pinealis | 0.02 | Tooth | 0.02 |
| Glandula salivaria | 0.20 | Trachea | 0.30 |
| Glandula pituitaria | 0.02 | Urine | 0.70 |
| Gray matter | 0.02 | Vitreous humor | 1.50 |
| Heart | 0.05 | White matter | 0.02 |
| Description | Code |
|---|---|
| Set L as in Equation (4) | for i = 1:3N |
| end for | |
| Estimated source location: | |
| Support vector: | |
| Current density: |
| Description | Code |
|---|---|
| Initialize variance-covariance matrix: | |
| Initialize quantity of state: | |
| for t = 1:N | |
| Prediction step: | |
| Update step: | |
| end for |
| LE (mm) | DE (◦) | |
|---|---|---|
| Homogeneous | 5.01 ± 4.07 | 1.91 ± 2.09 |
| Inhomogeneous | 12.64 ± 11.35 | 9.93 ± 11.67 |
| RMSE | Mean Distance Error (mm) | |||
|---|---|---|---|---|
| x-Axis | y-Axis | z-Axis | ||
| OMP w/o Kalman | 4.63 | 10.37 | 13.19 | 15.30 |
| OMP w/ Kalman | 3.31 | 6.12 | 4.40 | 7.26 |
| (Proposed) | Svehlikova, 2018. [53] | Potyagaylo, 2016. [54] | |
|---|---|---|---|
| Source | dipole | dipole | double layer |
| Electrode | 9 | 100 | 9 |
| Resolution (mm) | 2.0 | - | 6.7 ± 1.5 |
| SNR (dB) | |||
| Localization error (mm) | 12.64 ± 11.35 | 10.13 ± 5.13 | 4.4 ± 5.4 |
| Number of tissue | 51 | 12 | 12 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nakano, Y.; Rashed, E.A.; Nakane, T.; Laakso, I.; Hirata, A. ECG Localization Method Based on Volume Conductor Model and Kalman Filtering. Sensors 2021, 21, 4275. https://doi.org/10.3390/s21134275
Nakano Y, Rashed EA, Nakane T, Laakso I, Hirata A. ECG Localization Method Based on Volume Conductor Model and Kalman Filtering. Sensors. 2021; 21(13):4275. https://doi.org/10.3390/s21134275
Chicago/Turabian StyleNakano, Yuki, Essam A. Rashed, Tatsuhito Nakane, Ilkka Laakso, and Akimasa Hirata. 2021. "ECG Localization Method Based on Volume Conductor Model and Kalman Filtering" Sensors 21, no. 13: 4275. https://doi.org/10.3390/s21134275
APA StyleNakano, Y., Rashed, E. A., Nakane, T., Laakso, I., & Hirata, A. (2021). ECG Localization Method Based on Volume Conductor Model and Kalman Filtering. Sensors, 21(13), 4275. https://doi.org/10.3390/s21134275







