Modeling the Piezoelectric Cantilever Resonator with Different Width Layers
Abstract
1. Introduction
2. Piezoelectric Cantilever Resonator Model
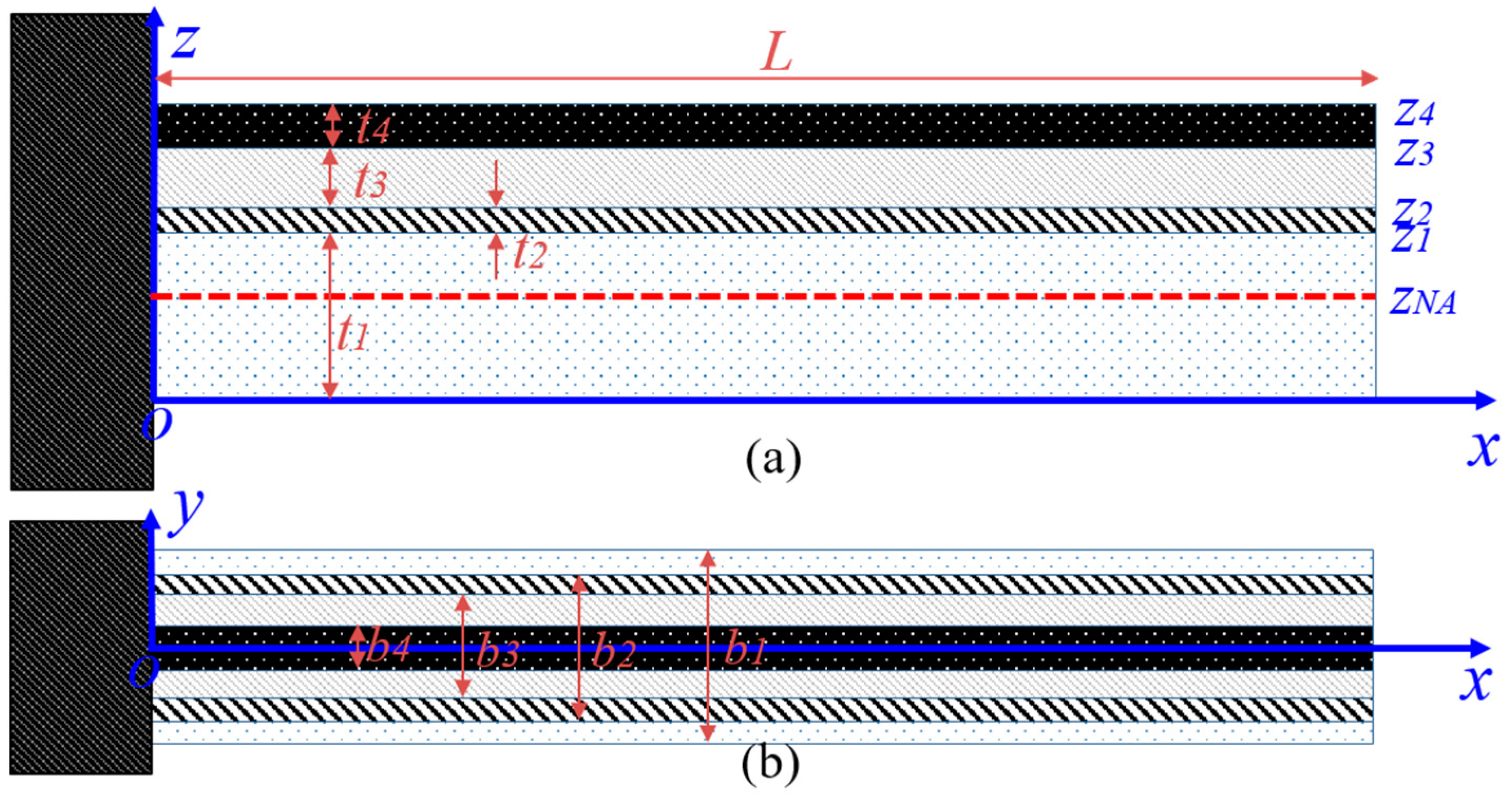
2.1. Geometry and Structure of Piezoelectric Cantilever Resonator
2.2. Assumptions and Theoretical Basis of the Model
2.3. Tip Displacement
2.4. Resonance Frequency
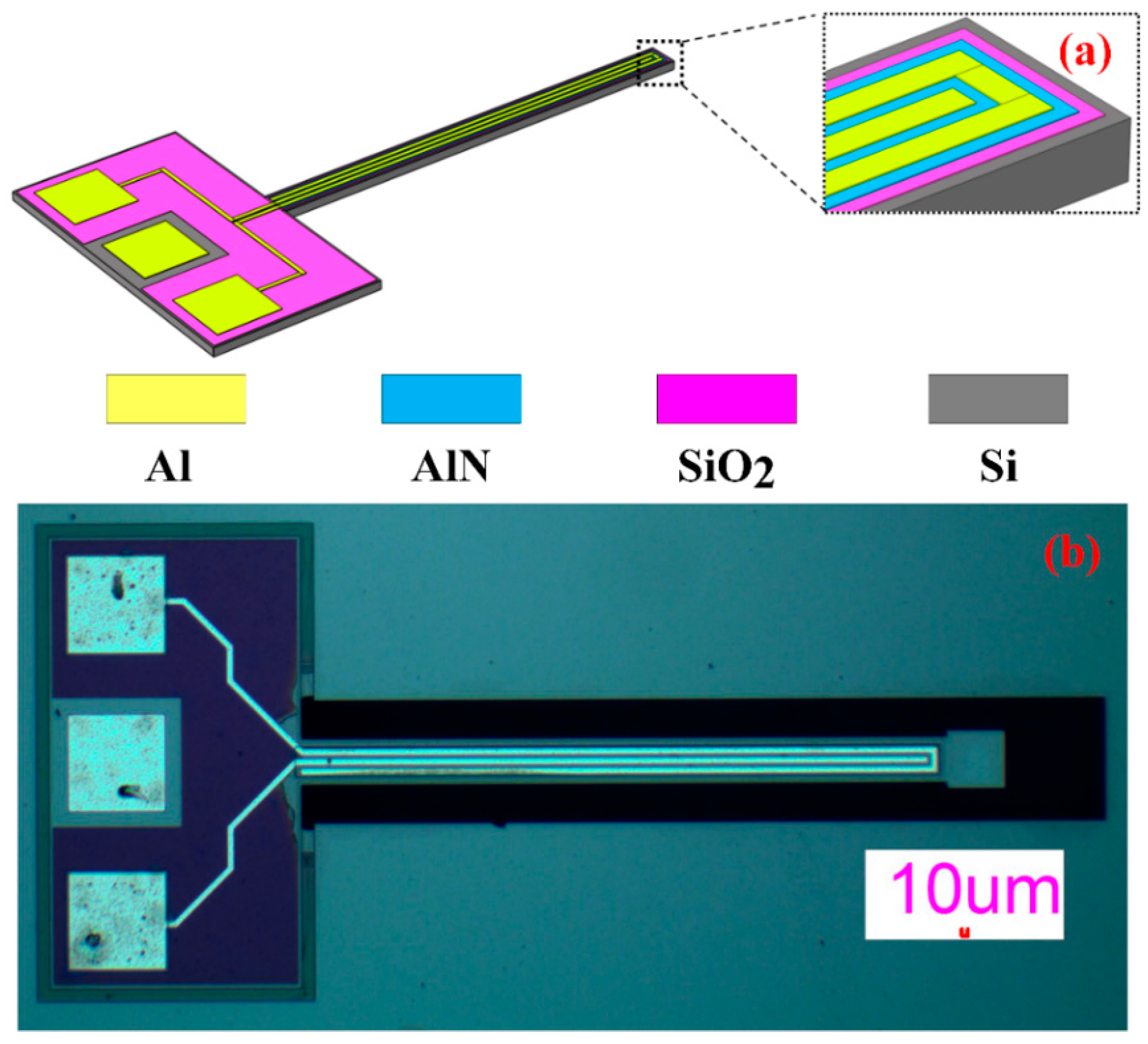
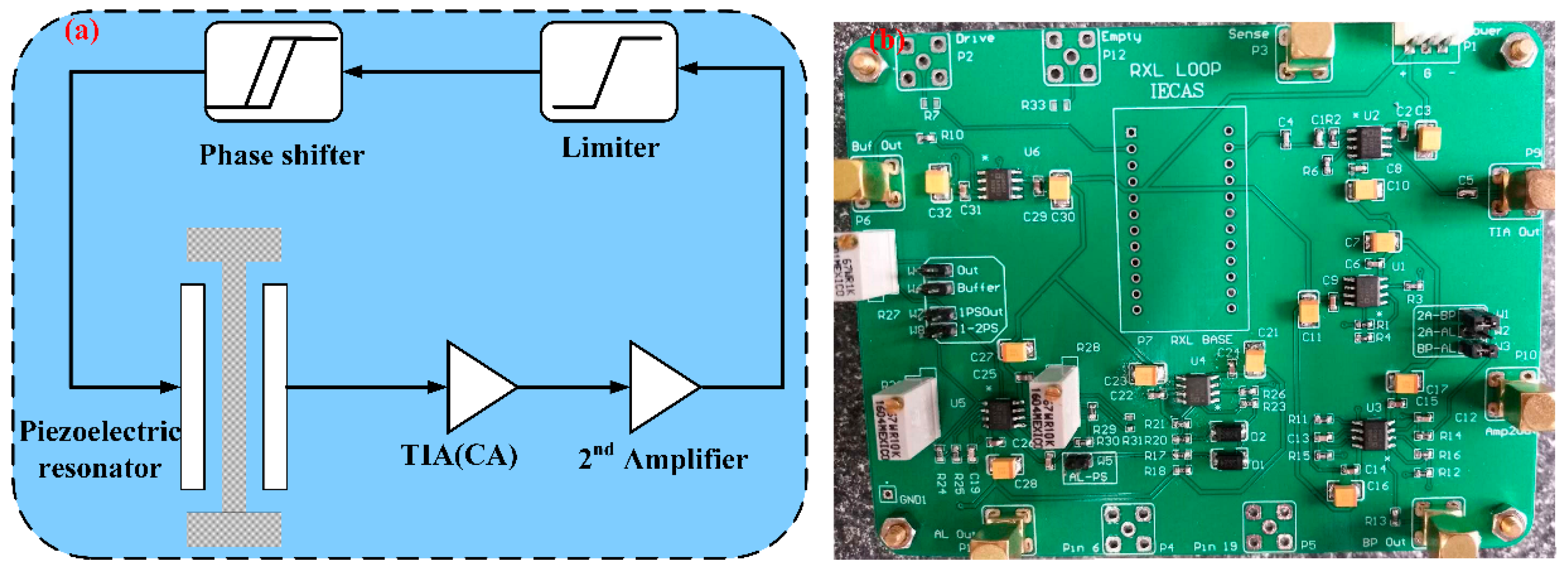
3. Device and Fabrication
4. Results and Discussion
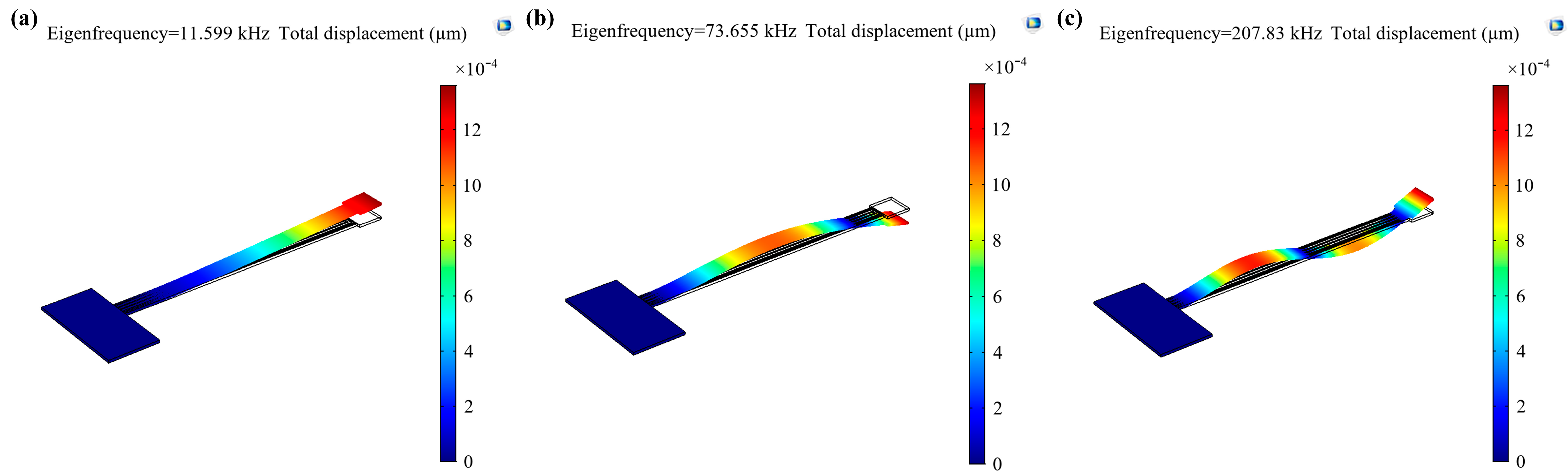
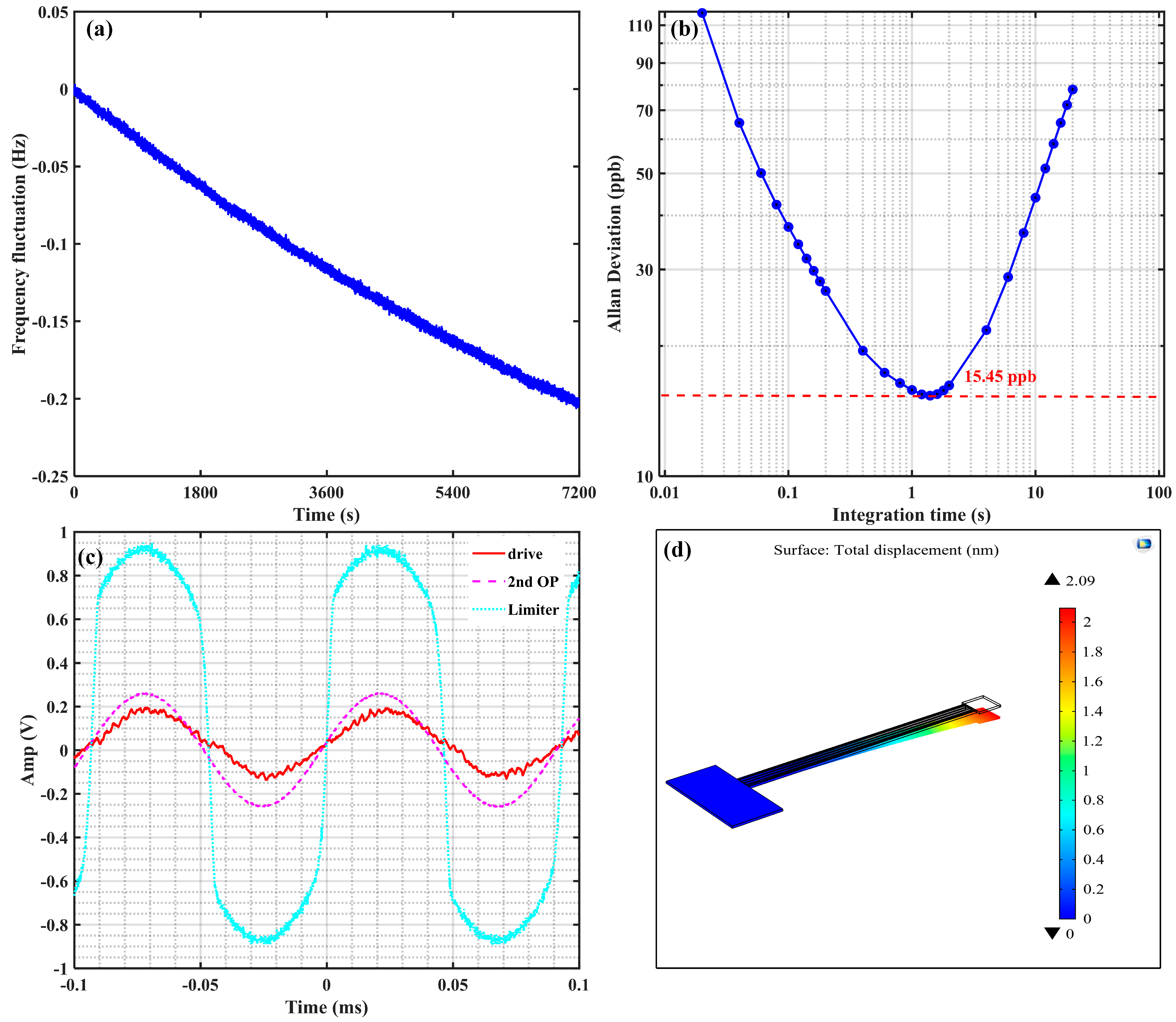
4.1. Measurements and Results
4.2. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Lee, C.S.; Nam, H.J.; Kim, Y.S.; Jin, W.H.; Cho, S.M.; Bu, J.U. Microcantilevers integrated with heaters and piezoelectric detectors for nano data-storage application. Appl. Phys. Lett. 2003, 83, 4839–4841. [Google Scholar] [CrossRef]
- Saadon, S.; Sidek, O. Shape Optimization of Cantilever-based MEMS Piezoelectric Energy Harvester for Low Frequency Applications. In Proceedings of the 2013 UKSim 15th International Conference on Computer Modelling and Simulation, Cambridge, UK, 10–12 April 2013; pp. 202–208. [Google Scholar] [CrossRef]
- Majstrzyk, W.; Mognaschi, M.E.; Orlowska, K.; Di Barba, P.; Sierakowski, A.; Dobrowolski, R.; Grabiec, P.; Gotszalk, T. Electromagnetic cantilever reference for the calibration of optical nanodisplacement systems. Sens. Actuators A Phys. 2018, 282, 149–156. [Google Scholar] [CrossRef]
- Zamanian, M.; Javadi, S.; Firouzi, B.; Hosseini, S.A.A. Modeling and analysis of power harvesting by a piezoelectric layer coated on an electrostatically actuated microcantilever. Mater. Res. Express 2018, 5, 125502. [Google Scholar] [CrossRef]
- Gibus, D.; Gasnier, P.; Morel, A.; Formosa, F.; Charleux, L.; Boisseau, S.; Pillonnet, G.; Berlitz, C.A.; Quelen, A.; Badel, A. Strongly coupled piezoelectric cantilevers for broadband vibration energy harvesting. Appl. Energy 2020, 277, 115518. [Google Scholar] [CrossRef]
- Habibnejad Korayem, M.; Hashemi, A.; Habibnejad Korayem, A. Multilayered non-uniform atomic force microscope piezoelectric microcantilever control and vibration analysis considering different excitation based on the modified couple stress theory. Microsc. Res. Tech. 2020. [Google Scholar] [CrossRef]
- Toledo, J.; Ruiz-Díez, V.; Hernando-García, J.; Sánchez-Rojas, J.L. Piezoelectric Actuators for Tactile and Elasticity Sensing. Actuators 2020, 9, 21. [Google Scholar] [CrossRef]
- Yu, H.W.; Kim, J.-M. Low-voltage micromechanical RF switch based on a piezoelectric micro-cantilever integrated with a transmission line. J. Korean Phys. Soc. 2015, 67, 1942–1946. [Google Scholar] [CrossRef]
- Timoshenko, S. Analysis of bi-metal thermostats. J. Opt. Soc. Am. Rev. Sci. Instrum. 1925, 11, 233–255. [Google Scholar] [CrossRef]
- Smits, J.G.; Dalke, S.I.; Cooney, T.K. THE CONSTITUENT EQUATIONS OF PIEZOELECTRIC BIMORPHS. Sens. Actuators A Phys. 1991, 28, 41–61. [Google Scholar] [CrossRef]
- DeVoe, D.L.; Pisano, A.P. Modeling and optimal design of piezoelectric cantilever microactuators. J. Microelectromech. Syst. 1997, 6, 266–270. [Google Scholar] [CrossRef]
- Huang, C.; Lin, Y.Y.; Tang, T.A. Theoretical study on the tip-deflection of multilayer piezoelectric cantilever structures. Integr. Ferroelectr. 2003, 54, 721–731. [Google Scholar] [CrossRef]
- Edqvist, E.; Hedlund, E.; Lundberg, B. Quasi-static and dynamic electromechanical response of piezoelectric multilayer cantilever beams. Sens. Actuators A Phys. 2010, 157, 198–209. [Google Scholar] [CrossRef]
- Mieczkowski, G. Electromechanical characteristics of piezoelectric converters with freely defined boundary conditions and geometry. Mechanika 2016, 22, 265–272. [Google Scholar] [CrossRef][Green Version]
- Mieczkowski, G. The Constituent equations of piezoelelctric cantilevered three-layer actuators with various external loads and geometry. J. Theor. Appl. Mech. 2017, 55, 69–86. [Google Scholar] [CrossRef]
- Nguyen, C.H.; Hanke, U.; Halvorsen, E. Actuation of Piezoelectric Layered Beams With d(31) and d(33) Coupling. Ieee Trans. Ultrason. Ferroelectr. Freq. Control 2018, 65, 815–827. [Google Scholar] [CrossRef]
- Harmeet Bhugra, G.P. Piezoelectric MEMS Resonators; Spring International Publishing: Cham, Switzerland, 2017; Volume 6, pp. 153–157. [Google Scholar] [CrossRef]
- Zhou, W.; Wang, B.; Lim, C.W.; Yang, Z. A distributed-parameter electromechanical coupling model for a segmented arc-shaped piezoelectric energy harvester. Mech. Syst. Signal Process. 2021, 146, 107005. [Google Scholar] [CrossRef]
- Huang, C.; Lin, Y.Y.; Tang, T.A. Study on the tip-deflection of a piezoelectric bimorph cantilever in the static state. J. Micromech. Microeng. 2004, 14, 530–534. [Google Scholar] [CrossRef]
- Anton, S.R.; Erturk, A.; Inman, D.J. Multifunctional self-charging structures using piezoceramics and thin-film batteries. Smart Mater. Struct. 2010, 19, 115021. [Google Scholar] [CrossRef]
- Wang, Y.; Inman, D.J. Finite element analysis and experimental study on dynamic properties of a composite beam with viscoelastic damping. J. Sound Vib. 2013, 332, 6177–6191. [Google Scholar] [CrossRef]
- Silva, T.M.P.; Clementino, M.A.; Erturk, A.; De Marqui, C. Equivalent electrical circuit framework for nonlinear and high quality factor piezoelectric structures. Mechatronics 2018, 54, 133–143. [Google Scholar] [CrossRef]
- Zhou, S.; Yan, B.; Inman, D.J. A Novel Nonlinear Piezoelectric Energy Harvesting System Based on Linear-Element Coupling: Design, Modeling and Dynamic Analysis. Sensors 2018, 18, 1492. [Google Scholar] [CrossRef] [PubMed]
- de Carvalho Dias, J.A.; Candido de Sousa, V.; Erturk, A.; De Marqui Junior, C. Nonlinear piezoelectric plate framework for aeroelastic energy harvesting and actuation applications. Smart Mater. Struct. 2020, 29, 105006. [Google Scholar] [CrossRef]
- Lee, A.J.; Inman, D.J. Electromechanical modelling of a bistable plate with Macro Fiber Composites under nonlinear vibrations. J. Sound Vib. 2019, 446, 326–342. [Google Scholar] [CrossRef]
- PiezoMUMPS Design Handbook. Available online: http://www.memscap.com/products/mumps/piezomumps (accessed on 24 November 2020).
- Alassi, A.; Benammar, M.; Brett, D. Quartz Crystal Microbalance Electronic Interfacing Systems: A Review. Sensors 2017, 17, 2799. [Google Scholar] [CrossRef]
- Zou, X.; Seshia, A.A. A high-resolution resonant MEMS accelerometer. In Proceedings of the 2015 Transducers-2015 18th International Conference on Solid-State Sensors, Actuators and Microsystems (TRANSDUCERS), Anchorage, AK, USA, 21–25 June 2015. [Google Scholar]
- Zou, X.; Seshia, A.A. The Impact of Damping on the Frequency Stability of Nonlinear MEMS Oscillators. J. Microelectromech. Syst. 2015, 24, 537–544. [Google Scholar] [CrossRef]
- Zou, X.; Seshia, A.A. Non-Linear Frequency Noise Modulation in a Resonant MEMS. IEEE Sens. J. 2017, 17, 4122–4127. [Google Scholar] [CrossRef]
- DeVoe, D.L. Piezoelectric thin film micromechanical beam resonators. Sens. Actuators A Phys. 2001, 88, 263–272. [Google Scholar] [CrossRef]
- Zhang, Y.; Bao, J.-F.; Li, X.-Y.; Zhou, X.; Wu, Z.-H.; Zhang, X.-S. Fully-Differential TPoS Resonators Based on Dual Interdigital Electrodes for Feedthrough Suppression. Micromachines 2020, 11, 119. [Google Scholar] [CrossRef]




| Mode | |||
|---|---|---|---|
| 1st mode | 0.3669 | 1.8746 | −1.3629 |
| 2nd mode | −0.5093 | 4.6927 | −0.9818 |
| 3rd mode | 0.4996 | 7.8500 | −1.0080 |
| Layer | t (µm) | b (µm) | L (µm) | Y (GPa) | ρ (kg/m3) | ε | |
|---|---|---|---|---|---|---|---|
| 1: Si | 10 | 70 | 1100 | 160 | 0.22 | 2320 | 4.5 |
| 2: SiO2 | 0.2 | 60 | 1100 | 70 | 0.17 | 2700 | 4.2 |
| 3: AlN | 0.5 | 50 | 1100 | 345 | 0.32 | 3300 | 9 |
| 4: Al | 1.0 | 30 | 1100 | 70 | 0.33 | 2700 | - |
| Piezoelectric coupling coefficient: d31 = −1.9159 × 10−12 C/N | |||||||
| Freq. | Simulation (KHz) (1) | Measured (KHz) (2) | Proposed Model (3) | Error (%) (1) and (2) | Error (%) (2) and (3) | Error (%) (1) and (3) |
|---|---|---|---|---|---|---|
| 1st order | 11.599 | 11.463 | 11.654 | 1.17 | 1.63 | 0.47 |
| 2nd order | 73.655 | 72.208 | 73.071 | 1.96 | 1.18 | 0.80 |
| 3rd order | 207.83 | 202.701 | 201.66 | 2.47 | 0.52 | 3.06 |
| Layer | t (µm) | L (µm) | Y (GPa) | ρ (kg/m3) | ||
|---|---|---|---|---|---|---|
| 1: Si | 10 | 1000 | 160 | 0.22 | 2320 | 4.5 |
| 2: Al | 0.2 | 1000 | 70 | 0.33 | 2700 | - |
| 3: AlN | 0.5 | 1000 | 345 | 0.32 | 3300 | 9 |
| 4: Al | 1.0 | 1000 | 70 | 0.33 | 2700 | - |
| Piezoelectric coupling coefficient: d31 = −1.9159 × 10−12 C/N | ||||||
| Test | b1 (µm) | b2 (µm) | b3 (µm) | b4 (µm) | Ref [11] (nm) | Ref [17] (nm) | Proposed (nm) | FEM (nm) | Error (%) |
|---|---|---|---|---|---|---|---|---|---|
| #1 | 70 | 70 | 70 | 70 | 88.42 | 78.83 | 88.42 | 88.77 | 0.39 |
| #2 | 70 | 70 | 70 | 20 | 93.04 | 23.70 | 26.58 | 27.70 | 4.04 |
| #3 | 70 | 70 | 20 | 20 | 35.08 | 31.28 | 35.08 | 34.35 | 2.13 |
| #4 | 70 | 20 | 20 | 20 | 35.82 | 31.94 | 35.82 | 34.98 | 2.40 |
| #5 | 70 | 50 | 30 | 10 | 50.50 | 15.01 | 16.83 | 17.75 | 5.18 |
| #6 | 70 | 60 | 50 | 10 | 74.41 | 13.32 | 14.94 | 15.89 | 5.98 |
| Test | b1 (µm) | b3 (µm) | b4 (µm) | Proposed (nm) | FEM (nm) | Error (%) |
|---|---|---|---|---|---|---|
| #1 | 70 | 70 | 70 | 88.95 | 89.70 | 0.84 |
| #6 | 70 | 50 | 10 | 14.95 | 15.94 | 6.21 |
| Test | b1 (µm) | b2 (µm) | b3 (µm) | b4 (µm) | Proposed (nm) | FEM (nm) | Error (%) |
|---|---|---|---|---|---|---|---|
| #1 | 70 | 70 | 70 | 70 | 47.61 | 46.07 | 3.34 |
| #6 | 70 | 60 | 50 | 10 | 8.04 | 8.54 | 5.85 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Chen, J.; Zou, X. Modeling the Piezoelectric Cantilever Resonator with Different Width Layers. Sensors 2021, 21, 87. https://doi.org/10.3390/s21010087
Liu Z, Chen J, Zou X. Modeling the Piezoelectric Cantilever Resonator with Different Width Layers. Sensors. 2021; 21(1):87. https://doi.org/10.3390/s21010087
Chicago/Turabian StyleLiu, Zhenxi, Jiamin Chen, and Xudong Zou. 2021. "Modeling the Piezoelectric Cantilever Resonator with Different Width Layers" Sensors 21, no. 1: 87. https://doi.org/10.3390/s21010087
APA StyleLiu, Z., Chen, J., & Zou, X. (2021). Modeling the Piezoelectric Cantilever Resonator with Different Width Layers. Sensors, 21(1), 87. https://doi.org/10.3390/s21010087






