Author Contributions
Conceptualization, V.R.M., J.K.; Experiment design and execution, V.R.M., J.K.; Formal analysis, V.R.M., J.K., T.S.; Data analysis, V.R.M.; Software, V.R.M.; Writing–Original draft preparation, V.R.M.; Writing–Review & editing, J.K., T.S., J.R.; Supervision, J.K., T.S., J.R. All authors have read and agreed to the published version of the manuscript.
Figure 1.
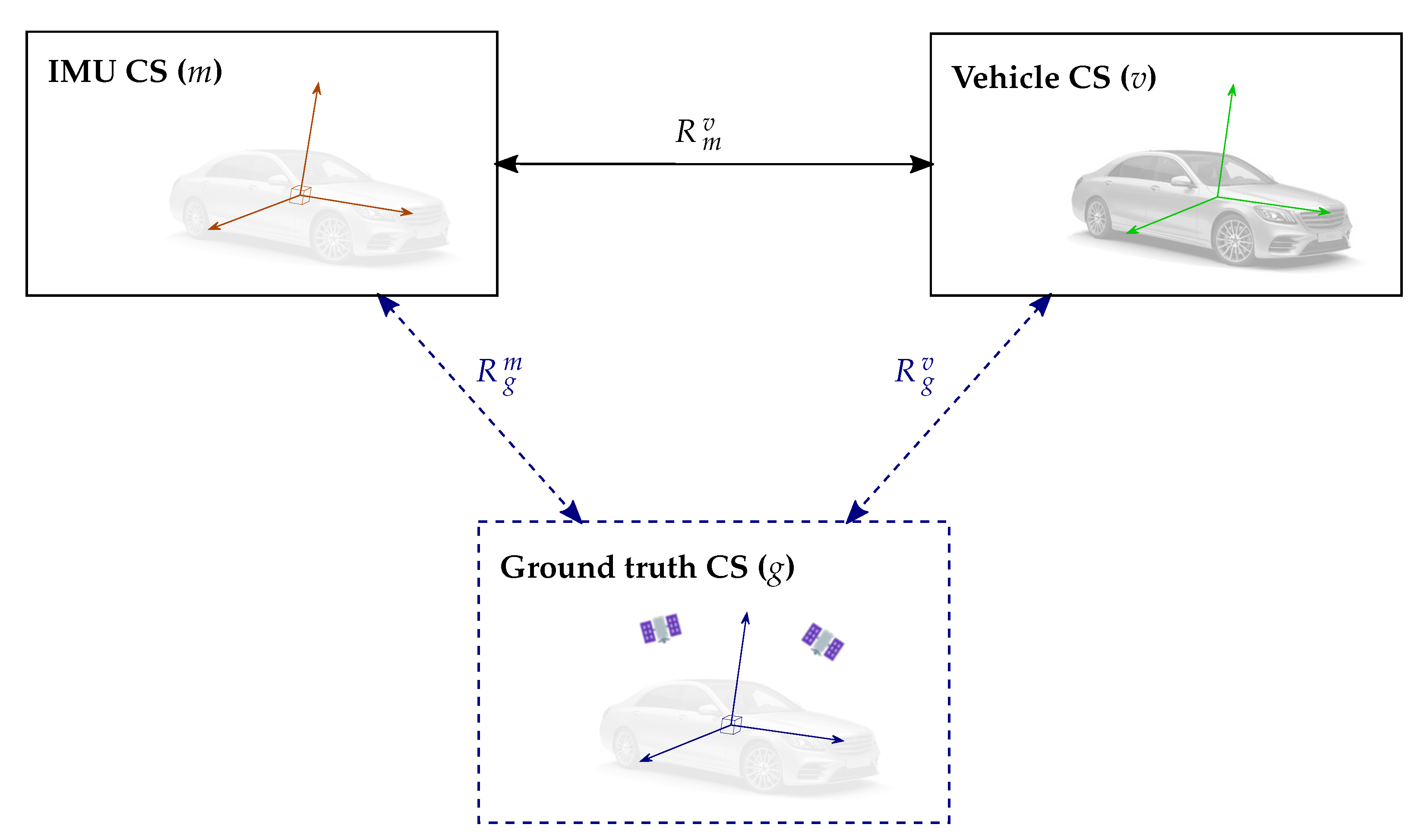
The present work proposes an approach to estimate the 3D rotation between the IMU and vehicle coordinate systems (). Additionally, calibration procedures are described to determine the 3D rotation between a ground-truth measurement system and both the IMU and vehicle coordinate systems ( and , respectively). These represent a reference to directly assess the accuracy of the estimated IMU–vehicle 3D rotation.
Figure 1.
The present work proposes an approach to estimate the 3D rotation between the IMU and vehicle coordinate systems (). Additionally, calibration procedures are described to determine the 3D rotation between a ground-truth measurement system and both the IMU and vehicle coordinate systems ( and , respectively). These represent a reference to directly assess the accuracy of the estimated IMU–vehicle 3D rotation.
Figure 2.
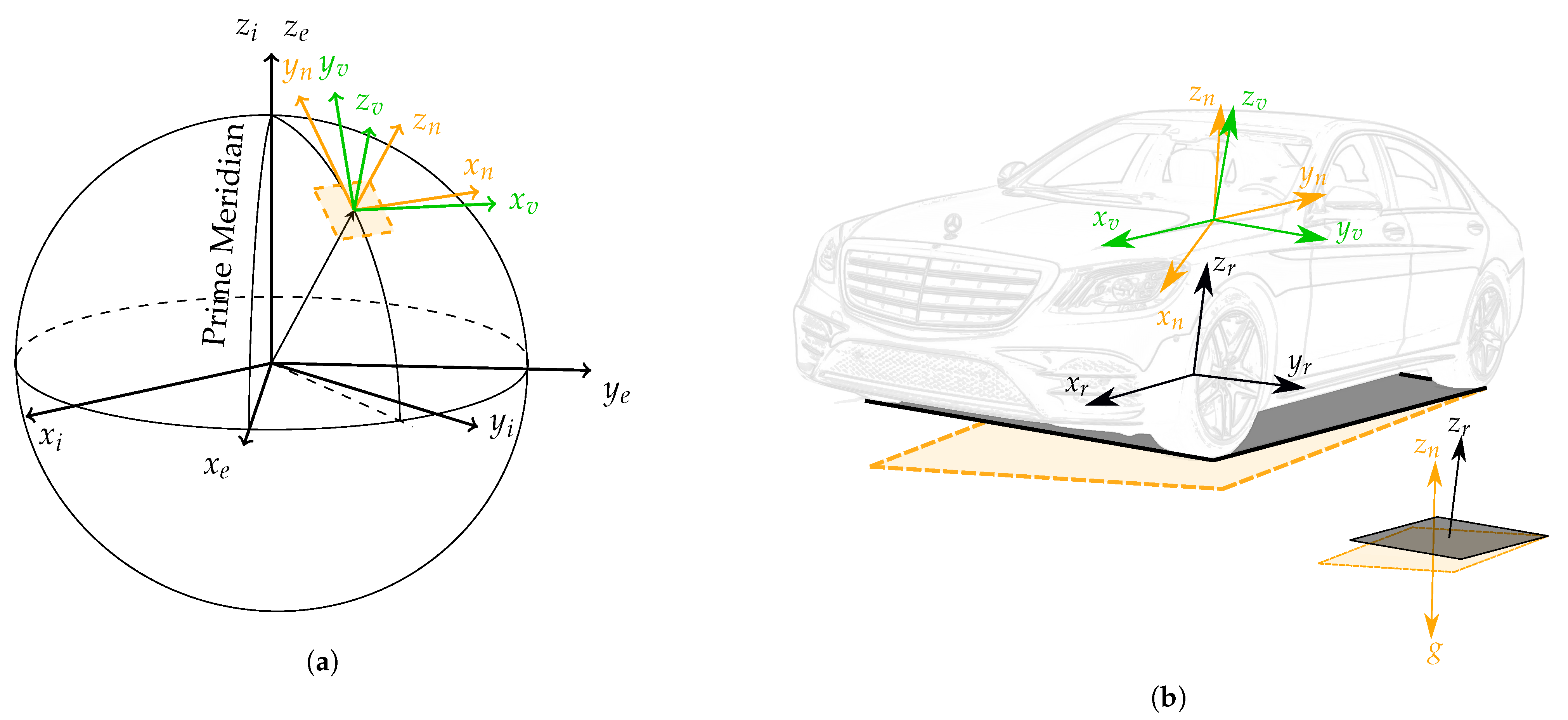
Representation of the inertial (i), ECEF (e), local navigation (n), vehicle (v) and road (r) coordinate systems. For a clear depiction, a world and vehicle perspectives are displayed, which corresponds with (a,b), respectively. The black and yellow planes respectively represent the road plane and the plane tangent to the Earth’s ellipsoid, which is considered to be normal to gravity. Please note that n and v share the same origin, and the origin of r lies on the road plane.
Figure 2.
Representation of the inertial (i), ECEF (e), local navigation (n), vehicle (v) and road (r) coordinate systems. For a clear depiction, a world and vehicle perspectives are displayed, which corresponds with (a,b), respectively. The black and yellow planes respectively represent the road plane and the plane tangent to the Earth’s ellipsoid, which is considered to be normal to gravity. Please note that n and v share the same origin, and the origin of r lies on the road plane.
Figure 3.
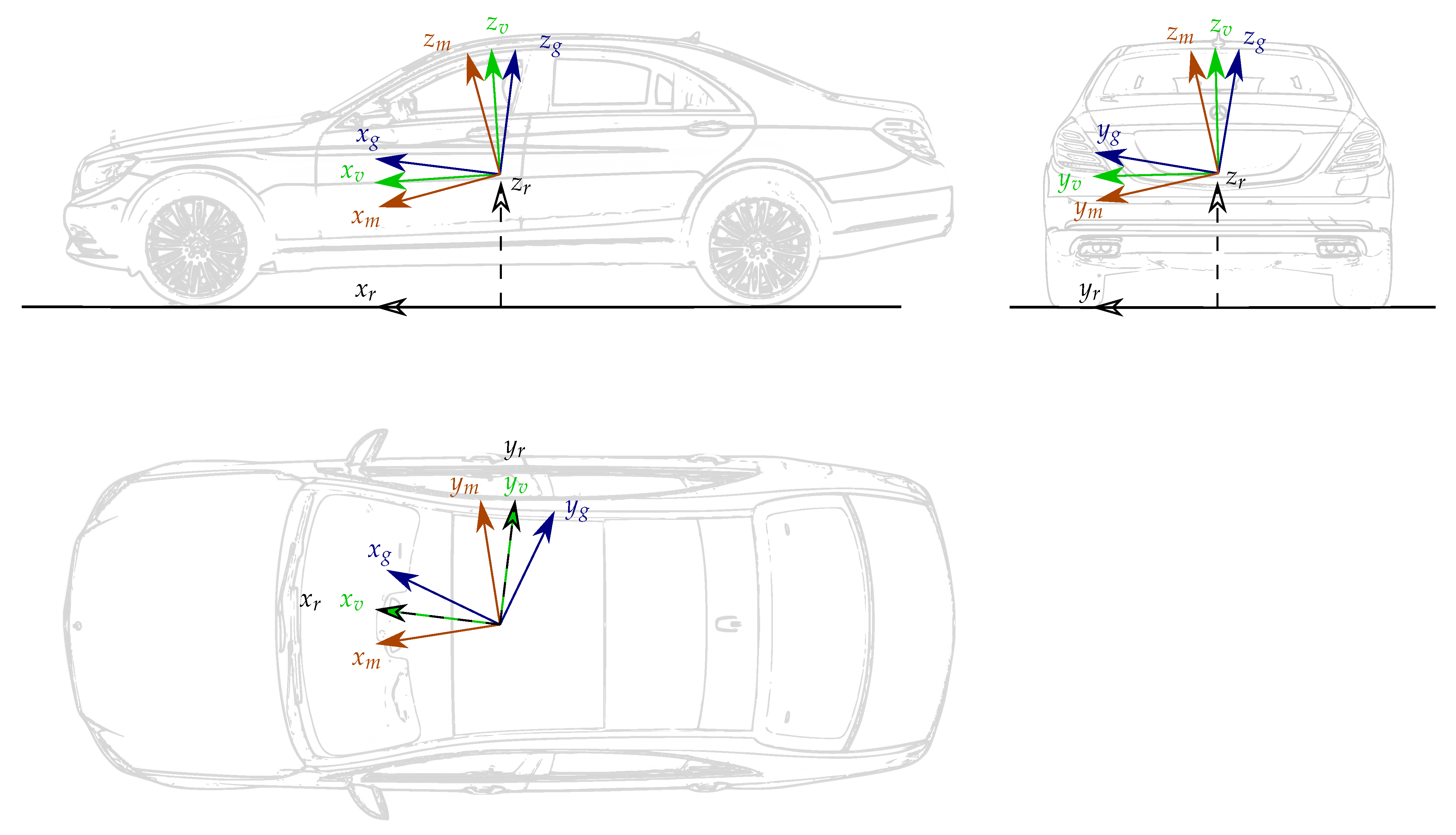
Representation of the ground-truth (g), IMU (m), vehicle (v) and road (r) coordinate systems. Please note that the origin of the ground-truth and IMU coordinate systems is not necessarily coincident with that of the vehicle coordinate system. This representation has been chosen to highlight the misalignment between the different coordinate systems.
Figure 3.
Representation of the ground-truth (g), IMU (m), vehicle (v) and road (r) coordinate systems. Please note that the origin of the ground-truth and IMU coordinate systems is not necessarily coincident with that of the vehicle coordinate system. This representation has been chosen to highlight the misalignment between the different coordinate systems.
Figure 4.
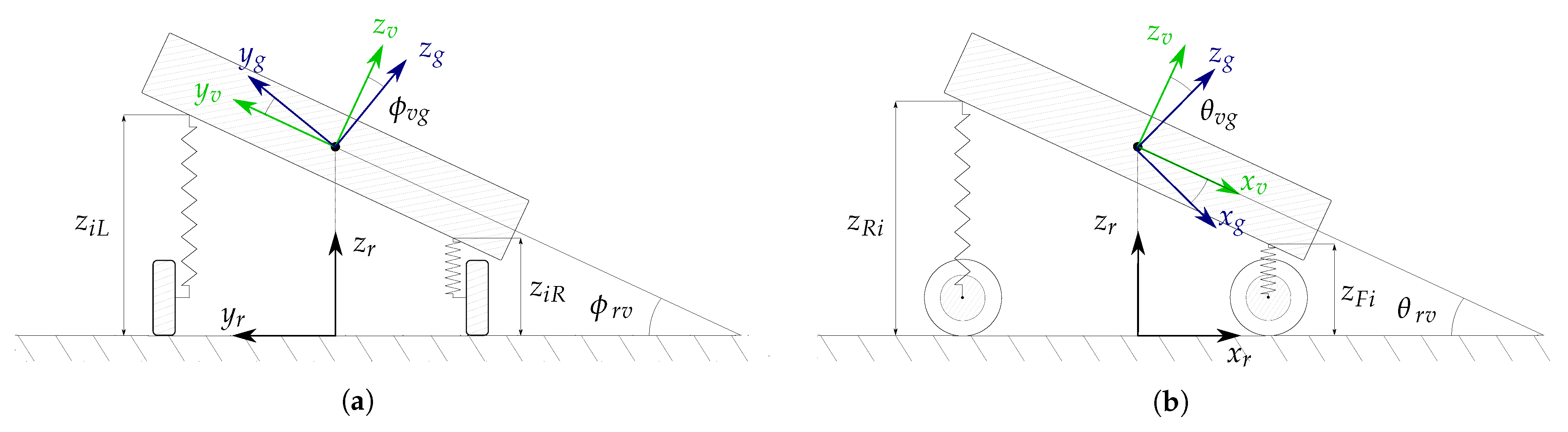
Vehicle-to-road pose [
3]. (
a) shows the roll model, where
; (
b) depicts the pitch model where
.
Figure 4.
Vehicle-to-road pose [
3]. (
a) shows the roll model, where
; (
b) depicts the pitch model where
.
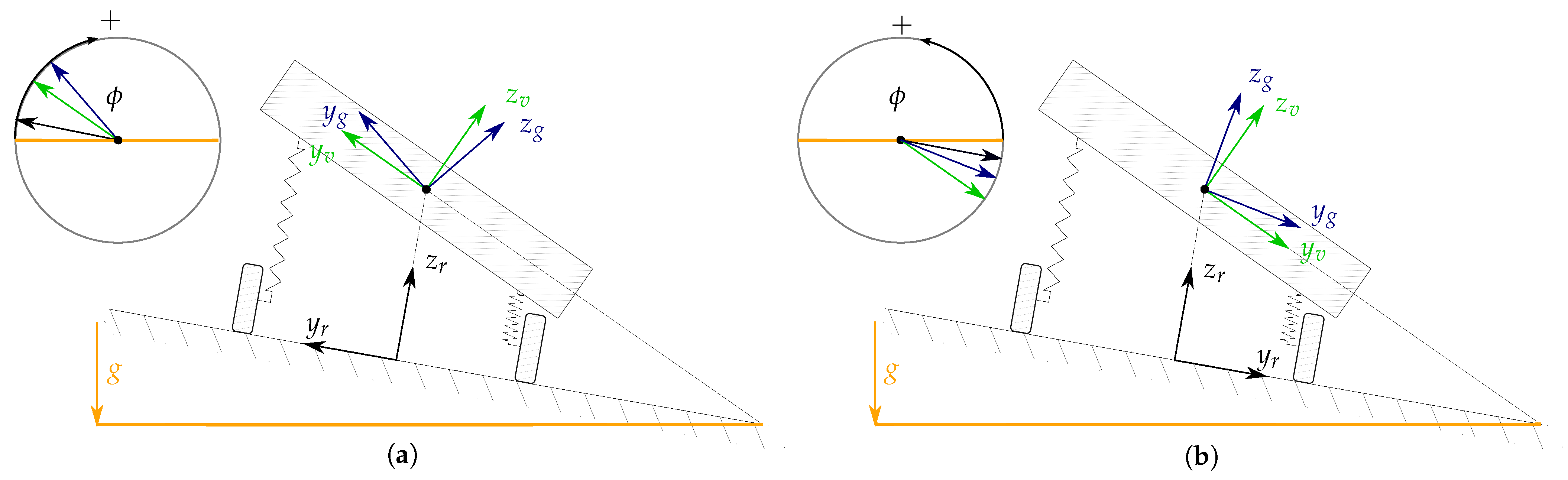
Figure 5.
Calibration procedure on non-horizontal road (roll angle perspective). (a) depicts the first standstill pose and (b) the second, which is equal to the first pose but facing the opposite direction. g, v and r denote the ground-truth, vehicle and road coordinate systems, respectively. (a,b) correspond with (10) and (11), respectively. The yellow line represents the horizontal plane. The circle on the upper left shows the direction of positive roll angles, and the arrows in it represent the y-axes of the corresponding coordinate systems. Note that, in the circles, the angle between the yellow line and the black arrow correspond with . It can then be seen that . The corresponding pitch angle perspective would be equivalent. It is omitted for the sake of conciseness.
Figure 5.
Calibration procedure on non-horizontal road (roll angle perspective). (a) depicts the first standstill pose and (b) the second, which is equal to the first pose but facing the opposite direction. g, v and r denote the ground-truth, vehicle and road coordinate systems, respectively. (a,b) correspond with (10) and (11), respectively. The yellow line represents the horizontal plane. The circle on the upper left shows the direction of positive roll angles, and the arrows in it represent the y-axes of the corresponding coordinate systems. Note that, in the circles, the angle between the yellow line and the black arrow correspond with . It can then be seen that . The corresponding pitch angle perspective would be equivalent. It is omitted for the sake of conciseness.
Figure 6.
Velocities of a vehicle while driving straight ahead with constant speed over a well-paved horizontal road.
Figure 6.
Velocities of a vehicle while driving straight ahead with constant speed over a well-paved horizontal road.
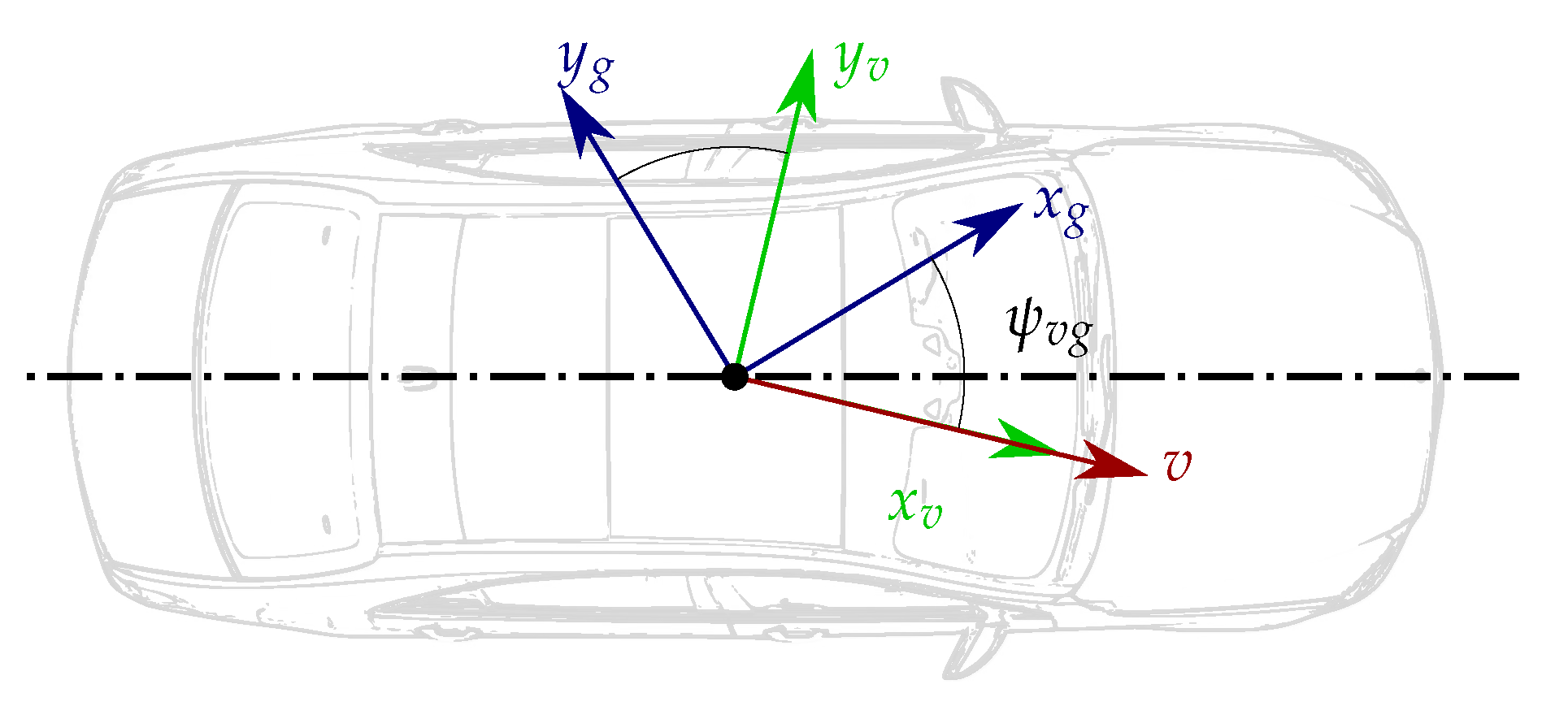
Figure 7.
Yaw calibration procedure on a non-horizontal road. The dashed and continuous lines respectively represent the visual division between lanes and the road limit. The vehicle drives on the same lane twice but in opposite directions. The upper left and right circles show the direction of positive yaw angles for the corresponding driving directions. The red, green and blue arrows in the circle depict the directions of the velocity vector, the x-axis of the vehicle CS and the x-axis of the ground-truth CS, respectively. is the side-slip angle stemming from the road bank and the direction in which the ground-truth perceives the velocity vector.
Figure 7.
Yaw calibration procedure on a non-horizontal road. The dashed and continuous lines respectively represent the visual division between lanes and the road limit. The vehicle drives on the same lane twice but in opposite directions. The upper left and right circles show the direction of positive yaw angles for the corresponding driving directions. The red, green and blue arrows in the circle depict the directions of the velocity vector, the x-axis of the vehicle CS and the x-axis of the ground-truth CS, respectively. is the side-slip angle stemming from the road bank and the direction in which the ground-truth perceives the velocity vector.
Figure 8.
Calibration procedure for the estimation of the misalignment between the ground-truth and IMU coordinate systems.
Figure 8.
Calibration procedure for the estimation of the misalignment between the ground-truth and IMU coordinate systems.
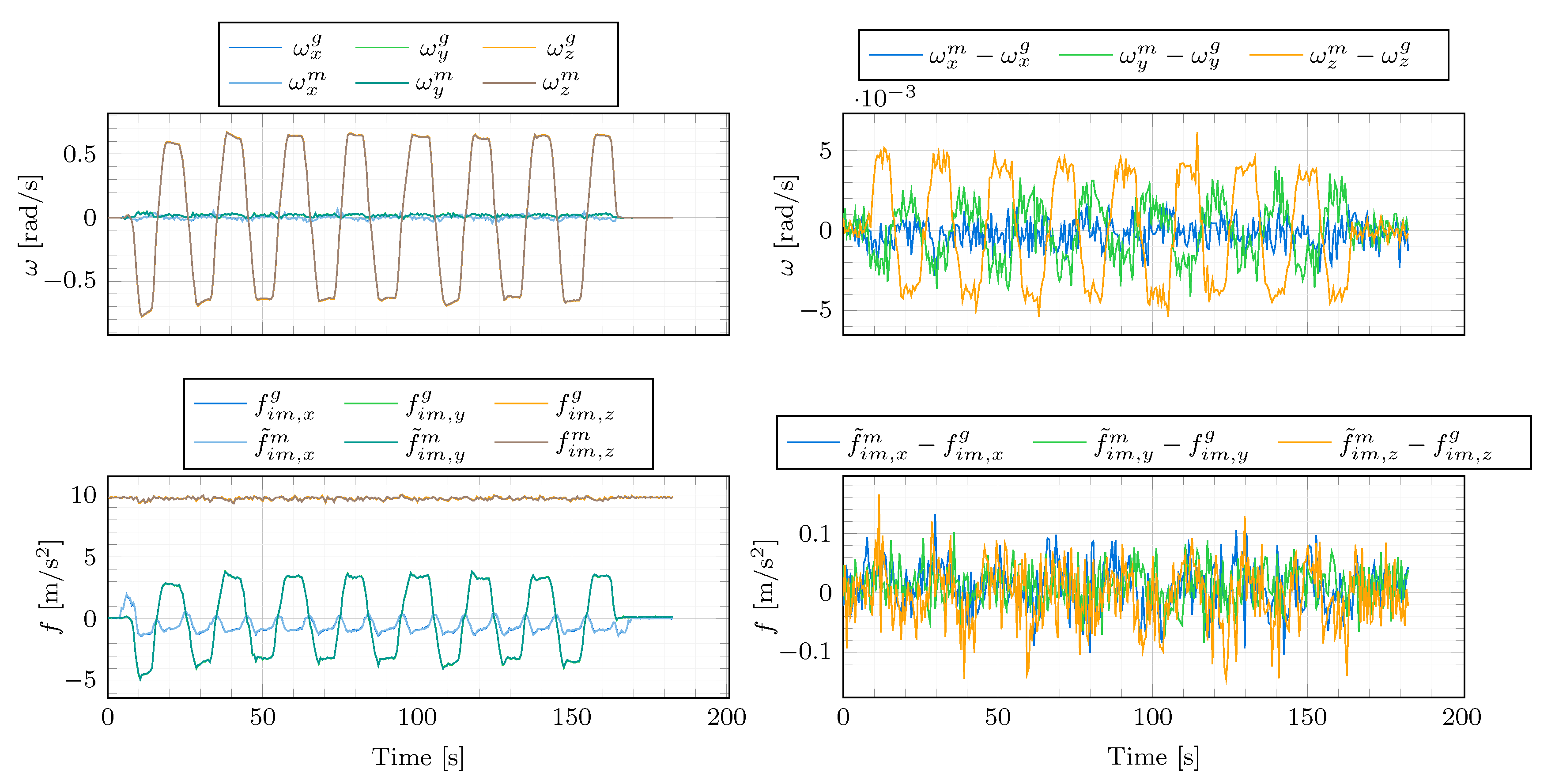
Figure 9.
Measurements during a figure eight manoeuvre. The ground-truth angular rates (, , ) and specific forces (, , ) obtained from the high-performance INS/GNSS system and transformed to the mounting position of the automotive-grade IMU, and the bias-corrected angular rates (, , ) and bias-corrupted specific forces (, , ) supplied by the automotive-grade IMU.
Figure 9.
Measurements during a figure eight manoeuvre. The ground-truth angular rates (, , ) and specific forces (, , ) obtained from the high-performance INS/GNSS system and transformed to the mounting position of the automotive-grade IMU, and the bias-corrected angular rates (, , ) and bias-corrupted specific forces (, , ) supplied by the automotive-grade IMU.
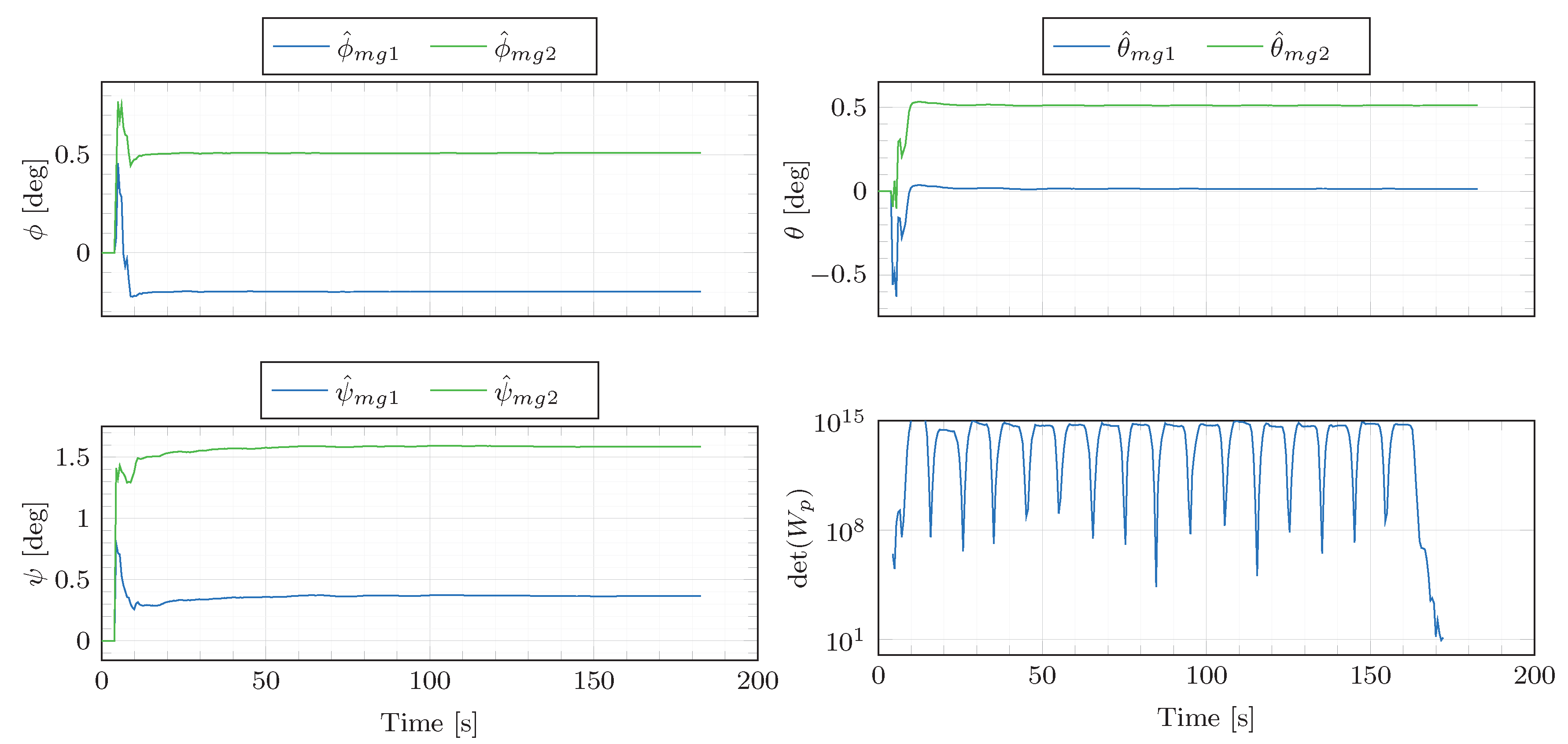
Figure 10.
Estimation results for the figure eight manoeuvre of
Figure 9.
,
,
are the parameter estimates obtained based on the original data.
,
,
are the parameter estimates obtained based on the data corrupted by the artificial misalignment error
for
,
and
, respectively. Finally, the determinant of the excitation matrix
is depicted in the last sub-plot.
Figure 10.
Estimation results for the figure eight manoeuvre of
Figure 9.
,
,
are the parameter estimates obtained based on the original data.
,
,
are the parameter estimates obtained based on the data corrupted by the artificial misalignment error
for
,
and
, respectively. Finally, the determinant of the excitation matrix
is depicted in the last sub-plot.
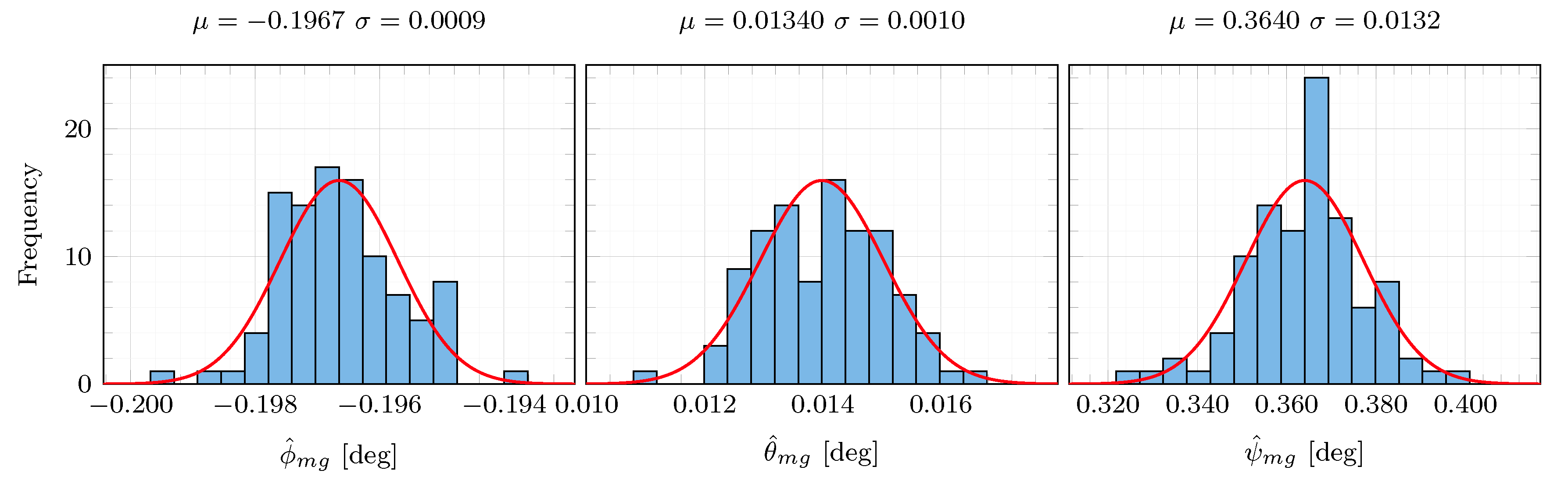
Figure 11.
Estimation robustness against noise. One hundred different sequences of additive Gaussian white noises with standard deviations and have been added to the original IMU angular rate and specific force data, respectively. The estimator has been run for each sequence. The last estimated values of each run have been collected in these histograms. The red curves represent the corresponding best Gaussian distribution fits. The corresponding mean and standard deviation are added on top of each plot.
Figure 11.
Estimation robustness against noise. One hundred different sequences of additive Gaussian white noises with standard deviations and have been added to the original IMU angular rate and specific force data, respectively. The estimator has been run for each sequence. The last estimated values of each run have been collected in these histograms. The red curves represent the corresponding best Gaussian distribution fits. The corresponding mean and standard deviation are added on top of each plot.
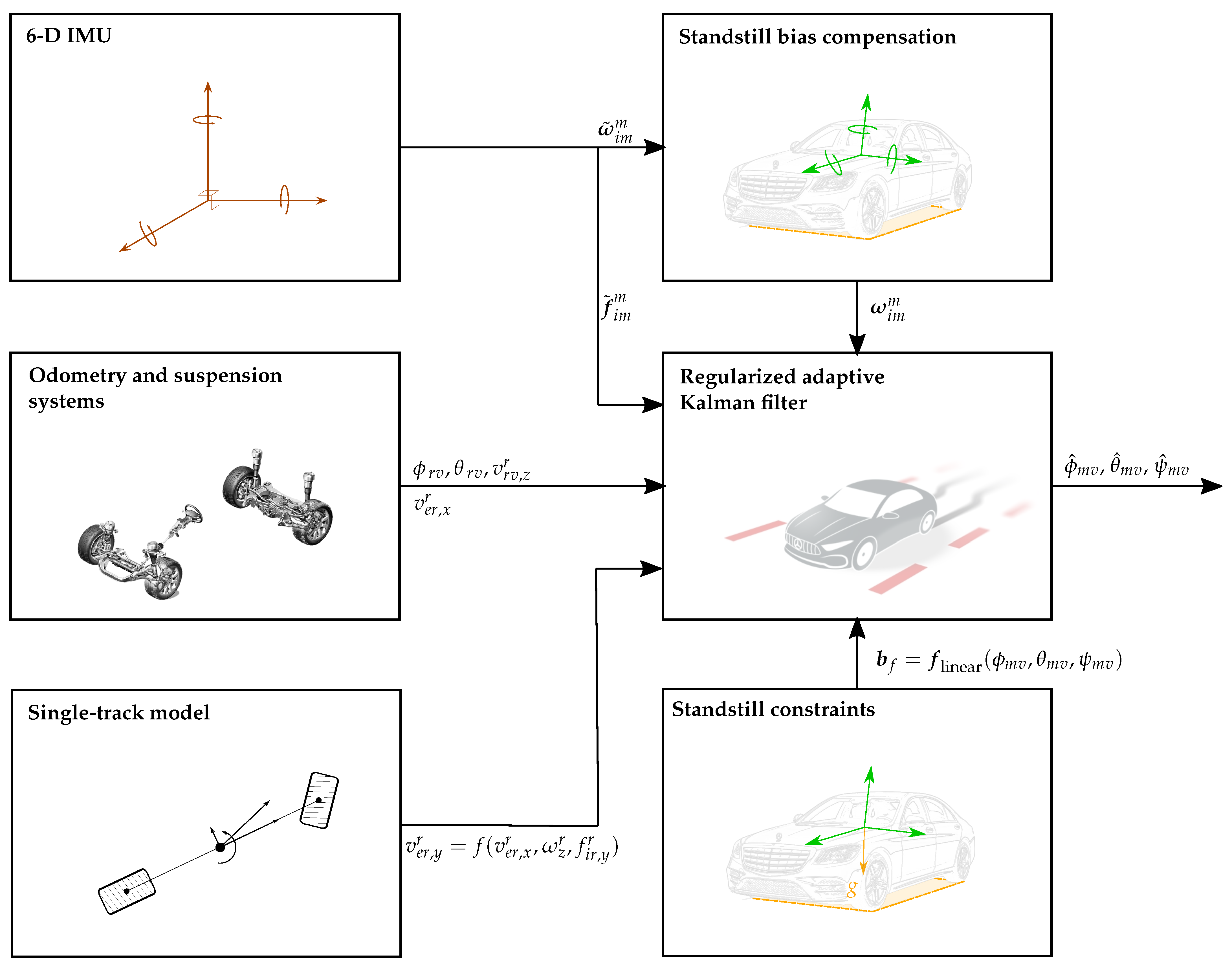
Figure 12.
Estimation approach for the IMU–vehicle misalignment estimation. The proposed regularized adaptive Kalman filter relies on the specific forces (
) supplied by an automotive-grade 6D IMU, its bias-compensated angular rates (
) as well as over-road longitudinal, lateral and vertical velocity information (
,
,
) mainly provided by the odometry, single-track model and suspension, respectively. Furthermore, the vehicle-to-road orientation (
,
), computed from the suspension signals, is used to relate the over-road velocities to the vehicle velocity (
), see
Figure 4. Finally, constraints stemming from a standstill phase are used to enhance the performance of the estimator.
Figure 12.
Estimation approach for the IMU–vehicle misalignment estimation. The proposed regularized adaptive Kalman filter relies on the specific forces (
) supplied by an automotive-grade 6D IMU, its bias-compensated angular rates (
) as well as over-road longitudinal, lateral and vertical velocity information (
,
,
) mainly provided by the odometry, single-track model and suspension, respectively. Furthermore, the vehicle-to-road orientation (
,
), computed from the suspension signals, is used to relate the over-road velocities to the vehicle velocity (
), see
Figure 4. Finally, constraints stemming from a standstill phase are used to enhance the performance of the estimator.
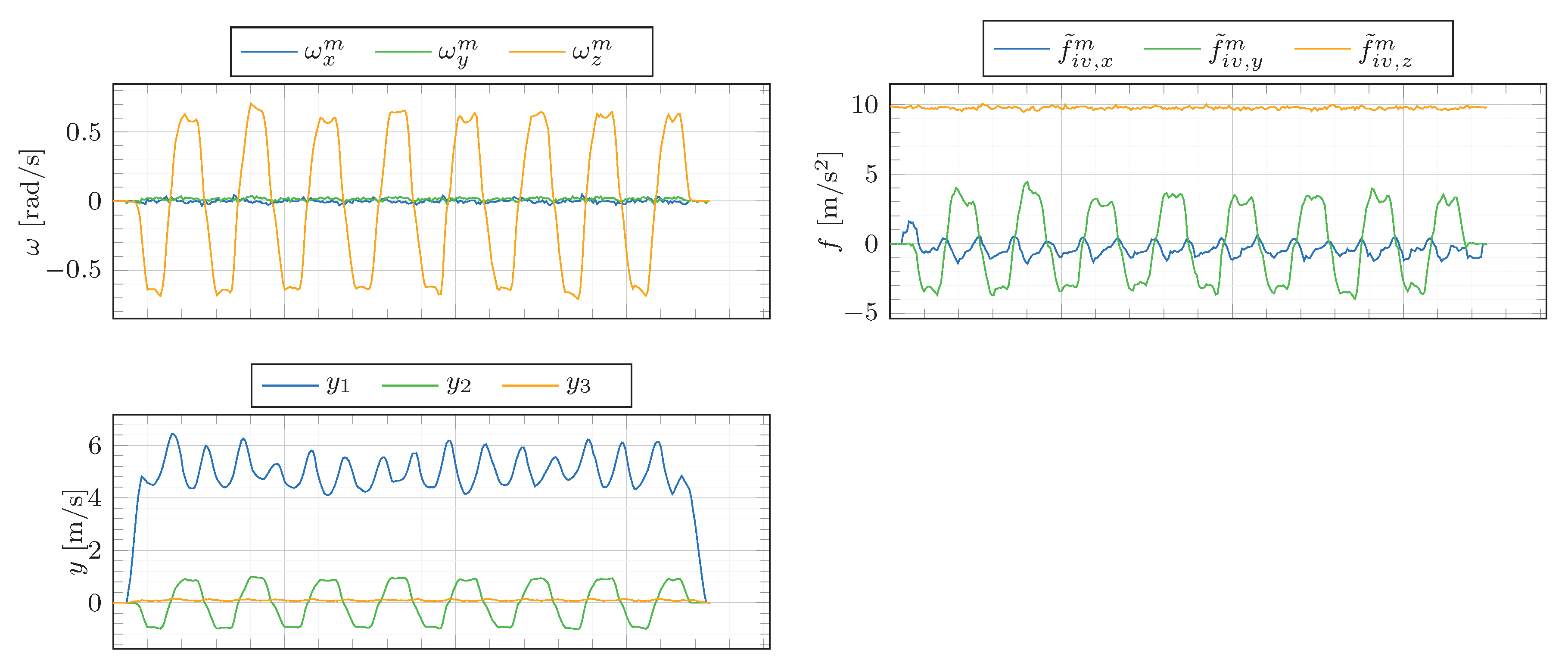
Figure 13.
Estimator inputs during a figure eight drive. The bias-free angular velocities (, , ), the uncorrected specific forces (, , ), the measurements (, , ).
Figure 13.
Estimator inputs during a figure eight drive. The bias-free angular velocities (, , ), the uncorrected specific forces (, , ), the measurements (, , ).
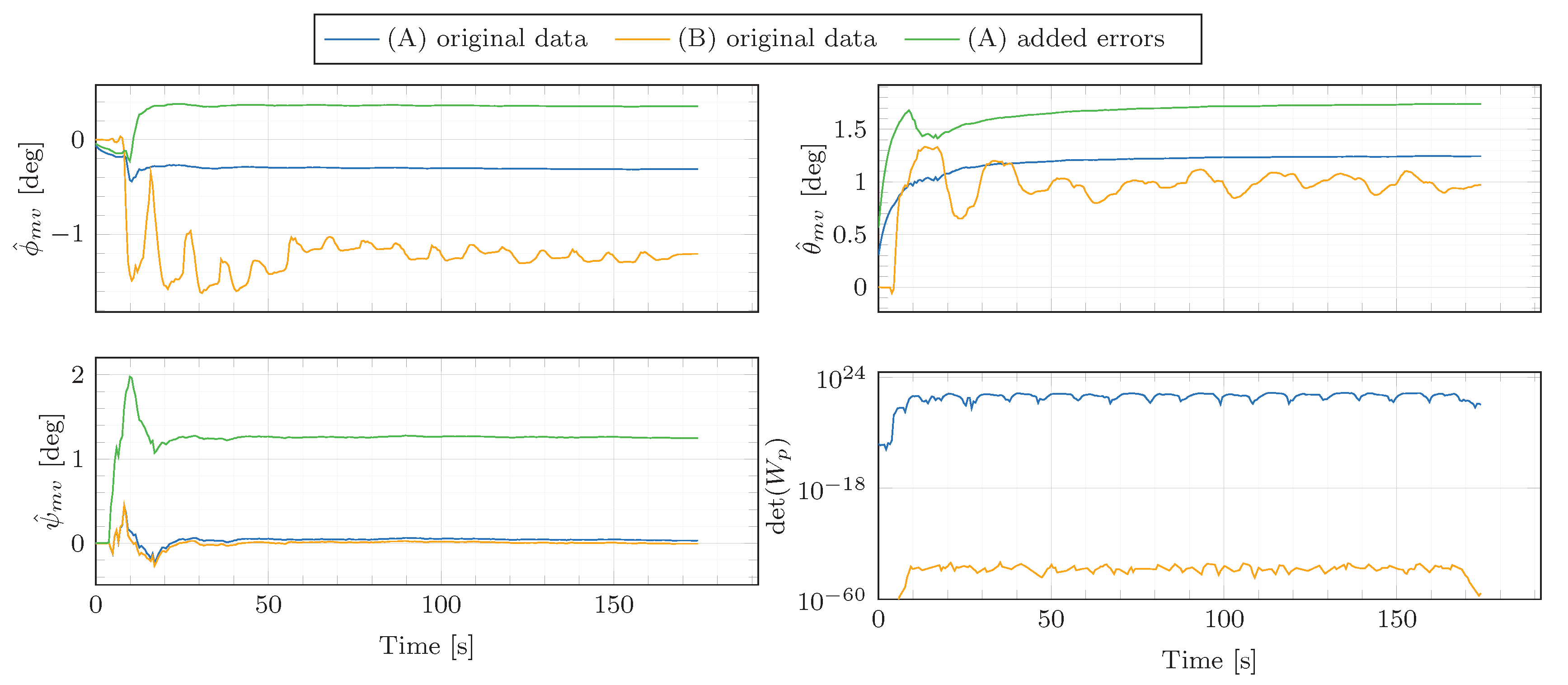
Figure 14.
Estimation results during the figure eight manoeuvre of
Figure 13 for both estimators (A) and (B). Additionally, in green, the parameter estimates obtained with estimator (A) based on the data corrupted by the artificial misalignment error
for
,
and
, respectively, and the artificial bias errors
for
,
and
, respectively. Finally, the determinant of the excitation matrix
is depicted in the last sub-plot.
Figure 14.
Estimation results during the figure eight manoeuvre of
Figure 13 for both estimators (A) and (B). Additionally, in green, the parameter estimates obtained with estimator (A) based on the data corrupted by the artificial misalignment error
for
,
and
, respectively, and the artificial bias errors
for
,
and
, respectively. Finally, the determinant of the excitation matrix
is depicted in the last sub-plot.
Table 1.
Estimation results of the v–g misalignment obtained from three calibration procedures performed on different dates. Results expressed in degrees.
Table 1.
Estimation results of the v–g misalignment obtained from three calibration procedures performed on different dates. Results expressed in degrees.
| Parameter | M1 | M2 | M3 | Mean |
|---|
| 0.100 | 0.128 | 0.122 | 0.117 |
| −1.178 | −1.158 | −1.177 | −1.171 |
| 0.265 | 0.292 | 0.320 | 0.292 |
Table 2.
Parameter choice, units according to the International System of Units.
Table 2.
Parameter choice, units according to the International System of Units.
| Parameter | Value |
|---|
| R | diag([2 × 10, 2 × 10, 2 × 10, 1 × 10, 1 × 10, 1 × 10]) |
| diag([3.0625 × 10, 3.0625 × 10, 3.0625 × 10]) |
| [0, 0, 0] |
| diag([3.2653 × 10, 3.2653 × 10, 3.2653 × 10]) |
| |
Table 3.
Variability misalignment estimation with angular rates and specific forces. Results expressed in degrees.
Table 3.
Variability misalignment estimation with angular rates and specific forces. Results expressed in degrees.
| Parameter | M1 | M2 | M3 | M4 | M5 | M6 | M7 | Max. Diff. | Mean |
|---|
| −0.187 | −0.188 | −0.193 | −0.193 | −0.191 | −0.193 | −0.195 | 0.008 | −0.192 |
| 0.011 | 0.012 | 0.006 | 0.006 | 0.007 | 0.008 | 0.005 | 0.007 | 0.009 |
| 0.434 | 0.373 | 0.367 | 0.367 | 0.402 | 0.401 | 0.394 | 0.067 | 0.396 |
Table 4.
Estimator scheme parameter choice, units according to the International System of Units.
Table 4.
Estimator scheme parameter choice, units according to the International System of Units.
| Parameter | Value |
|---|
| Q | diag([]) |
| R (A) | diag([]) |
| R (B) | diag([]) |
| diag([]) |
| diag([]) |
| |
| |
| diag([]) |
| |
Table 5.
Misalignment angles computed from the identified
m-
g and
v-
g misalignments in
Section 3 and
Section 4 (see
Table 1 and
Table 3). Results expressed in degrees.
Table 5.
Misalignment angles computed from the identified
m-
g and
v-
g misalignments in
Section 3 and
Section 4 (see
Table 1 and
Table 3). Results expressed in degrees.
| Misalignment Angle | | | |
|---|
| −0.192 | 0.117 | ≈−0.309 |
| 0.009 | −1.171 | ≈1.180 |
| 0.396 | 0.292 | ≈0.104 |
Table 6.
Estimation results of (A) for three different figure eight manoeuvres driven on different days.
is the manoeuvre displayed in
Figure 13 with
,
represents a less dynamic
Figure 8 drive with
and
corresponds with a more dynamic
Figure 8 drive with
.
Table 6.
Estimation results of (A) for three different figure eight manoeuvres driven on different days.
is the manoeuvre displayed in
Figure 13 with
,
represents a less dynamic
Figure 8 drive with
and
corresponds with a more dynamic
Figure 8 drive with
.
| Misalignment Angle | | | |
|---|
| −0.313 | −0.278 | −0.300 |
| 1.236 | 1.184 | 1.183 |
| 0.037 | 0.058 | 0.045 |