Modelling and Measurement of Magnetically Soft Nanowire Arrays for Sensor Applications
Abstract
1. Introduction
- The sensing direction is defined by the direction of the sensor core and not by the direction of the pickup coil. This allows the construction of highly stable gradiometers of the Foerster type [3].
- The high shape anisotropy reduces the Crossfield error (a non-linearity response to fields perpendicular to the primary sensing direction) [6].
- The low demagnetization of the sensor core increases sensitivity and thus allows miniaturization of sensors.
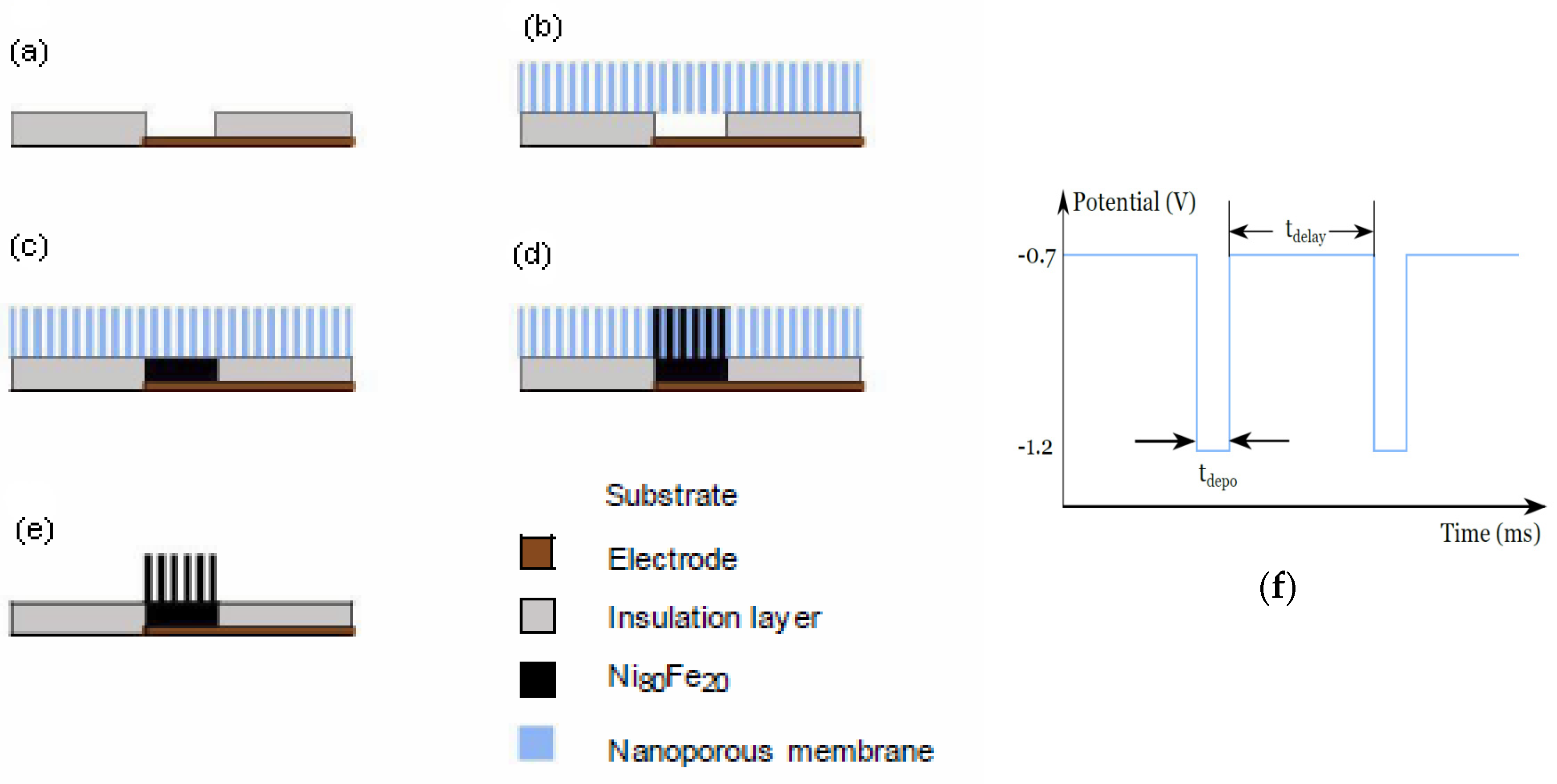
2. Nanowire Fabrication
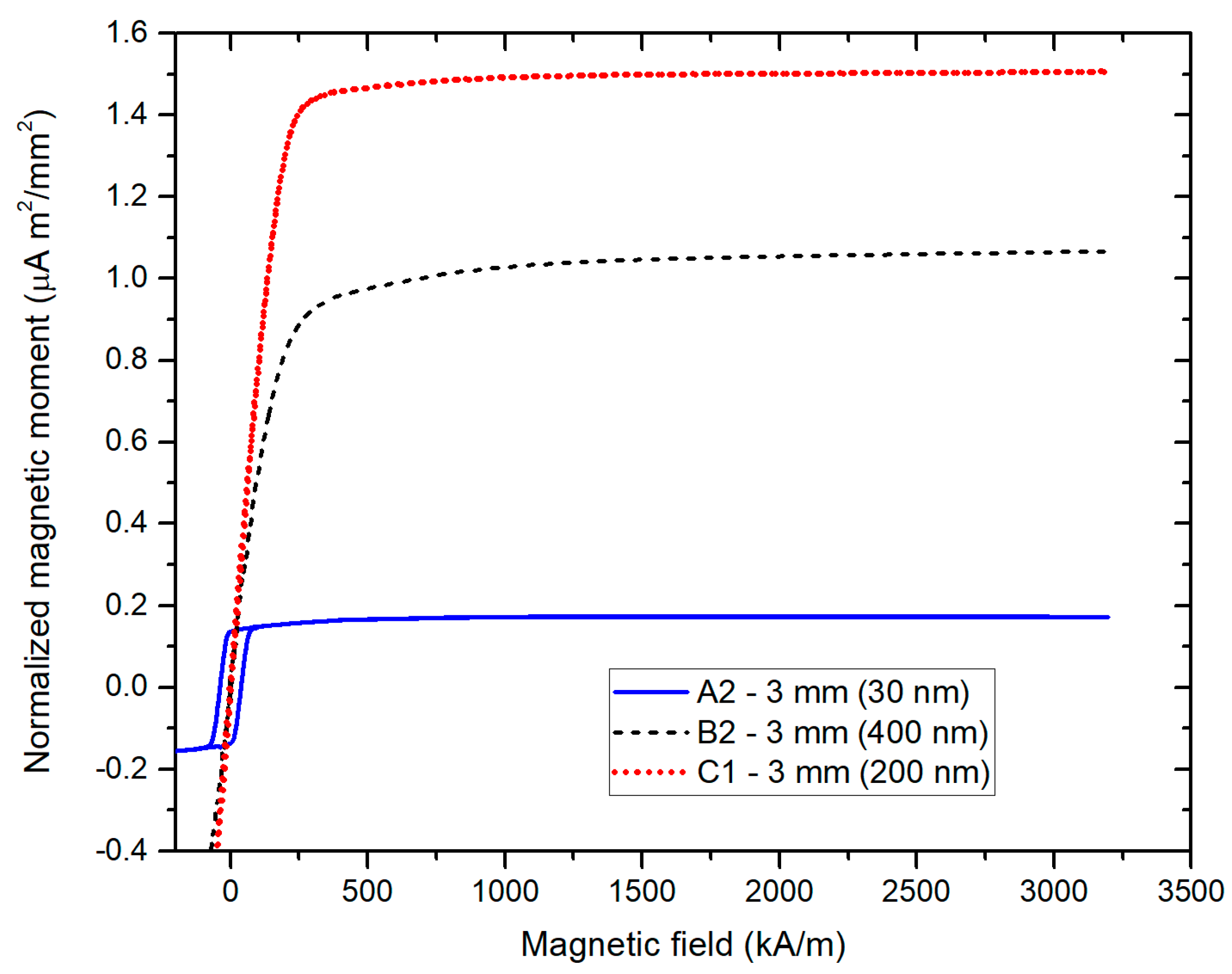
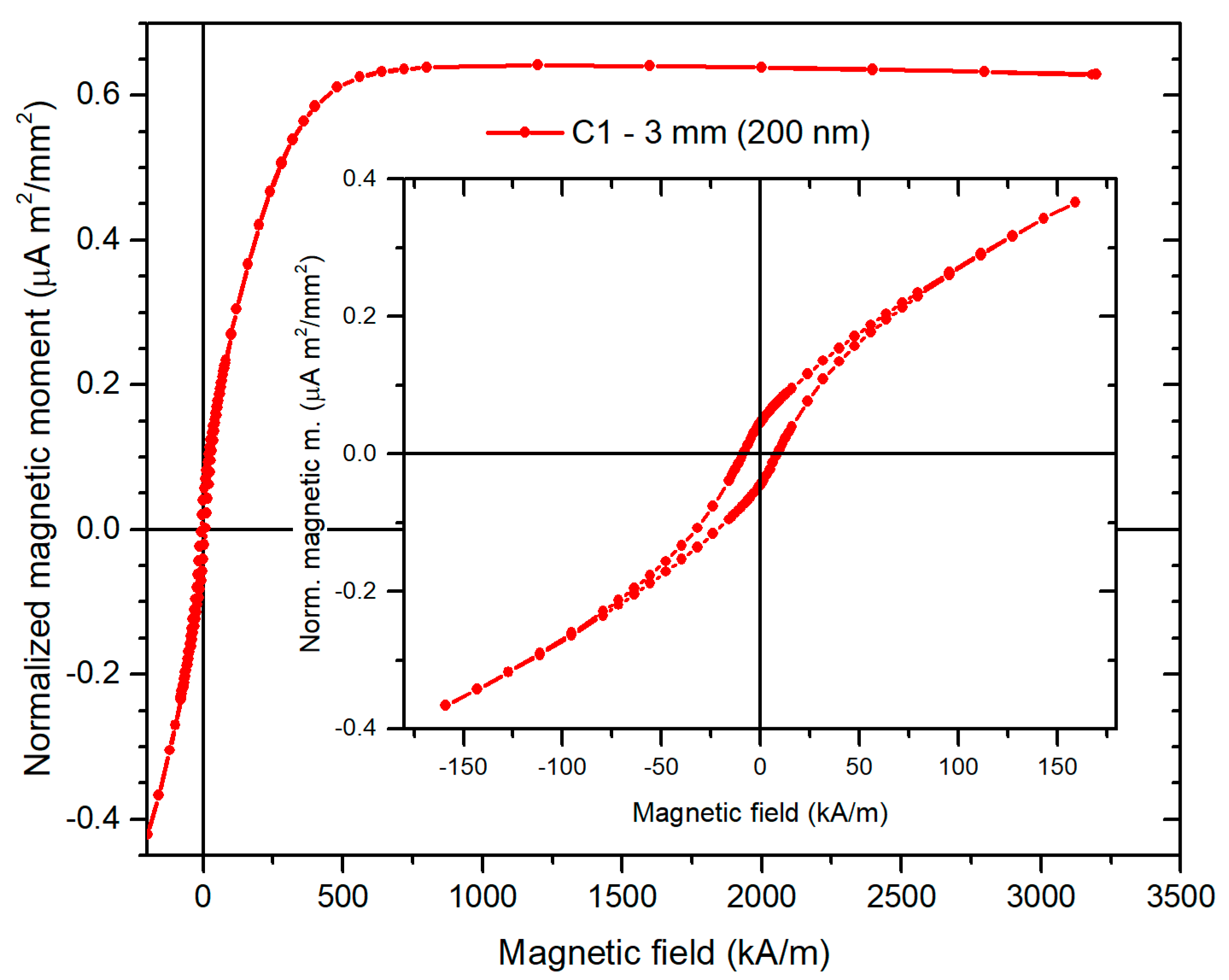
3. Nanowire Magnetic Characterization
4. Modelling Nanowire Arrays
4.1. Demagnetization, Apparent Permeability and Amplification Factor
4.2. 2D Model for Single Wire
4.3. 3D Model for Small Wire Array
4.4. Equivalent 2D Model for Large Wire Arrays
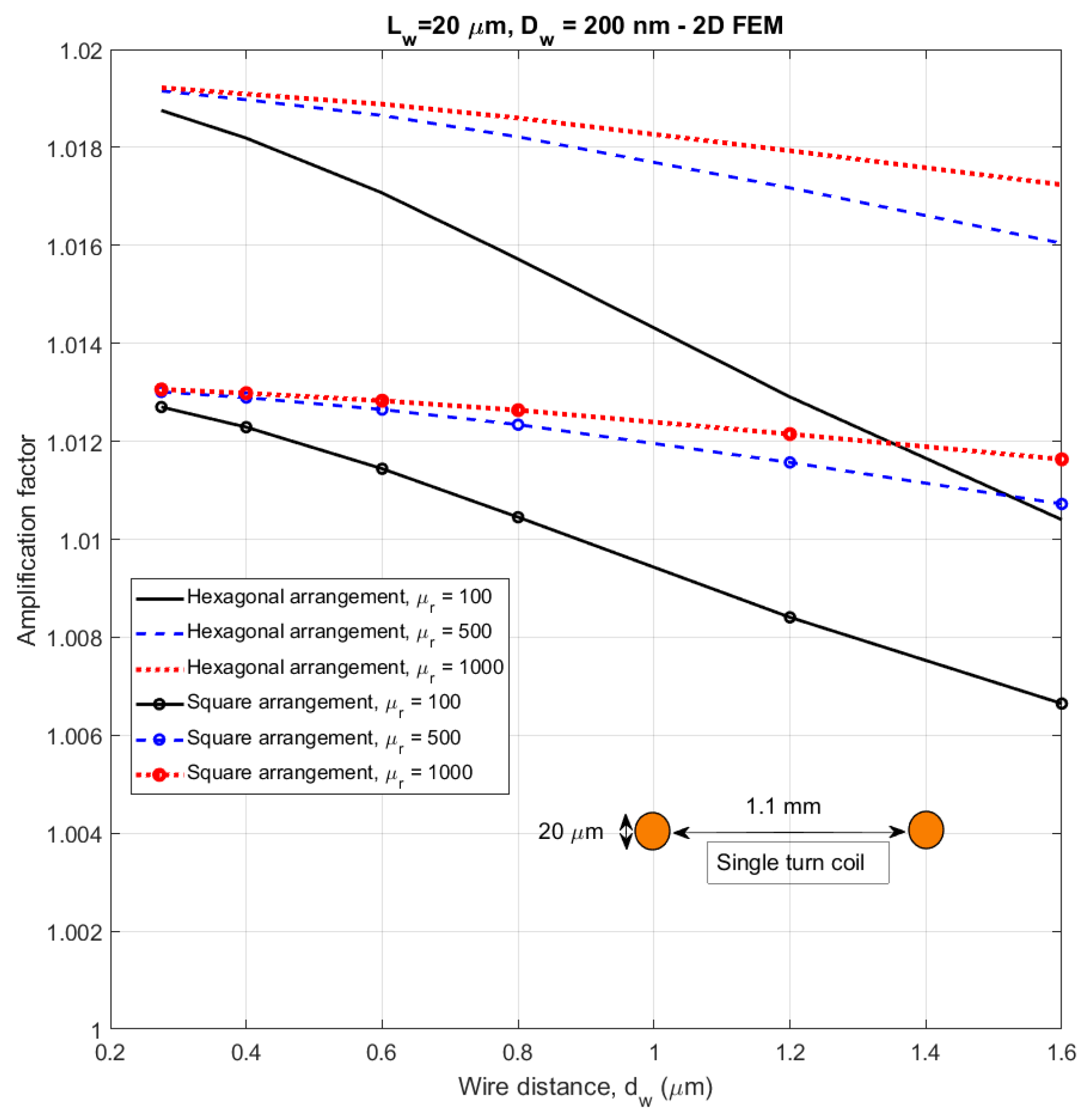
4.5. Verification of the 2D Model on Arrays of Thousands of Wires
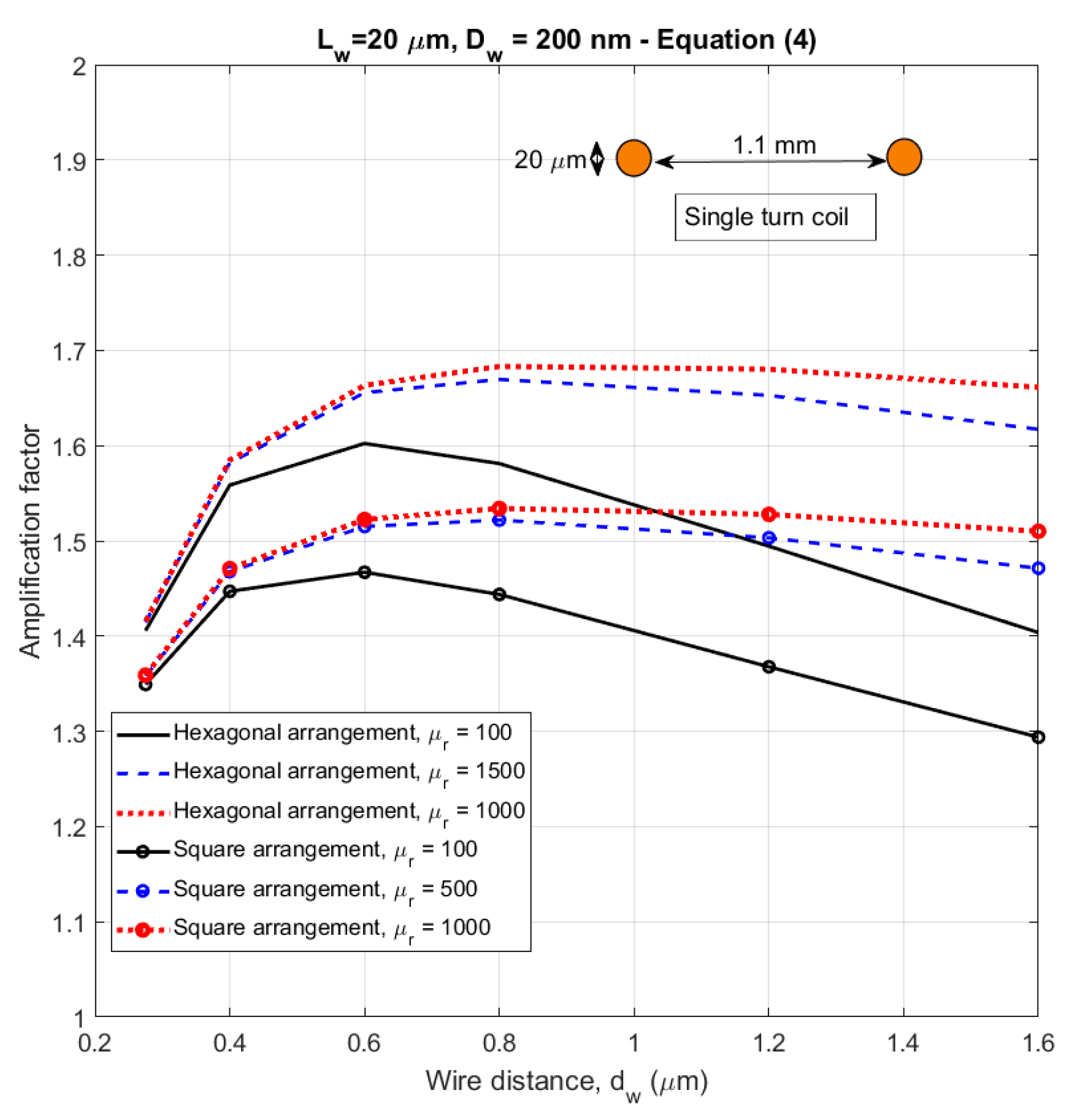
4.6. Using the 2D Model on Very Large Arrays
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Jordan, J.W.; Sternberg, B.; Dvorak, S.L. Size, Weight and Power Efficiency for High-power, Nonlinear, Geophysical-transmitter, Rod-core Antennas. J. Environ. Eng. Geophys. 2011, 16, 1–12. [Google Scholar] [CrossRef]
- Janosek, M. Parallel fluxgate magnetometers. In High Sensitivity Magnetometers; Grosz, A., Haji-Sheikh, M., Mukhopadhyay, S., Eds.; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Foerster, F. A method for the measurement of d-c field differences and its application to nondestructive testing. Nondestruct. Test. 1955, 13, 31–41. [Google Scholar]
- Lei, J.; Wang, T.; Lei, C.; Zhou, Y. Detection of Dynabeads using a micro-electro-mechanical-systems fluxgate sensor. Appl. Phys. Lett. 2013, 102, 022413. [Google Scholar] [CrossRef]
- Murzin, D.; Mapps, D.J.; Levada, K.; Belyaev, V.; Omelyanchik, A.; Panina, L.; Rodionova, V. Ultrasensitive Magnetic Field Sensors for Biomedical Applications. Sensors 2020, 20, 1569. [Google Scholar] [CrossRef]
- Ripka, P.; Janosek, M.; Butta, M.; Billingsley, S.W.; Wakefield, E.; IEEE. Crossfield Effect in Magnetic Sensors; IEEE: New York, NY, USA, 2009; p. 1860. [Google Scholar] [CrossRef]
- Delevoye, E.; Audoin, A.; Beranger, A.; Cuchet, R.; Hida, R.; Jager, T. Microfluxgate sensors for high frequency and low power applications. Sens. Actuators A Phys. 2008, 145, 271–277. [Google Scholar] [CrossRef]
- Sun, X.Y.; Yamada, T.; Takemura, Y. Output Characteristics and Circuit Modeling of Wiegand Sensor. Sensors 2019, 19, 2991. [Google Scholar] [CrossRef] [PubMed]
- Vazquez, M.; Chiriac, H.; Zhukov, A.; Panina, L.; Uchiyama, T. On the state-of-the-art in magnetic microwires and expected trends for scientific and technological studies. Phys. Status Solidi A Appl. Mater. Sci. 2011, 208, 493–501. [Google Scholar] [CrossRef]
- Zhukov, A.; Ipatov, M.; Corte-Leon, P.; Gonzalez-Legarreta, L.; Blanco, J.M.; Zhukova, V. Soft magnetic microwires for sensor applications. J. Magn. Magn. Mater. 2020, 498, 166180. [Google Scholar] [CrossRef]
- Alimohammadi, S.; Meydan, T.; Williams, P. Strain sensing by exploiting the Matteucci effect in amorphous wire. Int. J. Appl. Electromagn. Mech. 2019, 59, 115–121. [Google Scholar] [CrossRef]
- Fuzer, J.; Brauer, P.; Nielsen, O.V. Magnetic behaviour of amorphous ribbons with creep-induced helical anisotropy and their fluxgate properties. J. Magn. Magn. Mater. 1998, 188, 286–290. [Google Scholar] [CrossRef]
- Atalay, S.; Ripka, P.; Bayri, N. Coil-less fluxgate effect in (Co0.94Fe0.06)(72.5)Si12.5B15 amorphous wires. J. Magn. Magn. Mater. 2010, 322, 2238–2243. [Google Scholar] [CrossRef]
- Butta, M.; Ripka, P.; Infante, G.; Badini-Confalonieri, G.A.; Vazquez, M. Magnetic microwires with field-induced helical anisotropy for coil-less fluxgate. IEEE Trans. Magn. 2010, 46, 2562–2565. [Google Scholar] [CrossRef]
- Chizhik, A.; Zhukov, A.; Gonzalez, J.; Stupakiewicz, A. Control of the domain wall motion in cylindrical magnetic wires. Appl. Phys. Lett. 2016, 109, 4. [Google Scholar] [CrossRef]
- Olivera, J.; Aparicio, S.; Hernandez, M.G.; Zhukov, A.; Varga, R.; Campusano, M.; Echavarria, E.; Velayos, J.J.A. Microwire-Based Sensor Array for Measuring Wheel Loads of Vehicles. Sensors 2019, 19, 4658. [Google Scholar] [CrossRef] [PubMed]
- Chiriac, H.; Ovari, T.A. Amorphous glass-covered magnetic wires: Preparation, properties, applications. Prog. Mater. Sci. 1996, 40, 333–407. [Google Scholar] [CrossRef]
- Murata, N.; Nomura, R.; Matsuoka, A. Current annealing of amorphous wire core for performance improvement of fundamental mode orthogonal fluxgate. J. Magn. Magn. Mater. 2019, 484, 497–503. [Google Scholar] [CrossRef]
- Chiriac, H.; Lupu, N.; Stoian, G.; Ababei, G.; Corodeanu, S.; Ovari, T.A. Ultrathin Nanocrystalline Magnetic Wires. Crystals 2017, 7, 13. [Google Scholar] [CrossRef]
- Knobel, M.; Vazquez, M.; Kraus, L. Giant magnetoimpedance. In Handbook of Magnetic Materials; Buschow, K., Ed.; Elsevier: Amsterdam, The Netherlands, 2003. [Google Scholar]
- Sayad, A.; Skafidas, E.; Kwan, P. Magneto-Impedance Biosensor Sensitivity: Effect and Enhancement. Sensors 2020, 20, 5213. [Google Scholar] [CrossRef]
- He, D.F. PT-Level High-Sensitivity Magnetic Sensor with Amorphous Wire. Sensors 2020, 20, 161. [Google Scholar] [CrossRef]
- Nabias, J.; Asfour, A.; Yonnet, J.P. The Impact of Bending Stress on the Performance of Giant Magneto-Impedance (GMI) Magnetic Sensors. Sensors 2017, 17, 640. [Google Scholar] [CrossRef]
- Zhang, D.S.; Pan, Z.M.; Zhou, H.; Zhang, W.N. Magnetic sensor based on giant magneto-impedance effect using the self-regulating technology on the bias magnetic field. Sens. Actuators A Phys. 2016, 249, 225–230. [Google Scholar] [CrossRef]
- Garcia-Arribas, A. The Performance of the Magneto-Impedance Effect for the Detection of Superparamagnetic Particles. Sensors 2020, 20, 1961. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.W.; Li, J.H.; Li, Y.Y.; Chen, Y.L.; Xu, L.X. Design and Fabrication of a Miniaturized GMI Magnetic Sensor Based on Amorphous Wire by MEMS Technology. Sensors 2018, 18, 732. [Google Scholar] [CrossRef]
- Trigona, C.; Sinatra, V.; Ando, B.; Baglio, S.; Bulsara, A.R. Flexible Microwire Residence Times Difference Fluxgate Magnetometer. IEEE Trans. Instrum. Meas. 2017, 66, 559–568. [Google Scholar] [CrossRef]
- Schoinas, S.; El Guamra, A.M.; Moreillon, F.; Passeraub, P. Fabrication and Characterization of a Flexible Fluxgate Sensor with Pad-Printed Solenoid Coils. Sensors 2020, 20, 2275. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.Y.; Wang, Y.Z.; Lin, J. A SFTD Algorithm for Optimizing the Performance of the Readout Strategy of Residence Time Difference Fluxgate. Sensors 2018, 18, 3985. [Google Scholar] [CrossRef] [PubMed]
- Pang, N.; Cheng, D.F.; Wang, Y.Z. A High Stability Time Difference Readout Technique of RTD-Fluxgate Sensors. Sensors 2017, 17, 2325. [Google Scholar] [CrossRef]
- Ripka, P.; Janošek, M. Advances in magnetic field sensors. IEEE Sens. J. 2010, 10, 1108–1116. [Google Scholar] [CrossRef]
- Kraus, L.; Butta, M.; Ripka, P. Magnetic anisotropy and giant magnetoimpedance in NiFe electroplated on Cu wires. Sens. Lett. 2013, 11, 53–55. [Google Scholar] [CrossRef]
- El Kammouni, R.; Infante, G.; Torrejon, J.; Britel, M.R.; Brigui, J.; Vazquez, M. Microwave behavior in CoFe-based single- and two-phase magnetic microwires. Phys. Status Solidi A Appl. Mater. Sci. 2011, 208, 520–525. [Google Scholar] [CrossRef]
- Lu, C.C.; Huang, J.; Chiu, P.K.; Chiu, S.L.; Jeng, J.T. High-Sensitivity Low-Noise Miniature Fluxgate Magnetometers Using a Flip Chip Conceptual Design. Sensors 2014, 14, 13815–13829. [Google Scholar] [CrossRef] [PubMed]
- Ciudad, D.; Diaz-Michelena, M.; Perez, L.; Aroca, C. Small Fluxgate Magnetometers: Development and Future Trends in Spain. Sensors 2010, 10, 1859–1870. [Google Scholar] [CrossRef] [PubMed]
- Gooneratne, C.P.; Li, B.D.; Moellendick, T.E. Downhole Applications of Magnetic Sensors. Sensors 2017, 17, 2384. [Google Scholar] [CrossRef] [PubMed]
- Can, H.; Svec, P.; Tanriseven, S.; Bydzovsky, J.; Birlikseven, C.; Sozeri, H.; Topal, U. Optimizing the sensing performance of a single-rod fluxgate magnetometer using thin magnetic wires. Meas. Sci. Technol. 2015, 26. [Google Scholar] [CrossRef]
- Ripka, P.; Li, X.P.; Fan, J. Multiwire core fluxgate. Sens. Actuators A Phys. 2009, 156, 265–268. [Google Scholar] [CrossRef]
- Ripka, P.; Butta, M.; Jie, F.; Li, X. Sensitivity and noise of wire-core transverse fluxgate. IEEE Trans. Magn. 2010, 46, 654–657. [Google Scholar] [CrossRef]
- Vázquez, M. Magnetic Nano- and Microwires: Design, Synthesis, Properties and Applications; Elsevier Science: Amsterdam, The Netherlands, 2015. [Google Scholar]
- Ghaddar, A.; Gloaguen, F.; Gieraltowski, J. Magnetic properties of ferromagnetic nanowire arrays: Theory and experiment. In Proceedings of the International Conference on Magnetism (ICM 2009), Karlsruhe, Germany, 26–31 July 2010. [Google Scholar]
- Dmytriiev, O.; Al-Jarah, U.A.S.; Gangmei, P.; Kruglyak, V.V.; Hicken, R.J.; Mahato, B.K.; Rana, B.; Agrawal, M.; Barman, A.; Matefi-Tempfli, M.; et al. Static and dynamic magnetic properties of densely packed magnetic nanowire arrays. Phys. Rev. B 2013, 87, 174429. [Google Scholar] [CrossRef]
- Martinez-Banderas, A.I.; Aires, A.; Teran, F.J.; Perez, J.E.; Cadenas, J.F.; Alsharif, N.; Ravasi, T.; Cortajarena, A.L.; Kosel, J. Functionalized magnetic nanowires for chemical and magneto-mechanical induction of cancer cell death. Sci. Rep. 2016, 6, 35786. [Google Scholar] [CrossRef]
- Fert, A.; Piraux, L. Magnetic nanowires. J. Magn. Magn. Mater. 1999, 200, 338–358. [Google Scholar] [CrossRef]
- Lee, Y.C.; Chao, C.T.; Li, L.C.; Suen, Y.W.; Horng, L.; Wu, T.H.; Chang, C.R.; Wu, J.C. Magnetic tunnel junction based out-of-plane field sensor with perpendicular magnetic anisotropy in reference layer. J. Appl. Phys. 2015, 117, 3. [Google Scholar] [CrossRef]
- Ivanov, Y.P.; Vazquez, M.; Chubykalo-Fesenko, O. Magnetic reversal modes in cylindrical nanowires. J. Phys. D Appl. Phys. 2013, 46, 485001. [Google Scholar] [CrossRef]
- Salem, M.S.; Sergelius, P.; Zierold, R.; Moreno, J.M.M.; Gorlitz, D.; Nielsch, K. Magnetic characterization of nickel-rich NiFe nanowires grown by pulsed electrodeposition. J. Mater. Chem. 2012, 22, 8549–8557. [Google Scholar] [CrossRef]
- Torabinejad, V.; Aliofkhazraei, M.; Assareh, S.; Allahyarzadeh, M.H.; Rouhaghdam, A.S. Electrodeposition of Ni-Fe alloys, composites, and nano coatings-A review. J. Alloys Compd. 2017, 691, 841–859. [Google Scholar] [CrossRef]
- Chen, D.X.; Pardo, E.; Sanchez, A. Fluxmetric and magnetometric demagnetizing factors for cylinders. J. Magn. Magn. Mater. 2006, 306, 135–146. [Google Scholar] [CrossRef]
- Li, J.P.; Liu, S.B.; Feng, W.G.; Guo, B. Analysis of a fluxgate incorporating demagnetization field. In New Materials and Processes, Pts 1–3; Chen, W.Z., Li, Q., Chen, Y.L., Dai, P.Q., Jiang, Z.Y., Eds.; Trans Tech Publications Ltd.: Stafa-Zurich, Switzerland, 2012; Volume 476–478, pp. 1425–1428. [Google Scholar]
- Primdahl, F.; Petersen, J.R.; Olin, C.; Andersen, K.H. The short-circuited fluxgate output current. J. Phys. E Sci. Instrum. 1989, 22, 349–354. [Google Scholar] [CrossRef]


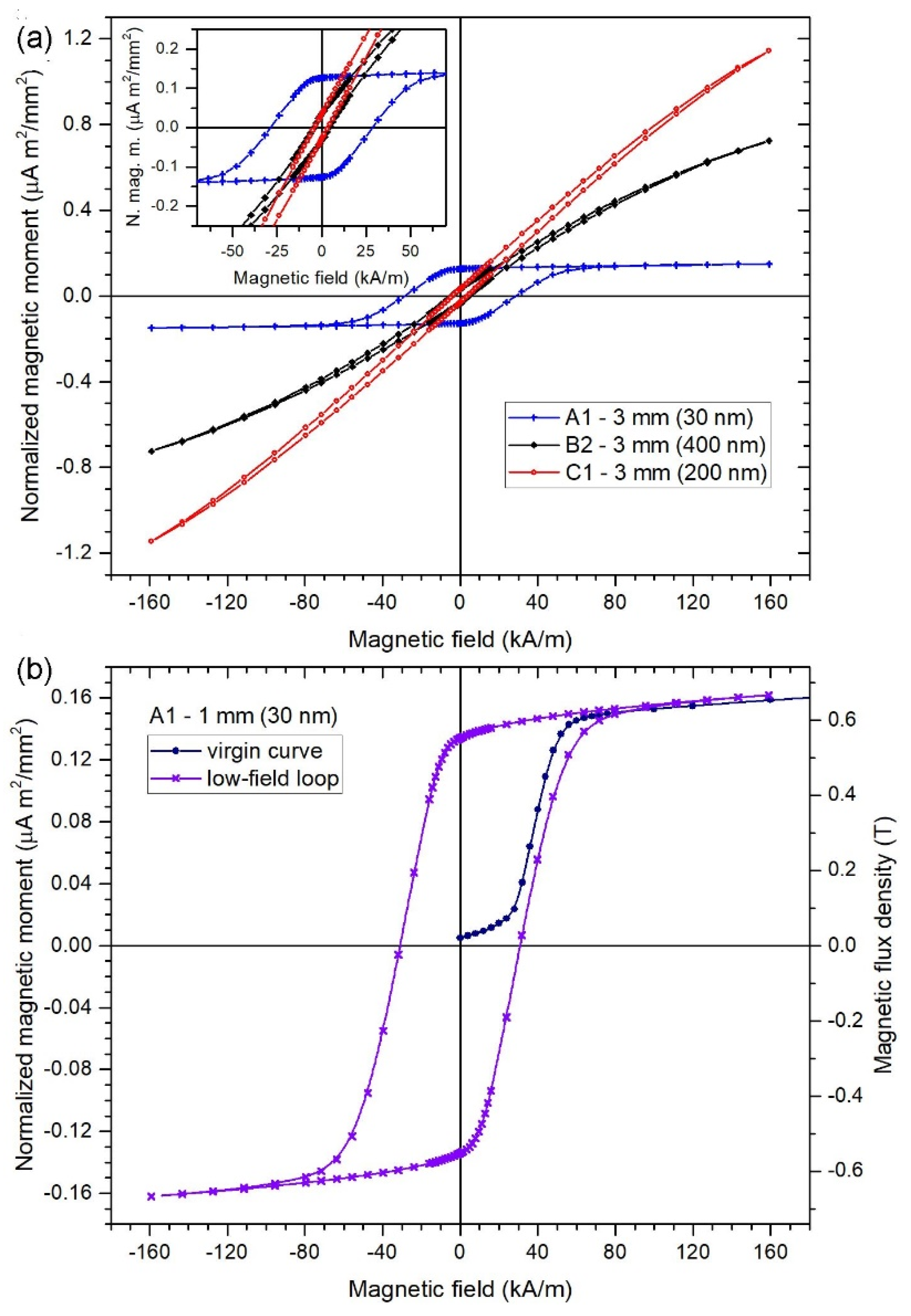
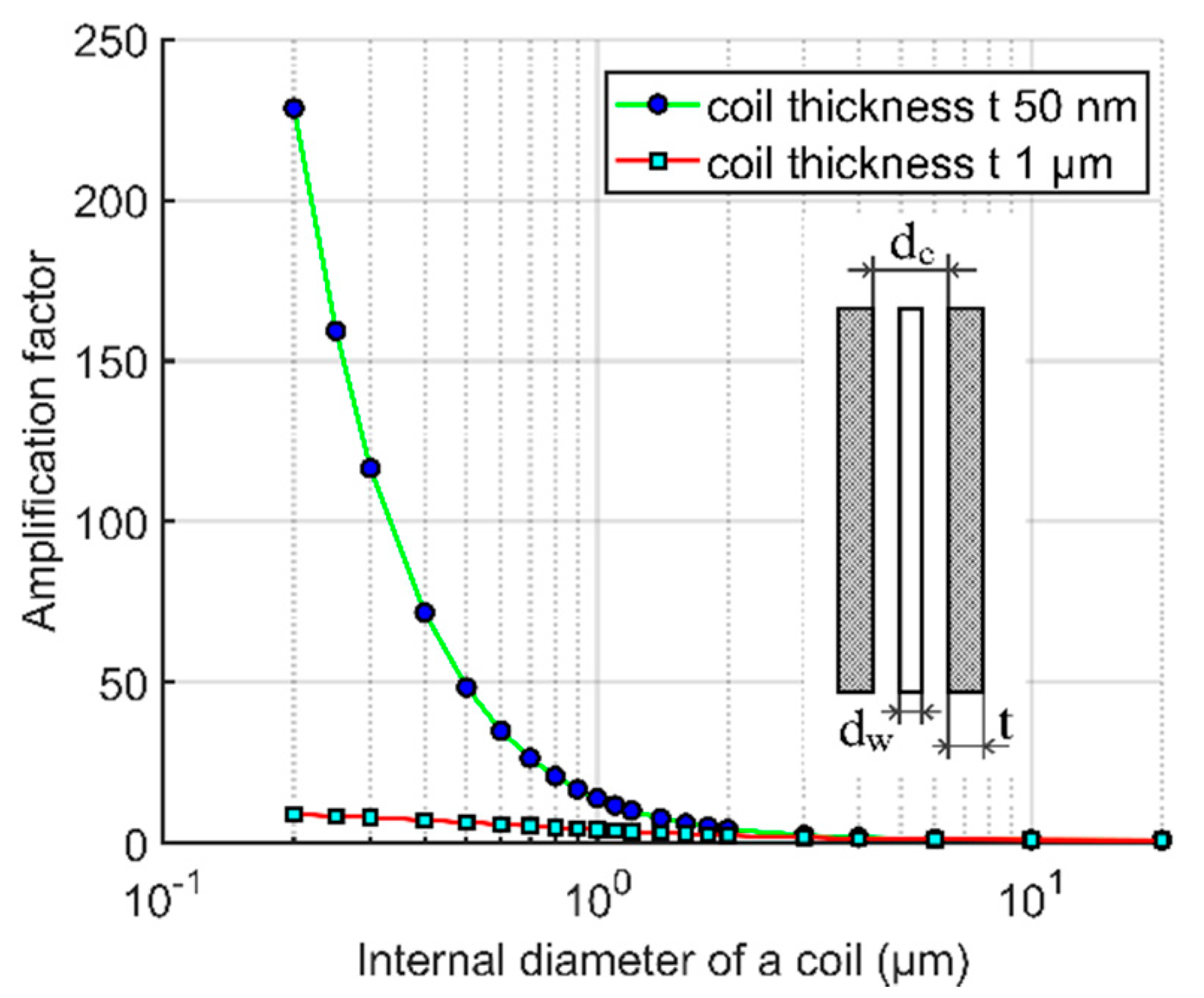
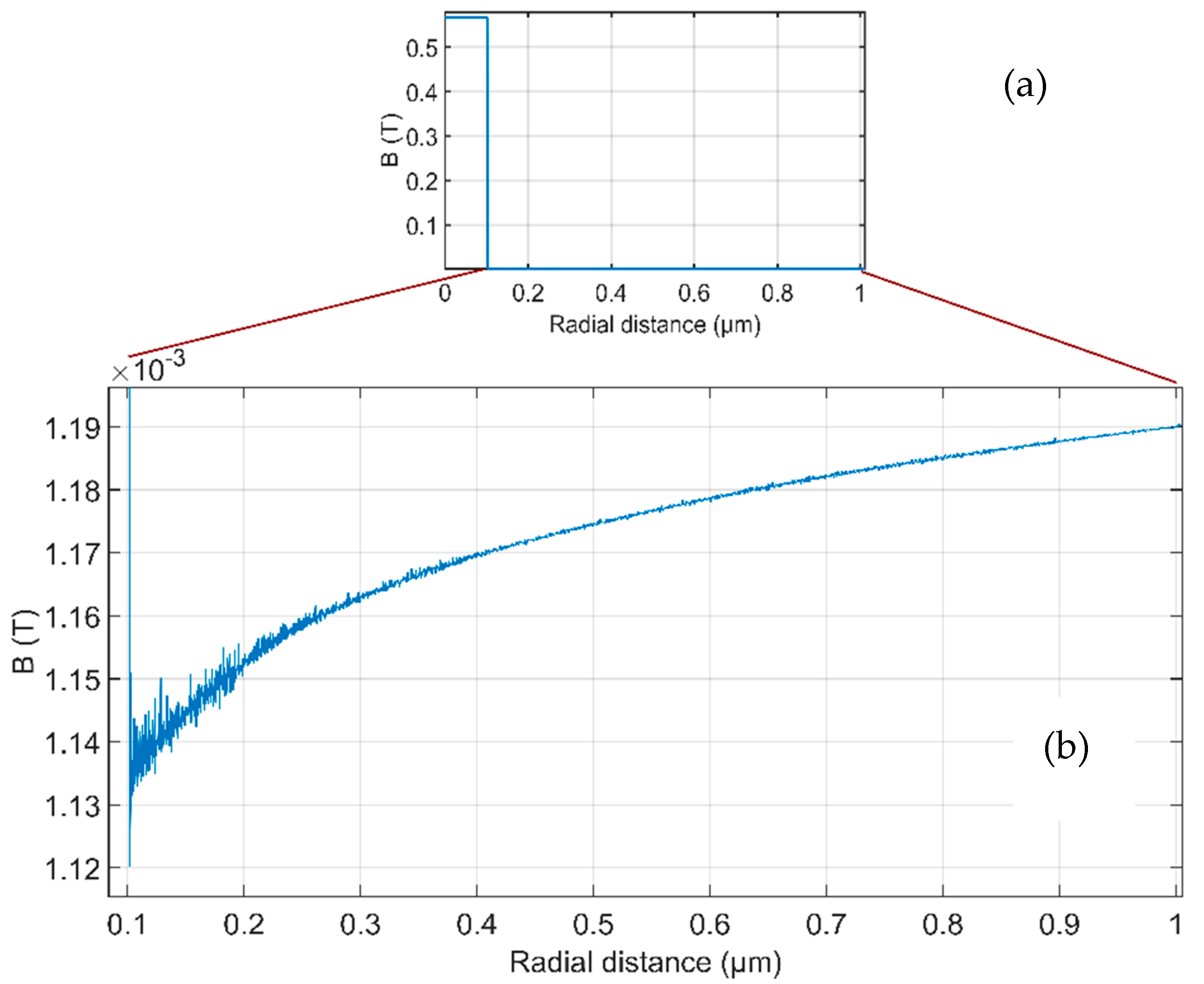
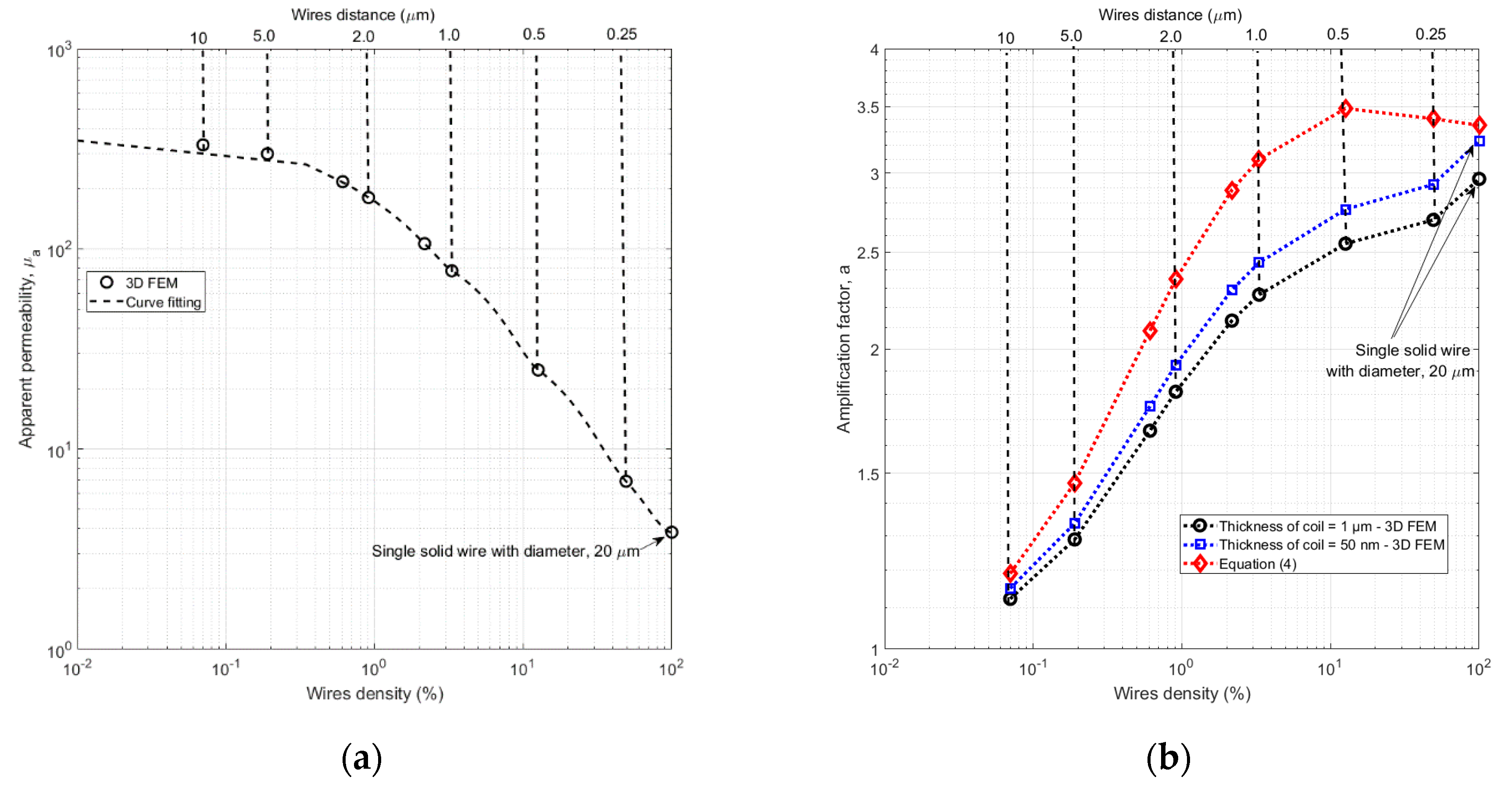


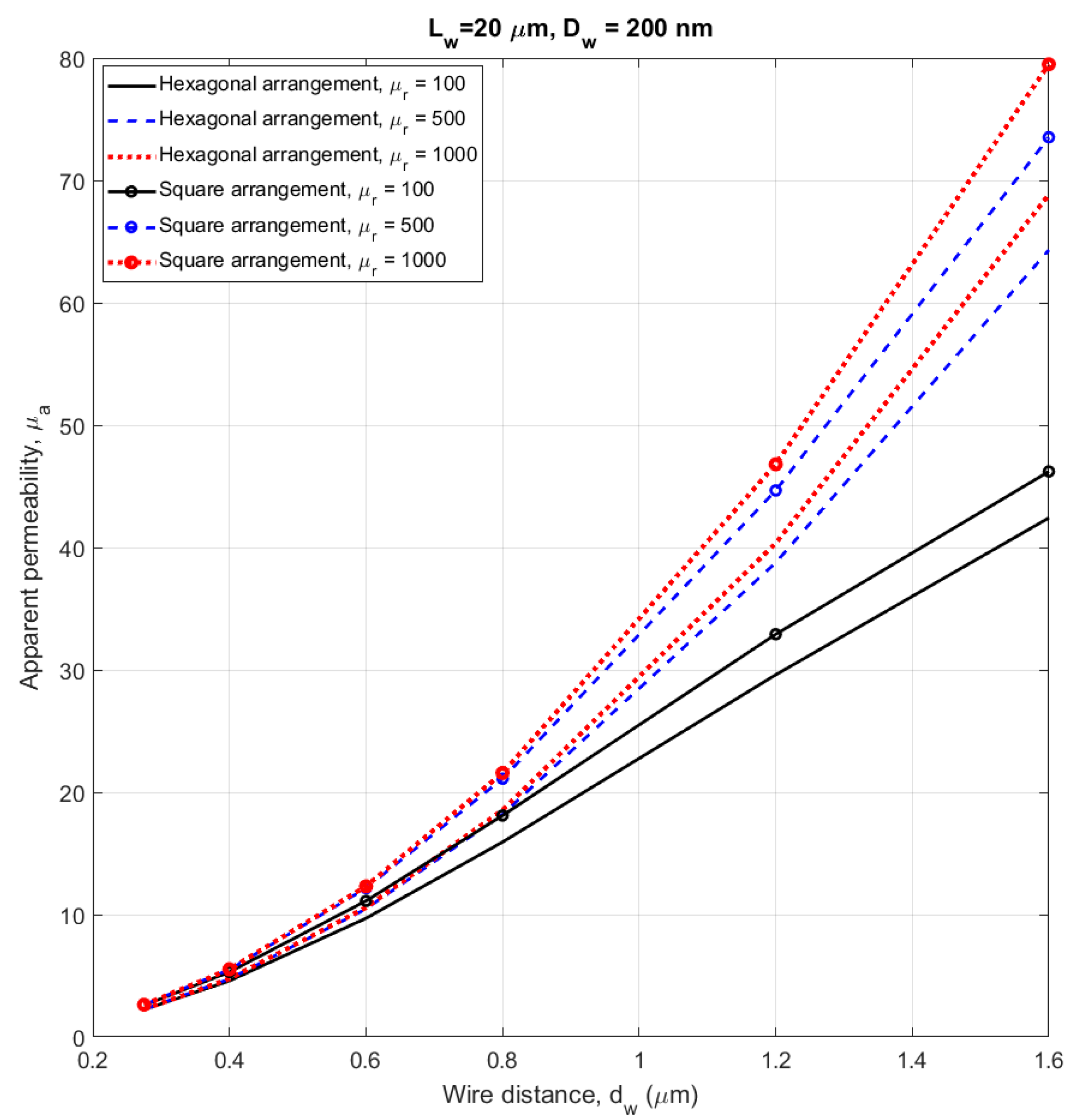
| # | Sample | Hc [kA/m] | μa |
|---|---|---|---|
| 1 | A1-1mm 30 nm | 31 | 20 |
| 2 | A1-3mm 30 nm | 29 | 18 |
| 3 | A2-3mm 30 nm | 39 | 16 |
| 4 | A4-1mm 30 nm | 31 | 14 |
| 5 | B2-1mm 400 nm | 3.9 | 3.3 |
| 6 | B2-3mm 400 nm | 4.5 | 3.4 |
| 7 | C1-1mm 200 nm | 4.6 | 3.7 |
| 8 | C1-3mm 200 nm | 2.6 | 3.3 |
| Case-µr = 500 Dw = 200 nm, Lw = 20 µm | µa 3D | µa 2D | Rel. Diff. (%) |
|---|---|---|---|
| 2791 wires–Hexagon, dw = 1.6 µm | 85.75 | 88.39 | 3.1 |
| 2791 wires–Hexagon, dw = 1.2 µm | 59.40 | 60.24 | 1.4 |
| 2791 wires–Hexagon, dw = 0.8 µm | 34.91 | 34.94 | 0.1 |
| 2791 wires–Hexagon, dw = 0.6 µm | 24.13 | 23.97 | −0.7 |
| 2791 wires–Hexagon, dw = 0.4 µm | 14.72 | 14.51 | −1.4 |
| 2791 wires–Hexagon, dw = 0.275 µm | 9.68 | 9.49 | −2.0 |
| 2521 wires–Square, dw = 1.6 µm | 97.06 | 98.98 | 2.0 |
| 2521 wires–Square, dw = 1.2 µm | 67.13 | 67.90 | 1.1 |
| 2521 wires–Square, dw = 0.8 µm | 39.84 | 39.52 | −0.8 |
| 2521 wires–Square, dw = 0.6 µm | 27.83 | 27.13 | −2.5 |
| 2521 wires–Square, dw = 0.4 µm | 16.92 | 16.40 | −3.1 |
| 2521 wires–Square, dw = 0.275 µm | 11.13 | 10.70 | −3.9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ripka, P.; Grim, V.; Mirzaei, M.; Hrakova, D.; Uhrig, J.; Emmerich, F.; Thielemann, C.; Hejtmanek, J.; Kaman, O.; Tesar, R. Modelling and Measurement of Magnetically Soft Nanowire Arrays for Sensor Applications. Sensors 2021, 21, 3. https://doi.org/10.3390/s21010003
Ripka P, Grim V, Mirzaei M, Hrakova D, Uhrig J, Emmerich F, Thielemann C, Hejtmanek J, Kaman O, Tesar R. Modelling and Measurement of Magnetically Soft Nanowire Arrays for Sensor Applications. Sensors. 2021; 21(1):3. https://doi.org/10.3390/s21010003
Chicago/Turabian StyleRipka, Pavel, Vaclav Grim, Mehran Mirzaei, Diana Hrakova, Janis Uhrig, Florian Emmerich, Christiane Thielemann, Jiri Hejtmanek, Ondrej Kaman, and Roman Tesar. 2021. "Modelling and Measurement of Magnetically Soft Nanowire Arrays for Sensor Applications" Sensors 21, no. 1: 3. https://doi.org/10.3390/s21010003
APA StyleRipka, P., Grim, V., Mirzaei, M., Hrakova, D., Uhrig, J., Emmerich, F., Thielemann, C., Hejtmanek, J., Kaman, O., & Tesar, R. (2021). Modelling and Measurement of Magnetically Soft Nanowire Arrays for Sensor Applications. Sensors, 21(1), 3. https://doi.org/10.3390/s21010003





