Uncertainty-Aware Visual Perception System for Outdoor Navigation of the Visually Challenged
Abstract
1. Introduction
2. Related Work
2.1. Assistive Navigation Systems for the VCP
2.2. Obstacle Detection
2.3. Object Recognition
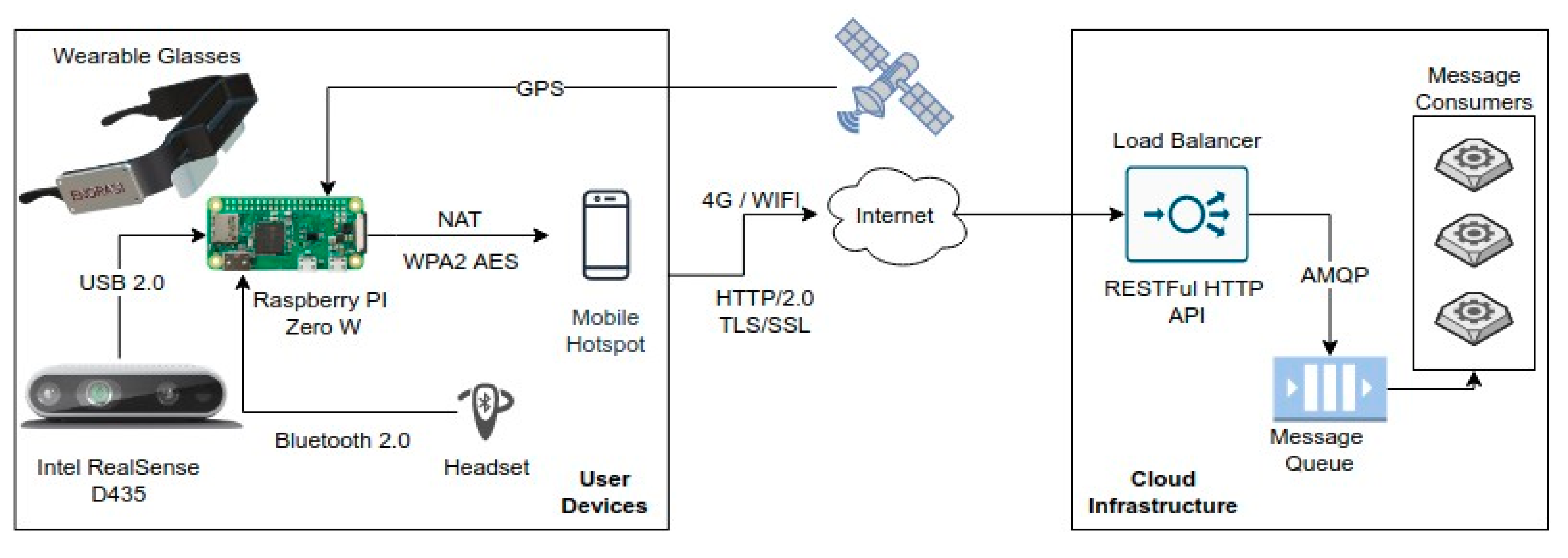
3. System Architecture
3.1. System Components and Infrastructure
3.2. Smart Glasses Design
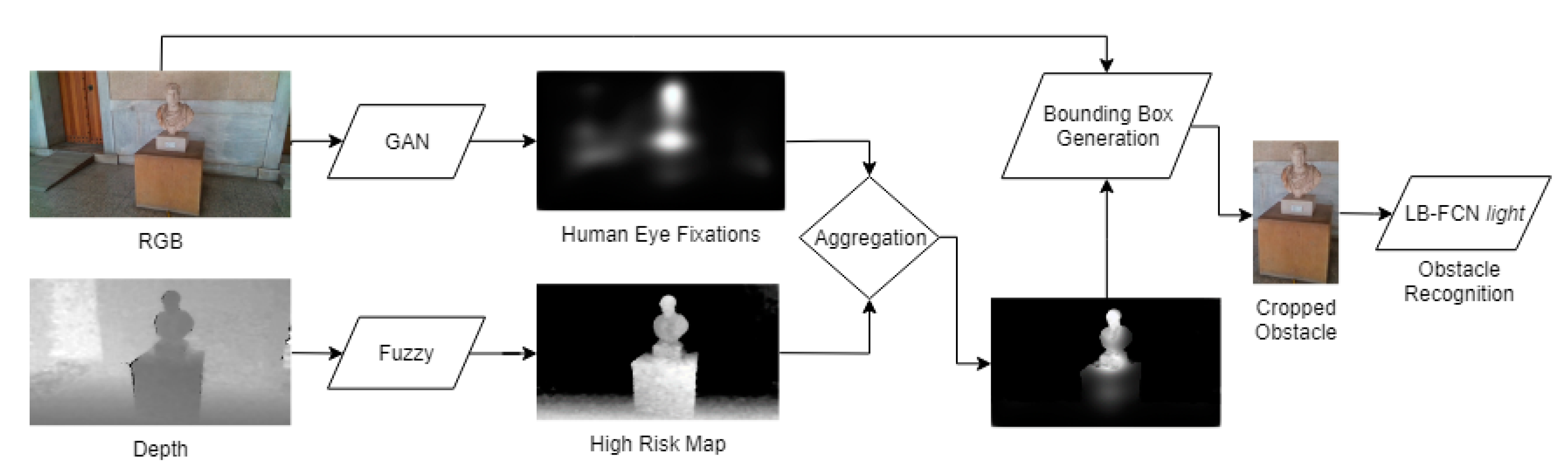
4. Obstacle Detection and Recognition Component
4.1. Obstacle Detection
- (a)
- Eye human fixation estimation model;
- (b)
- Depth-aware fuzzy risk assessment in the form of risk maps;
- (c)
- Obstacle detection and localization via the fuzzy aggregation of saliency maps, produced in Step (a) and the risk maps produced in Step (b);
- (d)
- Obstacle recognition using a deep learning model based on probable obstacle regions obtained in Step (c).
4.1.1. Human Eye Fixation Estimation
4.1.2. Uncertainty-Aware Obstacle Detection
4.1.3. Personalized Obstacle Detection Refinement
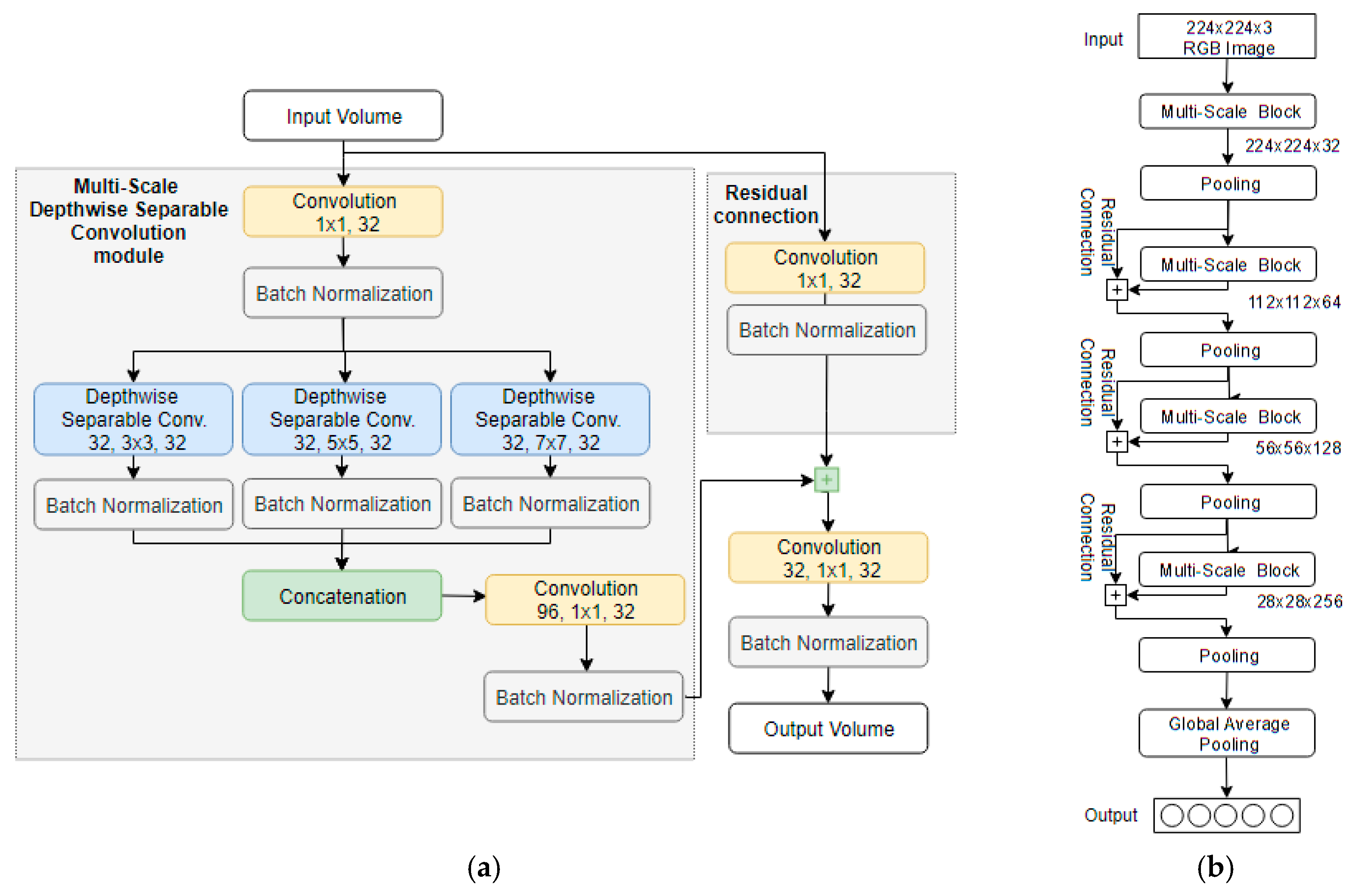
4.2. Obstacle Recognition
5. Experimental Framework and Results
5.1. Experimental Framework
5.2. Obstacle Detection Results
5.3. Obstacle Recognition Results
6. Discussion
7. Conclusions
- A novel uncertainty-aware obstacle detection methodology, exploiting the human eye-fixation saliency estimation and person-specific characteristics;
- Integration of obstacle detection and recognition methodologies in a unified manner;
- A novel system architecture that allows horizontal resource scaling and processing module interchange ability.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- WHO. World Health Organization-Blindness and Visual Impairement; WHO: Geneva, Switzerland, 2018. [Google Scholar]
- Suresh, A.; Arora, C.; Laha, D.; Gaba, D.; Bhambri, S. Intelligent Smart Glass for Visually Impaired Using Deep Learning Machine Vision Techniques and Robot Operating System (ROS). In Proceedings of the International Conference on Robot Intelligence Technology and Applications, Daejeon, Korea, 14–15 December 2017; pp. 99–112. [Google Scholar]
- Tapu, R.; Mocanu, B.; Zaharia, T. DEEP-SEE: Joint Object Detection, Tracking and Recognition with Application to Visually Impaired Navigational Assistance. Sensors 2017, 17, 2473. [Google Scholar] [CrossRef] [PubMed]
- Schwarze, T.; Lauer, M.; Schwaab, M.; Romanovas, M.; Böhm, S.; Jürgensohn, T. A camera-Based mobility aid for visually impaired people. KI Künstliche Intell. 2016, 30, 29–36. [Google Scholar] [CrossRef]
- Caraiman, S.; Morar, A.; Owczarek, M.; Burlacu, A.; Rzeszotarski, D.; Botezatu, N.; Herghelegiu, P.; Moldoveanu, F.; Strumillo, P.; Moldoveanu, A. Computer Vision for the Visually Impaired: The Sound of Vision System. In Proceedings of the IEEE International Conference on Computer Vision Workshops, Venice, Italy, 22–29 October 2017; pp. 1480–1489. [Google Scholar]
- Mahmood, Z.; Bibi, N.; Usman, M.; Khan, U.; Muhammad, N. Mobile cloud based-Framework for sports applications. Multidimens. Syst. Signal Process. 2019, 30, 1991–2019. [Google Scholar] [CrossRef]
- Ahmed, H.; Ullah, I.; Khan, U.; Qureshi, M.B.; Manzoor, S.; Muhammad, N.; Khan, S.; Usman, M.; Nawaz, R. Adaptive Filtering on GPS-Aided MEMS-IMU for Optimal Estimation of Ground Vehicle Trajectory. Sensors 2019, 19, 5357. [Google Scholar] [CrossRef]
- Khan, S.N.; Muhammad, N.; Farwa, S.; Saba, T.; Khattak, S.; Mahmood, Z. Early Cu depth decision and reference picture selection for low complexity Mv-Hevc. Symmetry 2019, 11, 454. [Google Scholar] [CrossRef]
- Bashiri, F.S.; LaRose, E.; Badger, J.C.; D’Souza, R.M.; Yu, Z.; Peissig, P. Object Detection to Assist Visually Impaired People: A Deep Neural Network Adventure; Springer International Publishing: Cham, Switzerland, 2018; pp. 500–510. [Google Scholar]
- Yang, K.; Wang, K.; Zhao, X.; Cheng, R.; Bai, J.; Yang, Y.; Liu, D. IR stereo realsense: Decreasing minimum range of navigational assistance for visually impaired individuals. J. Ambient Intell. Smart Environ. 2017, 9, 743–755. [Google Scholar] [CrossRef]
- Long, N.; Wang, K.; Cheng, R.; Hu, W.; Yang, K. Unifying obstacle detection, recognition, and fusion based on millimeter wave radar and RGB-Depth sensors for the visually impaired. Rev. Sci. Instrum. 2019, 90, 044102. [Google Scholar] [CrossRef]
- Pardasani, A.; Indi, P.N.; Banerjee, S.; Kamal, A.; Garg, V. Smart Assistive Navigation Devices for Visually Impaired People. In Proceedings of the IEEE 4th International Conference on Computer and Communication Systems (ICCCS), Singapore, 23–25 February 2019; pp. 725–729. [Google Scholar]
- Jiang, B.; Yang, J.; Lv, Z.; Song, H. Wearable vision assistance system based on binocular sensors for visually impaired users. IEEE Internet Things J. 2019, 6, 1375–1383. [Google Scholar] [CrossRef]
- Chen, S.; Yao, D.; Cao, H.; Shen, C. A Novel Approach to Wearable Image Recognition Systems to Aid Visually Impaired People. Appl. Sci. 2019, 9, 3350. [Google Scholar] [CrossRef]
- Adegoke, A.O.; Oyeleke, O.D.; Mahmud, B.; Ajoje, J.O.; Thomase, S. Design and Construction of an Obstacle-Detecting Glasses for the Visually Impaired. Int. J. Eng. Manuf. 2019, 9, 57–66. [Google Scholar]
- Islam, M.T.; Ahmad, M.; Bappy, A.S. Microprocessor-Based Smart Blind Glass System for Visually Impaired People. In Proceedings of the International Joint Conference on Computational Intelligence, Seville, Spain, 18–20 September 2018; pp. 151–161. [Google Scholar]
- Iakovidis, D.K.; Diamantis, D.; Dimas, G.; Ntakolia, C.; Spyrou, E. Digital Enhancement of Cultural Experience and Accessibility for the Visually Impaired. In Digital Enhancement of Cultural Experience and Accessibility for the Visually Impaired; Springer: Cham, Switzerland, 2020; pp. 237–271. [Google Scholar]
- Zhang, J.; Ong, S.; Nee, A. Navigation systems for individuals with visual impairment: A survey. In Proceedings of the 2nd International Convention on Rehabilitation Engineering & Assistive Technology, Bangkok, Thailand, 13–18 May 2008; pp. 159–162. [Google Scholar]
- Dakopoulos, D.; Bourbakis, N.G. Wearable obstacle avoidance electronic travel aids for blind: A survey. IEEE Trans. Syst. Man Cybern. Part C 2009, 40, 25–35. [Google Scholar] [CrossRef]
- Elmannai, W.; Elleithy, K. Sensor-Based assistive devices for visually-Impaired people: Current status, challenges, and future directions. Sensors 2017, 17, 565. [Google Scholar] [CrossRef] [PubMed]
- Poggi, M.; Mattoccia, S. A wearable mobility aid for the visually impaired based on embedded 3D vision and deep learning. In Proceedings of the 2016 IEEE Symposium on Computers and Communication (ISCC), Messina, Italy, 27–30 June 2016; pp. 208–213. [Google Scholar]
- Wang, H.-C.; Katzschmann, R.K.; Teng, S.; Araki, B.; Giarré, L.; Rus, D. Enabling independent navigation for visually impaired people through a wearable vision-Based feedback system. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Marina Bay Sands, Singapore, 29 May–3 June 2017; pp. 6533–6540. [Google Scholar]
- Lin, B.-S.; Lee, C.-C.; Chiang, P.-Y. Simple smartphone-based guiding system for visually impaired people. Sensors 2017, 17, 1371. [Google Scholar] [CrossRef] [PubMed]
- Hu, W.; Wang, K.; Chen, H.; Cheng, R.; Yang, K. An indoor positioning framework based on panoramic visual odometry for visually impaired people. Meas. Sci. Technol. 2019, 31, 014006. [Google Scholar] [CrossRef]
- Yu, X.; Yang, G.; Jones, S.; Saniie, J. AR Marker Aided Obstacle Localization System for Assisting Visually Impaired. In Proceedings of the 2018 IEEE International Conference on Electro/Information Technology (EIT), Rochester, MA, USA, 3–5 May 2018; pp. 271–276. [Google Scholar]
- Kaur, B.; Bhattacharya, J. A scene perception system for visually impaired based on object detection and classification using multi-Modal DCNN. arXiv 2018, arXiv:1805.08798. [Google Scholar]
- Cheng, R.; Wang, K.; Bai, J.; Xu, Z. OpenMPR: Recognize places using multimodal data for people with visual impairments. Meas. Sci. Technol. 2019, 30, 124004. [Google Scholar] [CrossRef]
- Yang, K.; Wang, K.; Bergasa, L.M.; Romera, E.; Hu, W.; Sun, D.; Sun, J.; Cheng, R.; Chen, T.; López, E. Unifying terrain awareness for the visually impaired through real-Time semantic segmentation. Sensors 2018, 18, 1506. [Google Scholar] [CrossRef]
- Lin, S.; Wang, K.; Yang, K.; Cheng, R. KrNet: A kinetic real-time convolutional neural network for navigational assistance. In International Conference on Computers Helping People with Special Needs; Springer: Cham, Germany, 2018; pp. 55–62. [Google Scholar]
- Potdar, K.; Pai, C.D.; Akolkar, S. A Convolutional Neural Network based Live Object Recognition System as Blind Aid. arXiv 2018, arXiv:1811.10399. [Google Scholar]
- Bai, J.; Liu, Z.; Lin, Y.; Li, Y.; Lian, S.; Liu, D. Wearable Travel Aid for Environment Perception and Navigation of Visually Impaired People. Electronics 2019, 8, 697. [Google Scholar] [CrossRef]
- Maadhuree, A.N.; Mathews, R.S.; Robin, C.R.R. Le Vision: An Assistive Wearable Device for the Visually Challenged. In Proceedings of the International Conference on Intelligent Systems Design and Applications, Vellore, India, 6–8 December 2018; pp. 353–361. [Google Scholar]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster r-CNN: Towards real-time object detection with region proposal networks. In Proceedings of the Neural Information Processing Systems, Montreal, QC, Canada, 7–9 December 2015; pp. 91–99. [Google Scholar]
- Redmon, J.; Farhadi, A. YOLO9000: Better, faster, stronger. arXiv 2017.
- Liu, W.; Anguelov, D.; Erhan, D.; Szegedy, C.; Reed, S.; Fu, C.-Y.; Berg, A.C. SSD: Single shot multibox detector. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 8–16 October 2016; pp. 21–37. [Google Scholar]
- Lee, C.-H.; Su, Y.-C.; Chen, L.-G. An intelligent depth-Based obstacle detection system for visually-Impaired aid applications. In Proceedings of the 2012 13th International Workshop on Image Analysis for Multimedia Interactive Services, Dublin, Ireland, 23–25 May 2012; pp. 1–4. [Google Scholar]
- Mancini, M.; Costante, G.; Valigi, P.; Ciarfuglia, T.A. J-MOD 2: Joint monocular obstacle detection and depth estimation. IEEE Robot. Autom. Lett. 2018, 3, 1490–1497. [Google Scholar] [CrossRef]
- Dimas, G.; Ntakolia, C.; Iakovidis, D.K. Obstacle Detection Based on Generative Adversarial Networks and Fuzzy Sets for Computer-Assisted Navigation. In Proceedings of the International Conference on Engineering Applications of Neural Networks, Crete, Greece, 24–26 May 2019; pp. 533–544. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. In Proceedings of the Neural Information Processing Systems, Lake Tahoe, NV, USA, 3–6 December 2012; pp. 1097–1105. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Howard, A.G.; Zhu, M.; Chen, B.; Kalenichenko, D.; Wang, W.; Weyand, T.; Andreetto, M.; Adam, H. Mobilenets: Efficient convolutional neural networks for mobile vision applications. arXiv 2017, arXiv:1704.04861. [Google Scholar]
- Zhang, X.; Zhou, X.; Lin, M.; Sun, J. ShuffleNet: An Extremely Efficient Convolutional Neural Network for Mobile Devices. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, San Juan, PR, USA, 17–19 June 1997; pp. 6848–6856. [Google Scholar]
- Chollet, F. Xception: Deep learning with depthwise separable convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 22–25 July 2017; pp. 1251–1258. [Google Scholar]
- Badrinarayanan, V.; Kendall, A.; Cipolla, R. Segnet: A deep convolutional encoder-Decoder architecture for image segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 2481–2495. [Google Scholar] [CrossRef] [PubMed]
- Diamantis, D.E.; Koutsiou, D.-C.C.; Iakovidis, D.K. Staircase Detection Using a Lightweight Look-Behind Fully Convolutional Neural Network. In Proceedings of the International Conference on Engineering Applications of Neural Networks, Crete, Greece, 24–26 May 2019; pp. 522–532. [Google Scholar]
- Diamantis, D.E.; Iakovidis, D.K.; Koulaouzidis, A. Look-Behind fully convolutional neural network for computer-Aided endoscopy. Biomed. Signal Process. Control. 2019, 49, 192–201. [Google Scholar] [CrossRef]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial nets. In Proceedings of the Neural Information Processing Systems, Montreal, QC, Canada, 8–13 December 2014; pp. 2672–2680. [Google Scholar]
- Deng, J.; Dong, W.; Socher, R.; Li, L.-J.; Li, K.; Li, F.-F. Imagenet: A large-scale hierarchical image database. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 248–255. [Google Scholar]
- Nguyen, H.T.; Walker, C.L.; Walker, E.A. A First Course in Fuzzy Logic; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Feferman, S.; Dawson, J.W.; Kleene, S.C.; Moore, G.H.; Solovay, R.M. Kurt Gödel: Collected Works; Oxford University Press: Oxford, UK, 1998; pp. 1929–1936. [Google Scholar]
- Rivest, J.-F.; Soille, P.; Beucher, S. Morphological gradients. J. Electron. Imaging 1993, 2, 326. [Google Scholar]
- Suzuki, S.; Abe, K. Topological structural analysis of digitized binary images by border following. Comput. Vision Graph. Image Process. 1985, 29, 396. [Google Scholar] [CrossRef]
- Kotoulas, L.; Andreadis, I. Image analysis using moments. In Proceedings of the 5th International. Conference on Technology and Automation, Thessaloniki, Greece, 15–16 October 2005. [Google Scholar]
- Heikkilä, J.; Silven, O. A four-step camera calibration procedure with implicit image correction. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Juan, PR, USA, 17–19 June 1997; pp. 1106–1112. [Google Scholar]
- Iakovidis, D.K.; Dimas, G.; Karargyris, A.; Bianchi, F.; Ciuti, G.; Koulaouzidis, A. Deep endoscopic visual measurements. IEEE J. Biomed. Heal. Informatics 2019, 23, 2211–2219. [Google Scholar] [CrossRef]
- Springenberg, J.T.; Dosovitskiy, A.; Brox, T.; Riedmiller, M. Striving for simplicity: The all convolutional net. arXiv 2014, arXiv:1412.6806. [Google Scholar]
- Ioffe, S.; Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. arXiv 2015, arXiv:1502.03167. [Google Scholar]
- Jiang, M.; Huang, S.; Duan, J.; Zhao, Q. Salicon: Saliency in context. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1072–1080. [Google Scholar]
- Flickr Inc. Find your inspiration. Available online: www.flickr.com/ (accessed on 21 April 2020).
- Keras. The Python Deep Learning library. Available online: www.keras.io/ (accessed on 21 April 2020).
- Abadi, M.; Barham, P.; Chen, J.; Chen, Z.; Davis, A.; Dean, J.; Devin, M.; Ghemawat, S.; Irving, G.; Isard, M.; et al. Tensorflow: A system for large-Scale machine learning. In Proceedings of the 12th USENIX Symposium on Operating Systems Design and Implementation, Savannah, GA, USA, 2–4 November 2016; pp. 265–283. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Sanders, J.; Kandrot, E. CUDA by Example: An Introduction to General-Purpose GPU Programming; Addison-Wesley Professional: Boston, MA, USA, 2010. [Google Scholar]
- Sandler, M.; Howard, A.; Zhu, M.; Zhmoginov, A.; Chen, L.-C. Mobilenetv2: Inverted residuals and linear bottlenecks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 4510–4520. [Google Scholar]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1–9. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 770–778. [Google Scholar]
- Ogden, S.S.; Guo, T. Characterizing the Deep Neural Networks Inference Performance of Mobile Applications. arXiv 2019, arXiv:1909.04783. [Google Scholar]
- Mattoccia, S.; Macrı, P. 3D Glasses as Mobility Aid for Visually Impaired People. In Proceedings of the European Conference on Computer Vision, Zurich, Switzerland, 6–12 September 2014; pp. 539–554. [Google Scholar]
- Ioannides, M.; Hadjiprocopi, A.; Doulamis, N.; Doulamis, A.; Protopapadakis, E.; Makantasis, K.; Santos, P.; Fellner, D.; Stork, A.; Balet, O.; et al. Online 4D reconstruction using multi-images available under Open Access. ISPRS Ann. Photogramm. Remote. Sens. Spat. Inf. Sci. 2013, 2, 169–174. [Google Scholar] [CrossRef]
- Rodríguez-Gonzálvez, P.; Muñoz-Nieto, A.L.; Del Pozo, S.; Sanchez, L.J.; Micoli, L.; Barsanti, S.G.; Guidi, G.; Mills, J.; Fieber, K.; Haynes, I.; et al. 4D Reconstruction and visualization of Cultural Heritage: Analyzing our legacy through time. Int. Arch. Photogramm. Remote. Sens. Spat. Inf. Sci. 2017, 42, 609–616. [Google Scholar] [CrossRef]













| Detected | ||
|---|---|---|
| Actual | Positive (%) | Negative (%) |
| Positive (%) | 55.1 | 9.0 |
| Negative (%) | 5.3 | 30.6 |
| Metrics | Proposed (%) | Method [38] (%) | Method [36] (%) |
|---|---|---|---|
| Accuracy | 85.7 | 72.6 | 63.7 |
| Sensitivity | 86.0 | 91.7 | 87.3 |
| Specificity | 85.2 | 38.6 | 21.6 |
| Metrics | LB-FCN Light [45] (%) | MobileNet-v2 [64] (%) |
|---|---|---|
| Accuracy | 93.8 | 91.4 |
| Sensitivity | 92.4 | 90.5 |
| Specificity | 91.3 | 91.1 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dimas, G.; Diamantis, D.E.; Kalozoumis, P.; Iakovidis, D.K. Uncertainty-Aware Visual Perception System for Outdoor Navigation of the Visually Challenged. Sensors 2020, 20, 2385. https://doi.org/10.3390/s20082385
Dimas G, Diamantis DE, Kalozoumis P, Iakovidis DK. Uncertainty-Aware Visual Perception System for Outdoor Navigation of the Visually Challenged. Sensors. 2020; 20(8):2385. https://doi.org/10.3390/s20082385
Chicago/Turabian StyleDimas, George, Dimitris E. Diamantis, Panagiotis Kalozoumis, and Dimitris K. Iakovidis. 2020. "Uncertainty-Aware Visual Perception System for Outdoor Navigation of the Visually Challenged" Sensors 20, no. 8: 2385. https://doi.org/10.3390/s20082385
APA StyleDimas, G., Diamantis, D. E., Kalozoumis, P., & Iakovidis, D. K. (2020). Uncertainty-Aware Visual Perception System for Outdoor Navigation of the Visually Challenged. Sensors, 20(8), 2385. https://doi.org/10.3390/s20082385






