Spectrometer-Free Graphene Plasmonics Based Refractive Index Sensor
Abstract
1. Introduction
2. Results
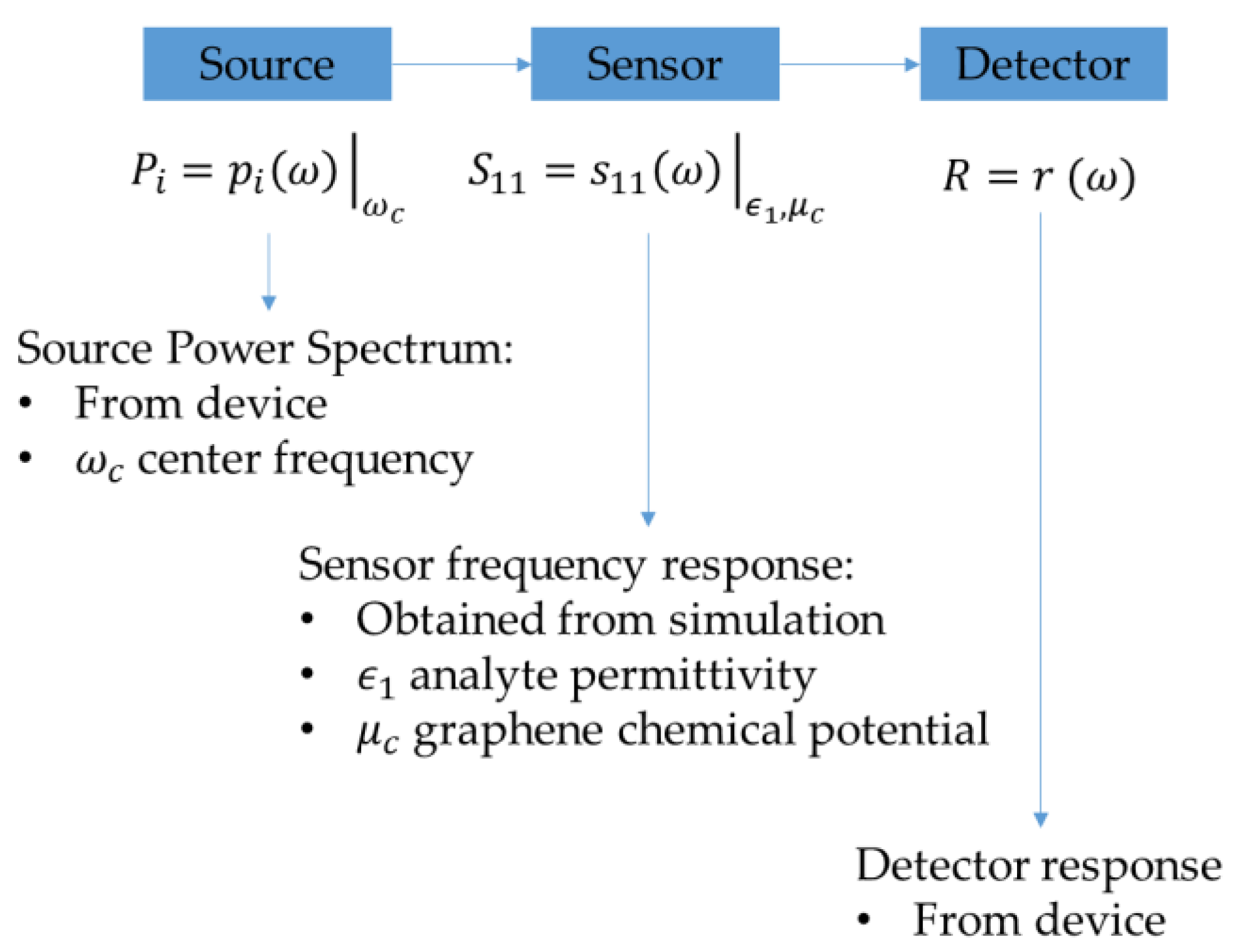
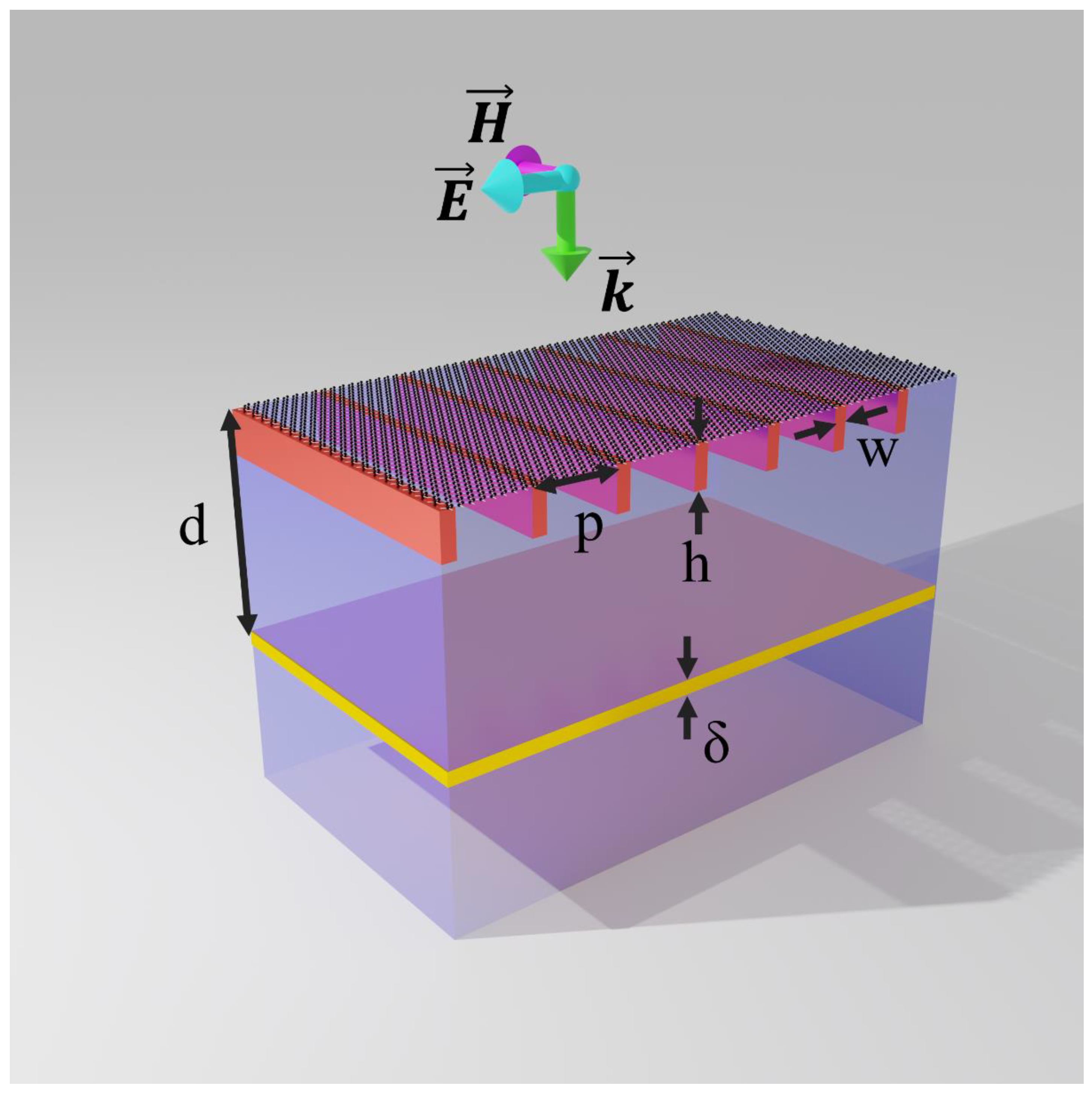
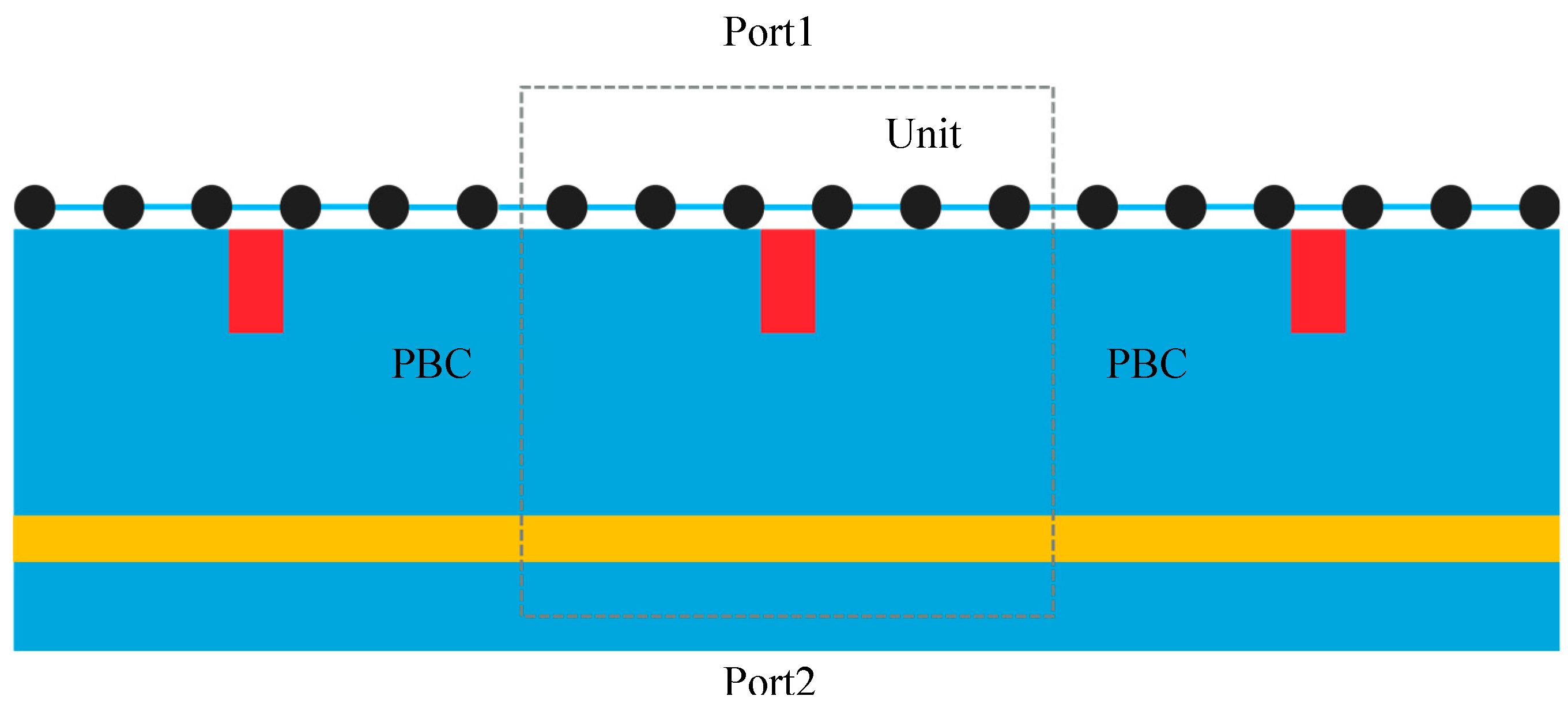
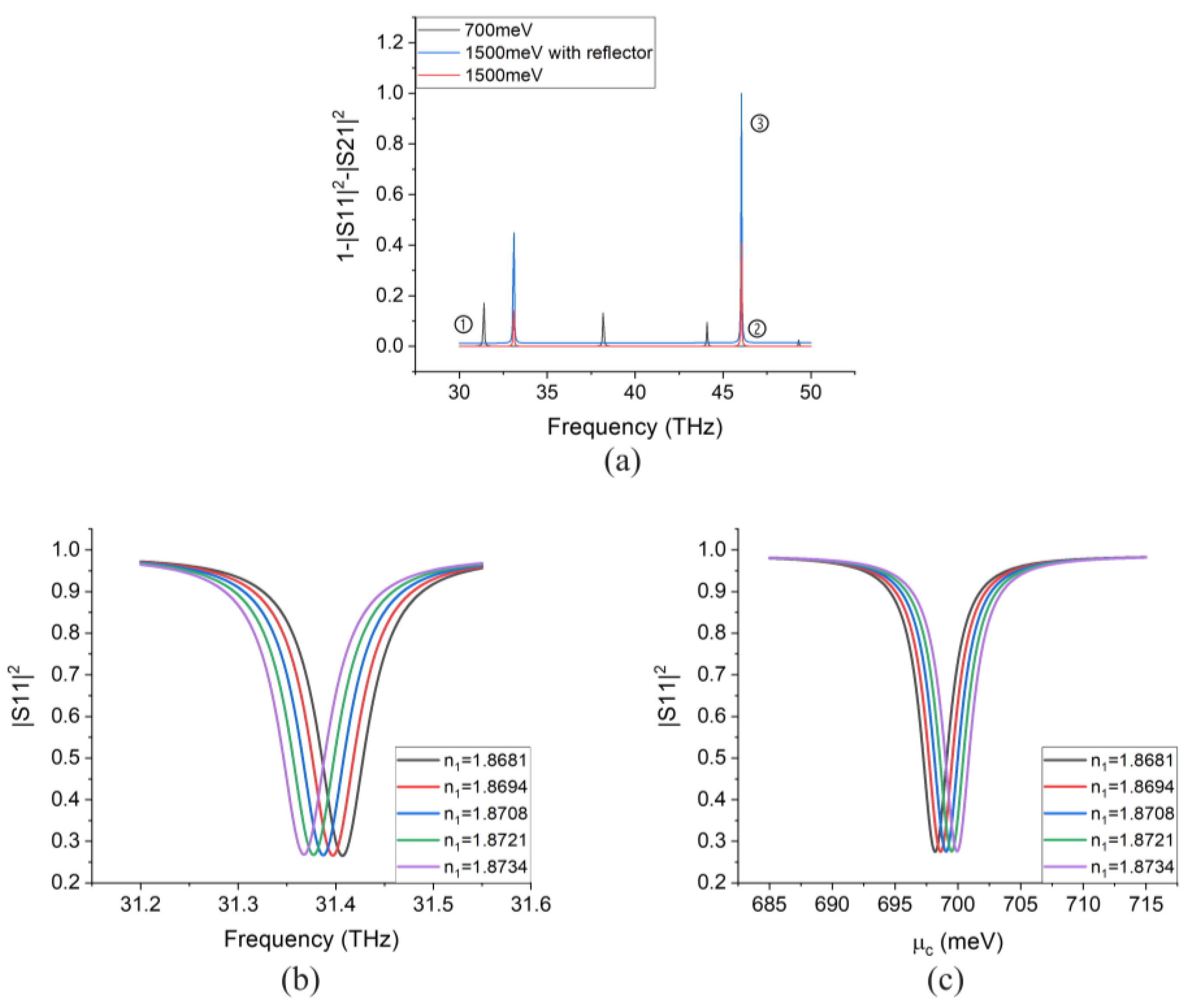
2.1. Sensing Mechanism and Sensor Design
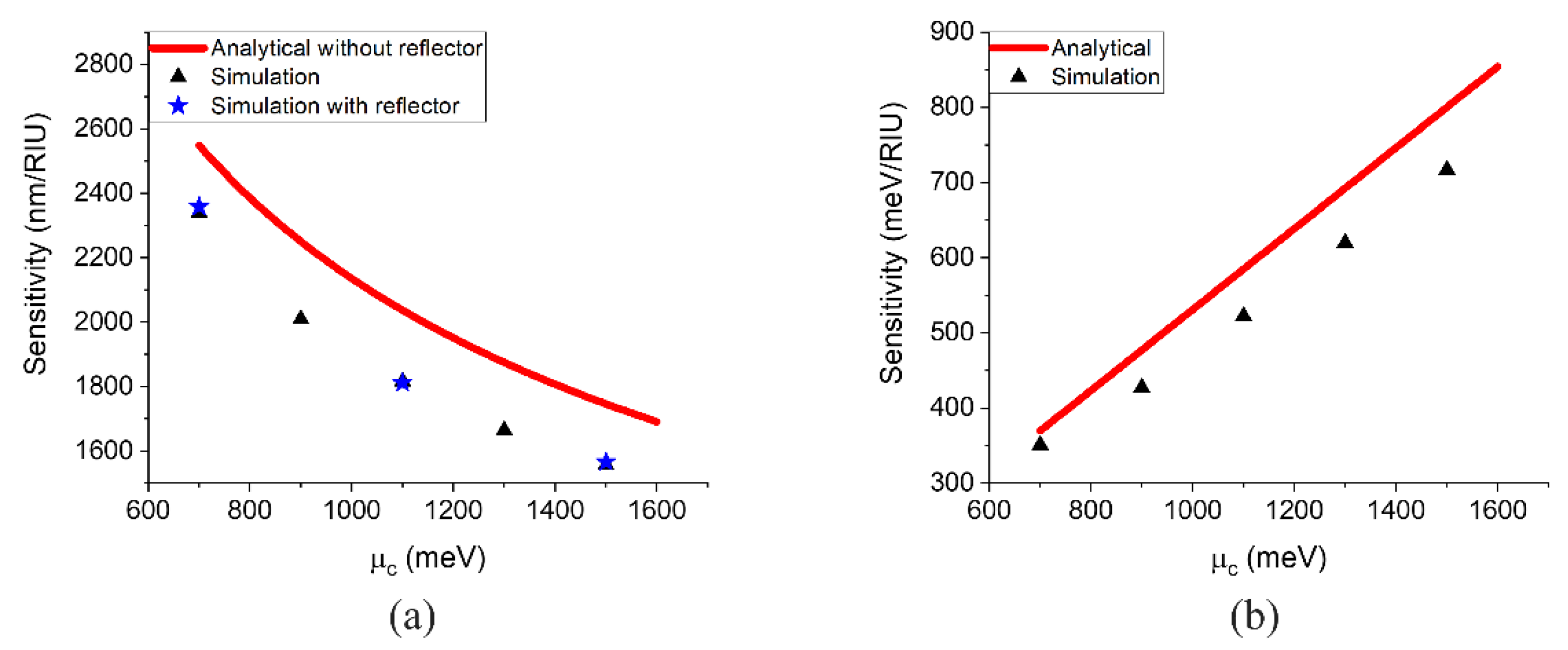
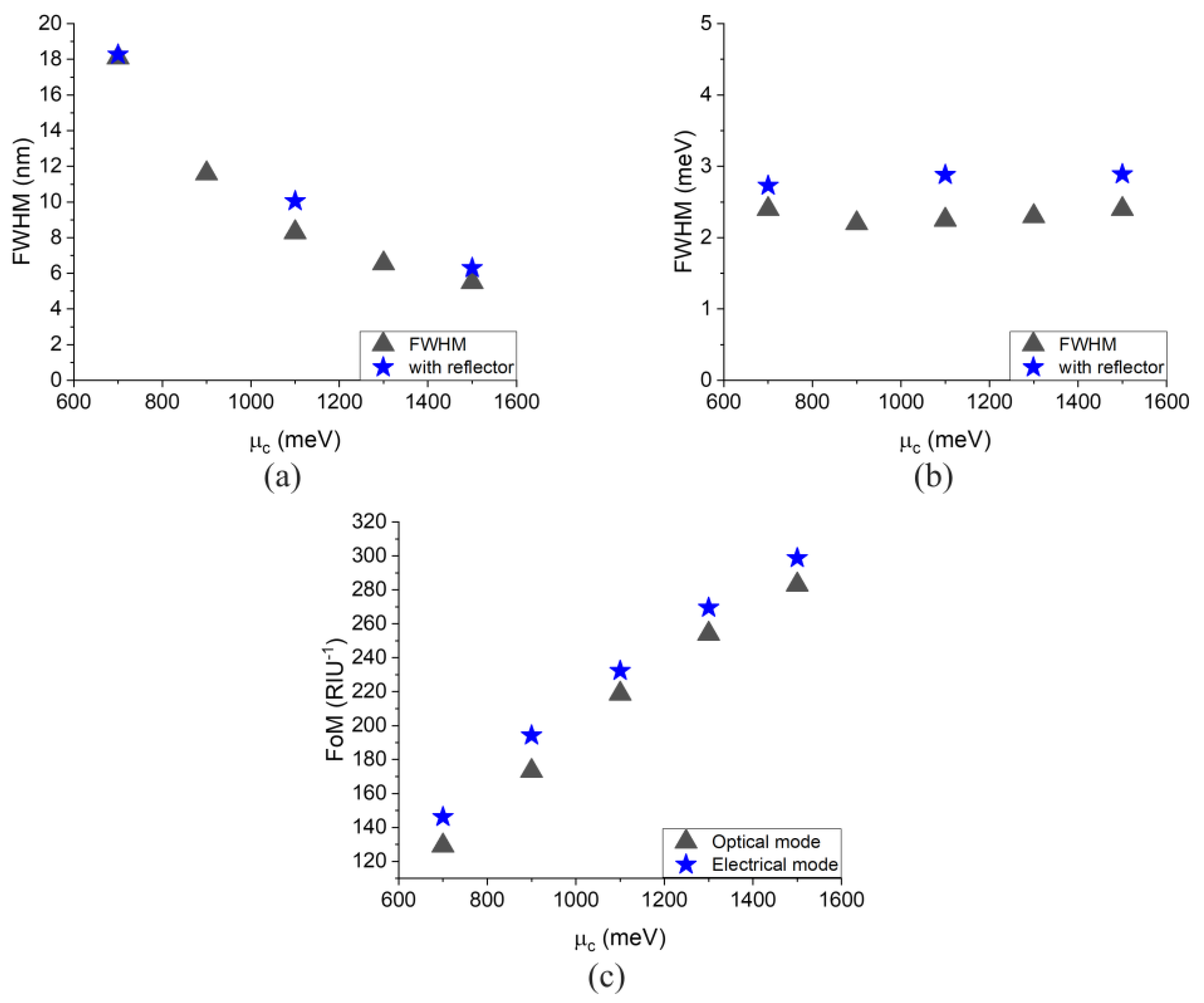
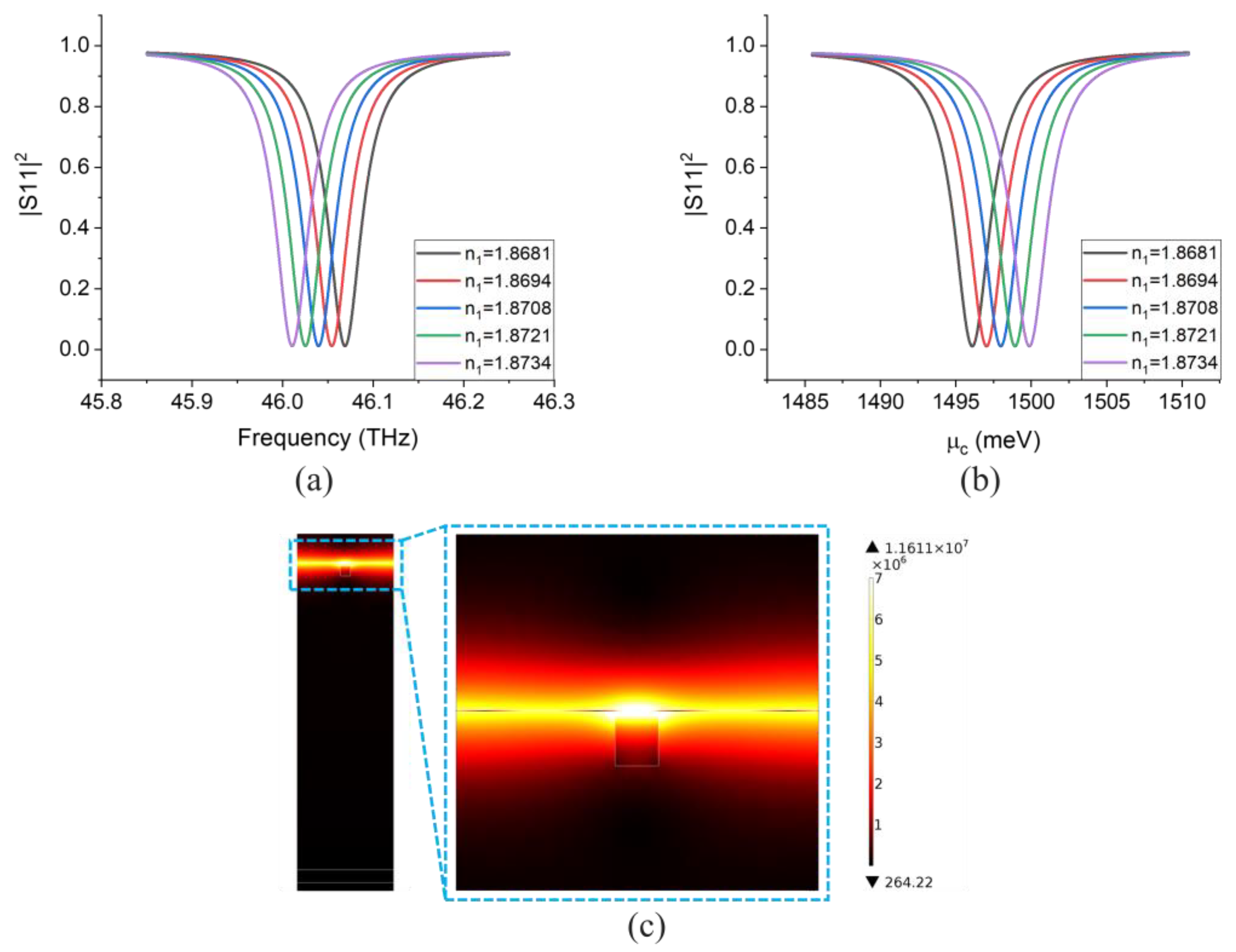
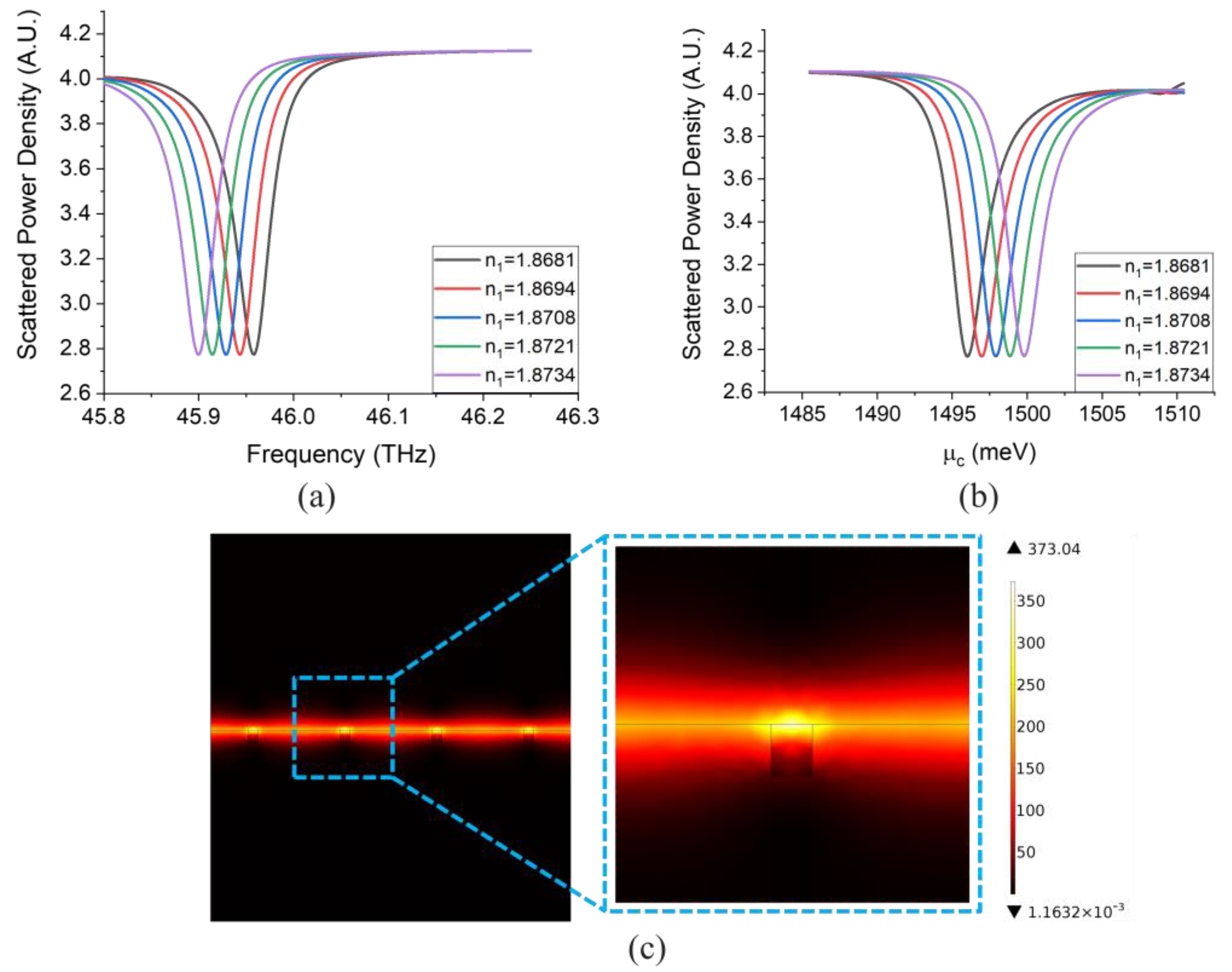
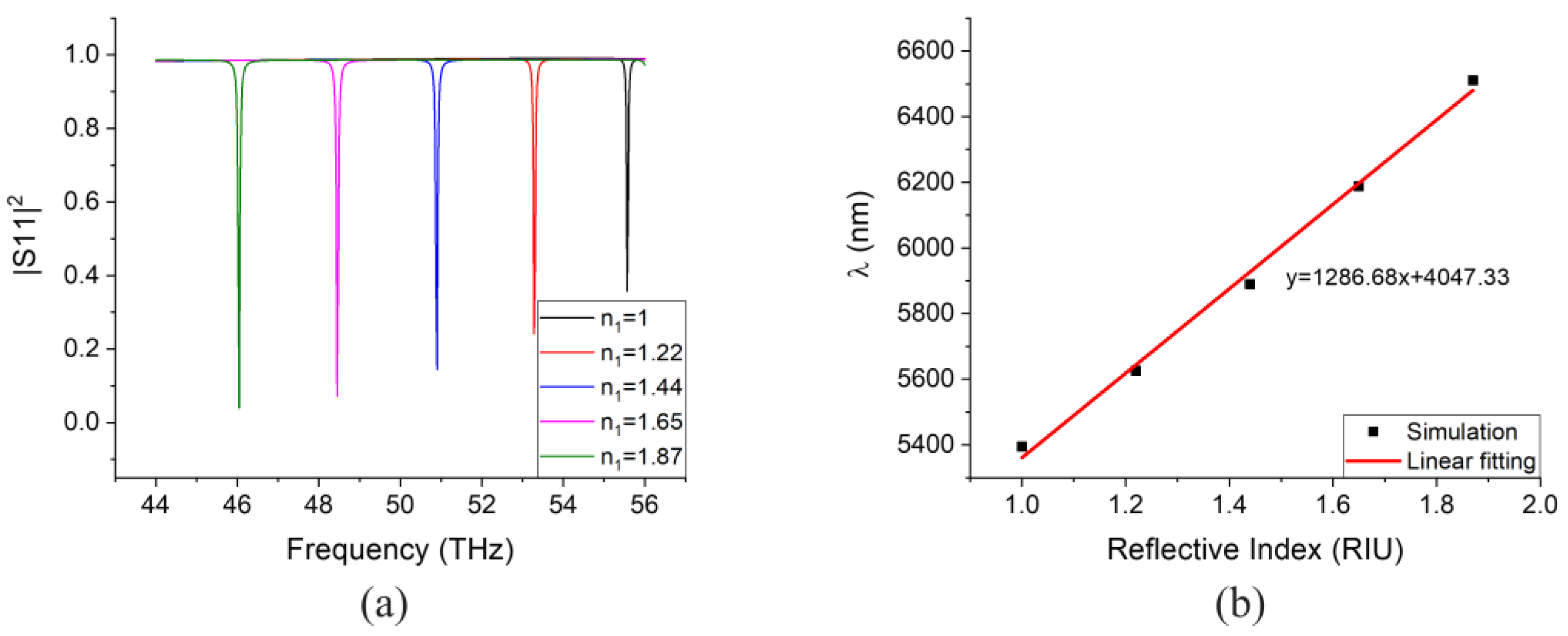
2.2. Performance Analysis and Simulation Results
3. Discussion
3.1. Geometrical Optimization
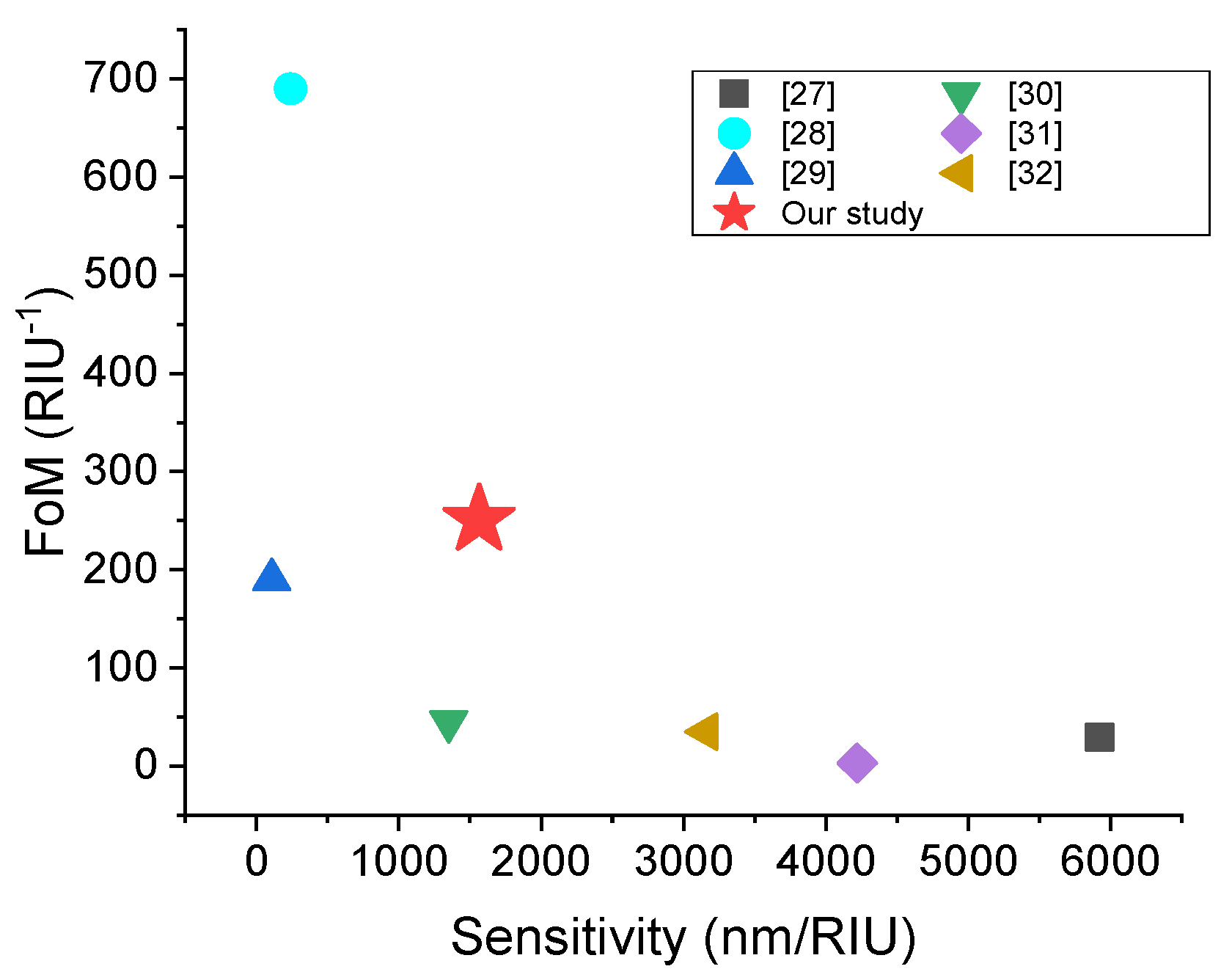
3.2. Performance Comparison
3.3. Mobility, Gating, and Advantages of the Sensor
- (1)
- Spectrometer-free: The design does not require the use of a spectrometer, which relaxes the design and reduces its complexity, via the electrical mode of operation.
- (2)
- Higher performance: The GSPR sensor possesses simultaneously a high FoM and sensitivity. This equips the proposed design with a higher precision in detection, in the terahertz range.
- (3)
- Geometry robustness: The operation is insensitive to the height of the grating, which gives more flexibility in the design and robustness regarding the imperfections in nanofabrication.
- (4)
- Dynamic tunability: The spectral location of the EM absorption peak can be tuned by changing . This shows that the same device can be optimized for different frequency ranges (with reconfigurability, by use of electrostatic biasing).
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Dispersion Relation and Graphene Conductivity
Appendix B. Device Performance Under Finite Band Excitation
| Mode of Operation | Sigma (THz) | FoM (RIU−1) | Sensitivity |
|---|---|---|---|
| Optical | 0.02 | 149.7 | 1557.1 nm/RIU |
| 0.01 | 204.8 | 1556.6 nm/RIU | |
| Electrical | 0.02 | 148.9 | 714.5 meV/RIU |
| 0.01 | 204.1 | 714.4 meV/RIU |
References
- Jing, J.-Y.; Li, S.-Y.; Wang, X.-Z.; Zhu, Q.; Meng, F.-L.; Wang, Q. A D-type fiber based symmetrical long-range surface plasmon resonance sensor with high quality factor. Measurement 2019, 140, 395. [Google Scholar] [CrossRef]
- Chen, C.; Hou, X.; Si, J. Design of a multi-analyte resonant photonic platform for label-free biosensing. Nanotechnology 2019, 30, 275501. [Google Scholar] [CrossRef]
- Lee, K.L.; Hsu, H.Y.; You, M.L.; Chang, C.C.; Pan, M.Y.; Shi, X.; Ueno, K.; Misawa, H.; Wei, P.K. Highly Sensitive Aluminum-Based Biosensors using Tailorable Fano Resonances in Capped Nanostructures. Sci. Rep. 2017, 7, 44104. [Google Scholar] [CrossRef] [PubMed]
- Liu, D.; Fu, W.; Shao, J.; Wang, J.; Zhang, Q.; Han, B.; Teng, D. Plasmon-Induced Transparency and Refractive Index Sensing Based on a Trapezoid Cavity Coupled with a Hexagonal Resonator. Plasmonics 2018, 14, 663. [Google Scholar] [CrossRef]
- Zhang, J.; Li, J.; Tang, S.; Fang, Y.; Wang, J.; Huang, G.; Liu, R.; Zheng, L.; Cui, X.; Mei, Y. Whispering-gallery nanocavity plasmon-enhanced Raman spectroscopy. Sci. Rep. 2015, 5, 15012. [Google Scholar] [CrossRef] [PubMed]
- Baaske, M.D.; Vollmer, F. Optical observation of single atomic ions interacting with plasmonic nanorods in aqueous solution. Nat. Photonics 2016, 10, 733. [Google Scholar] [CrossRef]
- Hackett, L.P.; Ameen, A.; Li, W.; Dar, F.K.; Goddard, L.L.; Liu, G.L. Spectrometer-Free Plasmonic Biosensing with Metal-Insulator-Metal Nanocup Arrays. ACS Sens. 2018, 3, 290. [Google Scholar] [CrossRef]
- Lin, F.C.; See, K.M.; Ouyang, L.; Huang, Y.X.; Chen, Y.J.; Popp, J.; Huang, J.S. Designable Spectrometer-Free Index Sensing Using Plasmonic Doppler Gratings. Anal. Chem. 2019, 91, 9382. [Google Scholar] [CrossRef]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Katsnelson, M.I.; Grigorieva, I.V.; Dubonos, S.V.; Firsov, A.A. Two-dimensional gas of massless Dirac fermions in graphene. Nature 2005, 438, 197. [Google Scholar] [CrossRef]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric Field Effect in Atomically Thin Carbon Films. Science 2004, 306, 666. [Google Scholar] [CrossRef]
- Chen, P.-Y.; Argyropoulos, C.; Farhat, M.; Gomez-Diaz, J.S. Flatland plasmonics and nanophotonics based on graphene and beyond. Nanophotonics 2017, 6, 1239. [Google Scholar] [CrossRef]
- Grigorenko, A.N.; Polini, M.; Novoselov, K.S. Graphene plasmonics. Nat. Photonics 2012, 6, 749. [Google Scholar] [CrossRef]
- Koppens, F.H.; Chang, D.E.; de Abajo, F.J.G. Graphene plasmonics: a platform for strong light-matter interactions. Nano Lett. 2011, 11, 3370. [Google Scholar] [CrossRef]
- Thongrattanasiri, S.; Koppens, F.H.; de Abajo, F.J.G. Complete optical absorption in periodically patterned graphene. Phys. Rev. Lett. 2012, 108, 047401. [Google Scholar] [CrossRef]
- Amin, M.; Farhat, M.; Bağcı, H. An ultra-broadband multilayered graphene absorber. Opt. Express 2013, 21, 29938. [Google Scholar] [CrossRef]
- Perrakis, G.; Tsilipakos, O.; Kenanakis, G.; Kafesaki, M.; Soukoulis, C.M.; Economou, E.N. Perfect optical absorption with nanostructured metal films: design and experimental demonstration. Opt. Express 2019, 27, 6842. [Google Scholar] [CrossRef]
- Chen, P.Y.; Farhat, M.; Bagci, H. Graphene metascreen for designing compact infrared absorbers with enhanced bandwidth. Nanotechnology 2015, 26, 164002. [Google Scholar] [CrossRef]
- Cen, C.; Chen, Z.; Xu, D.; Jiang, L.; Chen, X.; Yi, Z.; Wu, P.; Li, G.; Yi, Y. High Quality Factor, High Sensitivity Metamaterial Graphene-Perfect Absorber Based on Critical Coupling Theory and Impedance Matching. Nanomaterials 2020, 10, 95. [Google Scholar] [CrossRef]
- Christensen, J.; Manjavacas, A.; Thongrattanasiri, S.; Koppens, F.H.L.; de Abajo, F.J.G. Graphene Plasmon Waveguiding and Hybridization in Individual and Paired Nanoribbons. ACS Nano 2012, 6, 431. [Google Scholar] [CrossRef]
- Gan, X.; Mak, K.F.; Gao, Y.; You, Y.; Hatami, F.; Hone, J.; Heinz, T.F.; Englund, D. Strong Enhancement of Light–Matter Interaction in Graphene Coupled to a Photonic Crystal Nanocavity. Nano Lett. 2012, 12, 5626. [Google Scholar] [CrossRef]
- Lee, S.H.; Choi, M.; Kim, T.T.; Lee, S.; Liu, M.; Yin, X.; Choi, H.K.; Lee, S.S.; Choi, C.G.; Choi, S.Y.; et al. Switching terahertz waves with gate-controlled active graphene. Nat. Mater. 2012, 11, 936. [Google Scholar] [CrossRef]
- Vakil, A.; Engheta, N. Transformation Optics Using Graphene. Science 2011, 332, 1291. [Google Scholar] [CrossRef] [PubMed]
- Rodrigo, D.; Limaj, O.; Janner, D.; Etezadi, D.; de Abajo, F.J.G.; Pruneri, V.; Altug, H. Mid-infrared plasmonic biosensing with graphene. Science 2015, 349, 165. [Google Scholar] [CrossRef]
- Verma, R.; Gupta, B.D.; Jha, R. Sensitivity enhancement of a surface plasmon resonance based biomolecules sensor using graphene and silicon layers. Sens. Actuators B Chem. 2011, 160, 623. [Google Scholar] [CrossRef]
- Wang, P.; Liang, O.; Zhang, W.; Schroeder, T.; Xie, Y.H. Ultra-sensitive graphene-plasmonic hybrid platform for label-free detection. Adv. Mater. 2013, 25, 4918. [Google Scholar] [CrossRef] [PubMed]
- Marini, A.; Silveiro, I.; de Abajo, F.J.G. Molecular Sensing with Tunable Graphene Plasmons. ACS Photonics 2015, 2, 876. [Google Scholar] [CrossRef]
- Hanson, G.W. Dyadic Green’s Functions for an Anisotropic, Non-Local Model of Biased Graphene. IEEE Trans. Antennas Propag. 2008, 56, 747. [Google Scholar] [CrossRef]
- Maier, S.A. Plasmonics: Fundamentals and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Bludov, Y.V.; Ferreira, A.; Peres, N.M.R.; Vasilevskiy, M.I. A primer on surface plasmon-polaritons in graphene. Int. J. Mod. Phys. B 2013, 27, 1341001. [Google Scholar] [CrossRef]
- de La Fuente, J. Properties of Graphene. Available online: https://www.graphenea.com/pages/graphene-properties#.XeJaNOgzY2w (accessed on 10 January 2020).
- Ordal, M.A.; Long, L.L.; Bell, R.J.; Bell, S.E.; Bell, R.R.; Alexander, R.W.; Ward, C.A. Optical properties of the metals Al, Co, Cu, Au, Fe, Pb, Ni, Pd, Pt, Ag, Ti, and W in the infrared and far infrared. Appl. Opt. 1983, 22, 1099. [Google Scholar] [CrossRef]
- White, I.M.; Fan, X. On the performance quantification of resonant refractive index sensors. Opt. Express 2008, 16, 1020. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, Z.; Xu, D.; Yi, Z.; Chen, X.; Chen, J.; Tang, Y.; Wu, P.; Li, G.; Yi, Y. Triple-band perfect metamaterial absorber with good operating angle polarization tolerance based on split ring arrays. Results Phys. 2020, 16, 102951. [Google Scholar] [CrossRef]
- Jiang, X.; Wang, Q. Refractive index sensitivity enhancement of optical fiber SPR sensor utilizing layer of MWCNT/PtNPs composite. Opt. Fiber Technol. 2019, 51, 118. [Google Scholar] [CrossRef]
- Qian, L.; Wang, K.; Zhu, W.; Han, C.; Yan, C. Enhanced sensing ability in a single-layer guided-mode resonant optical biosensor with deep grating. Opt. Commun. 2019, 452, 273. [Google Scholar] [CrossRef]
- Yildirim, D.U.; Ghobadi, A.; Soydan, M.C.; Gokbayrak, M.; Toprak, A.; Butun, B.; Ozbay, E. Colorimetric and Near-Absolute Polarization-Insensitive Refractive-Index Sensing in All-Dielectric Guided-Mode Resonance Based Metasurface. J. Phys. Chem. C 2019, 123, 19125. [Google Scholar] [CrossRef]
- Azarian, A.; Sheikhy, L. Dark Plasmon with a High Figure of Merit in a Single Au Triangular Nano Frame. J. Clust. Sci. 2019, 30, 1633. [Google Scholar] [CrossRef]
- Tavousi, A.; Mansouri-Birjandi, M.A.; Janfaza, M. Graphene Nanoribbon Assisted Refractometer Based Biosensor for Mid-Infrared Label-Free Analysis. Plasmonics 2019, 14, 1207. [Google Scholar] [CrossRef]
- Tabassum, R.; Kant, R. Mechanistic understanding of excitation of surface plasmons in a fiber-optic SPR sensor utilizing Al/Cu bimetallic configuration: mode field approach. Phys. Scr. 2019, 94, 125012. [Google Scholar] [CrossRef]
- Chen, J.H.; Jang, C.; Xiao, S.; Ishigami, M.; Fuhrer, M.S. Intrinsic and extrinsic performance limits of graphene devices on SiO 2. Nat. Nanotechnol. 2008, 3, 206. [Google Scholar] [CrossRef]
- Akturk, A.; Goldsman, N. Electron transport and full-band electron-phonon interactions in graphene. J. Appl. Phys. 2008, 103, 053702. [Google Scholar] [CrossRef]
- Geim, A.K.; Novoselov, K.S. The rise of graphene. In Nanoscience and Technology: A Collection of Reviews from Nature Journals; World Scientific: Singapore, 2010; p. 11. [Google Scholar]
- Fang, Z.; Thongrattanasiri, S.; Schlather, A.; Liu, Z.; Ma, L.; Wang, Y.; Ajayan, P.M.; Nordlander, P.; Halas, N.J.; García de Abajo, F.J. Gated Tunability and Hybridization of Localized Plasmons in Nanostructured Graphene. ACS Nano 2013, 7, 2388. [Google Scholar] [CrossRef]
- Hinkov, B.; Hayden, J.; Szedlak, R.; Martin-Mateos, P.; Jerez, B.; Acedo, P.; Strasser, G.; Lendl, B. High frequency modulation and (quasi) single-sideband emission of mid-infrared ring and ridge quantum cascade lasers. Opt. Express 2019, 27, 14716. [Google Scholar] [CrossRef]
- Peng, Y.; Wei, X.; Nie, Z.; Luo, X.; Peng, J.; Wang, Y.; Shen, D. High-power, narrow-bandwidth mid-infrared PPMgLN optical parametric oscillator with a volume Bragg grating. Opt. Express 2015, 23, 30827. [Google Scholar] [CrossRef]
| Geometry Dimensions | Value (nm) |
|---|---|
| p | 384.8 |
| w | 40 |
| h | 50 |
| 50 | |
| d | 1244.4 |
| Grating Width (nm) | FWHM (nm) | Sensitivity (nm/RIU) |
|---|---|---|
| 40 | 6.3 | 1566.03 |
| 26 | 4.5 | 1603.8 |
| 18 | 3 | 1641.5 |
| Grating Height (nm) | FWHM (nm) | Sensitivity (nm/RIU) |
|---|---|---|
| 50 | 6.3 | 1566.03 |
| 25 | 6.25 | 1566.04 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Farhat, M.; Salama, K.N. Spectrometer-Free Graphene Plasmonics Based Refractive Index Sensor. Sensors 2020, 20, 2347. https://doi.org/10.3390/s20082347
Zhang L, Farhat M, Salama KN. Spectrometer-Free Graphene Plasmonics Based Refractive Index Sensor. Sensors. 2020; 20(8):2347. https://doi.org/10.3390/s20082347
Chicago/Turabian StyleZhang, Li, Mohamed Farhat, and Khaled Nabil Salama. 2020. "Spectrometer-Free Graphene Plasmonics Based Refractive Index Sensor" Sensors 20, no. 8: 2347. https://doi.org/10.3390/s20082347
APA StyleZhang, L., Farhat, M., & Salama, K. N. (2020). Spectrometer-Free Graphene Plasmonics Based Refractive Index Sensor. Sensors, 20(8), 2347. https://doi.org/10.3390/s20082347






