Extracting Common Mode Errors of Regional GNSS Position Time Series in the Presence of Missing Data by Variational Bayesian Principal Component Analysis
Abstract
1. Introduction
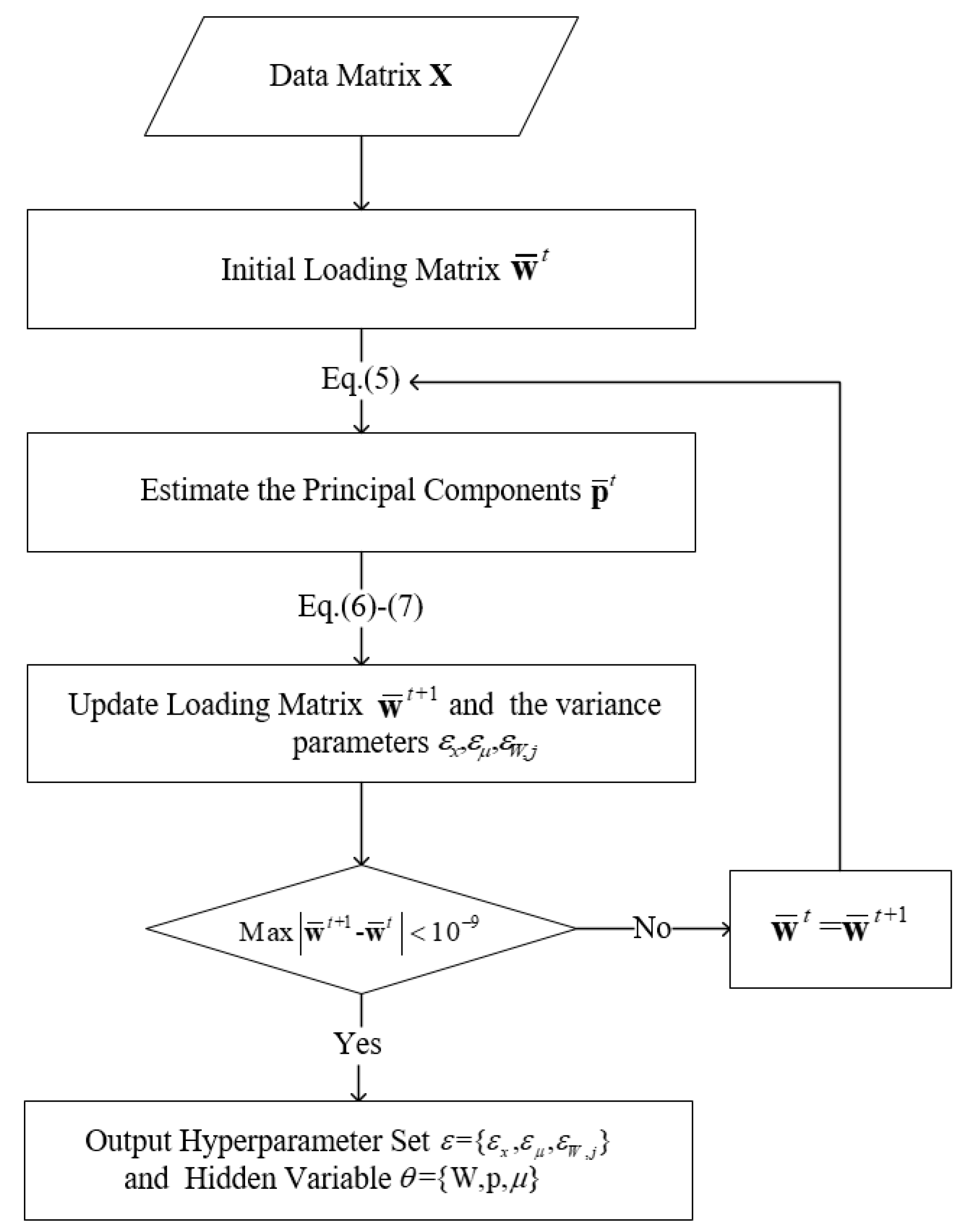
2. Methodology
Variational Bayesian PCA
3. Experiment and Analysis
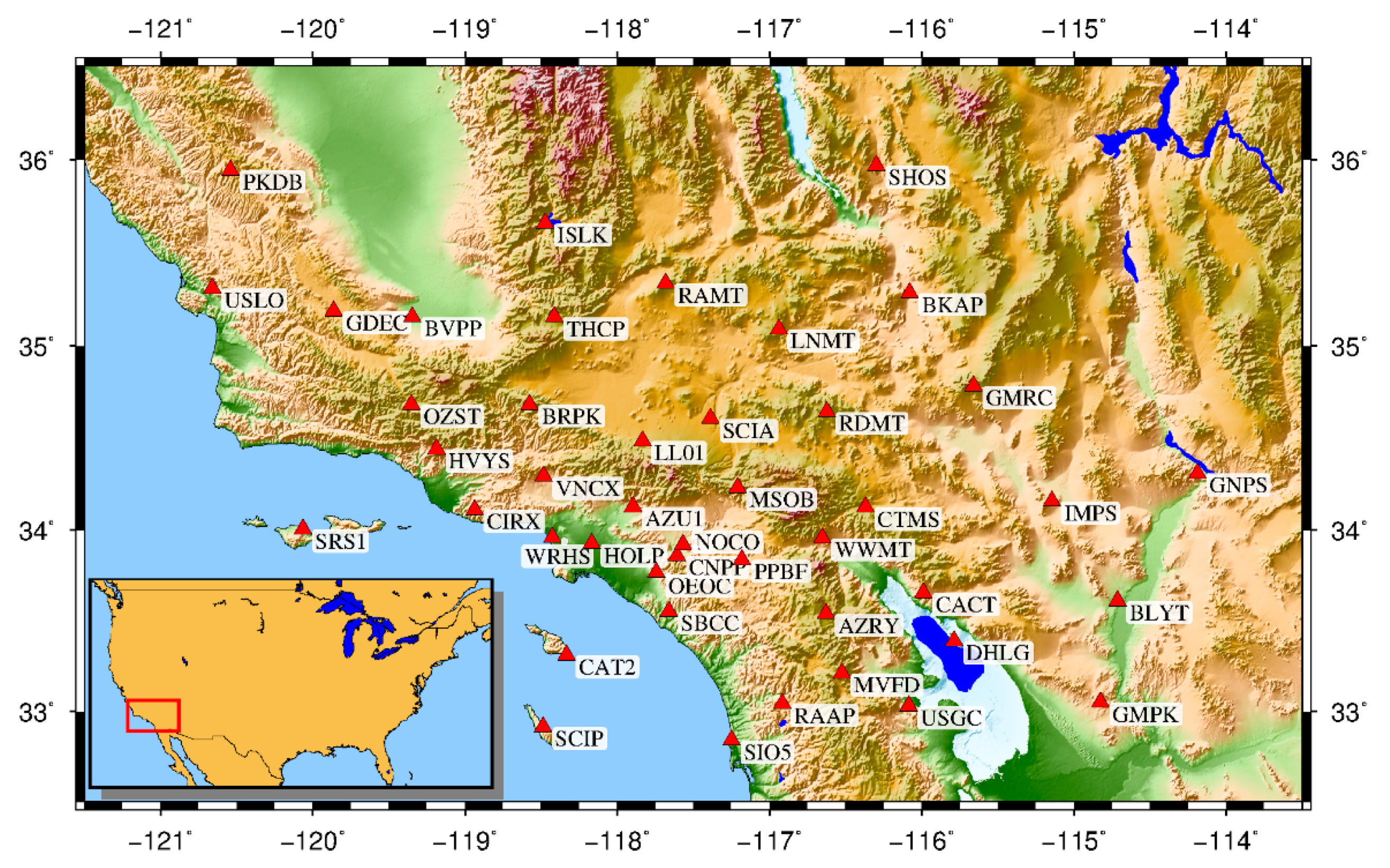
3.1. GNSS Data Processing
3.2. Comparison of CME Relative Errors from Different Methods
3.3. The Performance of Missing Value Estimation
4. Results and Discussion
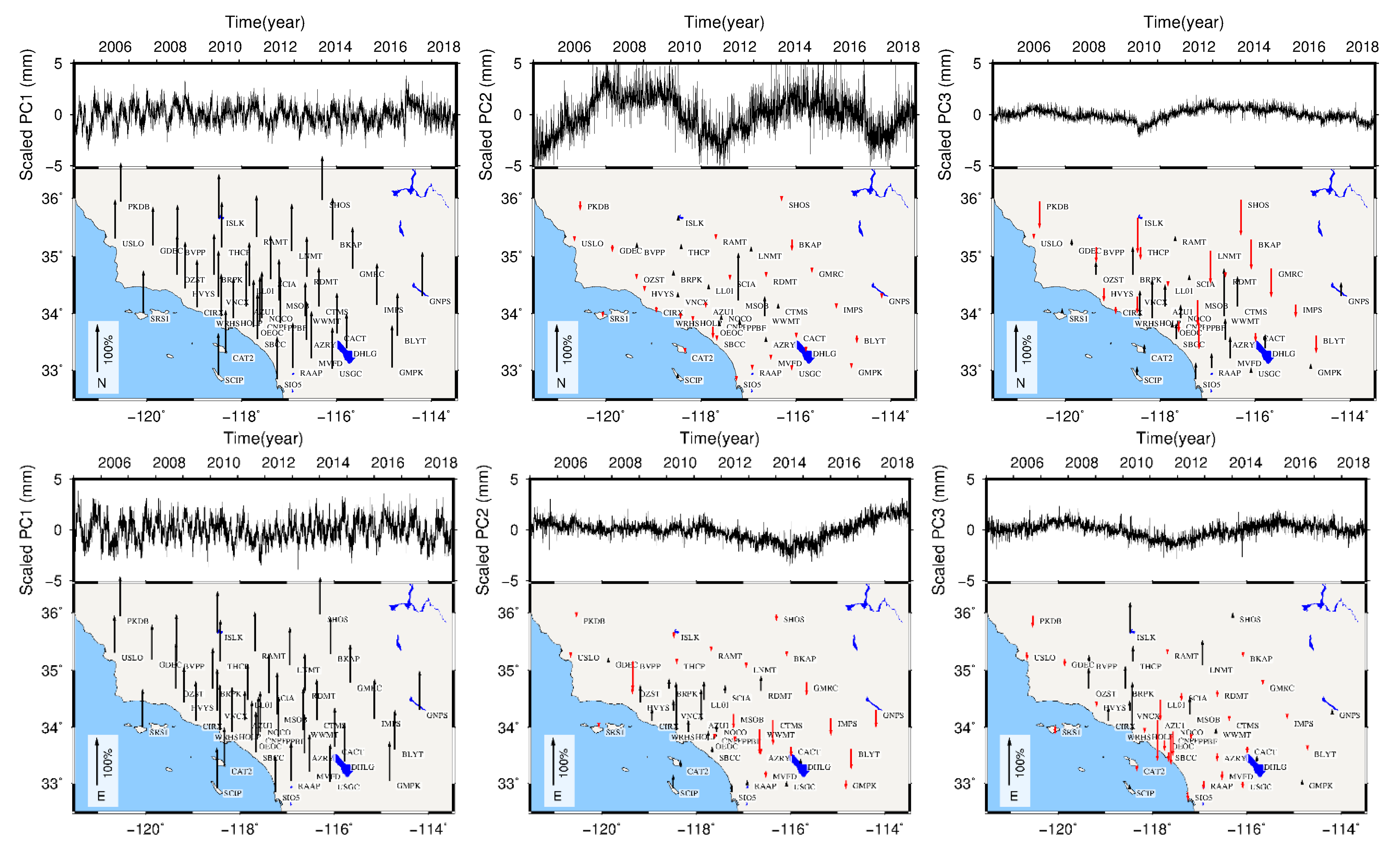
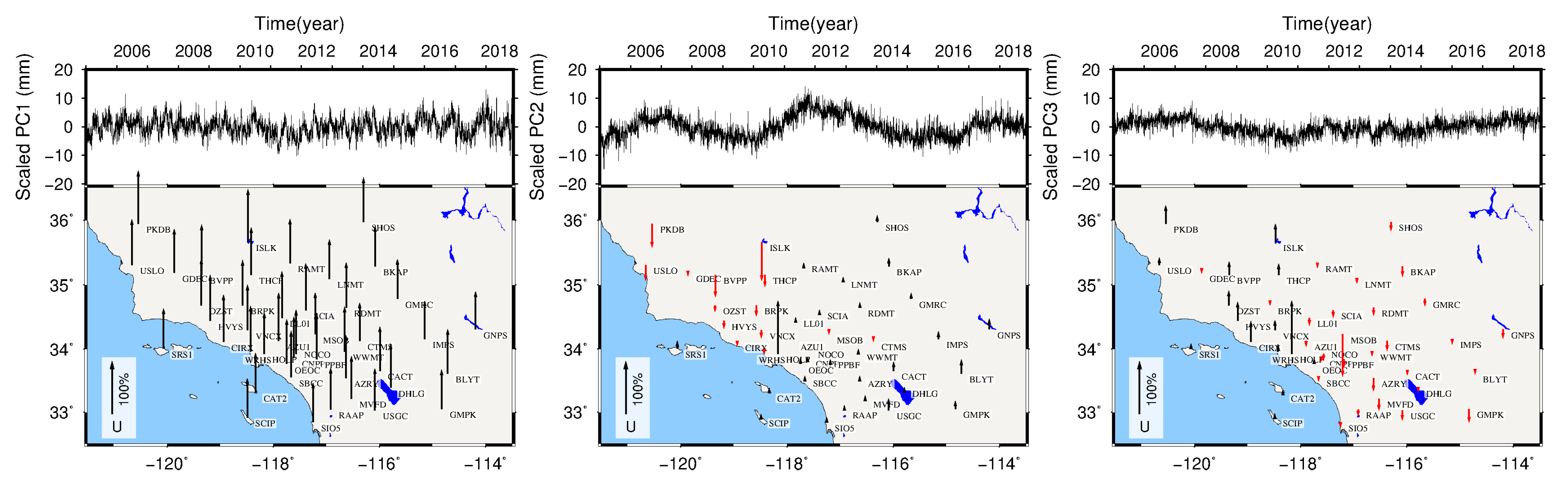
4.1. Extraction of CME Using the VBPCA Method
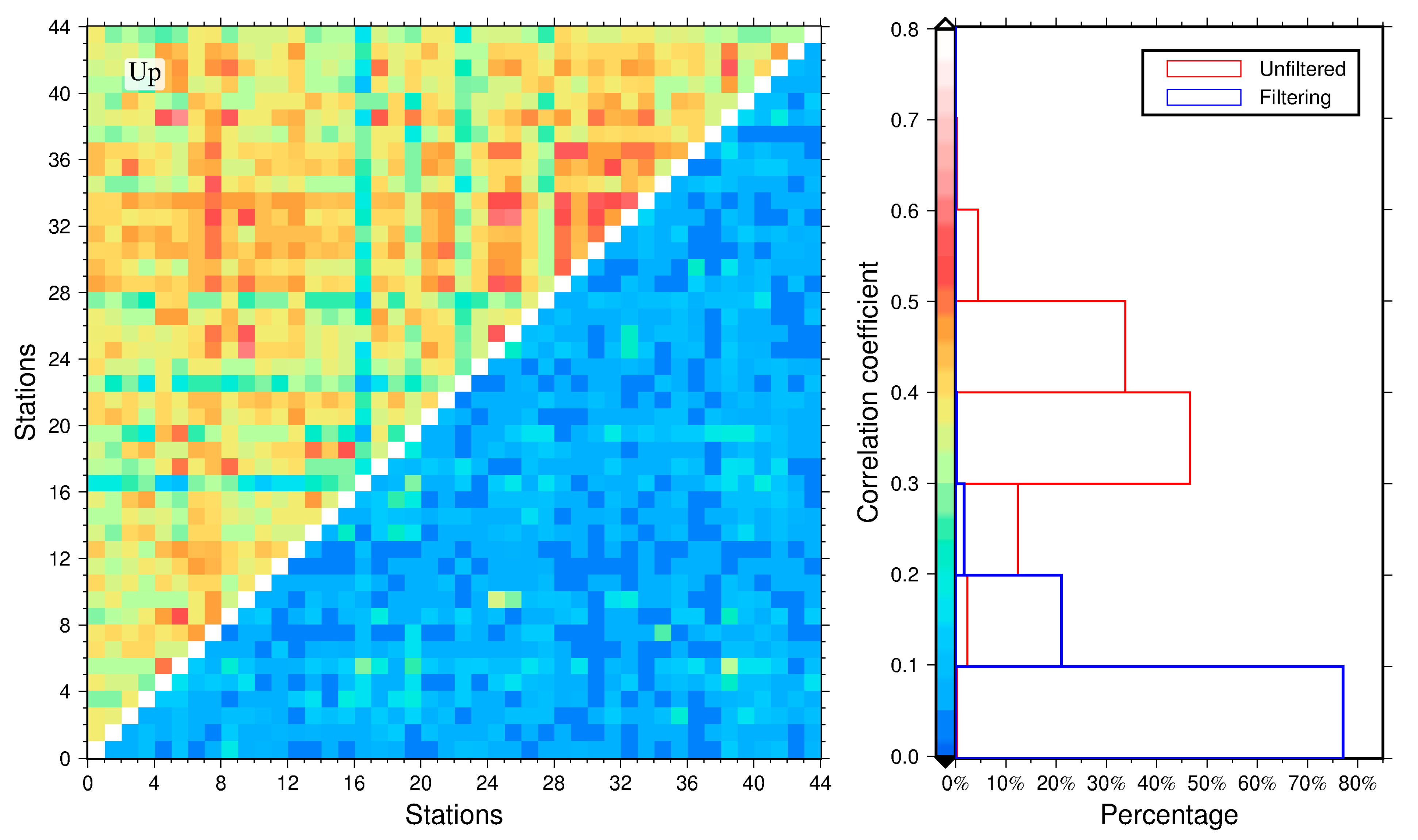
4.2. Interstation Correlation Analysis
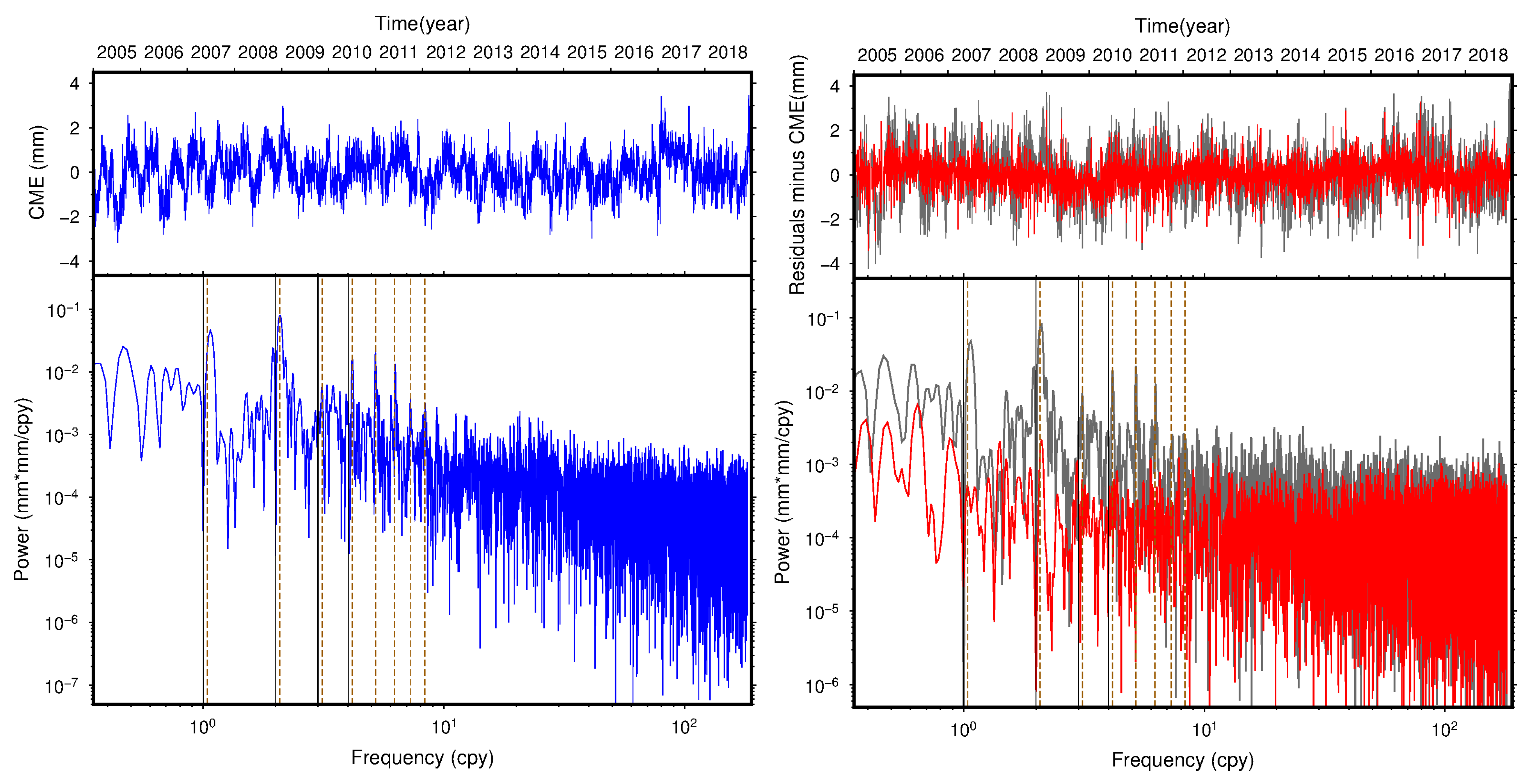
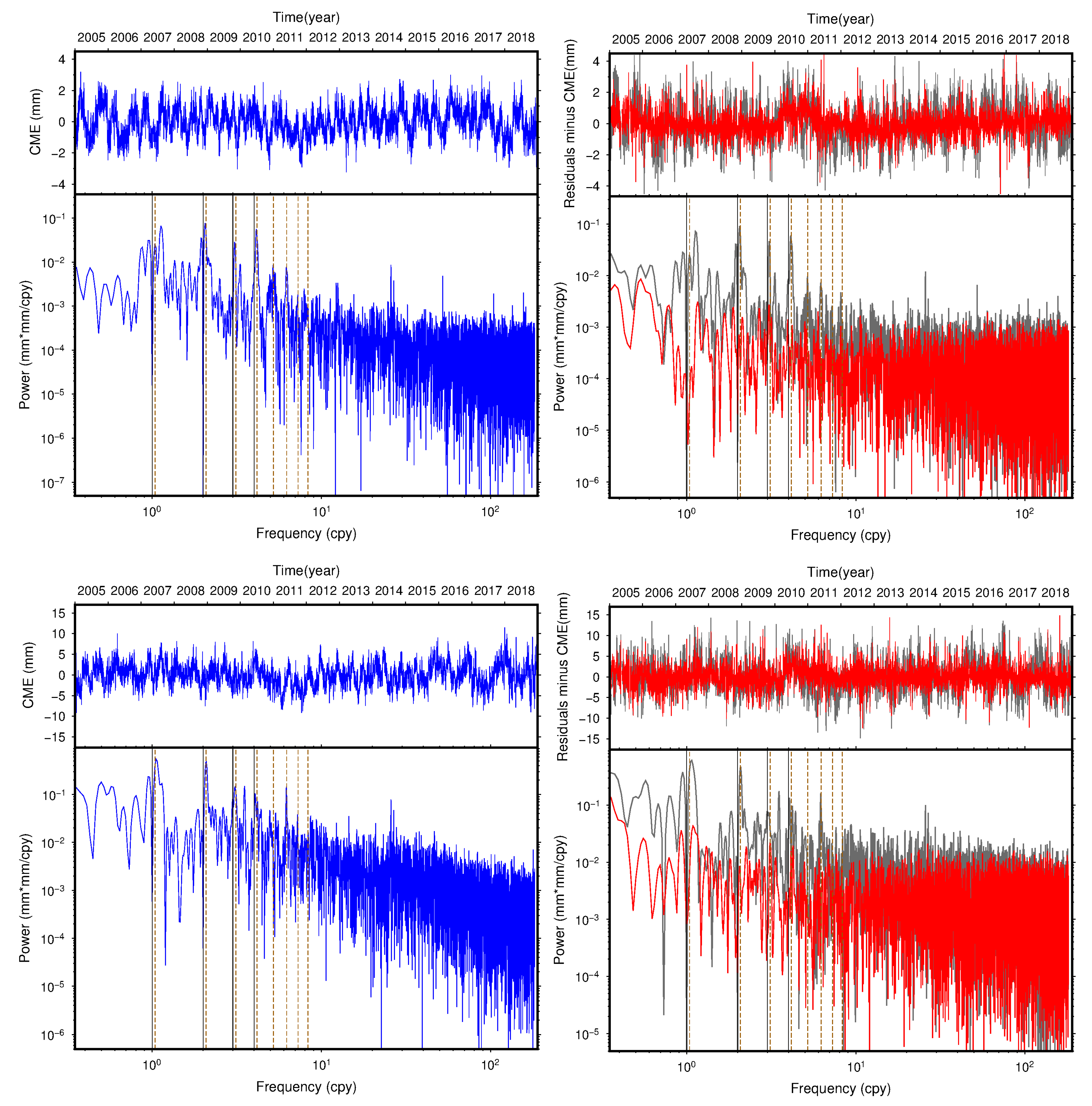
4.3. Time Series Analysis
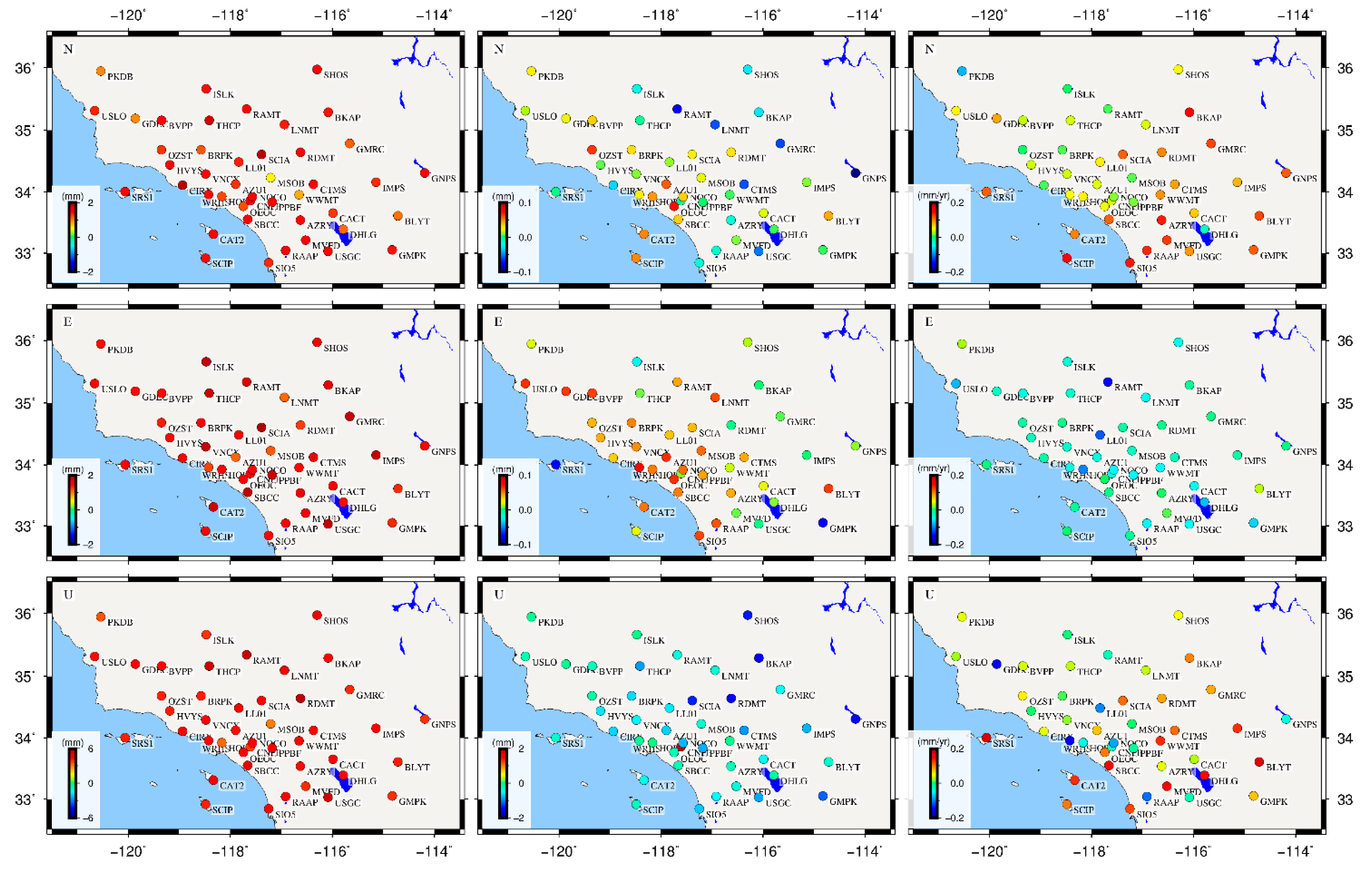
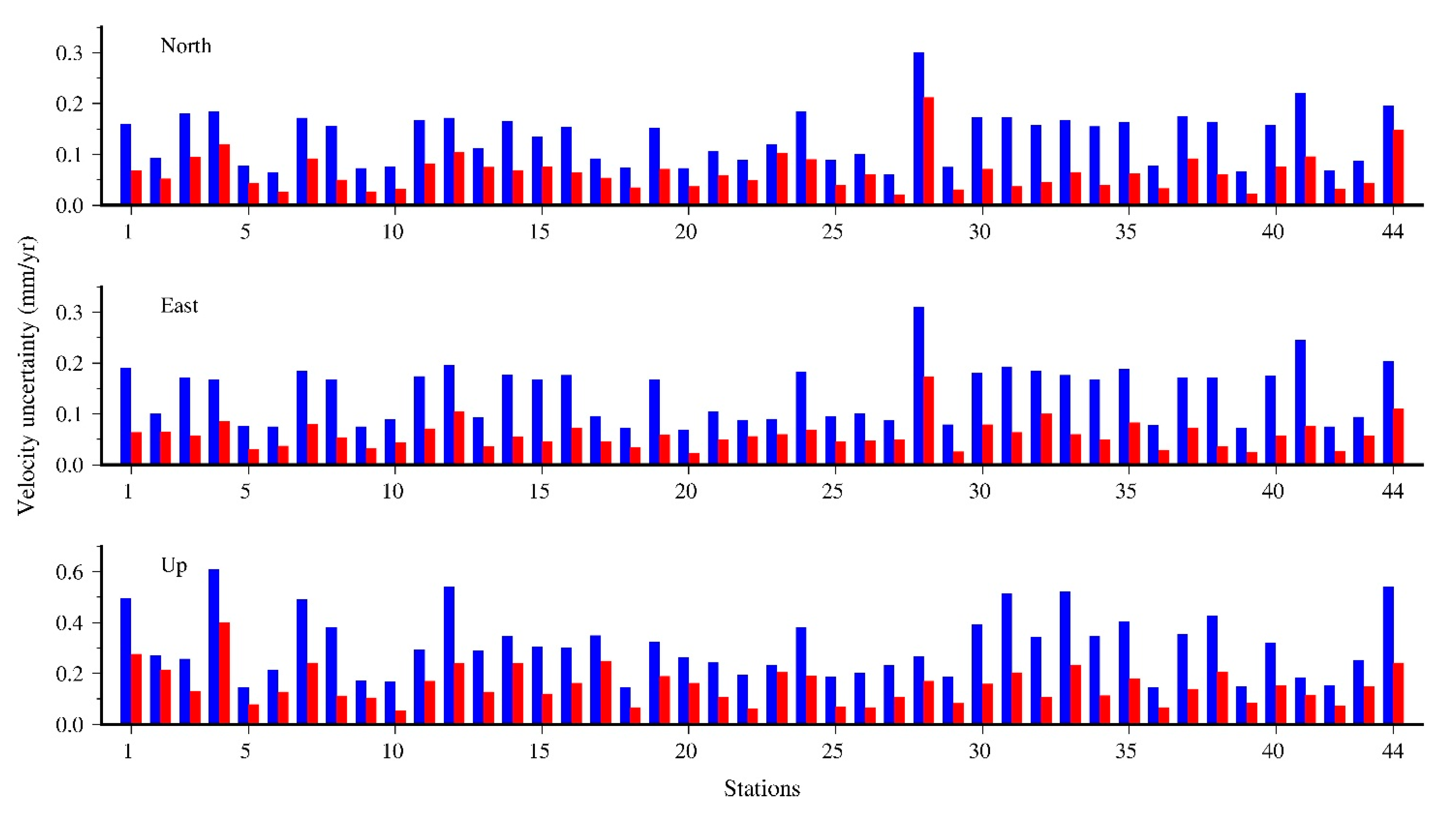
4.4. Effect of CME on Noise Amplitude and Velocity Estimation
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| CME | common mode error |
| GNSS | global navigation satellite systems |
| VBPCA | variational Bayesian principal component analysis |
| PC | principal component |
| NEU | north, east, and up |
| RMS | root mean square |
| WN | white noise |
| PLN | power-law noises |
| MLE | maximum likelihood estimation |
| PCA | principal component analysis |
| IPCA | improved principal component analysis |
| PPCA | probabilistic principal component analysis |
| VBPCA | variational Bayesian principal component analysis |
| MSSA | multi-channel singular spectrum analysis |
| ICA | independent component analysis |
| SOPAC | SCRIPPS ORBIT AND PERMANENT ARRAY CENTER |
| IQR | interquartile range |
| ARD | automatic relevance determination |
| RegEM | regularized expectation-maximization |
| NRMSE | normalized root mean squared error |
| cpy | cycle per year |
| the number of epochs | |
| the number of GNSS stations | |
| the number of principal components | |
| data matrix | |
| j-th column of | |
| loading matrix | |
| j-th column of the loading matrix | |
| the column vector corresponding to the th row of | |
| posterior mean of | |
| posterior covariance of | |
| the -th element on the diagonal of | |
| matrix of principal components | |
| j-th column of | |
| posterior mean of | |
| posterior covariance of | |
| the bias vector | |
| posterior mean of | |
| posterior variance of | |
| j-th out of n noise vector | |
| the noise variance | |
| priori variance of | |
| priori variance of | |
| the hyperparameter set () | |
| the Identity Matrices | |
| the hidden variable () | |
| C | cost function to be minimized |
| the set of indices for which is observed | |
| the set of indices j for which is observed | |
| the number of elements in | |
| Gaussian normal probability density function over variable with mean and covariance |
References
- Rebischung, P.; Altamimi, Z.; Springer, T. A collinearity diagnosis of the GNSS geocenter determination. J. Geod. 2014, 88, 65–85. [Google Scholar] [CrossRef]
- Männel, B.; Rothacher, M. Geocenter variations derived from a combined processing of LEO- and ground-based GPS observations. J. Geod. 2017, 91, 933–944. [Google Scholar] [CrossRef]
- Van Dam, T.; Wahr, J.; Lavallée, D. A comparison of annual vertical crustal displacements from GPS and Gravity Recovery and Climate Experiment (GRACE) over Europe. J. Geophys. Res. Solid Earth 2007, 112, B03404. [Google Scholar] [CrossRef]
- Zheng, G.; Wang, H.; Wright, T.J.; Lou, Y.; Zhang, R.; Zhang, W.; Shi, C.; Huang, J.; Wei, N. Crustal Deformation in the India-Eurasia Collision Zone from 25 Years of GPS Measurements. J. Geophys. Res. Solid Earth 2017, 122, 9290–9312. [Google Scholar] [CrossRef]
- Yadav, R.K.; Kundu, B.; Gahalaut, K.; Catherine, J.; Gahalaut, V.K.; Ambikapthy, A.; Naidu, M.S. Coseismic offsets due to the 11 April 2012 Indian Ocean earthquakes (Mw 8.6 and 8.2) derived from GPS measurements. Geophys. Res. Lett. 2013, 40, 3389–3393. [Google Scholar] [CrossRef]
- Blewitt, G.; Hammond, W.C.; Kreemer, C.; Plag, H.-P.; Stein, S.; Okal, E. GPS for real-time earthquake source determination and tsunami warning systems. J. Geod. 2009, 83, 335–343. [Google Scholar] [CrossRef]
- Lidberg, M.; Johansson, J.M.; Scherneck, H.-G.; Davis, J.L. An improved and extended GPS-derived 3D velocity field of the glacial isostatic adjustment (GIA) in Fennoscandia. J. Geod. 2007, 81, 213–230. [Google Scholar] [CrossRef]
- Bogusz, J.; Klos, A.; Pokonieczny, K. Optimal Strategy of a GPS Position Time Series Analysis for Post-Glacial Rebound Investigation in Europe. Remote Sens. 2019, 11, 1209. [Google Scholar] [CrossRef]
- Williams, S.D.P.; Bock, Y.; Fang, P.; Jamason, P.; Nikolaidis, R.M.; Prawirodirdjo, L.; Miller, M.; Johnson, D.J. Error analysis of continuous GPS position time series. J. Geophys. Res. Solid Earth 2004, 109, B03412. [Google Scholar] [CrossRef]
- He, X.; Montillet, J.-P.; Fernandes, R.; Bos, M.; Yu, K.; Hua, X.; Jiang, W. Review of current GPS methodologies for producing accurate time series and their error sources. J. Geodyn. 2017, 106, 12–29. [Google Scholar] [CrossRef]
- Gruszczynski, M.; Klos, A.; Bogusz, J. Orthogonal transformation in extracting of common mode error from continuous gps networks. Acta Geodyn. Geomater. 2016, 13, 291–298. [Google Scholar] [CrossRef]
- Wdowinski, S.; Bock, Y.; Zhang, J.; Fang, P.; Genrich, J. Southern California permanent GPS geodetic array: Spatial filtering of daily positions for estimating coseismic and postseismic displacements induced by the 1992 Landers earthquake. J. Geophys. Res. Solid Earth 1997, 102, 18057–18070. [Google Scholar] [CrossRef]
- Nikolaidis, R. Observation of geodetic and seismic deformation with the Global Positioning System. Ph.D. Thesis, University of California, San Diego, CA, USA, 2002. [Google Scholar]
- Márquez-Azúa, B.; DeMets, C. Crustal velocity field of Mexico from continuous GPS measurements, 1993 to June 2001: Implications for the neotectonics of Mexico. J. Geophys. Res. Solid Earth 2003, 108, 2450. [Google Scholar] [CrossRef]
- Tian, Y.; Shen, Z.-K. Correlation weighted stacking filtering of common-mode component in GPS observation network. Acta Seismol. Sin. 2011, 33, 198–208. [Google Scholar] [CrossRef]
- Tian, Y.; Shen, Z.-K. Extracting the regional common-mode component of GPS station position time series from dense continuous network. J. Geophys. Res. Solid Earth 2016, 121, 1080–1096. [Google Scholar] [CrossRef]
- Ji, K.H.; Herring, T.A. Transient signal detection using GPS measurements: Transient inflation at Akutan volcano, Alaska, during early 2008. Geophys. Res. Lett. 2011, 38, L06307. [Google Scholar] [CrossRef]
- Blewitt, G.; Kreemer, C.; Hammond, W.C.; Goldfarb, J.M. Terrestrial reference frame NA12 for crustal deformation studies in North America. J. Geodyn. 2013, 72, 11–24. [Google Scholar] [CrossRef]
- Dong, D.; Fang, P.; Bock, Y.; Webb, F.; Prawirodirdjo, L.; Kedar, S.; Jamason, P. Spatiotemporal filtering using principal component analysis and Karhunen-Loeve expansion approaches for regional GPS network analysis. J. Geophys. Res. Solid Earth 2006, 111, B03405. [Google Scholar] [CrossRef]
- He, X.; Hua, X.; Yu, K.; Xuan, W.; Lu, T.; Zhang, W.; Chen, X. Accuracy enhancement of GPS time series using principal component analysis and block spatial filtering. Adv. Space Res. 2015, 55, 1316–1327. [Google Scholar] [CrossRef]
- Yuan, P.; Jiang, W.; Wang, K.; Sneeuw, N. Effects of Spatiotemporal Filtering on the Periodic Signals and Noise in the GPS Position Time Series of the Crustal Movement Observation Network of China. Remote Sens. 2018, 10, 1472. [Google Scholar] [CrossRef]
- Zhou, M.; Guo, J.; Shen, Y.; Kong, Q.; Yuan, J. Extraction of common mode errors of GNSS coordinate time series based on multi-channel singular spectrum analysis. Chin. J. Geophys. 2018, 61, 4383–4395. [Google Scholar] [CrossRef]
- Gruszczynska, M.; Rosat, S.; Klos, A.; Gruszczynski, M.; Bogusz, J. Multichannel Singular Spectrum Analysis in the Estimates of Common Environmental Effects Affecting GPS Observations. In Geodynamics and Earth Tides Observations from Global to Micro Scale; Braitenberg, C., Rossi, G., Geodynamics, Geodynamics and Earth Tides Editor Group, Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 211–228. [Google Scholar] [CrossRef]
- Ming, F.; Yang, Y.; Zeng, A.; Zhao, B. Spatiotemporal filtering for regional GPS network in China using independent component analysis. J. Geod. 2017, 91, 419–440. [Google Scholar] [CrossRef]
- Liu, B.; Dai, W.; Peng, W.; Meng, X. Spatiotemporal analysis of GPS time series in vertical direction using independent component analysis. Earth Planets Space 2015, 67, 189. [Google Scholar] [CrossRef]
- Shen, Y.; Li, W.; Xu, G.; Li, B. Spatiotemporal filtering of regional GNSS network’s position time series with missing data using principle component analysis. J. Geod. 2014, 88, 1–12. [Google Scholar] [CrossRef]
- Li, W.; Shen, Y. The Consideration of Formal Errors in Spatiotemporal Filtering Using Principal Component Analysis for Regional GNSS Position Time Series. Remote Sens. 2018, 10, 534. [Google Scholar] [CrossRef]
- Li, W.; Shen, Y.; Li, B. Weighted spatiotemporal filtering using principal component analysis for analyzing regional GNSS position time series. Acta Geod. Geophys. 2015, 50, 419–436. [Google Scholar] [CrossRef]
- Gruszczynski, M.; Klos, A.; Bogusz, J. A filtering of incomplete GNSS position time series with probabilistic Principal Component Analysis. Pure. Appl. Geophys. 2018, 175, 1841–1867. [Google Scholar] [CrossRef]
- Ilin, A.; Raiko, T. Practical Approaches to Principal Component Analysis in the Presence of Missing Values. J. Mach. Learn. Res. 2010, 11, 1957–2000. [Google Scholar]
- Bishop, C.M. Variational principal components. In Proceedings of the 9th International Conference on Artificial Neural Networks (ICANN99), Edinburgh, UK, 7–10 September 1999; pp. 509–514. [Google Scholar]
- Liu, N.; Dai, W.; Santerre, R.; Kuang, C. A MATLAB-based Kriged Kalman Filter software for interpolating missing data in GNSS coordinate time series. GPS Solut. 2017, 22, 25. [Google Scholar] [CrossRef]
- Kwon, O.-W.; Chan, K.; Lee, T.-W. Speech feature analysis using variational Bayesian PCA. IEEE Signal. Process. Lett. 2003, 10, 137–140. [Google Scholar] [CrossRef]
- Klos, A.; Olivares, G.; Teferle, F.N.; Hunegnaw, A.; Bogusz, J. On the combined effect of periodic signals and colored noise on velocity uncertainties. GPS Solut. 2017, 22, 1–13. [Google Scholar] [CrossRef]
- Bevis, M.; Brown, A. Trajectory models and reference frames for crustal motion geodesy. J. Geod. 2014, 88, 283–311. [Google Scholar] [CrossRef]
- Schneider, T. Analysis of incomplete climate data: Estimation of mean values and covariance matrices and imputation of missing values. J. Clim. 2001, 14, 853–871. [Google Scholar] [CrossRef]
- Szekely, G.J.; Rizzo, M.L.; Bakirov, N.K. Measuring and testing dependence by correlation of distances. Ann. Stat. 2007, 35, 2769–2794. [Google Scholar] [CrossRef]
- Bos, M.S.; Fernandes, R.M.S.; Williams, S.D.P.; Bastos, L. Fast error analysis of continuous GNSS observations with missing data. J. Geod. 2013, 87, 351–360. [Google Scholar] [CrossRef]



| Filtering Methods | Advantages | Disadvantages |
|---|---|---|
| Stacking | Simple to calculate Ability to handle missing data | Not suitable for larger scale GNSS networks Inability to identify stations with strong local effects Need to determine realistic weight values |
| Reference frame transformation | Simple to calculate Ability to handle missing data | Distorted signal or residual CME may appear at the edge of the region GNSS positions cannot reveal movement from the global point of view |
| Statistical signal decomposition techniques | Rigorous mathematical framework Ability to identify stations with strong local effects Suitable for larger scale GNSS networks | Inability to handle missing data for the traditional methods Any two time series need common epochs for the modified methods |
| Principal Component | Difference | Proportion (%) | Histogram | |
|---|---|---|---|---|
| 1 | 0.78 | 0.64 | 54.71 |  |
| 2 | 0.14 | 0.07 | 10.00 |  |
| 3 | 0.07 | 0.01 | 5.01 |  |
| 4 | 0.06 | 0.01 | 4.02 |  |
| 5 | 0.05 | - | 3.48 |  |
| Principal Component | Difference | Proportion (%) | Histogram | |
|---|---|---|---|---|
| 1 | 0.94 | 0.84 | 60.84 |  |
| 2 | 0.10 | 0.04 | 6.43 |  |
| 3 | 0.06 | 0.01 | 3.97 |  |
| 4 | 0.06 | 0.01 | 3.59 |  |
| 5 | 0.05 | - | 3.00 |  |
| Principal Component | Difference | Proportion (%) | Histogram | |
|---|---|---|---|---|
| 1 | 7.29 | 6.26 | 54.84 |  |
| 2 | 1.03 | 0.42 | 7.74 |  |
| 3 | 0.61 | 0.17 | 4.60 |  |
| 4 | 0.44 | 0.05 | 3.33 |  |
| 5 | 0.39 | - | 2.96 |  |
| No. | Station | Unfiltered | Filtered | No. | Station | Unfiltered | Filtered | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| N | E | U | N | E | U | N | E | U | N | E | U | ||||
| 1 | AZRY | 1.23 | 1.44 | 4.27 | 0.94 | 1.08 | 3.36 | 23 | MSOB | 2.42 | 1.63 | 5.36 | 2.24 | 1.26 | 4.74 |
| 2 | AZU1 | 1.45 | 1.55 | 4.96 | 1.09 | 1.36 | 3.96 | 24 | MVFD | 1.41 | 1.54 | 4.55 | 1.01 | 1.23 | 3.70 |
| 3 | BKAP | 1.39 | 1.30 | 4.18 | 1.09 | 0.93 | 3.35 | 25 | NOCO | 1.27 | 1.41 | 3.99 | 0.84 | 1.01 | 2.91 |
| 4 | BLYT | 1.36 | 1.38 | 4.65 | 1.04 | 1.01 | 3.77 | 26 | OEOC | 1.48 | 1.32 | 3.93 | 1.10 | 0.88 | 2.82 |
| 5 | BRPK | 1.42 | 1.43 | 4.12 | 1.15 | 1.02 | 3.04 | 27 | OZST | 1.31 | 1.62 | 4.61 | 1.04 | 1.15 | 3.56 |
| 6 | BVPP | 1.13 | 1.65 | 4.72 | 0.72 | 1.17 | 3.56 | 28 | PKDB | 1.41 | 1.44 | 5.79 | 1.16 | 1.07 | 4.78 |
| 7 | CACT | 1.21 | 1.36 | 4.25 | 0.88 | 0.96 | 3.23 | 29 | PPBF | 1.31 | 1.20 | 3.85 | 0.91 | 0.69 | 2.59 |
| 8 | CAT2 | 1.11 | 1.22 | 3.40 | 0.67 | 0.76 | 2.35 | 30 | RAAP | 1.18 | 1.22 | 3.84 | 0.71 | 0.77 | 2.86 |
| 9 | CIRX | 1.32 | 1.35 | 4.28 | 0.88 | 0.92 | 3.13 | 31 | RAMT | 1.14 | 1.26 | 3.78 | 0.74 | 0.81 | 2.61 |
| 10 | CNPP | 1.27 | 1.47 | 4.09 | 0.86 | 1.12 | 3.20 | 32 | RDMT | 1.15 | 1.50 | 3.97 | 0.80 | 1.19 | 2.82 |
| 11 | CTMS | 1.28 | 1.41 | 3.91 | 1.00 | 0.99 | 3.11 | 33 | SBCC | 1.15 | 1.24 | 3.96 | 0.64 | 0.72 | 2.73 |
| 12 | DHLG | 1.22 | 1.49 | 4.36 | 0.98 | 1.16 | 3.41 | 34 | SCIA | 1.11 | 1.24 | 3.92 | 0.65 | 0.77 | 2.61 |
| 13 | GDEC | 1.33 | 1.18 | 3.79 | 1.07 | 0.83 | 2.72 | 35 | SCIP | 1.21 | 1.44 | 4.06 | 0.84 | 1.05 | 3.23 |
| 14 | GMPK | 1.19 | 1.42 | 4.10 | 0.82 | 1.04 | 3.29 | 36 | SHOS | 1.31 | 1.28 | 4.14 | 0.94 | 0.88 | 3.10 |
| 15 | GMRC | 1.52 | 1.33 | 4.14 | 1.26 | 0.93 | 3.34 | 37 | SIO5 | 1.19 | 1.19 | 3.49 | 0.79 | 0.76 | 2.50 |
| 16 | GNPS | 1.31 | 1.34 | 3.92 | 0.93 | 0.93 | 3.13 | 38 | SRS1 | 1.25 | 1.34 | 4.07 | 0.88 | 0.96 | 3.26 |
| 17 | HOLP | 1.41 | 1.47 | 6.48 | 1.13 | 0.97 | 5.97 | 39 | THCP | 1.22 | 1.38 | 4.03 | 0.77 | 0.92 | 2.78 |
| 18 | HVYS | 1.37 | 1.33 | 4.39 | 0.97 | 1.00 | 3.35 | 40 | USGC | 1.26 | 1.39 | 4.44 | 0.93 | 1.05 | 3.62 |
| 19 | IMPS | 1.20 | 1.35 | 3.76 | 0.86 | 0.95 | 2.91 | 41 | USLO | 1.29 | 1.50 | 4.69 | 1.01 | 1.19 | 3.75 |
| 20 | ISLK | 1.51 | 1.75 | 5.98 | 1.22 | 1.43 | 5.00 | 42 | VNCX | 1.34 | 1.33 | 4.21 | 0.94 | 0.84 | 3.13 |
| 21 | LL01 | 1.43 | 1.42 | 4.38 | 1.11 | 1.11 | 3.30 | 43 | WRHS | 1.23 | 1.99 | 4.23 | 0.87 | 1.66 | 3.16 |
| 22 | LNMT | 1.46 | 1.59 | 3.62 | 1.09 | 1.30 | 2.67 | 44 | WWMT | 1.75 | 1.77 | 5.10 | 1.61 | 1.44 | 4.28 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, W.; Jiang, W.; Li, Z.; Chen, H.; Chen, Q.; Wang, J.; Zhu, G. Extracting Common Mode Errors of Regional GNSS Position Time Series in the Presence of Missing Data by Variational Bayesian Principal Component Analysis. Sensors 2020, 20, 2298. https://doi.org/10.3390/s20082298
Li W, Jiang W, Li Z, Chen H, Chen Q, Wang J, Zhu G. Extracting Common Mode Errors of Regional GNSS Position Time Series in the Presence of Missing Data by Variational Bayesian Principal Component Analysis. Sensors. 2020; 20(8):2298. https://doi.org/10.3390/s20082298
Chicago/Turabian StyleLi, Wudong, Weiping Jiang, Zhao Li, Hua Chen, Qusen Chen, Jian Wang, and Guangbin Zhu. 2020. "Extracting Common Mode Errors of Regional GNSS Position Time Series in the Presence of Missing Data by Variational Bayesian Principal Component Analysis" Sensors 20, no. 8: 2298. https://doi.org/10.3390/s20082298
APA StyleLi, W., Jiang, W., Li, Z., Chen, H., Chen, Q., Wang, J., & Zhu, G. (2020). Extracting Common Mode Errors of Regional GNSS Position Time Series in the Presence of Missing Data by Variational Bayesian Principal Component Analysis. Sensors, 20(8), 2298. https://doi.org/10.3390/s20082298





