Exploiting Direct Link in Two-Way Half-Duplex Sensor Network over Block Rayleigh Fading Channel: Upper Bound Ergodic Capacity and Exact SER Analysis
Abstract
1. Introduction
- (1)
- Energy harvesting based two-way half-duplex relaying cooperative network using selection combining over block Rayleigh fading channel is proposed and investigated
- (2)
- The closed-form of the upper bound EC and exact SER of the model system is derived.
- (3)
- All the results are convinced by Monte Carlo simulation in connection with all primary system parameters.
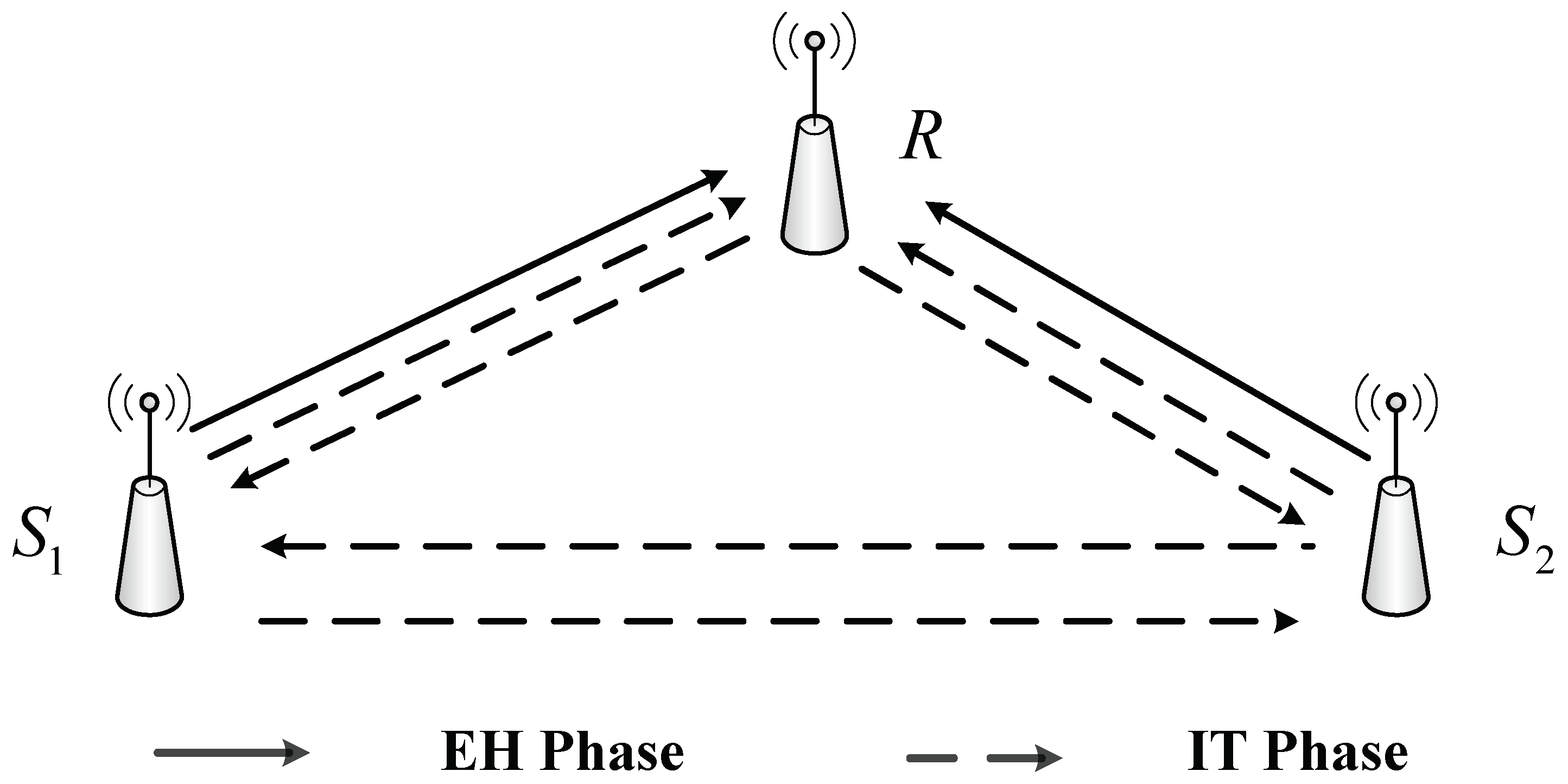
2. Relaying Network Model
2.1. Energy Harvesting Phase
2.2. Information Transmission Phase
3. Upper Bound Ergodic Capacity and Exact SER Analysis
3.1. Upper Bound Ergodic Capacity Analysis
3.2. SER Analysis
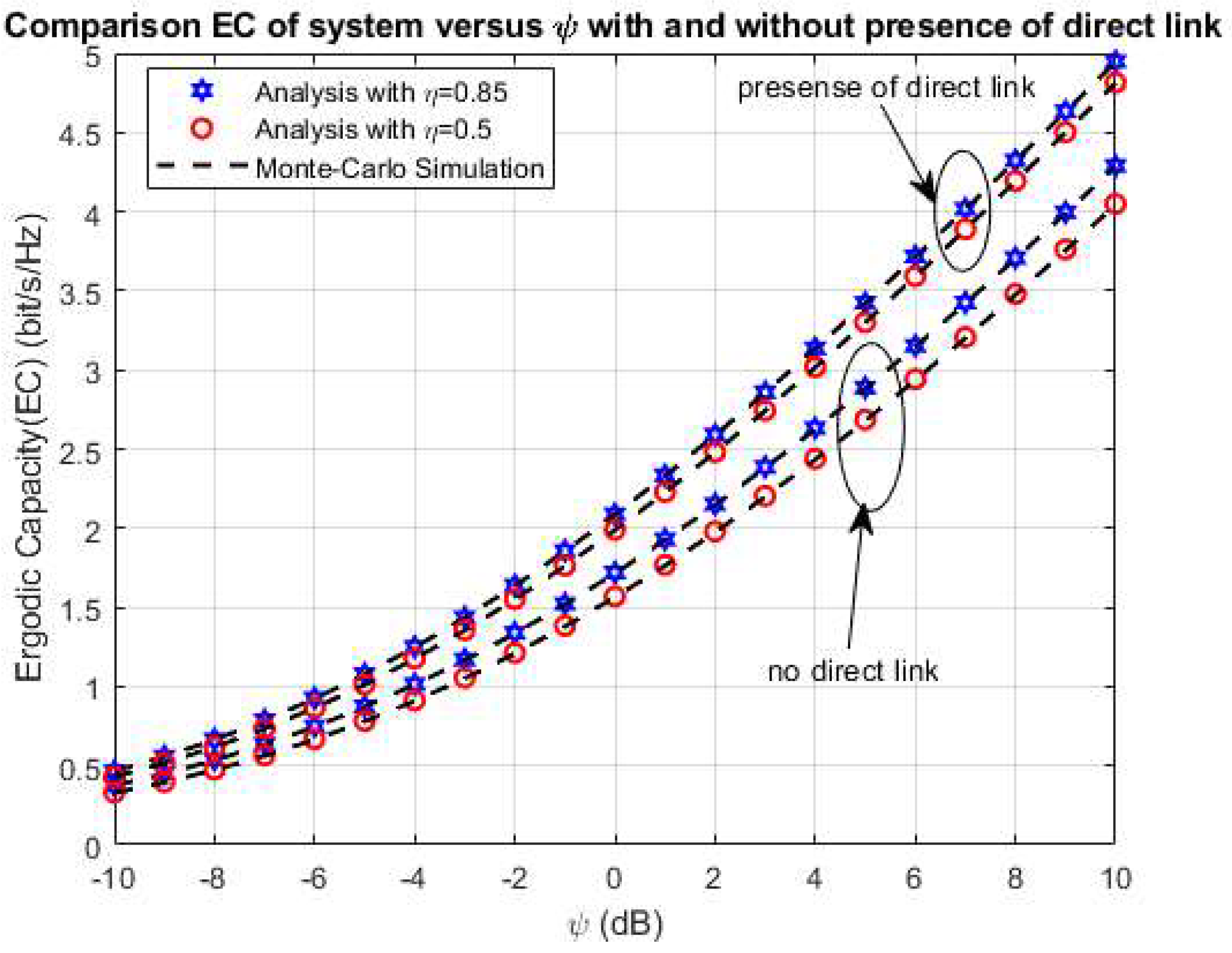
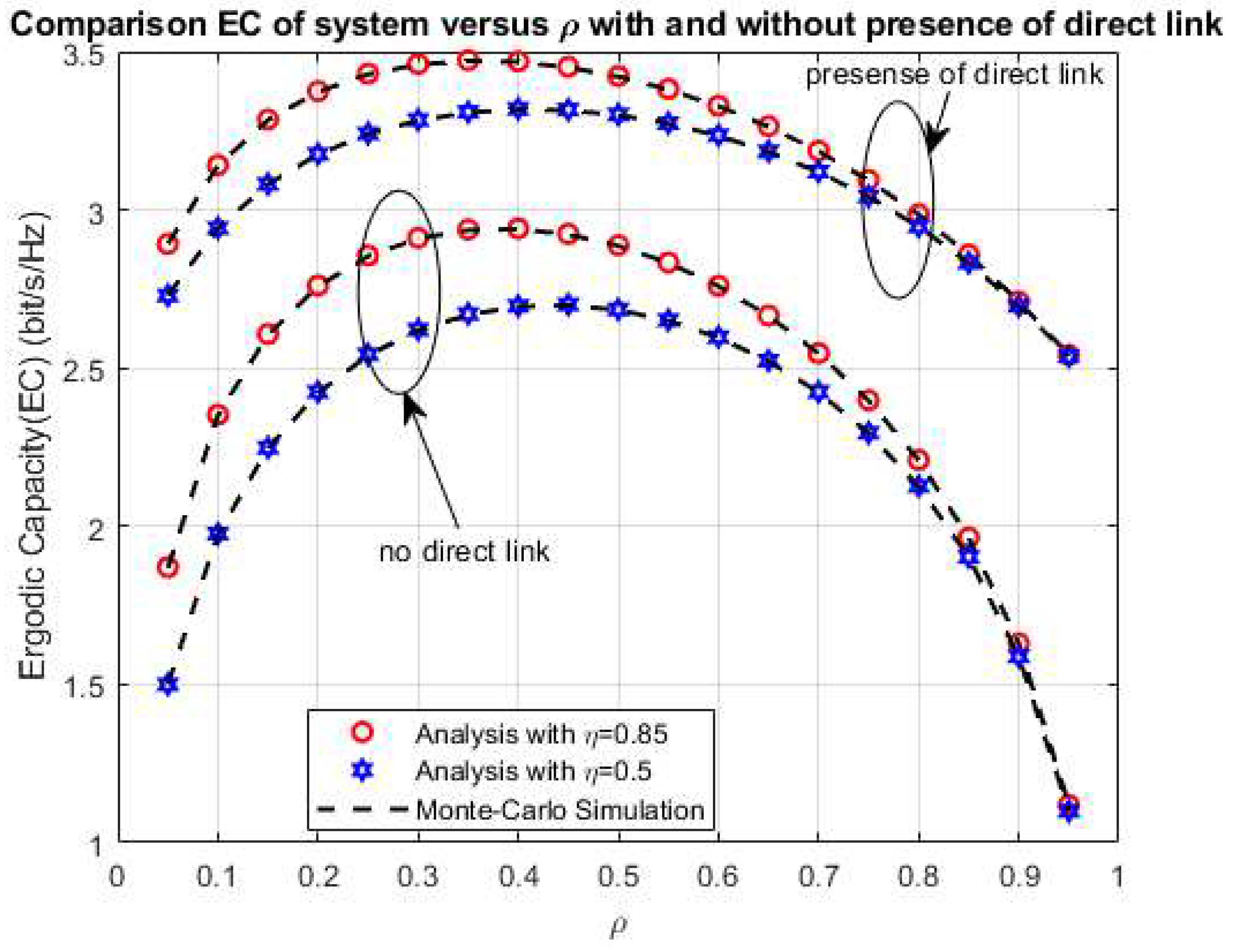
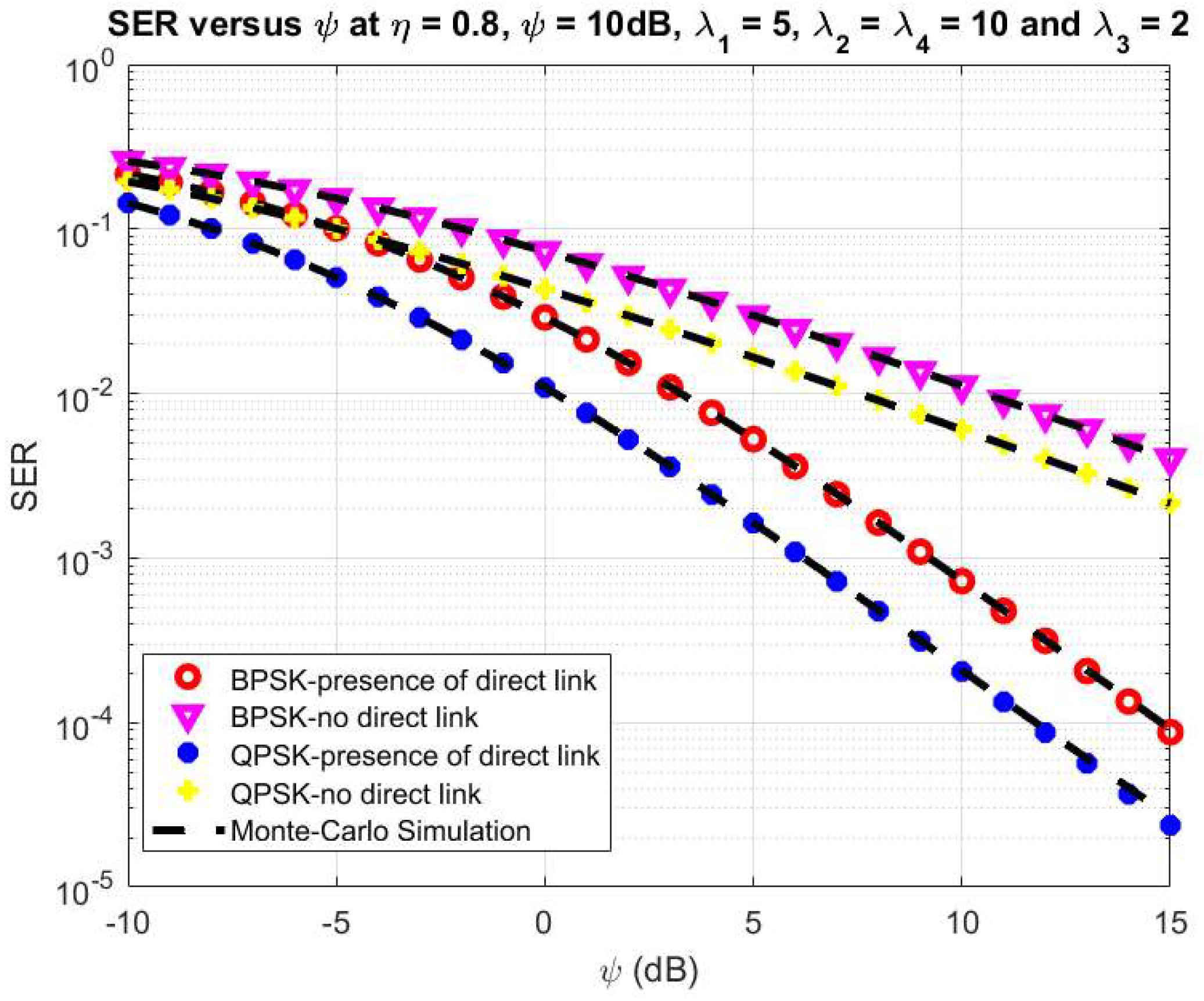
4. Numerical Results and Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Bi, S.; Ho, C.K.; Zhang, R. Wireless powered communication: Opportunities and challenges. IEEE Commun. Mag. 2015, 53, 117–125. [Google Scholar] [CrossRef]
- Niyato, D.; Kim, D.I.; Maso, M.; Han, Z. Wireless Powered Communication Networks: Research Directions and Technological Approaches. IEEE Wirel. Commun. 2017, 24, 2–11. [Google Scholar] [CrossRef]
- Yu, H.; Lee, H.; Jeon, H. What is 5G? Emerging 5G Mobile Services and Network Requirements. Sustainability 2017, 9, 1848. [Google Scholar] [CrossRef]
- Salem, A.; Khairi, A.H.; Khaled, M.R. Physical Layer Security with RF Energy Harvesting in AF Multi-Antenna Relaying Networks. IEEE Trans. Commun. 2016, 64, 3025–3038. [Google Scholar] [CrossRef]
- Liu, W.; Zhou, X.; Durrani, S.; Popovski, P. Secure Communication with a Wireless-Powered Friendly Jammer. IEEE Trans. Wirel. Commun. 2016, 15, 401–415. [Google Scholar] [CrossRef]
- Varshney, L.R. Transporting Information Energy Simultaneously. In Proceedings of the 2008 IEEE International Symposium on Information Theory, Toronto, ON, Canada, 6–11 July 2008. [Google Scholar] [CrossRef]
- Zhou, X.; Zhang, R.; Ho, C.K. Wireless Information and Power Transfer: Architecture Design and Rate-Energy Tradeoff. IEEE Trans. Commun. 2013, 61, 4754–4767. [Google Scholar] [CrossRef]
- Liu, L.; Zhang, R.; Chua, C.-K. Wireless Information Transfer with Opportunistic Energy Harvesting. IEEE Trans. Wirel. Commun. 2013, 12, 288–300. [Google Scholar] [CrossRef]
- Xiang, Z.; Tao, M. Robust Beamforming for Wireless Information and Power Transmission. IEEE Wirel. Commun. Lett. 2012, 1, 372–375. [Google Scholar] [CrossRef]
- Bhargav, M.; Mehta, N.B. Voluntary Energy Harvesting Relays and Selection in Cooperative Wireless Networks. IEEE Trans. Wirel. Commun. 2010, 9, 3543–3553. [Google Scholar] [CrossRef]
- Nasir, A.A.; Zhou, X.; Durrani, S.; Kennedy, R.A. Relaying Protocols for Wireless Energy Harvesting and Information Processing. IEEE Trans. Wirel. Commun. 2013, 12, 3622–3636. [Google Scholar] [CrossRef]
- Grover, P.; Sahai, A. Shannon Meets Tesla: Wireless Information and Power Transfer. In Proceedings of the 2010 IEEE International Symposium on Information Theory, Austin, TX, USA, 13–18 June 2010. [Google Scholar] [CrossRef]
- Huang, K.; Lau, V.K.N. Enabling Wireless Power Transfer in Cellular Networks: Architecture, Modeling and Deployment. IEEE Trans. Wirel. Commun. 2014, 13, 902–912. [Google Scholar] [CrossRef]
- Nguyen, T.N.; Minh, T.; Long, N.T.; Hung, D.H.; Voznak, M. Multisource Power Splitting Energy Harvesting Relaying Network in Half-Duplex System over Block Rayleigh Fading Channel: System Performance Analysis. Electronics 2019, 8, 67. [Google Scholar] [CrossRef]
- Shi, Q.; Liu, L.; Xu, W.; Zhang, R. Joint Transmit Beamforming and Receive Power Splitting for MISO SWIPT Systems. IEEE Trans. Wirel. Commun. 2014, 13, 3269–3280. [Google Scholar] [CrossRef]
- Zhang, R.; Ho, C.K. MIMO Broadcasting for Simultaneous Wireless Information and Power Transfer. IEEE Trans. Wirel. Commun. 2013, 12, 1989–2001. [Google Scholar] [CrossRef]
- Ju, H.; Zhang, R. Throughput Maximization in Wireless Powered Communication Networks. IEEE Trans. Wirel. Commun. 2014, 13, 418–428. [Google Scholar] [CrossRef]
- Krikidis, I.; Timotheou, S.; Sasaki, S. RF Energy Transfer for Cooperative Networks: Data Relaying or Energy Harvesting? IEEE Commun. Lett. 2012, 16, 1772–1775. [Google Scholar] [CrossRef]
- Michalopoulos, D.S.; Suraweera, H.A.; Schober, R. Relay Selection for Simultaneous Information Transmission and Wireless Energy Transfer: A Tradeoff Perspective. IEEE J. Sel. Areas Commun. 2015, 1. [Google Scholar] [CrossRef]
- Park, J.; Clerckx, B. Joint Wireless Information and Energy Transfer in a Two-User MIMO Interference Channel. IEEE Trans. Wirel. Commun. 2013, 12, 4210–4221. [Google Scholar] [CrossRef]
- Park, J.; Clerckx, B. Joint Wireless Information and Energy Transfer with Reduced Feedback in MIMO Interference Channels. IEEE J. Sel. Areas Commun. 2015, 1. [Google Scholar] [CrossRef]
- Ding, Z.; Perlaza, S.M.; Esnaola, I.; Poor, H.V. Power Allocation Strategies in Energy Harvesting Wireless Cooperative Networks. IEEE Trans. Wirel. Commun. 2014, 13, 846–860. [Google Scholar] [CrossRef]
- Chen, Z.; Xia, B.; Liu, H. Wireless Information and Power Transfer in Two-way Amplify-and-forward Relaying Channels. In Proceedings of the 2014 IEEE Global Conference on Signal and Information Processing (GlobalSIP), Atlanta, GA, USA, 3–5 December 2014. [Google Scholar] [CrossRef]
- Krikidis, I.; Sasaki, S.; Timotheou, S.; Ding, Z. A Low Complexity Antenna Switching for Joint Wireless Information and Energy Transfer in MIMO Relay Channels. IEEE Trans. Commun. 2014, 62, 1577–1587. [Google Scholar] [CrossRef]
- Tin, P.T.; Hung, D.T.; Nguyen, T.; Duy, T.; Voznak, M. Secrecy Performance Enhancement for Underlay Cognitive Radio Networks Employing Cooperative Multi-Hop Transmission with and without Presence of Hardware Impairments. Entropy 2019, 21, 217. [Google Scholar] [CrossRef]
- Tran, H.D.; Tran, D.T.; Choi, S.G. Secrecy Performance of a Generalized Partial Relay Selection Protocol in Underlay Cognitive Networks. Int. J. Commun. Syst. 2018, 31. [Google Scholar] [CrossRef]
- Nguyen, T.L.N.; Shin, Y. Performance Analysis for Energy Harvesting Based Wireless Relay Systems. In Proceedings of the 2019 IEEE VTS Asia Pacific Wireless Communications Symposium (APWCS), Singapore, 28–30 August 2019. [Google Scholar] [CrossRef]
- Gui, L.; He, B.; Zhou, X.; Yu, C.; Shu, F.; Li, J. Energy-Efficient Wireless Powered Secure Transmission with Cooperative Jamming for Public Transportation. IEEE Trans. Green Commun. Netw. 2019, 3, 876–885. [Google Scholar] [CrossRef]
- Bhowmick, A.; Chatterjee, A.; Verma, T. Performance of DF Relaying in an Energy Harvesting Full Duplex Cognitive Radio Network. In Proceedings of the 2019 International Conference on Vision towards Emerging Trends in Communication and Networking (ViTECoN), Vellore, India, 30–31 March 2019. [Google Scholar] [CrossRef]
- Zhao, M.; Zhao, J.; Zhou, W.; Zhu, J.; Zhang, S. Energy Efficiency Optimization in Relay-assisted Networks with Energy Harvesting Relay Constraints. China Commun. 2015, 12, 84–94. [Google Scholar] [CrossRef]
- Nguyen, T.N.; Minh, Q.; Hoang, T.; Tran, P.T.; Vozňák, M. Energy Harvesting over Rician Fading Channel: A Performance Analysis for Half-Duplex Bidirectional Sensor Networks under Hardware Impairments. Sensors 2018, 18, 1781. [Google Scholar] [CrossRef]
- Bhatnagar, M.R. On the Capacity of Decode-and-Forward Relaying over Rician Fading Channels. IEEE Commun. Lett. 2013, 17, 1100–1103. [Google Scholar] [CrossRef]
- Nguyen, T.N.; Minh TH, Q.; Tran, P.T.; Voznak, M.; Duy, T.T.; Nguyen, T.L.; Tin, P.T. Performance Enhancement for Energy Harvesting Based Two-Way Relay Protocols in Wireless Ad-hoc Networks with Partial and Full Relay Selection Methods. Ad Hoc Netw. 2019, 84, 178–187. [Google Scholar] [CrossRef]
- Luo, S.; Zhang, R.; Lim, T.J. Optimal save-then-transmit protocol for energy harvesting wireless transmitters. IEEE Trans. Wirel. Commun. 2013, 13, 1196–1207. [Google Scholar] [CrossRef]
- Nguyen, T.N.; Minh TH, Q.; Tran, P.T.; Voznak, M. Adaptive Energy Harvesting Relaying Protocol for Two-Way Half Duplex System Network over Rician Fading Channel. Wirel. Commun. Mob. Comput. 2018, 2018, 7693016. [Google Scholar] [CrossRef]
- Gradshteyn, I.S.; Ryzhik, I.M. Table of Integrals, Series, and Products; Elsevier: San Diego, CA, USA, 2015. [Google Scholar]
- McKay, M.R.; Grant, A.J.; Collings, I.B. Performance analysis of MIMO-MRC in double-correlated Rayleigh environments. IEEE Trans. Commun. 2007, 55, 497–507. [Google Scholar] [CrossRef]
- Chu, Z.; Zhou, F.; Zhu, Z.; Hu, R.Q.; Xiao, P. Wireless Powered Sensor Networks for Internet of Things: Maximum Throughput and Optimal Power Allocation. IEEE Internet Things J. 2018, 5, 310–321. [Google Scholar] [CrossRef]
- Wang, C.-X.; Haider, F.; Gao, X.; You, X.-H.; Yang, Y.; Yuan, D.; Aggoune, H.; Haas, H.; Fletcher, S.; Hepsaydir, E. Cellular Architecture and Key Technologies for 5G Wireless Communication Networks. IEEE Commun. Mag. 2014, 52, 122–130. [Google Scholar] [CrossRef]
- Valenta, C.R.; Durgin, G.D. Harvesting wireless power: Survey of energy-harvester conversion efficiency in far-field, wireless power transfer systems. IEEE Microw. Mag. 2014, 15, 108–120. [Google Scholar]
- Louie, R.H.Y.; Li, Y.; Vucetic, B. Practical physical layer network coding for two-way relay channels: Performance analysis and comparison. IEEE Trans. Wirel. Commun. 2010, 9, 764–777. [Google Scholar] [CrossRef]
- Phan, V.D.; Nguyen, T.N.; Tran, M.; Trang, T.T.; Voznak, M.; Ha, D.H.; Nguyen, T.L. Power Beacon-Assisted Energy Harvesting in a Half-Duplex Communication Network under Co-Channel Interference over a Rayleigh Fading Environment: Energy Efficiency and Outage Probability Analysis. Energies 2019, 12, 2579. [Google Scholar] [CrossRef]
- Nguyen, T.N.; Tran, M.; Ha, D.H.; Trang, T.T.; Vozňák, M. Multi-Source in DF Cooperative Networks with PSR protocol Based Full-Duplex Energy Harvesting over Rayleigh Fading Channel: Performance Analysis. Proc. Est. Acad. Sci. 2019, 68, 264–275. [Google Scholar] [CrossRef]
- Nguyen, T.N.; Tran, M.; Ha, D.H.; Nguyen, T.L.; Vozňák, M. Energy harvesting based two-way full-duplex relaying network over Rician fading environment: Performance analysis. Proc. Est. Acad. Sci. 2019, 68, 111–123. [Google Scholar] [CrossRef]
- Li, L.; Cimini, L.J.; Xia, X.G. Impact of Direct Link on Outage of Cooperative Full-Duplex Relaying. In Proceedings of the 2015 49th Annual Conference on Information Sciences and Systems (CISS), Baltimore, MD, USA, 18–20 March 2015. [Google Scholar] [CrossRef]




© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tin, P.T.; Nguyen, T.N.; Tran, M.; Trang, T.T.; Sevcik, L. Exploiting Direct Link in Two-Way Half-Duplex Sensor Network over Block Rayleigh Fading Channel: Upper Bound Ergodic Capacity and Exact SER Analysis. Sensors 2020, 20, 1165. https://doi.org/10.3390/s20041165
Tin PT, Nguyen TN, Tran M, Trang TT, Sevcik L. Exploiting Direct Link in Two-Way Half-Duplex Sensor Network over Block Rayleigh Fading Channel: Upper Bound Ergodic Capacity and Exact SER Analysis. Sensors. 2020; 20(4):1165. https://doi.org/10.3390/s20041165
Chicago/Turabian StyleTin, Phu Tran, Tan N. Nguyen, Minh Tran, Tran Thanh Trang, and Lukas Sevcik. 2020. "Exploiting Direct Link in Two-Way Half-Duplex Sensor Network over Block Rayleigh Fading Channel: Upper Bound Ergodic Capacity and Exact SER Analysis" Sensors 20, no. 4: 1165. https://doi.org/10.3390/s20041165
APA StyleTin, P. T., Nguyen, T. N., Tran, M., Trang, T. T., & Sevcik, L. (2020). Exploiting Direct Link in Two-Way Half-Duplex Sensor Network over Block Rayleigh Fading Channel: Upper Bound Ergodic Capacity and Exact SER Analysis. Sensors, 20(4), 1165. https://doi.org/10.3390/s20041165




