Ambient Effect Filtering Using NLPCA-SVR in High-Rise Buildings
Abstract
1. Introduction
1.1. Background
1.2. Motivation and Objectives
2. Fundamentals of NLPCA-SVR
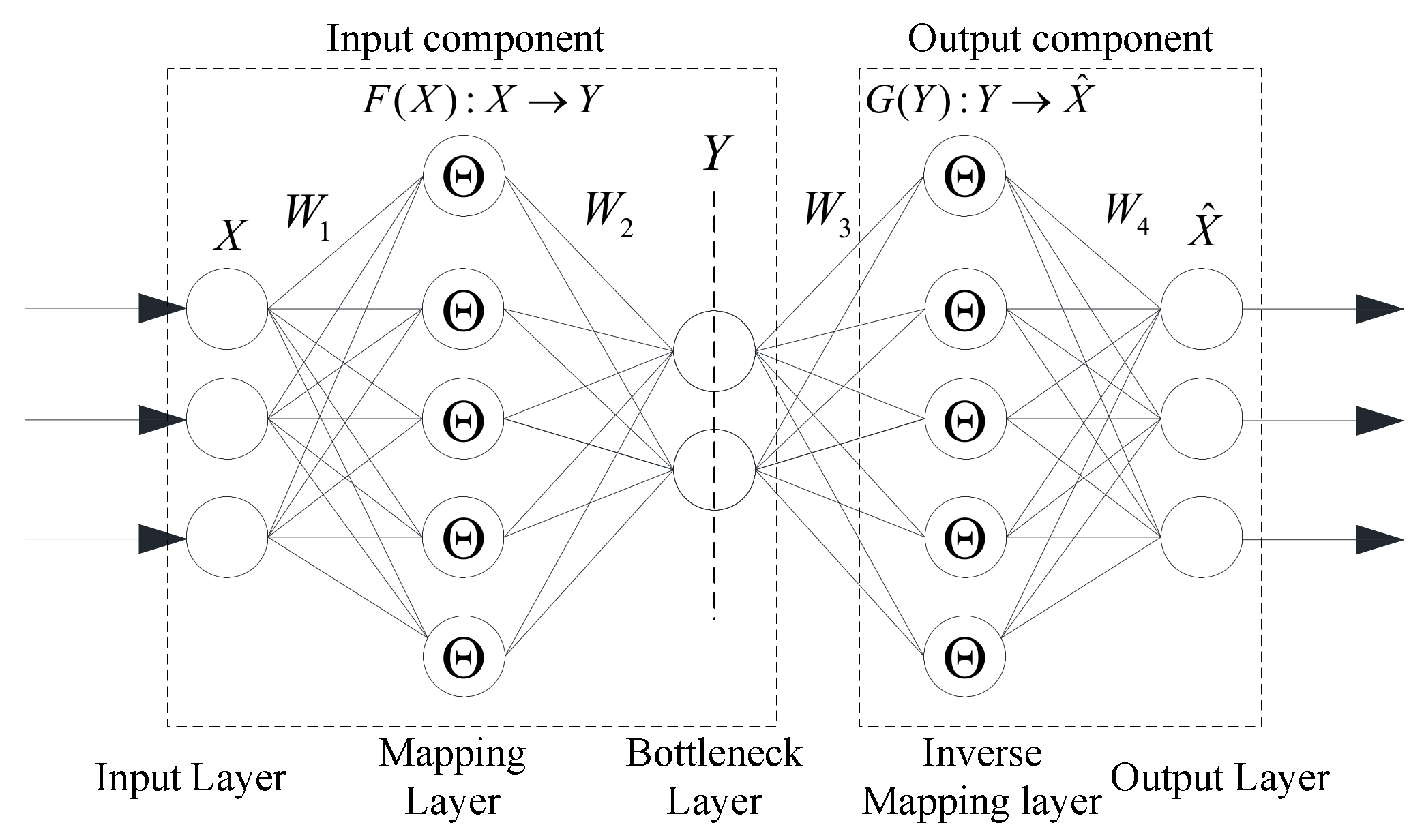
2.1. NLPCA
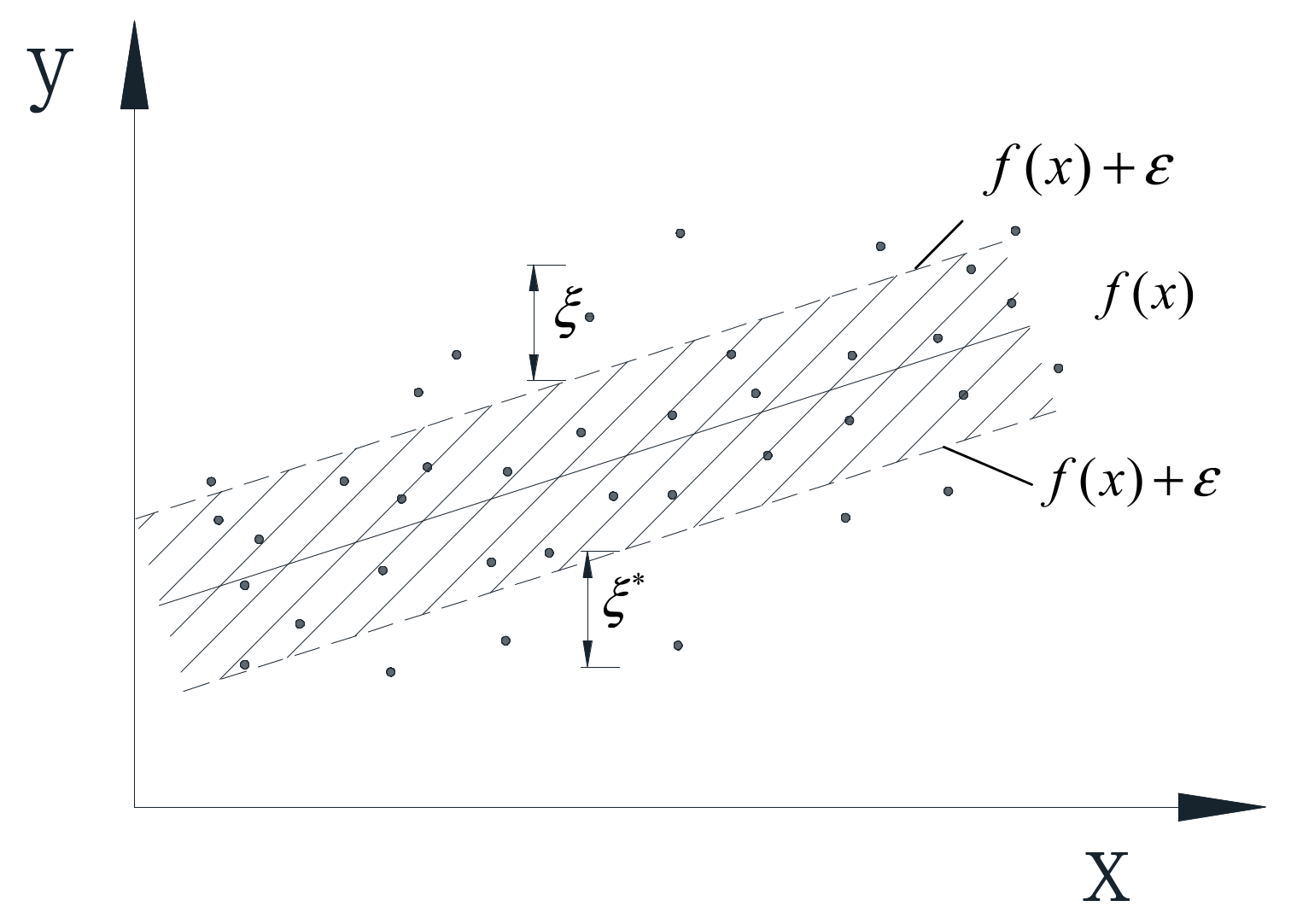
2.2. Support Vector Regression (SVR)
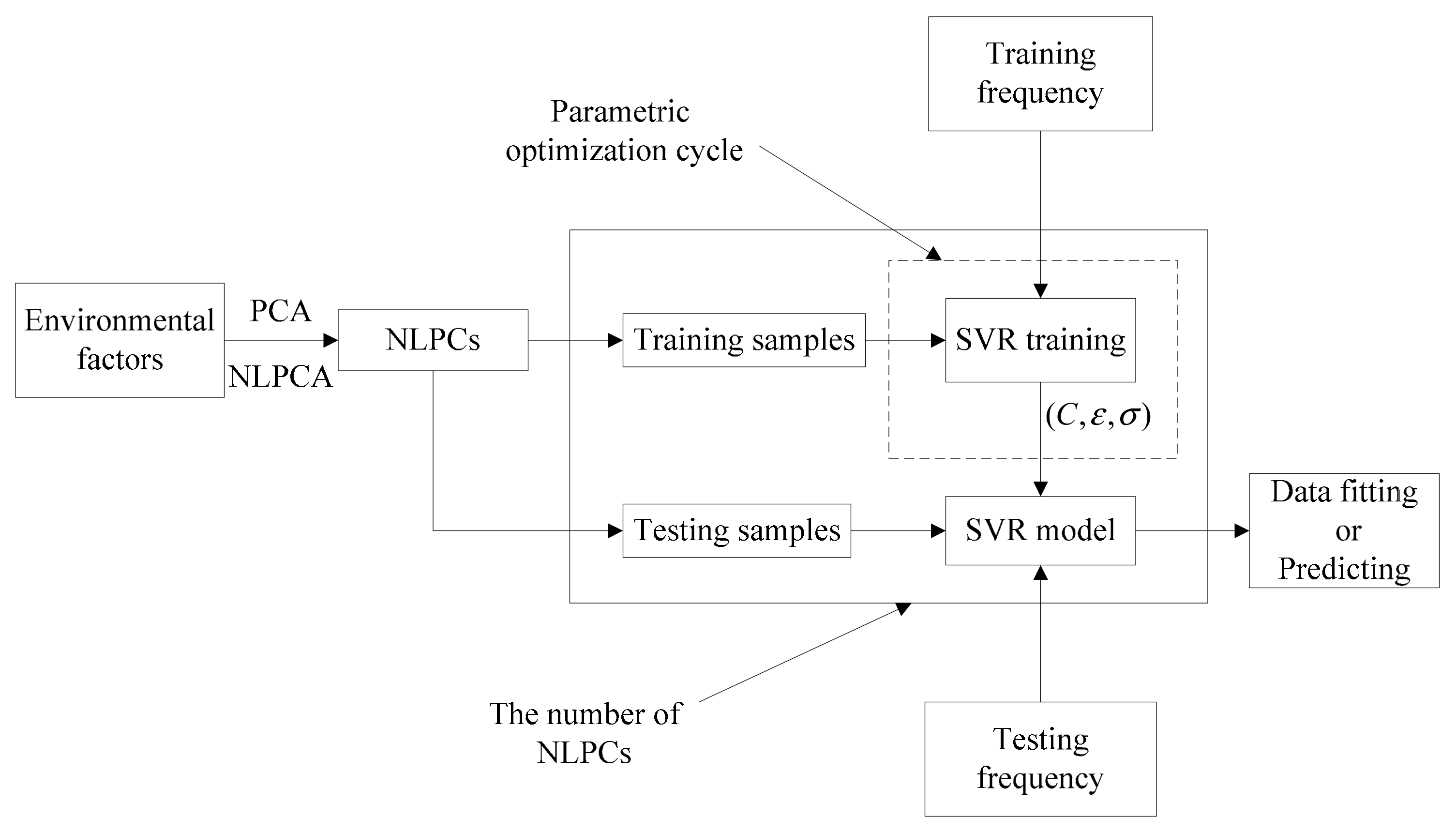
2.3. Flowchart
3. Modal Identification of GNTVT
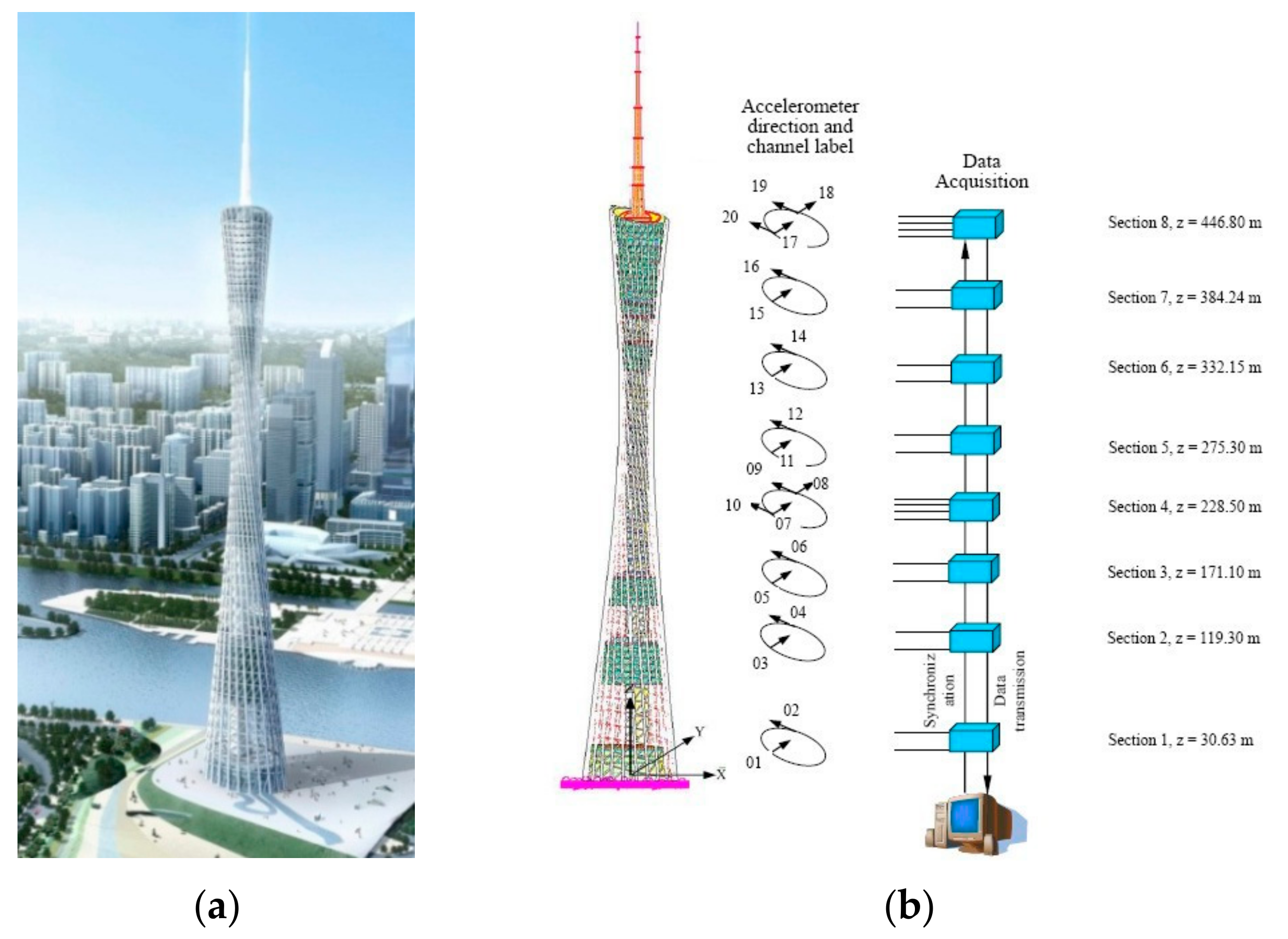
3.1. Introduction of the GNTVT Benchmark
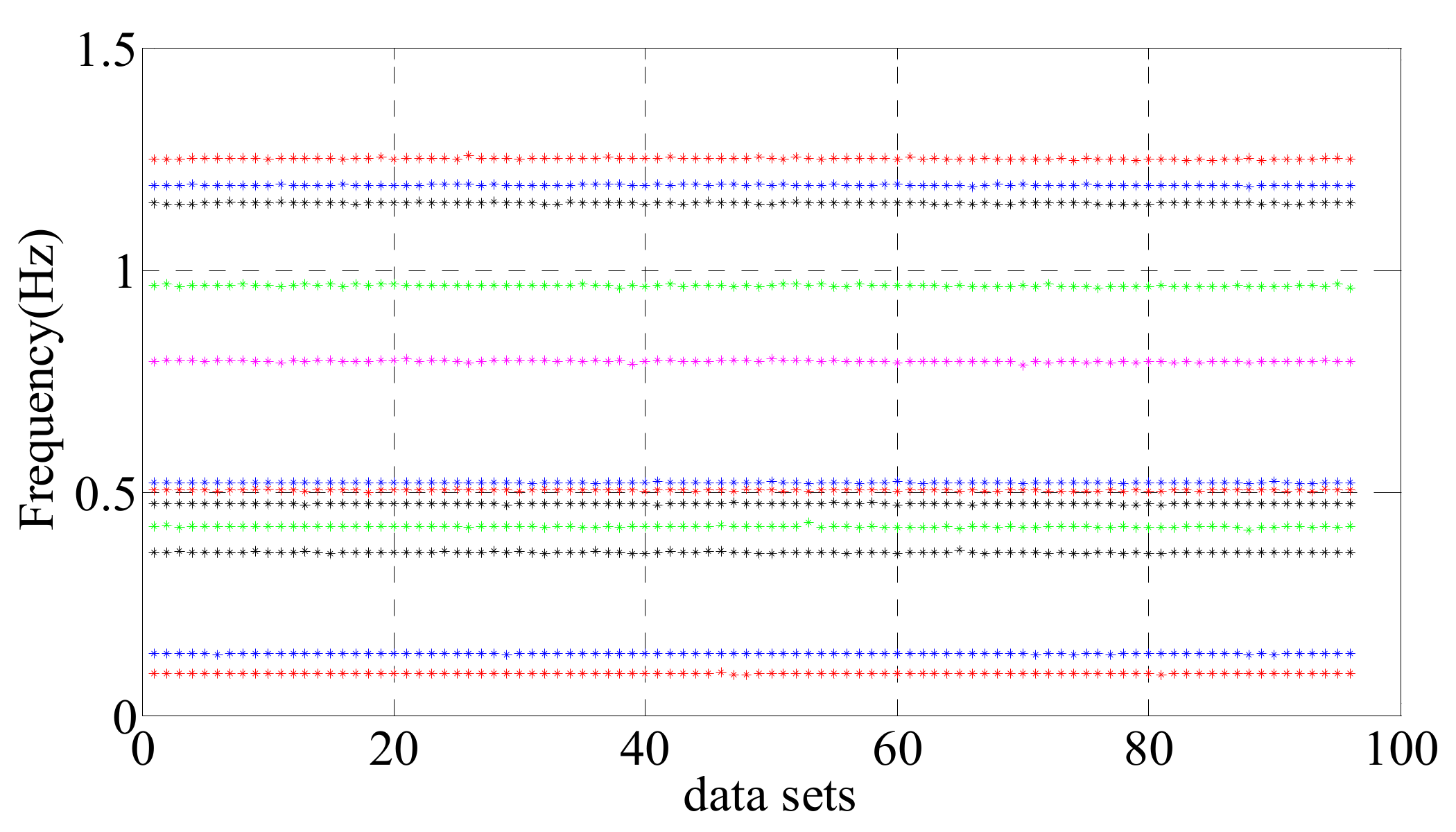
3.2. Modal Identification
4. Data Model
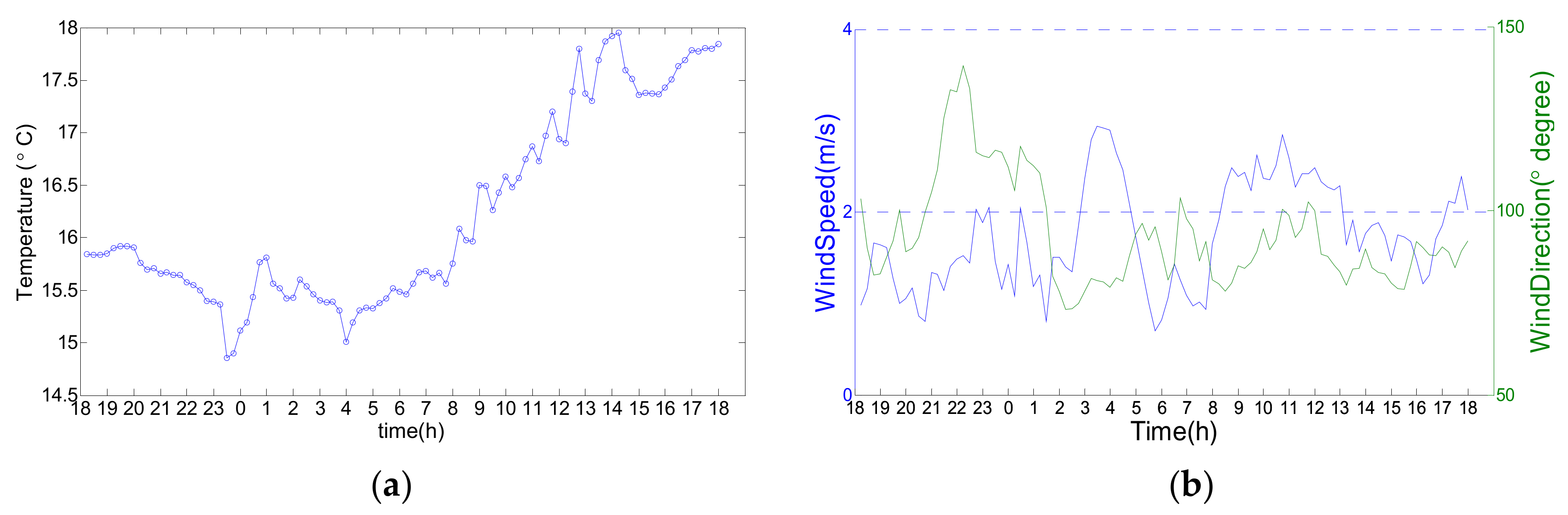
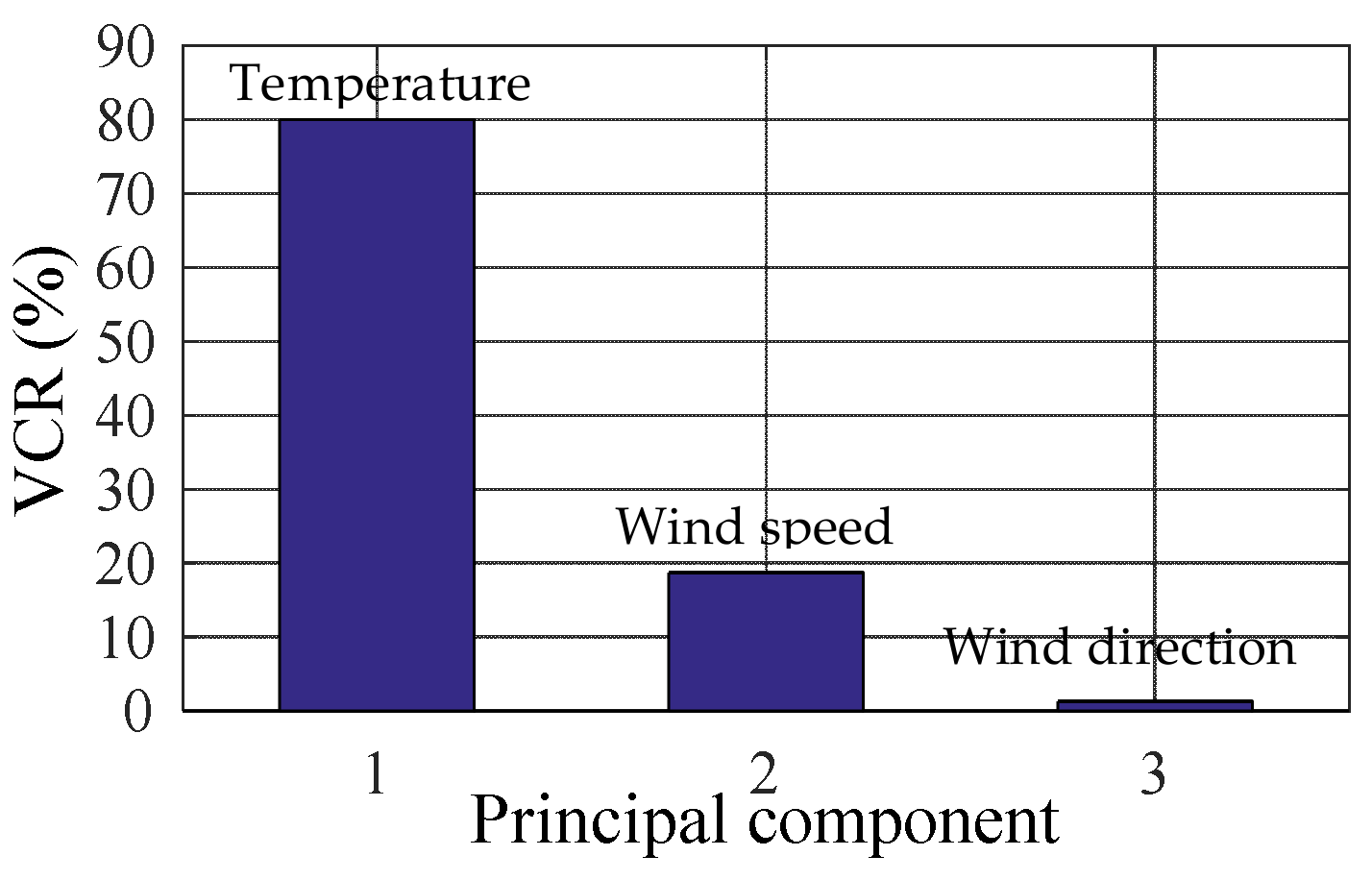
4.1. Data Preprocessing
4.2. NLPCA-SVR Model
Optimization of hyperparameters
- GSM
- (1)
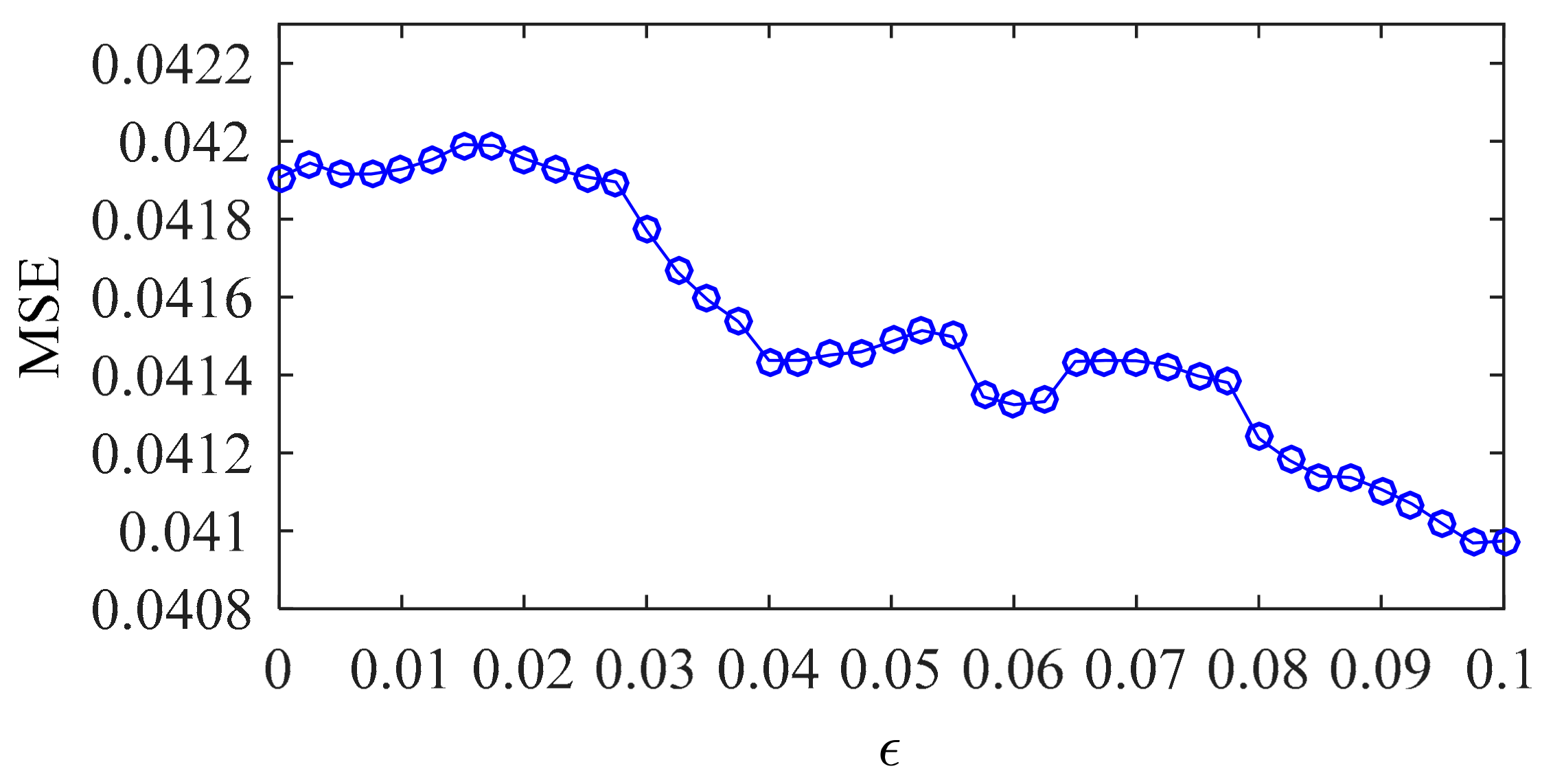
- With a step size of εstep = 0.0025, the insensitive coefficient ε is set to vary from 0 to 0.1. For each ε, the best combination of (C, σ) is determined by steps (2) to (4);
- (2)
- The step sizes of the penalty parameters C and kernel functions σ are both set as 0.5. With a step size of 0.5, C and σ are both set to vary from 2.8 to 28;
- (3)
- A different combination of (C, σ) is substituted into the SVR model in turn. K-fold cross validation is applied to reduce the influence of the data set partitioning differences. The training data set is randomly divided into K groups of subsets (approximately equal sizes) that are not included in each other. (K-1) groups of the subset are set as the training sets, and the others are set as the testing sets. This process is repeated K times so that each subset is tested, the mean square error (MSEcv) of k times is obtainedwhere and yi are the training and expected output values in the SVR model, respectively, and m is the training sample number;
- (4)
- For different combinations of (C, σ), their MSEs are plotted with contour lines to obtain a contour map. According to this contour map, the best combination of (C, σ) is determined by ;
- (5)
- For each εstep, the best combination of (εstep, C, σ) can obtain E. The optimal combination (ε, C, σ) can be determined by .
- 2.
- GA
- (1)
- The ranges of the three parameters (C, ε, σ) are set as [0,200], [0,1], [0,200], respectively.
- (2)
- The generation number, population number, crossover probability, and mutation probability are set to 200, 20, 0.7, and 0.05, respectively.
- (3)
- K-fold cross-validation is applied in GA. MSECV is set as the fitness function, expressed as
- 3.
- FOA
4.3. Original Data-SVR Model
Optimization of hyperparameters
- GSM
- 2.
- GA
- 3.
- FOA
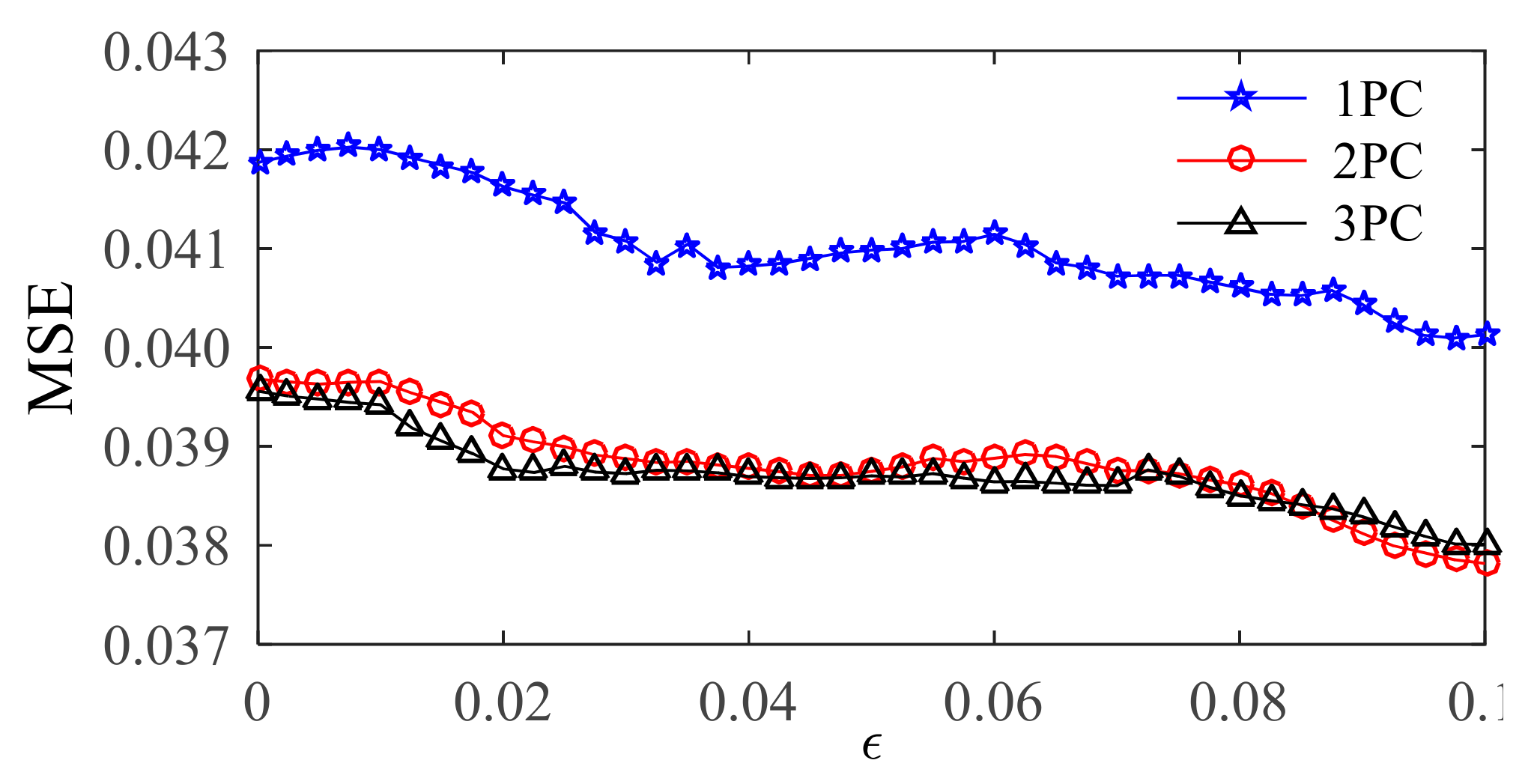
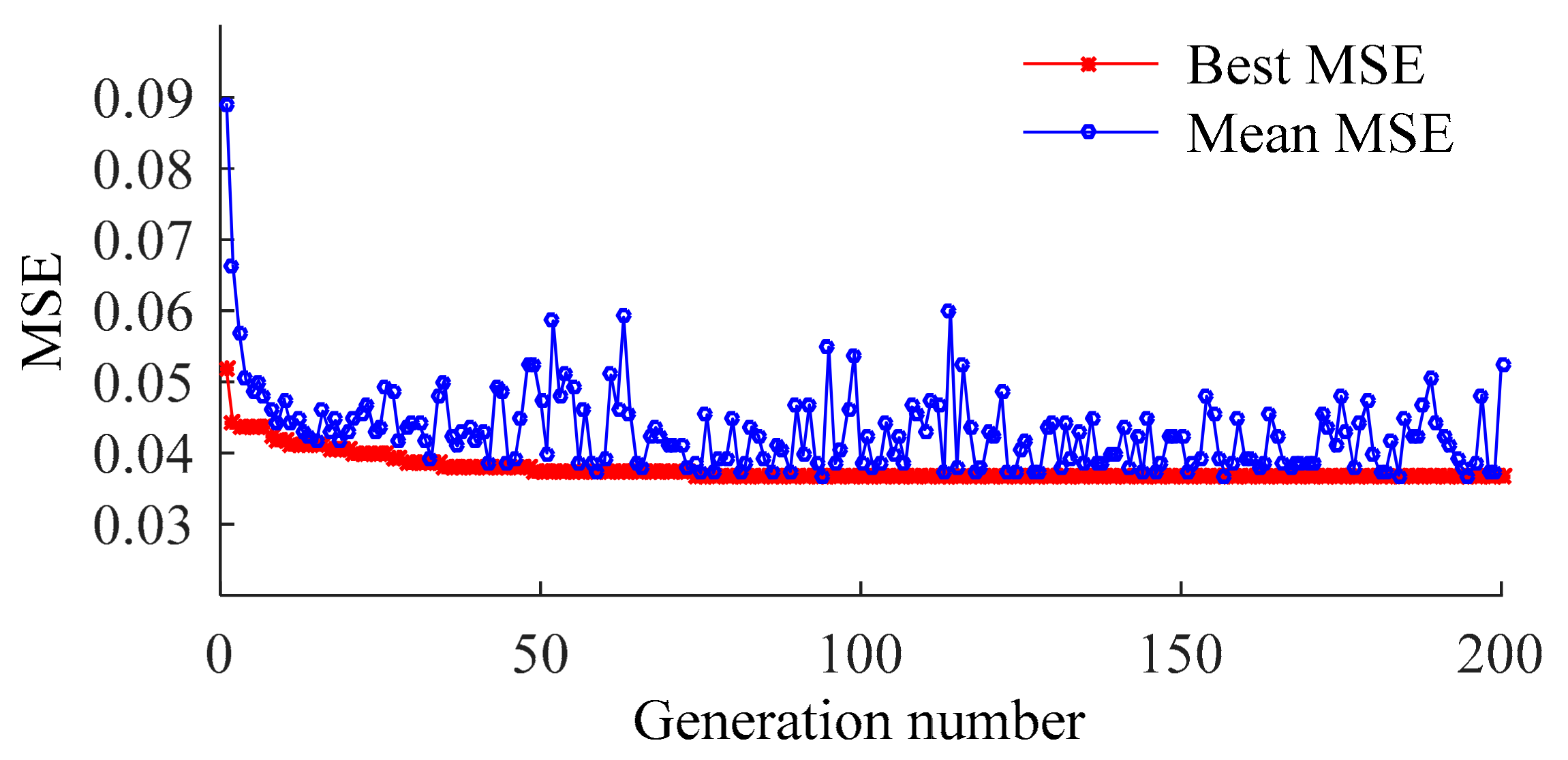
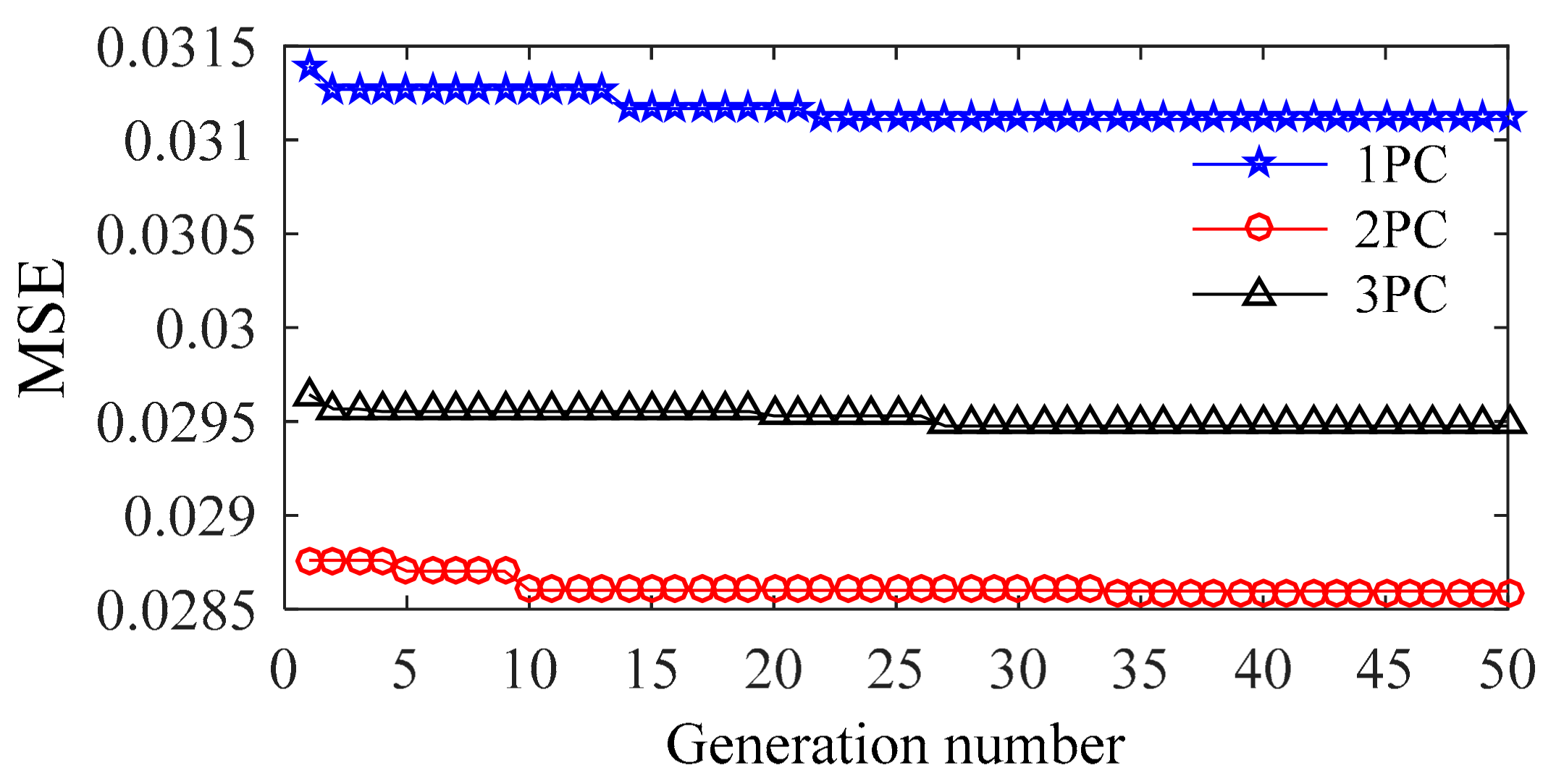
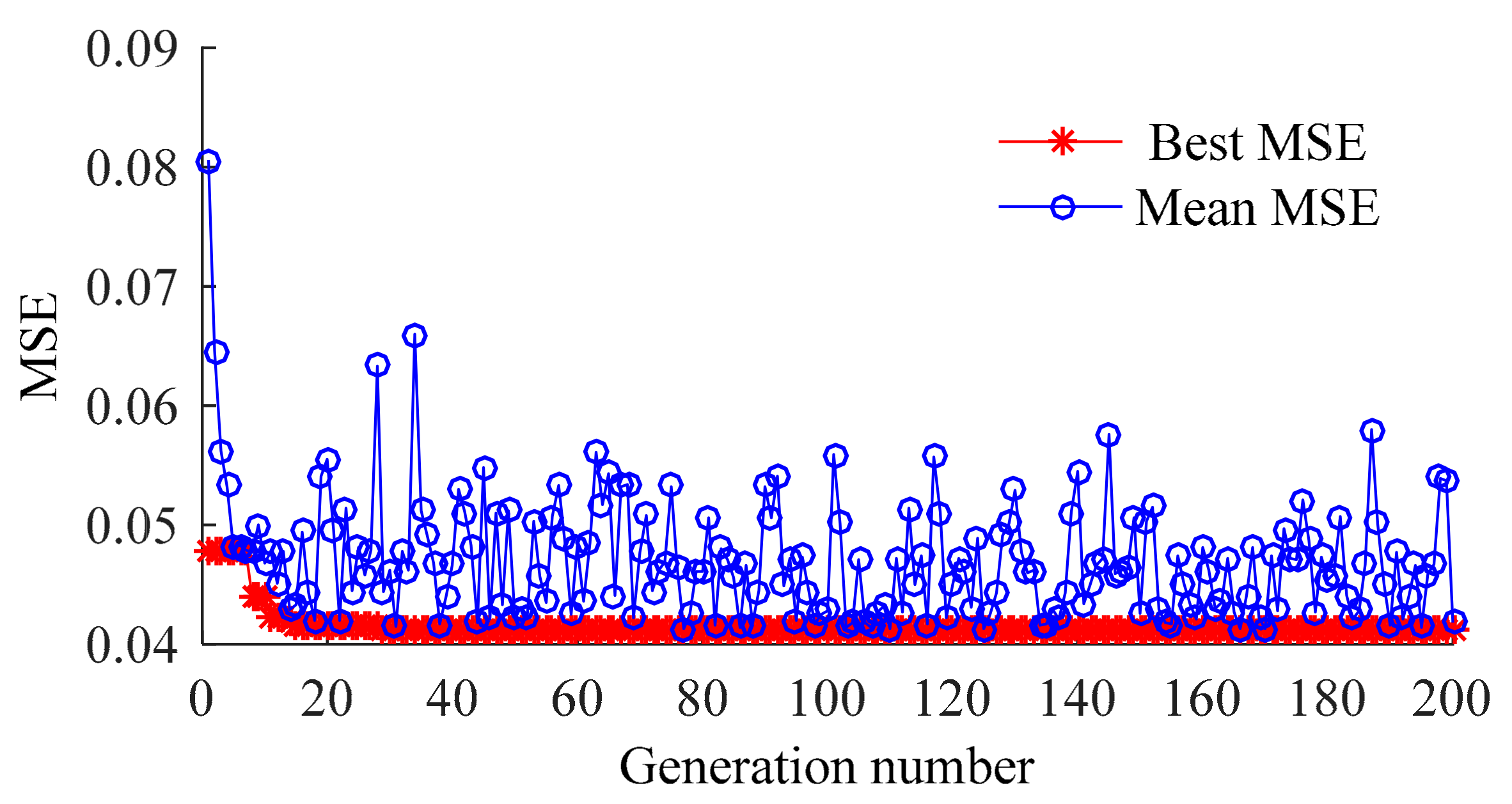
4.4. Optimization Results
5. Estimation of the NLPCA-SVR Model
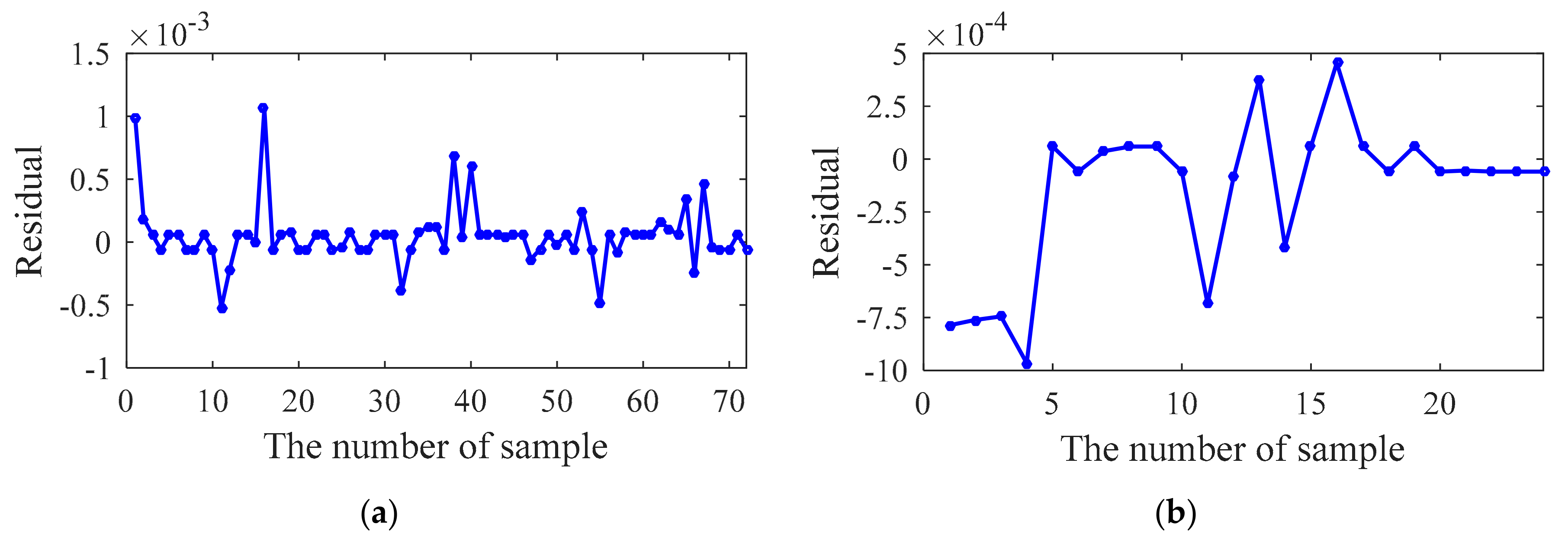
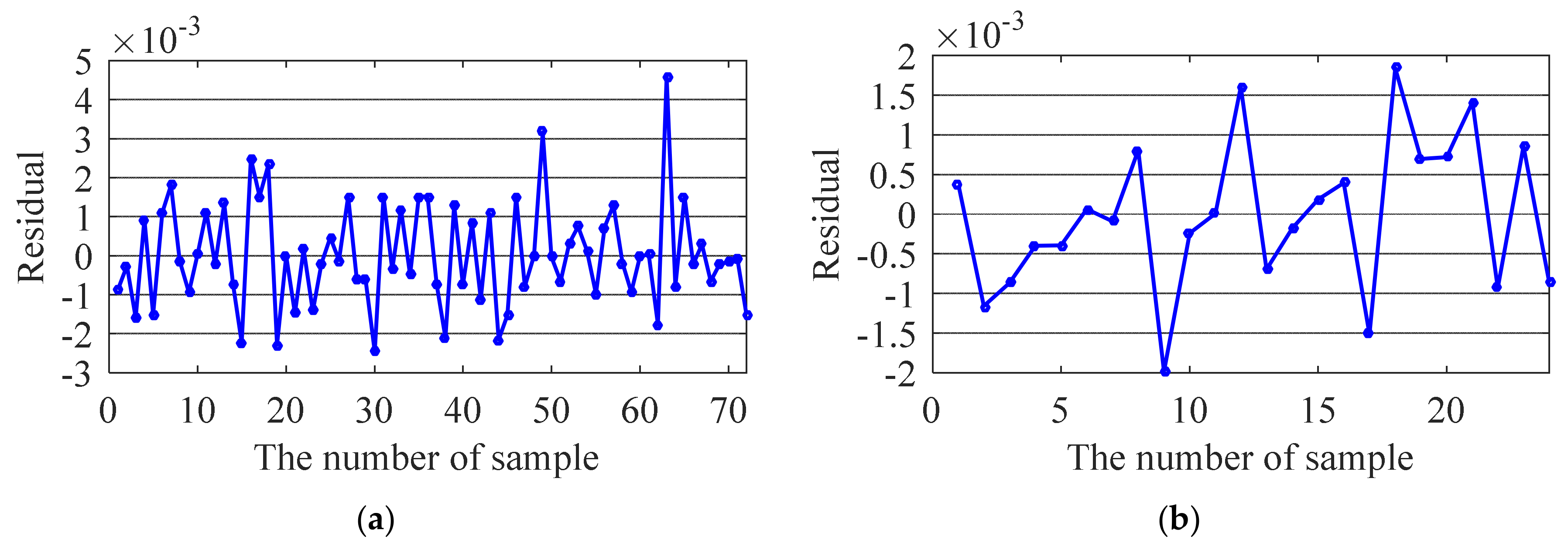
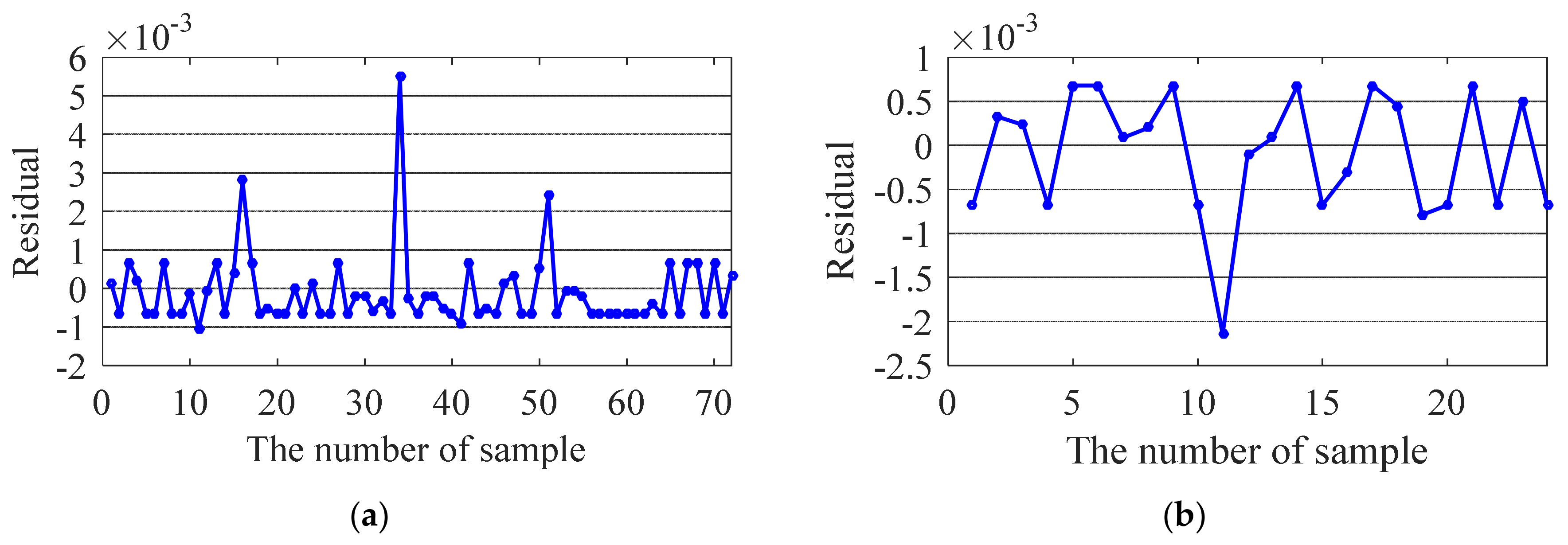
5.1. Generalization Performance
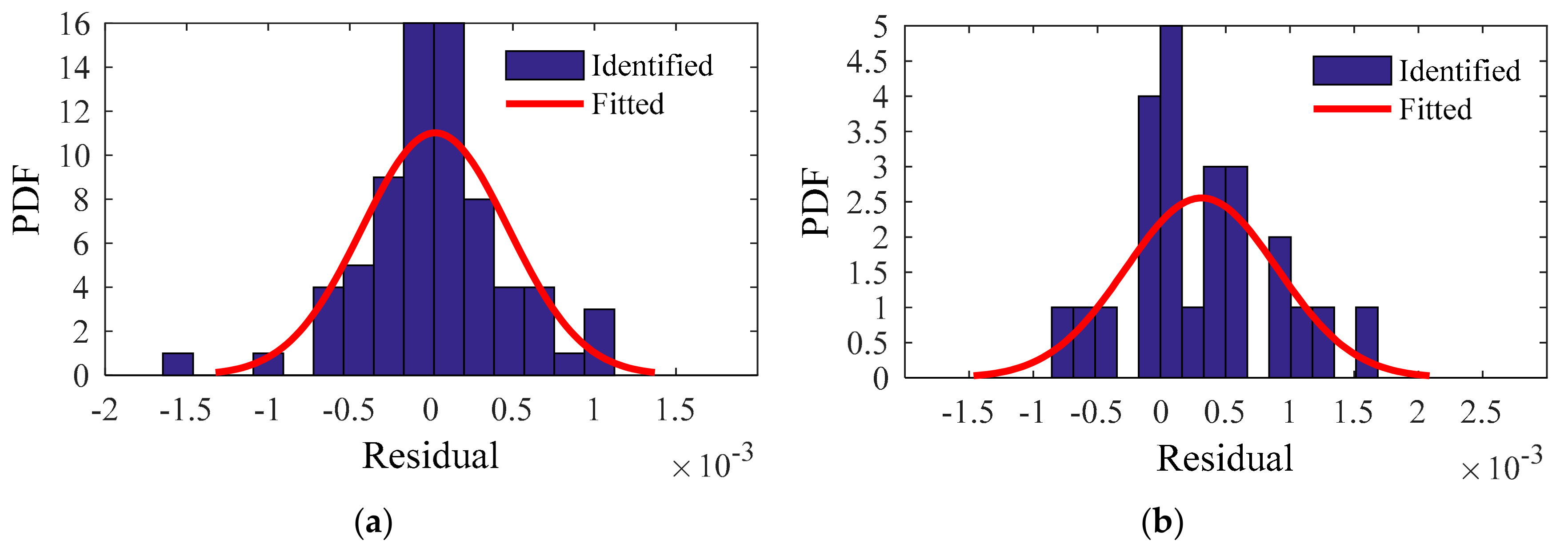
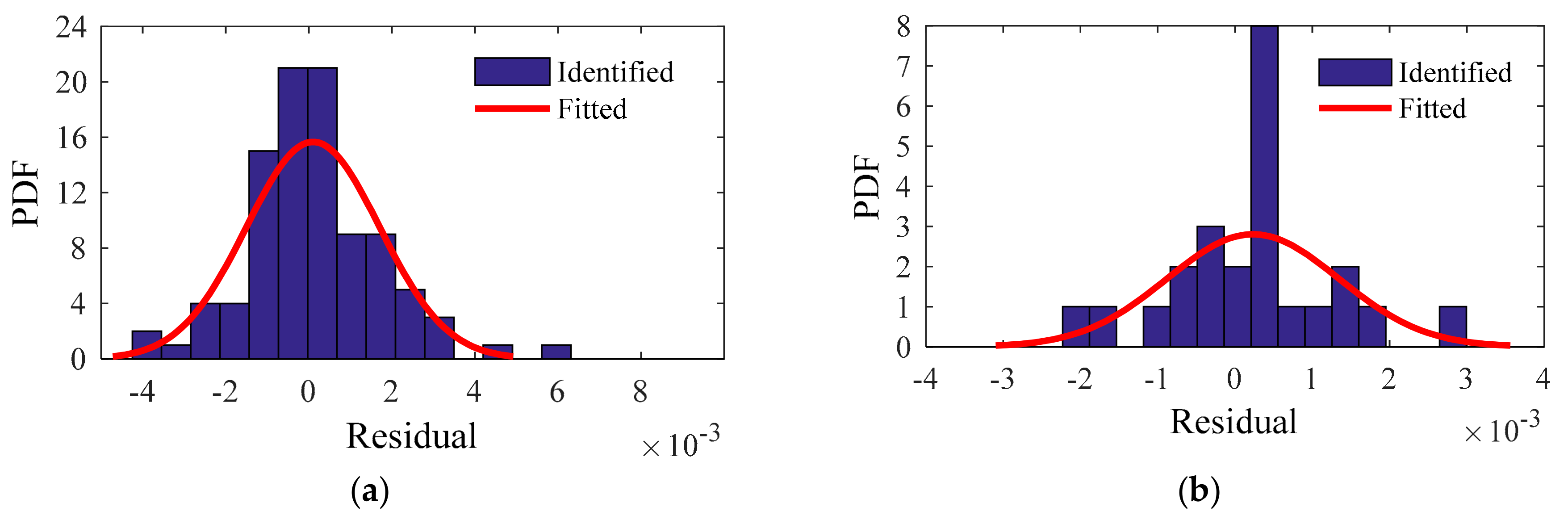
5.2. Hypothesis Test
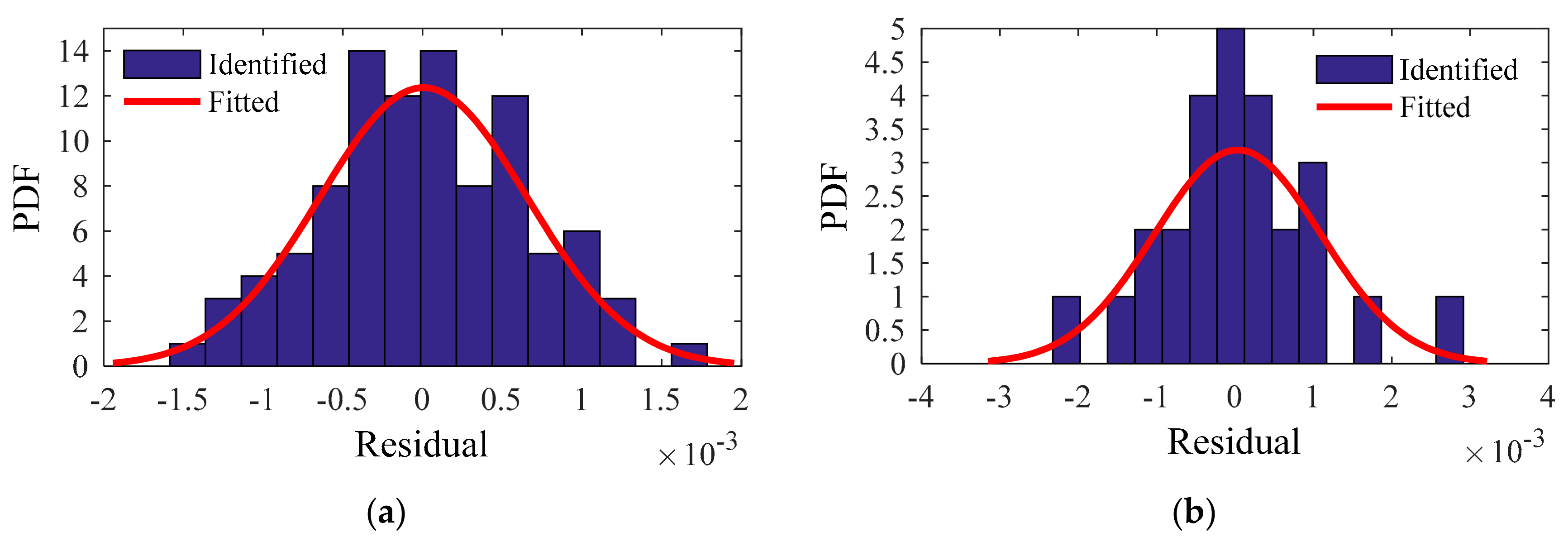
5.3. Goodness-of-Fit Test
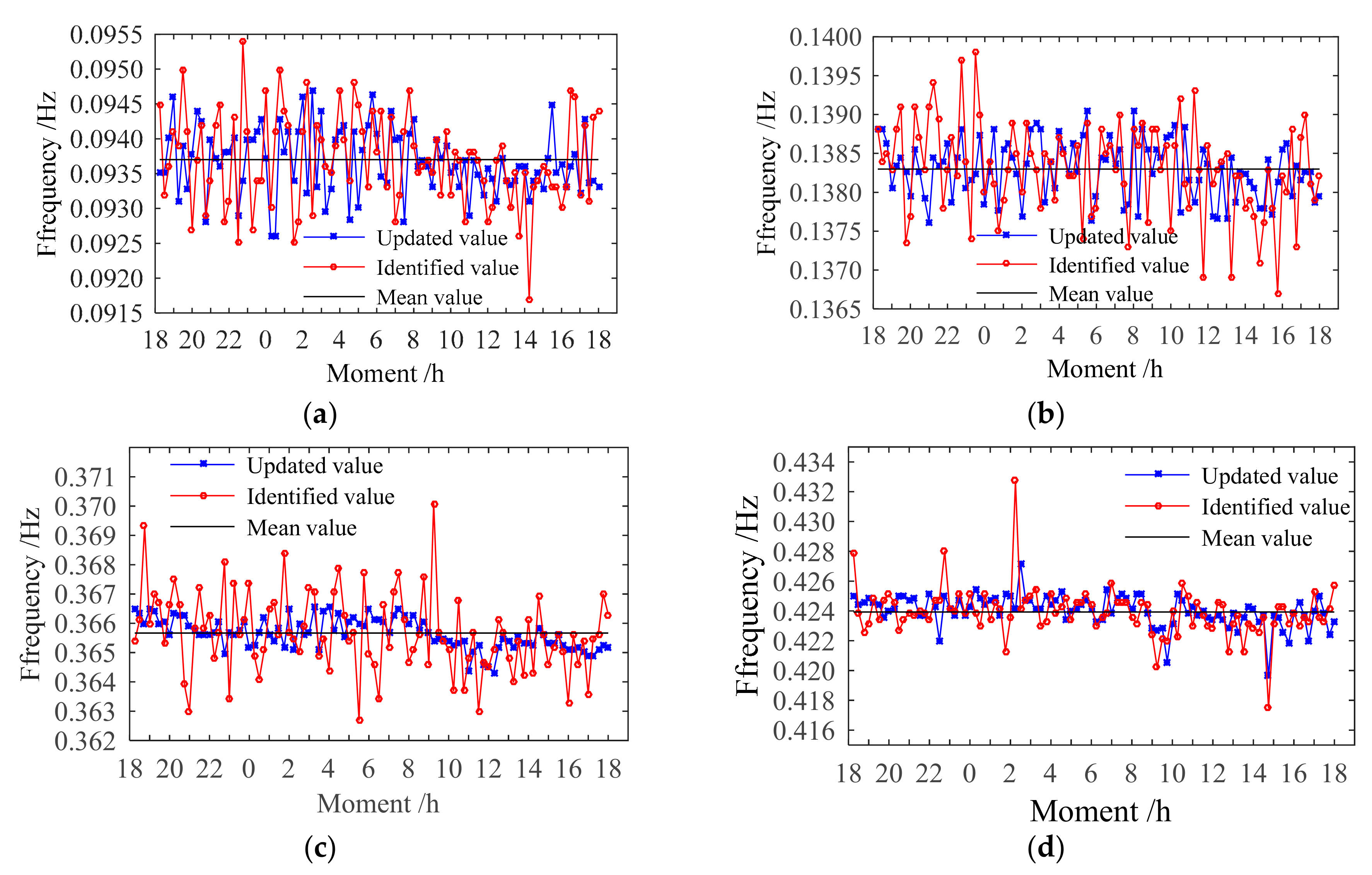
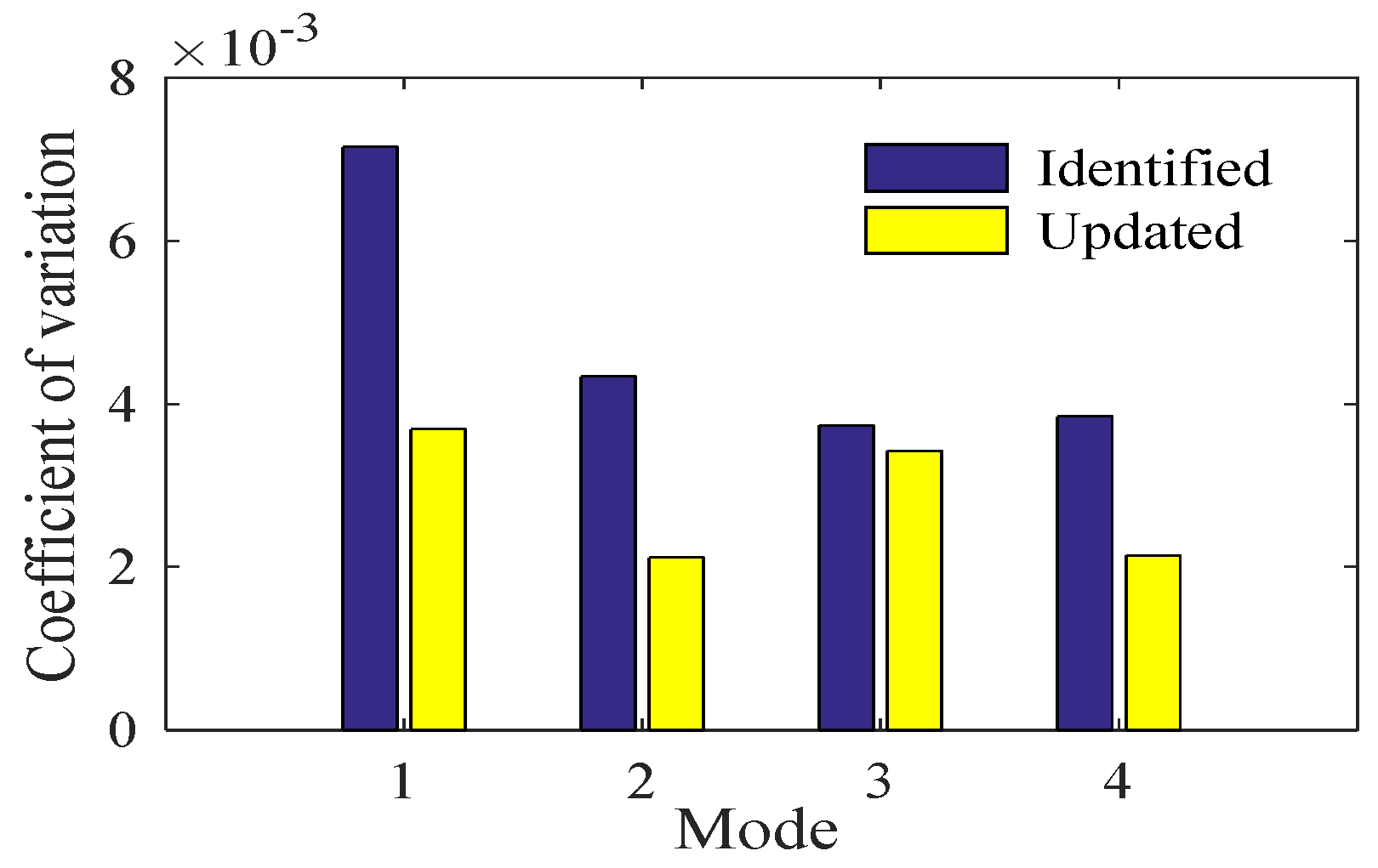
5.4. Updated Modal Frequency
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Xia, Y.; Chen, B.; Weng, S.; Ni, Y.; Xu, Y. Temperature effect on vibration properties of civil structures: A literature review and case studies. J. Civ. Struct. Health Monit. 2012, 2, 29–46. [Google Scholar] [CrossRef]
- Hu, W.; Cunha, A.; Caetano, E.; Rohrmann, R.G.; Said, S.; Teng, J. Comparison of different statistical approaches for removing environmental/operational effects for massive data continuously collected from footbridges. Struct. Control Health Monit. 2017, 24, e1955. [Google Scholar] [CrossRef]
- Deng, Y.; Ding, Y.; Li, A. Structural condition assessment of long-span suspension bridges using long-term monitoring data. Earthq. Eng. Eng. Vibr. 2010, 9, 123–131. [Google Scholar]
- Nayeri, R.; Masri, S.; Ghanem, R.; Nigbor, R. A novel approach for the structural identification and monitoring of a full-scale 17-story building based on ambient vibration measurements. Smart Mater. Struct. 2008, 17, 1–19. [Google Scholar] [CrossRef]
- Yuen, K.; Kuok, S. Ambient interference in long-term monitoring of buildings. Eng. Struct. 2010, 32, 2379–2386. [Google Scholar] [CrossRef]
- Faravelli, L.; Ubertini, F.; Fuggini, C. System identification of a super high-rise building via a stochastic subspace approach. Smart Struct.Syst. 2011, 7, 133–152. [Google Scholar] [CrossRef]
- Zhang, F.; Xiong, H.; Shi, W.; Ou, X. Structural health monitoring of Shanghai Tower during different stages using a Bayesian approach. Struct. Control Health Monit. 2016, 23, 1366–1384. [Google Scholar] [CrossRef]
- Demarie, G.; Sabia, D. A machine learning approach for the automatic long-term structural health monitoring. Struct. Health Monit. 2018, 18, 819–837. [Google Scholar] [CrossRef]
- Ni, Y.; Lu, X.; Lu, W. Operational modal analysis of a high-rise multi-function building with dampers by a Bayesian approach. Mech. Syst. Sig. Process. 2017, 86, 286–307. [Google Scholar] [CrossRef]
- Wu, W.; Wang, S.; Chen, C. Assessment of environmental and nondestructive earthquake effects on modal parameters of an office building based on long-term vibration measurements. Smart Mater. Struct. 2017, 26, 055034. [Google Scholar] [CrossRef]
- Behmanesh, I.; Moaveni, B.; Lombaert, G.; Lai, G. Hierarchical Bayesian model updating for structural identification. Mech. Syst. Sig. Process. 2015, 64–65, 360–376. [Google Scholar] [CrossRef]
- Jesus, A.; Brommer, P.; Westgate, R.; Koo, K.; Brownjohn, J.; Laory, I. Bayesian structural identification of a long suspension bridge considering temperature and traffic load effects. Struct. Health Monit. 2018, 4. [Google Scholar] [CrossRef]
- Worden, K.; Baldacchino, T.; Rowson, J.; Cross, E.J. Some recent developments in SHM based on nonstationary time series analysis. Proc. IEEE 2016, 104, 1589–1603. [Google Scholar] [CrossRef]
- Omenzetter, P.; Brownjohn, J.M.W. Application of time series analysis for bridge monitoring. Smart Mater. Struct. 2006, 15, 129–138. [Google Scholar] [CrossRef]
- Liu, C.; DeWolf, J.T.; Kim, J.H. Development of a baseline for structural health monitoring for a curved post-tensioned concrete box-girder bridge. Eng. Struct. 2009, 31, 3107–3115. [Google Scholar] [CrossRef]
- Li, H.; Li, S.; Ou, J.; Li, H. Modal identification of bridges under varying environmental conditions: Temperature and wind effects. Struct. Control Health Monit. 2010, 17, 495–512. [Google Scholar] [CrossRef]
- Shan, W.; Wang, X.; Jiao, Y. Vibration Analysis of Reinforced Concrete Simply Supported Beam versus Variation Temperature. Shock Vibr. 2017, 2017, 4931749. [Google Scholar]
- Teng, J.; Tang, D.; Zhang, X.; Hu, W.; Said, S.; Rohrmann, R. Automated Modal Analysis for Tracking Structural Change during Construction and Operation Phases. Sensors 2019, 19, 927. [Google Scholar] [CrossRef]
- Gui, G.; Pan, H.; Lin, Z.; Li, Y.; Yuan, Z. Data-driven support vector machine with optimization techniques for structural health monitoring and damage detection. KSCE J. Civ. Eng. 2017, 21, 523. [Google Scholar] [CrossRef]
- Li, G.; Zhao, X.; Du, K.; Ru, F.; Zhang, Y. Recognition and evaluation of bridge cracks with modified active contour model and greedy search-based support vector machine. Autom. Constr. 2017, 78, 51–61. [Google Scholar] [CrossRef]
- Ni, Y.; Hua, X.; Fan, K.; Ko, J.M. Correlating modal properties with temperature using long-term monitoring data and support vector machine technique. Eng. Struct. 2005, 27, 1762–1773. [Google Scholar] [CrossRef]
- Tibaduiza, D.A.; Mujica, L.E.; Rodellar, J.; Guemes, A. Structural damage detection using principal component analysis and damage indices. J. Intell. Mater. Syst. Struct. 2015, 27, 233–248. [Google Scholar] [CrossRef]
- Silva, M.; Santos, A.; Santos, R.; Figueiredo, E.; Sales, C.; Costa, J.C. Deep principal component analysis: An enhanced approach for structural damage identification. Struct. Health Monit. 2018, 18, 1444–1463. [Google Scholar] [CrossRef]
- Scholz, M.; Kaplan, F.; Guy, C.L.; Kopka, J.; Selbig, J. Nonlinear PCA: A missing data approach. Bioinformatics 2005, 21, 3887–3895. [Google Scholar] [CrossRef]
- Soares, C.; Brazdil, P.B.; Kuba, P. A meta-learning method to select the kernel width in support vector regression. Mach. Learn. 2004, 54, 195–209. [Google Scholar] [CrossRef]
- Liu, Z.; Xu, H. Kernel Parameter Selection for Support Vector Machine Classification. J. Algorithms Comput. Technol. 2014, 8, 163–177. [Google Scholar] [CrossRef]
- Ni, Y.; Xia, Y.; Lin, W.; Chen, W.; Ko, J.M. SHM benchmark for high-rise structures: A reduced-order finite element model and field measurement data. Smart Struct. Syst. 2012, 10, 411–426. [Google Scholar] [CrossRef]
- Ye, X.; Yan, Q.; Wang, W.; Yu, X. Modal identification of Canton Tower under uncertain environmental conditions. Smart Struct. Syst. 2012, 10, 353–373. [Google Scholar] [CrossRef]
- Zhang, H.; Chen, L.; Qu, Y.; Zhao, G.; Guo, Z. Support Vector Regression Based on Grid-Search Method for Short-Term Wind Power Forecasting. J. Appl. Math. 2014, 1–4, 1–11. [Google Scholar] [CrossRef]
- Tran-Ngoc, H.; Khatir, S.; De Roeck, G.; Bui-Tien, T.; Nguyen-Ngoc, L.; Abdel-Wahab, M. Model Updating for Nam O Bridge Using Particle Swarm Optimization Algorithm and Genetic Algorithm. Sensors 2018, 18, 4131. [Google Scholar] [CrossRef]
- Kanarachos, S.; Griffin, J.; Fitzpatrick, M. Efficient truss optimization using the contrast-based fruit fly optimization algorithm. Comput. Struct. 2017, 182, 137–148. [Google Scholar] [CrossRef]



| Data | Item | Correlation Coefficient | ||
|---|---|---|---|---|
| Original ambient data | - | Temperature | Wind speed | Wind direction |
| Temperature | 1 | 0.2547 | −0.3090 | |
| Wind speed | 0.2547 | 1 | −0.2736 | |
| Wind direction | −0.3090 | −0.2736 | 1 | |
| NLPCs | - | NLPC1 | NLPC2 | NLPC3 |
| NLPC1 | 1 | −2.46 × 10−17 | 5.66 × 10−17 | |
| NLPC2 | −2.46 × 10−17 | 1 | 9.73 × 10−17 | |
| NLPC3 | −5.66 × 10−17 | 9.73 × 10−17 | 1 | |
| Input | Method | Parameter | Optimal MSE | ||
|---|---|---|---|---|---|
| C | σ | ε | |||
| 1NLPC | GSM | 2.8284 | 8.8323 | 0.0975 | 0.040094 |
| GA | 26.5678 | 4.7221 | 0.0973 | 0.040131 | |
| FOA | 1.1628 | 0.1197 | 0.1057 | 0.031218 | |
| 2NLPC | GSM | 0.0884 | 16.0739 | 0.1000 | 0.037817 |
| GA | 0.3343 | 10.5849 | 0.1028 | 0.036574 | |
| FOA | 0.8325 | 0.0938 | 0.0882 | 0.028612 | |
| 3NLPC | GSM | 0.0625 | 11.3137 | 0.1000 | 0.038008 |
| GA | 0.1855 | 7.6122 | 0.1157 | 0.036829 | |
| FOA | 0.9828 | 0.1168 | 0.1060 | 0.029503 | |
| Input | Method | Parameter | Optimal MSE | ||
|---|---|---|---|---|---|
| C | σ | ε | |||
| Original measured data | GSM | 0.08793 | 11.3137 | 0.0975 | 0.040969 |
| GA | 59.5333 | 0.06361 | 0.0927 | 0.041225 | |
| FOA | 0.94248 | 0.1067 | 0.10587 | 0.031023 | |
| Mode | µ | s | df | t | T |
|---|---|---|---|---|---|
| 1 | −4.7481 × 10−5 | 2.9386 × 10−4 | 71 | −1.3710 | 1.993 |
| 2 | −5.1555 × 10−5 | 2.4383 × 10−4 | 71 | −1.7941 | 1.993 |
| 3 | −3.0228× 10−5 | 1.3211 × 10−3 | 71 | −0.1914 | 1.993 |
| 4 | 1.1689 × 10−5 | 9.6769 × 10−4 | 71 | 1.0249 | 1.993 |
| Mode | µ | s | df | t | T |
|---|---|---|---|---|---|
| 1 | 2.6099 × 10−5 | 4.7299 × 10−4 | 23 | 0.2703 | 2.069 |
| 2 | 1.5349 × 10−4 | 3.7102 × 10−4 | 23 | 2.0266 | 2.069 |
| 3 | 1.5427 × 10−5 | 9.6760 × 10−4 | 23 | 0.0781 | 2.069 |
| 4 | 8.9497 × 10−5 | 7.1578 × 10−4 | 23 | 0.6125 | 2.069 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ye, X.; Wu, Y.; Zhang, L.; Mei, L.; Zhou, Y. Ambient Effect Filtering Using NLPCA-SVR in High-Rise Buildings. Sensors 2020, 20, 1143. https://doi.org/10.3390/s20041143
Ye X, Wu Y, Zhang L, Mei L, Zhou Y. Ambient Effect Filtering Using NLPCA-SVR in High-Rise Buildings. Sensors. 2020; 20(4):1143. https://doi.org/10.3390/s20041143
Chicago/Turabian StyleYe, Xijun, Yingfeng Wu, Liwen Zhang, Liu Mei, and Yunlai Zhou. 2020. "Ambient Effect Filtering Using NLPCA-SVR in High-Rise Buildings" Sensors 20, no. 4: 1143. https://doi.org/10.3390/s20041143
APA StyleYe, X., Wu, Y., Zhang, L., Mei, L., & Zhou, Y. (2020). Ambient Effect Filtering Using NLPCA-SVR in High-Rise Buildings. Sensors, 20(4), 1143. https://doi.org/10.3390/s20041143






