On the Use of Weighted Least-Squares Approaches for Differential Interferometric SAR Analyses: The Weighted Adaptive Variable-lEngth (WAVE) Technique
Abstract
1. Introduction
2. Weighted Least-Squares Inversion of SB Differential SAR Interferograms
2.1. Summary of the Un-Weighted SBAS Inversion Technique
2.2. EMCF-Based Multi-Temporal Phase Unwrapping
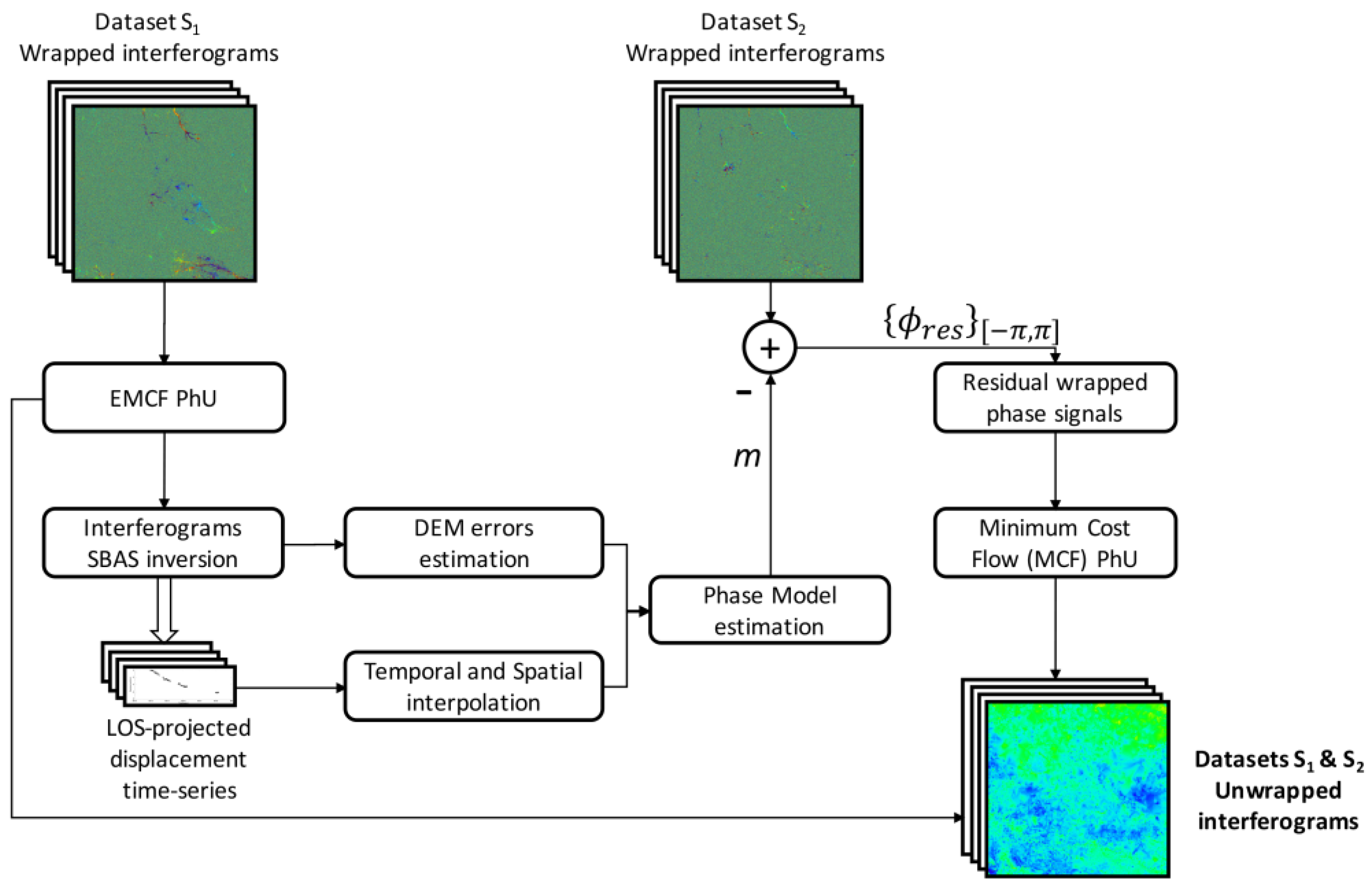
2.3. Weighted Adaptive Variable-lEngth (WAVE) InSAR Method
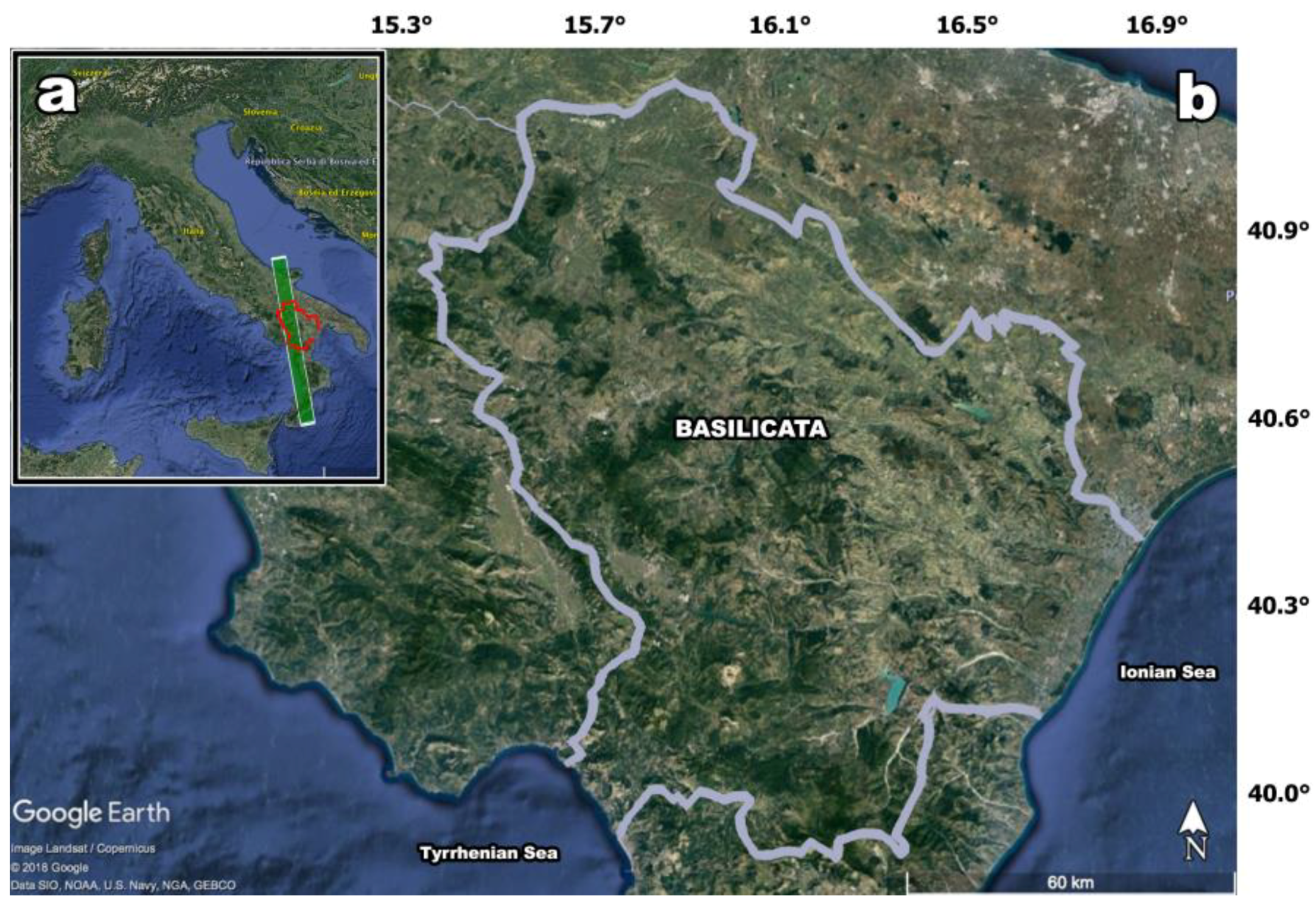
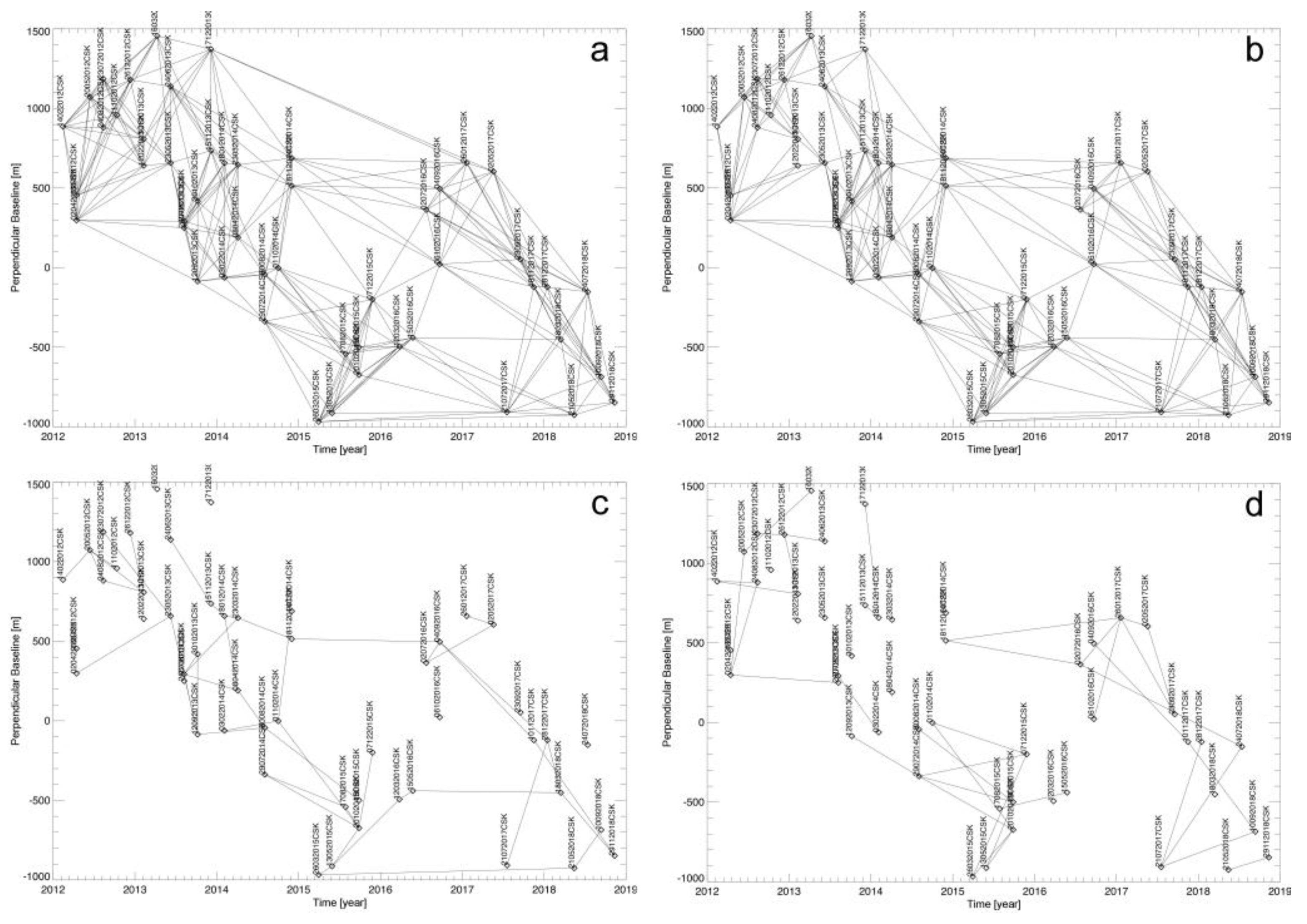
3. Dataset and Study Area
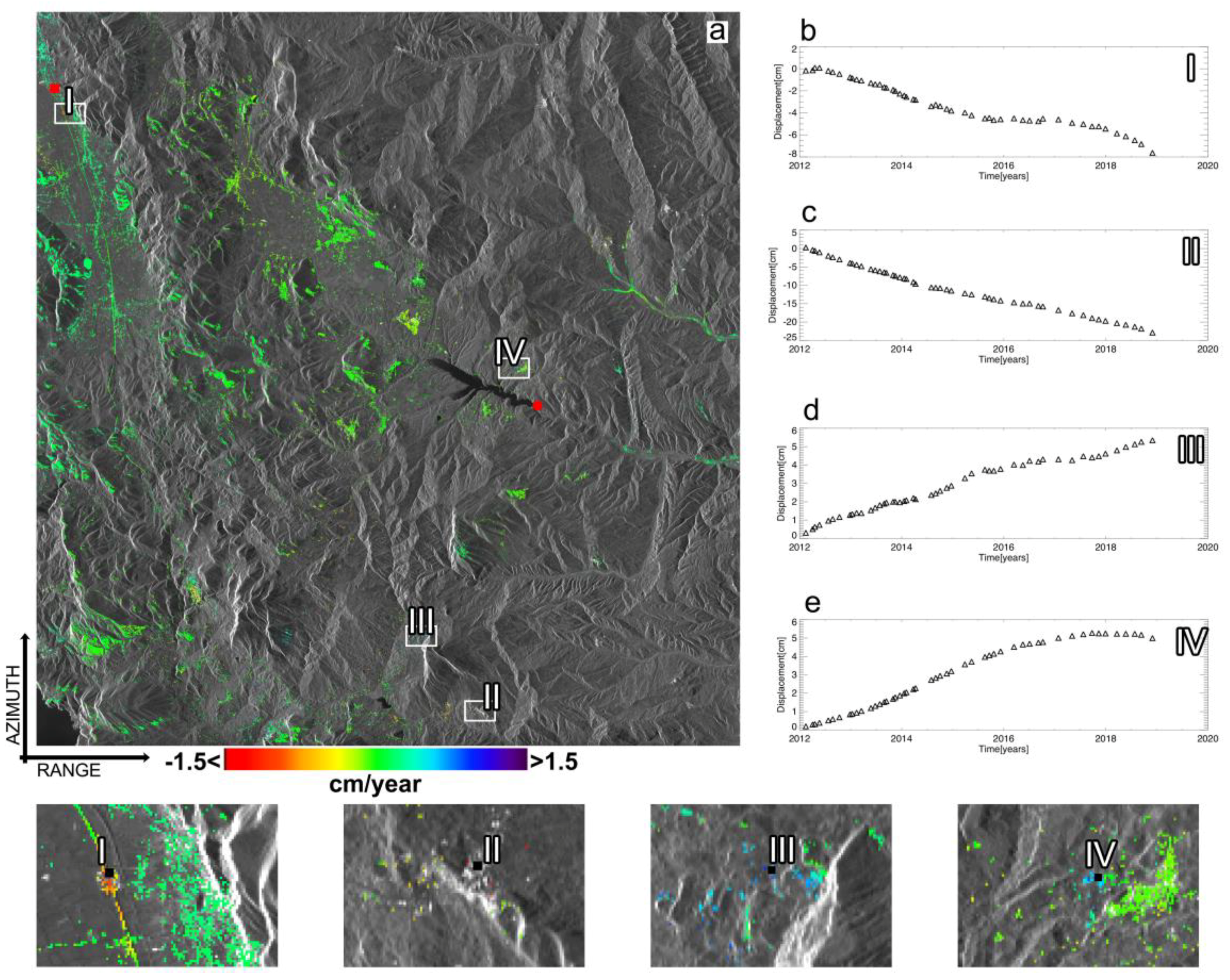
4. Experimental Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Strutz, T. Data Fitting and Uncertainty: A Practical Introduction to Weighted Least Squares and Beyond; Springer Vieweg: Wiesbaden, Germany; ISBN 978-3-658-11455-8.
- Massonnet, D.; Rossi, M.; Carmona, C.; Ardagna, F.; Peltzer, G.; Feigl, K.; Rabaute, T. The displacement field of the Landers earthquake mapped by radar interferometry. Nature 1993, 364, 138–142. [Google Scholar] [CrossRef]
- Gabriel, A.K.; Goldstein, R.M.; Zebker, H.A. Mapping small elevation changes over large areas: Differential interferometry. J. Geophys. Res. 1989, 94, 9183–9191. [Google Scholar] [CrossRef]
- Peltzer, G.; Rosen, P.A. Surface displacement of the 17 May 1993 Eureka Valley earthquake observed by SAR interferometry. Science 1995, 268, 1333–1336. [Google Scholar] [CrossRef] [PubMed]
- Zebker, H.A.; Villasenor, J. Decorrelation in interferometric radar echoes. IEEE Trans. Geosci. Remote Sens. 1992, 30, 950–959. [Google Scholar] [CrossRef]
- Bamler, R.; Hartl, P. Synthetic Aperture Radar interferometry. Inverse Probl. 1998, 14, R1–R54. [Google Scholar] [CrossRef]
- Lee, J.S.; Lee, K.W.; Hoppel, S.; Mango, A.; Miller, A.R. Intensity and Phase Statistics of Multilook Polarimetric and Interferometric SAR Imagery. IEEE Trans. Geosci. Remote Sens. 1994, 32, 1017–1028. [Google Scholar]
- Massonnet, D.; Briole, P.; Arnaud, A. Deflation of Mount Etna monitored by spaceborne Radar interferometry. Nature 1995, 375, 567–570. [Google Scholar] [CrossRef]
- Fialko, Y.; Simons, M.; Agnew, D. The complete (3-D) surface displacement field in the epicentral area of the 1999 Mw 7.1 Hector Mine earthquake, California, from space geodetic observations. Geophys. Res. Lett. 2001, 28, 3063–3066. [Google Scholar] [CrossRef]
- Ferretti, A.; Prati, C.; Rocca, F. Permanent scatterers in SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2001, 39, 8–20. [Google Scholar] [CrossRef]
- Kampes, B.M. Radar Interferometry: Persistent Scatterer Technique; Springer: New York, NY, USA, 2006. [Google Scholar]
- Werner, C.; Wegmuller, U.; Strozzi, T.; Wiesmann, A. Interferometric point target analysis for deformation mapping. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Toulouse, France, 21–25 July 2003; pp. 4362–4364. [Google Scholar]
- Hooper, A.; Zebker, H.; Segall, P.; Kampes, B.M. A new method for measuring deformation on volcanoes and other natural terrains using InSAR persistent scatterers. Geophys. Res. Lett. 2004, 31, L23611. [Google Scholar] [CrossRef]
- Berardino, P.; Fornaro, G.; Lanari, R.; Sansosti, E. A new algorithm for surface deformation monitoring based on small baseline differential SAR interferograms. IEEE Trans. Geosci. Remote Sens. 2004, 40, 2375–2383. [Google Scholar] [CrossRef]
- Lanari, R.; Mora, O.; Manunta, M.; Mallorquì, J.J.; Berardino, P.; Sansosti, E. A small baseline approach for investigating deformation on full resolution differential SAR interferograms. IEEE Trans. Geosci Remote Sens. 2004, 42, 1377–1386. [Google Scholar] [CrossRef]
- Mora, O.; Mallorqui, J.J.; Broquetas, A. Linear and nonlinear terrain deformation maps from a reduced set of interferometric SAR images. IEEE Trans. Geosci. Remote Sens., 2003, 41, 2243–2253. [Google Scholar] [CrossRef]
- Usai, S. A least squares database approach for SAR interferometric data. IEEE Trans. Geosci. Remote Sens. 2003, 41, 753–760. [Google Scholar] [CrossRef]
- Shirzaei, M. A Wavelet-Based Multitemporal DInSAR Algorithm for Monitoring Ground Surface Motion. IEEE Geosci. Remote Sens. Lett. 2013, 10, 456–460. [Google Scholar] [CrossRef]
- Schmidt, D.; Burgmann, R. Time-Dependent Land Uplift and Subsidence in the Santa Clara Valley, California, from a large interferometric synthetic aperture radar data set. J. Geophys. Res. Solid Earth 2003. [Google Scholar]
- Hetland, E.A.; Muse, P.; Simons, M.; Lin, Y.N.; Agram, P.S.; DiCaprio, C.J. Multiscale InSAR time series (MInTS) analysis of surface deformation. J. Geophys. Res. Solid Earth 2012, 117, B02404. [Google Scholar] [CrossRef]
- Hooper, A. A multi-temporal InSAR method incorporating both persistent scatterer and small baseline approaches. Geophys. Res. Lett. 2008, 35, L16302. [Google Scholar] [CrossRef]
- Pepe, A.; Yang, Y.; Manzo, M.; Lanari, R. Improved EMCF-SBAS Processing Chain Based on Advanced Techniques for the Noise-Filtering and Selection of Small Baseline Multi-look DInSAR Interferograms. IEEE Trans. Geosci. Remote Sens. 2015, 53, 4394–4417. [Google Scholar] [CrossRef]
- Ferretti, A.; Fumagalli, A.; Novali, F.; Prati, C.; Rocca, V.; Rucci, A. A New Algorithm for Processing Interferometric Data-Stacks: SqueeSAR. IEEE Trans. Geosci. Remote Sens. 2001, 49, 3460–3470. [Google Scholar] [CrossRef]
- Fornaro, G.; Verde, S.; Reale, D.; Pauciullo, A. CAESAR: An approach based on covariance matrix decomposition to improve multibaseline multitemporal interferometric SAR processing. IEEE Trans. Geosc. Remote Sens. 2015, 4, 2050–2065. [Google Scholar] [CrossRef]
- Parizzi, A.; Brcic, R. Adaptive InSAR stack multi-looking exploiting amplitude statistics: A comparison between different techniques and practical results. IEEE Geosci. Remote Sens. Lett. 2011, 8, 441–445. [Google Scholar] [CrossRef]
- Pinel-Puyssegur, B.; Michel, R.; Avouac, J.P. Multi-link InSAR time-series: Enhancement of a wrapped interferometric database. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 784–794. [Google Scholar] [CrossRef]
- Esfahany, S.S.; Martins, J.E.; van Leijen, F.; Hanssen, R.F. Phase Estimation for Distributed Scatterers in InSAR Stacks Using Integer Least Squares Estimation. IEEE Trans. Geosci. Remote Sens. 2016, 54, 5671–5687. [Google Scholar] [CrossRef]
- Hooper, A.; Spaans, K.; Bekaert, D.; Cuenca, M.C.; Arıkan, M.; Oyen, A. StaMPS/MTI Manual, Delft Institute of Earth Observation and Space Systems Delft University of Technology, Kluyverweg 1, 2629 HS, Delft, The Netherlands 2010. Available online: http://radar.tudelft.nl/~ahooper/stamps/StaMPS_Manual_v3.2.pdf (accessed on 13 February 2020).
- Yunjun, Z.; Fattahi, H.; Amelung, F. Small baseline InSAR time series analysis: Unwrapping error correction and noise reduction. Comput. Geosci. 2019, 133, 104331. [Google Scholar] [CrossRef]
- Ansari, H.; De Zan, F.; Bamler, R. Distributed Scatterer Interferometry Tailored to the Analysis of Big InSAR Data; EUSAR: Aachen, Germany, 2018. [Google Scholar]
- Lauknes, T.S.; Shanker, A.P.; Dehls, J.F.; Zebker, H.A.; Henderson, I.H.C.; Larsen, Y. Detailed rockslide mapping in northern Norway with small baseline and persistent scatterer interferometric SAR time series methods. Remote Sens. Environ. 2010, 114, 2097–2109. [Google Scholar] [CrossRef]
- Chaussard, E.; Wdowinski, S.; Cabral-Can, E. Land subsidence in central Mexico detected by ALOS InSAR time-series. Remote Sens. Environ. 2014, 140, 94–106. [Google Scholar] [CrossRef]
- Wright, T.J.; Parsons, B.; England, P.C.; Fielding, E.J. InSAR observations of low slip rates on the major faults of western Tibet. Science 2004, 305, 236–239. [Google Scholar] [CrossRef]
- Lanari, R.; Lundgren, P.; Manzo, M.; Casu, F. Satellite radar interferometry time-series analysis of surface deformation for Los Angeles, California. Geophys. Res. Lett. 2004, 31. [Google Scholar] [CrossRef]
- Manunta, M.; Marsella, M.; Zeni, G.; Sciotti, M.; Atzori, S.; Lanari, R. Two-scale surface deformation analysis using the SBAS-DInSAR technique: A case study of the city of Rome, Italy. Int. J. Remote Sens. 2008, 29, 1665–1684. [Google Scholar] [CrossRef]
- Stramondo, S.; Bozzano, F.; Marra, F.; Wegmuller, U.; Cinti, F.R.; Moro, M.; Saroli, M. Subsidence induced by urbanisation in the city of Rome detected by advanced InSAR technique and geotechnical investigations. Remote Sens. Environ. 2008, 112, 3160–3172. [Google Scholar] [CrossRef]
- Ding, X.L.; Liu, G.X.; Li, Z.W. Ground subsidence monitoring in Hong Kong with satellite SAR interferometry. Photogramm. Eng. Remote Sens. 2004, 70, 1151–1156. [Google Scholar] [CrossRef]
- Zeni, G.; Bonano, M.; Casu, F.; Manunta, M.; Manzo, M.; Marsella, M.; Pepe, A.; Lanari, R. Long-term deformation analysis of historical buildings through the advanced SBAS-DInSAR technique: The case study of the city of Rome, Italy. J. Geophys. Eng. 2011, 8, S1–S12. [Google Scholar] [CrossRef]
- Lauknes, R.T.; Zebker, H.A.; Yngvar, L. InSAR Deformation Time Series Using an L1-Norm Small-Baseline Approach. IEEE Trans. Geosci. Remote Sens. 2011, 49, 536–546. [Google Scholar] [CrossRef]
- Strang, G. Linear Algebra and Its Applications; Harcourt Brace Jovanovich: Orlando, FL, USA, 1988. [Google Scholar]
- Goldstein, R.M.; Zebker, H.A.; Werner, C.L. Satellite radar interferometry: Two-dimensional Phase unwrapping. Radio Sci. 1988, 23, 713–720. [Google Scholar] [CrossRef]
- Ghiglia, D.C.; Romero, L.A. Robust two-dimensional weighted and unweighted phase unwrapping that uses fast transforms and iterative methods. J. Opt. Soc. Amer. A 1994, 11, 107–117. [Google Scholar] [CrossRef]
- Pritt, M.D.; Shipman, J.S. Least-squares two-dimensional phase unwrapping using FFTs. IEEE Trans. Geosci. Remote Sens. 1994, 32, 706–708. [Google Scholar] [CrossRef]
- Fornaro, G.; Franceschetti, G.; Lanari, R. Interferometric SAR phase unwrapping using Green’s formulation. IEEE Trans. Geosci. Remote Sens. 1996, 34, 720–727. [Google Scholar] [CrossRef]
- Kerr, D.; Kaufmann, G.H.; Galizzi, G.E. Unwrapping of interferometric phase-fringe maps by the discrete cosine transform. Appl. Opt. 1996, 35, 810–816. [Google Scholar] [CrossRef]
- Pritt, M.D. Phase unwrapping by means of multigrid techniques for interferometric SAR. IEEE Trans. Geosci. Remote Sens. 1996, 34, 728–738. [Google Scholar] [CrossRef]
- Flynn, T. Two-dimensional phase unwrapping with minimum weighted discontinuity. J. Opt. Soc. Amer. A 1997, 14, 2692–2701. [Google Scholar] [CrossRef]
- Fornaro, G.; Franceschetti, G.; Lanari, R.; Rossi, D.; Tesauro, M. Interferometric SAR phase unwrapping using the finite element method. IEE Proc. Radar Sonar Navigat. 1997, 144, 266–274. [Google Scholar] [CrossRef]
- Costantini, M. A novel phase unwrapping method based on network programming. IEEE Trans. Geosci. Remote Sens. 1998, 36, 813–821. [Google Scholar] [CrossRef]
- Costantini, M.; Rosen, P.A. A generalized phase unwrapping approach for sparse data. In Proceedings of the IEEE 1999 International Geoscience and Remote Sensing Symposium. (IGARSS), Hamburg, Germany, 28 June–2 July 1999; pp. 267–269. [Google Scholar]
- Xu, W.; Cumming, I. A region-growing algorithm for InSAR phase unwrapping. IEEE Trans. Geosci. Remote Sens. 1999, 37, 124–134. [Google Scholar] [CrossRef]
- Su, X.; Chen, W. Reliability-guided phase unwrapping algorithm: A review. Opt. Lasers Eng. 2004, 42, 245–261. [Google Scholar] [CrossRef]
- Yuangang, L.; Xiangzhao, W.; Xuping, Z. Weighted least-squares phase unwrapping algorithm based on derivative variance correlation map. Optics Laser Eng. 2007, 118, 62–66. [Google Scholar]
- Lu, Y.; Zhao, W.; Zhang, X.; Xu, W.; Xu, G. Weighted-phase-gradient-based quality maps for two-dimensional quality-guided phase unwrapping. Optics Laser Eng. 2012, 50, 1397–1404. [Google Scholar] [CrossRef]
- Yuan, G.; Xiaotian, C.; Tao, Z. Robust phase unwrapping algorithm based on least squares. Optics Laser Eng. 2014, 63, 25–29. [Google Scholar]
- Delaunay, B. Sur la sphère vide. A la mémoire de Georges Voronoï. Bull. l’Académie des Sci. l’URSS, Cl. des. Sci. Mathématiques et Nat. 1934, 6, 793–800. [Google Scholar]
- Hoffman, J.; Zebker, H.A. Prospecting for horizontal surface displacements in Antelope Valley, California, using satellite radar interferometry. J. Geophys. Res. 2003, 108, F16011. [Google Scholar] [CrossRef]
- Hooper, A.; Zebker, H.A. Phase unwrapping in three dimensions with applications to InSAR time series. J. Opt. Soc. Amer. A 2007, 24, 2737–3747. [Google Scholar] [CrossRef]
- Costantini, M.; Falco, S.; Malvarosa, F.; Minati, F.; Trillo, F.; Vecchioli, F. A general formulation for robust integration of finite differences and phase unwrapping on sparse multidimensional domains. In Proceedings of the IEEE Transactions on Geoscience and Remote Sensing, Frascati, Italy, 30 November–4 December 2009. [Google Scholar]
- Pepe, A.; Lanari, R. On the extension of the minimum cost flow algorithm for phase unwrapping of multi-temporal differential SAR interferograms. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2374–2383. [Google Scholar] [CrossRef]
- Fornaro, G.; Pauciullo, A.; Reale, D. A null-space method for the phase unwrapping of multitemporal SAR interferometric stacks. IEEE Trans. Geosci. Remote Sens. 2011, 49, 2323–2334. [Google Scholar] [CrossRef]
- Akbari, V.; Motagh, M. Improved Ground Subsidence Monitoring Using Small Baseline SAR Interferograms and a Weighted Least Squares Inversion Algorithm. IEEE Geosci. Remote Sens. Lett. 2012, 9, 437–441. [Google Scholar] [CrossRef]
- Hu, J.; Li, Z.; Ding, X.; Zhu, J.; Sun, Q. Spatial-temporal surface deformation of Los Angeles over 2003–2007 from weighted least squares DInSAR. Int. J. Appl. Earth Obs. Geoinf. 2013, 21, 484–492. [Google Scholar] [CrossRef]
- Zhang, K.; Li, Z.; Meng, G.; Dai, Y. A very fast phase inversion approach for small baseline style interferogram stacks. ISPRS J. Photogramm. Remote Sens. 2014, 97, 1–8. [Google Scholar] [CrossRef]
- Ghaderpour, E.; Sinem Ince, E.; Spiros, D.; Pagiatakis, D. Least-squares cross-wavelet analysis and its applications in geophysical time series. J. Geod. 2018, 92, 1223–1236. [Google Scholar] [CrossRef]
- VanLoan, C.F. Generalized Singular Values with Algorithms and Applications. Ph.D. thesis, University of Michigan, Ann Arbor, Michigan, 1973. [Google Scholar]
- Golub, G.H.; Reinsch, C. Singular value decomposition and least squares solutions. Numer. Math. 1970, 14, 403–420. [Google Scholar] [CrossRef]
- Chan, T.F. An Improved Algorithm for Computing the Singular Value Decomposition. ACM Trans. Math. Softw. 1982, 8, 72–83. [Google Scholar] [CrossRef]
- Sowter, A.; Bateson, L.; Strange, P.; Ambrose, K.; Syafiudin, M. DInSAR estimation of land motion using intermittent coherence with application to the South Derbyshire and Leicestershire coalfield. Remote Sens. Lett. 2013, 4, 979–987. [Google Scholar] [CrossRef]
- Cigna, F.; Sowter, A. The relationship between intermittent coherence and precision of ISBAS InSAR ground motion velocities: ERS-1/2 case studies in the UK. Remote Sens. Environ. 2017, 202, 177–198. [Google Scholar] [CrossRef]
- Rosen, P.A.; Hensley, S.; Joughin, I.R.; Li, F.K.; Madsen, F.R.; Rodriguez, E.; Goldstein, R.M. Synthetic Aperture Radar interferometry. Proc. IEEE 2000, 88, 333–381. [Google Scholar] [CrossRef]
- Pepe, A.; Ortiz, B.; Lundgren, P.R.; Rosen, P.A.; Lanari, R. The Stripmap-ScanSAR SBAS Approach to Fill Gaps in Stripmap Deformation Time-Series With ScanSAR data. IEEE Trans. Geosci. Remote Sens. 2011, 49, 4788–4804. [Google Scholar] [CrossRef]
- Manunta, M.; De Luca, C.; Zinno, I.; Casu, F.; Manzo, M.; Bonano, M.; Fusco, A.; Pepe, A.; Onorato, G.; Berardino, P.; et al. The Parallel SBAS Approach for Sentinel-1 Interferometric Wide Swath Deformation Time-Series Generation: Algorithm Description and Products Quality Assessment. IEEE Trans. Geosci. Remote Sens. 2019, 57, 6259–6281. [Google Scholar] [CrossRef]
- Touzi, R.; Lopes, A. Statistics of the Stokes parameters and the complex coherence parameters in one-look and multilook speckle fields. IEEE Trans. Geosci. Remote Sens. 1996, 34, 519–531. [Google Scholar] [CrossRef]
- Tough, J.A.; Blacknell, D.; Quegan, S. A statistical description of polarimetric and interferometric synthetic aperture radar. Proc. Royal Soc. Lond. A 1995, 449, 567–589. [Google Scholar]
- Mardia, K.V.; Jupp, P.E. Directional Statistics; Wiley: New York, NY, USA, 2000. [Google Scholar]
- Draper, N.R.; Smith, H. Applied Regression Analysis; John Wiley & Sons: Hoboken, NJ, USA, 1988. [Google Scholar]
- Agram, P.; Simons, S. A noise model for InSAR time-series. J. Geophys. Res. Solid Earth 2015, 120, 2752–2771. [Google Scholar] [CrossRef]
- Van Loan, C.F. Generalizing the singular value decomposition. SIAM J. Numer. Anal. 1976, 13, 76–83. [Google Scholar] [CrossRef]
- Spizzichino, D.; Falconi, L.; Delmonaco, G.; Margottini, C.; Puglisi, V. Integrated approach for landslide risk assessment of Craco village (Italy). Landslides: Evaluation and Stabil-Ization. Balkema; Lacerda, W.A., Ehrlich, M., Fontoura, S.A.B., Sayao, A.S.F., Eds.; Taylor & Francis Group: London, UK, 2004; pp. 237–242. [Google Scholar]
- Guzzetti, F. Landslide fatalities and the evaluation of landslide risk in Italy. Eng. Geol. 2000, 58, 89–107. [Google Scholar] [CrossRef]
- Berardino, P.; Costantini, M.; Franceschetti, G.; Iodice, A.; Pietranera, L.; Rizzo, V. Use of differential SAR interferometry in monitoring and modelling large slope instability at Maratea (Basilicata, Italy). Eng. Geol. 2003, 68, 31–51. [Google Scholar]
- Di Maio, C.; Fornaro, G.; Gioia, D.; Reale, D.; Schiattarella, M.; Vassallo, R. In situ and satellite long-term monitoring of the Latronico landslide, Italy: Displacement evolution, damage to buildings, and effectiveness of remedial works. Eng. Geol. 2018, 245, 218–235. [Google Scholar] [CrossRef]
- Manconi, A.; Casu, F.; Ardizzone, F.; Bonano, M.; Cardinali, M.; De Luca, C.; Gueguen, E.; Marchesini, I.; Parise, M.; Vennari, C.; et al. Brief Communication: Rapid mapping of landslide events: The 3 December 2013 Montescaglioso landslide, Italy. Nat. Hazards Earth Syst. Sci. 2014, 14, 1835–1841. [Google Scholar] [CrossRef]
- Westaway, R.; Jackson, J. Surface faulting in the southern Italian Campania-Basilicata earthquake of 23 November. Nature 1984, 312, 436–438. [Google Scholar] [CrossRef]
- Westaway, R.; Jackson, J. The earthquake of 1980 November 23 in Campania—Basilicata (southern Italy). Geophys. J. Int. 1987, 90, 375–443. [Google Scholar] [CrossRef]
- Cello, G.; Tondi, E.; Micarelli, L.; Mattioni, L. Active tectonics and earthquake sources in the epicentral area of the 1857 Basilicata earthquake (Southern Italy). J. Geodyn. 2003, 36, 37–50. [Google Scholar] [CrossRef]
- Benedetti, L.; Tapponier, P.; King, G.C.; Piccardi, L. Surface rupture due to the 1857 Southern Italian Earthquake. Terra Nova. 1998, 10, 206–210. [Google Scholar] [CrossRef]
- Covello, F.; Battazza, F.; Coletta, A.; Lopinto, E.; Fiorentino, C.; Pietranera, L.; Valentini, G.; Zoffoli, S. COSMO-SkyMed an existing opportunity for observing the Earth. J. Geodyn. 2010, 49, 171–180. [Google Scholar] [CrossRef]
- Bamler, R. A comparison of range-Doppler and wavenumber domain SAR focusing algorithms. IEEE Trans. Geosci. Remote Sens. 1992, 30, 706–713. [Google Scholar] [CrossRef]
- Imperatore, P.; Pepe, A.; Lanari, R. Spaceborne Synthetic Aperture Radar Data Focusing on Multicore-Based Architectures. IEEE Trans. Geosci Remote Sens. 2016, 54, 4712–4731. [Google Scholar] [CrossRef]
- Goldstein, R.M.; Werner, C.L. Radar interferogram filtering for geophysical applications. Geophys. Res. Lett. 1998, 25, 4035–4038. [Google Scholar] [CrossRef]
- Blewitt, G.; Hammond, W.C.; Kreemer, C. Harnessing the GPS Data Explosion for Interdisciplinary Science. Eos 2018, 99, 1–2. [Google Scholar] [CrossRef]
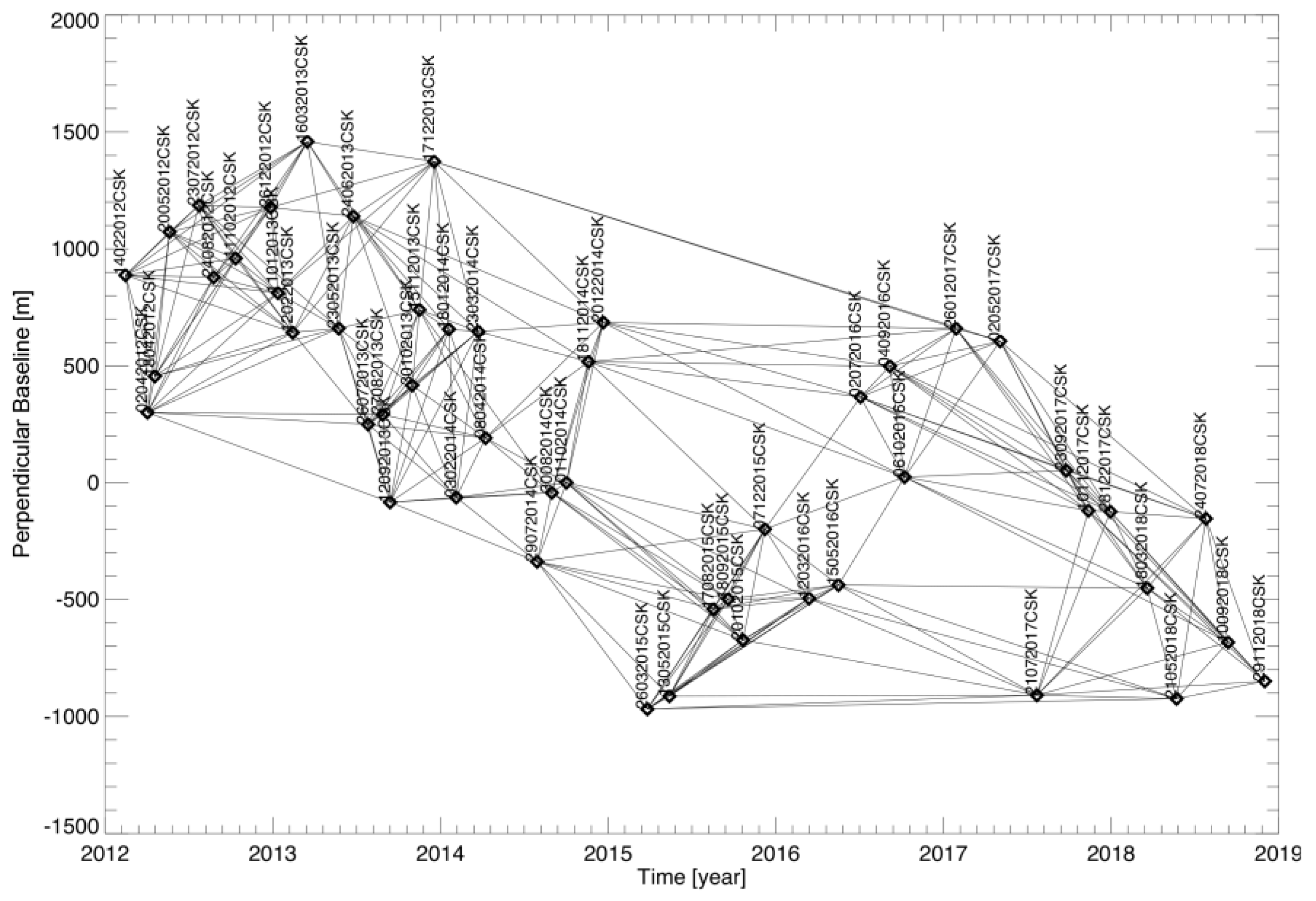








| Day | Month | Year | ||
|---|---|---|---|---|
| 14 | 02 | 2012 | 887.96 | −1164.2 |
| 02 | 04 | 2012 | 300.52 | −1136.8 |
| 18 | 04 | 2012 | 455.29 | −1074.5 |
| 20 | 05 | 2012 | 1072.3 | −1241.8 |
| 23 | 07 | 2012 | 1186.6 | −1133.3 |
| 24 | 08 | 2012 | 878.17 | −1176.1 |
| 11 | 10 | 2012 | 959.50 | −1235.1 |
| 26 | 12 | 2012 | 1177.6 | −653.37 |
| 11 | 01 | 2013 | 811.07 | −659.16 |
| 12 | 02 | 2013 | 642.53 | −681.40 |
| 16 | 03 | 2013 | 1458.4 | −536.96 |
| 23 | 05 | 2013 | 660.91 | −1092.4 |
| 24 | 06 | 2013 | 1139.4 | −1176.9 |
| 26 | 07 | 2013 | 249.04 | −1188.3 |
| 27 | 08 | 2013 | 291.91 | −1201.2 |
| 12 | 09 | 2013 | −83.779 | −1194.1 |
| 30 | 10 | 2013 | 416.50 | −1196.9 |
| 15 | 11 | 2013 | 739.37 | −1187.5 |
| 17 | 12 | 2013 | 1373.2 | −1231.9 |
| 18 | 01 | 2014 | 656.69 | −1237.0 |
| 03 | 02 | 2014 | −62.523 | −1206.4 |
| 23 | 03 | 2014 | 646.41 | −1163.4 |
| 08 | 04 | 2014 | 191.51 | −1099.6 |
| 29 | 07 | 2014 | −337.35 | −1227.3 |
| 30 | 08 | 2014 | −42.907 | −1206.0 |
| 01 M | 10 M | 2014 M | 0.0000 M | −1236.5 M |
| 18 | 11 | 2014 | 517.28 | −1194.4 |
| 20 | 12 | 2014 | 685.74 | −1211.9 |
| 26 | 03 | 2015 | −967.52 | −1224.9 |
| 13 | 05 | 2015 | −912.84 | −1182.2 |
| 17 | 08 | 2015 | −540.35 | −1245.1 |
| 18 | 09 | 2015 | −497.50 | −1325.8 |
| 20 | 10 | 2015 | −672.71 | −1384.0 |
| 07 | 12 | 2015 | −198.14 | −1189.8 |
| 12 | 03 | 2016 | −494.75 | −1284.2 |
| 15 | 05 | 2016 | −437.48 | −1081.5 |
| 02 | 07 | 2016 | 366.08 | −1185.4 |
| 04 | 09 | 2016 | 498.12 | −1258.2 |
| 06 | 10 | 2016 | 24.905 | −1266.8 |
| 26 | 01 | 2017 | 659.14 | −1252.1 |
| 02 | 05 | 2017 | 605.27 | −1209.8 |
| 21 | 07 | 2017 | −909.00 | −1334.3 |
| 23 | 09 | 2017 | 52.237 | −1414.1 |
| 10 | 11 | 2017 | −119.79 | −1291.0 |
| 28 | 12 | 2017 | −123.48 | −1521.1 |
| 18 | 03 | 2018 | −450.21 | −1258.0 |
| 21 | 05 | 2018 | −924.02 | −1275.6 |
| 24 | 07 | 2018 | −153.99 | −1218.1 |
| 10 | 09 | 2018 | −682.59 | −1296.5 |
| 29 | 11 | 2018 | −848.53 | −1290.5 |
| Figure Identifier | Name | RMSE [mm] |
|---|---|---|
| 13.b | AGR2 | 3.75 |
| 13.c | MTSN | 3.19 |
| 13.d | RVLO | 3.34 |
| 13.e | SCHR | 3.17 |
| 13.f | SIRI | 2.82 |
| 13.g | VIGG | 3.10 |
| 13.h | SLC1 | 3.49 |
| Mean RMSE | 3.27 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Falabella, F.; Serio, C.; Zeni, G.; Pepe, A. On the Use of Weighted Least-Squares Approaches for Differential Interferometric SAR Analyses: The Weighted Adaptive Variable-lEngth (WAVE) Technique. Sensors 2020, 20, 1103. https://doi.org/10.3390/s20041103
Falabella F, Serio C, Zeni G, Pepe A. On the Use of Weighted Least-Squares Approaches for Differential Interferometric SAR Analyses: The Weighted Adaptive Variable-lEngth (WAVE) Technique. Sensors. 2020; 20(4):1103. https://doi.org/10.3390/s20041103
Chicago/Turabian StyleFalabella, Francesco, Carmine Serio, Giovanni Zeni, and Antonio Pepe. 2020. "On the Use of Weighted Least-Squares Approaches for Differential Interferometric SAR Analyses: The Weighted Adaptive Variable-lEngth (WAVE) Technique" Sensors 20, no. 4: 1103. https://doi.org/10.3390/s20041103
APA StyleFalabella, F., Serio, C., Zeni, G., & Pepe, A. (2020). On the Use of Weighted Least-Squares Approaches for Differential Interferometric SAR Analyses: The Weighted Adaptive Variable-lEngth (WAVE) Technique. Sensors, 20(4), 1103. https://doi.org/10.3390/s20041103







