High Definition 3D Map Creation Using GNSS/IMU/LiDAR Sensor Integration to Support Autonomous Vehicle Navigation
Abstract
1. Introduction
2. Motivation
3. Data Acquisition System and Test Area
4. Platform Georeferencing and Inter-Sensor Calibration
4.1. Methodology
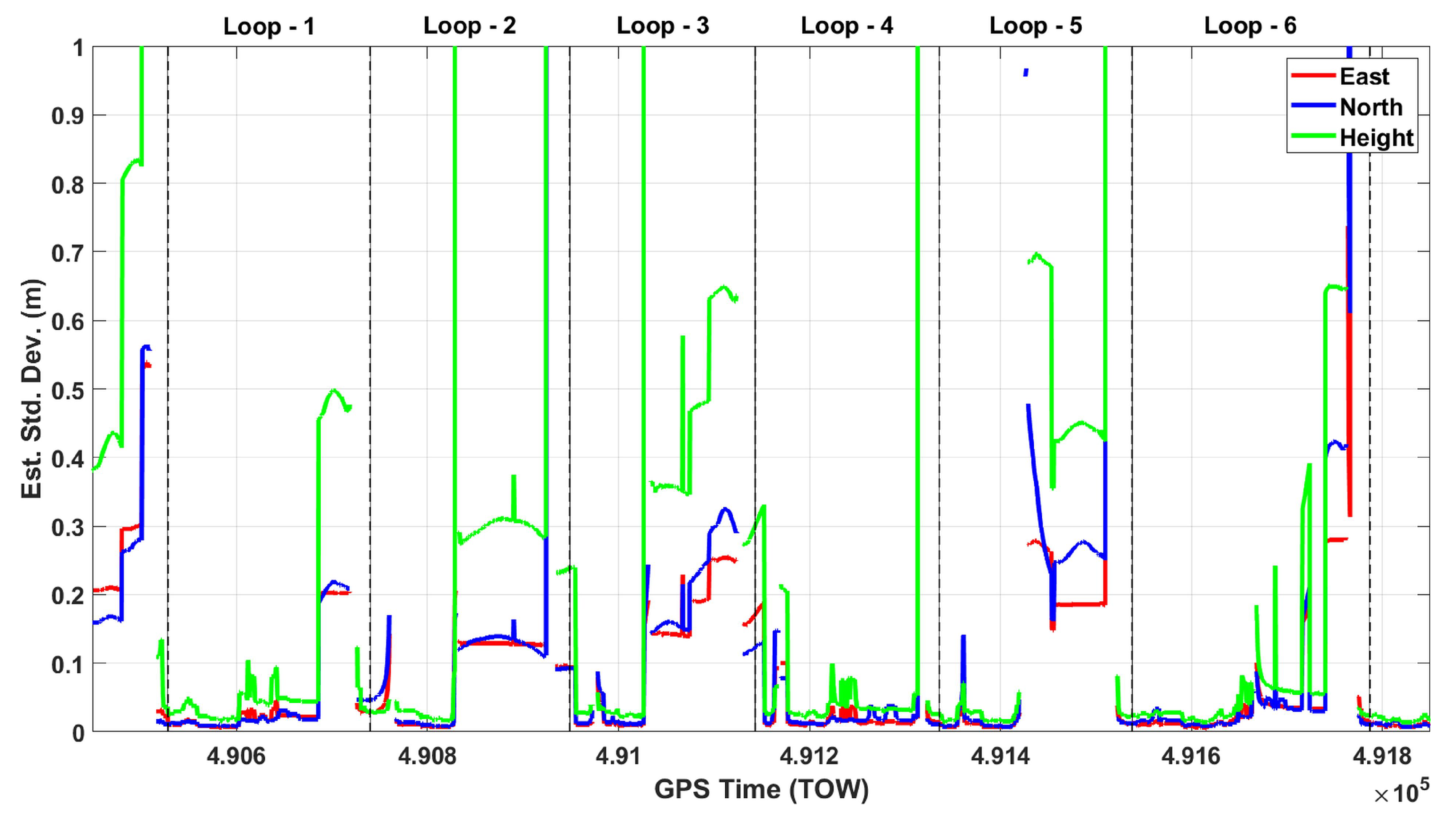
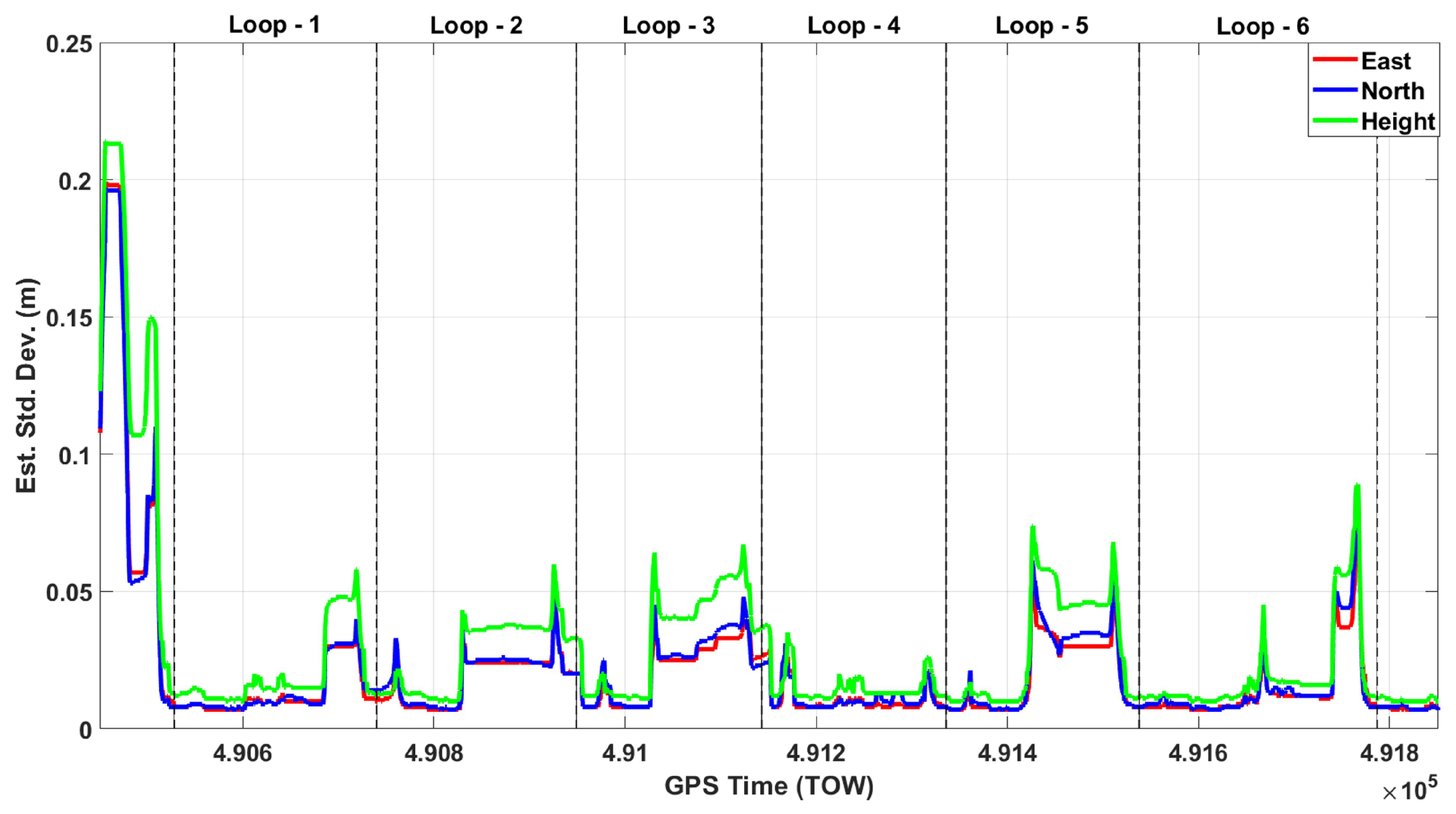
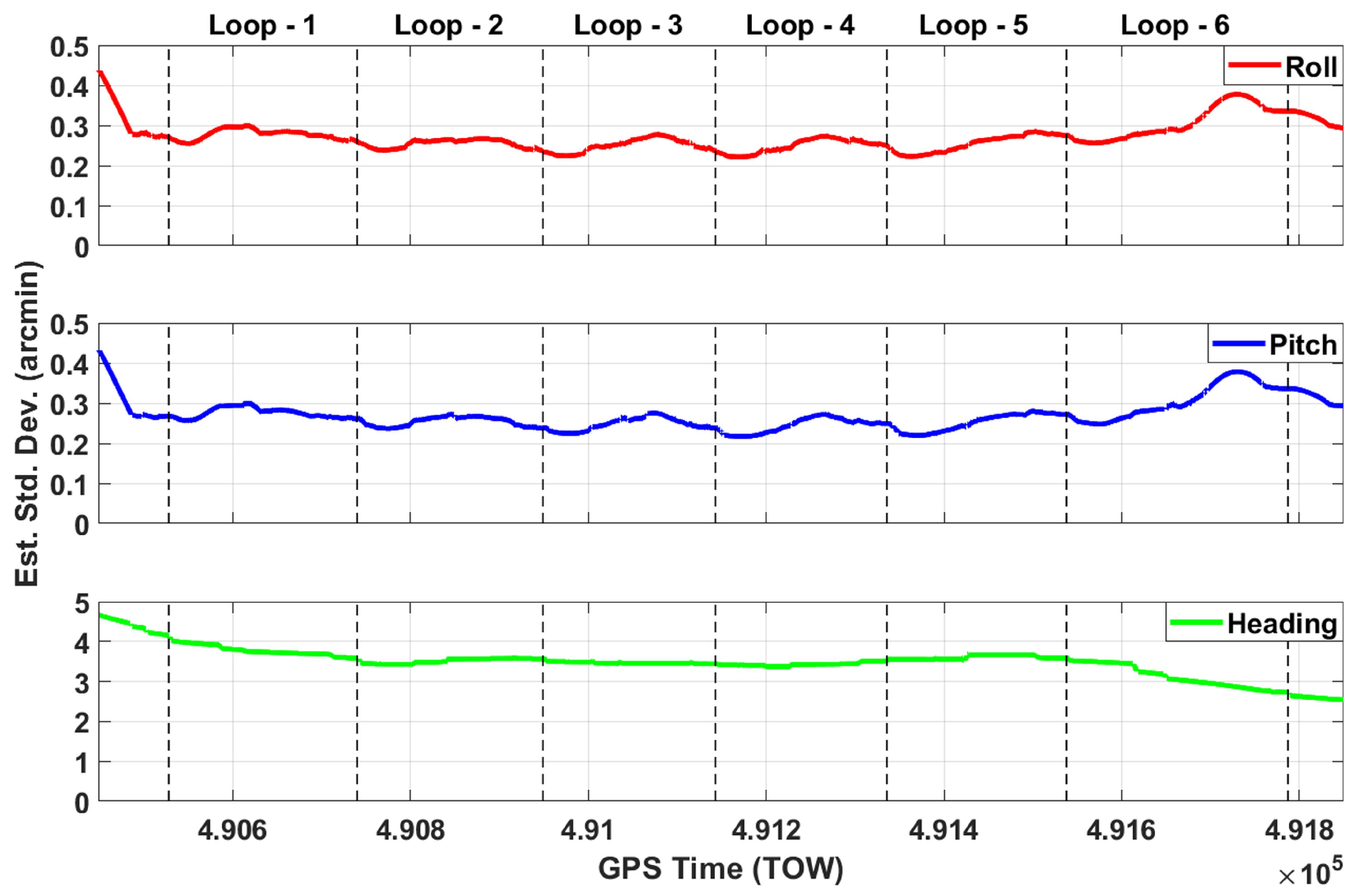
4.2. Georeferencing Solution
4.3. Boresighting Estimation
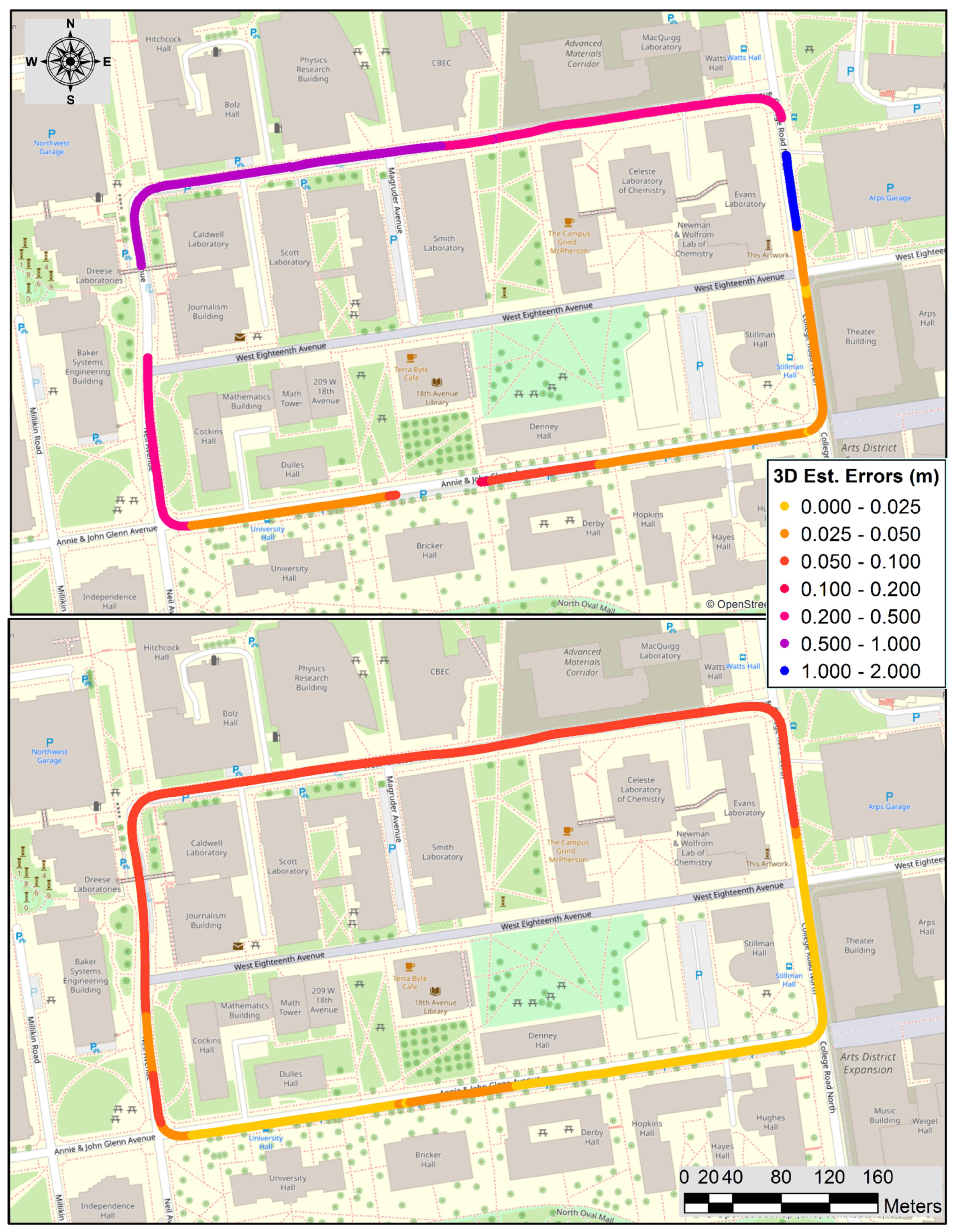
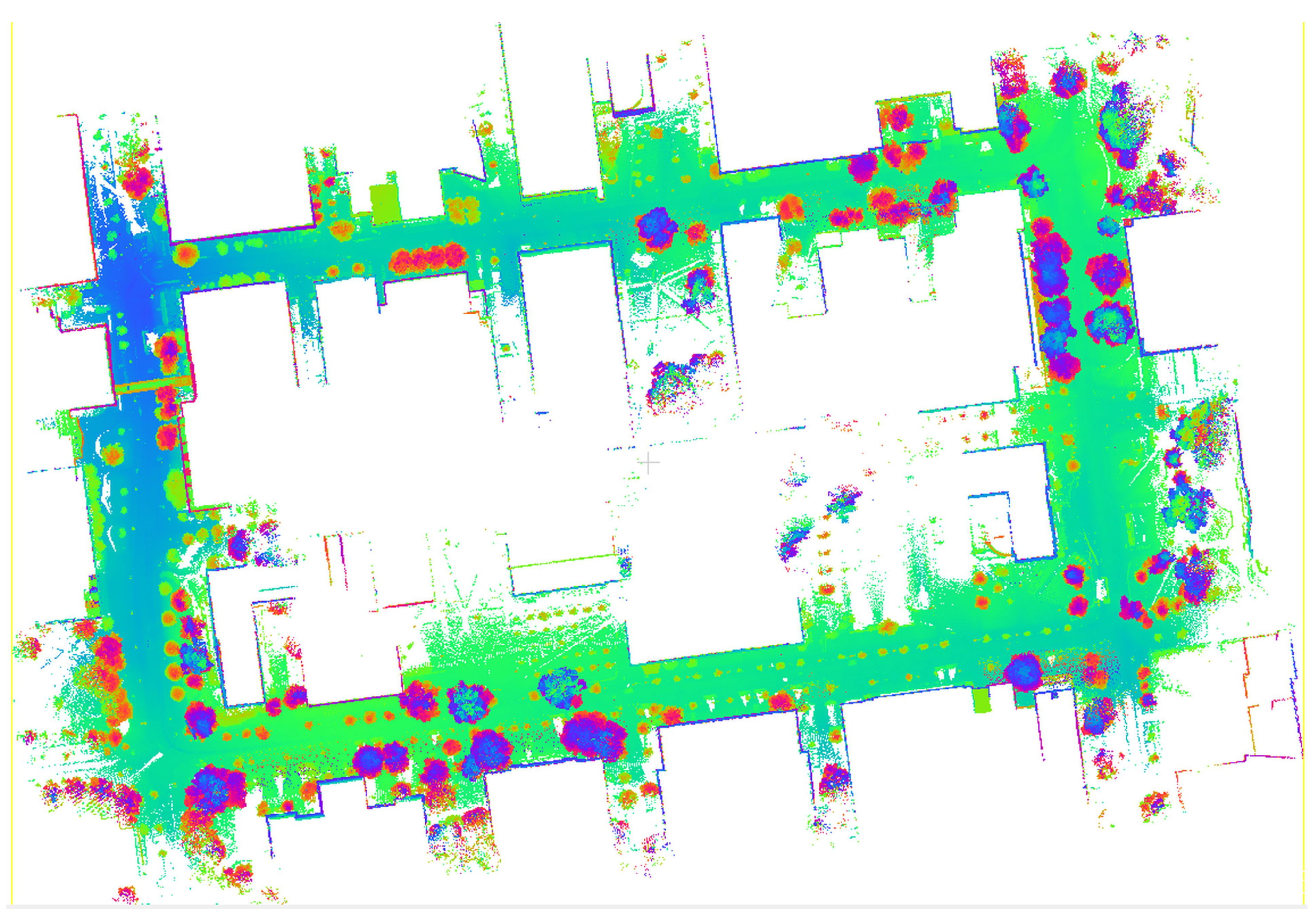
5. Point Cloud Generation and Performance Analysis
6. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Jiang, K.; Yang, D.; Liu, C.; Zhang, T.; Xiao, Z. A Flexible Multi-Layer Map Model Designed for Lane-Level Route Planning in Autonomous Vehicles. Engineering 2019. [Google Scholar] [CrossRef]
- Society of Automotive Engineer (SAE). Available online: https://www.sae.org/news/press-room/2018/12/sae-international-releases-updated-visual-chart-for-its-“levels-of-driving-automation”-standard-for-self-driving-vehicles/ (accessed on 18 January 2020).
- Ma, L.; Li, Y.; Li, J.; Zhong, Z.; Chapman, M.A. Generation of horizontally curved driving lines in HD maps using mobile laser scanning point clouds. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 1572–1586. [Google Scholar] [CrossRef]
- Hirabayashi, M.; Sujiwo, A.; Monrroy, A.; Kato, S.; Edahiro, M. Traffic light recognition using high-definition map features. Robot. Autom. Syst. 2019, 111, 62–72. [Google Scholar] [CrossRef]
- Peng, H.; Ye, Q.; Shen, X. Spectrum Management for Multi-Access Edge Computing in Autonomous Vehicular Networks. IEEE Trans. Intell. Transp. Syst. 2019, 1–12. [Google Scholar] [CrossRef]
- Jo, K.; Kim, C.; Sunwoo, M. Simultaneous localization and map change update for the high definition map-based autonomous driving car. Sensors 2018, 18, 3145. [Google Scholar] [CrossRef] [PubMed]
- Van Brummelen, J.; O’Brien, M.; Gruyer, D.; Najjaran, H. Autonomous vehicle perception: The technology of today and tomorrow. Transp. Res. Part C Emerg. Technol. 2018, 89, 384–406. [Google Scholar] [CrossRef]
- Min, H.; Wu, X.; Cheng, C.; Zhao, X. Kinematic and Dynamic Vehicle Model-Assisted Global Positioning Method for Autonomous Vehicles with Low-cost GPS/Camera/In-Vehicle Sensors. Sensors 2019, 19, 5430. [Google Scholar] [CrossRef]
- Javanmardi, E.; Javanmardi, M.; Gu, Y.; Kamijo, S. Factors to evaluate capability of map for vehicle localization. IEEE Access 2018, 6, 49850–49867. [Google Scholar] [CrossRef]
- Seif, H.G.; Hu, X. Autonomous Driving in the iCity—HD Maps as a Key Challenge of the Automotive Industry. Engineering 2016, 2, 159–162. [Google Scholar] [CrossRef]
- Toth, C.; Ozguner, U.; Brzezinska, D. Moving Toward Real-Time Mobile Mapping: Autonomous Vehicle Navigation. In Proceedings of the 5th International Symposium on Mobile Mapping Technology, Padova, Italy, 29–31 May 2007; pp. 1–6. [Google Scholar]
- Jo, K.; Kim, J.; Kim, D.; Jang, C.; Sunwoo, M. Development of Autonomous Car-Part II: A Case Study on the Implementation of an Autonomous Driving System Based on Distributed Architecture. IEEE Trans. Ind. Electron. 2015, 62, 5119–5132. [Google Scholar] [CrossRef]
- Toth, C.K.; Koppanyi, Z.; Lenzano, M.G. New source of geospatial data: Crowdsensing by assisted and autonomous vehicle technologies. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2018, 211–216. [Google Scholar] [CrossRef]
- Toth, C.; Jóźków, G. Remote sensing platforms and sensors: A survey. ISPRS J. Photogramm. Remote Sens. 2016, 115, 22–36. [Google Scholar] [CrossRef]
- Błaszczak-Ba̧k, W.; Koppanyi, Z.; Toth, C. Reduction Method for Mobile Laser Scanning Data. ISPRS Int. J. Geo-Inf. 2018, 7, 285. [Google Scholar] [CrossRef]
- Toth, C.K.; Koppanyi, Z.; Navratil, V.; Grejner-Brzezinska, D. Georeferencing in GNSS-challenged environment: Integrating UWB and IMU technologies. Int. Arch. Photogramm. Remote Sens. Spatial Inf. Sci. 2017, 175–180. [Google Scholar] [CrossRef]
- Reuper, B.; Becker, M.; Leinen, S. Benefits of multi-constellation/multi-frequency GNSS in a tightly coupled GNSS/IMU/Odometry integration algorithm. Sensors 2018, 18, 3052. [Google Scholar] [CrossRef]
- Dierenbach, K.; Ostrowski, S.; Jozkow, G.; Toth, C.K.; Grejner-Brzezinska, D.A.; Koppanyi, Z. UWB for navigation in GNSS compromised environments. In Proceeding of the 28th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS 2015), Tampa, FL, USA, 14–18 September 2015; pp. 2380–2389. [Google Scholar]
- Hata, A.Y.; Wolf, D.F. Feature Detection for Vehicle Localization in Urban Environments Using a Multilayer LIDAR. IEEE Trans. Intell. Transp. Syst. 2016, 17, 420–429. [Google Scholar] [CrossRef]
- Jang, E.S.; Suhr, J.K.; Jung, H.G. Lane endpoint detection and position accuracy evaluation for sensor fusion-based vehicle localization on highways. Sensors 2018, 18, 4389. [Google Scholar] [CrossRef]
- Milanés, V.; Naranjo, J.E.; González, C.; Alonso, J.; De Pedro, T. Autonomous vehicle based in cooperative GPS and inertial systems. Robotica 2008, 26, 627–633. [Google Scholar] [CrossRef]
- Zihajehzadeh, S.; Loh, D.; Lee, T.J.; Hoskinson, R.; Park, E.J. A cascaded Kalman filter-based GPS/MEMS-IMU integration for sports applications. Measurement 2015, 73, 200–210. [Google Scholar] [CrossRef]
- Liu, Y.; Fan, X.; Lv, C.; Wu, J.; Li, L.; Ding, D. An innovative information fusion method with adaptive Kalman filter for integrated INS/GPS navigation of autonomous vehicles. Mech. Syst. Sig. Process. 2018, 100, 605–616. [Google Scholar] [CrossRef]
- Wyglinski, A.M.; Huang, X.; Padir, T.; Lai, L.; Eisenbarth, T.R.; Venkatasubramanian, K. Security of autonomous systems employing embedded computing and sensors. IEEE Micro 2013, 33, 80–86. [Google Scholar] [CrossRef]
- Lahat, D.; Adali, T.; Jutten, C. Multimodal Data Fusion: An Overview of Methods, Challenges, and Prospects. Proc. IEEE 2015, 103, 1449–1477. [Google Scholar] [CrossRef]
- Luettel, T.; Himmelsbach, M.; Wuensche, H.J. Autonomous ground vehicles-concepts and a path to the future. Proc. IEEE 2012, 100, 1831–1839. [Google Scholar] [CrossRef]
- Pothou, A.; Toth, C.; Karamitsos, S.; Georgopoulos, A. An approach to optimize reference ground control requirements for estimating LIDAR/IMU boresight misalignment. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2008, 37, 301–307. [Google Scholar]
- Falco, G.; Pini, M.; Marucco, G. Loose and tight GNSS/INS integrations: Comparison of performance assessed in real Urban scenarios. Sensors 2017, 17, 255. [Google Scholar] [CrossRef] [PubMed]
- Ren, R.; Fu, H.; Wu, M. Large-scale outdoor slam based on 2d lidar. Electronics 2019, 8, 613. [Google Scholar] [CrossRef]
- Besl, P.J.; McKay, N.D. A Method for Registration of 3-D Shapes. IEEE Trans. Pattern Anal. Mach. Intell. 1992, 14, 239–256. [Google Scholar] [CrossRef]
- Yang, C.; Medioni, G. Object modelling by registration of multiple range images. Image Vis. Comput. 1992, 10, 145–155. [Google Scholar] [CrossRef]
- Stoyanov, T.; Magnusson, M.; Andreasson, H.; Lilienthal, A.J. Fast and accurate scan registration through minimization of the distance between compact 3D NDT representations. Int. J. Robot. Res. 2012. [Google Scholar] [CrossRef]
- Tian, Y.; Liu, X.; Li, L.; Wang, W. Intensity-assisted ICP for fast registration of 2D-LIDAR. Sensors 2019, 19, 2124. [Google Scholar] [CrossRef]
- Wang, Y.T.; Peng, C.C.; Ravankar, A.A.; Ravankar, A. A single LiDAR-based feature fusion indoor localization algorithm. Sensors 2018, 18, 1294. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Zhang, L.; Qin, S.; Tian, D.; Ouyang, S.; Chen, C. Optimized LOAM Using Ground Plane Constraints and SegMatch-Based Loop Detection. Sensors 2019, 19, 5419. [Google Scholar] [CrossRef] [PubMed]
- Chiang, K.W.; Tsai, G.J.; Li, Y.H.; El-Sheimy, N. Development of LiDAR-Based UAV System for Environment Reconstruction. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1790–1794. [Google Scholar] [CrossRef]
- Ren, Z.; Wang, L.; Bi, L. Robust GICP-based 3D LiDAR SLAM for underground mining environment. Sensors 2019, 19, 2915. [Google Scholar] [CrossRef]
- Javanmardi, E.; Gu, Y.; Javanmardi, M.; Kamijo, S. Autonomous vehicle self-localization based on abstract map and multi-channel LiDAR in urban area. IATSS Res. 2019. [Google Scholar] [CrossRef]
- Yue, R.; Xu, H.; Wu, J.; Sun, R.; Yuan, C. Data registration with ground points for roadside LiDAR sensors. Remote Sens. 2019, 11, 1354. [Google Scholar] [CrossRef]
- Ahtiainen, J.; Stoyanov, T.; Saarinen, J. Normal Distributions Transform Traversability Maps: LIDAR-Only Approach for Traversability Mapping in Outdoor Environments. J. Field Robot. 2017, 34, 600–621. [Google Scholar] [CrossRef]
- Vlaminck, M.; Luong, H.; Goeman, W.; Philips, W. 3D scene reconstruction using Omnidirectional vision and LiDAR: A hybrid approach. Sensors 2016, 16, 1923. [Google Scholar] [CrossRef]
- Wen, W.; Hsu, L.T.; Zhang, G. Performance Analysis of NDT-based Graph SLAM for Autonomous Vehicle in Diverse Typical Driving Scenarios of Hong Kong. Sensors 2018, 18, 3928. [Google Scholar] [CrossRef]
- Zhang, J.; Singh, S. LOAM: Lidar Odometry and Mapping in Real-time. Robot. Sci. Syst. 2015, 2. [Google Scholar] [CrossRef]
- Niu, X.; Yu, T.; Tang, J.; Chang, L. An Online Solution of LiDAR Scan Matching Aided Inertial Navigation System for Indoor Mobile Mapping. Mob. Inf. Syst. 2017, 2017, 1–11. [Google Scholar] [CrossRef]
- Ravi, R.; Lin, Y.J.; Elbahnasawy, M.; Shamseldin, T.; Habib, A. Simultaneous System Calibration of a Multi-LiDAR Multicamera Mobile Mapping Platform. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 1694–1714. [Google Scholar] [CrossRef]
- Rodríguez-Gonzálvez, P.; Fernández-Palacios, B.J.; Muñoz-Nieto, á.L.; Arias-Sanchez, P.; Gonzalez-Aguilera, D. Mobile LiDAR system: New possibilities for the documentation and dissemination of large cultural heritage sites. Remote Sens. 2017, 9, 189. [Google Scholar] [CrossRef]
- Zheng, L.; Li, B.; Yang, B.; Song, H.; Lu, Z. Lane-level road network generation techniques for lane-level maps of autonomous vehicles: A survey. Sustainability 2019, 11, 4511. [Google Scholar] [CrossRef]
- Wong, K.; Javanmardi, E.; Javanmardi, M.; Kamijo, S. Estimating autonomous vehicle localization error using 2D geographic information. ISPRS Int. J. Geo-Inf. 2019, 8, 288. [Google Scholar] [CrossRef]
- Meng, X.; Wang, H.; Liu, B. A robust vehicle localization approach based on GNSS/IMU/DMI/LiDAR sensor fusion for autonomous vehicles. Sensors 2017, 17, 2140. [Google Scholar] [CrossRef]
- Tan, C.; Ji, S.; Gui, Z.; Shen, J.; Fu, D.S.; Wang, J. An effective data fusion-based routing algorithm with time synchronization support for vehicular wireless sensor networks. J. Supercomput. 2018. [Google Scholar] [CrossRef]
- Li, J.; Jia, L.; Liu, G. Multisensor Time Synchronization Error Modeling and Compensation Method for Distributed POS. IEEE Trans. Instrum. Meas. 2016. [Google Scholar] [CrossRef]
- Toth, C.K.; Grejner-Brzezinska, D.A.; Shin, S.W.; Kwon, J. A Method for Accurate Time Synchronization of Mobile Mapping Systems. J. Appl. Geod. 2008, 2, 159–166. [Google Scholar]
- Grejner-Brzezinska, D.A. Positioning Accuracy of the GPSVan. In Proceedings of the 52nd Annual Meeting of The Institute of Navigation, Cambridge, MA, USA, 19–21 June 1996; pp. 657–665. [Google Scholar]
- Koppanyi, Z.; Toth, C.K. Experiences with Acquiring Highly Redundant Spatial Data to Support Driverless Vehicle Technologies. ISPRS Ann. Photogramm. Remote Sens. Spatial Inf. Sci. 2018, 161–168. [Google Scholar] [CrossRef]
- NovAtel Inertial Explorer. Available online: https://www.novatel.com/products/software/inertial-explorer/ (accessed on 4 December 2019).
- CloudCompare. Available online: https://www.danielgm.net/cc/ (accessed on 4 December 2019).
- OPUS: Online Positioning User Service. Available online: https://www.ngs.noaa.gov/OPUS/ (accessed on 4 December 2019).
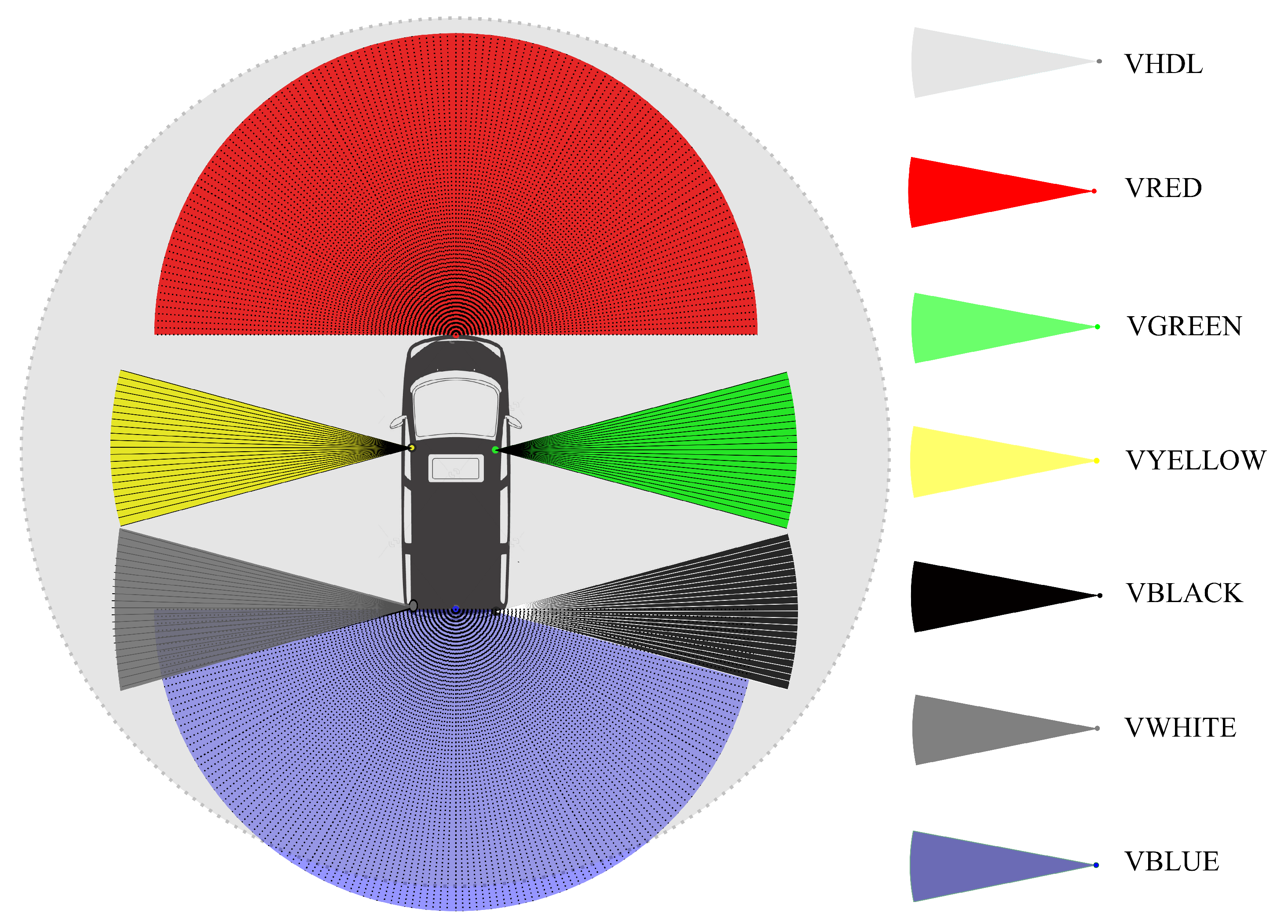



| Type | Sensor Model | Sensor ID | Location | Sampling Frequency | Angular Resolution H/V | Field of View H/V |
|---|---|---|---|---|---|---|
| GNSS | Septentrio | SEPT | Top | 10 Hz | - | - |
| PolaRx | ||||||
| GPS | Novatel DL-4 | NOVATEL | Top | 5 Hz | - | - |
| IMU | MicroStrain | MS | Inside | 200 Hz | - | - |
| 3DM-GX3 | ||||||
| IMU | H764G IMU1 | H764G | Inside | 200 Hz | - | - |
| IMU | H764G IMU2 | H764G | Inside | 200 Hz | - | - |
| LiDAR | Velodyne | VHDL | Front,Top | 20 Hz | 0.2°/1.33° | 360°/40° |
| HDL-32E | ||||||
| LiDAR | Velodyne | VRED | Front,Bottom | 20 Hz | 2.0°/0.2° | 30°/360° |
| VLP-16 | VBLUE | Back,Center | ||||
| LiDAR | Velodyne | VGREEN | Front,Right | 20 Hz | 0.2°/2.0° | 360°/30° |
| VLP-16 | VYELLOW | Front,Left | ||||
| VWHITE | Back,Left | |||||
| VBLACK | Back,Right |
| GNSS only | GNSS/IMU | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| East | North (m) | Height | East | North (m) | Height | Roll | Pitch (arcmin) | Heading | |
| min. | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 | 0.02 | 0.02 | 0.02 |
| average | 0.08 | 0.09 | 0.20 | 0.02 | 0.02 | 0.02 | 0.27 | 0.26 | 3.48 |
| max. | 7.28 | 4.02 | 16.97 | 0.08 | 0.08 | 0.09 | 0.38 | 0.38 | 4.13 |
| std. | 0.23 | 0.20 | 0.61 | 0.01 | 0.01 | 0.02 | 0.03 | 0.03 | 0.25 |
| Vertical Surface No | Mean Distance | Standard Deviation (m) | Horizontal Surface No | Mean Distance (m) | Standard Deviation (m) |
|---|---|---|---|---|---|
| VS-1 | 0.00 | 0.02 | HS-1 | 0.01 | 0.03 |
| VS-2 | 0.00 | 0.03 | HS-2 | 0.00 | 0.01 |
| VS-3 | −0.03 | 0.02 | HS-3 | −0.06 | 0.05 |
| VS-4 | 0.00 | 0.01 | HS-4 | 0.02 | 0.02 |
| VS-5 | −0.01 | 0.04 | HS-5 | 0.02 | 0.03 |
| VS-6 | −0.04 | 0.02 | HS-6 | −0.02 | 0.02 |
| VS-7 | −0.10 | 0.01 | |||
| VS-8 | 0.00 | 0.02 | |||
| VS-9 | −0.11 | 0.04 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ilci, V.; Toth, C. High Definition 3D Map Creation Using GNSS/IMU/LiDAR Sensor Integration to Support Autonomous Vehicle Navigation. Sensors 2020, 20, 899. https://doi.org/10.3390/s20030899
Ilci V, Toth C. High Definition 3D Map Creation Using GNSS/IMU/LiDAR Sensor Integration to Support Autonomous Vehicle Navigation. Sensors. 2020; 20(3):899. https://doi.org/10.3390/s20030899
Chicago/Turabian StyleIlci, Veli, and Charles Toth. 2020. "High Definition 3D Map Creation Using GNSS/IMU/LiDAR Sensor Integration to Support Autonomous Vehicle Navigation" Sensors 20, no. 3: 899. https://doi.org/10.3390/s20030899
APA StyleIlci, V., & Toth, C. (2020). High Definition 3D Map Creation Using GNSS/IMU/LiDAR Sensor Integration to Support Autonomous Vehicle Navigation. Sensors, 20(3), 899. https://doi.org/10.3390/s20030899





