Robust Acoustic Imaging Based on Bregman Iteration and Fast Iterative Shrinkage-Thresholding Algorithm
Abstract
1. Introduction
2. Bregman Iteration Based Acoustic Imaging
2.1. Bregman Iteration with FISTA
2.2. Refining the Computational Grid via the Wavelet Method
3. Simulations
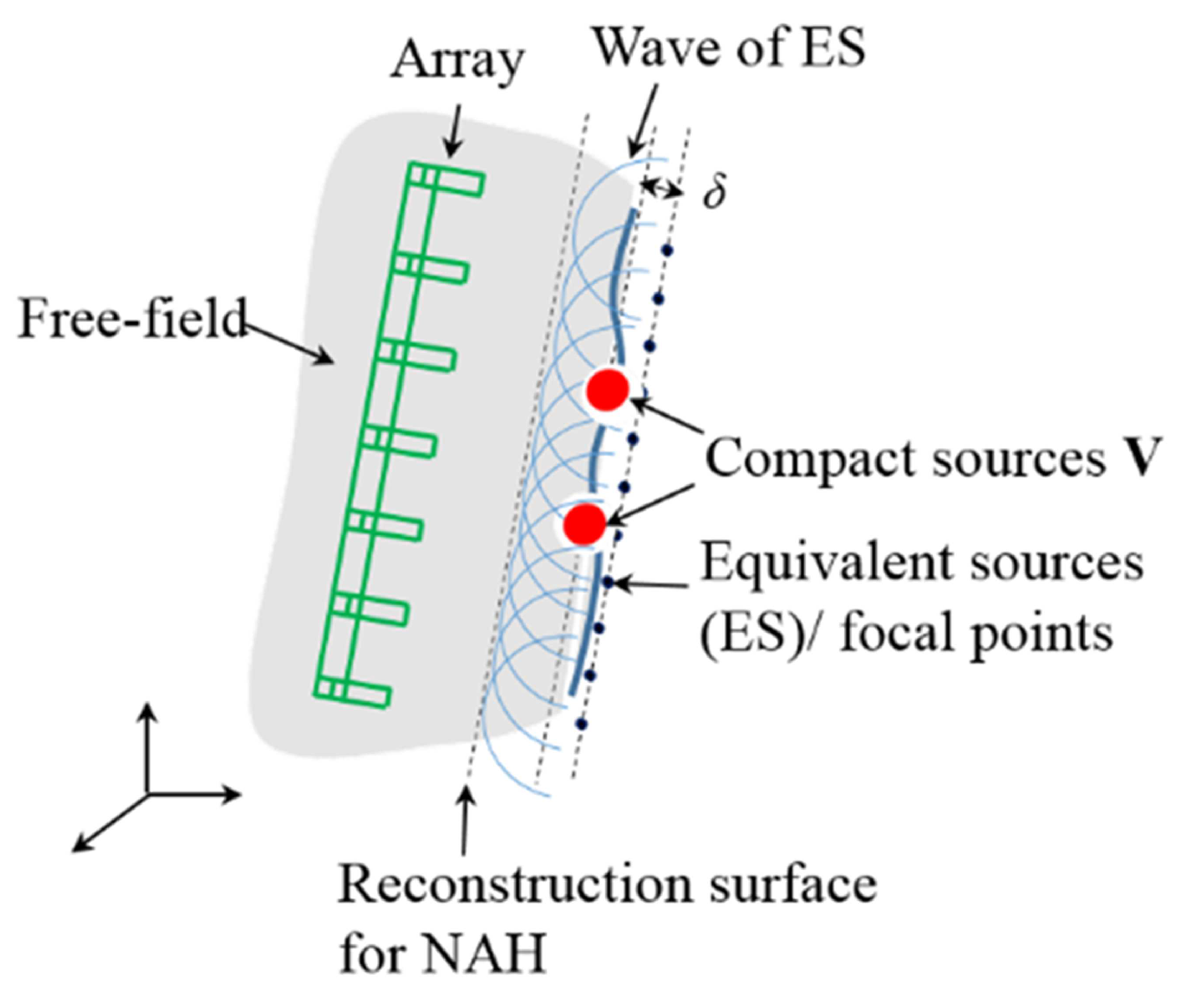
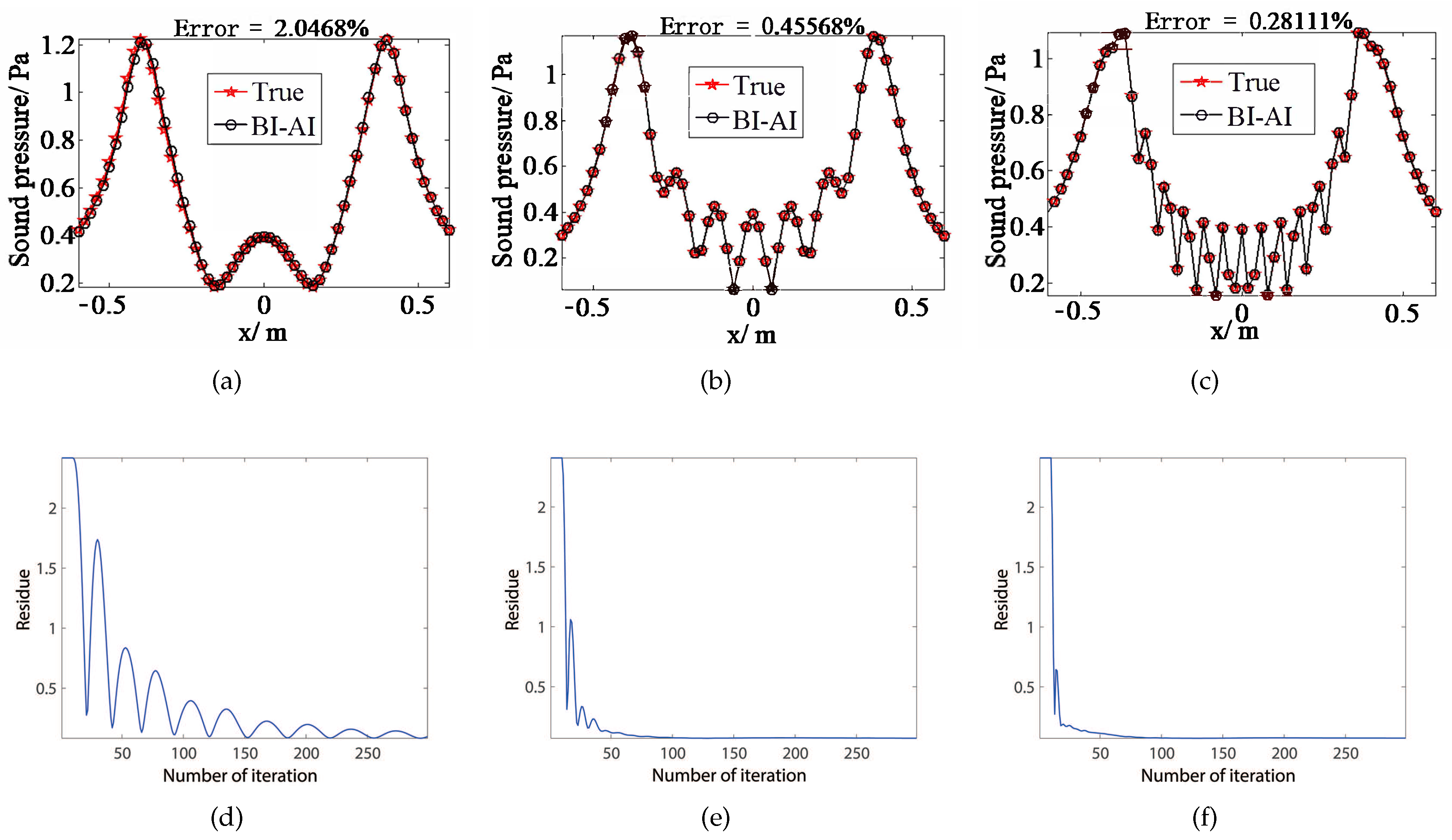
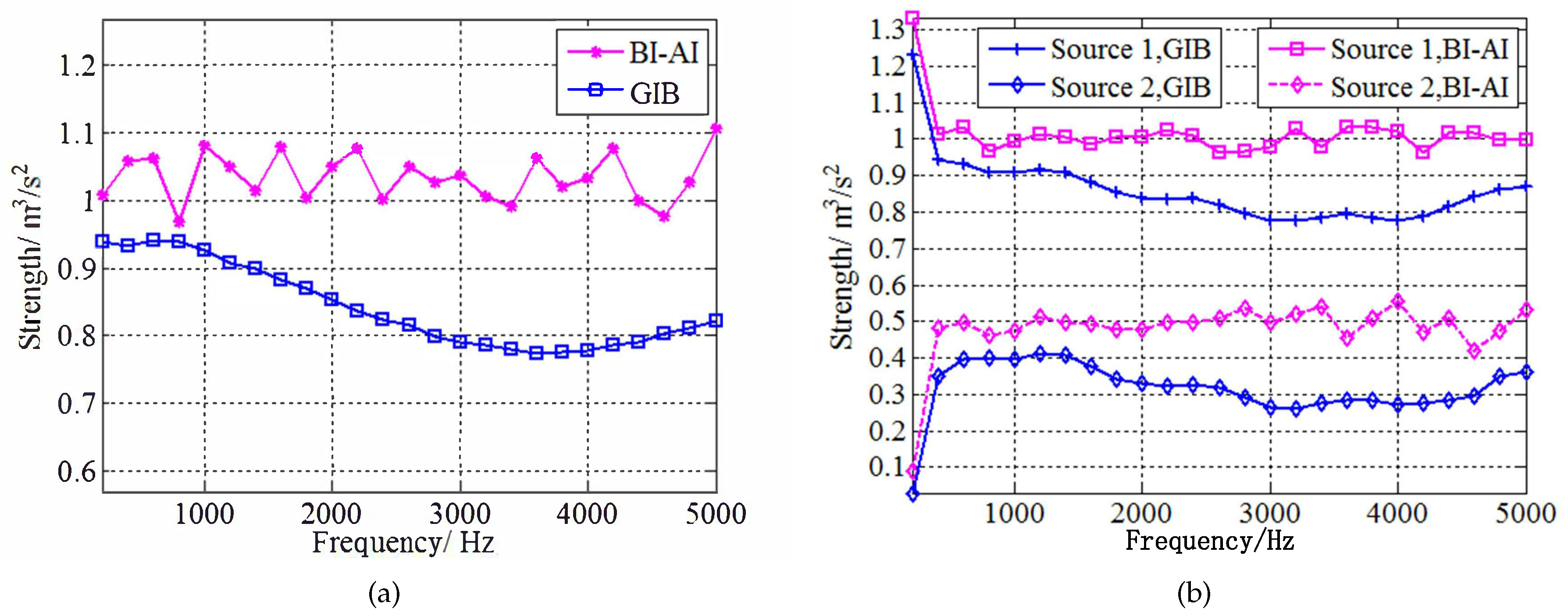
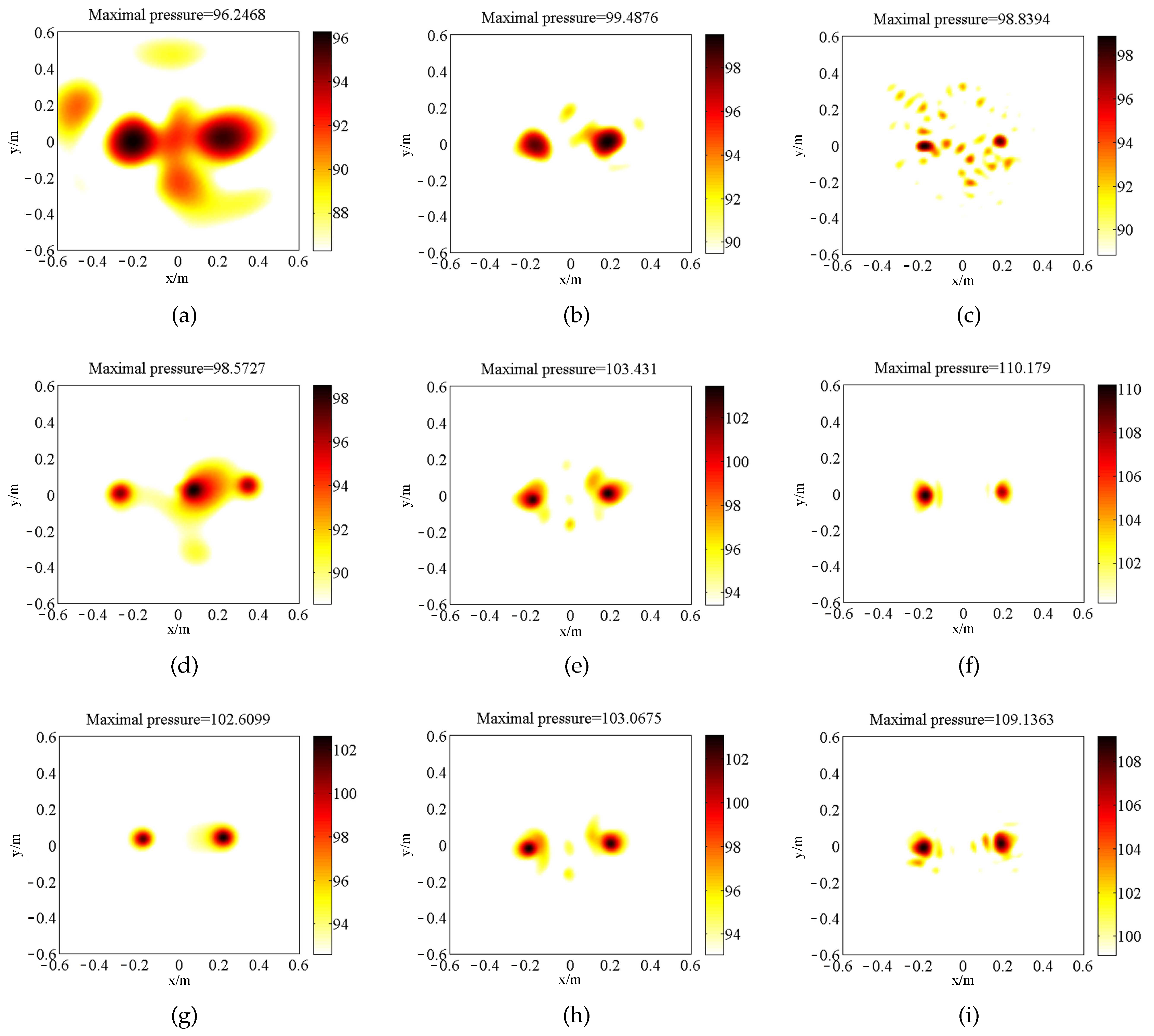
3.1. BI-AI in the Near-Field Measurements
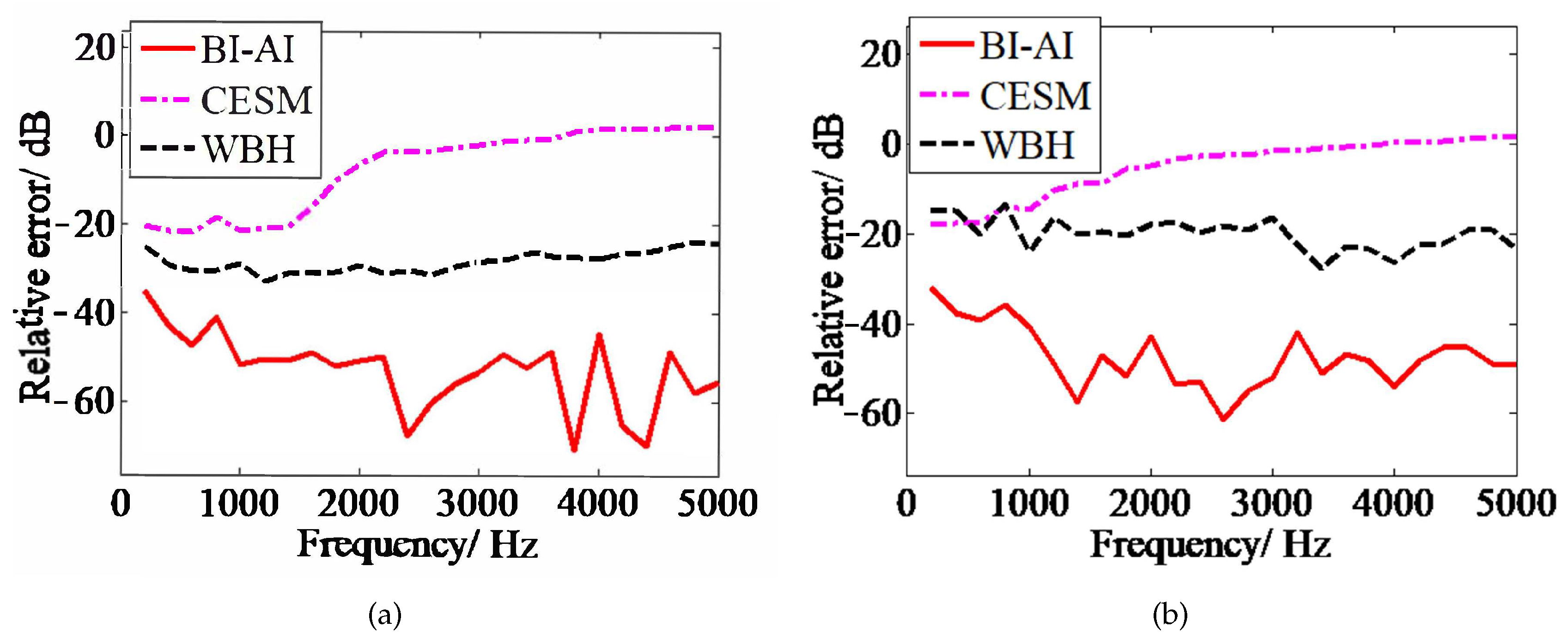
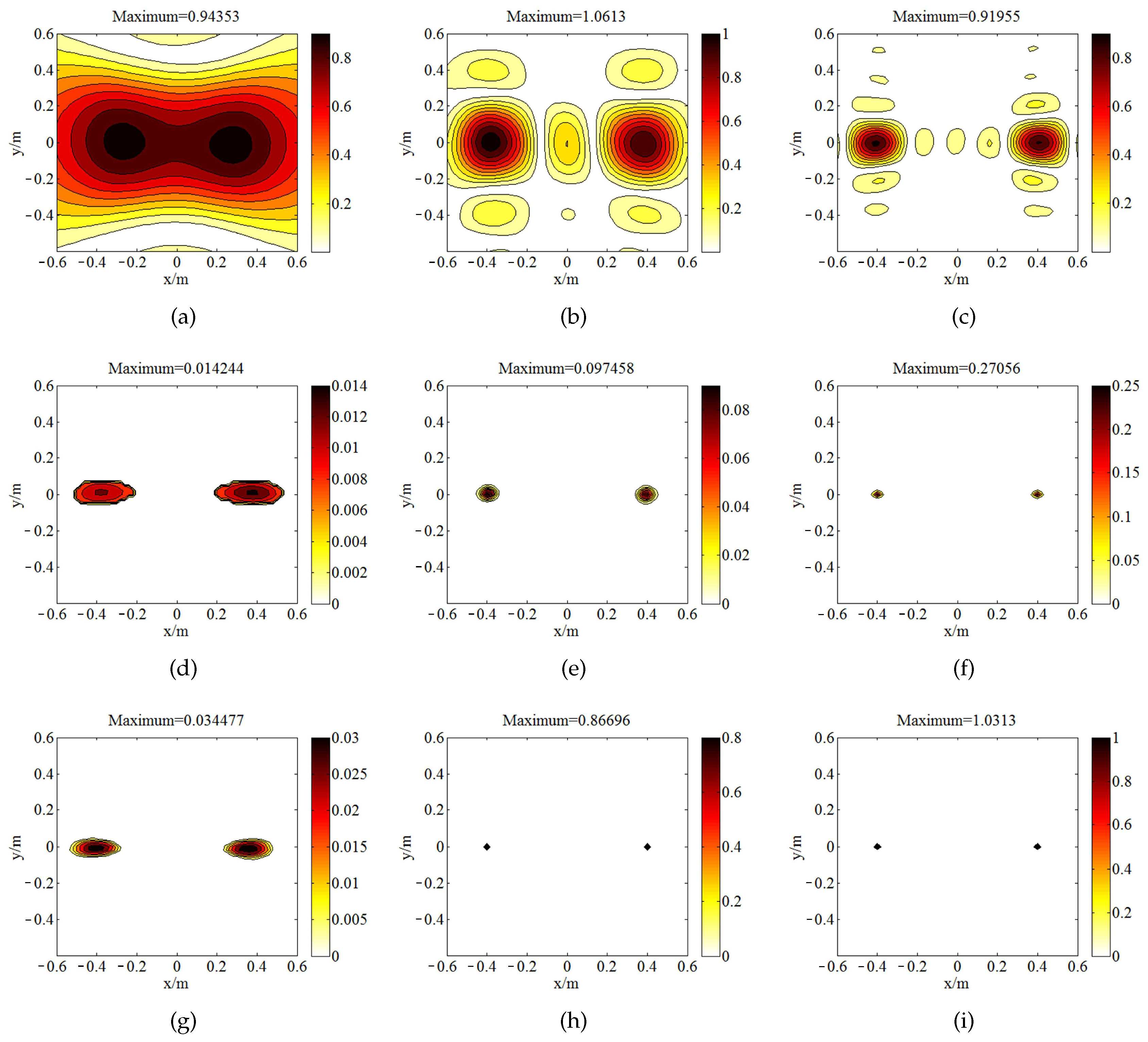
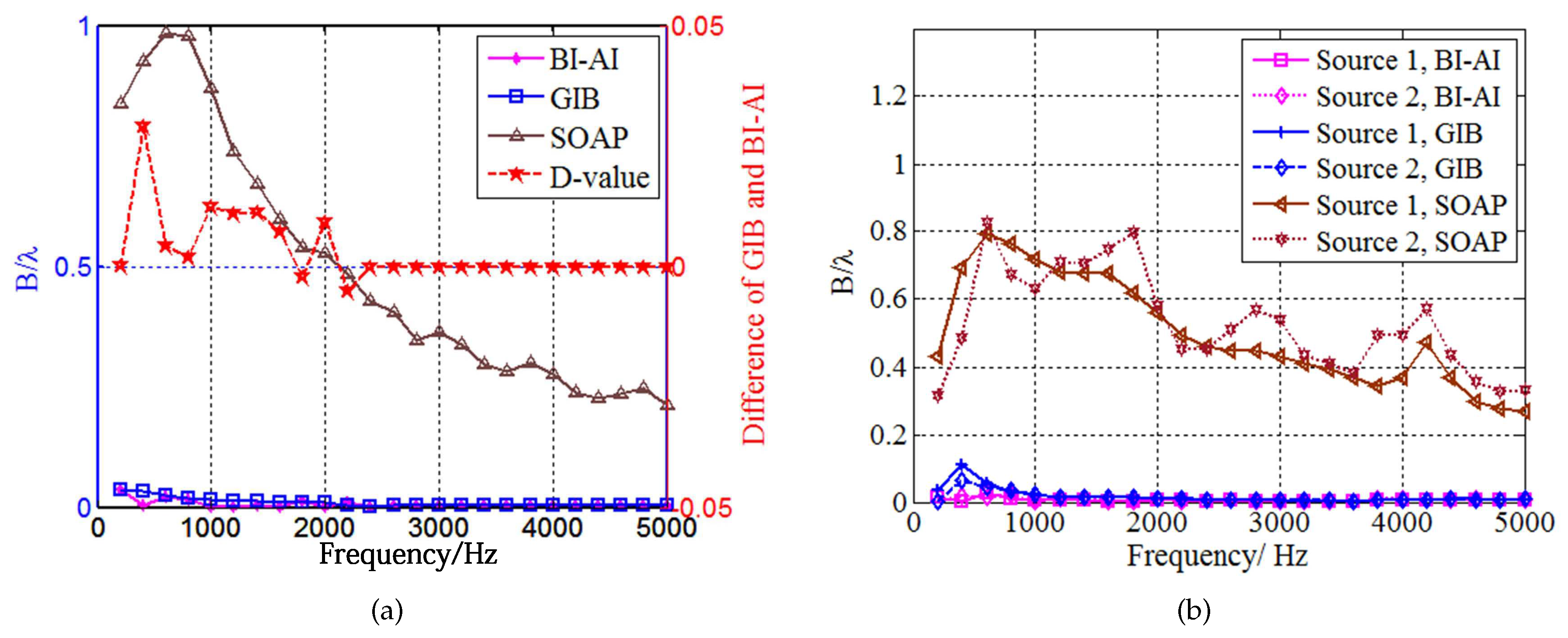
3.2. Source Detection in the Far-Field Measurements
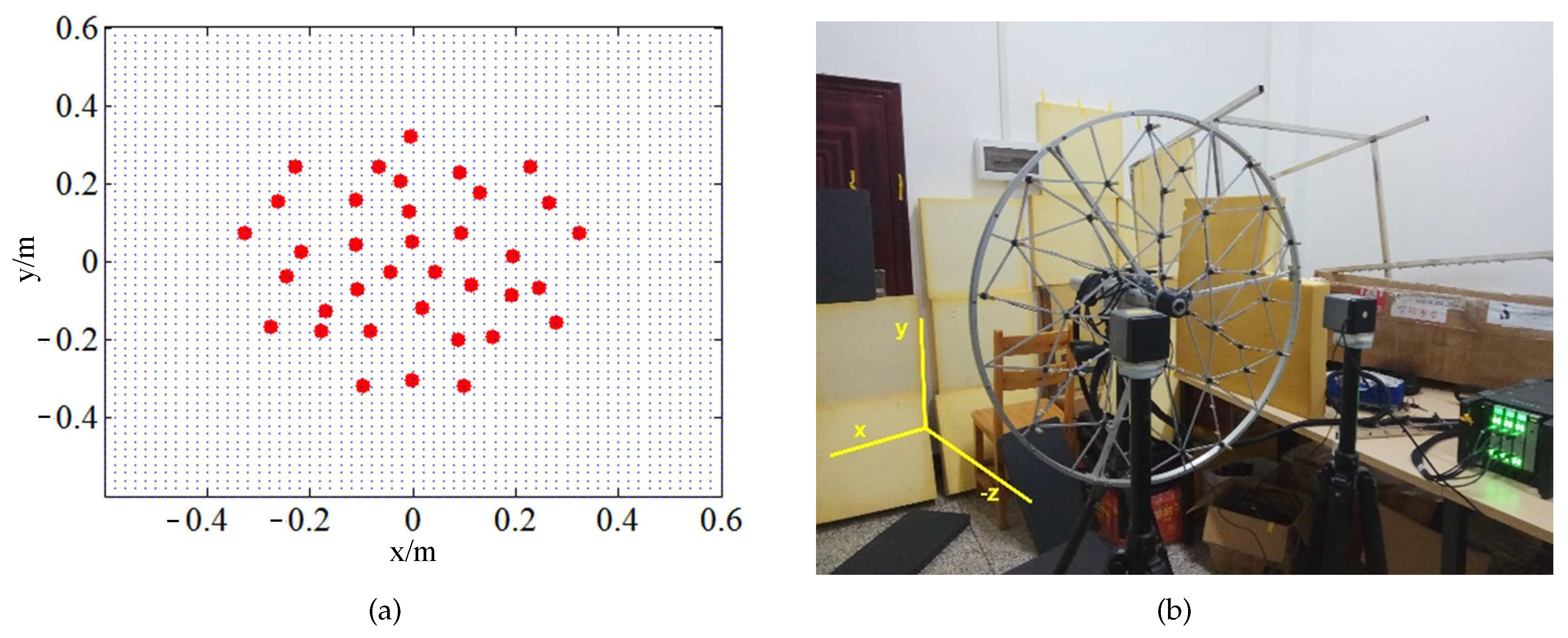
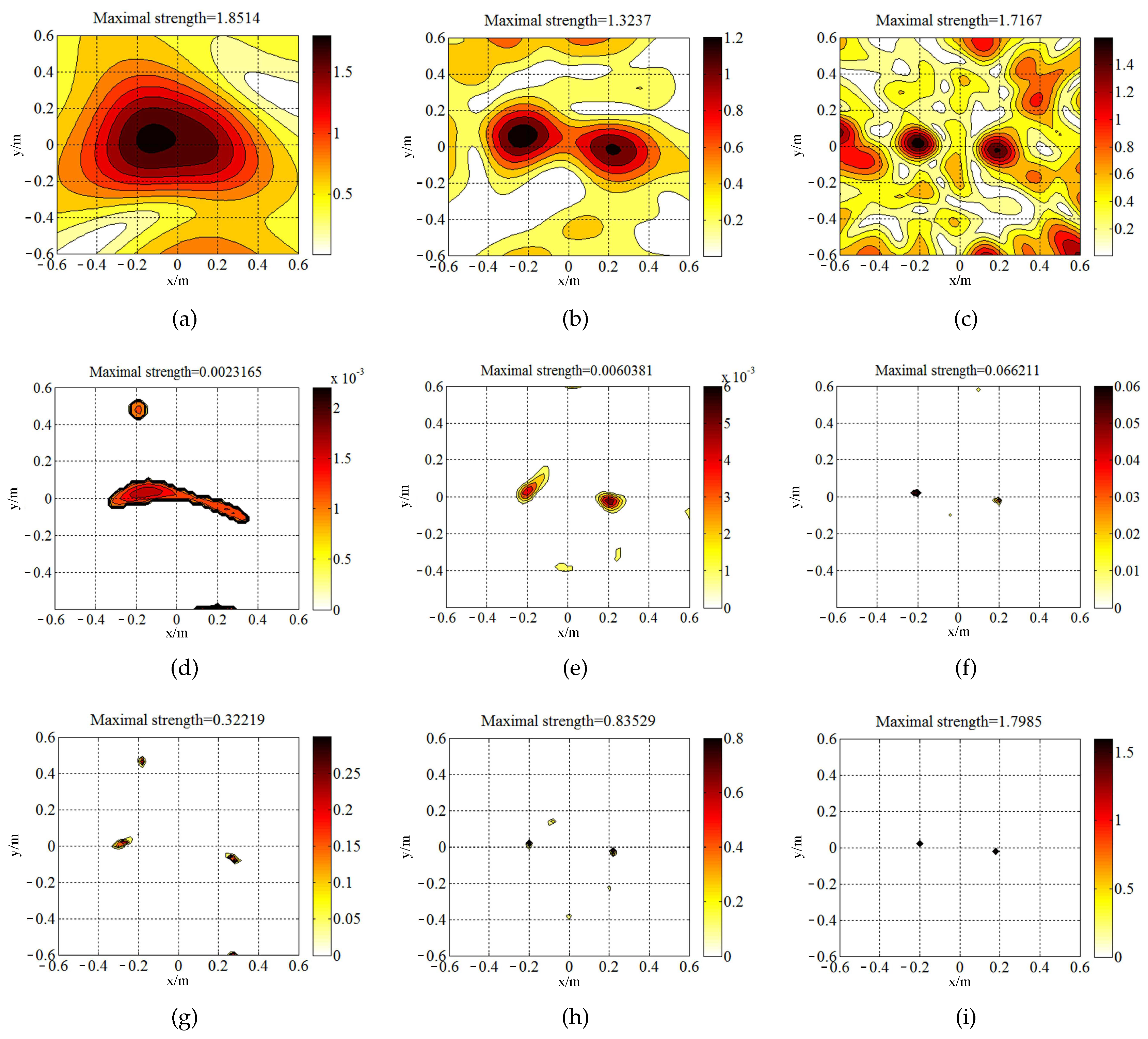
4. Experimental Application and Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Magalhães, M.; Tenenbaum, R. Sound sources reconstruction techniques: A review of their evolution and new trends. Acta Acust. United Acust. 2004, 90, 199–220. [Google Scholar]
- Lanslots, J.; Deblauwe, F.; Janssens, K. Selecting sound source localization techniques for industrial applications. Sound Vibr. 2010, 44, 6–10. [Google Scholar]
- Qiu, M.; Wang, D.; Liang, W.; Liu, L.; Zhang, Y.; Chen, X.; Sang, D.K.; Xing, C.; Li, Z.; Dong, B.; et al. Novel concept of the smart NIR-light–controlled drug release of black phosphorus nanostructure for cancer therapy. Proc. Natl. Acad. Sci. USA 2018, 115, 501–506. [Google Scholar] [CrossRef] [PubMed]
- Chiariotti, P.; Martarelli, M.; Castellini, P. Acoustic beamforming for noise source localization—Reviews, methodology and applications. Mech. Syst. Signal Process. 2019, 120, 422–448. [Google Scholar] [CrossRef]
- Yang, Y.; Chu, Z.; Shen, L.; Xu, Z. Functional delay and sum beamforming for three-dimensional acoustic source identification with solid spherical arrays. J. Sound Vibr. 2016, 373, 340–359. [Google Scholar] [CrossRef]
- Williams, E.G.; Maynard, J.D.; Skudrzyk, E. Sound source reconstructions using a microphone array. J. Acoust. Soc. Am. 1980, 68, 340–344. [Google Scholar] [CrossRef]
- Maynard, J.D.; Williams, E.G.; Lee, Y. Nearfield acoustic holography: I. Theory of generalized holography and the development of NAH. J. Acoust. Soc. Am. 1985, 78, 1395–1413. [Google Scholar] [CrossRef]
- Koopmann, G.H.; Song, L.; Fahnline, J.B. A method for computing acoustic fields based on the principle of wave superposition. J. Acoust. Soc. Am. 1989, 86, 2433–2438. [Google Scholar] [CrossRef]
- Chu, Z.; Yang, Y. Comparison of deconvolution methods for the visualization of acoustic sources based on cross-spectral imaging function beamforming. Mech. Syst. Signal Process. 2014, 48, 404–422. [Google Scholar] [CrossRef]
- Schmidt, R. Multiple emitter location and signal parameter estimation. IEEE Trans. Antennas Propag. 1986, 34, 276–280. [Google Scholar] [CrossRef]
- Li, J.; Stoica, P.; Wang, Z. On robust Capon beamforming and diagonal loading. IEEE Trans. Signal Process. 2003, 51, 1702–1715. [Google Scholar] [CrossRef]
- Wang, X.; Quost, B.; Chazot, J.D.; Antoni, J. Iterative beamforming for identification of multiple broadband sound sources. J. Sound Vibr. 2016, 365, 260–275. [Google Scholar] [CrossRef]
- Schuhmacher, A.; Hald, J.; Rasmussen, K.B.; Hansen, P.C. Sound source reconstruction using inverse boundary element calculations. J. Acoust. Soc. Am. 2003, 113, 114–127. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Wu, S.F. Helmholtz equation–least-squares method for reconstructing the acoustic pressure field. J. Acoust. Soc. Am. 1997, 102, 2020–2032. [Google Scholar] [CrossRef]
- Hald, J. Basic theory and properties of statistically optimized near-field acoustical holography. J. Acoust. Soc. Am. 2009, 125, 2105–2120. [Google Scholar] [CrossRef]
- Bi, C.; Chen, X.; Chen, J.; Zhou, R. Method of superposition applied to patch near-field acoustic holography. Sci. China Ser. E-Technol. Sci. 2005, 48, 338–353. [Google Scholar] [CrossRef]
- Sarkissian, A. Method of superposition applied to patch near-field acoustic holography. J. Acoust. Soc. Am. 2005, 118, 671–678. [Google Scholar] [CrossRef]
- Donoho, D.L. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Candes, E.J.; Romberg, J.; Tao, T. Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information. IEEE Trans. Inf. Theory 2006, 52, 489–509. [Google Scholar] [CrossRef]
- Suzuki, T. L1 generalized inverse beam-forming algorithm resolving coherent/incoherent, distributed and multipole sources. J. Sound Vibr. 2011, 330, 5835–5851. [Google Scholar] [CrossRef]
- Hald, J. Fast wideband acoustical holography. J. Acoust. Soc. Am. 2016, 139, 1508–1517. [Google Scholar] [CrossRef] [PubMed]
- Chardon, G.; Daudet, L.; Peillot, A.; Ollivier, F.; Bertin, N.; Gribonval, R. Near-field acoustic holography using sparse regularization and compressive sampling principles. J. Acoust. Soc. Am. 2012, 132, 1521–1534. [Google Scholar] [CrossRef] [PubMed]
- Huang, L.; Xu, Z.; He, Y.; Zhang, Z. A ratio model of ℓ1/ℓ2 norm for sound source identification. Sensors 2020, 20, 5290. [Google Scholar] [CrossRef] [PubMed]
- Shaoyu, S. Algorithm Study of Sound Sources Identification Based on Sparsity Regularization. Master’s Thesis, Chongqing University, Chongqing, China, 2018. [Google Scholar]
- Osher, S.; Burger, M.; Goldfarb, D.; Xu, J.; Yin, W. An iterative regularization method for total variation-based image restoration. Multiscale Model. Simul. 2005, 4, 460–489. [Google Scholar] [CrossRef]
- Antonelli, L.; De Simone, V.; di Serafino, D. Spatially adaptive regularization in image segmentation. Algorithms 2020, 13, 226. [Google Scholar] [CrossRef]
- Ma, S.; Goldfarb, D.; Chen, L. Fixed point and Bregman iterative methods for matrix rank minimization. Math Program 2011, 128, 321–353. [Google Scholar] [CrossRef]
- Ho, M.; Sun, Z.; Xin, J. Weighted elastic net penalized mean-variance portfolio design and computation. SIAM J. Financ. Math. 2015, 6, 1220–1244. [Google Scholar] [CrossRef]
- Corsaro, S.; De Simone, V.; Marino, Z. Split Bregman iteration for multi-period mean variance portfolio optimization. Appl. Math. Comput. 2021, 392, 125715. [Google Scholar] [CrossRef]
- Goldstein, T.; Osher, S. The split Bregman method for ℓ1-regularized problems. SIAM J. Imaging Sci. 2009, 2, 323–343. [Google Scholar] [CrossRef]
- Alqadah, H.F.; Valdivia, N.; Williams, E.G. A super-resolving near-Field electromagnetic holographic method. IEEE Trans. Antennas Propag. 2014, 62, 3679–3692. [Google Scholar] [CrossRef]
- Hale, E.T.; Yin, W.; Zhang, Y. Fixed-Point continuation for ℓ1-minimization: Methodology and convergence. SIAM J. Optim. 2008, 19, 1107–1130. [Google Scholar] [CrossRef]
- Bai, M.R.; Chen, C.C.; Lin, J.H. On optimal retreat distance for the equivalent source method-based nearfield acoustical holography. J. Acoust. Soc. Am. 2011, 129, 1407–1416. [Google Scholar] [CrossRef] [PubMed]
- Hald, J. A comparison of iterative sparse equivalent source methods for near-field acoustical holography. J. Acoust. Soc. Am. 2018, 143, 3758–3769. [Google Scholar] [CrossRef] [PubMed]
- Pereira, A.; Antoni, J.; Leclère, Q. Empirical Bayesian regularization of the inverse acoustic problem. Appl. Acoust. 2015, 97, 11–29. [Google Scholar] [CrossRef]
- Xenaki, A.; Gerstoft, P.; Mosegaard, K. Compressive beamforming. J. Acoust. Soc. Am. 2014, 136, 260–271. [Google Scholar] [CrossRef]
- Yin, W.; Osher, S.; Goldfarb, D.; Darbon, J. Bregman iterative algorithms for ℓ1 minimization with applications to compressed sensing. SIAM J. Imaging Sci. 2008, 1, 143–168. [Google Scholar] [CrossRef]
- Purkait, P.; Chanda, B. Super resolution image reconstruction through bregman iteration using morphologic regularization. IEEE Trans. Image Process. 2012, 21, 4029–4039. [Google Scholar] [CrossRef]
- Beck, A.; Teboulle, M. A fast iterative shrinkage-thresholding algorithm for linear inverse problems. SIAM J. Imaging Sci. 2009, 2, 183–202. [Google Scholar] [CrossRef]
- Yin, W.; Osher, S. Error forgetting of Bregman iteration. J. Sci. Comput. 2013, 54, 684–695. [Google Scholar] [CrossRef]
- Schneider, K.; Vasilyev, O.V. Wavelet methods in computational fluid dynamics. Annu. Rev. Fluid Mech. 2010, 42, 473–503. [Google Scholar] [CrossRef]
- Rastigejev, Y.A.; Paolucci, S. Wavelet-based adaptive multiresolution computation of viscous reactive flows. Int. J. Numer. Methods Fluids 2006, 52, 749–784. [Google Scholar] [CrossRef]
- Wirasaet, D.; Paolucci, S. Adaptive wavelet method for incompressible flows in complex domains. J. Fluids Eng. 2005, 127, 656–665. [Google Scholar] [CrossRef]
- Ma, W.; Liu, X. Improving the efficiency of DAMAS for sound source localization via wavelet compression computational grid. J. Sound Vibr. 2017, 395, 341–353. [Google Scholar] [CrossRef]
- Zavala, P.; DeRoeck, W.; Janssens, K.; Arruda, J.; Sas, P.; Desmet, W. Generalized inverse beamforming with optimized regularization strategy. Mech. Syst. Signal Process. 2011, 25, 928–939. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, L.; Song, S.; Xu, Z.; Zhang, Z.; He, Y. Robust Acoustic Imaging Based on Bregman Iteration and Fast Iterative Shrinkage-Thresholding Algorithm. Sensors 2020, 20, 7298. https://doi.org/10.3390/s20247298
Huang L, Song S, Xu Z, Zhang Z, He Y. Robust Acoustic Imaging Based on Bregman Iteration and Fast Iterative Shrinkage-Thresholding Algorithm. Sensors. 2020; 20(24):7298. https://doi.org/10.3390/s20247298
Chicago/Turabian StyleHuang, Linsen, Shaoyu Song, Zhongming Xu, Zhifei Zhang, and Yansong He. 2020. "Robust Acoustic Imaging Based on Bregman Iteration and Fast Iterative Shrinkage-Thresholding Algorithm" Sensors 20, no. 24: 7298. https://doi.org/10.3390/s20247298
APA StyleHuang, L., Song, S., Xu, Z., Zhang, Z., & He, Y. (2020). Robust Acoustic Imaging Based on Bregman Iteration and Fast Iterative Shrinkage-Thresholding Algorithm. Sensors, 20(24), 7298. https://doi.org/10.3390/s20247298




