1. Introduction
Cellular licensed IoT technology has been an emerging and evolving Low Power Wide Area (LPWA) technology which provides long range, low power and low cost connectivity for IoT devices [
1]. It can be deployed in existing cellular networks from which it inherits many of the features that determine its behavior [
2], such as Long Term Evolution (LTE) networks. With the booming development of Fifth Generation (5G) technology, evolutions of cellular IoT standards have been proposed and put into practice by 3rd Generation Partnership Project (3GPP) [
3]. It will further promote the development of IoT technology. 5G technologies primarily include non-standalone and standalone technologies. The former is the early-drop technology that operators plan to connect new radio 5G base stations to the Fourth Generation (4G) core network until 5G connectivity migrates to the native 5G Core network mode which means shifts to standalone mode [
4]. For the 4G and nonstandalone 5G connections, Orthogonal Frequency Division Multiple Access (OFDMA) technology can be employed to enable multi-carrier transmission and network access. OFDMA can take advantage of multiuser diversity and robustness to multipath fading for the uplink communications. Moreover, it provides more degrees of freedom for resource allocation and facilitates multiplexing and diversity gains [
5,
6]. Due to the limited spectrum of licensed IoT, as the network gradually scales up, one of the key issues we face is how to effectively use these resources to support large-scale IoT devices. In addition, the cost of IoT has been a major concern, and the improvement of spectrum efficiency can help reduce the cost of cellular IoT networks.
In this paper, we focus on the uplink of OFDMA-based cellular IoT networks with multiple antennas receiver. The average statistical behavior of the network is considered where the active sensors and collectors are randomly distributed in a given area according to a random Poisson Point Process (PPP). The randomness of the wireless channel is considered as a mark of the Poisson position and results from stochastic geometry using marked PPP as in [
7,
8,
9,
10,
11,
12,
13,
14,
15,
16,
17,
18,
19] will be invoked. These tools were investigated in [
20,
21,
22,
23] to compute an upper-bound on the resource outage probability in a cellular network considering random PPP marked by the random fading. Unlike the previous contributions in [
20,
21,
22,
23] where the network is considered as noise limited, this study is more general as it takes into account the impact of interference on the statistical dimensioning. In [
24], our dimensioning model is restricted to the single user case with multiple antennas receivers, in which only the receiver diversity, namely, the antenna selection technique, is performed without exploiting the spatial multiplexing gain. This paper generalizes our previous contribution in [
24] by considering MU-MIMO schemes where multiple users can be scheduled over one RR. It introduces indeed a new criterion for performing dimensioning based upon low delay access. We also provide a comparison between the energy consumption of the different considered transmission modes.
We consider first single-user (SU) communication with receiver diversity transmission modes such as antenna selection considered in [
24] and the Maximum Ratio Combining (MRC). Next, we consider multiuser (MU) transmission where a distance-based scheduling algorithm is proposed with neighboring sensors nodes that are scheduled on the same RR. The interuser interferences are canceled using a Zero-Forcing decoder. The remaining diversity when not all the degrees of freedom are consumed is extracted using a MRC. The number of RR required by a single node in the SU case of by a group of nodes in the MU case is limited by the lowest Modulation and Coding Scheme (MCS). We define the network outage as the event that occurs when the number of request RRs exceed the number of the available ones. Whenever this event occurs, the sensor node has to delay its transmission to the next time transmission interval (TTI). Our goal is to determine the number of required RR to be allocated at the network side depending on the network load and the collector density in order to guarantee that the average delay access does not exceed a preset threshold.
The rest of the paper is organized as follows. We introduce in
Section 2 the network model and its properties. In
Section 3, we review first the dimensioning concentration inequality used in [
21,
22,
23,
24] that provides an upper-bound on the network outage probability and hence on the number of required RR. This upper-bounds depends on the average total number of required RR that we computed for the single-user case as in [
24] and for the multiuser case that we introduce in this paper. We also characterize in each case the power distribution. The results presented in this section are general and are not related to the transmission mode fading distribution observed by the collector or the statistical behavior of interference that are characterized in
Section 4. Numerical results are provided in
Section 5 to compare the transmission mode in terms of required RRs and energy consumption in function of the collectors density and the average required delay. Finally,
Section 6 concludes the paper.
2. IoT Network Model
We consider a sensor network in which a random number of active nodes sensors and collectors are distributed in a given area
according to two independent homogeneous PPP with intensities
and
. We assume that the sensors are equipped with a single antenna and that the collector is equipped with
receiver antennas. We assume that a sensor is active
times per day, the mean service time is
(s) and the interarrival rate is
per second and per km
2. The active sensors nodes form then a spatial PPP
with intensity
The frequency reuse pattern in the network is equal to 1. At a given collector situated at
, the received power on a given RR from a sensor
transmitting with power
(mW per RR) is computed as,
where
and
are respectively the attenuation factor (that includes the average shadowing) and the path-loss exponent that are computed from the Okumura-Hata model,
is the fading coefficient with distribution depending on the antenna configuration and the used transmission mode (single-user or multiuser). The sensor nodes are considered as static and the fading channel is considered as flat during the transmission. The Channel State Information (CSI) is only available at the receiver side and not at the transmitter side. Each sensor is connected to the collector on which the average received power (by averaging over the fading and the shadowing) is the highest. This is equivalent to connect the sensor to the nearest collector. Assuming a collector
, the set of the sensors connected to this latter is defined as
Nodes transmitting in the same frequency band generate additive interference with power
with
The received SINR at the given collector
is,
with
being the random exponential noise power with mean power of
where
K is the Boltzmann’s constant
W Hz
−1 K
−1,
T the absolute temperature in kelvins
K and
B the bandwidth. The power of the random exponential noise power is characterized by its Laplace transform as,
Due to Slivnyak-Mecke Theorem in [
8], the statistical behavior in the PPP remains unchanged when adding a collector at the center of this region. This defines the typical cell centered at the origin
as illustrated in
Figure 1. The typical cell properties are reviewed in Proposition 1.
Proposition 1 (Typical cell properties)
. The typical cell average number of sensors is, The probability distribution function of the distances between and the o collector is, The average radius of the typical cell is .
Proof. We provide for completeness the proof in
Appendix A. □
3. Proposed Statistical Dimensioning Model
Given the density of collectors in the network, we propose a statistical method for resource planning in the uplink of cellular IoT networks. We assume the network access is an OFDMA and consider only the Narrowband Physical Uplink Shared Channel (NPUSCH) which carries the uplink user data and uplink control information. In an NB-IoT network or LTE-M, identical to the LTE network, the smallest block of radio resource elements that can be invoked is called the Resource Block (RB) or Radio Resource Block (RRB). It contains several OFDM symbols. Each RR corresponds to 180 kHz in the frequency domain and ms in the time domain. In the 5G, different numerologies were defined to reduce the RR duration and hence the latency by increasing the RR bandwidth. In the following, the RR corresponds to the LTE resource block and the RR with numerology 0 in the 5G terminology. For the single-user and multiuser cases, our main objective here is to statistically determine the total number of required RRs to minimize the occurrence of the network outage event. When the total number of RRs required is larger than the number of RRs available on the collector side, this is considered as an outage event.
3.1. Dimensioning Objectives in a Typical Cell
In the typical cell illustrated in
Figure 1, the collector o allocates according to the level of the received SINR, 1 to
RRs to the sensor node in order to achieve its target data rate
. The required number of RRs is,
with
being the threshold SINR required to achieve a target rate of
within a single RR and
and
. Note that
(respectively
) is the threshold SINR to decode the highest (respectively lowest) Modulation and Coding (MCS) scheme. If
, the sensor will not be able to decode the lowest MCS and the collector does not attribute any RR to this user. This event of having insufficient SINR occurs with probability, we intentionally do not refer to this probability as outage to avoid confusion with the network outage probability.
By setting
with
the threshold fading to achieve a rate
over one RR, the number of RR can be rewritten as,
The total of required RR in this typical cell depicted in
Figure 1 is,
The network is in outage if,
In order to ensure an optimized network dimensioning, the number of total radio resources
that ensure a network outage probability of
, should be found. Using the concentration inequality, the typical cell outage probability is upper-bounded by,
where
with
the function
and
. By setting a threshold
on the network outage,
3.2. Average Delay and Choice of the Network Threshold
In this subsection, we compute the average delay to connect the sensor device to the network independently of its transmitting rate. This average delay should not exceed a maximal delay
that we assume proportional to the Time Transmission Interval (TTI). As long as the sensor is not accepted by the network due to the lack of resource, a new trial will be performed after TTI. We assume that the probabilities of being rejected after
are independent and are equal to
. The average delay to access to the network is hence,
This expression can be simplified to,
By choosing
such that
we make sure that the average delay in the network does not exceed
. By letting
, the network threshold is,
3.3. Expressions of and
In this subsection, we derive the expressions of
and
in (
16) and (
17) considering the single-user and multiuser cases. We recall that all sensor devices are equipped with a single antenna and the number of antennas at the collector is
. The distribution of the fading coefficient in (
4) will be specified in the next section depending on the antenna configuration and transmission mode.
3.3.1. Single-User Case
Proposition 2 (Single-user case)
. The expressions of and are,with the average number of sensors as shown in (6), and with defined in (7). Note that (
22) can be interpreted as following:
is the average number of sensor in the typical cell; each sensor requires each 1 to
RRs depending on their distance to the collector, the channel conditions and the additive interference and noise.
3.3.2. Multiuser Case
In the multiuser case, we assume that each RR is shared by
users simultaneously as depicted in
Figure 2. To cancel the interuser interference, the collectors uses a Zero-Forcing (ZF) decoder. The equivalent fading observed by each sensor
j device is denoted by
having a distribution that will be specified in the next section.
Distance based multiuser scheduling scheme: In this scheme, the active users are sorted according to their proximity to the collector into different groups of
users, each independently of their fading. As shown in
Figure 3, the first group contains the
nearest neighbor to the typical collector, the second group the
to
collector neighbor and so on. We adjust the number of allocated RRs to the furthest user from the collector in each group independently of the fading coefficient experienced by other users. The furthest node
x in each group
i is the
neighbor of the collector and it corresponds to the radius of the ball
with radius
containing
nodes.
Proposition 3 (Multiuser case)
. The expressions of and arewhere is the ball with radius r, andwith being the set of nonzero positive integers. The distribution of r in the typical cell is given by defined in (7). Note that Proposition 3 is a generalization of Proposition 2 with
. For
,
and the expressions of
in (
24) becomes equal to (
22).
3.4. Distribution of the Sensor Power Consumption
We assume that the transmitted power is fixed to per RR and the total power over RRs does not exceed . The power is then a discrete random variable and its Probability Mass Function (PMF) is given in Proposition 4.
Proposition 4 (Total sensor power PMF)
. For the general case, the sensor power PMF is,with , the number of the groups of sensors in the typical cell such that,and . Proof. The proof is similar to Proposition 3 and the PMF can be obtained by averaging over the whole power in the typical cell normalized by the size of this latter. In each ring delimited by the and neighbor, the sensors adjust their power to the the furthest neighbor. □
5. Numerical Results
In this section, we consider the uplink of a sensor network corresponding to the licensed IoT with parameters summarized in
Table 1.
We assume that the density of nodes
sensors per km
2 transmitting on average once each half-an-hour,
during 20 seconds. The active node density is then
sensors per km
2. We consider a cellular network with ranges between 500 m to
km corresponding to a collector density of
nodes per km
2 down to
nodes per km
2 (the ranges are obtained with a confidence margin of 95%). The maximal power is limited to 14 dBm and is uniformly distributed among the allocated RRs.
Table 2 gives the matching between the SINR range with the required number of RRs to achieve a target rate of
bps. This data are derived from the Link Layer Simulation (LLS) provided in [
26] on the Physical Uplink Shared Channel (PUSCH) of LTE-Cat M. To evaluate network performances, we consider a path-loss in an urban/suburban environment with
and
. We consider the following antenna configurations: SISO, single SIMO with
, multiuser SIMO with
and
or
.
5.1. Accuracy of the Theoretical Model
Table 3 indicates the percentage difference between the mean number of RRs required in the typical cell derived by using our statistical dimensioning tools and the empirical network simulation results. The mean number of required RRs using former method is denoted as
, the simulation one is denoted as
. Consequently, the percentage difference is
. We consider different collector intensities (from 0.1 to 0.9 nodes/km
2) and different antenna configurations as well as transmission modes. As presented in the
Table 3, the comparison shows that the difference between the results obtained by our statistical tools and the simulated values is very small, which verifies the accuracy of our model and approach.
5.2. Average and Total Number of RR
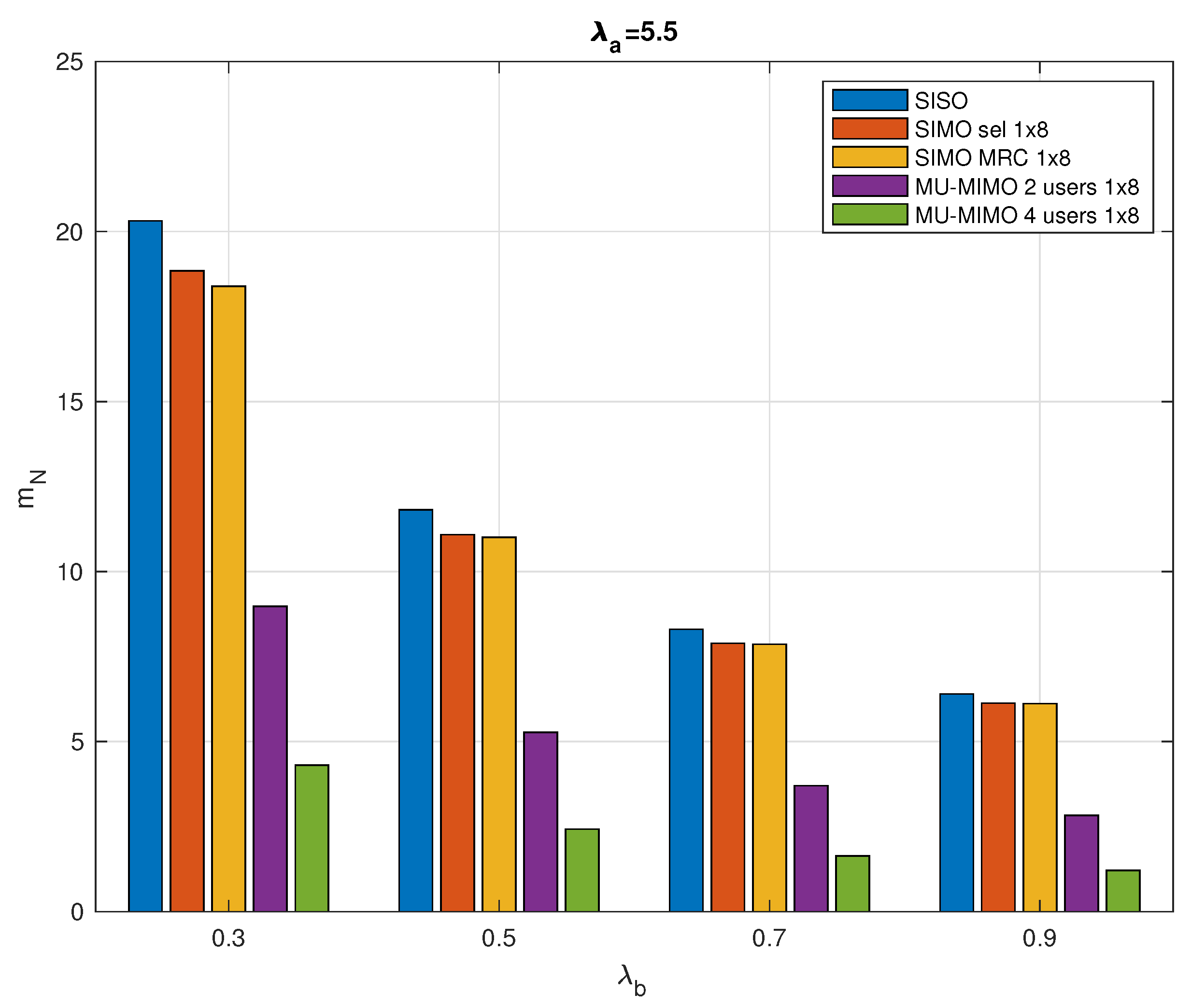
Figure 5 further illustrates the specific value of
considering different network configurations. As shown in the figure, for the given active sensor and collector intensities
and
, respectively, assuming a maximum delay of 1 ms, the SISO system always requires the highest mean number of RRs.
With the use of SIMO and MU-MIMO, multiantenna techniques achieve higher data rates through increased spectral efficiency, with a corresponding reduction in the required RRs. The multiple receive antennas system has the potential to enhance signal robustness and increase system capacity. In particular, the MU-MIMO system significantly reduces the mean number of RRs required in a typical cluster. Meanwhile, as collector intensity increases, the mean number of RRs required for various configurations decreases. When increases, the radius of the typical cell will decrease, while the number of active sensor nodes per unit area remains the same, which means that each collector needs to serve fewer nodes in the cell and thus the number of RRs required decreases.
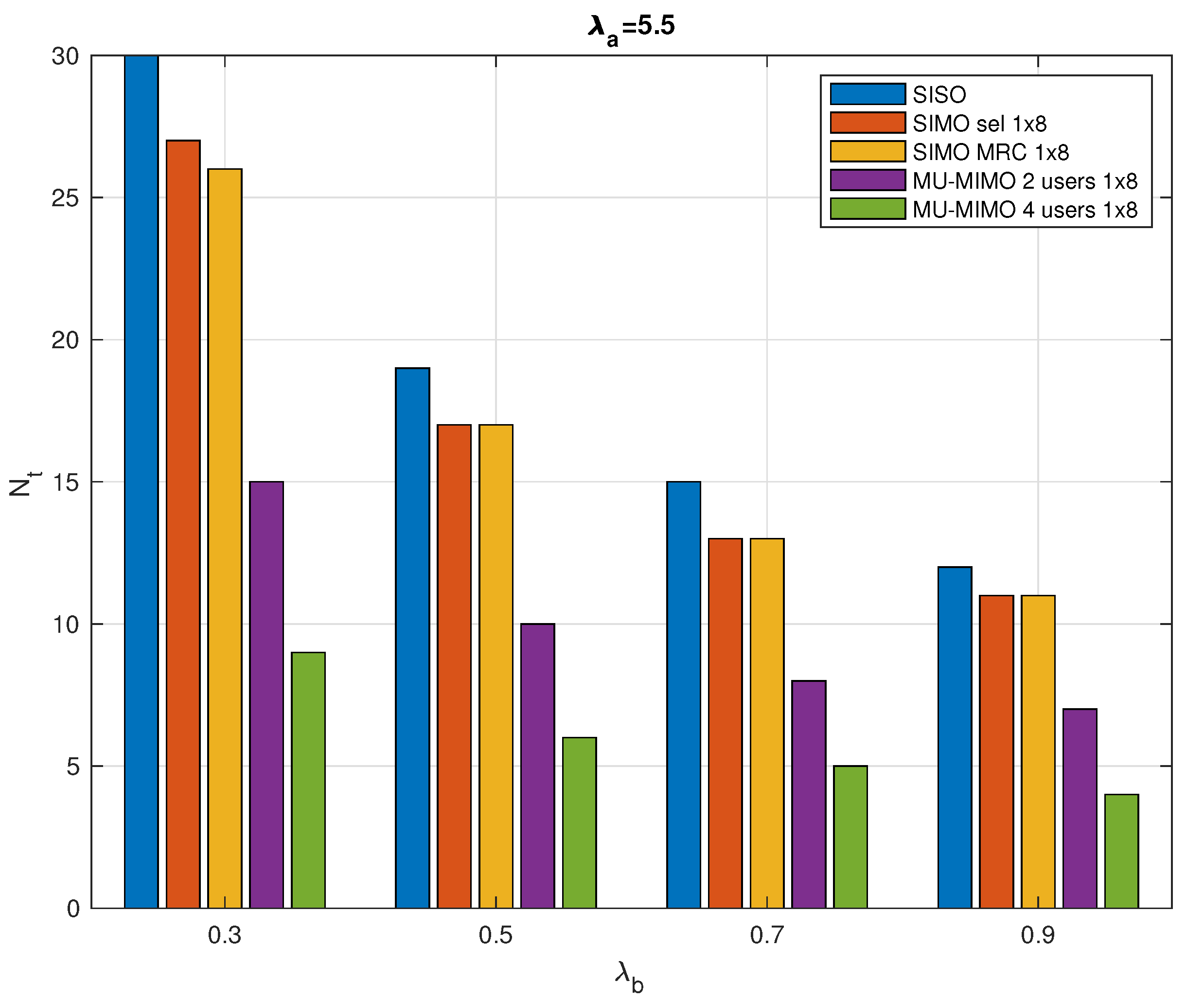
Figure 6 presents the total number of required RRs in a typical cell versus the collector intensity. It maintains the same trend as in
Figure 5, with MU-MIMO being the best performing case, followed by SIMO and then SISO.
5.3. Empirical Distribution and Actual Average Delay
Figure 7 illustrates the empirical Cumulative Distribution Function (CDF) of the total number
of RRs required for the typical cell with
nodes/
and
nodes/
.
For example, according to
Figure 6, for the same value of
,
, we find that the
value required for the SISO system is 19. In
Figure 7, we can see that
corresponds to a CDF value of
. This means that there is a network outage probability of
meaning that the network cannot attributed RR to
of nodes in the typical cell. The corresponding average delay can be then computed using (
19).
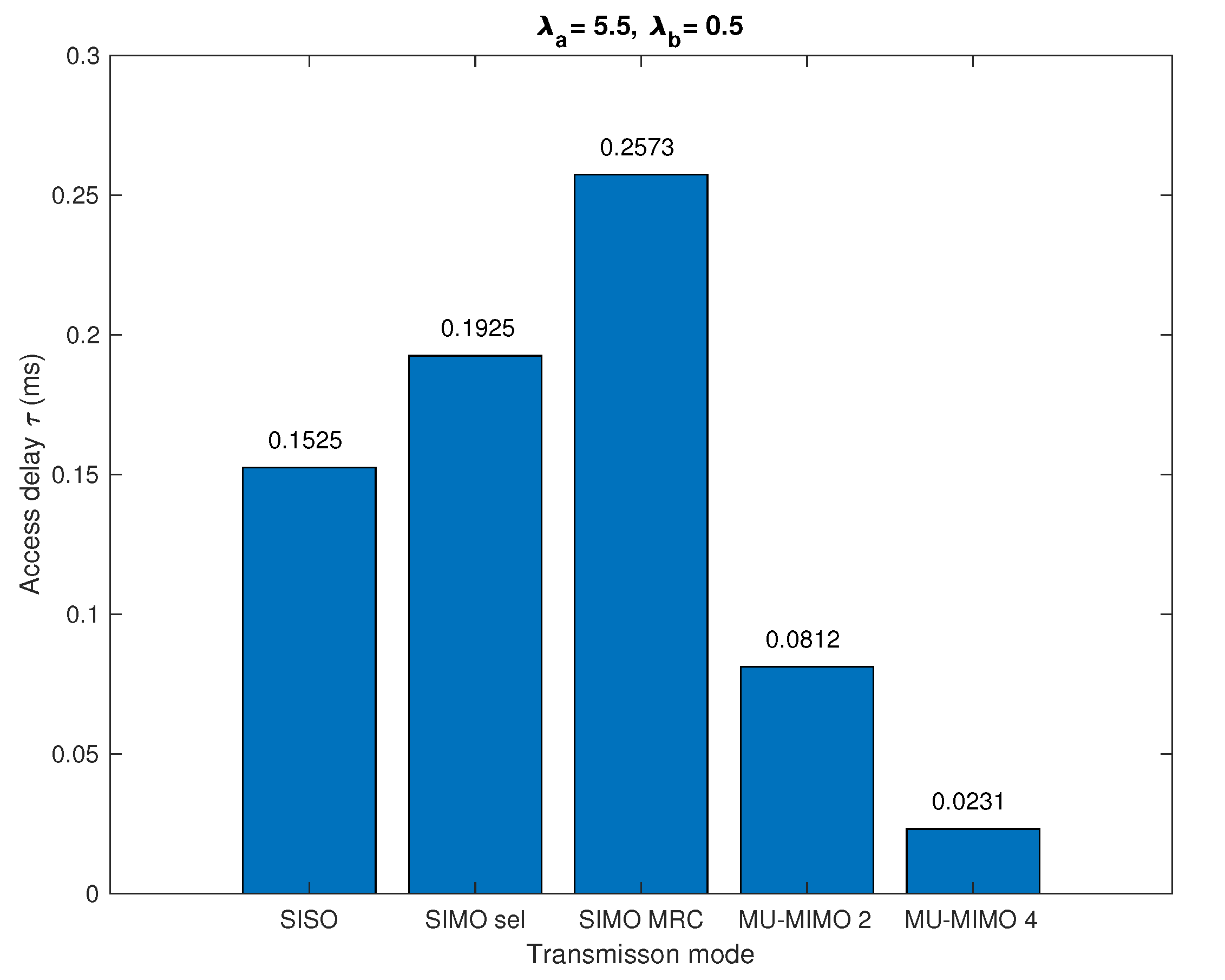
Figure 8 show the actual average access delay corresponding to different antenna configurations and transmission modes for given intensities of active sensors and collectors
,
and the maximum access delay
ms. It can be seen from the figure that the average access delay
is less than the maximum access delay
. SIMO with MRC transmission mode requires the longest access time because it has the lowest individual off probability, i.e., it serves the largest percentage of active nodes. The second highest access delay is the SIMO with antenna selection scheme. For the SISO configuration, the average access delay is relatively lower because in this mode, many nodes are in off state and not served. For the MU-MIMO system, each time there are
nodes transmitting information simultaneously and being processed by the collector. The larger the
is, the shorter the average access delay required.
5.4. Tolerated Delay and Overdimensioning
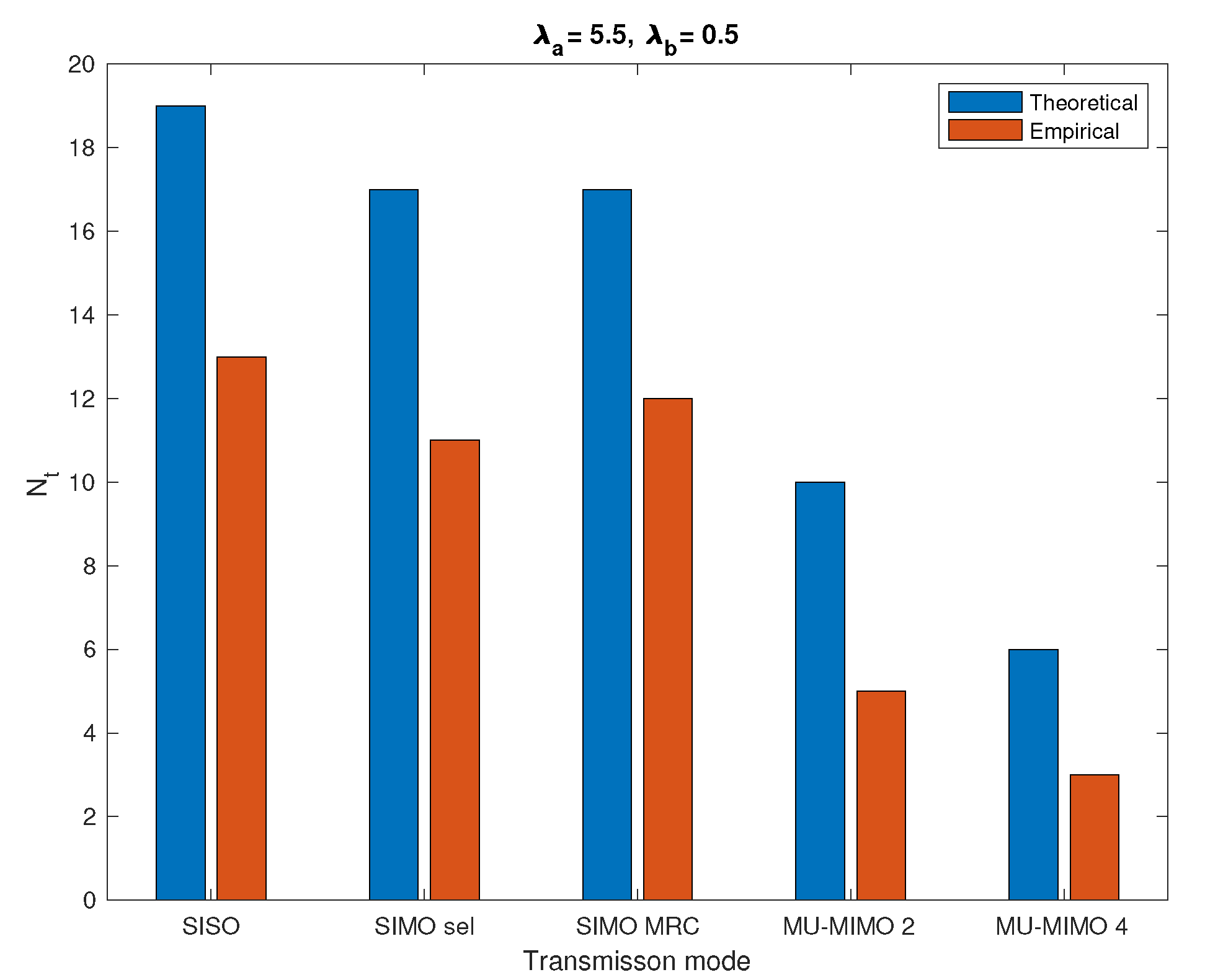
Figure 9 gives a comparison of the theoretical and empirical values of
for a typical cell that guarantee an average delay of 1 ms.
From the figure, it can be seen that the derived by our statistical tool is always larger than the empirical , i.e., it is overdimensioning. The excess in the radio-resource provided by the theoretical model ensures that the expected data rate is achieved and the access to the cellular IoT network does not exceed the predefined average access delay.
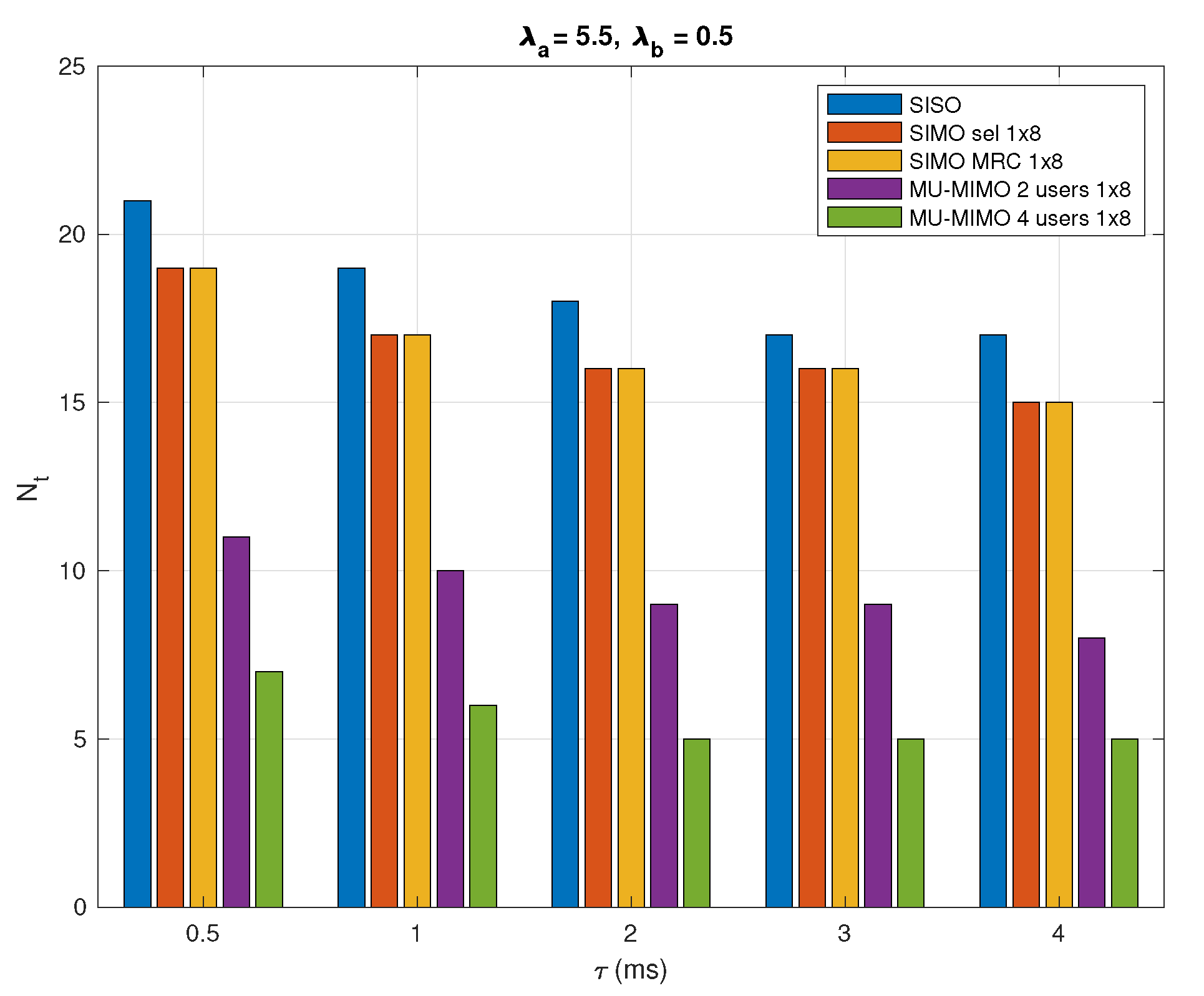
In
Figure 10, it shows the relationship between the total number of required RRs and the maximal access delay
with
nodes/
and
nodes/
. Assuming that
ranges from
to 4 ms, a larger
means that the node can wait longer for access to the network. The average access delay
of the active nodes must not exceed the maximal delay
. In general, a lower total number of RRs is required to response to the demands of active sensor nodes with a larger
.
5.5. Individual Sensor off Probability
As mentioned in
Section 3.1, when the SINR received on the collector side is below the SINR threshold
, no RR will be assigned to this sensor. In other words, this active sensor is forced to be off in this trial.
Table 4 illustrates the individual off probability in the typical cell according to the different antenna configurations, including SISO,
SIMO with antenna selection and MRC, 2 users and 4 users
MU-MIMO. From the table, we can see the
SIMO with MRC outperforms other modes in the individual off probability. Although it does not reduce the number of RRs required in the typical cell significantly compared to the SIMO with antenna selection or the MU-MIMO, it does reduce the sensor individual off probability, ensuring more sensors to be served. This result gives us a new way of thinking about resource planning, i.e., we need to take into account both the total number of RRs assigned to the network and the individual off probability to improve network service.
5.6. Power Distribution
In
Table 5, for a given pair of
and
, we elaborate the power distribution with the different transmission modes in the typical cell. The transmission power of each RR is fixed to
mW (
dBm), so the maximal transmission power is
mW (14 dBm) with
. For each transmission mode,
Table 5 shows the specific percentage share of each transmit power. Where off represents a number of nodes to which no RR is assigned and therefore have a transmission power of 0 mW. From
to
corresponds to the transmission power of the nodes that are assigned the corresponding number of 1 to 6 RRs, respectively. As marked in the light grey part of the table, it can be noticed that SIMO with MRC mode has the least number of off nodes, meanwhile with
of the nodes being transmitting information at
power. Therefore, it has the best power distribution. MU-MIMO with
also has a good power distribution, with only
of nodes off and
of nodes transmitting at
. SISO has the worst performance, with up to
of nodes unable to transmit information and only
of nodes transmitting at low power.
6. Conclusions
In this paper, we focus on licensed OFDMA-based IoT networks which corresponds to NB-IoT, LTE-M and to some extent 5G network using the numerology 0. We assume a wireless sensor network in which sensor nodes and collectors are distributed according a spatial PPP. A statistical method based on PPP is proposed to model and analyze the average behavior of the cellular IoT networks. This method is used for statistical resource planning to support the dominant uplink communications in the IoT networks and fulfill the network requirements in terms of limited transmission power per RR, low access delay, preset network outage probability and target data rate. Different antenna configurations and transmission modes are taken into account, e.g., SISO, SIMO, and MU-MIMO. Based on the preset tolerated average access delay and target data rate, the specific total number of RRs required for the typical cell is further calculated. Numerical results are finally given to assess our statistical analysis. We compare the theoretical results with the empirical simulation results in detail. The comparison shows that the results obtained from our statistical model are very close to the empirical results. Moreover, the results highlight and quantify the radio resources gain obtained by the receiver diversity techniques and the multiuser gains.