Motion Inference Using Sparse Inertial Sensors, Self-Supervised Learning, and a New Dataset of Unscripted Human Motion
Abstract
1. Introduction
2. Materials and Methods
2.1. Overview
2.2. Data Collection
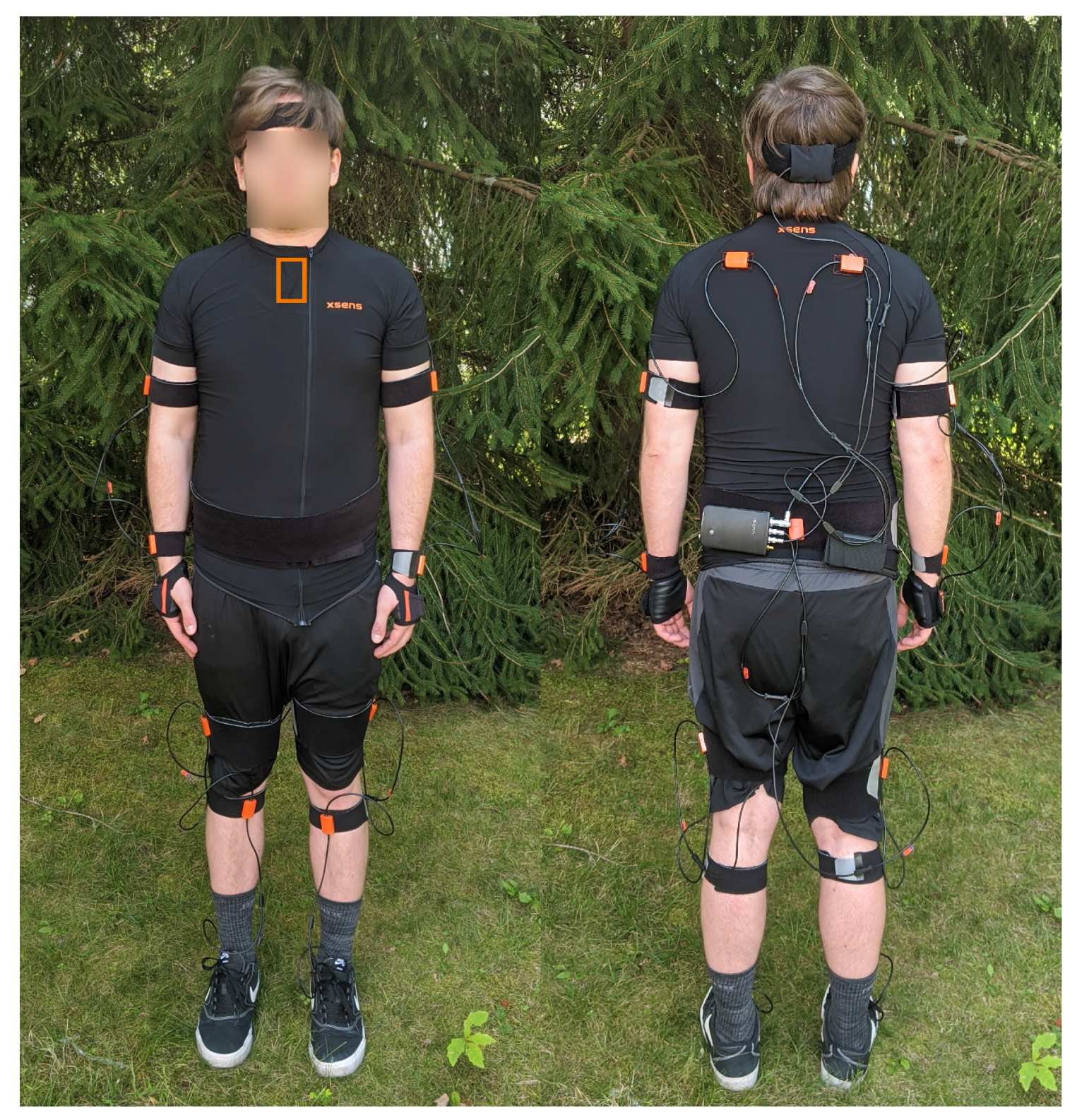
2.2.1. Data Collection System
2.2.2. Data Collection Study Design
2.2.3. Manual Material Handlers
2.2.4. Virginia Tech Participants
2.2.5. Quality Assurance
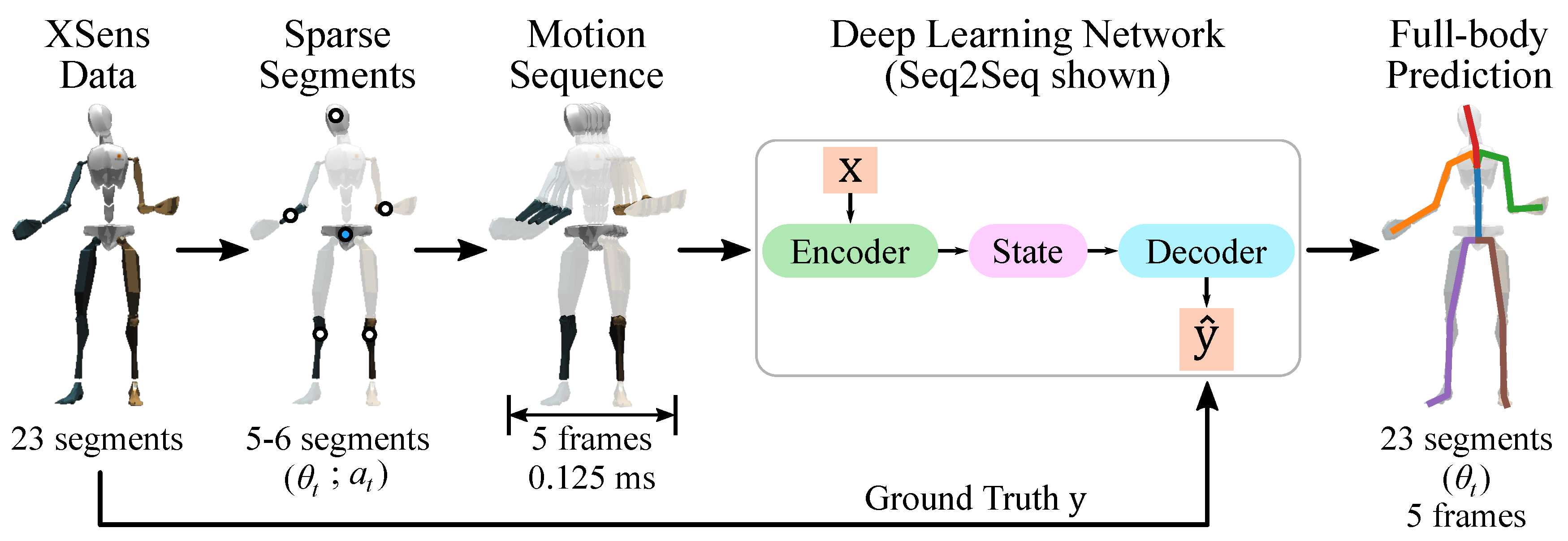
2.3. Human Motion Inference Using Sparse Sensors
2.3.1. Overview
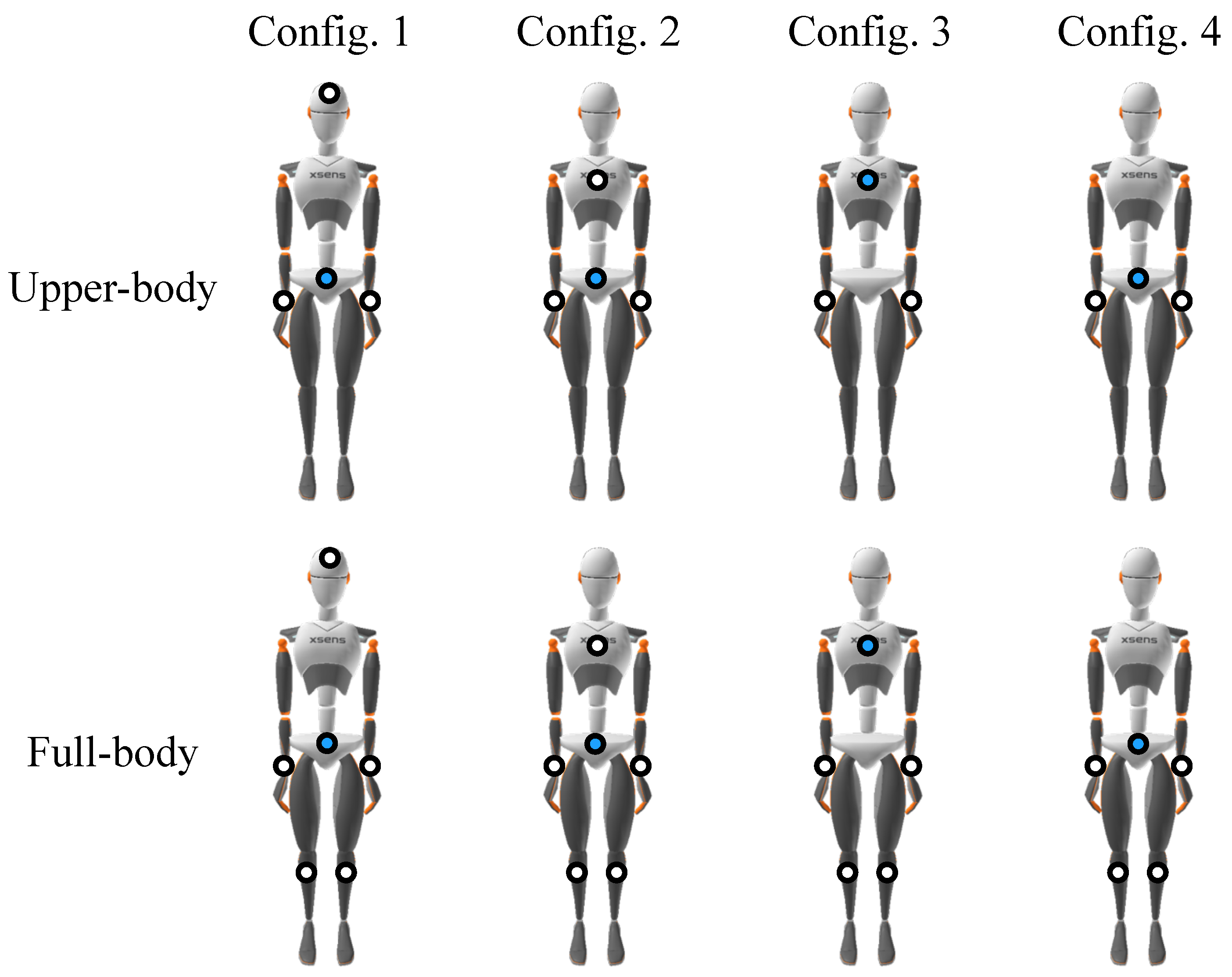
2.3.2. Inputs and Outputs
2.3.3. Representing Rotations
2.3.4. Normalization
2.4. Deep Learning for Human Motion Inference
2.4.1. Seq2seq Architectures
2.4.2. Transformer Architectures
2.4.3. Training
2.4.4. Evaluation
3. Results and Discussion
3.1. Dataset
3.2. Evaluation Overview
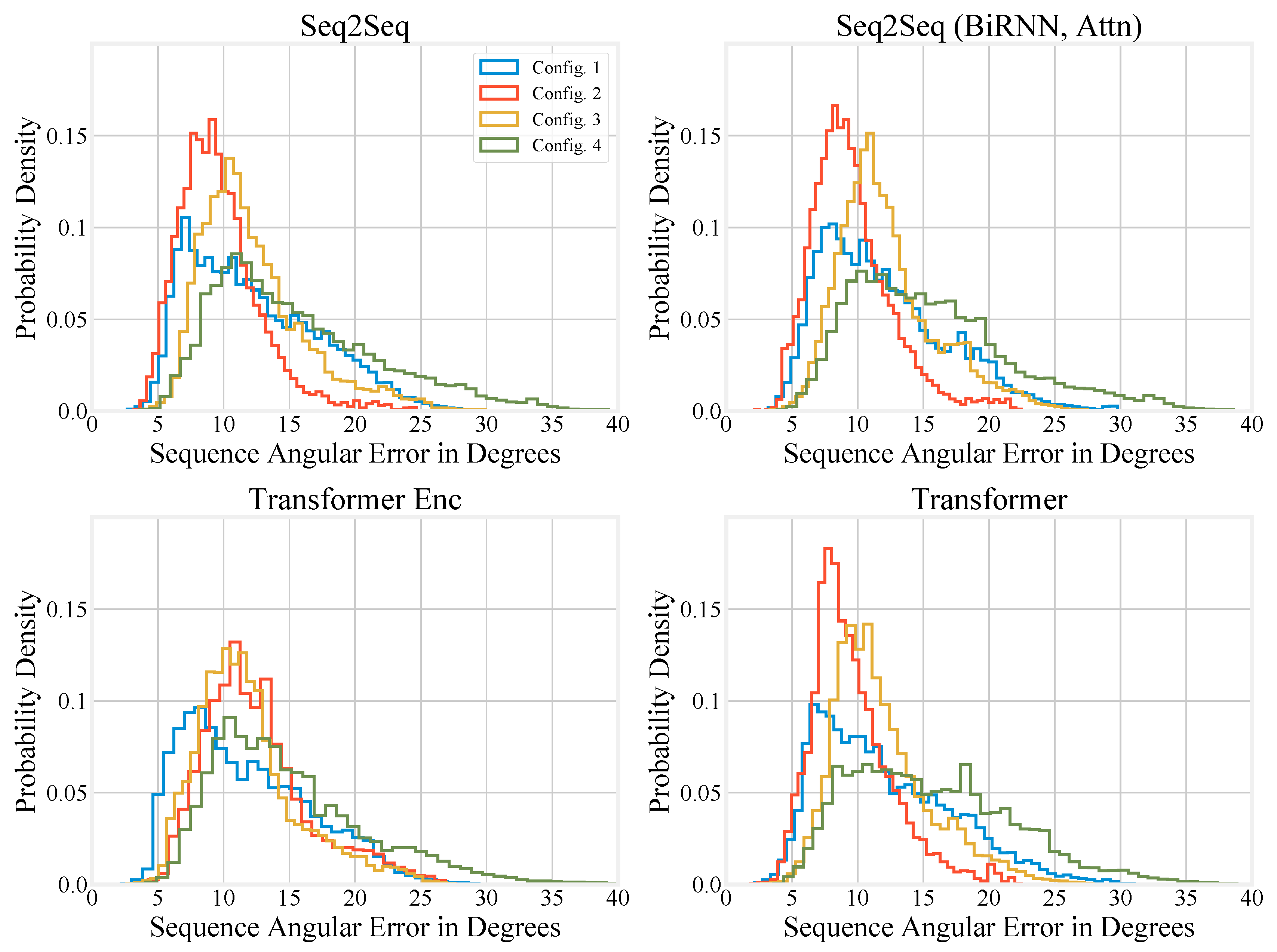
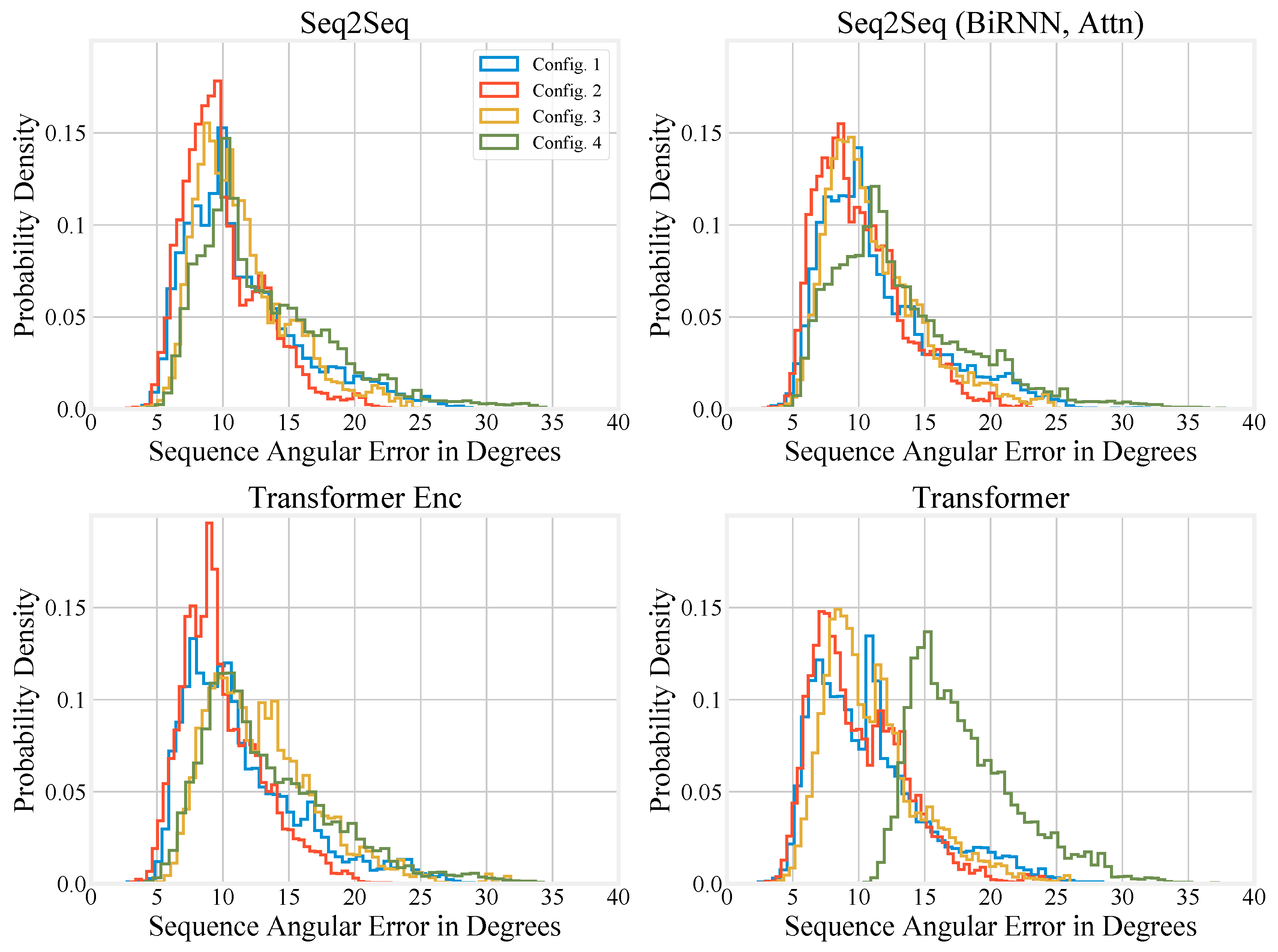
3.3. Quantitative Evaluation
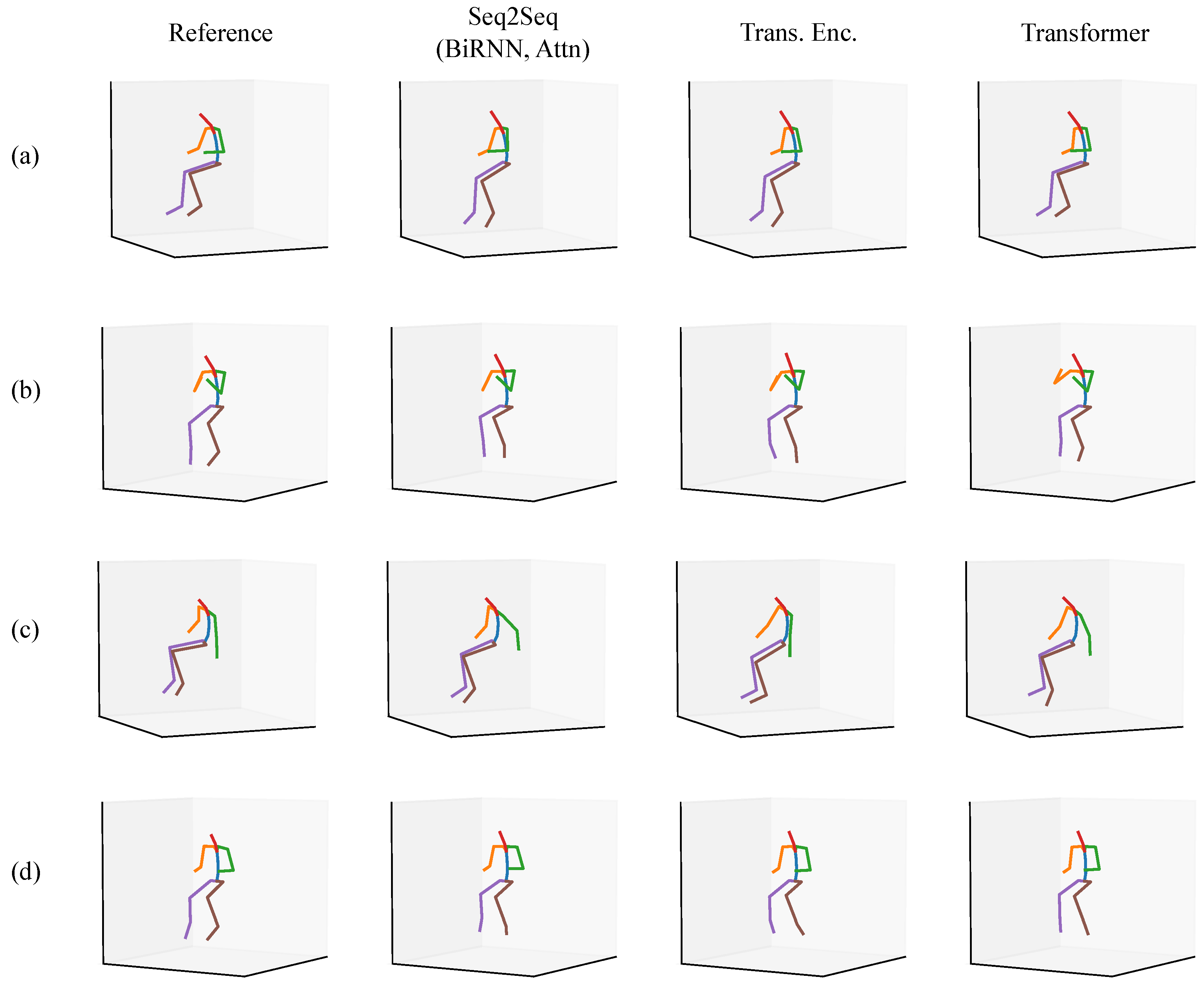
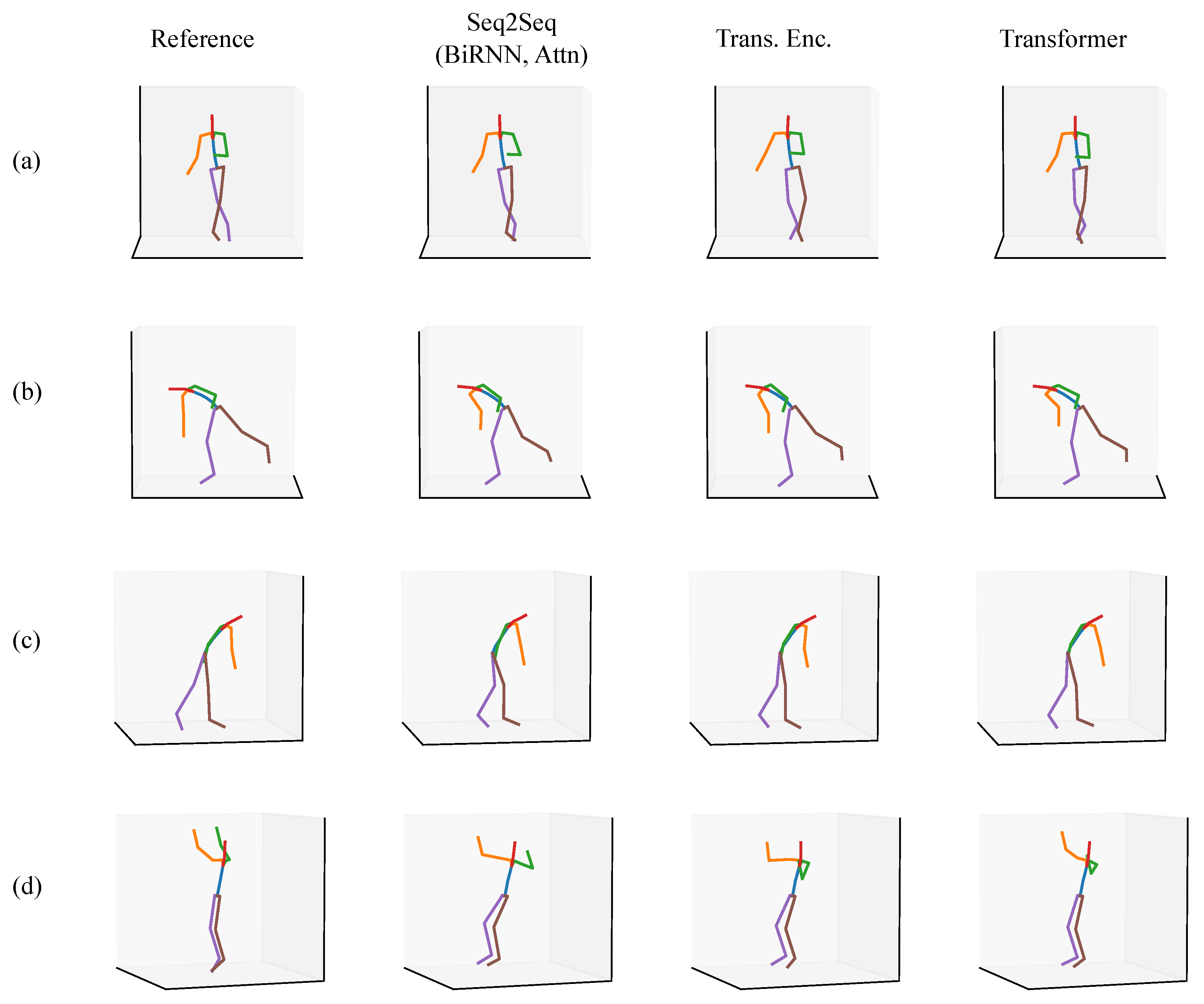
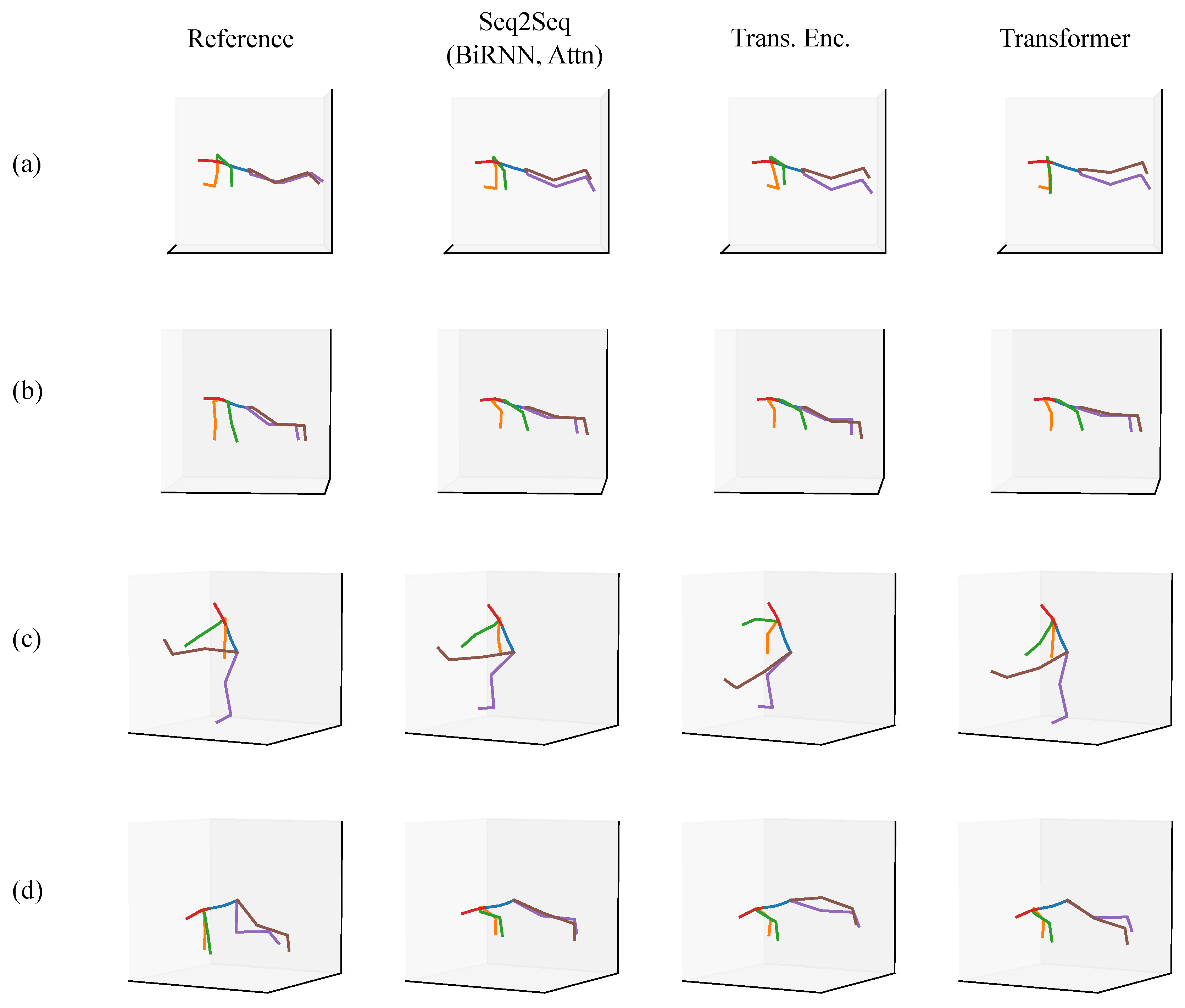
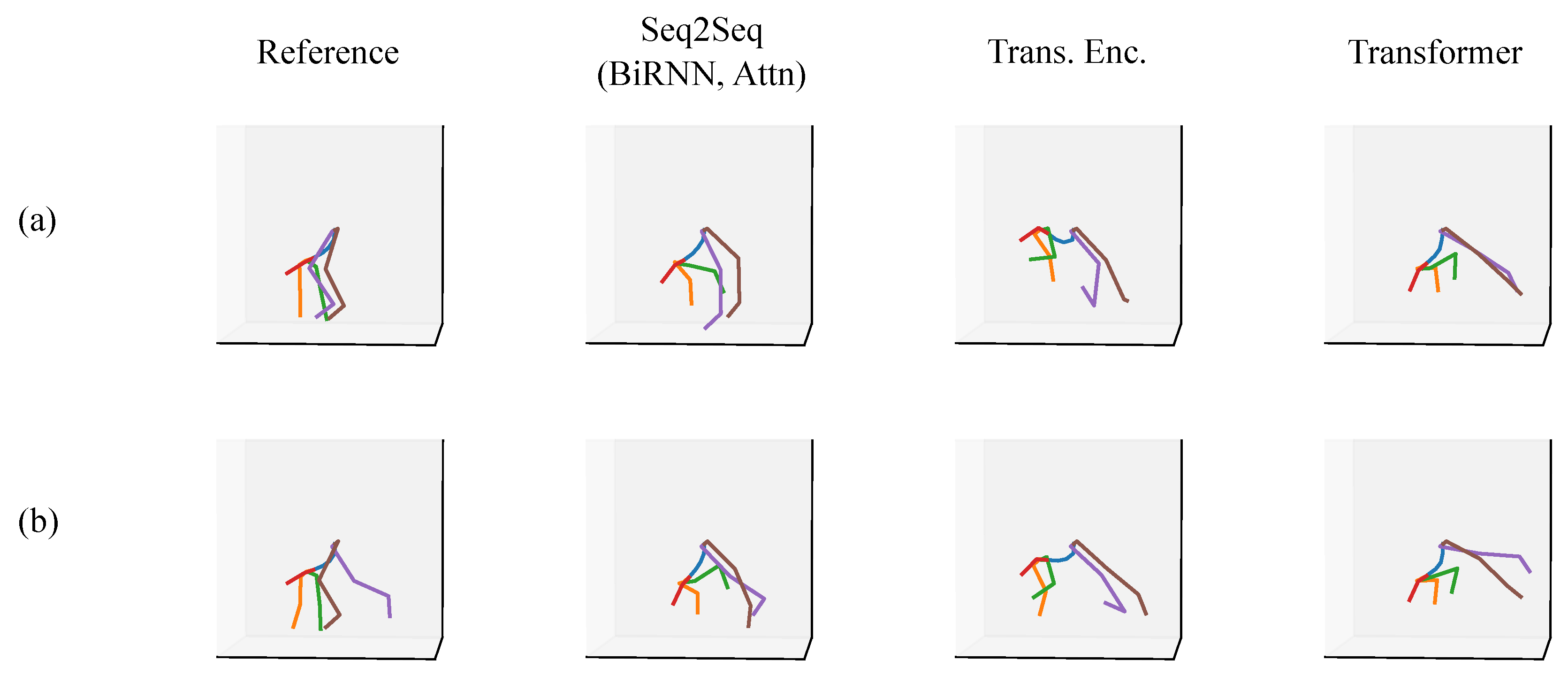
3.4. Qualitative Evaluation
3.5. Comparison to Prior Works
3.6. Limitations and Future Work
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Dataset Description
| Subj. | Day | # Frames | Dur. | Notes |
|---|---|---|---|---|
| All | All | 35087845 | 40.59 | |
| P1 | Day 1 | 1557894 | 1.8 | The participant was in a lab environment operating an experiment involving a virtual reality setup and other hardware. They stand and sit repeatedly to make adjustments. They manipulated many things with their hands. |
| P2 | Day 1 | 1103415 | 1.27 | The participant was sitting in a chair in an office environment, performing work on a computer that included CAD design. The participant was also talking with others and walking around. The participant was having a technical discussion with another person throughout the duration of the data collection. |
| Day 2 | 1293893 | 1.5 | The participant was working in a lab environment, manipulating scrap metal and other materials with their hands. They also operated a drill press. The participant was talking with other people, working with his hands, and walking around an office. | |
| Day 3 | 1604016 | 1.85 | The participant was working in a lab environment, manipulating scrap metal and other materials with their hands. They also operated a drill press. The participant was talking with other people, working with his hands, and walking around an office. | |
| Day 4 | 1349583 | 1.56 | The participant was cleaning up a lab environment and machine shop. They stand and walk around for most of the trial while manipulating objects with their hands. | |
| P3 | Day 1 | 1377289 | 1.6 | The participant was in an open office/lab environment at their desk. The participant was reading and writing on a tablet while sitting and reclining in their chair. The participant also walked around some, spoke with others, and manipulated things with their hands. |
| P4 | Day 1 | 1709725 | 1.97 | The participant was sitting in an office environment working at a computer. The participant was sitting and manipulating things at their desk for the majority of the trial. |
| Day 2 | 529900 | 0.61 | The participant was sitting at a desk in a lab environment doing office work. | |
| P5 | Day 1 | 272731 | 0.32 | The participant attended a sketching session. They walked to the sketching session and drew for the remainder of the log. They did other interesting things, like hold the door open for people, reach into their backpack while sitting down, and operate their laptop in their lap. |
| P6 | Day 1 | 1709741 | 1.98 | The participant was sitting at a desk, working on a computer, and talking with others. |
| Day 2 | 1242864 | 1.44 | The participant was standing for the duration of the log and operating an experiment. They were primarily interacting and talking with an experiment collaborator and the participant who was testing an exoskeleton and assisting with data collection. They were leading a person through the experiment, handing them weights, standing, and performing other actions. | |
| P7 | Day 1 | 1256115 | 1.45 | The participant walked around Virginia Tech’s campus, went to class, and also drove around in their car to a local department store. |
| P8 | Day 1 | 1894520 | 2.19 | The participant walked around campus, attended office hours, and worked on homework with their computer while sitting down. |
| P9 | Day 1 | 3299680 | 3.82 | The participant walked across campus to meet a friend for lunch, sat down, ate food, and did stretching motions to show their friend how the XSens worked. They also went to class, took notes, and spoke with people about the XSens suit. |
| P10 | Day 1 | 1358481 | 1.57 | The participant walked around campus to a teacher’s office hours and worked in the office. They worked on a computer and on their homework while standing up. |
| P11 | Day 1 | 2574733 | 2.98 | The participant walked across Virginia Tech’s campus to attend class. The participant then walked back across campus, got take-out food from a restaurant, and returned to the starting location. |
| P12 | Day 1 | 1709704 | 1.98 | The participant walked across campus to a lab meeting and their office where they sat and discussed things with other people. |
| P13 | Day 1 | 1587648 | 1.84 | The participant was at their home near Virginia Tech’s campus. They were doing Spring cleaning activities, such as sweeping and vacuuming. They also emptied a dishwasher, played the piano, played video games, and took a nap. |
| Day 2 | 209547 | 0.24 | The participant did exercises at their home near Virginia Tech’s campus, including Frankensteins, jumping jacks, pushups, mountain climbers, burpees, and some jogging. The participant was working at a standing desk and using their smartphone at their home. The participant also walked to their car and started to drive to complete some errands. The later data in the car had errors so it was trimmed to only include the participant reversing out of their parking spot. | |
| W1 | Day 1 | 1707956 | 1.98 | The participant pushed and pulled carts, looked at and wrote on a clipboard or a touchpad, placed items on shelves, and bent down to objects low to the ground. |
| W2 | Day 1 | 506650 | 0.59 | The participant pushed/pulled carts, bent over to objects low to the floor and knelt on the ground to pull something once. |
| Day 2 | 1159655 | 1.35 | The participant operated a small touchscreen, spent some time interacting with something overhead, leaned far forward for something and bent over in other postures, as well. They also poured some material, pulled and pushed a cart, sat down for a small time, and operated machinery. The participant also operated a dolly, including putting an object onto it. | |
| Day 3 | 715716 | 0.83 | The participant walked around while pushing an object similar to a wheelbarrow. They also pushed and pulled carts. They did some overhead lifting of materials and low-height object manipulation with various bending postures. The participant carried objects on their shoulders and spent some time looking upwards at something. | |
| W3 | Day 1 | 1709720 | 1.97 | The participant sorted materials and placed objects in containers. They carried objects around. The participant also did low-height object manipulation with various bending postures. They also pushed and pulled carts. |
| W4 | Day 1 | 1646669 | 1.9 | The participant did low-height object manipulation, including squatting. They operated machinery while standing up (possibly a stand-up forklift), pushed and pulled carts, and spent a lot of time sorting bins and other containers. |
Appendix B. Histograms for the Special Test Sets
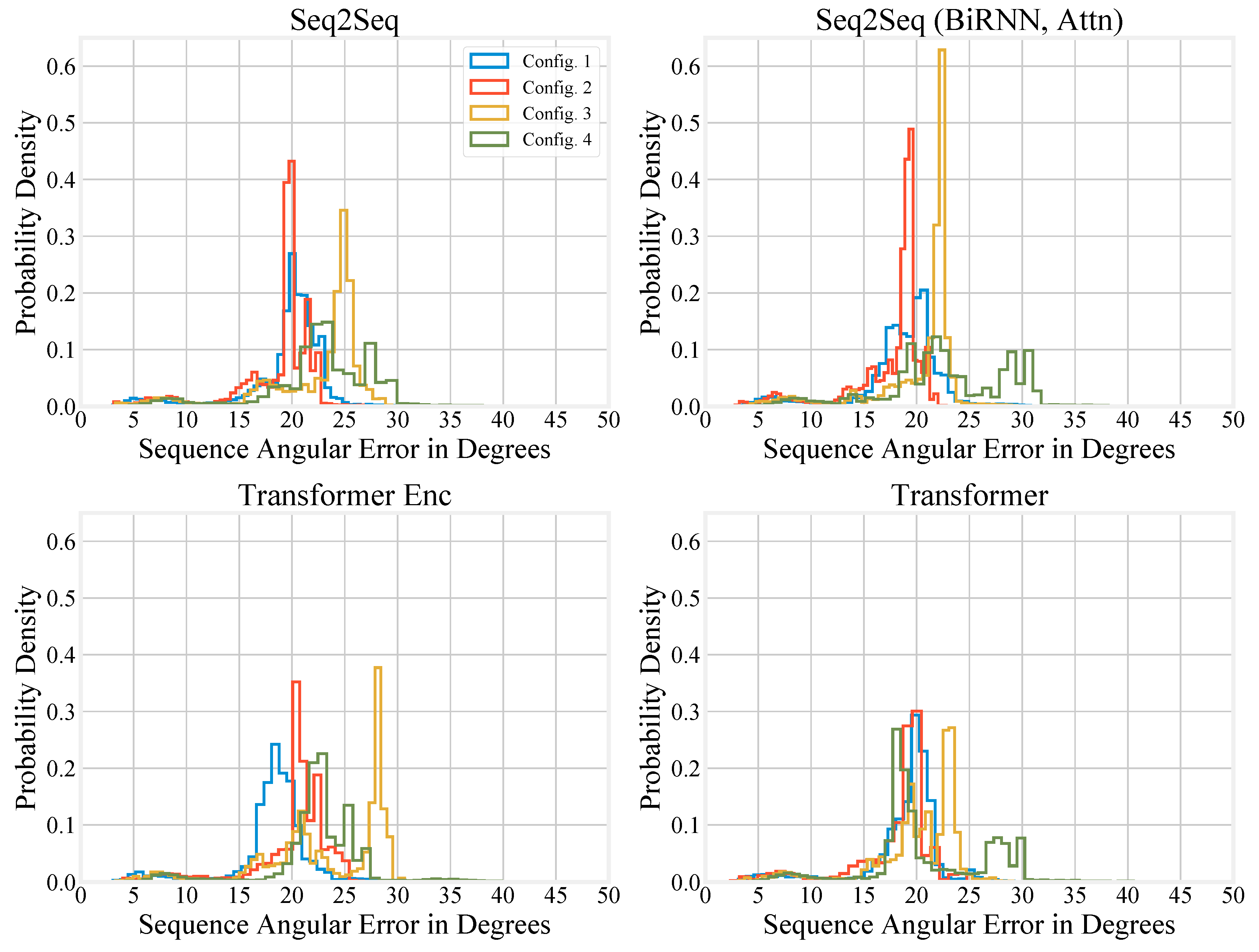
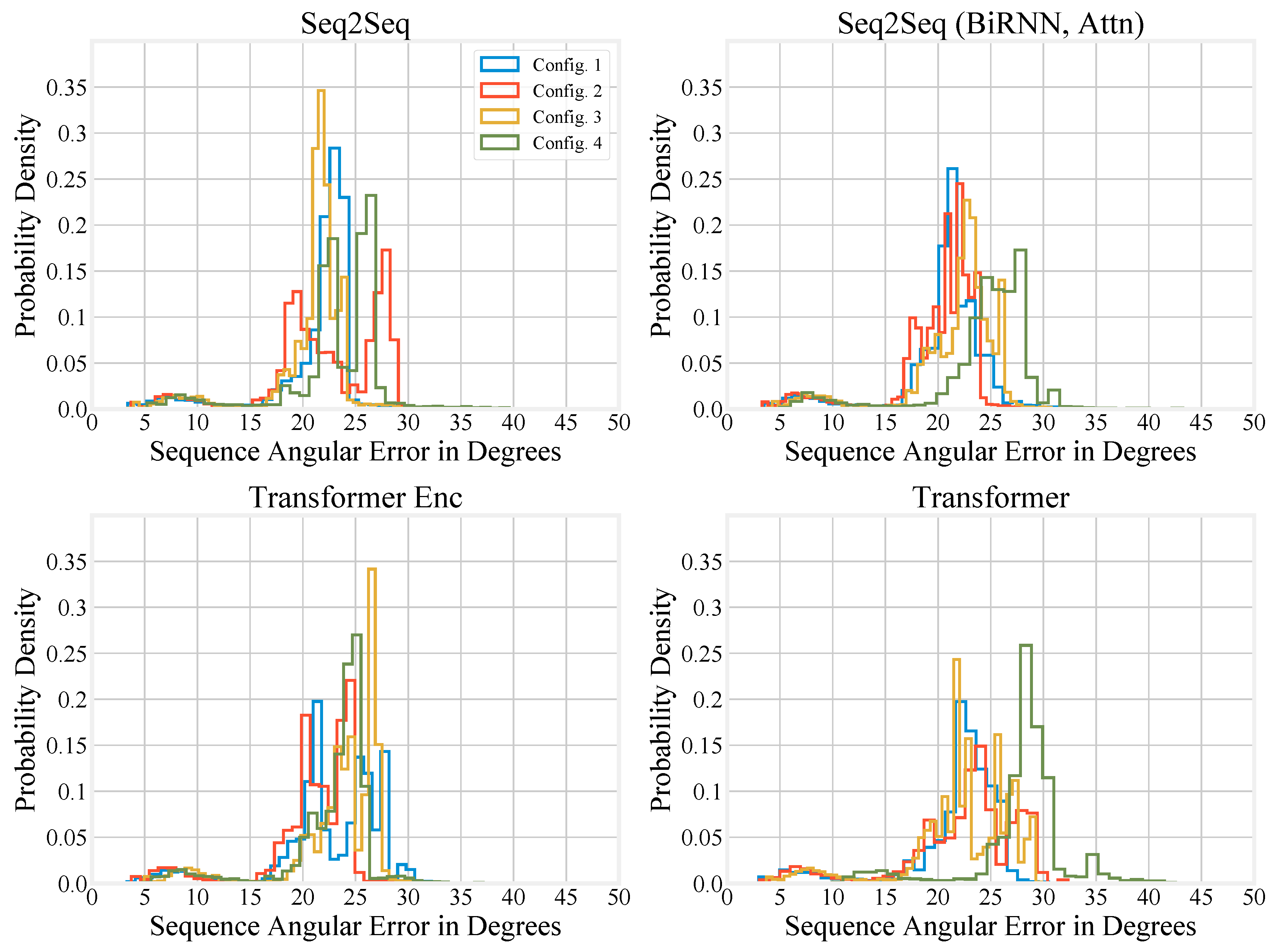
References
- Troje, N.F. Decomposing biological motion: A framework for analysis and synthesis of human gait patterns. J. Vis. 2002, 2, 2. [Google Scholar]
- Müller, M.; Röder, T.; Clausen, M.; Eberhardt, B.; Krüger, B.; Weber, A. Documentation Mocap Database HDM05; Technical Report CG-2007-2; Universität Bonn: Bonn, Germany, 2007. [Google Scholar]
- De la Torre, F.; Hodgins, J.; Montano, J.; Valcarcel, S.; Forcada, R.; Macey, J. Guide to the Carnegie Mellon University Multimodal Activity (CMU-MMAC) Database; Robotics Institute, Carnegie Mellon University: Pittsburgh, PA, USA, 2009; Volume 5. [Google Scholar]
- Ionescu, C.; Papava, D.; Olaru, V.; Sminchisescu, C. Human3.6M: Large scale datasets and predictive methods for 3D human sensing in natural environments. IEEE Trans. Pattern Anal. Mach. Intell. 2014, 36, 1325–1339. [Google Scholar] [PubMed]
- Mandery, C.; Terlemez, Ö.; Do, M.; Vahrenkamp, N.; Asfour, T. The KIT whole-body human motion database. In Proceedings of the 2015 International Conference on Advanced Robotics (ICAR), Istanbul, Turkey, 27–31 July 2015; pp. 329–336. [Google Scholar]
- Akhter, I.; Black, M.J. Pose-conditioned joint angle limits for 3D human pose reconstruction. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1446–1455. [Google Scholar]
- Trumble, M.; Gilbert, A.; Malleson, C.; Hilton, A.; Collomosse, J. Total Capture: 3D Human Pose Estimation Fusing Video and Inertial Sensors. In Proceedings of the British Machine Vision Conference, BMVC 2017, London, UK, 4–7 September 2017; Volume 2, p. 3. [Google Scholar]
- Mahmood, N.; Ghorbani, N.; Troje, N.F.; Pons-Moll, G.; Black, M.J. AMASS: Archive of motion capture as surface shapes. arXiv 2019, arXiv:1904.03278. [Google Scholar]
- Loper, M.; Mahmood, N.; Romero, J.; Pons-Moll, G.; Black, M.J. SMPL: A skinned multi-person linear model. ACM Trans. Graph. (TOG) 2015, 34, 248. [Google Scholar]
- Loper, M.; Mahmood, N.; Black, M.J. MoSh: Motion and shape capture from sparse markers. ACM Trans. Graph. (TOG) 2014, 33, 220. [Google Scholar]
- Fragkiadaki, K.; Levine, S.; Felsen, P.; Malik, J. Recurrent network models for human dynamics. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 4346–4354. [Google Scholar]
- Jain, A.; Zamir, A.R.; Savarese, S.; Saxena, A. Structural-RNN: Deep learning on spatio-temporal graphs. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 5308–5317. [Google Scholar]
- Butepage, J.; Black, M.J.; Kragic, D.; Kjellstrom, H. Deep representation learning for human motion prediction and classification. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 6158–6166. [Google Scholar]
- Martinez, J.; Black, M.J.; Romero, J. On human motion prediction using recurrent neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 2891–2900. [Google Scholar]
- Pavllo, D.; Grangier, D.; Auli, M. Quaternet: A quaternion-based recurrent model for human motion. arXiv 2018, arXiv:1805.06485. [Google Scholar]
- Gui, L.Y.; Wang, Y.X.; Liang, X.; Moura, J.M. Adversarial geometry-aware human motion prediction. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 786–803. [Google Scholar]
- Gui, L.Y.; Wang, Y.X.; Ramanan, D.; Moura, J.M. Few-shot human motion prediction via meta-learning. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 432–450. [Google Scholar]
- Shotton, J.; Fitzgibbon, A.; Cook, M.; Sharp, T.; Finocchio, M.; Moore, R.; Kipman, A.; Blake, A. Real-time human pose recognition in parts from single depth images. In Proceedings of the CVPR, Providence, RI, USA, 20–25 June 2011; pp. 1297–1304. [Google Scholar]
- Cao, Z.; Hidalgo, G.; Simon, T.; Wei, S.E.; Sheikh, Y. OpenPose: Realtime multi-person 2D pose estimation using Part Affinity Fields. arXiv 2018, arXiv:1812.08008. [Google Scholar]
- Roetenberg, D.; Luinge, H.; Slycke, P. XSens MVN: Full 6DOF Human Motion Tracking Using Miniature Inertial Sensors; Technical Report; Xsens Motion Technologies B.V.: Enschede, The Netherlands, 2009; Volume 1. [Google Scholar]
- Vlasic, D.; Adelsberger, R.; Vannucci, G.; Barnwell, J.; Gross, M.; Matusik, W.; Popović, J. Practical motion capture in everyday surroundings. ACM Trans. Graph. (TOG) 2007, 26, 35. [Google Scholar]
- Jung, S.; Michaud, M.; Oudre, L.; Dorveaux, E.; Gorintin, L.; Vayatis, N.; Ricard, D. The Use of Inertial Measurement Units for the Study of Free Living Environment Activity Assessment: A Literature Review. Sensors 2020, 20, 5625. [Google Scholar]
- van der Kruk, E.; Reijne, M.M. Accuracy of human motion capture systems for sport applications; state-of-the-art review. Eur. J. Sport Sci. 2018, 18, 806–819. [Google Scholar]
- Johansson, D.; Malmgren, K.; Murphy, M.A. Wearable sensors for clinical applications in epilepsy, Parkinson’s disease, and stroke: A mixed-methods systematic review. J. Neurol. 2018, 265, 1740–1752. [Google Scholar]
- von Marcard, T.; Rosenhahn, B.; Black, M.J.; Pons-Moll, G. Sparse inertial poser: Automatic 3D human pose estimation from sparse IMUs. Comput. Graph. Forum 2017, 36, 349–360. [Google Scholar]
- Huang, Y.; Kaufmann, M.; Aksan, E.; Black, M.J.; Hilliges, O.; Pons-Moll, G. Deep inertial poser: Learning to reconstruct human pose from sparse inertial measurements in real time. ACM Trans. Graph. (TOG) 2018, 37, 185. [Google Scholar]
- Pons-Moll, G.; Baak, A.; Helten, T.; Müller, M.; Seidel, H.P.; Rosenhahn, B. Multisensor-fusion for 3D full-body human motion capture. In Proceedings of the 2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Francisco, CA, USA, 13–18 June 2010; pp. 663–670. [Google Scholar]
- Pons-Moll, G.; Baak, A.; Gall, J.; Leal-Taixe, L.; Mueller, M.; Seidel, H.P.; Rosenhahn, B. Outdoor human motion capture using inverse kinematics and Von Mises-Fisher sampling. In Proceedings of the 2011 International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011; pp. 1243–1250. [Google Scholar]
- Malleson, C.; Gilbert, A.; Trumble, M.; Collomosse, J.; Hilton, A.; Volino, M. Real-time full-body motion capture from video and IMUs. In Proceedings of the 2017 International Conference on 3D Vision (3DV), Qingdao, China, 10–12 October 2017; pp. 449–457. [Google Scholar]
- von Marcard, T.; Henschel, R.; Black, M.J.; Rosenhahn, B.; Pons-Moll, G. Recovering accurate 3D human pose in the wild using IMUs and a moving camera. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 601–617. [Google Scholar]
- Helten, T.; Muller, M.; Seidel, H.P.; Theobalt, C. Real-time body tracking with one depth camera and inertial sensors. In Proceedings of the IEEE International Conference on Computer Vision, Sydney, Australia, 1–8 December 2013; pp. 1105–1112. [Google Scholar]
- Andrews, S.; Huerta, I.; Komura, T.; Sigal, L.; Mitchell, K. Real-time physics-based motion capture with sparse sensors. In Proceedings of the 13th European Conference on Visual Media Production (CVMP 2016), London, UK, 12–13 December 2016; pp. 1–10. [Google Scholar]
- Badler, N.I.; Hollick, M.J.; Granieri, J.P. Real-time control of a virtual human using minimal sensors. Presence Teleoperators Virtual Environ. 1993, 2, 82–86. [Google Scholar]
- Semwal, S.K.; Hightower, R.; Stansfield, S. Mapping algorithms for real-time control of an avatar using eight sensors. Presence 1998, 7, 1–21. [Google Scholar]
- Yin, K.; Pai, D.K. Footsee: An interactive animation system. In Proceedings of the 2003 ACM SIGGRAPH/Eurographics Symposium on Computer Animation, San Diego, CA, USA, 26–27 July 2003; Eurographics Association: Geneve, Switzerland, 2003; pp. 329–338. [Google Scholar]
- Slyper, R.; Hodgins, J.K. Action Capture with Accelerometers. In Proceedings of the Symposium on Computer Animation, Dublin, Ireland, 7–9 July 2008; pp. 193–199. [Google Scholar]
- Tautges, J.; Zinke, A.; Krüger, B.; Baumann, J.; Weber, A.; Helten, T.; Müller, M.; Seidel, H.P.; Eberhardt, B. Motion reconstruction using sparse accelerometer data. ACM Trans. Graph. (ToG) 2011, 30, 18. [Google Scholar]
- Liu, H.; Wei, X.; Chai, J.; Ha, I.; Rhee, T. Realtime human motion control with a small number of inertial sensors. In Proceedings of the Symposium on Interactive 3D Graphics and Games, San Francisco, CA, USA, 18–20 February 2011; pp. 133–140. [Google Scholar]
- Schwarz, L.A.; Mateus, D.; Navab, N. Discriminative human full-body pose estimation from wearable inertial sensor data. In 3D Physiological Human Workshop; Springer: Berlin/Heidelberg, Germany, 2009; pp. 159–172. [Google Scholar]
- Wouda, F.J.; Giuberti, M.; Bellusci, G.; Veltink, P.H. Estimation of full-body poses using only five inertial sensors: An eager or lazy learning approach? Sensors 2016, 16, 2138. [Google Scholar]
- Roetenberg, D.; Luinge, H.; Veltink, P. Inertial and magnetic sensing of human movement near ferromagnetic materials. In Proceedings of the Second IEEE and ACM International Symposium on Mixed and Augmented Reality, Tokyo, Japan, 10 October 2003; pp. 268–269. [Google Scholar]
- Roetenberg, D.; Luinge, H.J.; Baten, C.T.; Veltink, P.H. Compensation of magnetic disturbances improves inertial and magnetic sensing of human body segment orientation. IEEE Trans. Neural Syst. Rehabil. Eng. 2005, 13, 395–405. [Google Scholar]
- Kim, S.; Nussbaum, M.A. Performance evaluation of a wearable inertial motion capture system for capturing physical exposures during manual material handling tasks. Ergonomics 2013, 56, 314–326. [Google Scholar] [PubMed]
- Al-Amri, M.; Nicholas, K.; Button, K.; Sparkes, V.; Sheeran, L.; Davies, J.L. Inertial measurement units for clinical movement analysis: Reliability and concurrent validity. Sensors 2018, 18, 719. [Google Scholar]
- Geissinger, J.; Alemi, M.M.; Simon, A.A.; Chang, S.E.; Asbeck, A.T. Quantification of Postures for Low-Height Object Manipulation Conducted by Manual Material Handlers in a Retail Environment. IISE Trans. Occup. Ergon. Hum. Factors 2020, 8, 88–98. [Google Scholar] [CrossRef]
- Schepers, M.; Giuberti, M.; Bellusci, G. XSens MVN: Consistent Tracking of Human Motion Using Inertial Sensing; XSENS Technologies B.V.: Enschede, The Netherlands, 2018; pp. 1–8. [Google Scholar]
- Taylor, G.W.; Hinton, G.E.; Roweis, S.T. Modeling human motion using binary latent variables. In Advances in Neural Information Processing Systems; Neural Information Processing Systems Foundation: Vancouver, BC, Canada, 2007; pp. 1345–1352. [Google Scholar]
- Grassia, F.S. Practical parameterization of rotations using the exponential map. J. Graph. Tools 1998, 3, 29–48. [Google Scholar] [CrossRef]
- Sutskever, I.; Vinyals, O.; Le, Q.V. Sequence to sequence learning with neural networks. In Advances in Neural Information Processing Systems; Neural Information Processing Systems Foundation: Montreal, QC, Canada, 2014; pp. 3104–3112. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Chung, J.; Gulcehre, C.; Cho, K.; Bengio, Y. Empirical evaluation of gated recurrent neural networks on sequence modeling. arXiv 2014, arXiv:1412.3555. [Google Scholar]
- Bahdanau, D.; Cho, K.; Bengio, Y. Neural machine translation by jointly learning to align and translate. arXiv 2014, arXiv:1409.0473. [Google Scholar]
- Schuster, M.; Paliwal, K.K. Bidirectional recurrent neural networks. IEEE Trans. Signal Process. 1997, 45, 2673–2681. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. In Advances in Neural Information Processing Systems; Neural Information Processing Systems Foundation: Long Beach, CA, USA, 2017; pp. 5998–6008. [Google Scholar]
- Radford, A.; Narasimhan, K.; Salimans, T.; Sutskever, I. Improving Language Understanding by Generative Pre-Training. 2018. Available online: https://s3-us-west-2.amazonaws.com/openai-assets/research-covers/language-unsupervised/language_understanding_paper.pdf (accessed on 25 April 2020).
- Devlin, J.; Chang, M.W.; Lee, K.; Toutanova, K. BERT: Pre-training of deep bidirectional transformers for language understanding. arXiv 2018, arXiv:1810.04805. [Google Scholar]
- Radford, A.; Wu, J.; Child, R.; Luan, D.; Amodei, D.; Sutskever, I. Language models are unsupervised multitask learners. OpenAI Blog 2019, 1, 9. [Google Scholar]
- Raffel, C.; Shazeer, N.; Roberts, A.; Lee, K.; Narang, S.; Matena, M.; Zhou, Y.; Li, W.; Liu, P.J. Exploring the limits of transfer learning with a unified text-to-text transformer. arXiv 2019, arXiv:1910.10683. [Google Scholar]
- Brown, T.B.; Mann, B.; Ryder, N.; Subbiah, M.; Kaplan, J.; Dhariwal, P.; Neelakantan, A.; Shyam, P.; Sastry, G.; Askell, A. Language models are few-shot learners. arXiv 2020, arXiv:2005.14165. [Google Scholar]
- Rush, A.M. The annotated transformer. In Proceedings of the Workshop for NLP Open Source Software (NLP-OSS), Melbourne, Australia, 20 July 2018; pp. 52–60. [Google Scholar]
- Alammar, J. The Illustrated Transformer. 2018. Available online: http://jalammar.github.io/illustrated-transformer (accessed on 25 April 2020).
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L. PyTorch: An imperative style, high-performance deep learning library. In Advances in Neural Information Processing Systems; Neural Information Processing Systems Foundation: Vancouver, BC, Canada, 2019; pp. 8024–8035. [Google Scholar]
- Loshchilov, I.; Hutter, F. Decoupled weight decay regularization. arXiv 2017, arXiv:1711.05101. [Google Scholar]
- Huynh, D.Q. Metrics for 3D rotations: Comparison and analysis. J. Math. Imaging Vis. 2009, 35, 155–164. [Google Scholar] [CrossRef]
- Geissinger, J.; Alemi, M.M.; Chang, S.E.; Asbeck, A.T. Virginia Tech Natural Motion Dataset [Data Set]; University Libraries, Virginia Tech: Blacksburg, VA, USA, 2020. [Google Scholar] [CrossRef]
- Rhodin, H.; Richardt, C.; Casas, D.; Insafutdinov, E.; Shafiei, M.; Seidel, H.P.; Schiele, B.; Theobalt, C. Egocap: Egocentric marker-less motion capture with two fisheye cameras. ACM Trans. Graph. (TOG) 2016, 35, 162. [Google Scholar] [CrossRef]

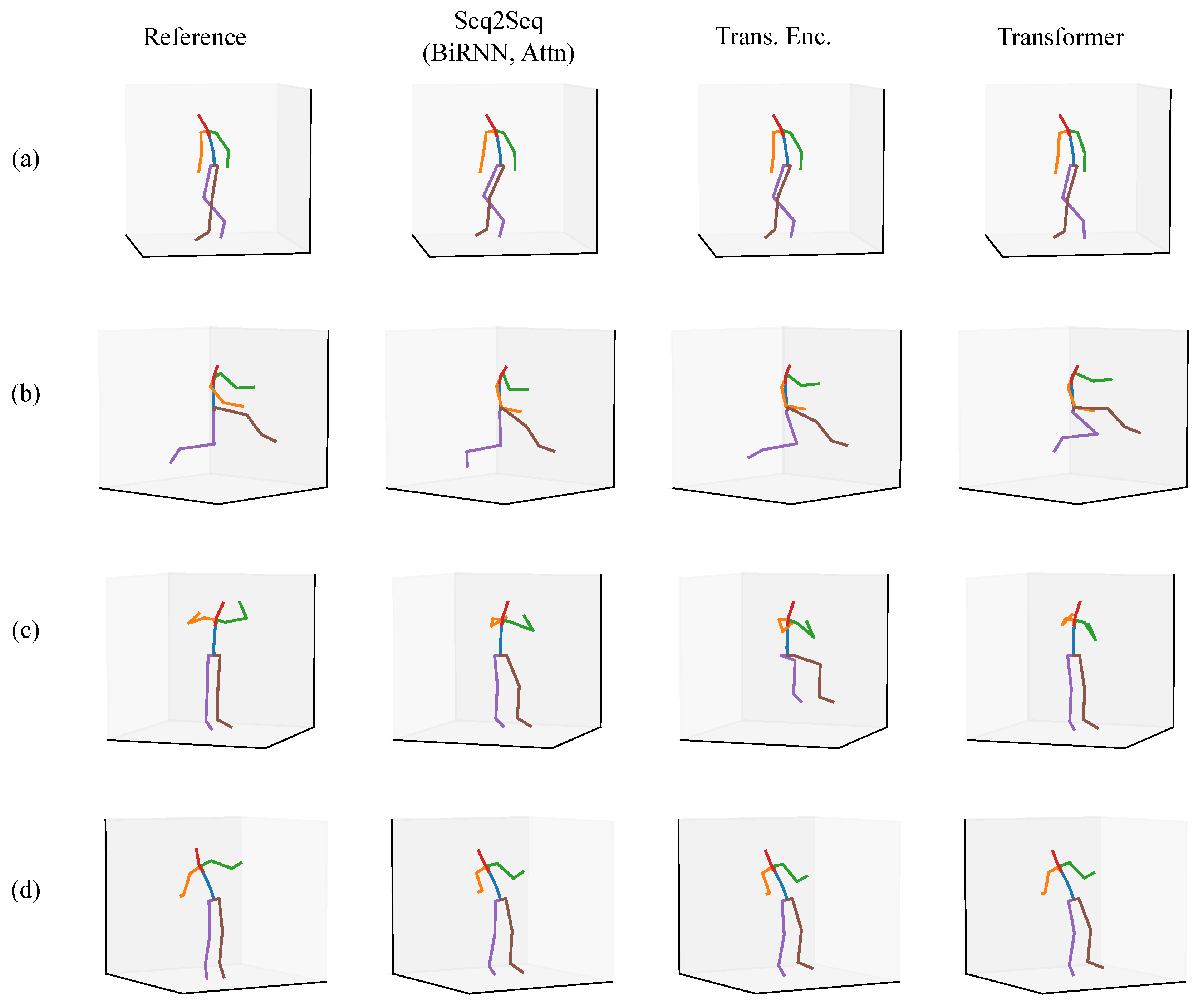
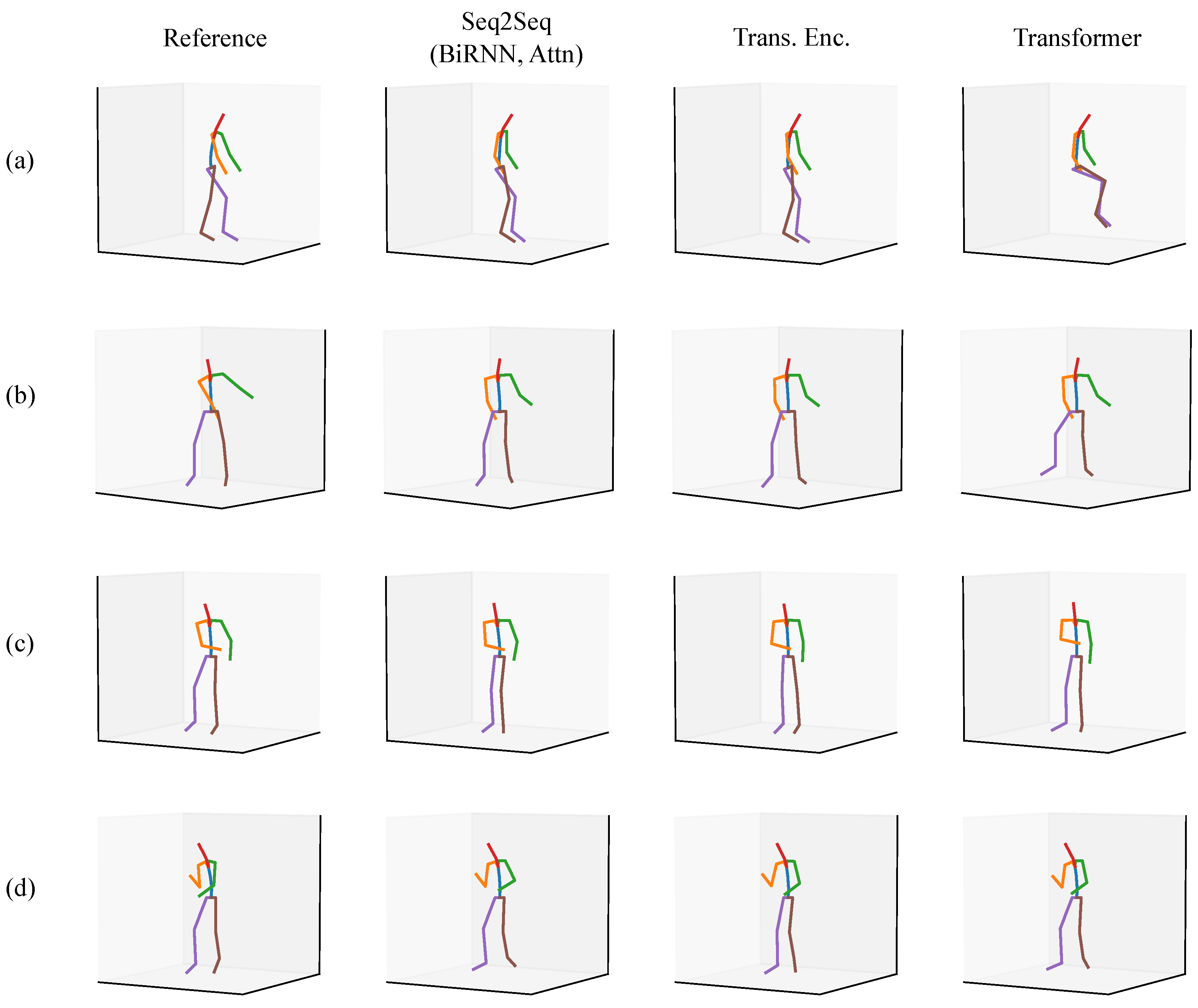
| Ours | AMASS [8] | KIT [5] | |
|---|---|---|---|
| Hours of Data | 40.6 | 45.2 | 37.2 |
| Number of Subjects | 17 | 460 | 224 |
| M/F | 13/4 | N/A | 106/37 |
| Avg. Hours/Subject | 2.39 | 0.10 | 0.17 |
| Lab Environment | No | Yes | Yes |
| Body Kinematics Only | Yes | Yes | No |
| Methodology | Inertial MoCap | SMPL [9], MoSh++ | Optical MoCap |
| Model | Config. 1 | Config. 2 | Config. 3 | Config. 4 |
|---|---|---|---|---|
| Seq2Seq | 12.29 | 9.64 | 12.26 | 15.64 |
| Seq2Seq (BiRNN, Attn) | 11.99 | 9.55 | 12.30 | 15.69 |
| Transformer Enc. | 11.82 | 12.56 | 11.88 | 15.08 |
| Transformer | 12.17 | 9.58 | 11.87 | 15.77 |
| Model | Config. 1 | Config. 2 | Config. 3 | Config. 4 |
|---|---|---|---|---|
| Seq2Seq | 11.54 | 10.00 | 11.44 | 13.25 |
| Seq2Seq (BiRNN, Attn) | 11.48 | 10.05 | 11.16 | 13.34 |
| Transformer Enc. | 11.53 | 9.98 | 12.97 | 13.45 |
| Transformer | 10.94 | 10.06 | 11.00 | 18.16 |
| Model | Config. 1 | Config. 2 | Config. 3 | Config. 4 |
|---|---|---|---|---|
| Seq2Seq | 19.38 | 18.52 | 22.18 | 22.85 |
| Seq2Seq (BiRNN, Attn) | 18.49 | 17.40 | 20.23 | 22.83 |
| Transformer Enc. | 18.12 | 19.95 | 22.92 | 22.52 |
| Transformer | 18.71 | 17.98 | 19.96 | 21.02 |
| Model | Config. 1 | Config. 2 | Config. 3 | Config. 4 |
|---|---|---|---|---|
| Seq2Seq | 21.35 | 22.03 | 20.65 | 23.17 |
| Seq2Seq (BiRNN, Attn) | 20.58 | 19.86 | 21.48 | 24.51 |
| Transformer Enc. | 22.54 | 20.78 | 23.36 | 22.83 |
| Transformer | 21.64 | 22.30 | 22.08 | 28.12 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Geissinger, J.H.; Asbeck, A.T. Motion Inference Using Sparse Inertial Sensors, Self-Supervised Learning, and a New Dataset of Unscripted Human Motion. Sensors 2020, 20, 6330. https://doi.org/10.3390/s20216330
Geissinger JH, Asbeck AT. Motion Inference Using Sparse Inertial Sensors, Self-Supervised Learning, and a New Dataset of Unscripted Human Motion. Sensors. 2020; 20(21):6330. https://doi.org/10.3390/s20216330
Chicago/Turabian StyleGeissinger, Jack H., and Alan T. Asbeck. 2020. "Motion Inference Using Sparse Inertial Sensors, Self-Supervised Learning, and a New Dataset of Unscripted Human Motion" Sensors 20, no. 21: 6330. https://doi.org/10.3390/s20216330
APA StyleGeissinger, J. H., & Asbeck, A. T. (2020). Motion Inference Using Sparse Inertial Sensors, Self-Supervised Learning, and a New Dataset of Unscripted Human Motion. Sensors, 20(21), 6330. https://doi.org/10.3390/s20216330





