Exploring the Potential of HySpex Hyperspectral Imagery for Extraction of Copper Content
Abstract
1. Introduction
2. Materials and Methods
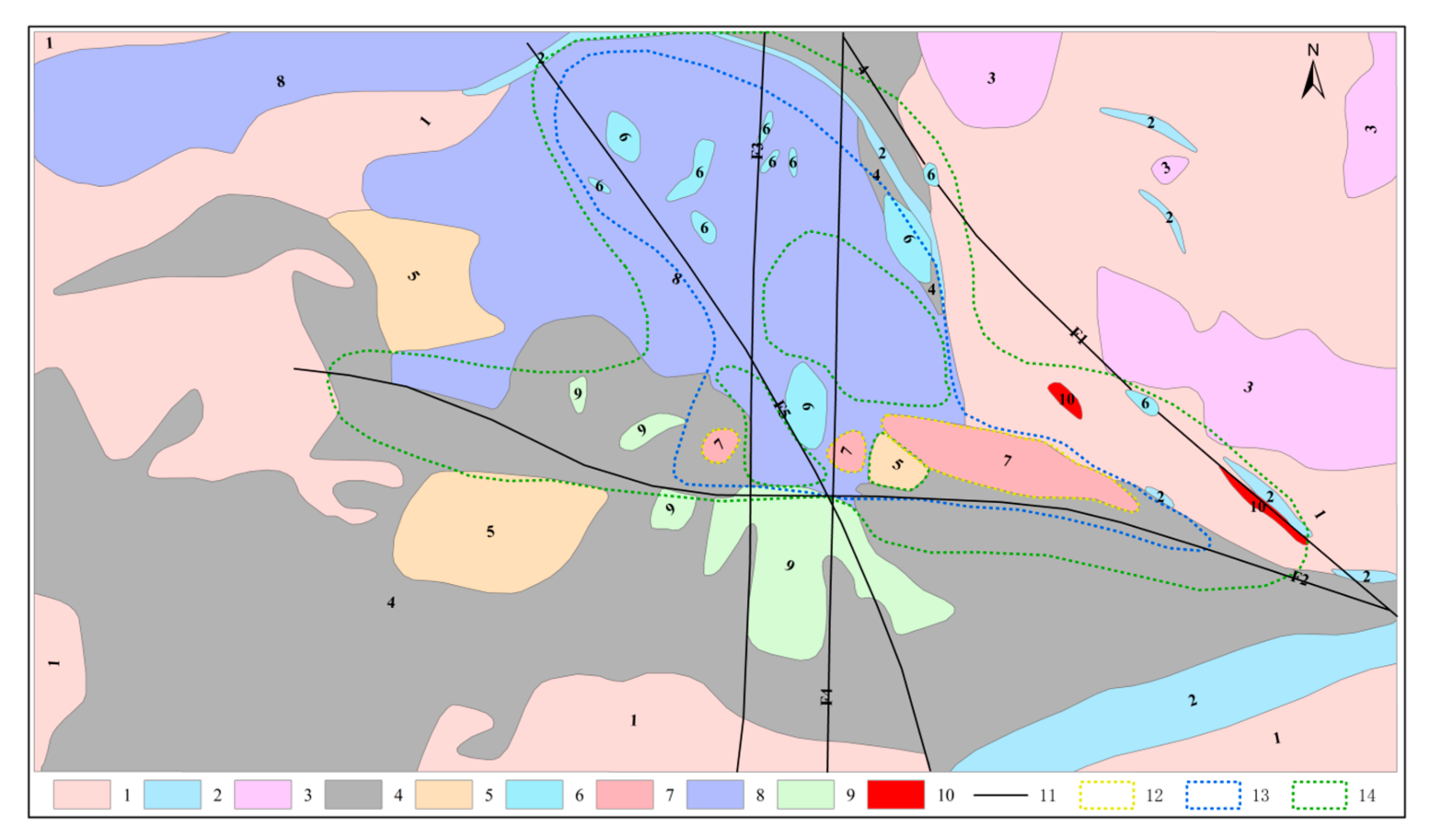
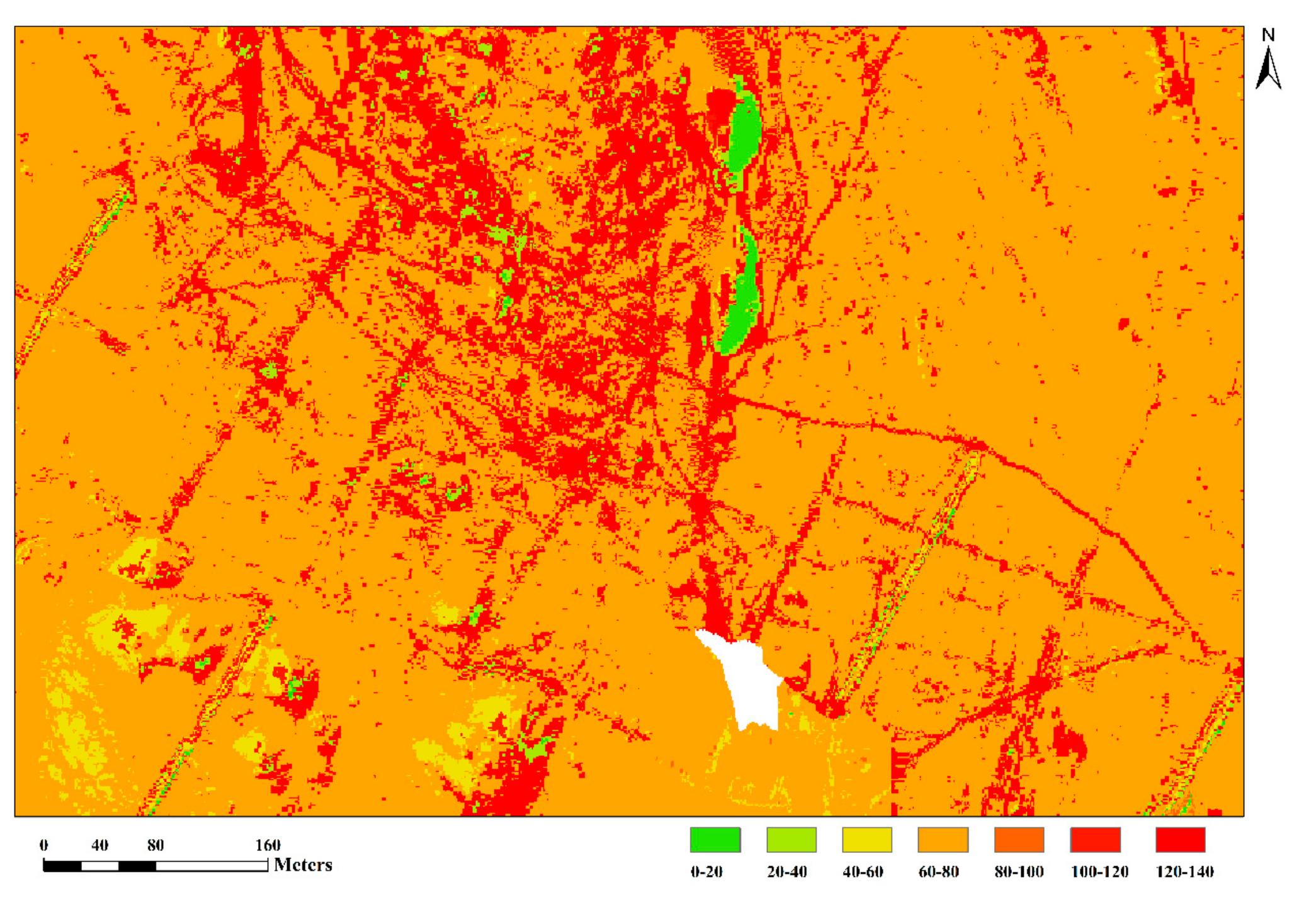
2.1. Study Area
2.2. Data Acquisition and Preprocessing
2.3. Spectral Transform
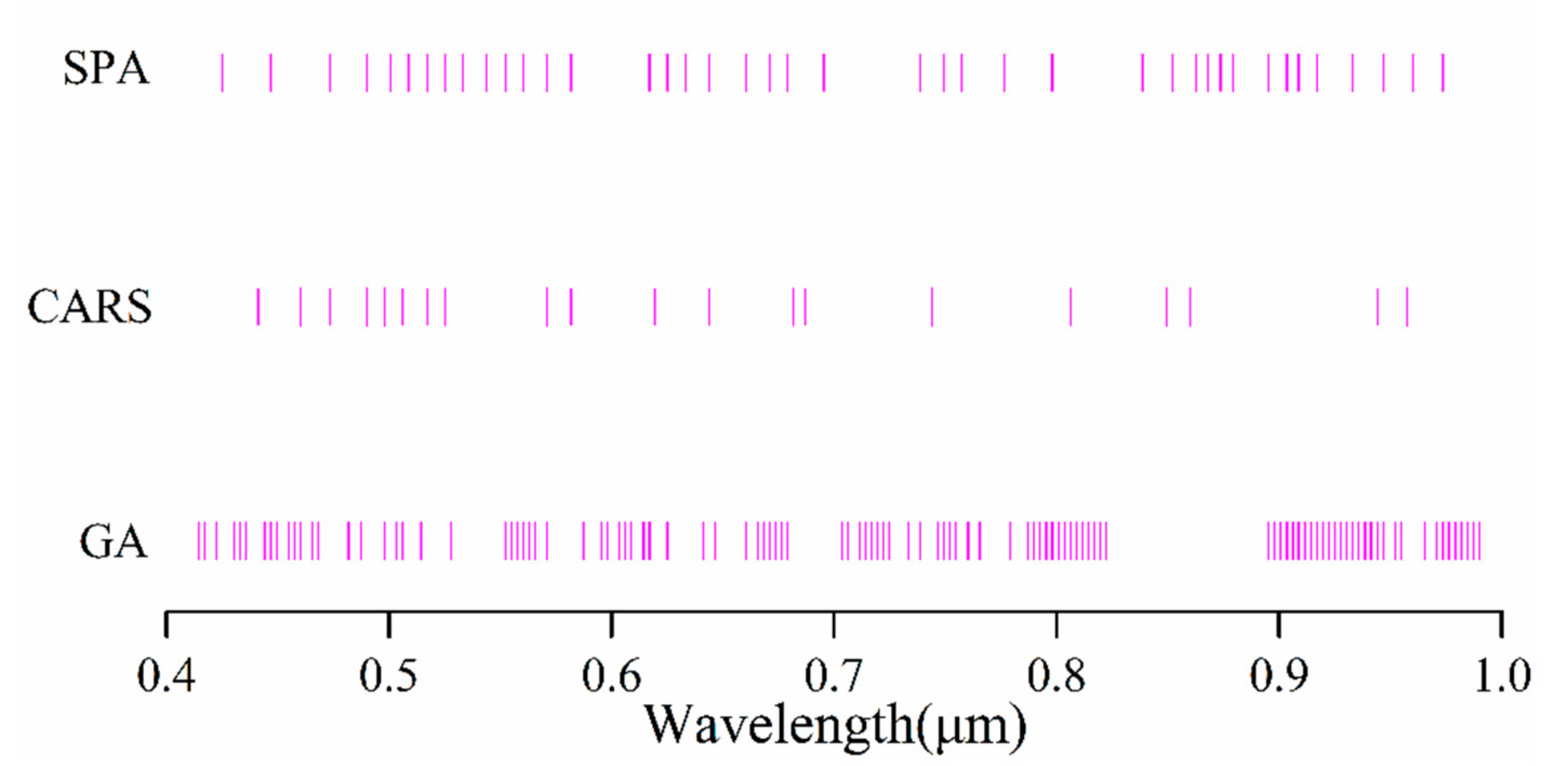
2.4. Spectral Variable Selection
2.5. Model Establishment and Accuracy Evaluation
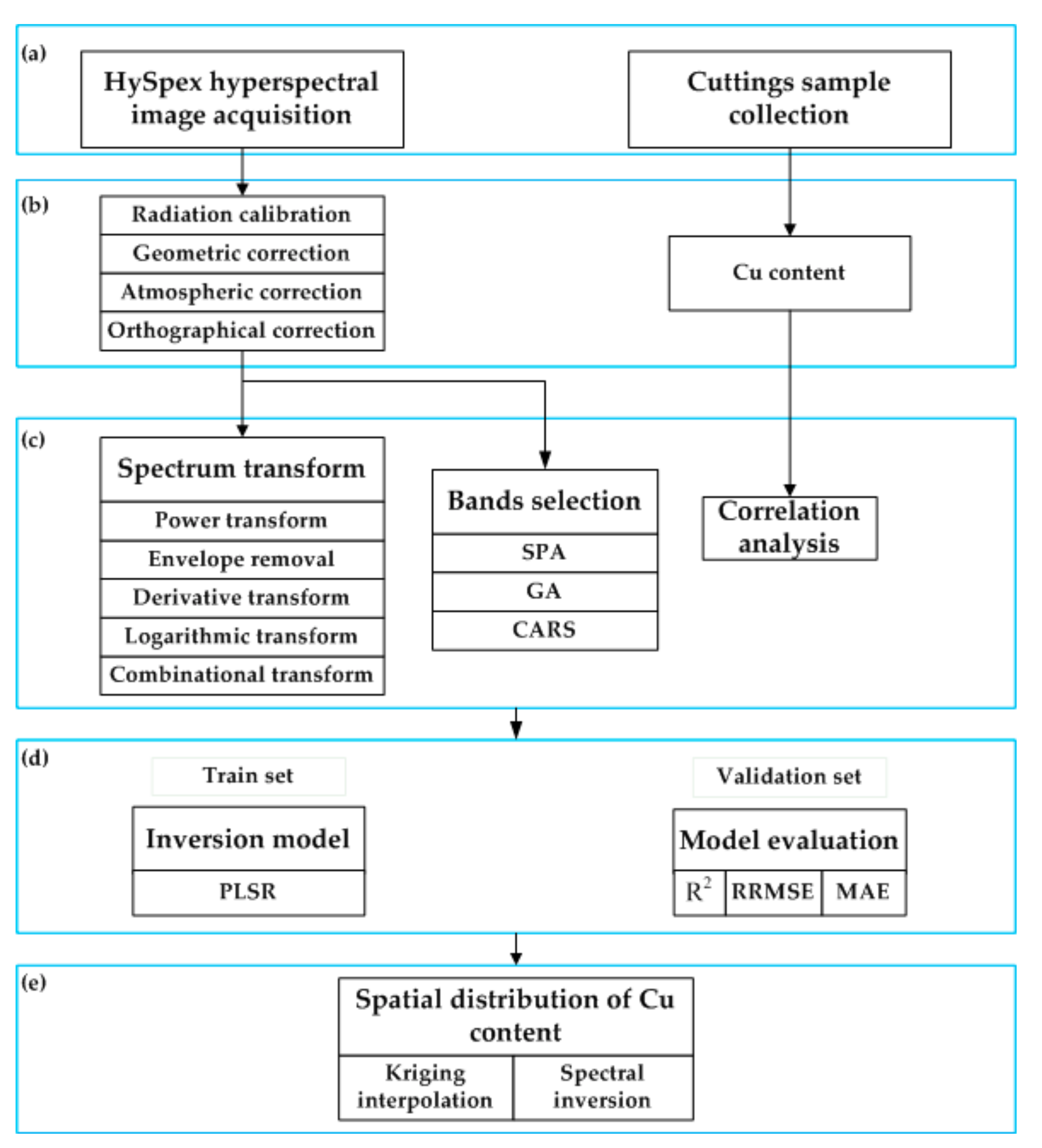
2.6. Flowchart
3. Results
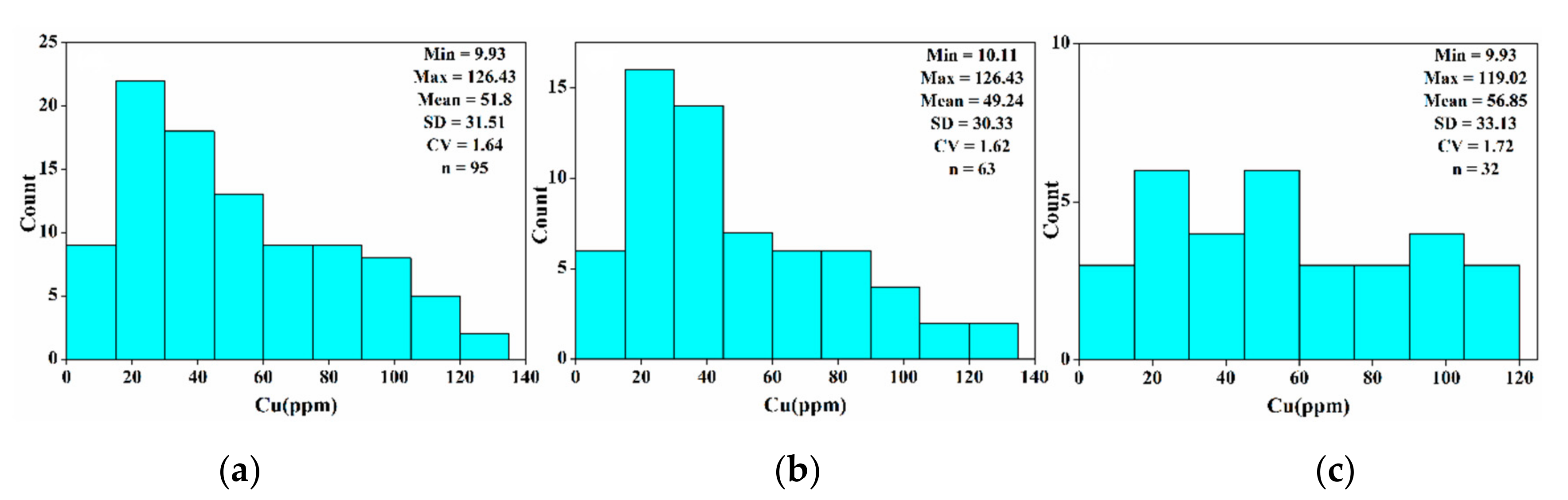
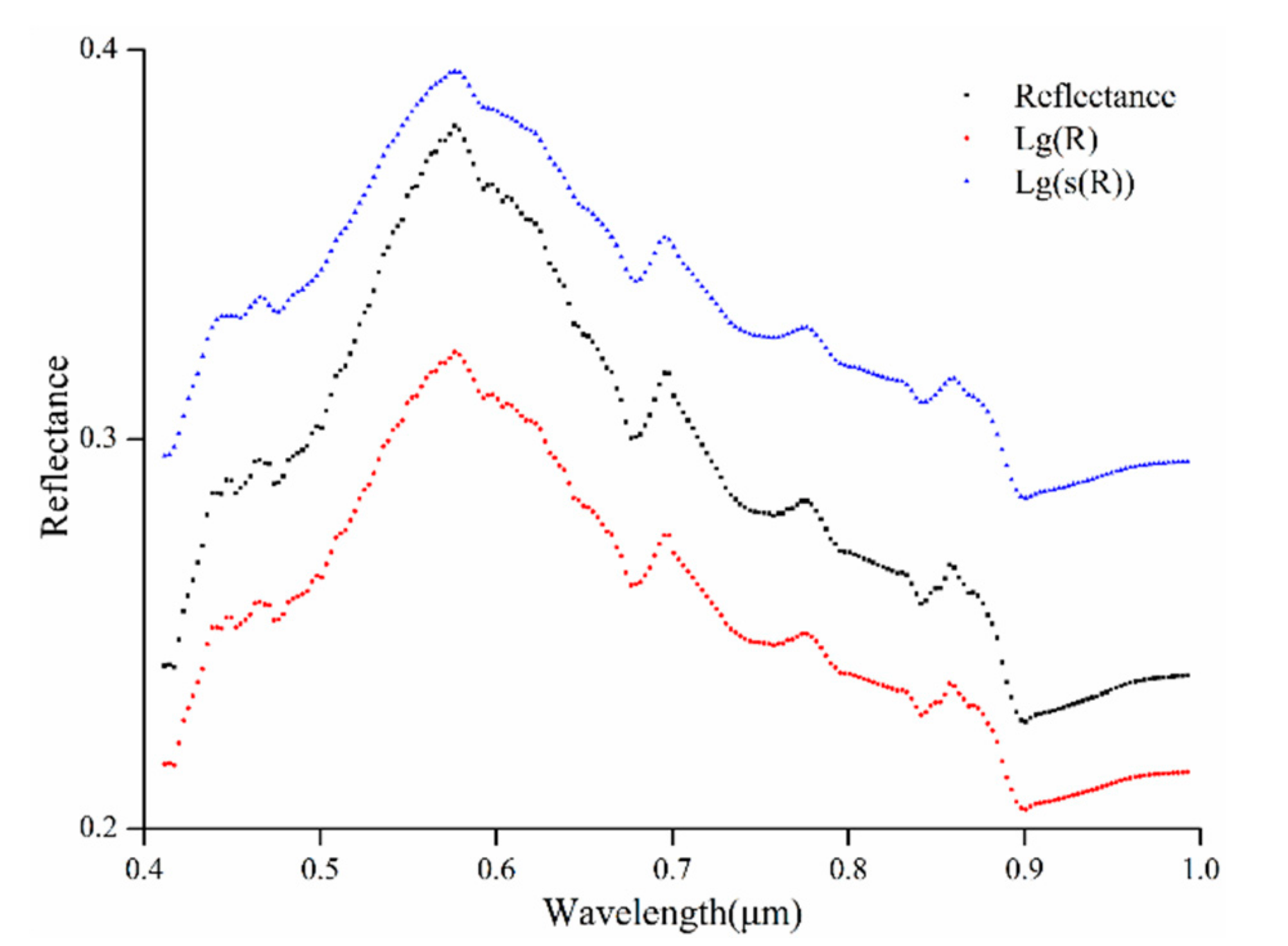
3.1. Element Content and Visible-Near-Infrared Spectral Reflectance
3.2. Correlation between Different Transform Spectra and Cu Content
3.3. PLS Model of Different Transform Spectra
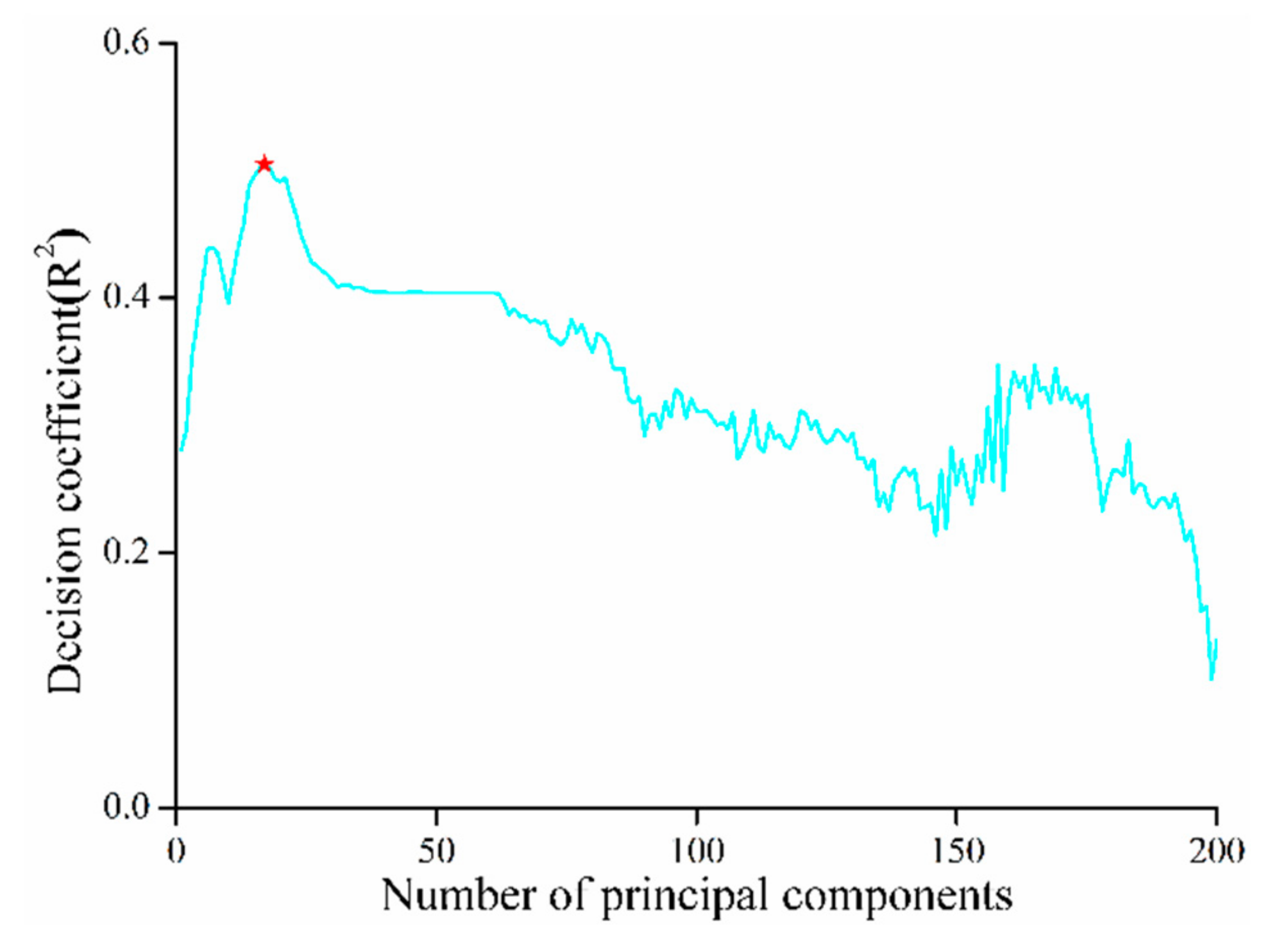
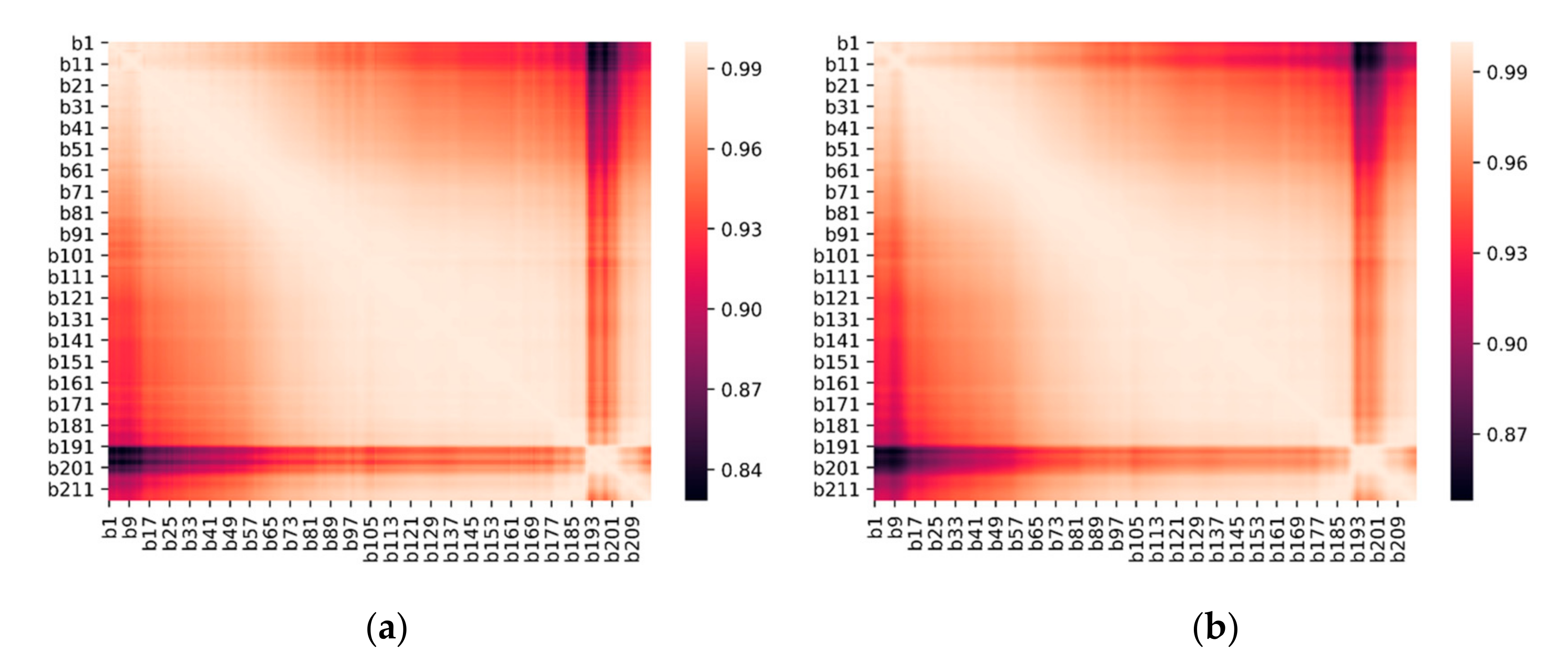
3.4. PLS Models of Different Band Selection Methods
3.5. HySpex Imaging Hyperspectral Cu Content Extraction
4. Discussion
5. Conclusions
- (1)
- Spectral transformation technology can highlight the band that is characteristically reflected by the element content, thereby improving the predictive ability of the model;
- (2)
- The 20 characteristic bands selected from the transform spectrum by the CARS method were input as independent variables into the PLS method to construct the detritus copper content inversion model with the highest accuracy. R2 (0.7342) was highest and MAE (19.926) was lowest in the verification set, indicating that the HySpex pixel spectrum could be used to quickly and accurately estimate the copper content in detritus;
- (3)
- GA, CARS, and SPA can be used for quickly selecting feature bands, and the use of these feature bands for modeling can simplify the model complexity and improve prediction accuracy. CARS is the optimal feature band screening method; it reduced the complexity of the model to the greatest extent and improved the stability of the model while ensuring the accuracy of the inversion, and has a wider application prospect;
- (4)
- Ultra-low HySpex imaging hyperspectral data have high spatial and spectral resolutions, but there were problems with information redundancy. Adopting appropriate spectral transformation technology and band selection methods to improve the prediction accuracy and data-processing efficiency can provide a low-cost and efficient method for the delineation and reduction of key mining research areas in the future.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Xiao, Y.P.; Zheng, R.C.; Deng, J.H. Petrology Concise Course; Geological Publishing House: Beijing, China, 2009. (In Chinese) [Google Scholar]
- Ye, H.G.; Zhang, D.H.; Cheng, Z.H.; Ye, H.F.; Wu, H. The prospecting effect of debris geochemincal survey in the xiaobinggou lead-zinc mining area in subei, Gansu rovince. Geophys. Geochem. Explor. 2014, 38, 295–303. (In Chinese) [Google Scholar]
- Zhang, Y.S.; Liu, Y.P.; An, X.Y. Application of cuttings geochemistry survey in a survey area of Mandahesumu, Donggobi Province, Mongolia. Kejifeng 2016, 2, 180–182. (In Chinese) [Google Scholar]
- Liu, C.M.; Li, Y.G.; Shi, C.Y. A study of geochemical exploration techniques suitable for different landscape regions. Geophys. Geochem. Explor. 2002, 1, 23–26. (In Chinese) [Google Scholar]
- Tao, Z.; Cui, X.; Sun, X.; Wang, J.; Chen, H. Rock mass quality prediction of open-pit gold mine slope based on the kriging interpolation method. Geotech. Geol. Eng. 2020, 4. [Google Scholar] [CrossRef]
- Abed, A.M.; Saffarini, G.A.; Sadaqah, R.M. Spatial distribution of uranium and vanadium in the upper phosphorite member in eshidiyya basin, southern jordan. Arab. J. Geosci. 2014, 7, 253–271. [Google Scholar] [CrossRef]
- Fernandez-Caliani, J.C.; Romero-Baena, A.; Gonzalez, I.; Galan, E. Geochemical anomalies of critical elements (Be, Co, Hf, Sb, Sc, Ta, V, W, Y and REE) in soils of western Andalusia (Spain). Appl. Clay Sci. 2020, 191, 105610. [Google Scholar] [CrossRef]
- Habibnia, A.; Rahimipour, G.; Ranjbar, H. Equivalence assessment and leveling of geochemical datasets to generate integrated geochemical maps: Application to mineral exploration. J. Geochem. Explor. 2020, 212, 106507. [Google Scholar] [CrossRef]
- Van der Meer, F.D.; Van der Werff, H.M.; Van Ruitenbeek, F.J.; Hecker, C.A.; Bakker, W.H.; Noomen, M.F.; Van Der Meijde, M.; Carranza, E.J.; De Smeth, J.B.; Woldai, T. Multi- and hyperspectral geologic remote sensing: A review. Int. J. Appl. Earth Obs. Geoinf. 2012, 14, 112–128. [Google Scholar] [CrossRef]
- Hunt, G.R. Spectral signatures of particulate minerals in the visible and near infrared. Geophysics 2012, 42, 501. [Google Scholar] [CrossRef]
- Abrams, M.J.; Ashley, R.P.; Rowan, L.C.; Goetz, A.F.H.; Kahle, A.B. Mapping of hydrothermal alteration in the cuprite mining district, nevada, using aircraft scanner images for the spectral region 0.46 to 2.36 µm. Geology 1977, 5, 713–718. [Google Scholar] [CrossRef]
- Okwuashi, O.; Ndehedehe, C.E. Deep support vector machine for hyperspectral image classification. Pattern Recognit. 2020, 103, 107298. [Google Scholar] [CrossRef]
- Pour, A.B.; Park, T.Y.S.; Park, Y.; Hong, J.K.; Zoheir, B.; Pradhan, B.; Ayoobi, I.; Hashim, M. Application of multi-sensor satellite data for exploration of zn-pb sulfide mineralization in the franklinian Basin, north Greenland. Remote Sens. 2018, 10, 1186. [Google Scholar] [CrossRef]
- Mohammadi, N.M.; Hezarkhani, A. A comparative study of SVM and RF methods for classification of alteration zones using remotely sensed data. J. Min. Environ. 2020, 11, 49–61. [Google Scholar]
- Choe, E.; Freek, V.D.M.; Frank, V.R.; Harald, V.D.W.; Boudewijn, D.S.; Kyoung-Woong, K. Mapping of heavy metal pollution in stream sediments using combined geochemistry, field spectroscopy, and hyperspectral remote sensing: A case study of the Rodalquilar mining area, SE Spain. Remote Sens. Environ. 2008, 112, 3222–3233. [Google Scholar] [CrossRef]
- Ren, H.Y.; Zhuang, D.F.; Singh, A.N.; Pan, J.J.; Qiu, D.S.; Shi, R.H. Estimation of As and Cu contamination in agricultural soils around a mining area by reflectance spectroscopy: A case study. Pedosphere 2009, 19, 719–726. [Google Scholar] [CrossRef]
- Kemper, T.; Sommer, S. Estimate of heavy metal contamination in soils after a mining accident using reflectance spectroscopy. Environ. Sci. Technol. 2002, 36, 2742–2747. [Google Scholar] [CrossRef]
- Han, L.; Chen, R.; Zhu, H.; Zhao, Y.; Liu, Z.; Huo, H. Estimating soil arsenic content with visible and near-infrared hyperspectral reflectance. Sustainability 2020, 12, 1476. [Google Scholar] [CrossRef]
- Zhao, L.; Hu, Y.M.; Zhou, W.; Liu, Z.H.; Pan, Y.C.; Shi, Z.; Wang, L.; Wang, G.X. Estimation Methods for Soil Mercury Content Using Hyperspectral Remote Sensing. Sustainability 2018, 10, 2474. [Google Scholar] [CrossRef]
- Lancianese, V.; Dinelli, E. Different spatial methods in regional geochemical mapping at high density sampling: An application on stream sediment of romagna apennines, northern italy. J. Geochem. Explor. 2015, 154, 143–155. [Google Scholar] [CrossRef]
- Fard, R.S.; Matinfar, H.R. Capability of vis-NIR spectroscopy and Landsat 8 spectral data to predict soil heavy metals in polluted agricultural land (Iran). Arab. J. Geoences 2016, 9, 745. [Google Scholar] [CrossRef]
- Peng, Y.; Kheir, R.; Adhikari, K.; Greve, M.; Knadel, M.; Greve, M. Digital mapping of toxic metals in qatari soils using remote sensing and ancillary data. Remote Sens. 2016, 8, 1003. [Google Scholar] [CrossRef]
- Liu, M.; Wang, T.J.; Skidmore, A.K.; Liu, X.N. Heavy metal-induced stress in rice crops detected using multi-temporal Sentinel-2 satellite images. Sci. Total Environ. 2018, 637, 18–29. [Google Scholar] [CrossRef]
- Yu, S.Y.; Zhang, J.X.; Sun, D.Y.; Li, Y.S.; Gong, J.H. Partial melting of subducted continental plate during exhumation from the North Qaidam UHP terrane, western China. Acta Petrol. Sin. 2014, 30, 2287–2296. [Google Scholar]
- Liang, S.N.; Gan, F.P.; Yan, B.K.; Wei, H.Y.; Xiao, C.C. A study on the relationship between the composition and spectral feature parameters in chlorite. Spectrosc. Spectr. Anal. 2014, 34, 1763–1768. [Google Scholar]
- Keshava, N.; Mustard, J.F. Spectral unmixing. IEEE Signal Process. Mag. 2002, 19, 44–57. [Google Scholar] [CrossRef]
- Chen, J.; Ma, L.; Chen, X.H.; Rao, Y.H. Research progress of spectral mixture analysis. J. Remote Sens. 2016, 20, 1102–1109. [Google Scholar]
- Cui, T.W.; Ma, Y.; Zhang, J. The development and applications of the airborne hyperspectral remote sensing. Remote Sens. Technol. Appl. 2003, 18, 118–122. (In Chinese) [Google Scholar]
- Jia, J.X.; Wang, Y.M.; Chen, J.S.; Guo, R.; Shu, R.; Wang, J.Y. Status and application of advanced airborne hyperspectral imaging technology: A review. Infrared Phys. Technol. 2020, 104, 103115. [Google Scholar] [CrossRef]
- Gomez, C.; Lagacherie, P.; Coulouma, G. Regional predictions of eight common soil properties and their spatial structures from hyperspectral Vis-NIR data. Geoderma 2012, 189, 176–185. [Google Scholar] [CrossRef]
- Zhang, C.; Mishra, D.R.; Pennings, S.C. Mapping salt marsh soil properties using imaging spectroscopy. ISPRS J. Photogramm. Remote Sens. 2019, 148, 221–234. [Google Scholar] [CrossRef]
- Hummel, J.W.; Sudduth, K.A.; Hollinger, S.E. Soil moisture and organic matter prediction of surface and subsurface soils using an NIR soil sensor. Comput. Electron. Agric. 2001, 32, 149–165. [Google Scholar] [CrossRef]
- Kawamura, K.; Tsujimoto, Y.; Nishigaki, T.; Andriamananjara, A.; Rabenarivo, M.; Asai, H.; Rakotoson, T.; Razafimbelo, T. Laboratory visible and near-infrared spectroscopy with genetic algorithm-based partial least squares regression for assessing the soil phosphorus content of upland and lowland rice fields in madagascar. Remote Sens. 2019, 11, 506. [Google Scholar] [CrossRef]
- Du, L.; Long, X.P.; Yuan, C.; Zhang, Y.Y.; Huang, Z.Y.; Sun, M.; Zhao, G.C.; Xiao, W.J. Early paleozoic dioritic and granitic plutons in the eastern tianshan orogenic belt, NW China: Constraints on the initiation of a magmatic arc in the southern Central Asian Orogenic Belt. J. Asian Earth Sci. 2018, 153, 139–153. [Google Scholar] [CrossRef]
- Mao, Q.G.; Wang, J.B.; Fang, T.H.; Yu, M.J.; Sun, Y. Discovery of the middle Devonian Yudai porphyric Cu(Au) deposit in the Kalatage area of eastern Tianshan Mountain, Xinjiang and and its geological prospecting significance. Geol. Explor. 2017, 53, 1–11. (In Chinese) [Google Scholar]
- Zhuang, D.Z. The geochemical characteristics and anomaly verification methods of TuWu and YanDong copper-deposits in the eastern TianShan Mountains, XinJiang. Geol. Prospect. 2003, 39, 67–71. (In Chinese) [Google Scholar]
- Chen, T.; Tang, G.; Yuan, Y.; Guo, H.; Xu, Z.; Guo, J.; Chen, X. Unraveling the relative impacts of climate change and human activities on grassland productivity in Central Asia over last three decades. Sci. Total Environ. 2020, 743, 140649. [Google Scholar] [CrossRef]
- Lenhard, K.; Baumgartner, A.; Schwarzmaier, T. Independent laboratory characterization of NEO HySpex imaging spectrometers VNIR-1600 and SWIR-320m-e. IEEE Trans. Geoence Remote Sens. 2014, 53, 1828–1841. [Google Scholar] [CrossRef]
- Zhang, C.; Yu, Z.X.; Huang, T.; Zhang, Y.; Luo, H.C.; Niu, X.H. The study on fresh biomass estimation of zizania latifolia based on different spectral transformations of spectral reflectance. J. Southwest For. Univ. 2019, 39, 105–115. (In Chinese) [Google Scholar]
- Gomez, C.; Lagacherie, P.; Coulouma, G. Continuum removal versus PLSR method for clay and calcium carbonate content estimation from laboratory and airborne hyperspectral measurements. Geoderma 2008, 148, 141–148. [Google Scholar] [CrossRef]
- Chen, C.Q.; Jiang, Q.Q.; Zhang, Z.C.; Shi, P.F.; Xu, Y.; Liu, B.; Xi, J.; Chang, S.Z. Hyperspectral inversion of petroleum hydrocarbon contents in soil based on continuum removal and wavelet packet decomposition. Sustainability 2020, 12, 4218. [Google Scholar] [CrossRef]
- Liu, X.Y.; Zhang, J.L.; Yin, Y.F.; Yang, Y.; Wu, X.X. Underwater polarization image restoration based on logarithmic transformation and dark channel. Optoelectron. Lett. 2020, 16, 149–153. [Google Scholar] [CrossRef]
- Luan, M.J.; Cui, G.F.; Sun, W. Mammogram image enhancement method based on power—Law transformation and high frequency emphasis filtering. J. Bohai Univ. (Nat. Sci. Ed.) 2019, 40, 378–384. (In Chinese) [Google Scholar]
- Ma, S.Y.; Fu, Z.W.; Wang, X.D.; Kuai, Z.Q.; Huang, D.R. Gray image enhancement algorithm based on histogram equalization and power transform. Comput. Appl. Softw. 2013, 30, 261–263. (In Chinese) [Google Scholar]
- Sun, L.; Cheng, L.J. Analysis of spectral response of vegetation leaf biochemical components. Spectrosc. Spectr. Anal. 2010, 30, 3031–3035. (In Chinese) [Google Scholar]
- Wang, C.Y. Earth Observation Technology and Fine Agriculture; Science Press: Beijing, China, 2001. (In Chinese) [Google Scholar]
- Galvão, R.K.H.; Araújo, M.C.U.; Silva, E.C.; José, G.E.; Soares, S.F.C.; Paiva, H.M. Cross-validation for the selection of spectral variables using the successive projections algorithm. J. Braz. Chem. Soc. 2007, 18, 1580–1584. [Google Scholar] [CrossRef]
- Holland, J.H. Adaptation in Natural and Artificial Systems. An Introductory Analysis with Application to Biology, Control and Artificial Intelligence; Higher Education Press: Beijing, China, 1994. (In Chinese) [Google Scholar]
- Leardi, R.; Seasholtz, M.B.; Pell, R.J. Variable selection for multivariate calibration using a genetic algorithm: Prediction of additive concentrations in polymer films from Fourier transform-infrared spectral data. Anal. Chim. Acta 2002, 461, 189–200. [Google Scholar] [CrossRef]
- Sun, T.; Xu, W.L.; Lin, J.L.; Liu, M.H.; He, X.W. Determination of soluble solids content in navel oranges by vis/nir diffuse transmission spectra combined with CARS method. Spectrosc. Spectr. Anal. 2012, 32, 3229–3233. (In Chinese) [Google Scholar]
- Chin, W.W. The partial least squares approach to structural equation modeling. Mod. Methods Bus. Res. 1998, 295, 295–336. [Google Scholar]
- Shi, T.Z.; Chen, Y.Y.; Liu, Y.L.; Wu, G.F. Visible and near-infrared reflectance spectroscopy-An alternative for monitoring soil contamination by heavy metals. J. Hazard. Mater. 2014, 265, 166–176. [Google Scholar] [CrossRef]
- Malley, D.F.; Williams, P.C. Use of near-infrared reflectance spectroscopy in prediction of heavy metals in freshwater sediment by their association with organic matter. Environ. Sci. Technol. 1997, 31, 3461–3467. [Google Scholar] [CrossRef]
- Velasquez, E.; Lavelle, P.; Barrios, E.; Joffre, R.; Reversat, F. Evaluating soil quality in tropical agroecosystems of Colombia using NIRS. Soil Biol. Biochem. 2005, 375, 889–898. [Google Scholar] [CrossRef]
- Nicola, B.M.; Beullens, K.; Bobelyn, E.; Peirs, A.; Saeys, W.; Theron, K.I.; Jeroen, L. Nondestructive measurement of fruit and vegetable quality by means of nir spectroscopy: A review. Postharvest Biol. Technol. 2007, 46, 99–118. [Google Scholar] [CrossRef]
- Dematte, J.A.M.; Galdos, M.V.; Guimaraes, R.V.; Genu, A.M.; Nanni, M.R.; Zullo, J. Quantification of tropical soil attributes from ETM+/LANDSAT-7 data. Int. J. Remote Sens. 2007, 28, 3813–3829. [Google Scholar] [CrossRef]
- Stazi, S.R.; Antonucci, F.; Pallottino, F.; Costa, C.; Marabottini, R.; Petruccioli, M.; Menesatti, P. Hyperspectral visible–near infrared determination of arsenic concentration in soil. Commun. Soil Sci. Plant Anal. 2014, 45, 2911–2920. [Google Scholar] [CrossRef]
- Yang, J.Y.; Qian, L.X.; Zheng, Y.W.; Li, M.J. Estimation of the content of arsenic and copper in soil based on hyperspectral data. Bull. Sci. Technol. 2018, 34, 112–119. (In Chinese) [Google Scholar]
- Wang, X.P.; Zhang, F.; Kung, H.T.; Johnson, V.C. New methods for improving the remote sensing estimation of soil organic matter content (SOMC) in the Ebinur Lake Wetland National Nature Reserve (ELWNNR) in northwest China. Remote Sens. Environ. 2018, 218, 104–118. [Google Scholar] [CrossRef]
- Gholizadeh, A.; Borůvka, L.; Saberioon, M.M.; Kozák, J.; Vašát, R.; Němeček, K. Comparing different data preprocessing methods for monitoring soil heavy metals based on soil spectral features. Soil Water Res. 2015, 10, 218–227. [Google Scholar] [CrossRef]
- Qiao, X.X.; Wang, C.; Feng, M.C.; Yang, W.D.; Ding, G.W.; Sun, H.; Liang, Z.Y.; Shi, C.C. Hyperspectral estimation of soil organic matter based on different spectral preprocessing techniques. Spectrosc. Lett. 2017, 50, 156–163. [Google Scholar] [CrossRef]
- Hong, Y.S.; Chen, Y.Y.; Yu, L.; Liu, Y.F.; Liu, Y.L.; Zhang, Y.; Liu, Y.; Cheng, H. Combining fractional order derivative and spectral variable selection for organic matter estimation of homogeneous soil samples by VIS-NIR spectroscopy. Remote Sens. 2018, 10, 479. [Google Scholar] [CrossRef]
- Shen, L.Z.; Gao, M.F.; Yan, J.W.; Li, Z.L.; Duan, S.B. Hyperspectral estimation of soil organic matter content using different spectral preprocessing techniques and PLSR method. Remote Sens. 2020, 12, 1206. [Google Scholar] [CrossRef]
- Vohland, M.; Ludwig, M.; Sören, T.B.; Ludwig, B. Determination of soil properties with visible to near- and mid-infrared spectroscopy: Effects of spectral variable selection. Geoderma 2014, 223, 88–96. [Google Scholar] [CrossRef]
- Jiang, Q.H. Retrieval Model and Its Optimization for Estimating Soil Components with Hyperspectra in Lakeside Area; Wuhan University: Wuhan, China, 2014. (In Chinese) [Google Scholar]
- Qian, J.; Guo, Y.K.; Jiang, M.; Zhang, Q. Combined hyperspectral remote sensing based modeling of Cu content in different soil types. Sci. Surv. Mapp. 2020, 1, 1–8. [Google Scholar]







| Sensor Name | VNIR-1024 | Sensor Image |
|---|---|---|
| Detector | SiCCD 2048 × 2048 |  |
| Spectral range | 400–1000 nm | |
| Spatial pixels | 1024 | |
| Field of view angle | 17° | |
| Extension lens | 34° | |
| Instantaneous field of view | 0.18 mrad/0.36 mrad | |
| Spectral sampling | 2.8 nm | |
| Spectral number | 216 | |
| Camera weight | 4.6 kg | |
| Camera size(cm) | 31.5 × 8.4 × 13.8 | |
| Power consumption | ~6 W |
| Spectral Transformation | Formula |
|---|---|
| Reciprocal | |
| Logarithmic | |
| Power | |
| Envelope removal | |
| First-order derivatives | |
| Second-order derivatives | |
| Power-logarithmic | |
| Logarithmic-power |
| Spectral Transformations | Number of Principal Components | Validation Set | |||
|---|---|---|---|---|---|
| RRMSEP | MAE | ||||
| R | 17 | 0.5048 | 0.4860 | 2.133 | 22.774 |
| (R)′ | 11 | 0.3474 | 0.3167 | 1.906 | 25.949 |
| (R)″ | 5 | 0.2695 | 0.2612 | 1.761 | 27.755 |
| 15 | 0.5307 | 0.4905 | 2.137 | 22.712 | |
| 1/R | 4 | 0.2725 | 0.2714 | 0.804 | 29.705 |
| CR(R) | 13 | 0.3834 | 0.3634 | 1.638 | 22.829 |
| 17 | 0.5201 | 0.4901 | 2.127 | 22.690 | |
| 17 | 0.5913 | 0.5863 | 2.064 | 21.405 | |
| 17 | 0.5869 | 0.5628 | 2.079 | 23.035 | |
| Spectral Transformations | Number of Bands | Number of Principal Components | Determination Coefficient of Training Set (R2) | Validation Set | ||
|---|---|---|---|---|---|---|
| R2 | RRMSEP | MAE | ||||
| GA | 105 | 18 | 0.536 | 0.519 | 2.102 | 23.171 |
| CARS | 20 | 12 | 0.751 | 0.734 | 2.21 | 19.926 |
| SPA | 42 | 18 | 0.709 | 0.691 | 2.175 | 21.764 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, G.; Zhou, S.; Cui, S.; Chen, T.; Wang, J.; Chen, X.; Liao, S.; Zhou, K. Exploring the Potential of HySpex Hyperspectral Imagery for Extraction of Copper Content. Sensors 2020, 20, 6325. https://doi.org/10.3390/s20216325
Jiang G, Zhou S, Cui S, Chen T, Wang J, Chen X, Liao S, Zhou K. Exploring the Potential of HySpex Hyperspectral Imagery for Extraction of Copper Content. Sensors. 2020; 20(21):6325. https://doi.org/10.3390/s20216325
Chicago/Turabian StyleJiang, Guo, Shuguang Zhou, Shichao Cui, Tao Chen, Jinlin Wang, Xi Chen, Shibin Liao, and Kefa Zhou. 2020. "Exploring the Potential of HySpex Hyperspectral Imagery for Extraction of Copper Content" Sensors 20, no. 21: 6325. https://doi.org/10.3390/s20216325
APA StyleJiang, G., Zhou, S., Cui, S., Chen, T., Wang, J., Chen, X., Liao, S., & Zhou, K. (2020). Exploring the Potential of HySpex Hyperspectral Imagery for Extraction of Copper Content. Sensors, 20(21), 6325. https://doi.org/10.3390/s20216325





