Monitoring of PM2.5 Concentrations by Learning from Multi-Weather Sensors
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Machine Learning Methods
2.2.1. Multivariate Linear Regression
2.2.2. Multivariate Nonlinear Regression
| Algorithm 1: Nelder–Mead simplex method for multivariate nonlinear regression |
 |
2.2.3. Neural Network
3. Results
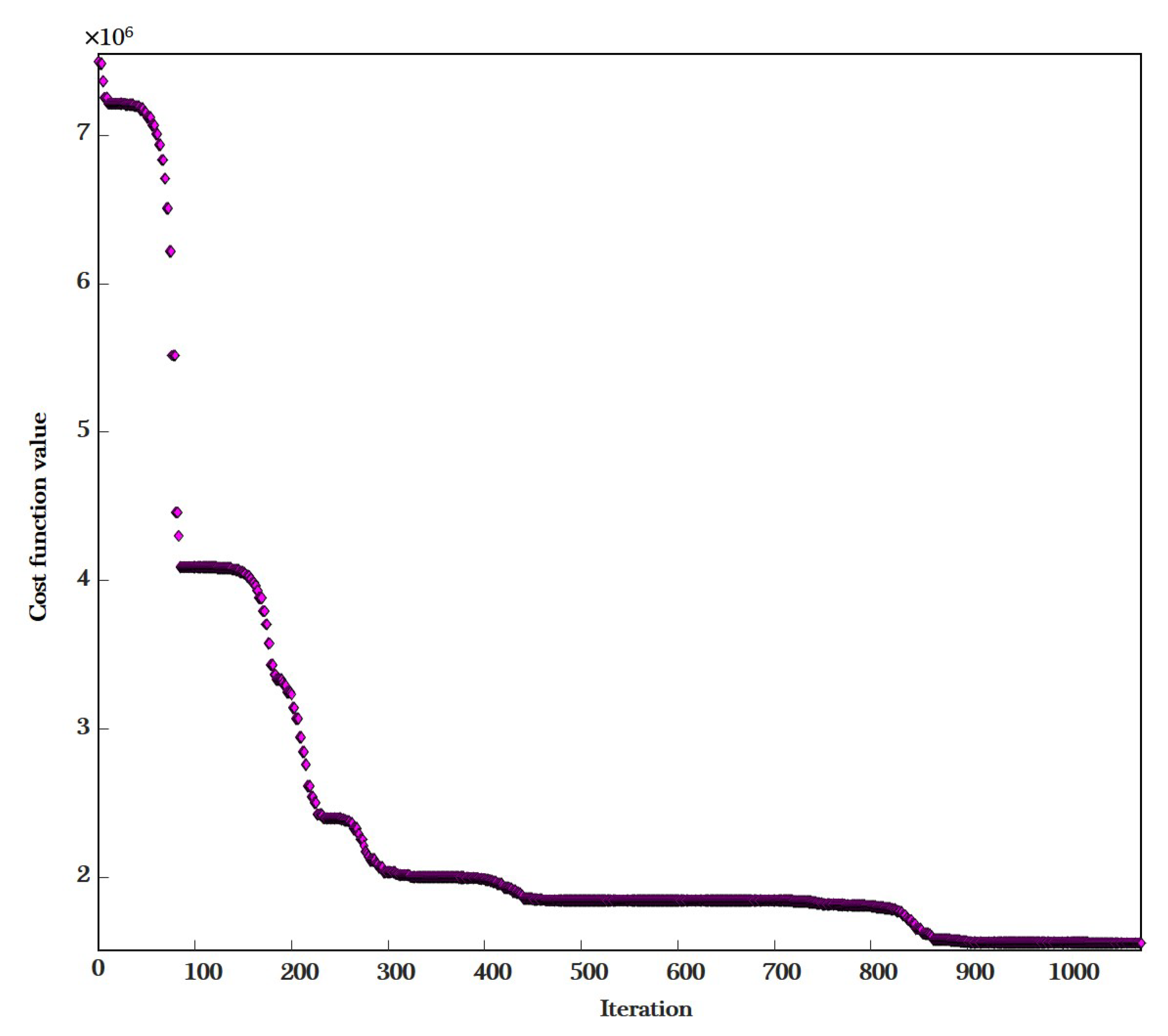
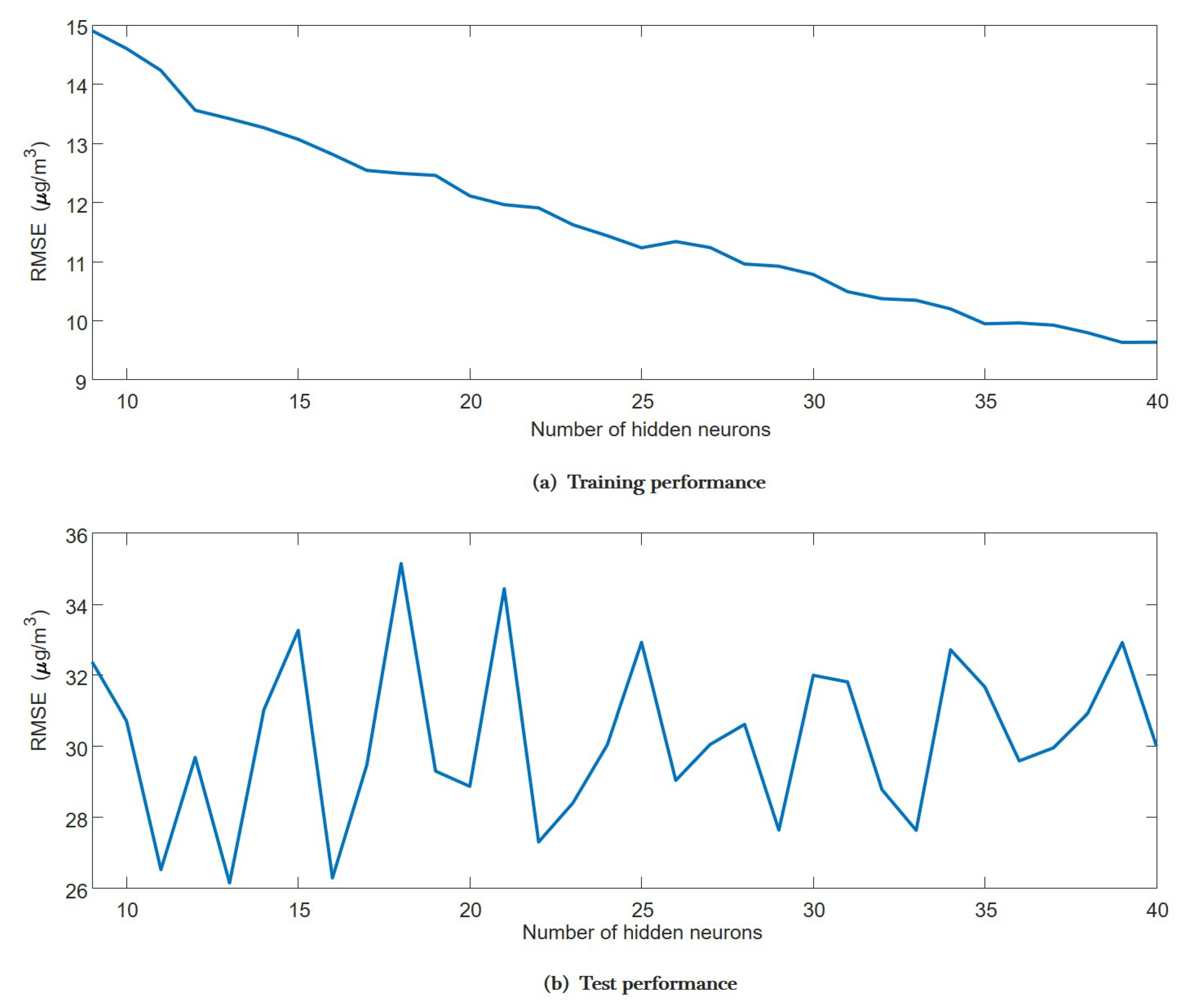
3.1. Models Training
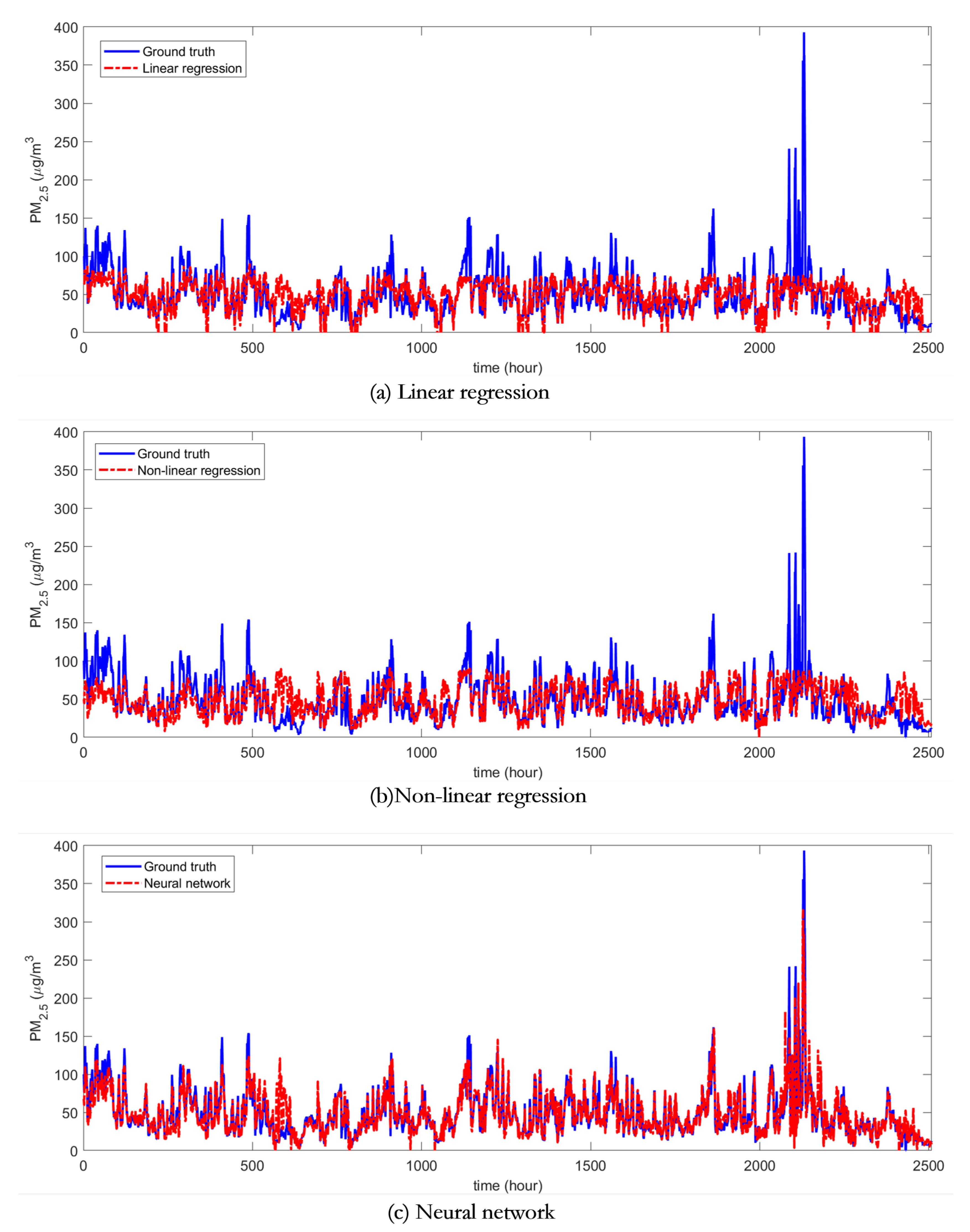
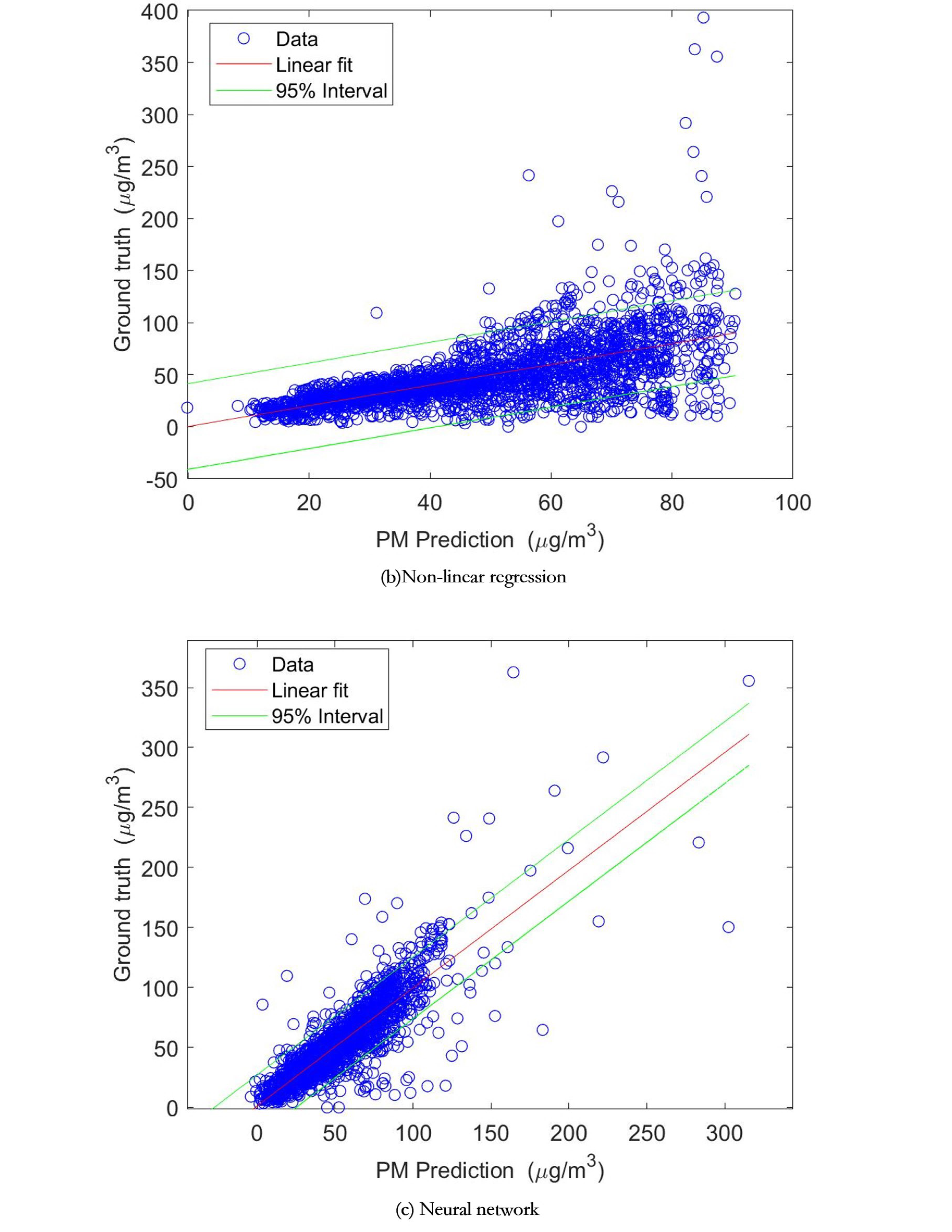
3.2. Predictions of PM Concentrations
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Mogireddy, K.; Devabhaktuni, V.; Kumar, A.; Aggarwal, P.; Bhattacharya, P. A new approach to simulate characterization of particulate matter employing support vector machines. J. Hazard. Mater. 2011, 186, 1254–1262. [Google Scholar] [CrossRef] [PubMed]
- Jo, H.Y.; Kim, C.H. Identification of long-range transported haze phenomena and their meteorological features over Northeast Asia. J. Appl. Meteorol. Climatol. 2013, 52, 1318–1328. [Google Scholar] [CrossRef]
- Lee, B.K.; Park, G.H. Characteristics of heavy metals in airborne particulate matter on misty and clear days. J. Hazard. Mater. 2010, 184, 406–416. [Google Scholar] [CrossRef] [PubMed]
- Kadiyala, A.; Kumar, A. Development and application of a methodology to identify and rank the important factors affecting in-vehicle particulate matter. J. Hazard. Mater. 2012, 213, 140–146. [Google Scholar] [CrossRef] [PubMed]
- Araujo, L.N.; Belotti, J.T.; Alves, T.A.; Tadano, Y.D.S.; Siqueira, H.V. Ensemble method based on Artificial Neural Networks to estimate air pollution health risks. Environ. Model. Softw. 2020, 123, 104567. [Google Scholar] [CrossRef]
- Tadano, Y.D.S.; Siqueira, H.V.; Alves, T.A. Unorganized machines to predict hospital admissions for respiratory diseases. In Proceedings of the 2016 IEEE Latin American Conference on Computational Intelligence (LA-CCI), Cartagena, Colombia, 2–4 November 2016; pp. 1–6. [Google Scholar]
- Jerrett, M.; Turner, M.C.; Beckerman, B.S.; Pope, C.A., III; Van Donkelaar, A.; Martin, R.V.; Serre, M.; Crouse, D.; Gapstur, S.M.; Krewski, D.; et al. Comparing the health effects of ambient particulate matter estimated using ground-based versus remote sensing exposure estimates. Environ. Health Perspect. 2017, 125, 552–559. [Google Scholar] [CrossRef] [PubMed]
- Harrison, R.M. Airborne particulate matter. Philos. Trans. R. Soc. A 2020, 378, 20190319. [Google Scholar] [CrossRef]
- Yang, X.; Li, Z. Increases in thunderstorm activity and relationships with air pollution in southeast China. J. Geophys. Res. Atmos. 2014, 119, 1835–1844. [Google Scholar] [CrossRef]
- Levy, R.C.; Pinker, R.T. Remote sensing of spectral aerosol properties: A classroom experience. Bull. Am. Meteorol. Soc. 2007, 88, 25–30. [Google Scholar] [CrossRef]
- Delp, W.W.; Singer, B.C. Wildfire smoke adjustment factors for low-cost and professional PM2.5 monitors with optical sensors. Sensors 2020, 20, 3683. [Google Scholar] [CrossRef]
- Franklin, M.; Kalashnikova, O.V.; Garay, M.J.; Fruin, S. Characterization of subgrid-scale variability in particulate matter with respect to satellite aerosol observations. Remote Sens. 2018, 10, 623. [Google Scholar] [CrossRef]
- Shin, M.; Kang, Y.; Park, S.; Im, J.; Yoo, C.; Quackenbush, L.J. Estimating ground-level particulate matter concentrations using satellite-based data: A review. GIScience Remote Sens. 2020, 57, 174–189. [Google Scholar] [CrossRef]
- Ma, X.; Huang, Z.; Qi, S.; Huang, J.; Zhang, S.; Dong, Q.; Wang, X. Ten-year global particulate mass concentration derived from space-borne CALIPSO lidar observations. Sci. Total Environ. 2020, 721, 137699. [Google Scholar] [CrossRef] [PubMed]
- Christopher, S.; Gupta, P. Global Distribution of Column Satellite Aerosol Optical Depth to Surface PM2.5 Relationships. Remote Sens. 2020, 12, 1985. [Google Scholar] [CrossRef]
- Veefkind, J.; Aben, I.; McMullan, K.; Forster, H.; De Vries, J.; Otter, G.; Claas, J.; Eskes, H.; De Haan, J.; Kleipool, Q.; et al. TROPOMI on the ESA Sentinel-5 Precursor: A GMES mission for global observations of the atmospheric composition for climate, air quality and ozone layer applications. Remote Sens. Environ. 2012, 120, 70–83. [Google Scholar] [CrossRef]
- Mei, H.; Han, P.; Wang, Y.; Zeng, N.; Liu, D.; Cai, Q.; Deng, Z.; Wang, Y.; Pan, Y.; Tang, X. Field evaluation of low-cost particulate matter sensors in Beijing. Sensors 2020, 20, 4381. [Google Scholar] [CrossRef]
- Zheng, M.; Yan, C.; Zhu, T. Understanding sources of fine particulate matter in China. Philos. Trans. R. Soc. A 2020, 378, 20190325. [Google Scholar] [CrossRef]
- Zhang, Y.; Guo, J.; Yang, Y.; Wang, Y.; Yim, S.H. Vertica Wind Shear Modulates Particulate Matter Pollutions: A Perspective from Radar Wind Profiler Observations in Beijing, China. Remote Sens. 2020, 12, 546. [Google Scholar] [CrossRef]
- Knobelspiesse, K.; Barbosa, H.M.; Bradley, C.; Bruegge, C.; Cairns, B.; Chen, G.; Chowdhary, J.; Cook, A.; Di Noia, A.; van Diedenhoven, B.; et al. The Aerosol Characterization from Polarimeter and Lidar (ACEPOL) airborne field campaign. Earth Syst. Sci. Data 2020, 12, 2183–2208. [Google Scholar] [CrossRef]
- Wang, T.; Han, W.; Zhang, M.; Yao, X.; Zhang, L.; Peng, X.; Li, C.; Dan, X. Unmanned Aerial Vehicle-Borne Sensor System for Atmosphere-Particulate-Matter Measurements: Design and Experiments. Sensors 2020, 20, 57. [Google Scholar] [CrossRef]
- Mølgaard, B.; Hussein, T.; Corander, J.; Hämeri, K. Forecasting size-fractionated particle number concentrations in the urban atmosphere. Atmos. Environ. 2012, 46, 155–163. [Google Scholar] [CrossRef]
- Reggente, M.; Peters, J.; Theunis, J.; Van Poppel, M.; Rademaker, M.; Kumar, P.; De Baets, B. Prediction of ultrafine particle number concentrations in urban environments by means of Gaussian process regression based on measurements of oxides of nitrogen. Environ. Model. Softw. 2014, 61, 135–150. [Google Scholar] [CrossRef]
- Commodore, S.; Metcalf, A.; Post, C.; Watts, K.; Reynolds, S.; Pearce, J. A Statistical Calibration Framework for Improving Non-Reference Method Particulate Matter Reporting: A Focus on Community Air Monitoring Settings. Atmosphere 2020, 11, 807. [Google Scholar] [CrossRef]
- Van Donkelaar, A.; Martin, R.V.; Brauer, M.; Hsu, N.C.; Kahn, R.A.; Levy, R.C.; Lyapustin, A.; Sayer, A.M.; Winker, D.M. Global estimates of fine particulate matter using a combined geophysical-statistical method with information from satellites, models, and monitors. Environ. Sci. Technol. 2016, 50, 3762–3772. [Google Scholar] [CrossRef] [PubMed]
- Van Donkelaar, A.; Martin, R.V.; Li, C.; Burnett, R.T. Regional estimates of chemical composition of fine particulate matter using a combined geoscience-statistical method with information from satellites, models, and monitors. Environ. Sci. Technol. 2019, 53, 2595–2611. [Google Scholar] [CrossRef]
- Hammer, M.S.; van Donkelaar, A.; Li, C.; Lyapustin, A.; Sayer, A.M.; Hsu, N.C.; Levy, R.C.; Garay, M.; Kalashnikova, O.; Kahn, R.A.; et al. Global Estimates and Long-Term Trends of Fine Particulate Matter Concentrations (1998-2018). Environ. Sci. Technol. 2020, 54, 7879–7890. [Google Scholar] [CrossRef]
- Dawson, J.P.; Bloomer, B.J.; Winner, D.A.; Weaver, C.P. Understanding the meteorological drivers of US particulate matter concentrations in a changing climate. Bull. Am. Meteorol. Soc. 2014, 95, 521–532. [Google Scholar] [CrossRef]
- Odman, M.T.; Hu, Y.; Unal, A.; Russell, A.G.; Boylan, J.W. Determining the sources of regional haze in the southeastern United States using the CMAQ model. J. Appl. Meteorol. Climatol. 2007, 46, 1731–1743. [Google Scholar] [CrossRef]
- Barker, H. Isolating the industrial contribution of PM2. 5 in Hamilton and Burlington, Ontario. J. Appl. Meteorol. Climatol. 2013, 52, 660–667. [Google Scholar] [CrossRef]
- Xu, M.; Wang, Y.X. Quantifying PM2.5 concentrations from multi-weather sensors using hidden Markov models. IEEE Sens. J. 2015, 16, 22–23. [Google Scholar] [CrossRef]
- Patten, M.L.; Newhart, M. Understanding Research Methods: An Overview of the Essentials; Taylor & Francis: Abingdon, UK, 2017. [Google Scholar]
- Powell, M.J. On search directions for minimization algorithms. Math. Program. 1973, 4, 193–201. [Google Scholar] [CrossRef]
- Lagarias, J.C.; Reeds, J.A.; Wright, M.H.; Wright, P.E. Convergence properties of the Nelder–Mead simplex method in low dimensions. SIAM J. Optim. 1998, 9, 112–147. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016; Available online: http://www.deeplearningbook.org (accessed on 28 September 2020).
- Haykin, S. Neural Networks and Learning Machine; Pearson Education, Inc.: Upper Saddle River, NJ, USA, 2009. [Google Scholar]
- MacKay, D.J. Bayesian interpolation. Neural Comput. 1992, 4, 415–447. [Google Scholar] [CrossRef]
- Foresee, F.D.; Hagan, M.T. Gauss–Newton approximation to Bayesian learning. In Proceedings of the IEEE International Conference on Neural Networks (ICNN’97), Houston, TX, USA, 12 June 1997; Volume 3, pp. 1930–1935. [Google Scholar]
- Burden, F.; Winkler, D. Bayesian regularization of neural networks. In Artificial Neural Networks; Springer: Berlin/Heidelberg, Germany, 2008; pp. 23–42. [Google Scholar]
- Kayri, M. Predictive abilities of bayesian regularization and Levenberg–Marquardt algorithms in artificial neural networks: A comparative empirical study on social data. Math. Comput. Appl. 2016, 21, 20. [Google Scholar] [CrossRef]
- Park, J.G.; Jo, S. Approximate Bayesian MLP regularization for regression in the presence of noise. Neural Netw. 2016, 83, 75–85. [Google Scholar] [CrossRef]
- Sariev, E.; Germano, G. Bayesian regularized artificial neural networks for the estimation of the probability of default. Quant. Financ. 2020, 20, 311–328. [Google Scholar] [CrossRef]
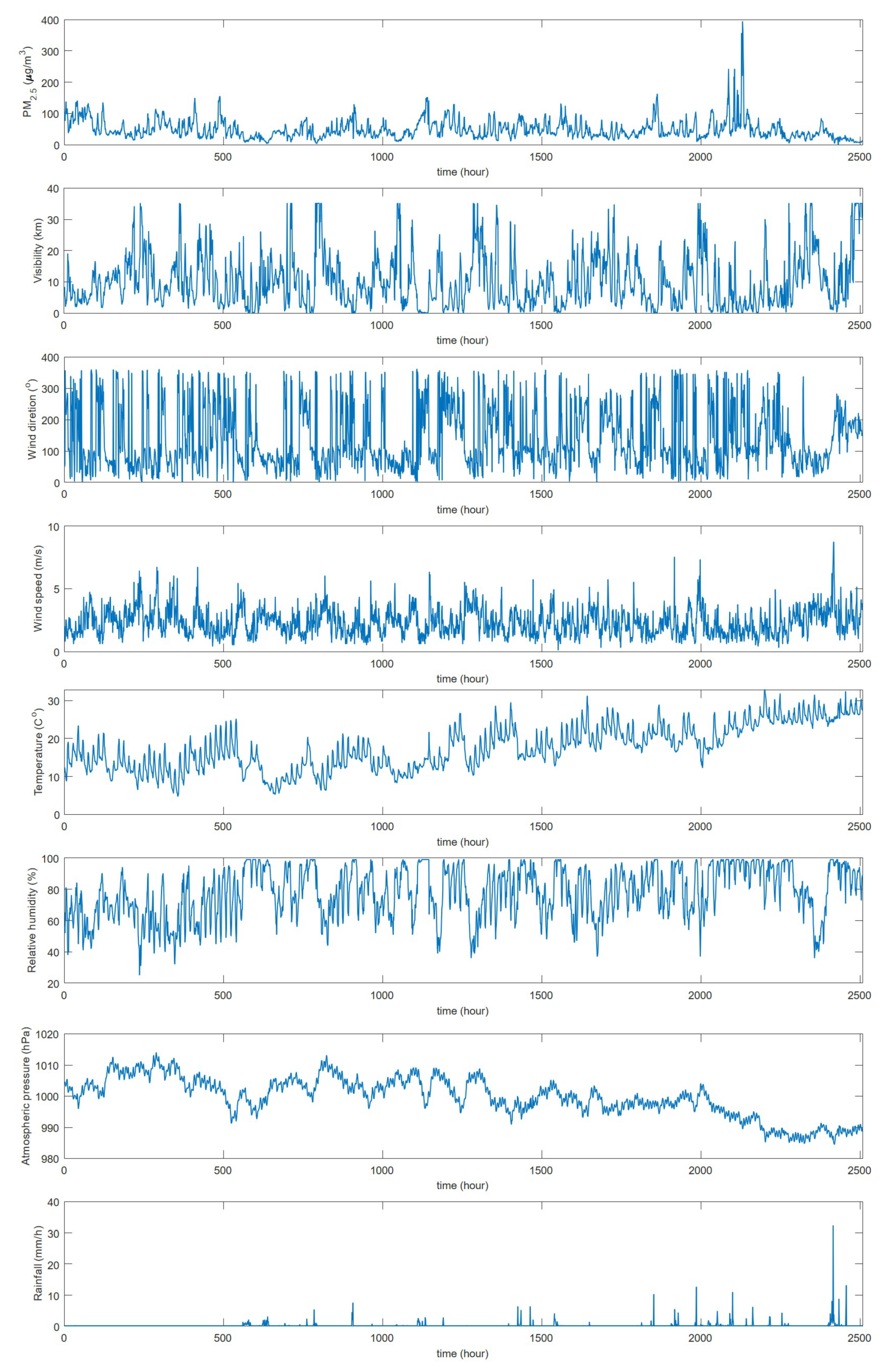
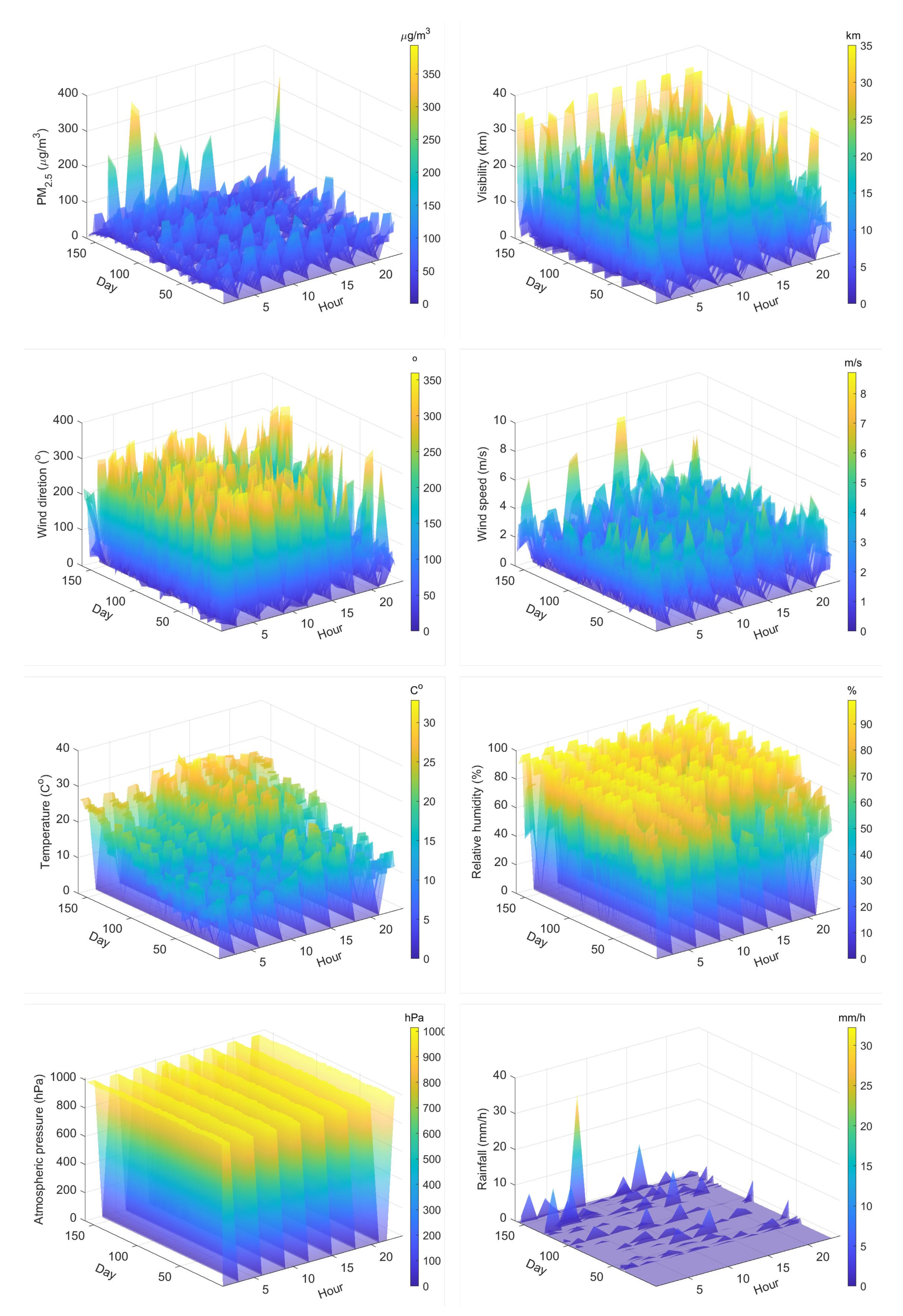
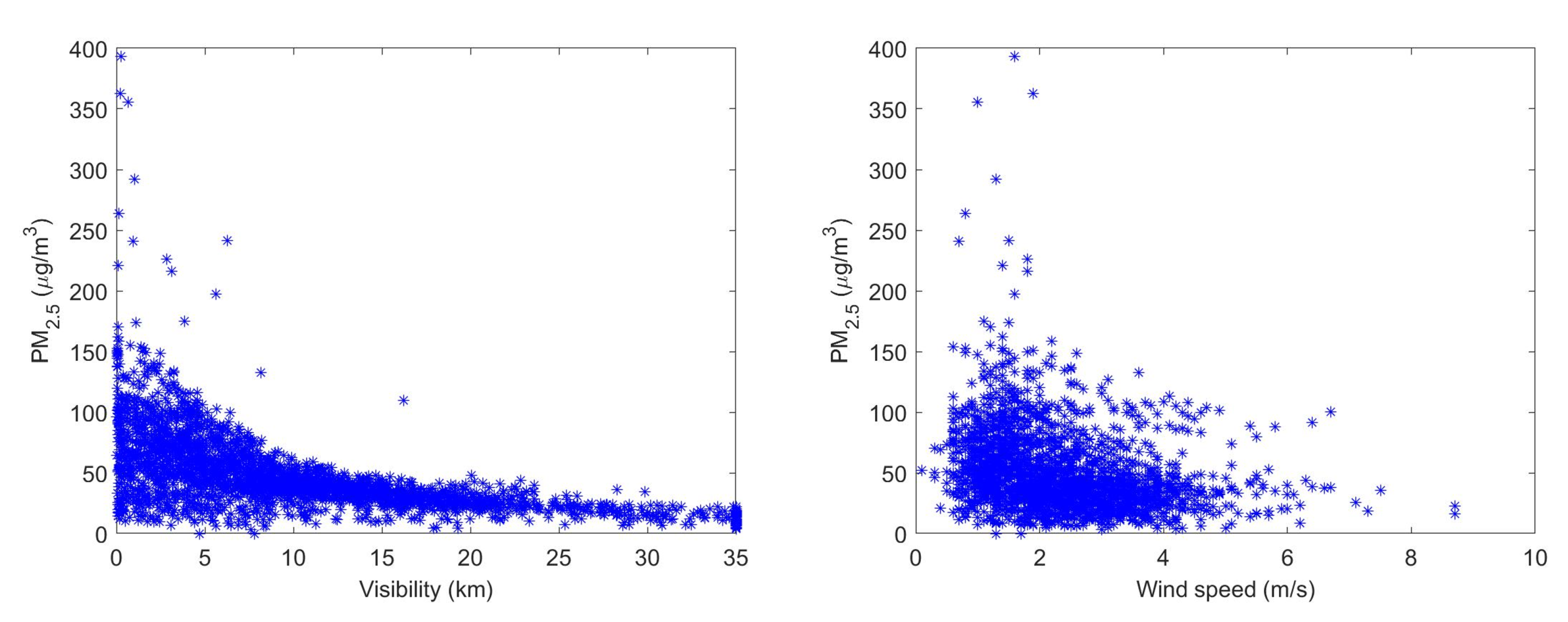



| Visibility | Wind Direction | Wind Speed | Relative Humidity | Temperature | Atmospheric Pressure | Rainfall Rate |
|---|---|---|---|---|---|---|
| −0.5639 | 0.2830 | −0.2839 | 0.1201 | −0.0424 | 0.0828 | −0.0308 |
| Linear Regression | Nonlinear Regression | Neural Network | |
|---|---|---|---|
| Averaged RMSE (g/m) | 24.6756 | 24.9191 | 15.6391 |
| Correlation coefficient | 0.6281 | 0.6184 | 0.8701 |
| Parameters | Linear Regression | Nonlinear Regression | Neural Network |
|---|---|---|---|
| visibility + wind + RH | 24.6756/0.6281 | 24.9191/0.6184 | 20.4548/0.7643 |
| visibility + wind + RH + temperature | 24.6670/0.6284 | 27.5901/0.5107 | 17.2791/ 0.8387 |
| visibility + wind + RH + temperature + air pressure | 24.5770/0.6319 | 30.1810/0.3093 | 17.1101/ 0.8460 |
| visibility + wind + RH + temperature + air pressure + rainfall | 24.5141/0.6343 | 29.0009/ 0.4132 | 15.6391/ 0.8701 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Xu, Z. Monitoring of PM2.5 Concentrations by Learning from Multi-Weather Sensors. Sensors 2020, 20, 6086. https://doi.org/10.3390/s20216086
Wang Y, Xu Z. Monitoring of PM2.5 Concentrations by Learning from Multi-Weather Sensors. Sensors. 2020; 20(21):6086. https://doi.org/10.3390/s20216086
Chicago/Turabian StyleWang, Yuexia, and Zhihuo Xu. 2020. "Monitoring of PM2.5 Concentrations by Learning from Multi-Weather Sensors" Sensors 20, no. 21: 6086. https://doi.org/10.3390/s20216086
APA StyleWang, Y., & Xu, Z. (2020). Monitoring of PM2.5 Concentrations by Learning from Multi-Weather Sensors. Sensors, 20(21), 6086. https://doi.org/10.3390/s20216086







