Compressing Deep Networks by Neuron Agglomerative Clustering
Abstract
1. Introduction
2. Related Work
2.1. Pruning
2.2. Low-Rank Decomposition
2.3. Compact Convolutional Filters Design
2.4. Knowledge Distillation
2.5. Weight Quantization
2.6. Agglomerative Clustering Method
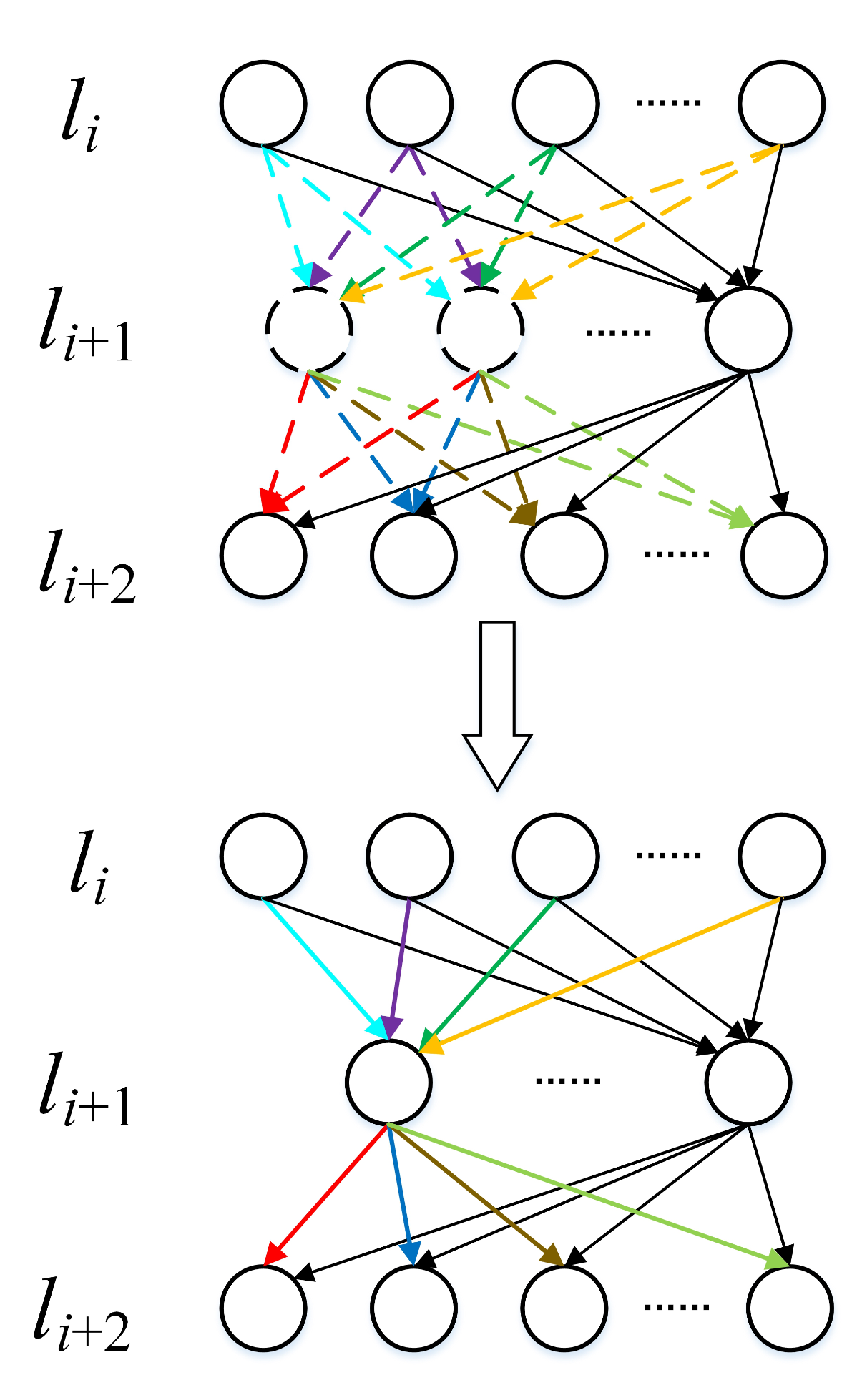
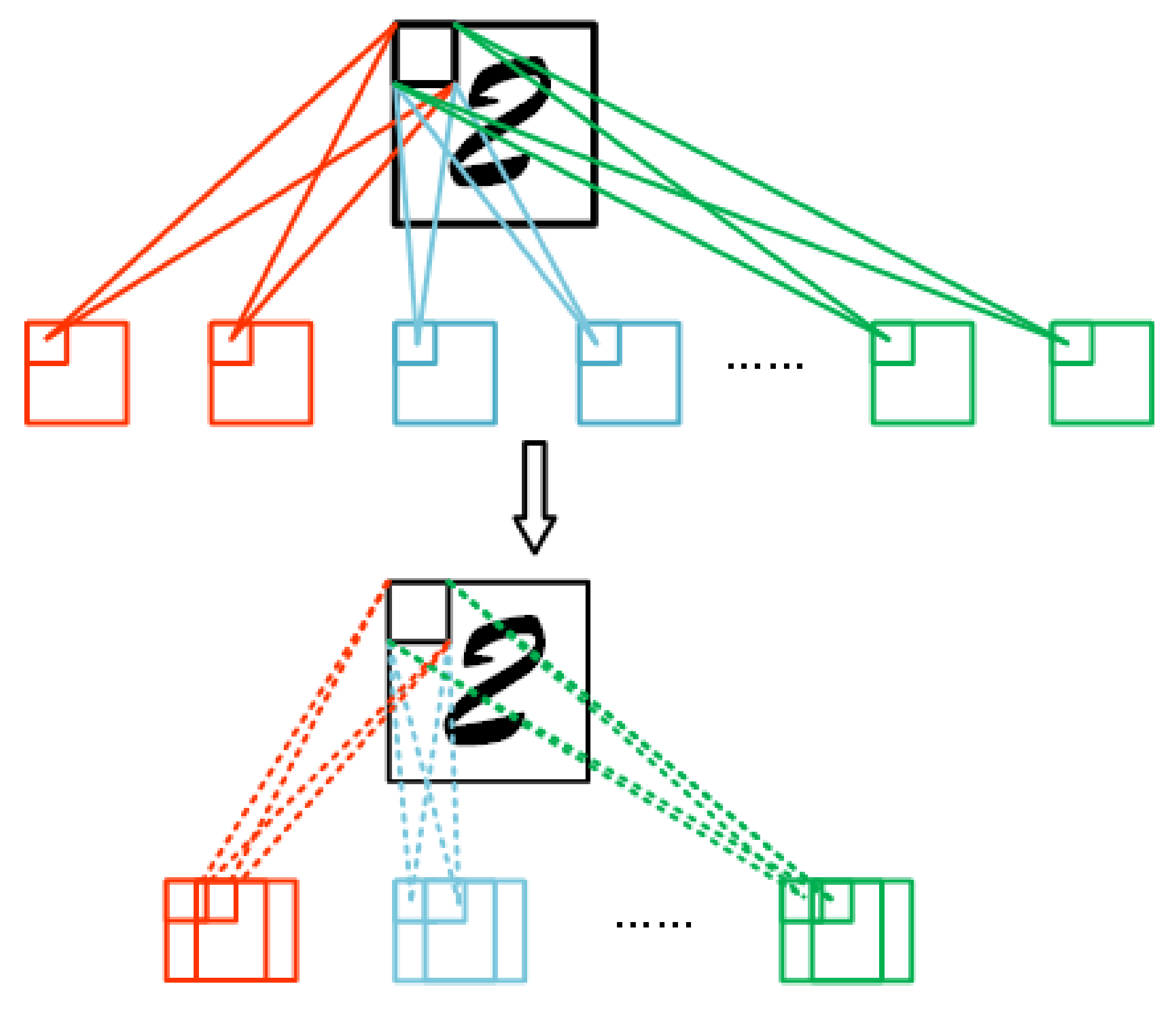
3. The Proposed Approach
3.1. Network Compression Based on Neuron Agglomerative Clustering
| Algorithm 1 Neuron agglomerative clustering. |
|
3.2. Applying NAC to Fully Connected Layers and Convolutional Layers
4. Experiments and Results
4.1. The Used Datasets
4.1.1. MNIST
4.1.2. CIFAR
4.2. Results on the MNIST Dataset
4.3. Results on the CIFAR Datasets
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- LeCun, Y.; Bengio, Y.; Hinton, G.E. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Zhong, G.; Yan, S.; Huang, K.; Cai, Y.; Dong, J. Reducing and Stretching Deep Convolutional Activation Features for Accurate Image Classification. Cogn. Comput. 2018, 10, 179–186. [Google Scholar] [CrossRef]
- Collobert, R.; Weston, J.; Bottou, L.; Karlen, M.; Kavukcuoglu, K.; Kuksa, P.P. Natural Language Processing (Almost) from Scratch. J. Mach. Learn. Res. 2011, 12, 2493–2537. [Google Scholar]
- Russakovsky, O.; Deng, J.; Su, H.; Krause, J.; Satheesh, S.; Ma, S.; Huang, Z.; Karpathy, A.; Khosla, A.; Bernstein, M.S.; et al. ImageNet Large Scale Visual Recognition Challenge. Int. J. Comput. Vis. 2015, 115, 211–252. [Google Scholar] [CrossRef]
- Li, H.; Kadav, A.; Durdanovic, I.; Samet, H.; Graf, H.P. Pruning Filters for Efficient ConvNets. arXiv 2017, arXiv:1608.08710. [Google Scholar]
- Srinivas, S.; Babu, R.V. Data-free Parameter Pruning for Deep Neural Networks. arXiv 2015, arXiv:1507.06149. [Google Scholar]
- Iandola, F.N.; Moskewicz, M.W.; Ashraf, K.; Han, S.; Dally, W.J.; Keutzer, K. SqueezeNet: AlexNet-level accuracy with 50x fewer parameters and <1MB model size. arXiv 2016, arXiv:1602.07360. [Google Scholar]
- Wang, K.; Liu, Z.; Lin, Y.; Lin, J.; Han, S. HAQ: Hardware-Aware Automated Quantization With Mixed Precision. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 16–19 June 2019; pp. 8612–8620. [Google Scholar]
- Han, S.; Cai, H.; Zhu, L.; Lin, J.; Wang, K.; Liu, Z.; Lin, Y. Design Automation for Efficient Deep Learning Computing. arXiv 2019, arXiv:1904.10616. [Google Scholar]
- Peng, B.; Tan, W.; Li, Z.; Zhang, S.; Xie, D.; Pu, S. Extreme Network Compression via Filter Group Approximation. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 307–323. [Google Scholar]
- Son, S.; Nah, S.; Lee, K.M. Clustering Convolutional Kernels to Compress Deep Neural Networks. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 225–240. [Google Scholar]
- Li, Y.; Gu, S.; Gool, L.V.; Timofte, R. Learning Filter Basis for Convolutional Neural Network Compression. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Seoul, Korea, 27 October–2 November 2019; pp. 5622–5631. [Google Scholar]
- Molchanov, P.; Tyree, S.; Karras, T.; Aila, T.; Kautz, J. Pruning Convolutional Neural Networks for Resource Efficient Inference. arXiv 2017, arXiv:1611.06440. [Google Scholar]
- Liu, X.; Li, W.; Huo, J.; Yao, L.; Gao, Y. Layerwise Sparse Coding for Pruned Deep Neural Networks with Extreme Compression Ratio. In Proceedings of the AAAI, New York, NY, USA, 7–12 February 2020; pp. 4900–4907. [Google Scholar]
- Frankle, J.; Carbin, M. The Lottery Ticket Hypothesis: Finding Sparse, Trainable Neural Networks. arXiv 2019, arXiv:1803.03635. [Google Scholar]
- Yu, J.; Tian, S. A Review of Network Compression Based on Deep Network Pruning. In Proceedings of the 3rd International Conference on Mechatronics Engineering and Information Technology (ICMEIT 2019), Dalian, China, 29–30 March 2019; pp. 308–319. [Google Scholar]
- LeCun, Y.; Denker, J.S.; Solla, S.A. Optimal Brain Damage. In Proceedings of the Advances in Neural Information Processing Systems, Denver, CO, USA, 26–29 November 1989; pp. 598–605. [Google Scholar]
- Hassibi, B.; Stork, D.G. Second Order Derivatives for Network Pruning: Optimal Brain Surgeon. In Proceedings of the Advances in Neural Information Processing Systems, Denver, CO, USA, 30 November–3 December 1989; pp. 164–171. [Google Scholar]
- Han, S.; Mao, H.; Dally, W.J. Deep Compression: Compressing Deep Neural Network with Pruning, Trained Quantization and Huffman Coding. In Proceedings of the Advances in Neural Information Processing Systems, Barcelona, Spain, 10–16 December 2016. [Google Scholar]
- Han, S.; Pool, J.; Tran, J.; Dally, W.J. Learning both Weights and Connections for Efficient Neural Network. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 7–12 December 2015; pp. 1135–1143. [Google Scholar]
- Anwar, S.; Hwang, K.; Sung, W. Structured Pruning of Deep Convolutional Neural Networks. ACM J. Emerg. Technol. Comput. Syst. 2017, 13, 32. [Google Scholar] [CrossRef]
- Figurnov, M.; Ibraimova, A.; Vetrov, D.P.; Kohli, P. PerforatedCNNs: Acceleration through Elimination of Redundant Convolutions. In Proceedings of the Advances in Neural Information Processing Systems, Barcelona, Spain, 10–16 December 2016; pp. 947–955. [Google Scholar]
- Hu, H.; Peng, R.; Tai, Y.; Tang, C. Network Trimming: A Data-Driven Neuron Pruning Approach towards Efficient Deep Architectures. arXiv 2016, arXiv:1607.03250. [Google Scholar]
- Rueda, F.M.; Grzeszick, R.; Fink, G.A. Neuron Pruning for Compressing Deep Networks Using Maxout Architectures. In Lecture Notes in Computer Science; CGC Press: New York, NY, USA, 2017; Volume 10496, pp. 177–188. [Google Scholar]
- Denton, E.L.; Zaremba, W.; Bruna, J.; LeCun, Y.; Fergus, R. Exploiting Linear Structure Within Convolutional Networks for Efficient Evaluation. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 8–13 December 2014; pp. 1269–1277. [Google Scholar]
- Lin, S.; Ji, R.; Guo, X.; Li, X. Towards Convolutional Neural Networks Compression via Global Error Reconstruction. In Proceedings of the 2016 International Joint Conference on Artificial Intelligence (IJCAI), New York, NY, USA, 9–15 July 2016; pp. 1753–1759. [Google Scholar]
- Wolter, M.; Lin, S.; Yao, A. Towards deep neural network compression via learnable wavelet transforms. arXiv 2020, arXiv:2004.09569. [Google Scholar]
- Jaderberg, M.; Vedaldi, A.; Zisserman, A. Speeding up Convolutional Neural Networks with Low Rank Expansions. arXiv 2014, arXiv:1405.3866. [Google Scholar]
- Zhang, X.; Zou, J.; He, K.; Sun, J. Accelerating Very Deep Convolutional Networks for Classification and Detection. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 38, 1943–1955. [Google Scholar] [CrossRef]
- Denil, M.; Shakibi, B.; Dinh, L.; Ranzato, M.; de Freitas, N. Predicting Parameters in Deep Learning. In Proceedings of the Advances in Neural Information Processing Systems, Lake Tahoe, CA, USA, 5–8 December 2013; pp. 2148–2156. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 26 June–1 July 2016; pp. 770–778. [Google Scholar]
- Chollet, F. Xception: Deep Learning with Depthwise Separable Convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 1800–1807. [Google Scholar]
- Zhang, X.; Zhou, X.; Lin, M.; Sun, J. ShuffleNet: An Extremely Efficient Convolutional Neural Network for Mobile Devices. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018; pp. 6848–6856. [Google Scholar]
- Qi, W.; Su, H.; Yang, C.; Ferrigno, G.; Momi, E.D.; Aliverti, A. A Fast and Robust Deep Convolutional Neural Networks for Complex Human Activity Recognition Using Smartphone. Sensors 2019, 19, 3731. [Google Scholar] [CrossRef]
- Liu, J.; Chen, F.; Yan, J.; Wang, D. CBN-VAE: A Data Compression Model with Efficient Convolutional Structure for Wireless Sensor Networks. Sensors 2019, 19, 3445. [Google Scholar] [CrossRef]
- Salakhutdinov, R.; Mnih, A.; Hinton, G.E. Restricted Boltzmann Machines for Collaborative Filtering. In Proceedings of the 24th International Conference on Machine Learning, Corvallis, OR, USA, 20–24 June 2007; pp. 791–798. [Google Scholar]
- Kingma, D.P.; Welling, M. Auto-Encoding Variational Bayes. arXiv 2014, arXiv:1312.6114. [Google Scholar]
- Pu, Y.; Gan, Z.; Henao, R.; Yuan, X.; Li, C.; Stevens, A.; Carin, L. Variational Autoencoder for Deep Learning of Images, Labels and Captions. In Proceedings of the Advances in Neural Information Processing Systems, Barcelona, Spain, 10–16 December 2016; pp. 2352–2360. [Google Scholar]
- Ba, J.; Caruana, R. Do Deep Nets Really Need to be Deep? In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 8–13 December 2014; pp. 2654–2662. [Google Scholar]
- Hinton, G.E.; Vinyals, O.; Dean, J. Distilling the Knowledge in a Neural Network. arXiv 2015, arXiv:1503.02531. [Google Scholar]
- Aguinaldo, A.; Chiang, P.; Gain, A.; Patil, A.; Pearson, K.; Feizi, S. Compressing GANs using Knowledge Distillation. arXiv 2019, arXiv:1902.00159. [Google Scholar]
- Chen, G.; Choi, W.; Yu, X.; Han, T.X.; Chandraker, M. Learning Efficient Object Detection Models with Knowledge Distillation. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 742–751. [Google Scholar]
- Li, T.; Li, J.; Liu, Z.; Zhang, C. Knowledge Distillation from Few Samples. CoRR 2018, abs/1812.01839. [Google Scholar]
- Luo, P.; Zhu, Z.; Liu, Z.; Wang, X.; Tang, X. Face Model Compression by Distilling Knowledge from Neurons. In Proceedings of the AAAI, Phoenix, AZ, USA, 12–17 February 2016; pp. 3560–3566. [Google Scholar]
- Yim, J.; Joo, D.; Bae, J.; Kim, J. A Gift from Knowledge Distillation: Fast Optimization, Network Minimization and Transfer Learning. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 7130–7138. [Google Scholar]
- Li, M.; Lin, J.; Ding, Y.; Liu, Z.; Zhu, J.; Han, S. GAN Compression: Efficient Architectures for Interactive Conditional GANs. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Montreal, QC, Canada, 14–19 July 2020. [Google Scholar]
- Goodfellow, I.J.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.C.; Bengio, Y. Generative Adversarial Nets. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 8–13 December 2014; pp. 2672–2680. [Google Scholar]
- Chen, H.; Wang, Y.; Xu, C.; Yang, Z.; Liu, C.; Shi, B.; Xu, C.; Xu, C.; Tian, Q. Data-Free Learning of Student Networks. In Proceedings of the IEEE International Conference on Computer Vision, Seoul, Korea, 27 October–2 November 2019. [Google Scholar]
- Peng, B.; Jin, X.; Liu, J.; Zhou, S.; Wu, Y.; Liu, Y.; Li, D.; Zhang, Z. Correlation Congruence for Knowledge Distillation. In Proceedings of the IEEE International Conference on Computer Vision, Seoul, Korea, 27 October–2 November 2019. [Google Scholar]
- Rastegari, M.; Ordonez, V.; Redmon, J.; Farhadi, A. XNOR-Net: ImageNet Classification Using Binary Convolutional Neural Networks. In Lecture Notes in Computer Science; ECCV: Prague, Czech, 2016; Volume 9908, pp. 525–542. [Google Scholar]
- Li, F.; Liu, B. Ternary Weight Networks. arXiv 2016, arXiv:1605.04711. [Google Scholar]
- Zhu, C.; Han, S.; Mao, H.; Dally, W.J. Trained Ternary Quantization. arXiv 2016, arXiv:1612.01064. [Google Scholar]
- Miao, H.; Li, A.; Davis, L.S.; Deshpande, A. Towards Unified Data and Lifecycle Management for Deep Learning. In Proceedings of the 2017 IEEE 33rd International Conference on Data Engineering (ICDE), San Diego, CA, USA, 19–22 April 2017; pp. 571–582. [Google Scholar]
- Louizos, C.; Ullrich, K.; Welling, M. Bayesian Compression for Deep Learning. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Li, Z.; Ni, B.; Zhang, W.; Yang, X.; Gao, W. Performance Guaranteed Network Acceleration via High-Order Residual Quantization. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2603–2611. [Google Scholar]
- Hu, Y.; Li, J.; Long, X.; Hu, S.; Zhu, J.; Wang, X.; Gu, Q. Cluster Regularized Quantization for Deep Networks Compression. In Proceedings of the 2019 IEEE International Conference on Image Processing (ICIP), Taipei, Taiwan, 22–25 September 2019. [Google Scholar]
- Cheng, Y.; Yu, F.X.; Feris, R.S.; Kumar, S.; Choudhary, A.N.; Chang, S. An Exploration of Parameter Redundancy in Deep Networks with Circulant Projections. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 3–7 December 2015; pp. 2857–2865. [Google Scholar]
- Ma, Y.; Suda, N.; Cao, Y.; Seo, J.; Vrudhula, S.B.K. Scalable and modularized RTL compilation of Convolutional Neural Networks onto FPGA. In Proceedings of the International Conference on Field Programmable Logic and Applications, FPL, Lausanne, Switzerland, 29 August–2 September 2016; pp. 1–8. [Google Scholar]
- Gysel, P. Ristretto: Hardware-Oriented Approximation of Convolutional Neural Networks. arXiv 2016, arXiv:1605.06402. [Google Scholar]
- Hubara, I.; Courbariaux, M.; Soudry, D.; El-Yaniv, R.; Bengio, Y. Binarized Neural Networks. In Proceedings of the Advances in Neural Information Processing Systems, Barcelona, Spain, 10–16 December 2016; pp. 4107–4115. [Google Scholar]
- Aggarwal, C.C.; Reddy, C.K. (Eds.) Data Clustering: Algorithms and Applications, 1st ed.; Data Mining and Knowledge Discovery; Chapman and Hall/CRC: New York, NY, USA, 2014. [Google Scholar]
- Duda, R.O.; Hart, P.E.; Stork, D.G. Pattern Classification, 2nd ed.; Wiley: New York, NY, USA, 2001. [Google Scholar]
- Liu, Z.; Li, J.; Shen, Z.; Huang, G.; Yan, S.; Zhang, C. Learning Efficient Convolutional Networks through Network Slimming. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2755–2763. [Google Scholar]
- Ding, X.; Ding, G.; Zhou, X.; Guo, Y.; Han, J.; Liu, J. Global Sparse Momentum SGD for Pruning Very Deep Neural Networks. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 8–14 December 2019; pp. 6382–6394. [Google Scholar]


| Original Network | Compressed Network | |
|---|---|---|
| 1st layer | 500 | 300 |
| 2nd layer | 500 | 300 |
| 3rd layer | 2000 | 1000 |
| Parameters | 1.67 M | 0.64 M |
| Error rate (%) | 1.03 | 1.17 |
| Error rate with fine-tuning (%) | - | 0.98 |
| Original Network | Compressed Network | |
|---|---|---|
| 1st layer | 500 | 200 |
| 2nd layer | 500 | 100 |
| 3rd layer | 2000 | 100 |
| Parameters | 1.67 M | 0.19 M |
| Error rate (%) | 1.03 | 15.8 |
| Error rate with fine-tuning (%) | - | 1.01 |
| Original Network | Compressed Network | |
|---|---|---|
| conv_1 | 6 | 6 |
| conv_2 | 6 | 5 |
| conv_3 | 16 | 12 |
| conv_4 | 16 | 12 |
| conv_5 | 120 | 80 |
| fc_1 | 120 | 60 |
| Parameters | 0.15 M | 0.05 M |
| Error rate (%) | 0.69 | 5.14 |
| Error rate with fine-tuning (%) | - | 0.63 |
| Datasets | Model | Test Error (%) | Parameters | P-Pruned | FLOPs | F-Pruned | Accuracy (%) |
|---|---|---|---|---|---|---|---|
| VGGNet (Baseline) | 6.38 | 33.65 M | - | 6.65 | - | - | |
| CIFAR-10 | VGGNet (Model-A) | 6.19 | 2.37 M | 92.96% | 3.72 | 44.06% | +0.19 |
| VGGNet (Model-B) | 6.08 | 2.37 M | 92.96% | 3.72 | 44.06% | +0.30 | |
| VGGNet (Baseline) | 26.38 | 34.02 M | - | 6.65 | - | - | |
| CIFAR-100 | VGGNet (Model-A) | 26.30 | 6.43 M | 81.10% | 4.93 | 25.86% | +0.08 |
| VGGNet (Model-B) | 26.21 | 6.43 M | 81.10% | 4.93 | 25.86% | +0.17 |
| Datasets | Method | Test Error (%) |
|---|---|---|
| Randomly merging neurons | 72.38 | |
| CIFAR-10 | Using k-means clustering | 6.35 |
| Using agglomerative clustering | 6.29 | |
| Randomly merging neurons | 87.53 | |
| CIFAR-100 | Using k-means clustering | 29.62 |
| Using agglomerative clustering | 26.93 |
| Datasets | Method | Parameters Pruned | Accuracy (%) |
|---|---|---|---|
| Network Slimming [63] | 88.5% | +0.14 | |
| CIFAR-10 | Pruning Filters [5] | 88.5% | -0.54 |
| Global Sparse Momentum [64] | 88.5% | +0.20 | |
| Our Method | 88.6% | +0.28 | |
| Network Slimming [63] | 76.0% | +0.22 | |
| CIFAR-100 | Pruning Filters [5] | 75.1% | -1.62 |
| Global Sparse Momentum [64] | 76.5% | +0.08 | |
| Our Method | 76.6% | +0.25 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.-N.; Liu, W.; Liu, X.; Zhong, G.; Roy, P.P.; Dong, J.; Huang, K. Compressing Deep Networks by Neuron Agglomerative Clustering. Sensors 2020, 20, 6033. https://doi.org/10.3390/s20216033
Wang L-N, Liu W, Liu X, Zhong G, Roy PP, Dong J, Huang K. Compressing Deep Networks by Neuron Agglomerative Clustering. Sensors. 2020; 20(21):6033. https://doi.org/10.3390/s20216033
Chicago/Turabian StyleWang, Li-Na, Wenxue Liu, Xiang Liu, Guoqiang Zhong, Partha Pratim Roy, Junyu Dong, and Kaizhu Huang. 2020. "Compressing Deep Networks by Neuron Agglomerative Clustering" Sensors 20, no. 21: 6033. https://doi.org/10.3390/s20216033
APA StyleWang, L.-N., Liu, W., Liu, X., Zhong, G., Roy, P. P., Dong, J., & Huang, K. (2020). Compressing Deep Networks by Neuron Agglomerative Clustering. Sensors, 20(21), 6033. https://doi.org/10.3390/s20216033








