Cache-Based Privacy Preserving Solution for Location and Content Protection in Location-Based Services
Abstract
1. Introduction
- (a)
- (b)
- (c)
- We provide the Cache-Based Privacy-Preserving (CBPP) solution for users in LBSs, which can protect the user’s location privacy and query privacy simultaneously. Meanwhile, we avoid the problem of TTP server by having users collaborate with each other in a mobile peer-to-peer (P2P) environment.
- We reduce the number of queries sent to the untrusted LBS by using the caching, which not only protects the user’s privacy effectively against the LBSs server, but also improves the user’s query efficiency and cache hit ratio.
- We analyze the availability and the security of proposed CBPP solution, which show that the proposed CBPP solution is a much more practical way to protect users’ privacy in LBSs.
2. Related Work
2.1. Present Research Situation
2.2. Most Related Work to Our Solution
3. Preliminaries
3.1. Motivation
3.2. Our Basic Idea
4. The Proposed Solution
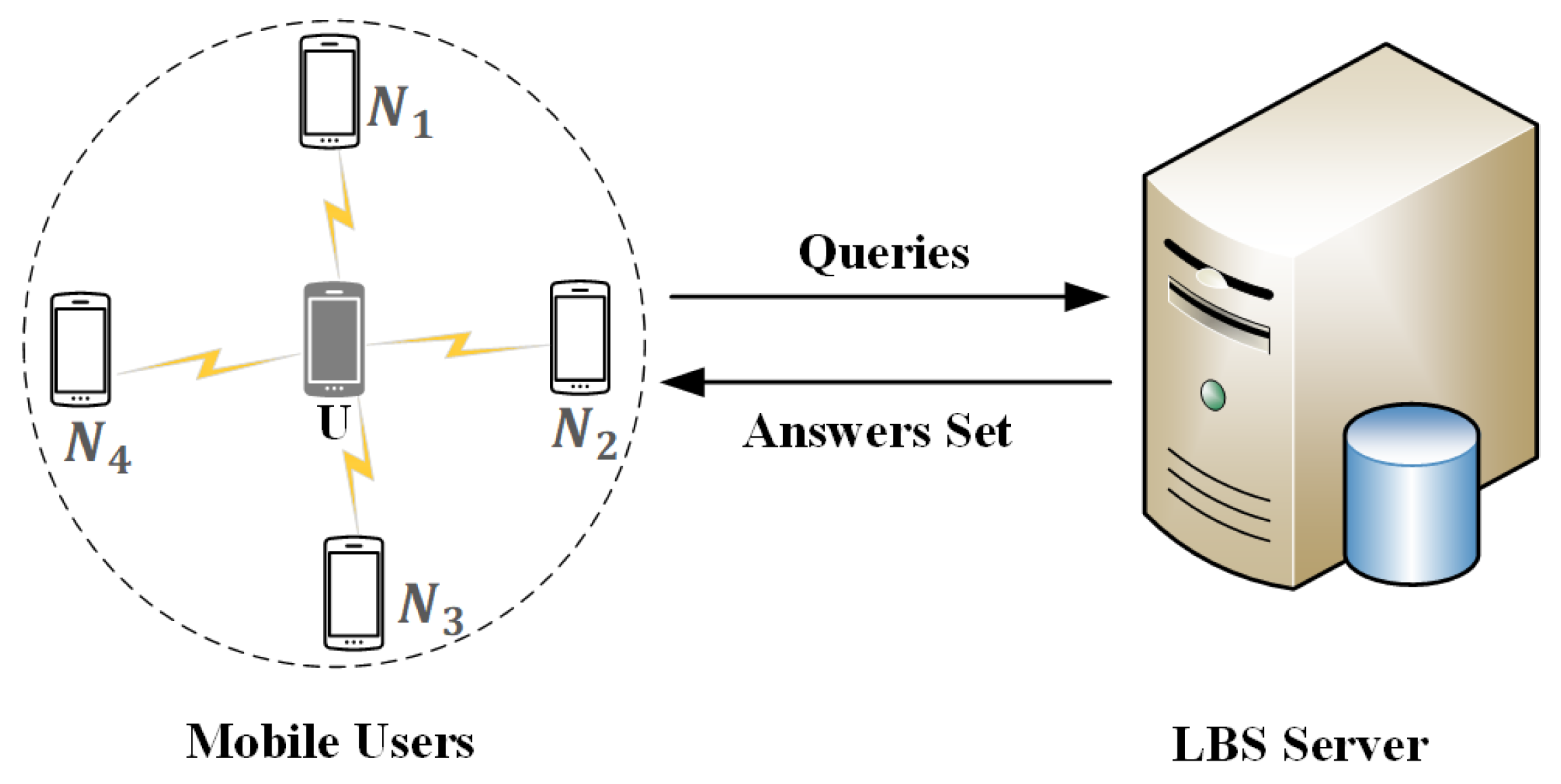
4.1. System Architecture and Threat Model
4.2. Proposed Cbpp Solution
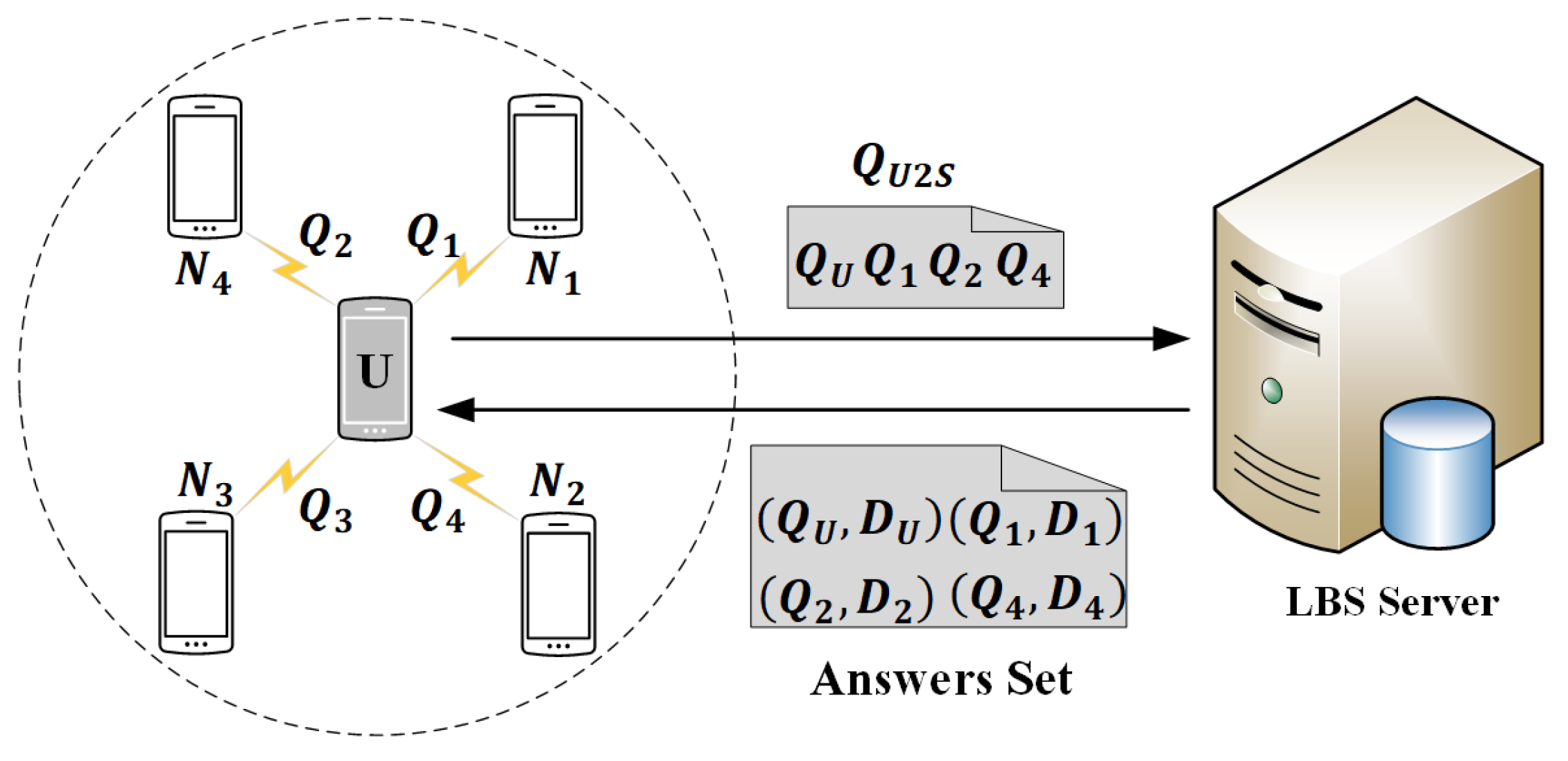
4.2.1. Query to Neighbors
| Algorithm 1: Query to Neighbors Algorithm. |
|
4.2.2. Query to LBS Server
| Algorithm 2: Query to LBS Server Algorithm. |
|
5. Solution Analysis
5.1. Security Analysis
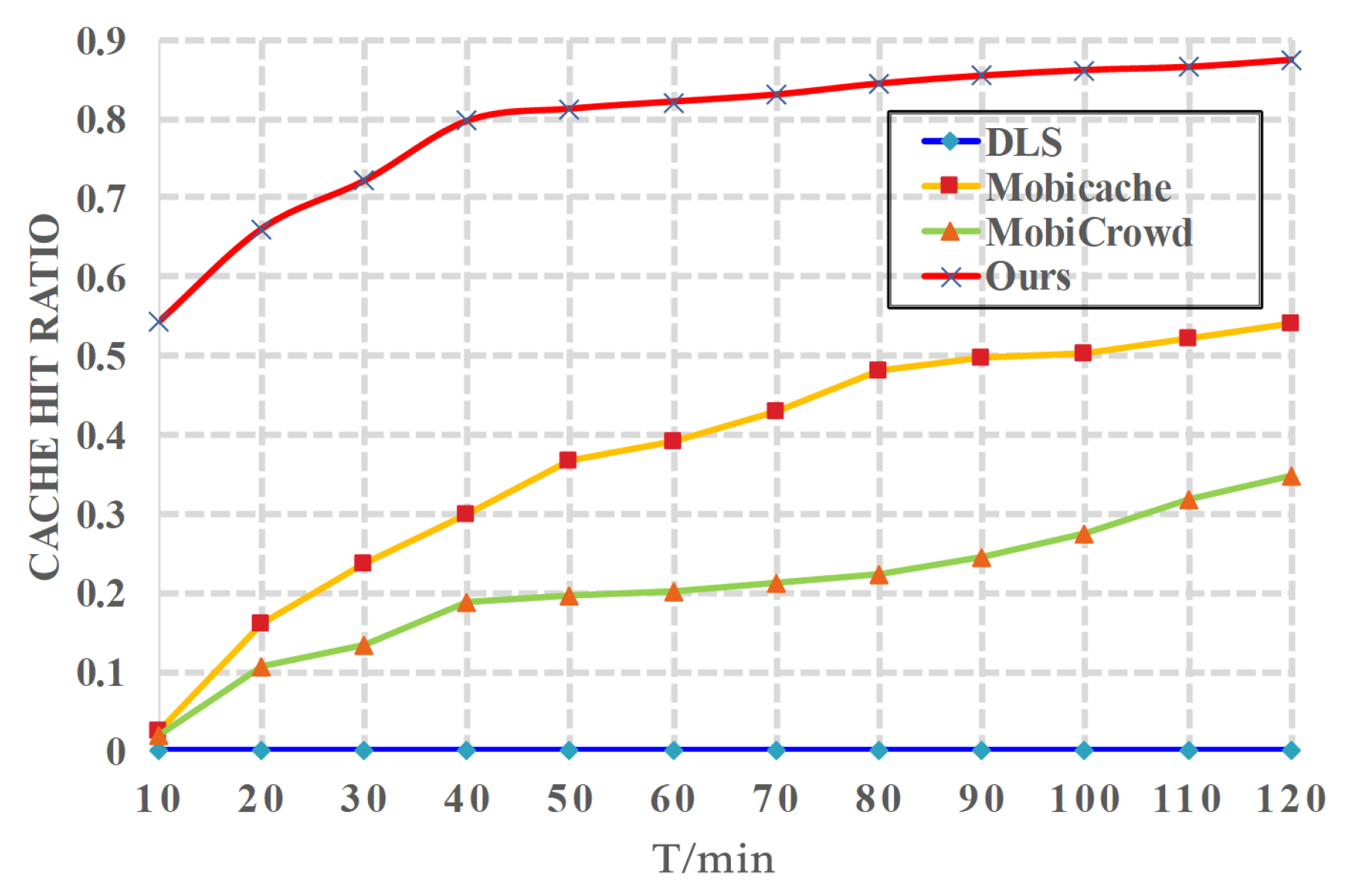
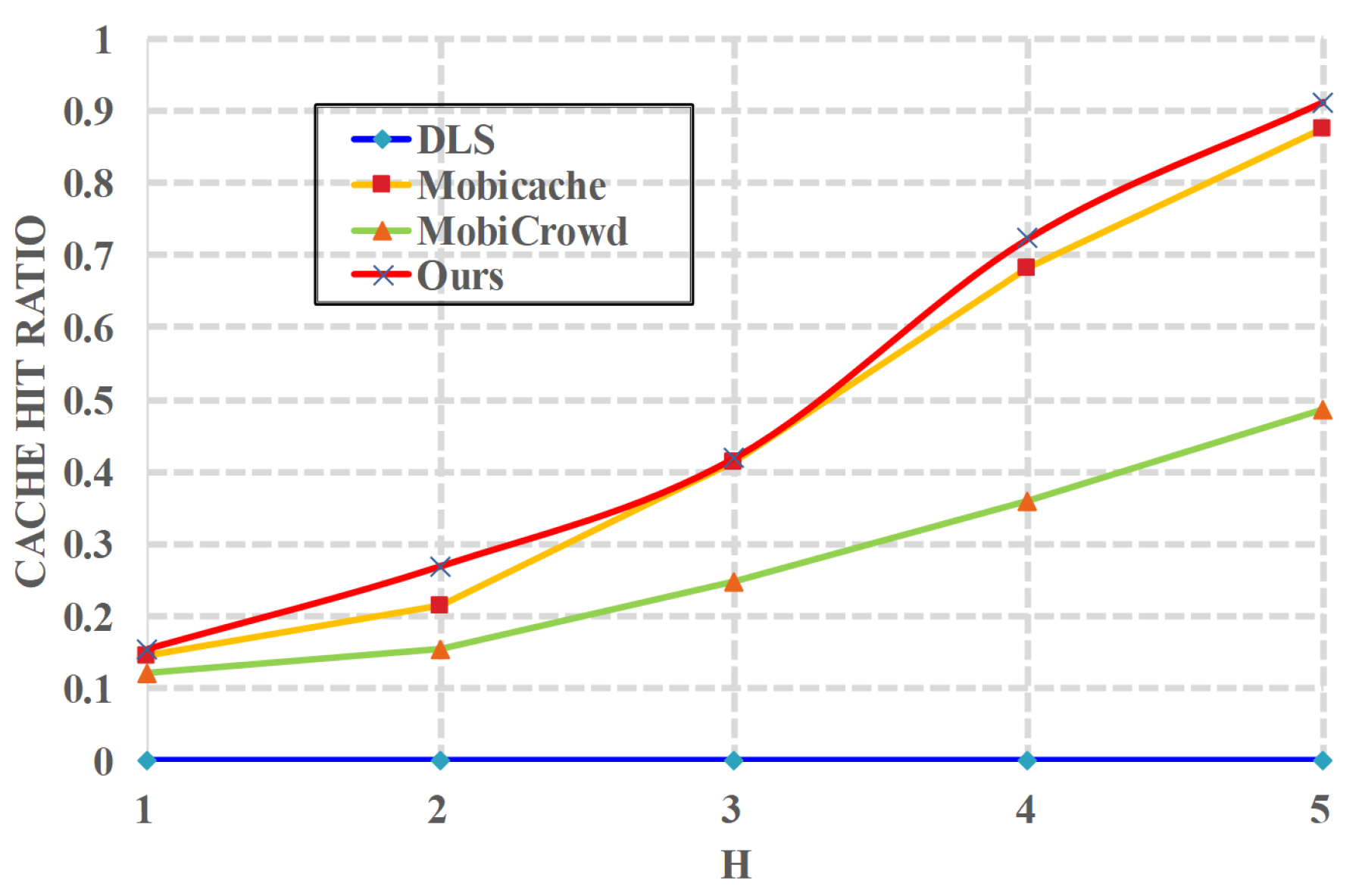
5.2. Cache Hit Ratio Analysis
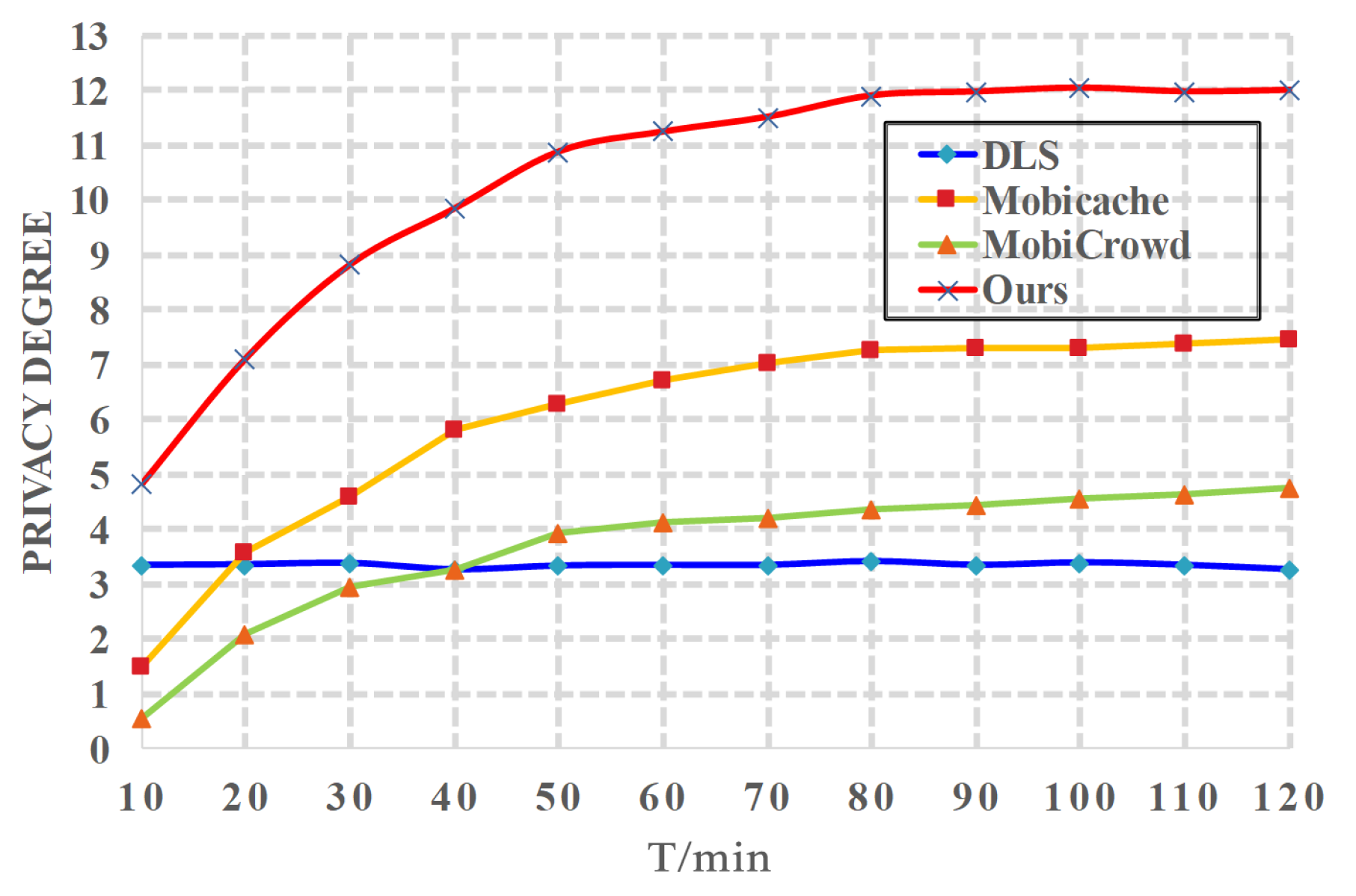
6. Performance Evaluation
6.1. Simulation Setup
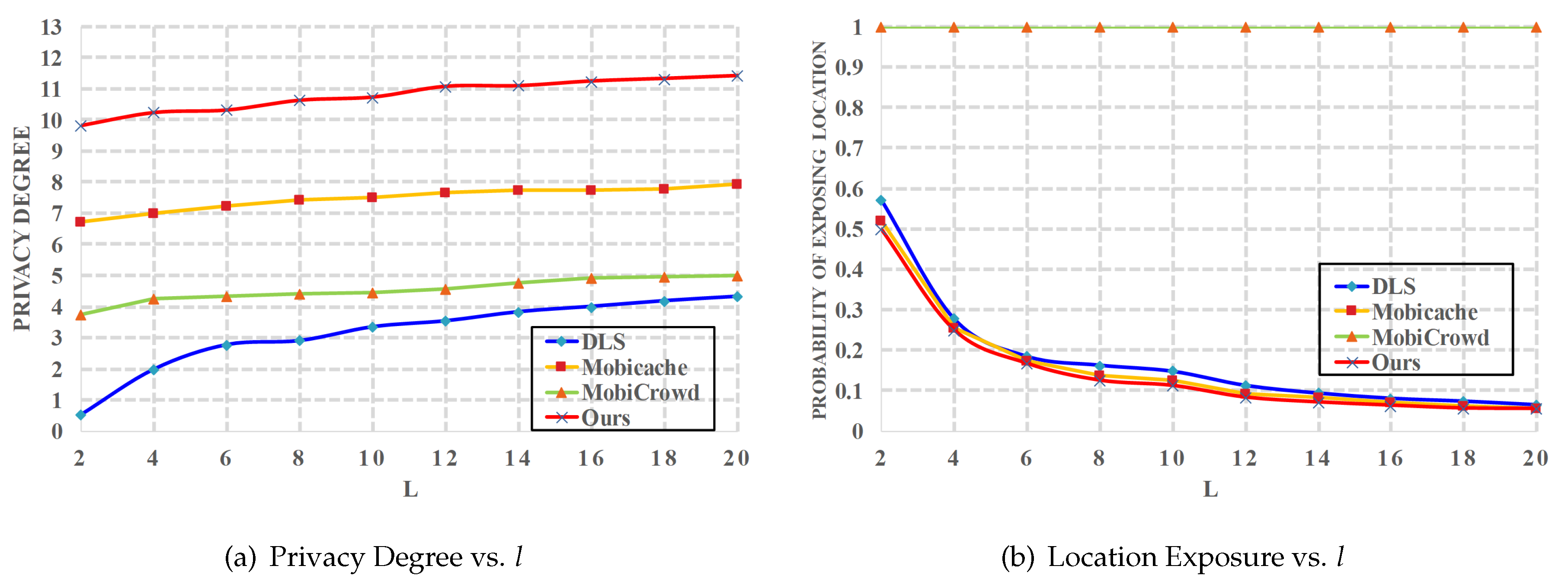
6.2. Evaluation Results
7. Conclusions and Future Work
7.1. Conclusions
7.2. Future Work
Author Contributions
Funding
Conflicts of Interest
References
- Niu, B.; Zhang, Z.; Li, X.; Li, H. Privacy-area aware dummy generation algorithms for location-based services. In Proceedings of the 2014 IEEE International Conference on Communications (ICC), Sydney, Australia, 10–14 June 2014; pp. 957–962. [Google Scholar]
- Niu, B.; Zhu, X.; Li, W.; Li, H.; Wang, Y.; Lu, Z. A personalized two-tier cloaking scheme for privacy-aware location-based services. In Proceedings of the 2015 International Conference on Computing, Networking and Communications (ICNC), Anaheim, CA, USA, 16–19 February 2015; pp. 94–98. [Google Scholar]
- Sun, G.; Sun, S.; Sun, J.; Yu, H.; Du, X.; Guizani, M. Security and privacy preservation in fog-based crowd sensing on the internet of vehicles. J. Netw. Comput. Appl. 2019, 134, 89–99. [Google Scholar] [CrossRef]
- Sun, G.; Song, L.; Liao, D.; Yu, H.; Chang, V. Towards privacy preservation for “check-in” services in location-based social networks. Inform. Sci. 2019, 481, 616–634. [Google Scholar] [CrossRef]
- Sun, G.; Liao, D.; Li, H.; Yu, H.; Chang, V. L2P2: A location-label based approach for privacy preserving in LBS. Future Gener. Comput. Syst. 2016, 74, 375–384. [Google Scholar] [CrossRef]
- Sun, G.; Chang, V.; Ramachandran, M.; Sun, Z.; Li, G.; Yu, H.; Liao, D. Efficient Location Privacy Algorithm for Internet of Things (IoT) Services and Applications. J. Netw. Comput. Appl. 2016, 89, 3–13. [Google Scholar] [CrossRef]
- Sun, G.; Xie, Y.; Liao, D.; Yu, H.; Chang, V. User-Defined Privacy Location-Sharing System in Mobile Online Social Networks. J. Netw. Comput. Appl. 2016, 86, 34–45. [Google Scholar] [CrossRef]
- Zhang, S.; Choo, K.K.R.; Qin, L.; Wang, G. Enhancing privacy through uniform grid and caching in location-based services. Future Gener. Comput. Syst. 2017, 86, S0167739X17312384. [Google Scholar] [CrossRef]
- Zhang, S.; Li, X.; Tan, Z.; Peng, T.; Wang, G. A caching and spatial K-anonymity driven privacy enhancement scheme in continuous location-based services. Future Gener. Comput. Syst. 2019, 94, 40–50. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, G.; Qin, L.; Abawajy, J.H. A trajectory privacy-preserving scheme based on query exchange in mobile social networks. Soft Comput. 2018, 22, 6121–6133. [Google Scholar] [CrossRef]
- Gruteser, M.; Grunwald, D. Anonymous usage of location-based services through spatial and temporal cloaking. In Proceedings of the 1st international conference on Mobile systems, applications and services, San Francisco, CA, USA, 5–8 May 2003; ACM: New York, NY, USA, 2003; pp. 31–42. [Google Scholar]
- Kido, H.; Yanagisawa, Y.; Satoh, T. An anonymous communication technique using dummies for location-based services. In Proceedings of the International Conference on Pervasive Services (ICPS’05), Santorini, Greece, 11–14 July 2005; IEEE: New York, NY, USA, 2005; pp. 88–97. [Google Scholar]
- Mokbel, M.F.; Chow, C.Y.; Aref, W.G. The new Casper: Query processing for location services without compromising privacy. In Proceedings of the 32nd international conference on Very large data bases, Seoul, Korea, 12–15 September 2006; pp. 763–774. [Google Scholar]
- Gedik, B.; Liu, L. Protecting location privacy with personalized k-anonymity: Architecture and algorithms. IEEE Trans. Mob. Comput. 2008, 7, 1–18. [Google Scholar] [CrossRef]
- Chow, C.Y.; Mokbel, M.F.; Liu, X. A peer-to-peer spatial cloaking algorithm for anonymous location-based service. In Proceedings of the ACM International Symposium on Advances in Geographic Information Systems, Arlington, VA, USA, 10–11 November 2006; pp. 171–178. [Google Scholar]
- Hu, H.; Xu, J. Non-exposure location anonymity. In Proceedings of the 2009 IEEE 25th International Conference on Data Engineering, Shanghai, China, 29 March–2 April 2009; pp. 1120–1131. [Google Scholar]
- Chow, C.Y.; Mokbel, M.F.; Liu, X. Spatial cloaking for anonymous location-based services in mobile peer-to-peer environments. GeoInformatica 2011, 15, 351–380. [Google Scholar] [CrossRef]
- Man, L.Y.; Jensen, C.S.; Huang, X.; Lu, H. SpaceTwist: Managing the Trade-Offs Among Location Privacy, Query Performance, and Query Accuracy in Mobile Services. In Proceedings of the IEEE International Conference on Data Engineering, Vancouver, BC, Canada, 21–24 August 2008; pp. 366–375. [Google Scholar]
- Lu, H.; Jensen, C.S.; Man, L.Y. PAD: Privacy-area aware, dummy-based location privacy in mobile services. In Proceedings of the ACM International Workshop on Data Engineering for Wireless and Mobile Access, Mobide 2008, Vancouver, BC, Canada, 13 June 2008; pp. 16–23. [Google Scholar]
- Niu, B.; Li, Q.; Zhu, X.; Cao, G.; Li, H. Achieving k-anonymity in privacy-aware location-based services. In Proceedings of the IEEE INFOCOM 2014-IEEE Conference on Computer Communications, Vancouver, BC, Canada, 27 April–25 May 2014; pp. 754–762. [Google Scholar]
- Zhu, X.; Chi, H.; Niu, B.; Zhang, W.; Li, Z.; Li, H. MobiCache: When k-anonymity meets cache. In Proceedings of the Global Communications Conference, Austin, TX, USA, 8–12 December 2014; pp. 820–825. [Google Scholar]
- Shokri, R.; Theodorakoupolos, G.; Papadimitratos, P.; Kazemi, E.; Hubaux, J.P. Hiding in the Mobile Crowd: Location Privacy through Collaboration. IEEE Trans. Dependable Secur. Comput. 2014, 11, 266–279. [Google Scholar]
- Niu, B.; Li, Q.; Zhu, X.; Li, H. A fine-grained spatial cloaking scheme for privacy-aware users in Location-Based Services. In Proceedings of the International Conference on Computer Communication and Networks, Shanghai, China, 4–7 August 2014; pp. 1–8. [Google Scholar]
- Pingley, A.; Zhang, N.; Fu, X.; Choi, H.A.; Subramaniam, S.; Zhao, W. Protection of query privacy for continuous location based services. Proc. IEEE INFOCOM 2011, 8, 1710–1718. [Google Scholar]
- Peng, T.; Liu, Q.; Wang, G. Enhanced Location Privacy Preserving Scheme in Location-Based Services. IEEE Syst. J. 2014, 1–12. [Google Scholar] [CrossRef]
- Peng, T.; Liu, Q.; Wang, G.; Xiang, Y. Privacy Preserving Scheme for Location and Content Protection in Location-Based Services; Springer International Publishing: New York, NY, USA, 2016; pp. 26–38. [Google Scholar]
- Qiu, Y.; Liu, Y.; Li, X.; Chen, J. A Novel Location Privacy-Preserving Approach Based on Blockchain. Sensors 2020, 20, 3519. [Google Scholar] [CrossRef] [PubMed]
- Daniel, K.; Baden, P.; Fakhrul, A.; Lai, M.K. Falcon: Fused Application of Light based positioning Coupled with Onboard Network localization. IEEE Access 2018, 6, 36155–36167. [Google Scholar]
- Amoretti, M.; Brambilla, G.; Medioli, F.; Zanichelli, F. Blockchain-Based Proof of Location. In Proceedings of the 2018 IEEE International Conference on Software Quality, Reliability and Security Companion (QRS-C), Lisbon, Portugal, 16–20 July 2018. [Google Scholar]
- Saia, R.; Carta, S.; Reforgiato Recupero, D.; Fenu, G. Internet of Entities (IoE): A Blockchain-based Distributed Paradigm for Data Exchange Between Wireless-based Devices. arXiv 2018, arXiv:1808.08809. [Google Scholar]
- Zhang, S.; Mao, X.; Choo, K.K.R.; Peng, T.; Wang, G. A Trajectory Privacy-preserving Scheme Based on a Dual-K Mechanism for Continuous Location-based Services. Inf. Sci. 2019, 527, 406–419. [Google Scholar] [CrossRef]
- Habibzadeh, H.; Nussbaum, B.H.; Anjomshoa, F.; Kantarci, B.; Soyata, T. A survey on cybersecurity, data privacy, and policy issues in cyber-physical system deployments in smart cities. Sustain. Cities Soc. 2019, 50. [Google Scholar] [CrossRef]
- Yang, Y.; Zheng, X.; Guo, W.; Liu, X.; Chang, V. Privacy-preserving smart IoT-based healthcare big data storage and self-adaptive access control system. Inf. Sci. 2019, 479, 567–592. [Google Scholar] [CrossRef]
- Challa, S.; Das, A.K.; Gope, P.; Kumar, N.; Wu, F.; Vasilakos, A.V. Design and analysis of authenticated key agreement scheme in cloud-assisted cyber–physical systems. Future Gener. Comput. Syst. 2020, 108, 1267–1286. [Google Scholar] [CrossRef]
- Machanavajjhala, A.; Kifer, D.; Gehrke, J. L-diversity:Privacy beyond k-anonymity. Acm Trans. Knowl. Discov. Data 2007, 1, 3. [Google Scholar]
- Amini, S.; Lindqvist, J.; Hong, J.I.; Lin, J.; Toch, E.; Sadeh, N.M. Cach: Caching location-enhanced content to improve user privacy. In Proceedings of the International Conference on Mobile Systems, Seoul, Korea, 17–21 June 2010. [Google Scholar]
- Stewart, R.R.; Xie, Q. Stream Control Transmission Protocol (SCTP):A Reference Guide: A Reference Guide; Addison-Wesley Longman Publishing Co., Inc.: Boston, MA, USA, 2001. [Google Scholar]
- Chow, C.Y.; Leong, H.; Chan, A. Distributed group-based cooperative caching in a mobile broadcast environment. In Proceedings of the 6th International Conference on Mobile Data Management (MDM 2005), Ayia Napa, Cyprus, 9–13 May 2005; pp. 97–106. [Google Scholar] [CrossRef]
- Zimmermann, R.; Wang, H.; Nguyen, T. ANNATTO: Adaptive nearest neighbor queries in travel time networks. In Proceedings of the 7th International Conference on Mobile Data Management (MDM’06), Nara, Japan, 10–12 May 2006. [Google Scholar] [CrossRef]
- Papadopouli, M.; Schulzrinne, H. Effects of power conservation, wireless coverage and cooperation on data dissemination among mobile devices. In Proceedings of the Symposium on Mobile Ad Hoc Networking and Computing (MobiHoc01), Long Beach, CA, USA, 4–5 October 2001; pp. 117–127. [Google Scholar] [CrossRef][Green Version]


| Notation | Meaning |
|---|---|
| U | User who submits query to neighbors or LBS server |
| Identity (pseudonym) of the node in P2P network | |
| Location of the node | |
| q | Query interest of the node |
| h | Number of hops |
| Query sent to Neighbor by the user | |
| Query sent to LBS server by the user | |
| l | Anonymity level |
| Z | Set of queries not answered by U |
| N | Neighbor of the user |
| M | Message sent to U by his neighboring peers |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cui, Y.; Gao, F.; Li, W.; Shi, Y.; Zhang, H.; Wen, Q.; Panaousis, E. Cache-Based Privacy Preserving Solution for Location and Content Protection in Location-Based Services. Sensors 2020, 20, 4651. https://doi.org/10.3390/s20164651
Cui Y, Gao F, Li W, Shi Y, Zhang H, Wen Q, Panaousis E. Cache-Based Privacy Preserving Solution for Location and Content Protection in Location-Based Services. Sensors. 2020; 20(16):4651. https://doi.org/10.3390/s20164651
Chicago/Turabian StyleCui, Yuanbo, Fei Gao, Wenmin Li, Yijie Shi, Hua Zhang, Qiaoyan Wen, and Emmanouil Panaousis. 2020. "Cache-Based Privacy Preserving Solution for Location and Content Protection in Location-Based Services" Sensors 20, no. 16: 4651. https://doi.org/10.3390/s20164651
APA StyleCui, Y., Gao, F., Li, W., Shi, Y., Zhang, H., Wen, Q., & Panaousis, E. (2020). Cache-Based Privacy Preserving Solution for Location and Content Protection in Location-Based Services. Sensors, 20(16), 4651. https://doi.org/10.3390/s20164651





