Weber Texture Local Descriptor for Identification of Group-Housed Pigs
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Setup
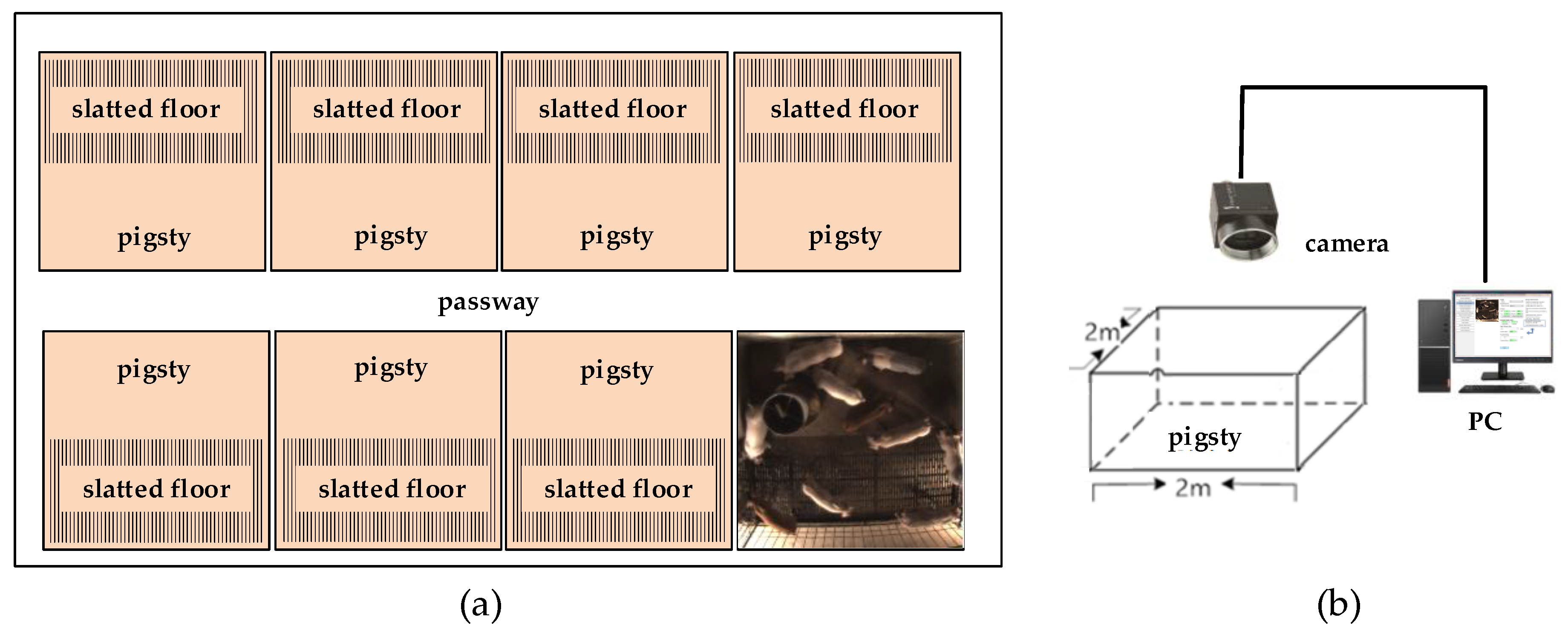
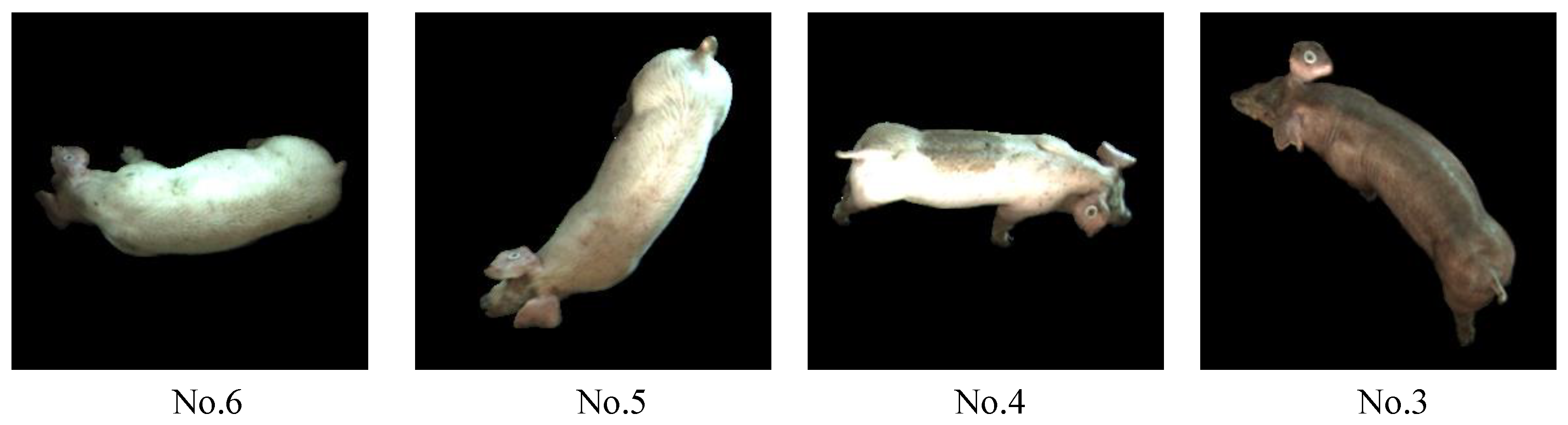
2.1.1. Animals and Farm
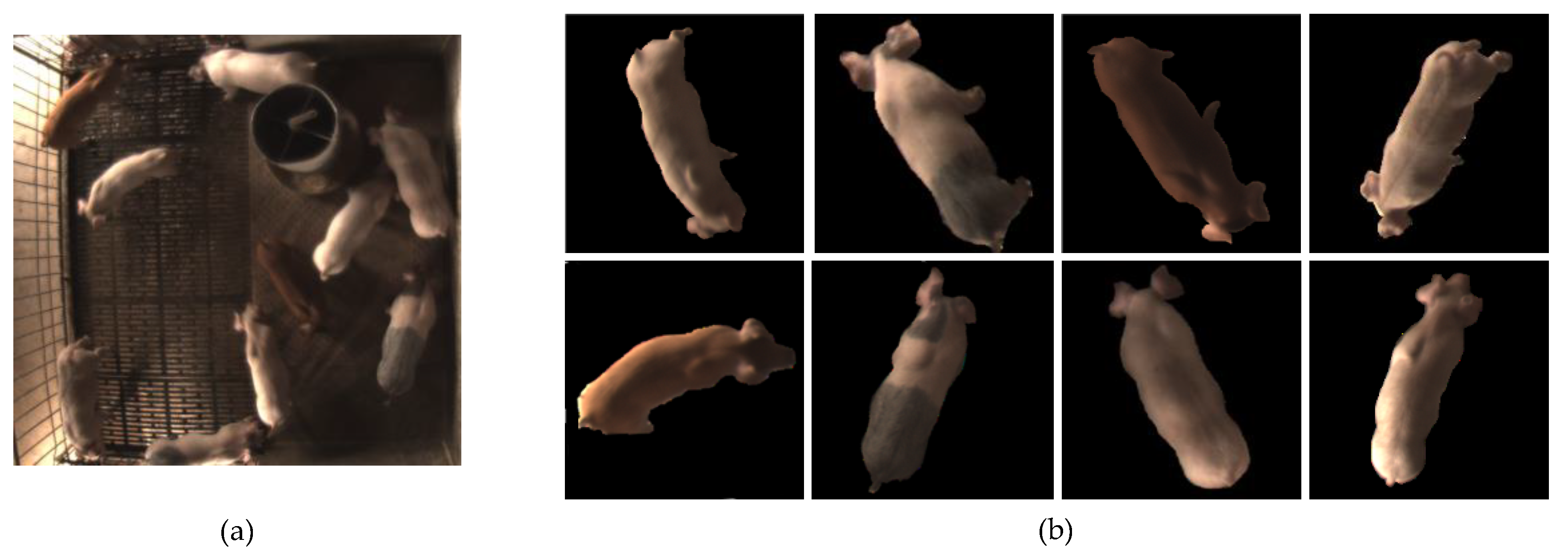
2.1.2. Image Collection
2.1.3. Image Preprocessing
2.1.4. Datasets
2.2. Weber Local Descriptor (WLD)
2.3. Weber Texture Local Descriptor (WTLD)
- 1.
- The differential excitation of each pixel is calculated by:
- 2.
- In order to extract the local multi-directional information, the multi-directional masks are used. The original image is convoluted with the multi-directional masks, as shown in Equation (5):
- 3.
- The difference excitation of the original WLD only calculates the difference between the central pixel and its neighborhood. Intensity variations of pixels in the neighborhood are not considered, which resulting in an insufficient expression of local structural information. To solve this problem, the gray intensity difference between pixels in the main direction is calculated, as shown in Equation (8):
3. Experimental Results and Analysis
3.1. Comparative Experiment and Analysis of WLD and WTLD
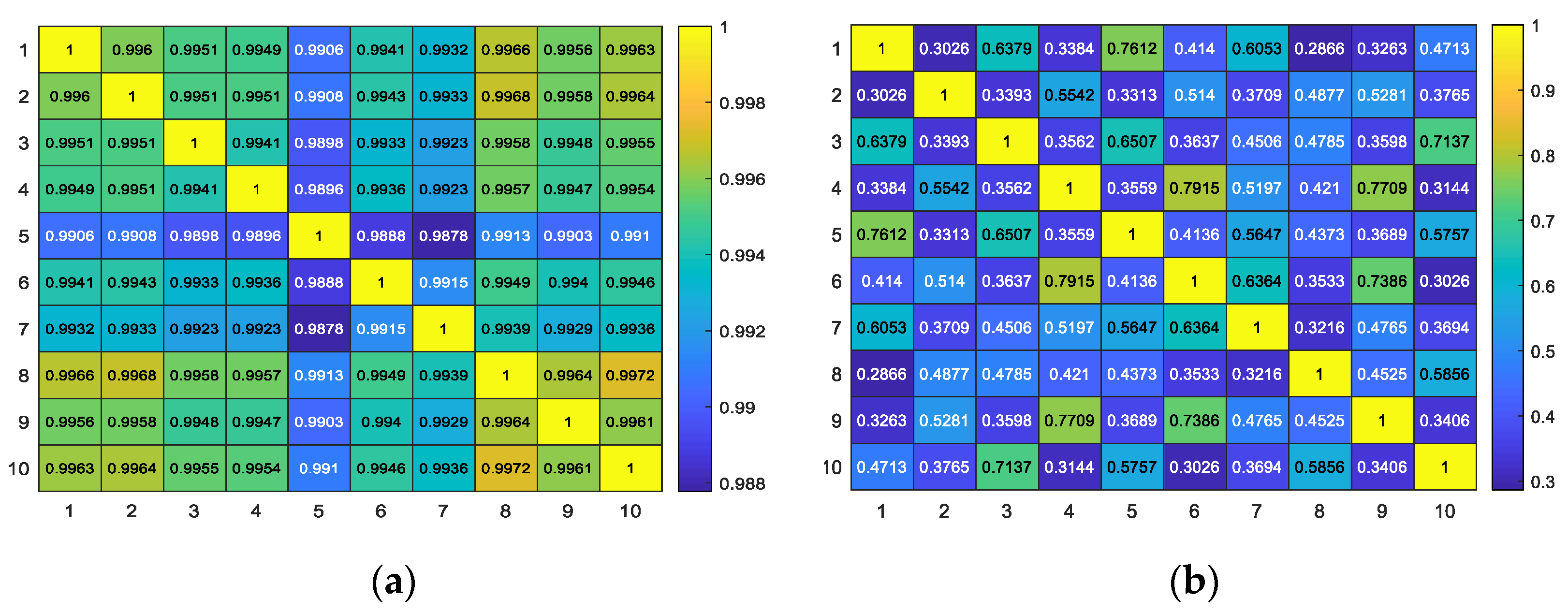
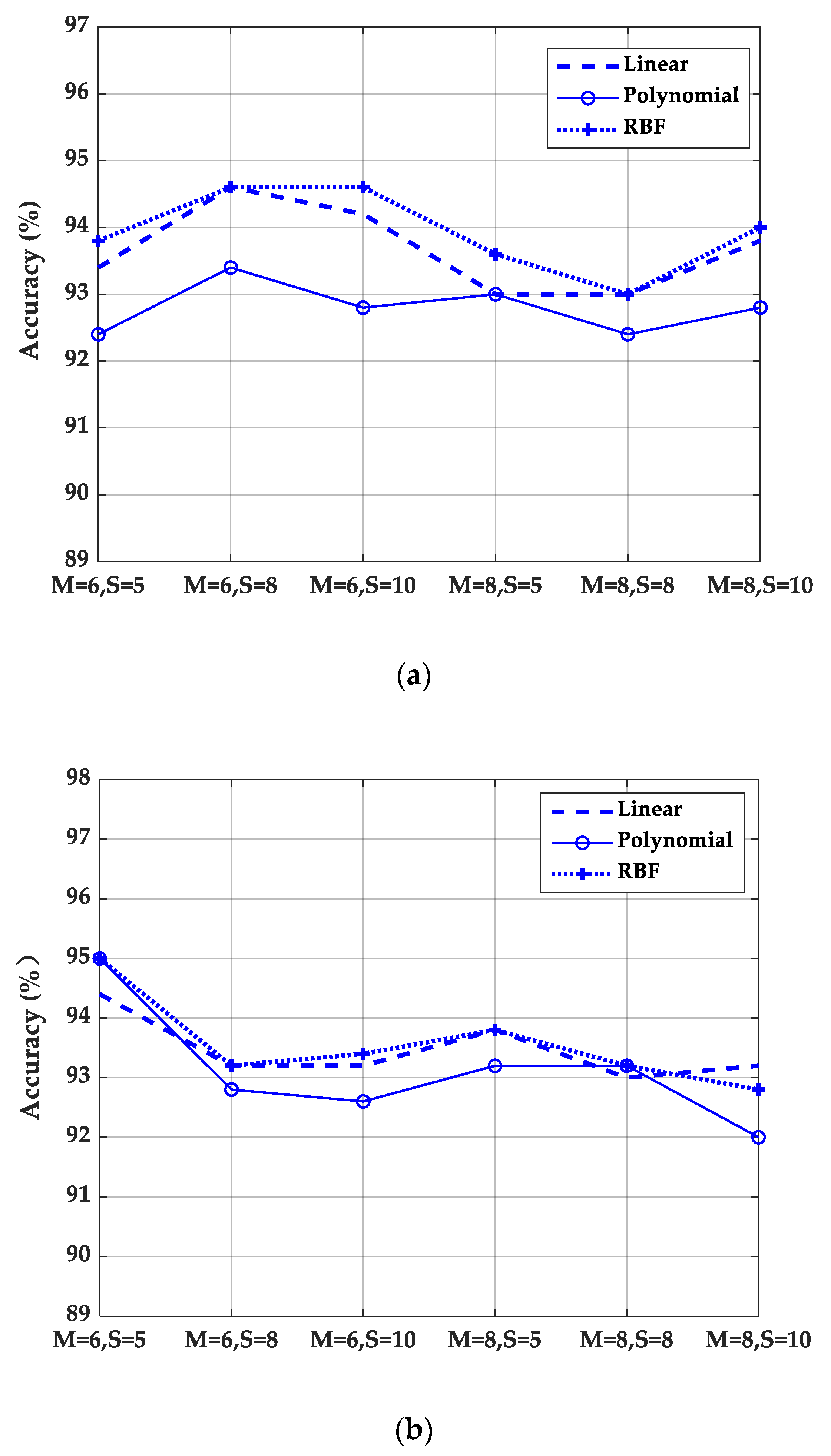
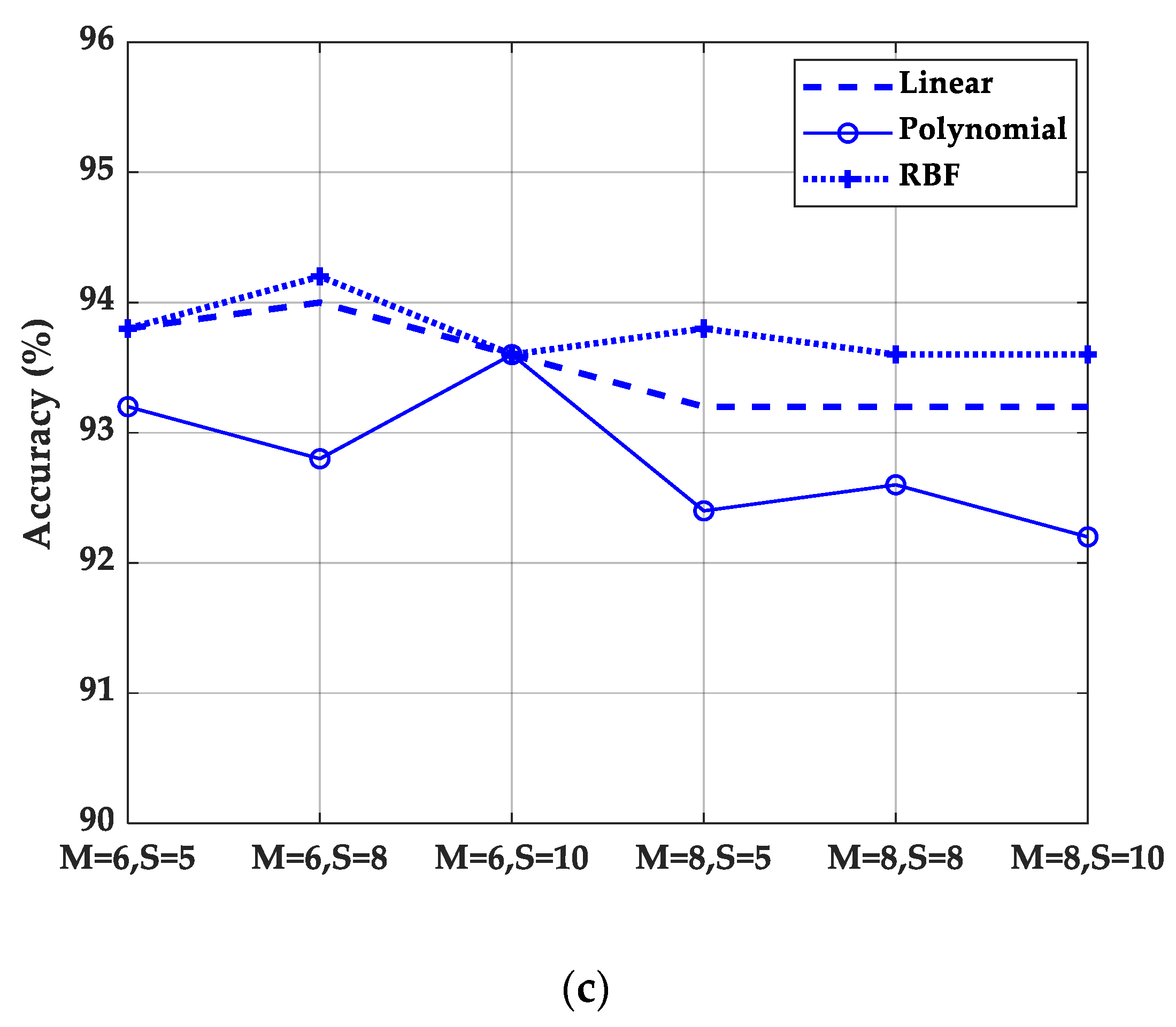
3.2. Experimental Results of Different Multi-Directional Masks and Mask Sizes
3.3. Experimental Results of Different Quantization Parameters
3.4. Performance Comparison Based on Different Local Descriptors
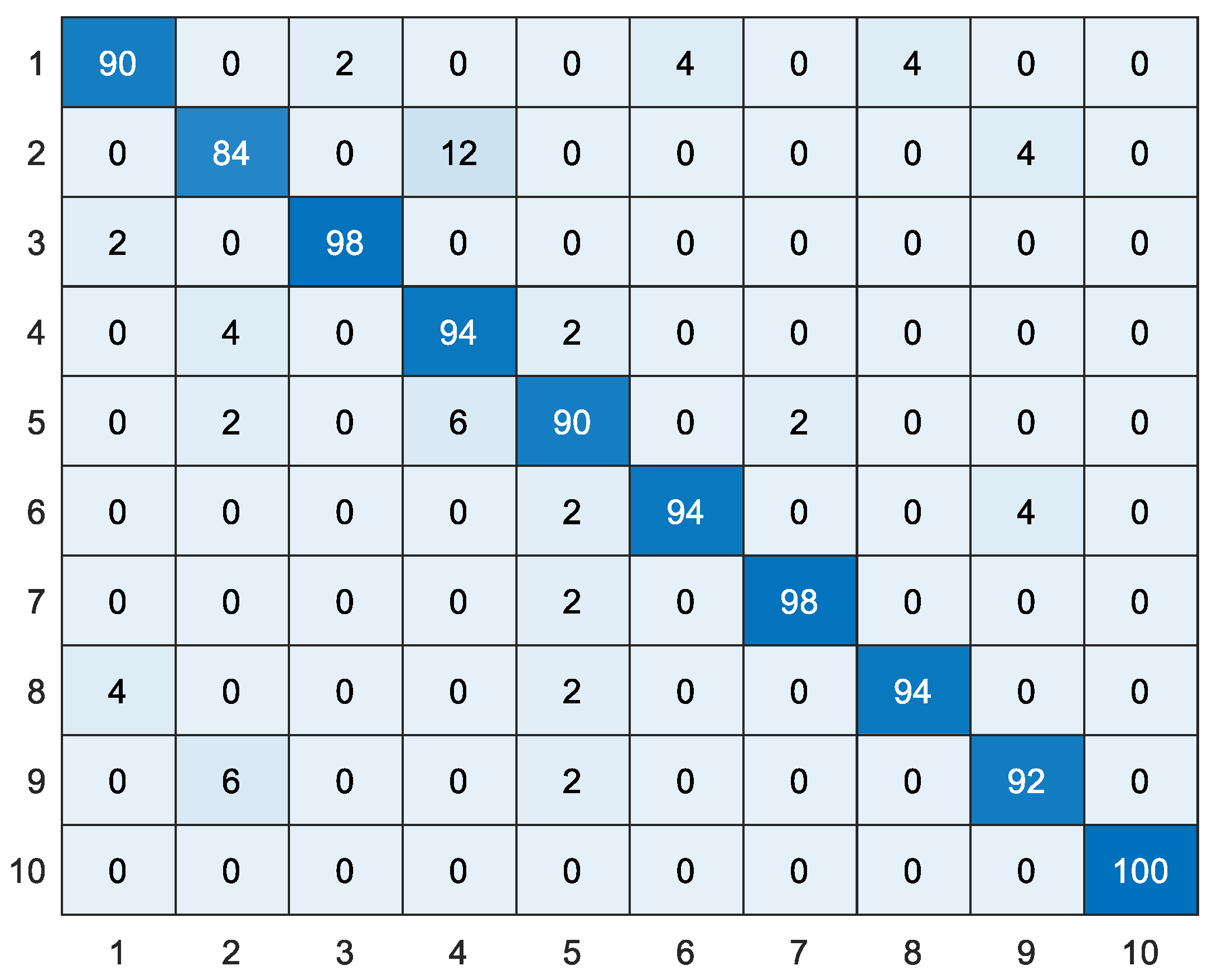
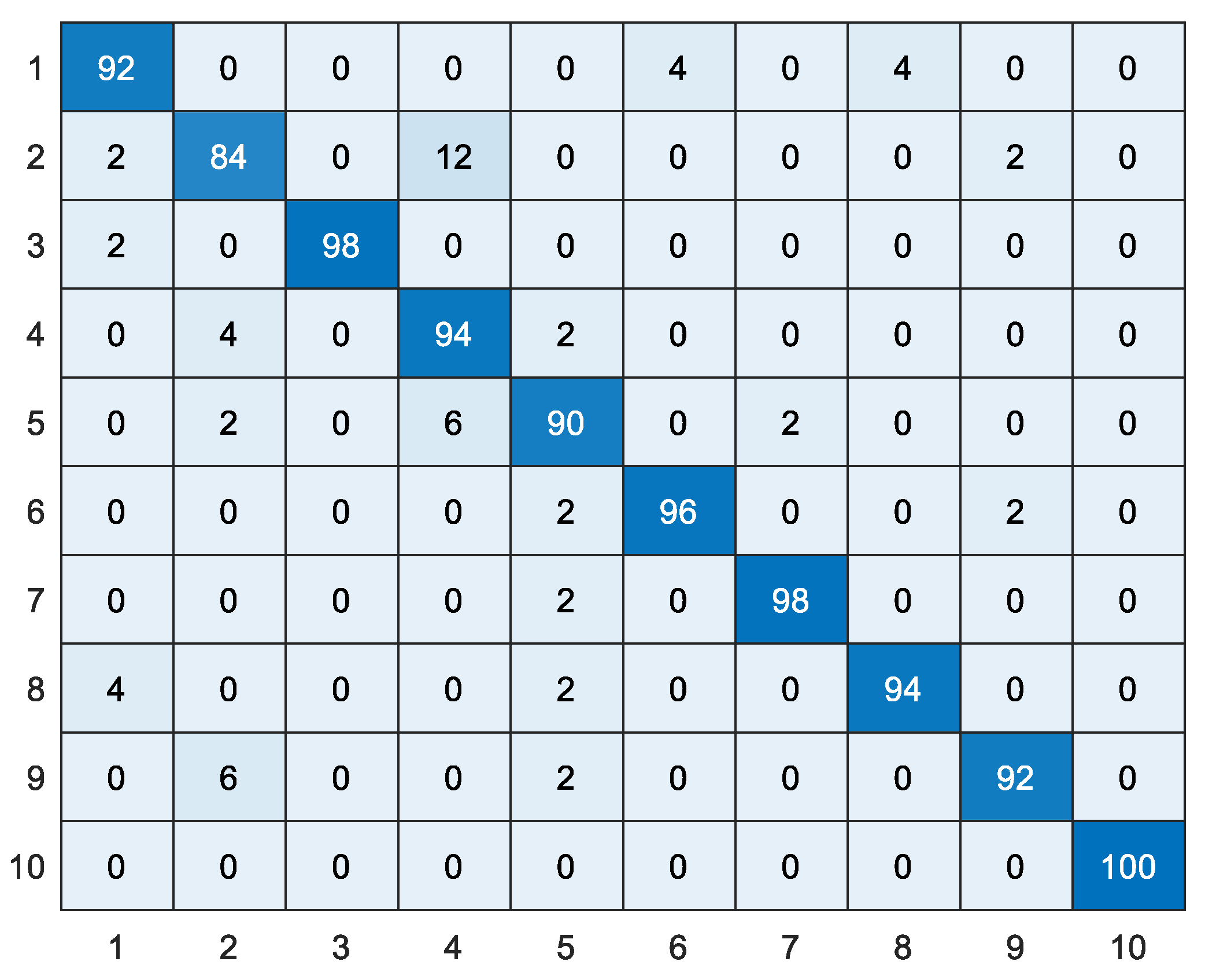
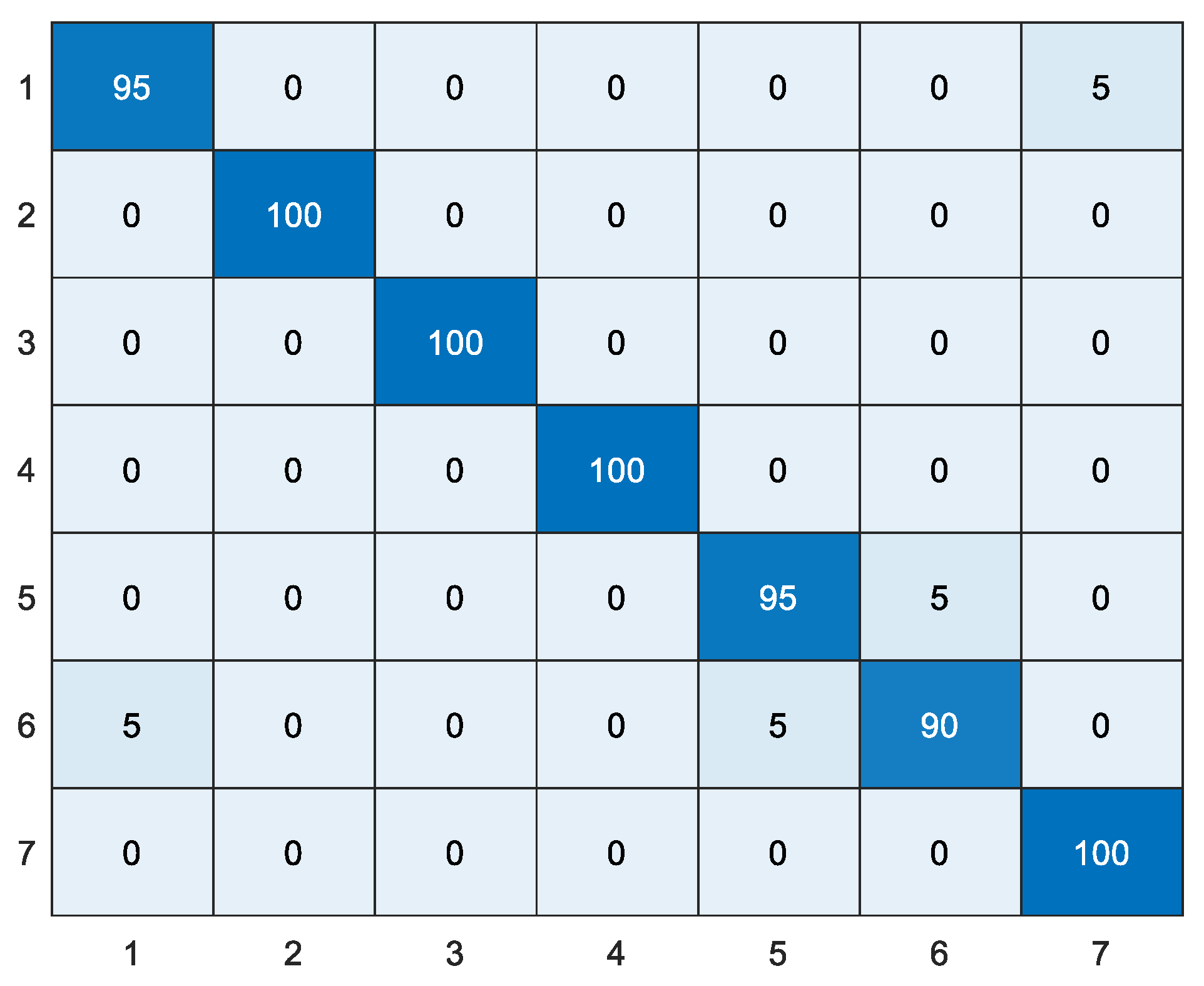
3.5. Results of WTLD Applied to Dataset 1
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Matthews, S.G.; Miller, A.L.; Clapp, J.; Plötz, T.; Kyriazakis, I. Early detection of health and welfare compromises through automated detection of behavioural changes in pigs. Vet. J. 2016, 217, 43–51. [Google Scholar] [CrossRef] [PubMed]
- Nasirahmadi, A.; Edwards, S.A.; Matheson, S.M.; Sturm, B. Using automated image analysis in pig behavioural research: Assessment of the influence of enrichment substrate provision on lying behaviour. Appl. Anim. Behav. Sci. 2017, 196, 30–35. [Google Scholar] [CrossRef]
- Guarino, M.; Jans, P.; Costa, A.; Aerts, J.-M.; Berckmans, D. Field test of algorithm for automatic cough detection in pig houses. Comput. Electron. Agric. 2008, 62, 22–28. [Google Scholar] [CrossRef]
- Zhao, J.; Li, X.; Liu, W.; Gao, Y.; Lei, M.; Tan, H.; Yang, D. DNN-HMM based acoustic model for continuous pig cough sound recognition. Int. J. Agric. Biol. Eng. 2020, 13, 186–193. [Google Scholar] [CrossRef]
- Kashiha, M.; Bahr, C.; Haredasht, S.A.; Ott, S.; Moons, C.P.; Niewold, T.A.; Ödberg, F.O.; Berckmans, D. The automatic monitoring of pigs water use by cameras. Comput. Electron. Agric. 2013, 90, 164–169. [Google Scholar] [CrossRef]
- Zhu, W.-X.; Guo, Y.; Jiao, P.-P.; Ma, C.-H.; Chen, C. Recognition and drinking behaviour analysis of individual pigs based on machine vision. Livest. Sci. 2017, 205, 129–136. [Google Scholar] [CrossRef]
- Yang, Q.; Xiao, D.; Lin, S. Feeding behavior recognition for group-housed pigs with the Faster R-CNN. Comput. Electron. Agric. 2018, 155, 453–460. [Google Scholar] [CrossRef]
- Matthews, S.G.; Miller, A.L.; PlÖtz, T.; Kyriazakis, I. Automated tracking to measure behavioural changes in pigs for health and welfare monitoring. Sci. Rep. 2017, 7, 17582. [Google Scholar] [CrossRef]
- Voulodimos, A.S.; Patrikakis, C.Z.; Sideridis, A.B.; Ntafis, V.A.; Xylouri, E.M. A complete farm management system based on animal identification using RFID technology. Comput. Electron. Agric. 2010, 70, 380–388. [Google Scholar] [CrossRef]
- Ruiz-Garcia, L.; Lunadei, L. The role of RFID in agriculture: Applications, limitations and challenges. Comput. Electron. Agric. 2011, 79, 42–50. [Google Scholar] [CrossRef]
- Fosgate, G.T.; Adesiyun, A.; Hird, D. Ear-tag retention and identification methods for extensively managed water buffalo (Bubalus bubalis) in Trinidad. Prev. Vet. Med. 2006, 73, 287–296. [Google Scholar] [CrossRef] [PubMed]
- Jover, J.N.; Alcañiz-Raya, M.; Gomez, V.; Balasch, S.; Moreno, J.; Colomer, V.G.; Torres, A. An automatic colour-based computer vision algorithm for tracking the position of piglets. Span. J. Agric. Res. 2009, 7, 535. [Google Scholar] [CrossRef]
- Kashiha, M.; Bahr, C.; Ott, S.; Moons, C.P.; ANiewold, T.; Ödberg, F.; Berckmans, D. Automatic identification of marked pigs in a pen using image pattern recognition. Comput. Electron. Agric. 2013, 93, 111–120. [Google Scholar] [CrossRef]
- Liakos, K.G.; Busato, P.; Moshou, D.; Pearson, S.; Bochtis, D. Machine learning in agriculture: A review. Sensors 2018, 18, 2674. [Google Scholar] [CrossRef] [PubMed]
- Ibrahim, M.E.; Hazem, M.E.; Hagar, M.E. A new muzzle classification model using decision tree classifier. Int. J. Electron. Inf. Eng. 2017, 6, 12–24. [Google Scholar]
- Trokielewicz, M.; Szadkowski, M. Iris and periocular recognition in Arabian race horses using deep convolutional neural networks. In Proceedings of the 2017 IEEE International Joint Conference on Biometrics (IJCB), Denver, CO, USA, 1–4 October 2017; pp. 510–516. [Google Scholar]
- Zhao, K.X.; He, D.J. Recognition of individual dairy cattle based on convolutional neural networks. Trans. Chin. Soc. Agric. Eng. 2015, 31, 181–187. [Google Scholar]
- Shen, W.; Hu, H.; Dai, B.; Dar, B.; Wei, X.; Sun, J.; Jiang, L.; Sun, Y. Individual identification of dairy cows based on convolutional neural networks. Multimed. Tools Appl. 2020, 79, 14711–14724. [Google Scholar] [CrossRef]
- Hansen, M.; Smith, M.L.; Smith, L.N.; Salter, M.G.; Baxter, E.M.; Farish, M.; Grieve, B. Towards on-farm pig face recognition using convolutional neural networks. Comput. Ind. 2018, 98, 145–152. [Google Scholar] [CrossRef]
- Marsot, M.; Mei, J.; Shan, X.; Ye, L.; Feng, P.; Yan, X.; Li, C.; Zhao, Y. An adaptive pig face recognition approach using Convolutional Neural Networks. Comput. Electron. Agric. 2020, 173, 105386. [Google Scholar] [CrossRef]
- Yuetong, L.; Lanying, Z.; Wei, J.; Jing, G.; Feng, X. Palmprint recognition method based on line feature Weber local descriptor. J. Image Graph. 2016, 21, 235–244. [Google Scholar]
- Turan, C.; Lam, K.-M. Histogram-based local descriptors for facial expression recognition (FER): A comprehensive study. J. Vis. Commun. Image Rep. 2018, 55, 331–341. [Google Scholar] [CrossRef]
- Huang, W.; Zhu, W.; Ma, C.; Guo, Y.; Chen, C. Identification of group-housed pigs based on Gabor and Local Binary Pattern features. Biosyst. Eng. 2018, 166, 90–100. [Google Scholar] [CrossRef]
- Guo, Y.; Zhu, W.-X.; Jiao, P.-P.; Ma, C.-H.; Yang, J.-J. Multi-object extraction from topview group-housed pig images based on adaptive partitioning and multilevel thresholding segmentation. Biosyst. Eng. 2015, 135, 54–60. [Google Scholar] [CrossRef]
- Jain, A.K. Fundamentals of Digital Image Processing; Prentice Hall: Upper Saddle River, NJ, USA, 1989. [Google Scholar]
- Chen, J.; Shan, S.; He, C.; Zhao, G.; Pietikäinen, M.; Chen, X.; Gao, W. WLD: A Robust Local Image Descriptor. IEEE Trans. Pattern Anal. Mach. Intell. 2009, 32, 1705–1720. [Google Scholar] [CrossRef]
- Chang, C.C.; Lin, C.J. LIBSVM: A library for support vector machines. ACM Trans. Intell. Syst. Technol. 2011, 2, 27. [Google Scholar] [CrossRef]
- Rivera, A.R.; Castillo, J.R.; Chae, O.O. Local directional number pattern for face analysis: Face and expression recognition. IEEE Trans. Image Process 2012, 22, 1740–1752. [Google Scholar] [CrossRef]
- Zhou, L.; Wang, H. Local gradient increasing pattern for facial expression recognition. In Proceedings of the 19th IEEE International Conference on Image Processing, Orlando, FL, USA, 30 September–3 October 2012; pp. 2601–2604. [Google Scholar]
- Ojala, T.; Pietikäinen, M.; Mäenpää, T. Multiresolution gray-scale and rotation invariant texture classification with local binary patterns. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 971–987. [Google Scholar] [CrossRef]
- Mohammad, T.; Ali, M.L. Robust facial expression recognition based on Local Monotonic Pattern (LMP). In Proceedings of the 2011 14th International Conference on Computer and Information Technology(ICCIT) Institute of Electrical and Electronics Engineers (IEEE), Dhaka, Bangladesh, 22–24 December 2011; pp. 572–576. [Google Scholar]
- Faisal, A.; Emam, H. Automated facial expression recognition using gradient-based ternary texture patterns. Chin. J. Eng. 2013, 2, 1–8. [Google Scholar]
- Islam, M.S.; Auwatanamo, S. Facial expression recognition using local arc pattern. Trends Appl. Sci. Res. 2014, 9, 113–120. [Google Scholar] [CrossRef]
- Yang, B.-Q.; Zhang, T.; Gu, C.-C.; Wu, K.-J.; Guan, X.-P. A novel face recognition method based on IWLD and IWBC. Multimed. Tools Appl. 2015, 75, 6979–7002. [Google Scholar] [CrossRef]
- Bashar, F.; Khan, A.; Ahmed, F.; Kabir, H. Robust facial expression recognition based on median ternary pattern (MTP). In Proceedings of the 2013 IEEE International Conference on Electrical Information and Communication Technology (EICT), Khulna, Bangladesh, 13–15 February 2014; pp. 1–5. [Google Scholar]


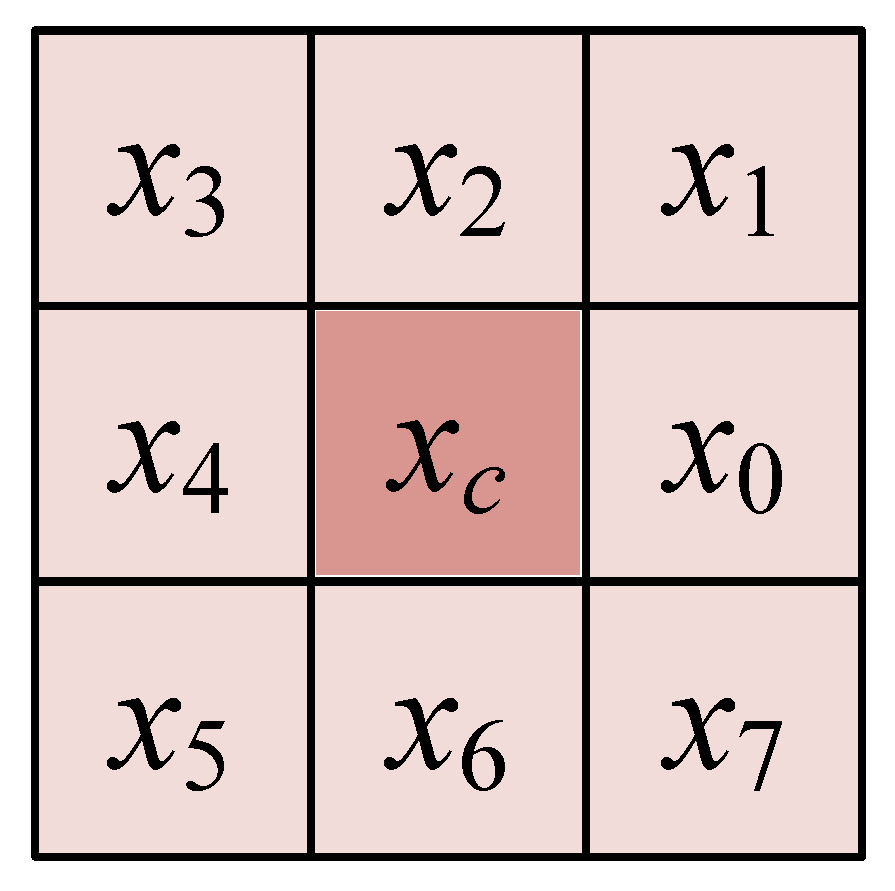
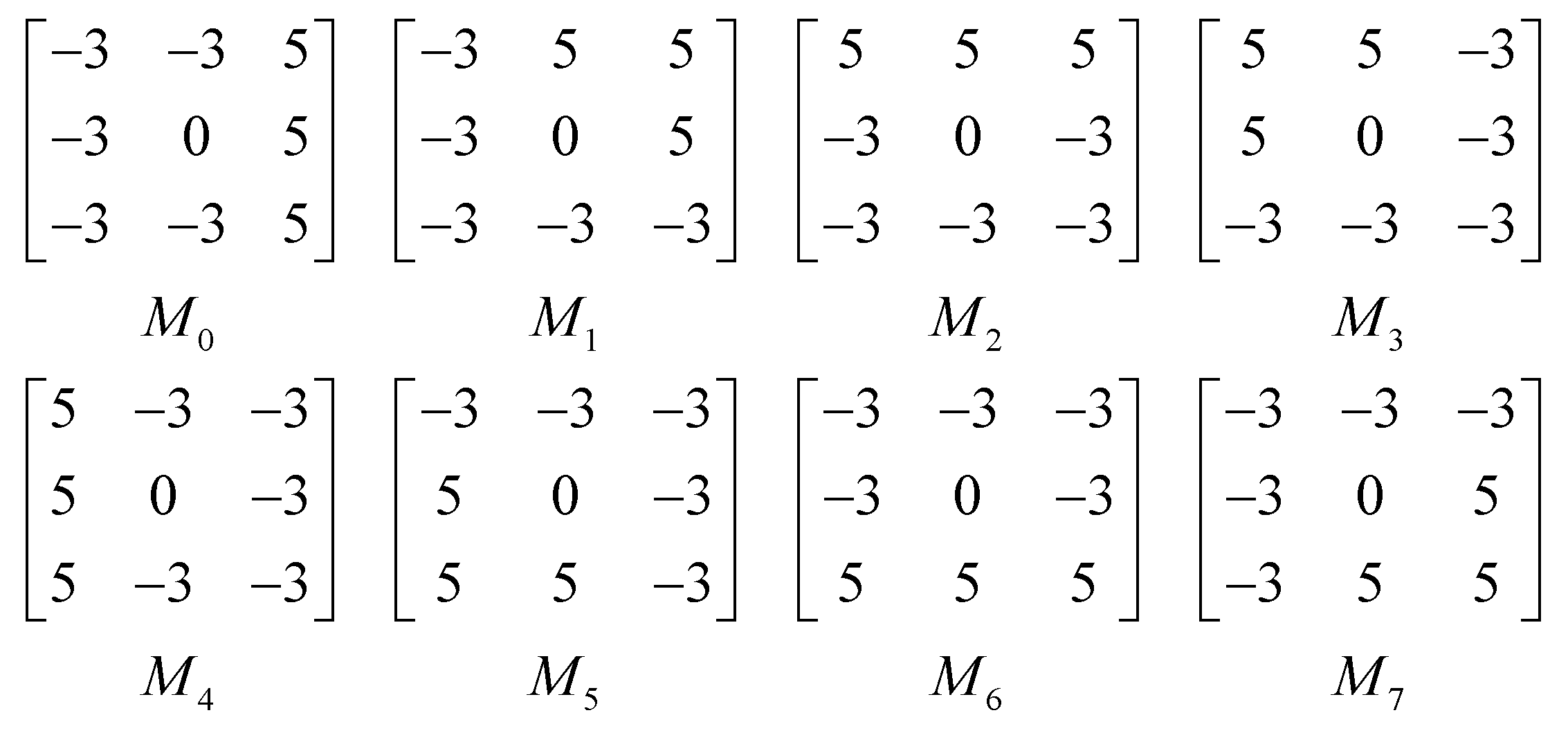




| Method | Linear | Polynomial | RBF (C = 100) |
|---|---|---|---|
| WLD | 91.4 | 90.8 | 91.4 |
| WLD + 1dir | 93.2 | 91.6 | 93.6 |
| WLD + 2dir | 92.6 | 90.4 | 93.2 |
| WLTD1dir | 93.4 | 92.4 | 93.8 |
| WLTD2dir | 94.0 | 92.4 | 94.0 |
| Method | Linear | Polynomial | RBF (C = 100) |
|---|---|---|---|
| WLD | 91.4 | 90.8 | 91.4 |
| WLD + 1dir | 92.8 | 92.0 | 93.0 |
| WLD + 2dir | 93.0 | 92.6 | 93.0 |
| WLTD1dir | 94.4 | 95.0 | 95.0 |
| WLTD2dir | 93.8 | 93.6 | 94.0 |
| Method | Linear | Polynomial | RBF (C = 100) |
|---|---|---|---|
| WLD | 91.4 | 90.8 | 91.4 |
| WLD + 1dir | 93.6 | 91.4 | 93.8 |
| WLD + 2dir | 92.8 | 91.4 | 93.4 |
| WLTD1dir | 93.8 | 93.2 | 93.8 |
| WLTD2dir | 93.8 | 92.6 | 94.0 |
| Method | Linear | Polynomial | RBF (C = 100) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Acc | PR | SP | F1 | Acc | PR | SP | F1 | Acc | PR | SP | F1 | |
| LDN | 0.890 | 0.897 | 0.988 | 0.889 | 0.862 | 0.868 | 0.985 | 0.857 | 0.886 | 0.895 | 0.987 | 0.885 |
| LGIP | 0.892 | 0.903 | 0.988 | 0.891 | 0.880 | 0.892 | 0.987 | 0.878 | 0.898 | 0.907 | 0.989 | 0.897 |
| LBP | 0.896 | 0.904 | 0.988 | 0.894 | 0.882 | 0.894 | 0.987 | 0.879 | 0.906 | 0.911 | 0.990 | 0.904 |
| LMP | 0.928 | 0.936 | 0.992 | 0.926 | 0.924 | 0.933 | 0.992 | 0.922 | 0.932 | 0.939 | 0.992 | 0.930 |
| WLD | 0.914 | 0.923 | 0.990 | 0.912 | 0.908 | 0.917 | 0.990 | 0.906 | 0.914 | 0.922 | 0.990 | 0.912 |
| GLTeP | 0.912 | 0.921 | 0.990 | 0.909 | 0.908 | 0.917 | 0.990 | 0.905 | 0.910 | 0.919 | 0.990 | 0.907 |
| LAP | 0.896 | 0.902 | 0.988 | 0.892 | 0.886 | 0.895 | 0.987 | 0.881 | 0.904 | 0.912 | 0.989 | 0.900 |
| IWBC | 0.930 | 0.937 | 0.992 | 0.928 | 0.930 | 0.938 | 0.992 | 0.928 | 0.934 | 0.941 | 0.993 | 0.932 |
| MBP | 0.894 | 0.904 | 0.988 | 0.892 | 0.882 | 0.891 | 0.987 | 0.880 | 0.898 | 0.908 | 0.989 | 0.896 |
| WTLD_kirsch | 0.934 | 0.941 | 0.993 | 0.933 | 0.924 | 0.933 | 0.992 | 0.922 | 0.938 | 0.944 | 0.993 | 0.937 |
| WTLD_sobel | 0.944 | 0.949 | 0.994 | 0.943 | 0.950 | 0.957 | 0.994 | 0.950 | 0.950 | 0.955 | 0.994 | 0.949 |
| WTLD_prewitt | 0.938 | 0.945 | 0.993 | 0.938 | 0.932 | 0.939 | 0.992 | 0.931 | 0.938 | 0.944 | 0.993 | 0.937 |
| Method | Feature Dimension | Eigenvector Length |
|---|---|---|
| LDN [28] | 56 | 896 |
| LGIP [29] | 37 | 592 |
| LBP [30] | 59 | 944 |
| LMP [31] | 256 | 4096 |
| WLD [26] | 32 | 512 |
| GLTeP [32] | 512 | 8192 |
| LAP [33] | 272 | 4352 |
| IWBC [34] | 2048 | 32,768 |
| MBP [35] | 256 | 4096 |
| WTLD | 256 (16 + 8 × 6 × 5) | 496 (16 × 4 × 4 + 8 × 6 × 5) |
| Method | Linear | Polynomial | RBF (C = 100) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Acc | PR | SP | F1 | Acc | PR | SP | F1 | Acc | PR | SP | F1 | |
| LDN | 0.914 | 0.926 | 0.986 | 0.911 | 0.921 | 0.936 | 0.987 | 0.919 | 0.921 | 0.928 | 0.987 | 0.917 |
| LGIP | 0.914 | 0.933 | 0.986 | 0.909 | 0.907 | 0.927 | 0.985 | 0.902 | 0.914 | 0.933 | 0.986 | 0.909 |
| LBP | 0.900 | 0.908 | 0.983 | 0.896 | 0.900 | 0.908 | 0.983 | 0.896 | 0.900 | 0.908 | 0.983 | 0.896 |
| LMP | 0.950 | 0.964 | 0.992 | 0.948 | 0.950 | 0.964 | 0.992 | 0.948 | 0.950 | 0.964 | 0.992 | 0.948 |
| WLD | 0.921 | 0.940 | 0.987 | 0.916 | 0.914 | 0.934 | 0.986 | 0.909 | 0.921 | 0.940 | 0.987 | 0.916 |
| GLTeP | 0.950 | 0.958 | 0.992 | 0.948 | 0.950 | 0.958 | 0.992 | 0.948 | 0.950 | 0.958 | 0.992 | 0.948 |
| LAP | 0.893 | 0.900 | 0.982 | 0.888 | 0.893 | 0.903 | 0.982 | 0.888 | 0.893 | 0.903 | 0.982 | 0.888 |
| IWBC | 0.964 | 0.973 | 0.994 | 0.963 | 0.964 | 0.973 | 0.994 | 0.963 | 0.964 | 0.973 | 0.994 | 0.963 |
| MBP | 0.929 | 0.933 | 0.988 | 0.927 | 0.929 | 0.933 | 0.988 | 0.927 | 0.929 | 0.933 | 0.988 | 0.927 |
| WTLD_kirsch | 0.971 | 0.979 | 0.995 | 0.970 | 0.971 | 0.979 | 0.995 | 0.970 | 0.971 | 0.979 | 0.995 | 0.970 |
| WTLD_sobel | 0.957 | 0.968 | 0.993 | 0.954 | 0.957 | 0.968 | 0.993 | 0.954 | 0.964 | 0.973 | 0.994 | 0.963 |
| WTLD_prewitt | 0.971 | 0.979 | 0.995 | 0.969 | 0.971 | 0.979 | 0.995 | 0.969 | 0.971 | 0.979 | 0.995 | 0.969 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, W.; Zhu, W.; Ma, C.; Guo, Y. Weber Texture Local Descriptor for Identification of Group-Housed Pigs. Sensors 2020, 20, 4649. https://doi.org/10.3390/s20164649
Huang W, Zhu W, Ma C, Guo Y. Weber Texture Local Descriptor for Identification of Group-Housed Pigs. Sensors. 2020; 20(16):4649. https://doi.org/10.3390/s20164649
Chicago/Turabian StyleHuang, Weijia, Weixing Zhu, Changhua Ma, and Yizheng Guo. 2020. "Weber Texture Local Descriptor for Identification of Group-Housed Pigs" Sensors 20, no. 16: 4649. https://doi.org/10.3390/s20164649
APA StyleHuang, W., Zhu, W., Ma, C., & Guo, Y. (2020). Weber Texture Local Descriptor for Identification of Group-Housed Pigs. Sensors, 20(16), 4649. https://doi.org/10.3390/s20164649




