A Multidimensional Hyperjerk Oscillator: Dynamics Analysis, Analogue and Embedded Systems Implementation, and Its Application as a Cryptosystem
Abstract
1. Introduction
Our Contributions
2. Dynamics of the Proposed Multidimensional Hyperjerk Oscillator
2.1. Mathematical Formulation of Proposed 5-D Hyperjerk Oscillator Network
2.2. Fixed Point and Stability
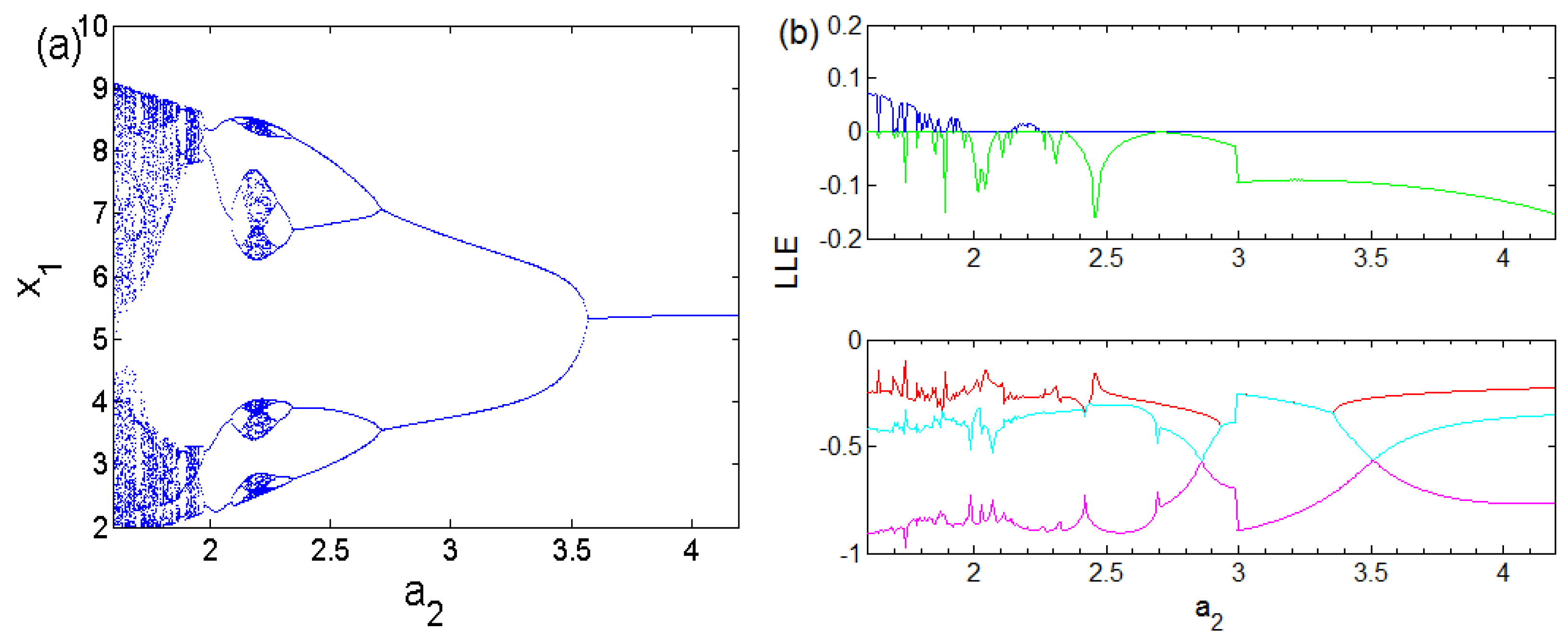
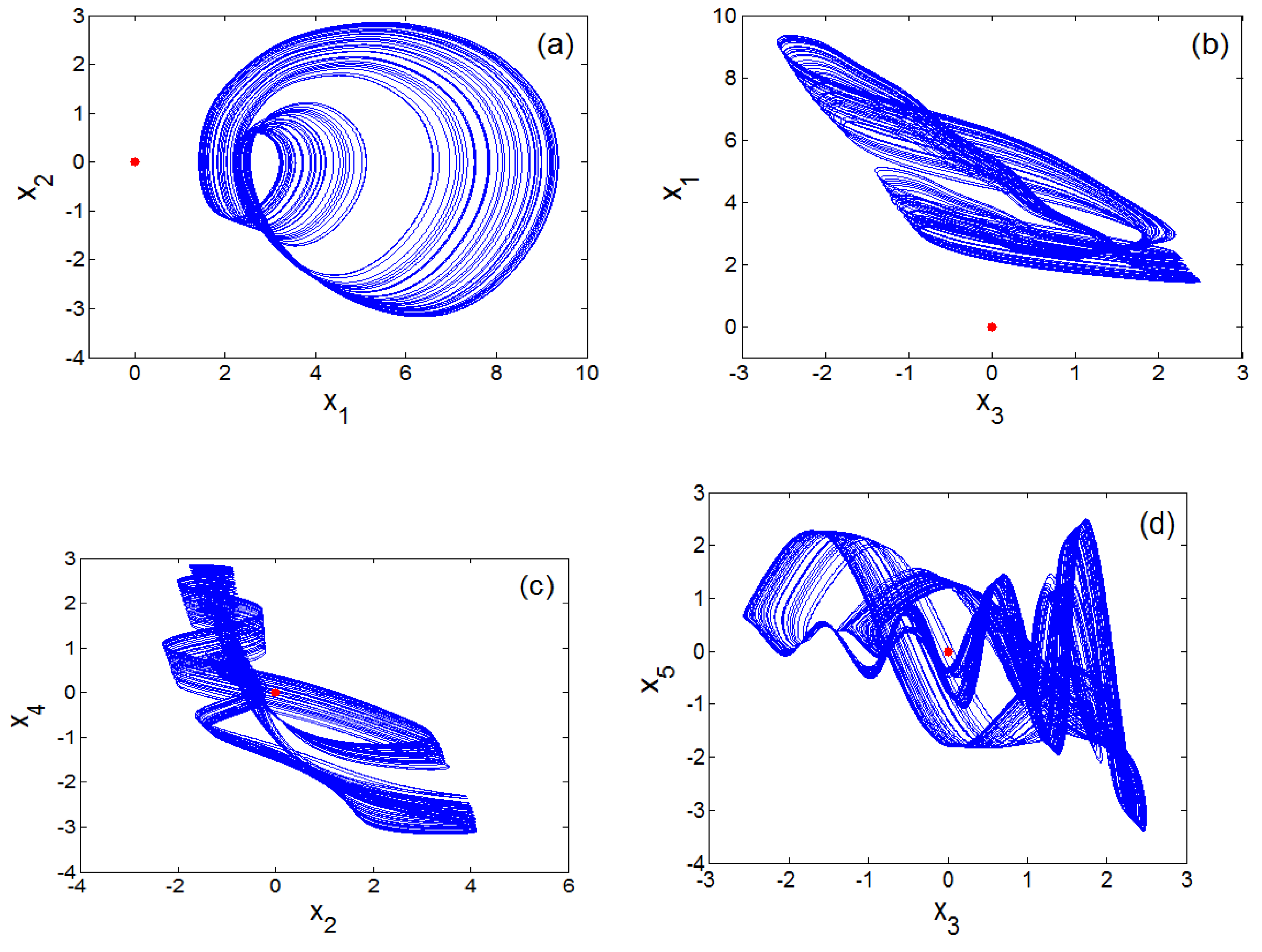
2.3. Bifurcations and Multistability
3. Experimental Analysis of Proposed Oscillator
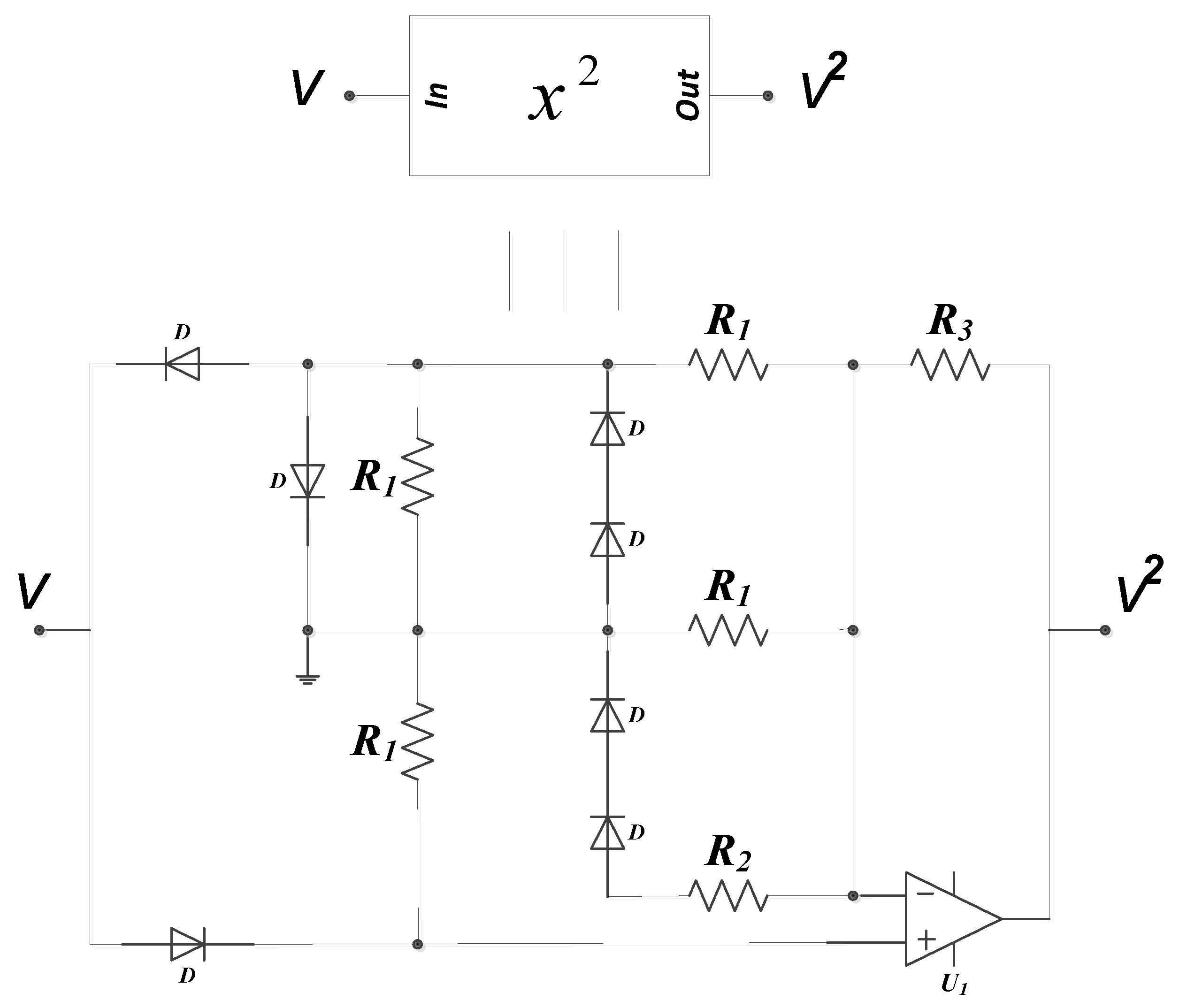
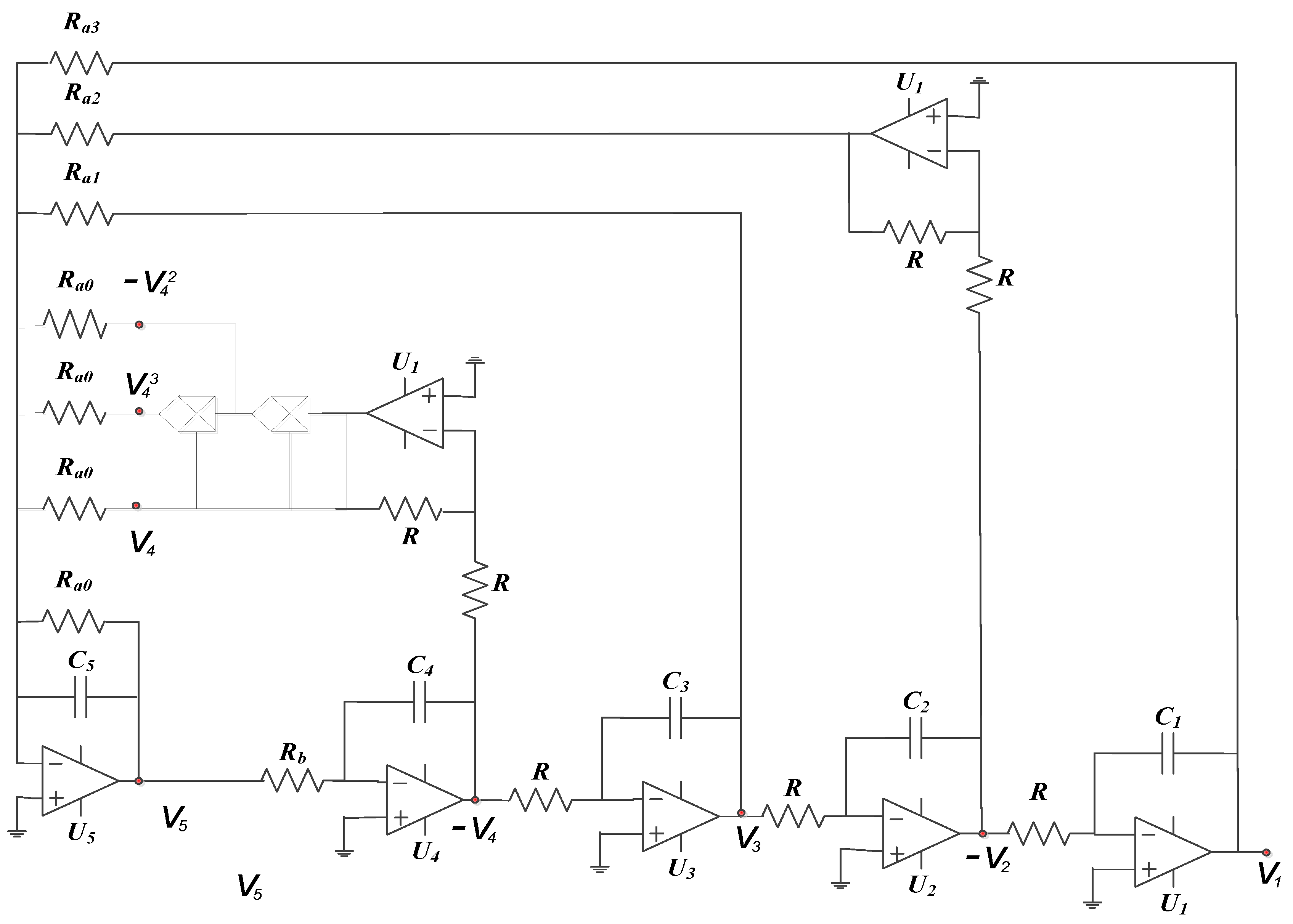
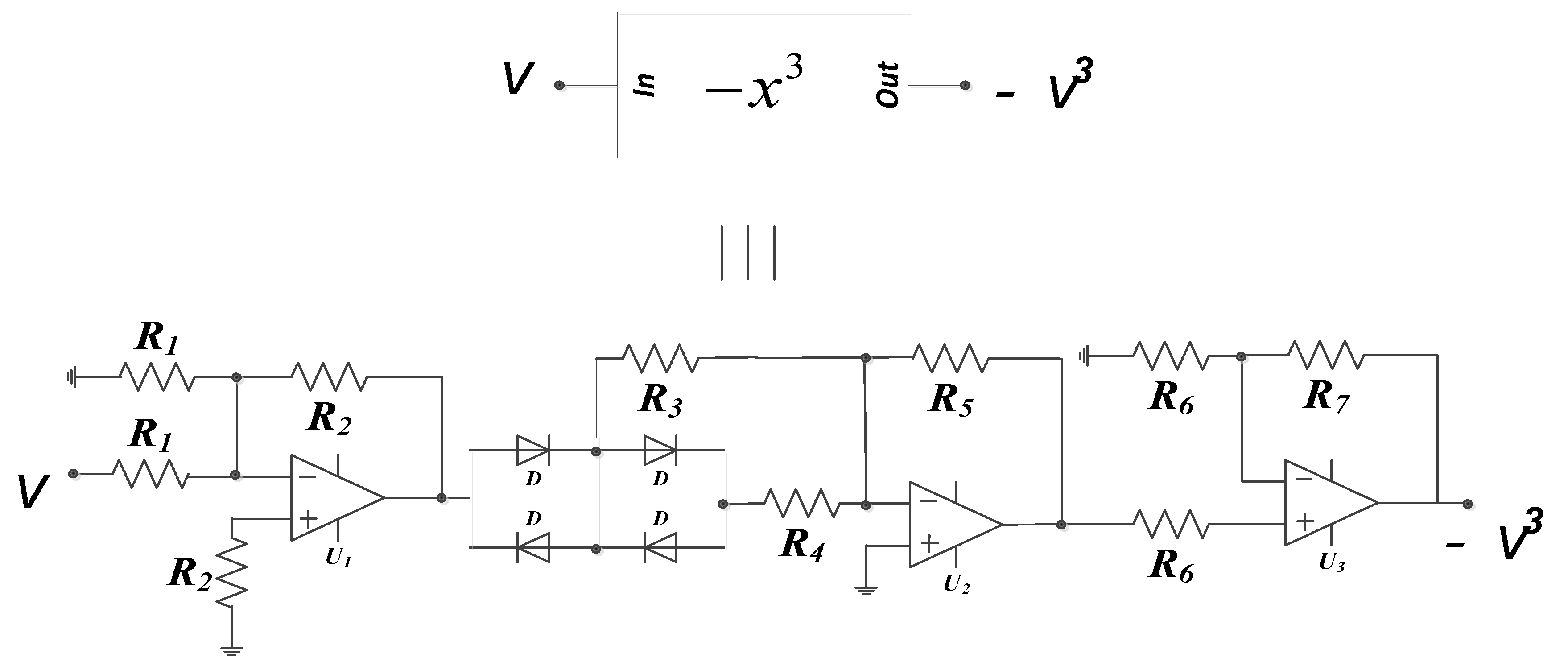
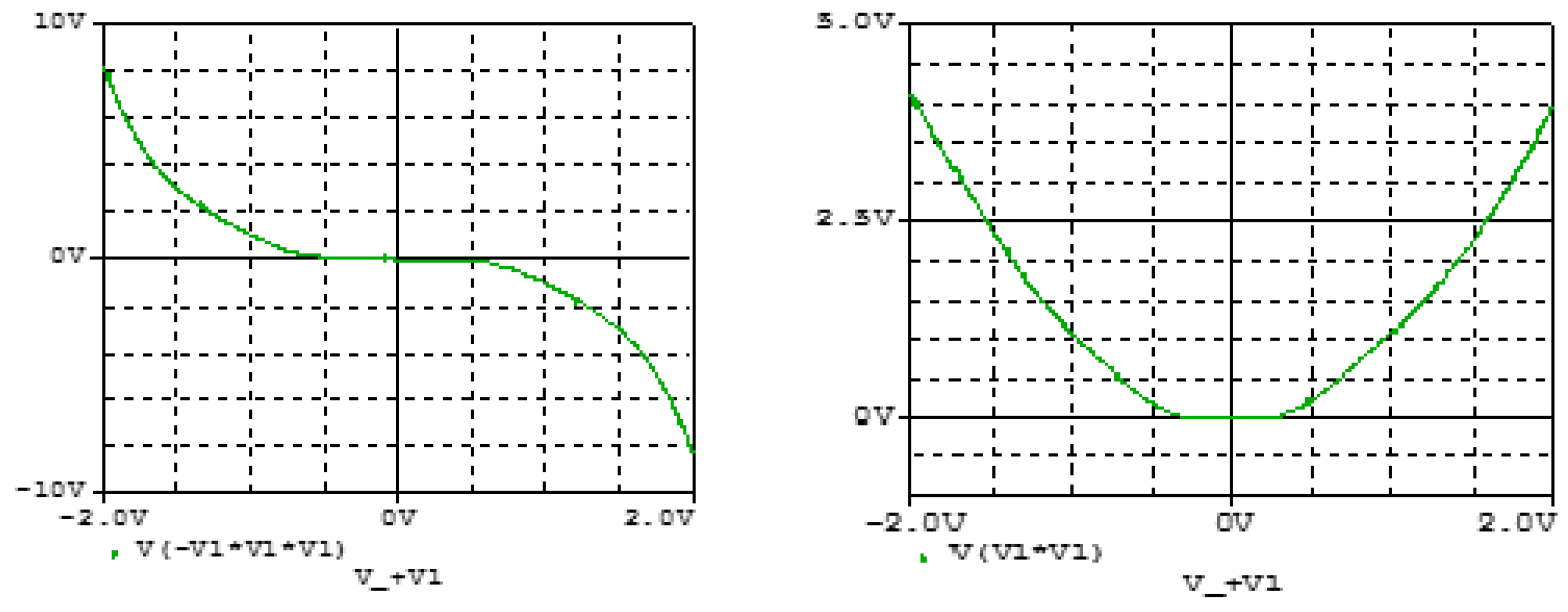
3.1. Analogue Simulation Results on the Designed Circuit Using Spice
3.2. Arduino Based Implementation of Proposed Oscillator
- Step 1: Set pins 1 and 2 as outputs. The solutions of our chaotic oscillator will be written here.
- Step 2: Define the discrete chaotic oscillator, its parameters and initial conditions under an infinite loop.
- Step 3: Write the solutions of the discrete chaotic oscillator on Arduino pins. Pin 1 is activated when x2 > 0.5 and pin 2 is activated when x1 > 1.
4. Application of Proposed Network as a Cryptosystem
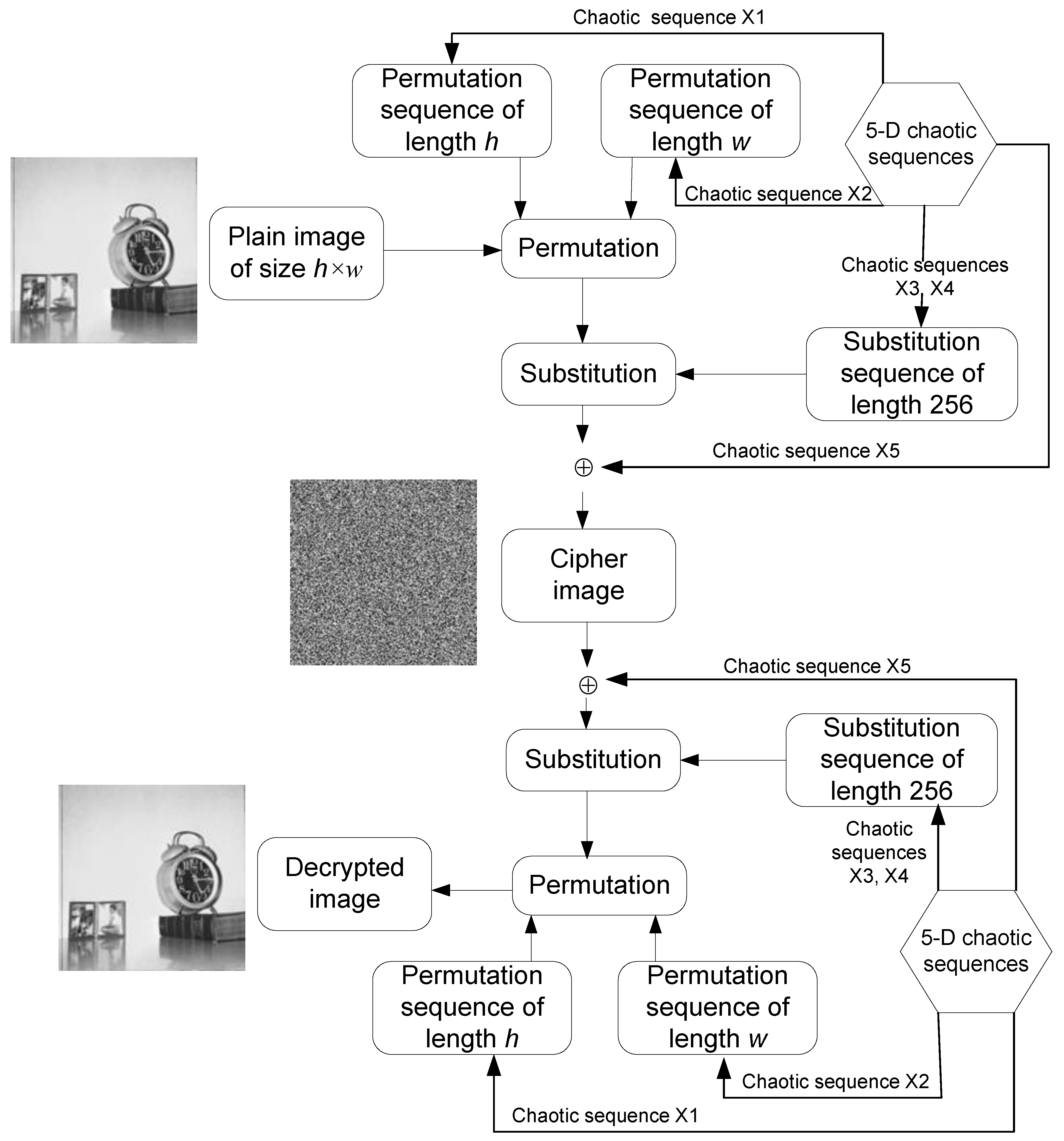
4.1. Chaos-Based Image Encryption Using Proposed 5-D Hyperjerk Oscillator Network
- Step 1: Iterate the 5-D hyperjerk chaos generator for h*w times, where h*w is the size of the plain image P, which produces output is five sequences x1, x2, x3, x4, and x5 as output.
- Step 2: Using the first sequence x1, construct a permutation sequence of length h with h distinct elements from 1 to h as follows:
- −
- Order the elements of first h elements and discard the first 10 elements in ascending order.Eh= order (x1(11:h+10))
- −
- Obtain the index of each element of the sequence Eh as a sequence x1(11:h+10).Ph=index (Eh in x1(11:h+10))
Step 3: Using the first sequence x2, construct a permutation sequence of length w with distinct elements from 1 to w.- −
- Order the elements of first w elements and discard the first 10 elements in ascending order.Ew= order (x2(11:w+10))
- −
- Obtain the index of each element of the sequence Ew as a sequence x2(11:h+10).Pw=index (Ew in x2(11:w+10))
- Step 4: Using the first sequence the third and fourth sequences x3 and x4, construct the substitution sequence of length 256, which have 256 distinct elements in the range 0 to 255
- −
- Y=x3(11:266) + x4(11:266)
- −
- Order the elements of Y sequence in ascending order.Ey= order(Y)
- −
- Obtain the index of each element of the sequence Ey as a sequence Y.Sb=index (Ey in Y)
- Step 5: Using the fifth sequence X5, construct the key matrix K with size h×w.
- Step 6: Permute the plain image P using the permutation sequences Ph and Pw (which originate from Step 2 and Step 3, respectively), each targeting the rows and columns.
- for i=1 to h
- for j=1 to w
- Per(i,j)=P(Ph(i),Pw(j));
- end
- end
- Step 7: Substitute the permutated image ‘Per’ (in Step 6) using Sb substitution sequence (in Step 4).
- Sub=zeros(a,b);
- for i=1 to h
- for j=1 to w
- Sub (i,j)=Sb(Per(i,j)+1);
- end
- end
- Step 8: Perform bitwise XOR operation on substituted image ‘Sub’ (in Step 7) using key matrix K (in Step 5). C=bitxor(Sub,K)
4.2. Performance Tests
4.2.1. Statistical Tests
Correlation of Adjacent Pixels
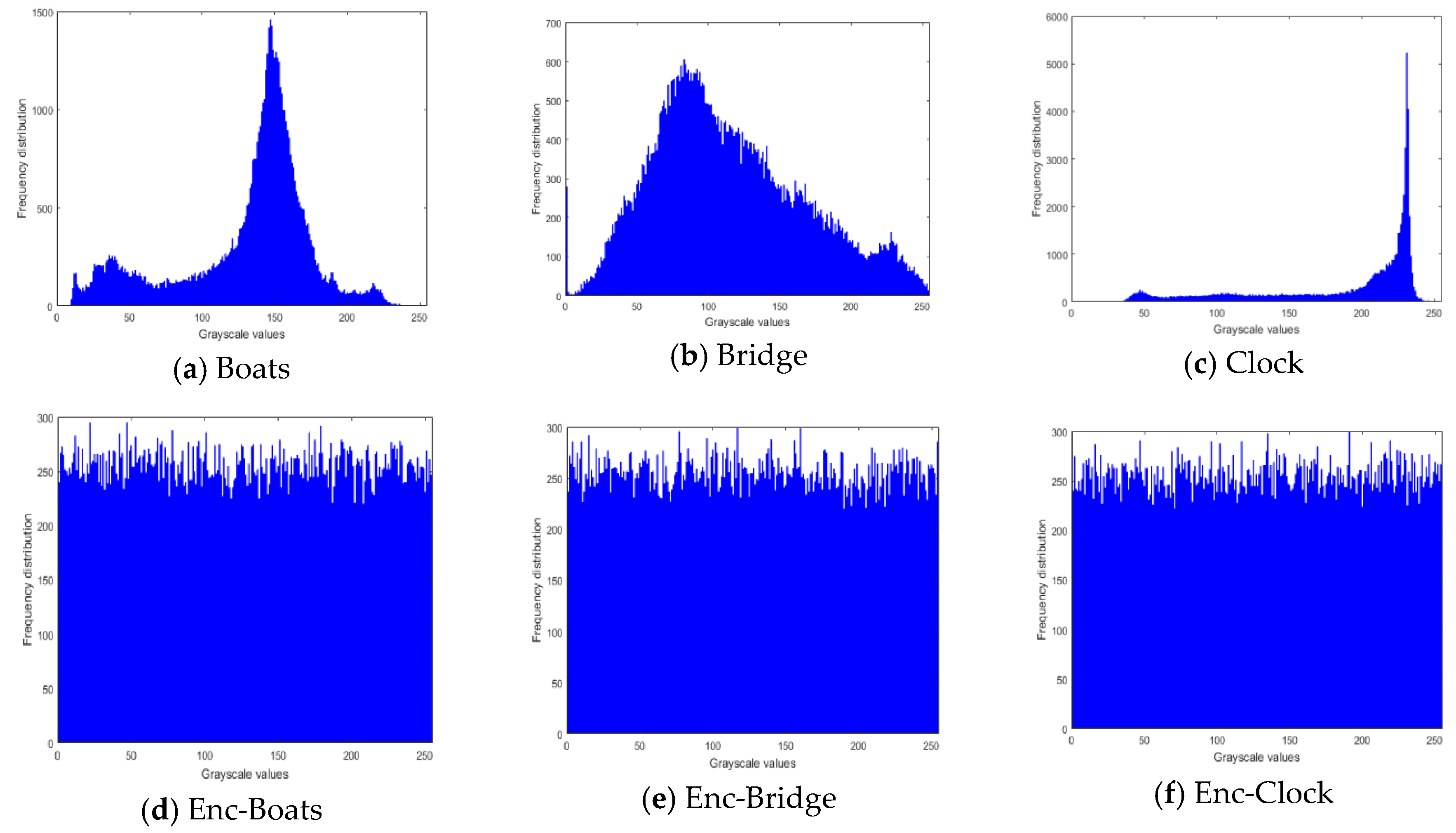
Histogram Tests
Information Entropy
4.2.2. Differential Test: NPCR and UACI
4.2.3. Key Sensitivity Test
4.2.4. Time and Complexity Analysis
- -
- Step 1: (5*h*w) steps are required to iterate the chaotic map
- -
- Step 2: (h2) steps each are required to retrieve h elements and obtain the index
- -
- Step 3: (w2) steps each are required to retrieve w elements and obtain the index
- -
- Step 4: (256*256) steps each are required to retrieve 256 elements, and obtain the index of h elements
- -
- Step 5: (h*w) steps are each required for the multiplication mod operations
- -
- Step 6: (h*w) steps are required for the permutation operation
- -
- Step 7: (h*w) steps are required for substitution operation
- -
- Step 8: (h*w) steps are required for number of exclusive-XOR operations in the final step
4.2.5. NIST Test
4.2.6. Key Space Analysis
4.2.7. Impact of Noise on the Transmission of Cipher Images
5. Concluding Remarks
Author Contributions
Funding
Conflicts of Interest
References
- FIPS PUB. Data Encryption Standard (DES); NIST, Publication 46; 1999. Available online: https://csrc.nist.gov/csrc/media/publications/fips/46/3/archive/1999-10-25/documents/fips46-3.pdf (accessed on 15 December 2019).
- Diffie, W.; Hellman, M. New direction in cryptograph. IEEE Trans. Inf. Theory 1976, 22, 644–654. [Google Scholar] [CrossRef]
- Abid, Z.; Wang, W. Countermeasures for hardware fault attack in multiprime RSA cryptosystems. Int. J. Netw. Secur. 2008, 6, 190–200. [Google Scholar]
- Li, S.; Chen, G.; Cheung, A.; Bhargava, B.; Lo, K.T. On the design of perceptual MPEG-video encryption algorithms. IEEE Trans. Circuits Syst. Video Technol. 2007, 17, 214–223. [Google Scholar] [CrossRef]
- Nkapkop, J.D.D.; Effa, J.Y.; Borda, M.; Terebes, R. A Novel Fast and Secure Chaos Based Algorithm for Image Encryption. In Innovative Security Solutions for Information Technology and Communications; Springer: Berlin, Germany, 2015; pp. 87–101. [Google Scholar]
- Tsafack, N.; Kengne, J.; Abd-El-Atty, B.; Iliyasu, A.M.; Hirota, K.; Abd EL-Latif, A.A. Design and implementation of a simple dynamical 4-D chaotic circuit with its cryptographic applications. Inf. Sci. 2020, 515C, 191–217. [Google Scholar] [CrossRef]
- El-Latif, A.A.A.; Li, L.; Wang, N.; Han, Q.; Niu, X. A new approach to chaotic image encryption based on quantum chaotic system, exploiting color spaces. Sign. Proces. 2013, 93, 2986–3000. [Google Scholar] [CrossRef]
- Li, L.; Abd-El-Atty, B.; El-Latif, A.A.A.; Ghoneim, A. Quantum color image encryption based on multiple discrete chaotic systems. In Proceedings of the 2017 Federated Conference on Computer Science and Information Systems (FedCSIS), Prague, Czech Republic, 3–6 September 2017; pp. 555–559. [Google Scholar]
- Luo, X.; Zhou, R.; Liu, J.; Cao, Y.; Ding, X. A parallel image encryption algorithm based on the piecewise linear chaotic map and hyper-chaotic map. Nonlinear Dyn. 2018, 93, 1165–1181. [Google Scholar] [CrossRef]
- Khan, J.S.; Ahmad, J. Chaos based efficient selective image encryption. Multidimens. Syst. Signal Process. 2019, 30, 943–961. [Google Scholar] [CrossRef]
- Ahmad, J.; Khan, M.A.; Ahmed, F.; Khan, J.S. A novel image encryption scheme based on orthogonal matrix, skew tent map, and XOR operation. Neural Comput. Appl. 2018, 30, 3847–3857. [Google Scholar] [CrossRef]
- Lu, Q.; Zhu, C.; Wang, G. A novel S-Box design Algorithm based on new compound chaotic system. Entropy 2019, 21, 1004. [Google Scholar] [CrossRef]
- Folifack, V.R.; Kengne, J. Coexistence of hidden attractors, 2-torus and 3-torus in a new simple 4-D chaotic system with hyperbolic cosine nonlinearity. Int. J. Bifurc. Chaos 2018, 6, 1421–1428. [Google Scholar]
- Njitacke, Z.T.; Kengne, J. Nonlinear Dynamics of Three-Neurons-Based Hopfield Neural Networks (HNNs): Remerging Feigenbaum Trees, Coexisting Bifurcations and Multiple Attractors. J. Circuits Syst. Comput. 2019, 28, 1950121. [Google Scholar] [CrossRef]
- Tsafack, N.; Kengne, J. A Particular Class of Simple Chaotic Circuits: Multistability Analysis; Lap LAMBERT Academic Publishing: Riga, Latvia, 2019; ISBN 978-613-9-46143-1. [Google Scholar]
- Kengne, J.; Jafari, S.; Njitacke, Z.T.; Yousefi, K.M.; Cheukem, A. Dynamic analysis and electronic circuit implementation of a novel 3D autonomous system without linear terms. Commun. Nonlinear Sci. Numer. Simul. 2017. [Google Scholar] [CrossRef]
- Kengne, J.; Njikam, S.M.; Folifack, V.R. A plethora of coexisting strange attractors in a simple jerk system with hyperbolic tangent nonlinearity. Chaos Solitons Fractals 2018, 106, 201–213. [Google Scholar] [CrossRef]
- Wang, B.; Xie, Y.; Zhou, C.; Zhou, S.; Zheng, X. Evaluating the permutation and diffusion operations used in image encryption based on chaotic map. Optik 2016, 127, 3541–3545. [Google Scholar] [CrossRef]
- Zhu, S.; Zhu, C.; Wang, W. A new image encryption algorithm based on chaos and secure Hash SHA-256. Entropy 2018, 20, 716. [Google Scholar] [CrossRef]
- Benrhouma, O.; Hermassi, H.; El-Latif, A.A.A.; Belghith, S. Cryptanalysis of a video encryption method based on mixing and permutation operations in the DCT domain. Signal Image Video Process. 2015, 9, 1281–1286. [Google Scholar] [CrossRef]
- Belazi, A.; Khan, M.; El-Latif, A.A.A.; Belghith, S. Efficient cryptosystem approaches: S-boxes and permutation–substitution-based encryption. Nonlinear Dyn. 2017, 87, 337–361. [Google Scholar] [CrossRef]
- De la Hoz, M.Z.; Leonardo, A.; Yolanda, V. An experimental realization of a chaos-based secure communication using arduino microcontrollers. Sci. World. J. 2015. [Google Scholar] [CrossRef]
- Adolfo, R.; Nicolás, V.; Luis, G.; Carlos, V.A.; Onofre, G. Design, implementation and evaluation of a solar tracking system based on a video processing sensor. Int. J. Adv. Res. Comput. Sci. Softw. Eng. 2013, 3, 172–178. [Google Scholar]
- Nikhil, L.; Paygude, S.S. Survey on traffic monitoring system using image processing. Int. J. Adv. Res. Comput. Eng. Technol. 2014, 3, 4374–4377. [Google Scholar]
- Pukale, D.D.; Palak, C.; Adhikari, S.S. Density based traffic control system using video processing (hardware and software implementation). Imp. J. Interdiscip. Res. 2016, 2, 293–297. [Google Scholar]
- Preeti, N.; Neha, K. Hardware Design of Embedded Systems for Security Applications; INTECH: Copenhagen, Denmark, 2012. [Google Scholar] [CrossRef]
- Tsafack, N.; Kengne, J. A novel autonomous 5-d hyperjerk RC circuit with hyperbolic sine function. Sci. World J. 2018, 17. [Google Scholar] [CrossRef] [PubMed]
- Fortuna, L.; Rizzo, A.; Xibilia, M.G. Modeling complex dynamics via extended PWL-based CNNS. Int. J. Bifurc. Chaos 2003, 13, 3273–3286. [Google Scholar] [CrossRef]
- Li, C.; Sprott, J.C. Coexisting hidden attractors in a 4-D simplified Lorenz system. Int. J. Bifurc. Chaos 2014, 24, 1450034. [Google Scholar] [CrossRef]
- Dudkowski, D.; Prasad, A.; Kapitaniak, T. Perpetual points and hidden attractors in dynamical systems. Phys. Lett. A 2015, 379, 2591–2596. [Google Scholar] [CrossRef]
- Prasad, A. Existence of perpetual points in nonlinear dynamical systems and its applications. Int. J. Bifurc. Chaos 2015, 25, 1530005. [Google Scholar] [CrossRef]
- Song, X.H.; Wang, H.Q.; Venegas-Andraca, S.E.; El-Latif, A.A.A. Quantum video encryption based on qubit-planes controlled-XOR operations and improved logistic map. Phys. A Stat. Mech. Appl. 2020, 537, 122660. [Google Scholar] [CrossRef]
- Azzaz, M.S.; Tanougast, C.; Sadoudi, S. A new auto-switched chaotic system and its FPGA implementation. Commun. Nonlinear Sci. Numer. Simul. 2013, 18, 1792–1804. [Google Scholar] [CrossRef]
- Murillo-Escobar, M.; Cruz-Hernández, C.; Abúndiz-Pérez, F. A robust embedded biometric authentication system based on fingerprint and chaotic encryption. Exp. Syst. Appl. 2015, 42, 8198–8211. [Google Scholar] [CrossRef]
- Jasio, L.D. Programming 32-Bit Microcontrollers in C: Exploring the PIC32; Newnes: Burlington, VT, USA, 2008. [Google Scholar]
- Rodrigo, M.; Adrian, A.; Cesar, C.; Fausto, A.; Rigoberto, M. Chaotic digital cryptosystem using serial peripheral interface protocol and its dsPIC implementation. Front. Inf. Technol. Electron. Eng. 2018. [Google Scholar] [CrossRef]
- Veronique, G.; Pierre, P.; Daniel, F.; Taha, A. Chaos based cryptosystem on DSP. Chaos Solitons Fractals 2009, 42, 2135–2144. [Google Scholar]
- Siddiqui, R.A.; Grosvenor, R.I.; Prickett, P.W. dsPIC-based advanced data acquisition system for monitoring, control and security applications. In Proceedings of the 12th International Bhurban Conference on Applied Sciences and Technology (IBCAST), Islamabad, Pakistan, 13–17 January 2015; pp. 293–298. [Google Scholar] [CrossRef]
- Uriz, A.J.; Agüero, P.D.; Moreira, J.C. Flexible pseudorandom number generator for tinnitus treatment implemented on a dsPIC. IEEE Latin Am. Trans. 2016, 14, 72–77. [Google Scholar] [CrossRef]
- Zhu, S.; Zhu, C. Image encryption algorithm with an avalanche effect based on a six-dimensional discrete chaotic system. Multimed. Tools Appl. 2018, 77, 29119–29142. [Google Scholar] [CrossRef]
- Zhu, C.; Wang, G.; Sun, K. Improved cryptanalysis and enhancements of an image encryption scheme using combined 1D chaotic maps. Entropy 2018, 20, 843. [Google Scholar] [CrossRef]
- Li, L.; Abd-El-Atty, B.; Elseuofi, S.; El-Rahiem, B.A.; El-Latif, A.A.A. Quaternion and multiple chaotic systems based pseudo-random number generator. In Proceedings of the 2019 2nd International Conference on Computer Applications & Information Security (ICCAIS), Riyadh, Saudi Arabia, 1–3 May 2019. [Google Scholar]
- Deng, Z.; Zhong, S. A digital image encryption algorithm based on chaotic mapping. J. Algorithms Comput. Technol. 2019, 13, 1–11. [Google Scholar] [CrossRef]
- Chong, F.; Chen, J.J.; Zou, H.; Meng, W.H.; Zhan, Y.F. A chaos-based digital image encryption with an improved permutation strategy. Opt. Express 2012, 20, 2363–2378. [Google Scholar]
- Hua, Z.; Zhou, Y.; Huang, H. Cosine-transform-based chaotic system for image encryption. Inf. Sci. 2019, 480, 403–419. [Google Scholar] [CrossRef]
- Wang, X.; Feng, L.; Zhao, H. Fast image encryption algorithm based on parallel computing system. Inf. Sci. 2019, 486, 340–358. [Google Scholar] [CrossRef]
- Ravichandran, D.; Praveenkumar, P.; Rayappan, J.B.B.; Amirtharajan, R. Dna chaos blend to secure medical privacy. IEEE Trans. Nanobiosci. 2017, 16, 850–858. [Google Scholar] [CrossRef]
- Lv, X.; Liao, X.; Yang, B. A novel scheme for simultaneous image compression and encryption based on wavelet packet transform and multi-chaotic systems. Multimed. Tools Appl. 2018, 77, 28633–28663. [Google Scholar] [CrossRef]
- Xu, M.; Tian, Z. A novel image cipher based on 3d bit matrix and latin cubes. Inf. Sci. 2019, 478, 1–14. [Google Scholar] [CrossRef]
- Abd-El-Atty, B.; El-Latif, A.A.A.; Venegas-Andraca, S.E. An encryption protocol for NEQR images based on one-particle quantum walks on a circle. Quantum Inf. Process. 2019, 18, 272. [Google Scholar] [CrossRef]
- Deb, S.; Biswas, B.; Bhuyan, B. Secure image encryption scheme using high efficiency word-oriented feedback shift register over finite field. Multimed. Tools Appl. 2019, 78, 34901–34925. [Google Scholar] [CrossRef]
- Behnis, S.; Akhshani, A.; Ahadpour, S.; Mahnodi, H.; Akhavan, A. A fast-chaotic encryption scheme based on piecewise nonlinear chaotic maps. Phys. Lett. A 2007, 366, 391–396. [Google Scholar] [CrossRef]
- Wang, X.Y.; Zhao, J.F.; Liu, H.J. A new image encryption algorithm based on chaos. Opt. Commun. 2012, 285, 562–566. [Google Scholar] [CrossRef]
- Gao, T.G.; Chen, Z.Q. A new image encryption algorithm based on hyper-chaos. Phys. Lett. A 2008, 372, 394–400. [Google Scholar] [CrossRef]
- Zhu, C.; Wang, G.; Sun, K. Cryptanalysis and improvement on an image encryption algorithm design using a novel chaos-based S-box. Symmetry 2018, 10, 399. [Google Scholar] [CrossRef]
- Zhu, S.; Wang, G.; Zhu, C. A secure and fast image encryption scheme based on double chaotic s-boxes. Entropy 2019, 21, 790. [Google Scholar] [CrossRef]
- Peng, J.; El-Latif, A.A.A.; Belazi, A.; Kotulski, Z. Efficient chaotic nonlinear component for secure cryptosystems. In Proceedings of the 2017 Ninth International Conference on Ubiquitous and Future Networks (ICUFN), Milan, Italy, 4–7 July 2017; pp. 989–993. [Google Scholar]

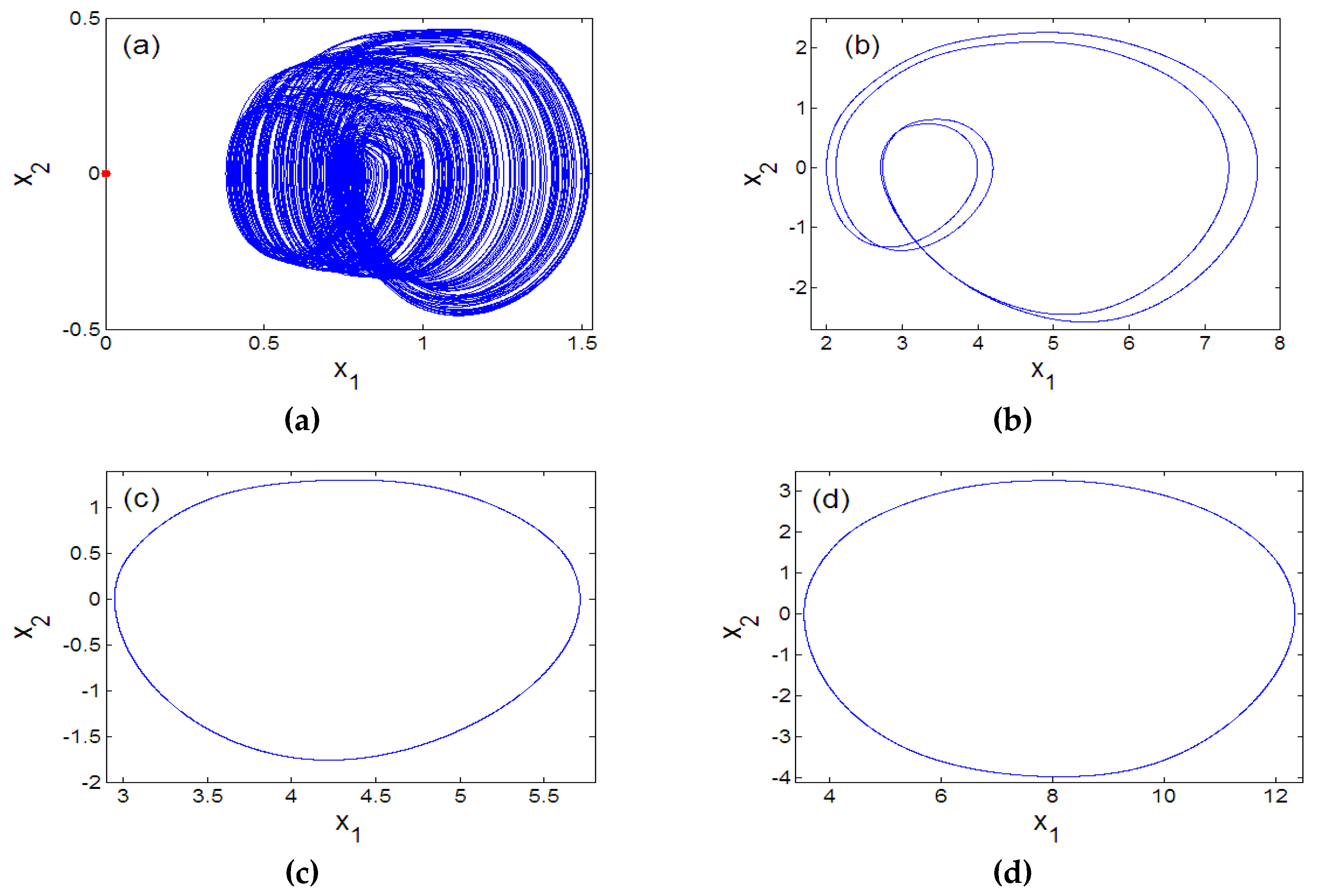
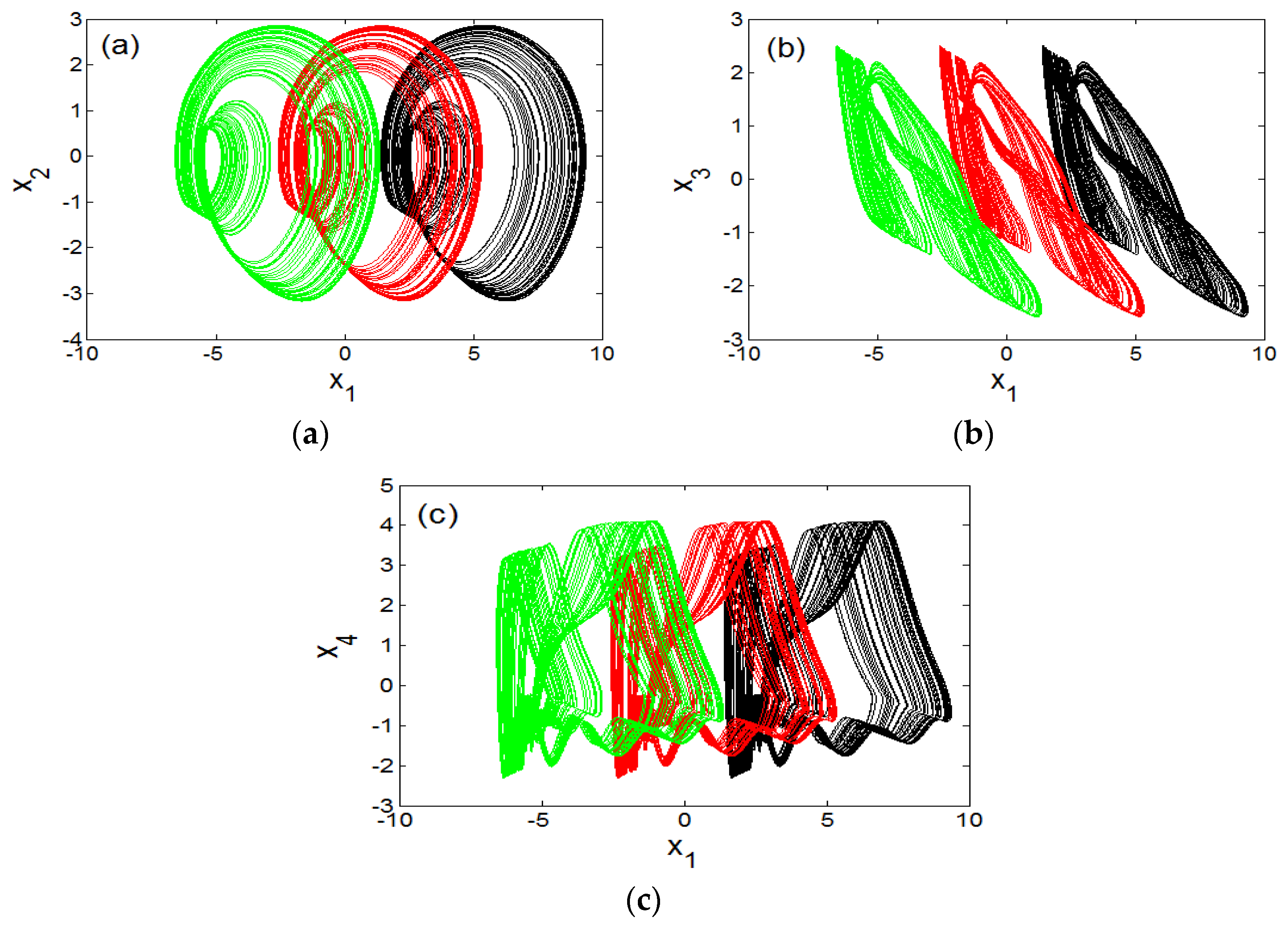
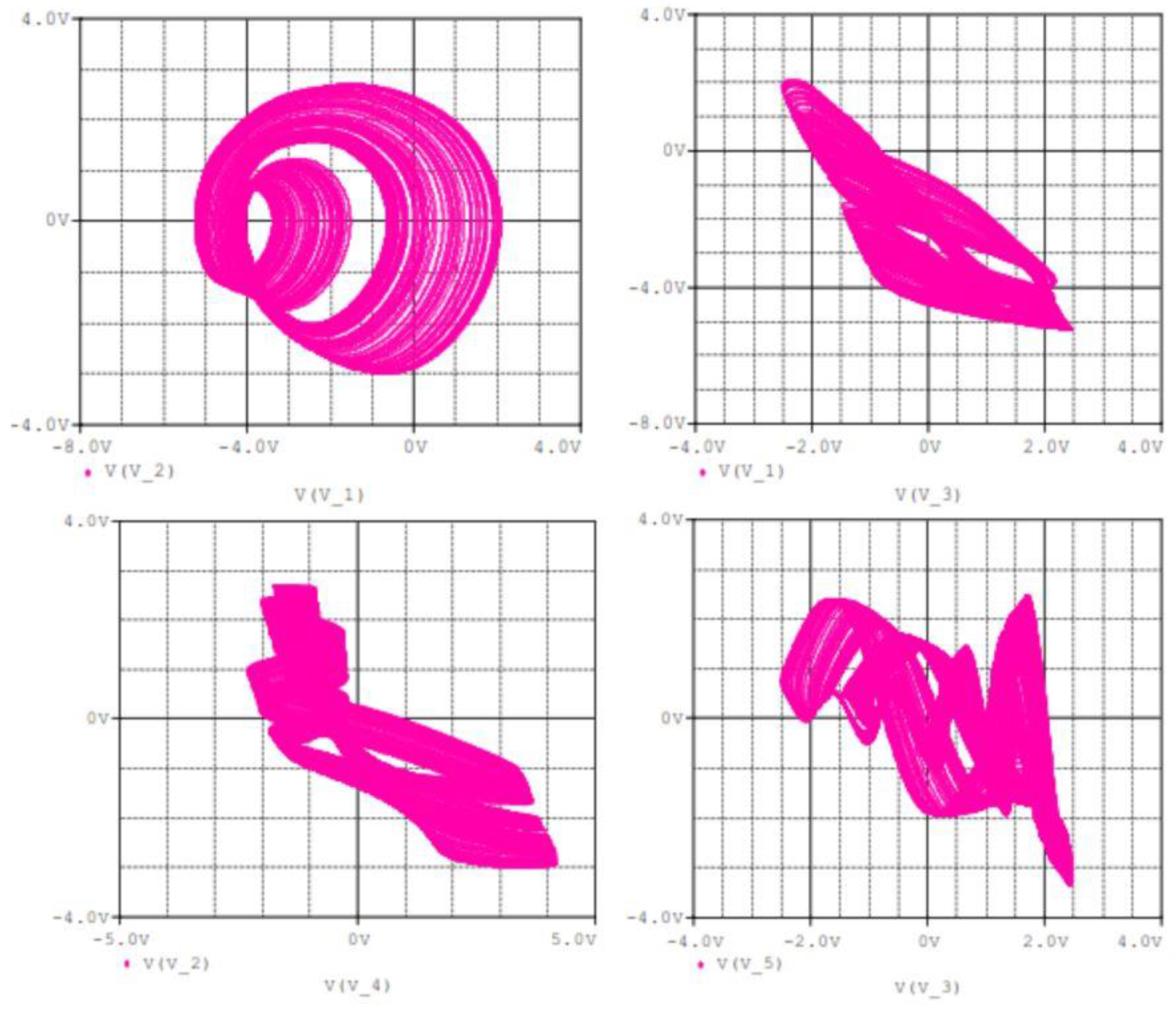
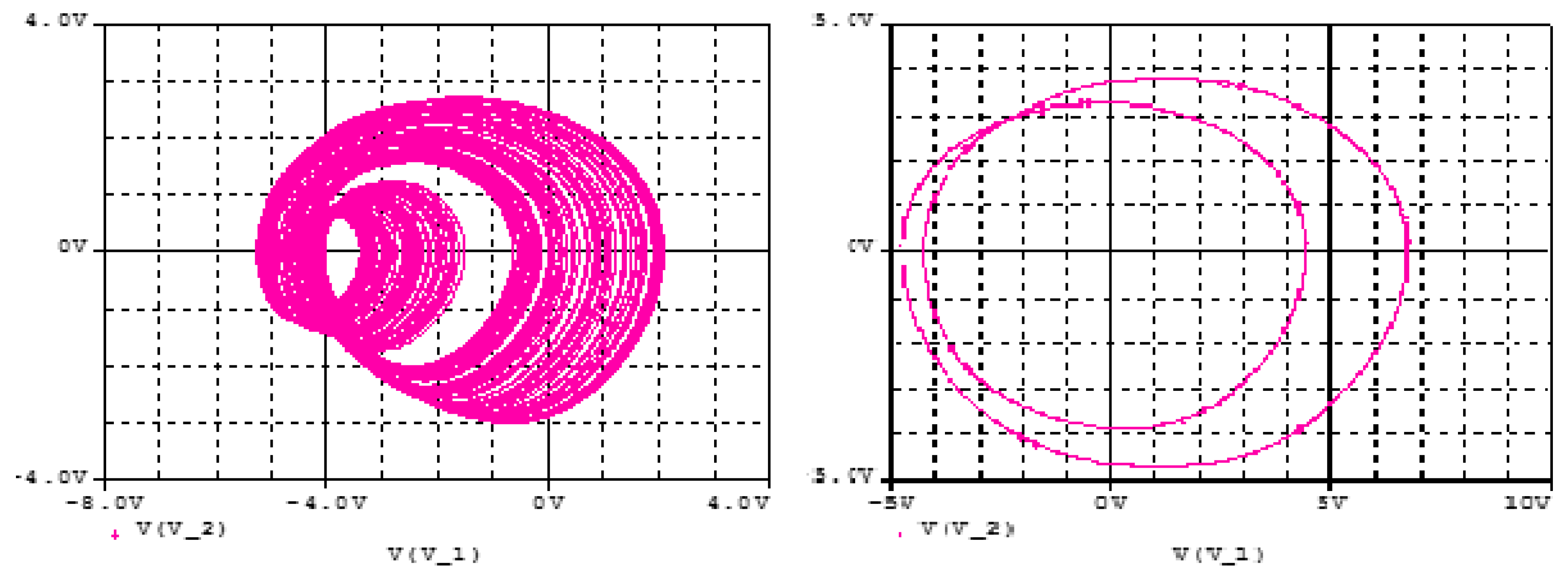





| Figure Number | Graph Colour | Parameter Range | Sweeping Direction | Initial State (x1(0),x2(0),x3(0),x4(0),x5(0)) |
|---|---|---|---|---|
| 7 | Green | Downward | (4,0,0,0,0,0) | |
| Red | Downward | (4.4,0,0,0,0,0) | ||
| Blue | Upward | (5.2,0,0,0,0,0) | ||
| Black | Downward | (0.4,0,0,0,0,0) | ||
| 10 | Green | Downward | (4,0,0,0,0,0) | |
| Red | Downward | (4.4,0,0,0,0,0) | ||
| Blue | Upward | (5.2,0,0,0,0,0) | ||
| Black | Downward | (0.4,0,0,0,0,0) | ||
| Cyan | Downward | (1.2,0,0,0,0) |
| Figure Number | Type of Coexistence | Control Parameter (a2) | Numerical Initial Conditions |
|---|---|---|---|
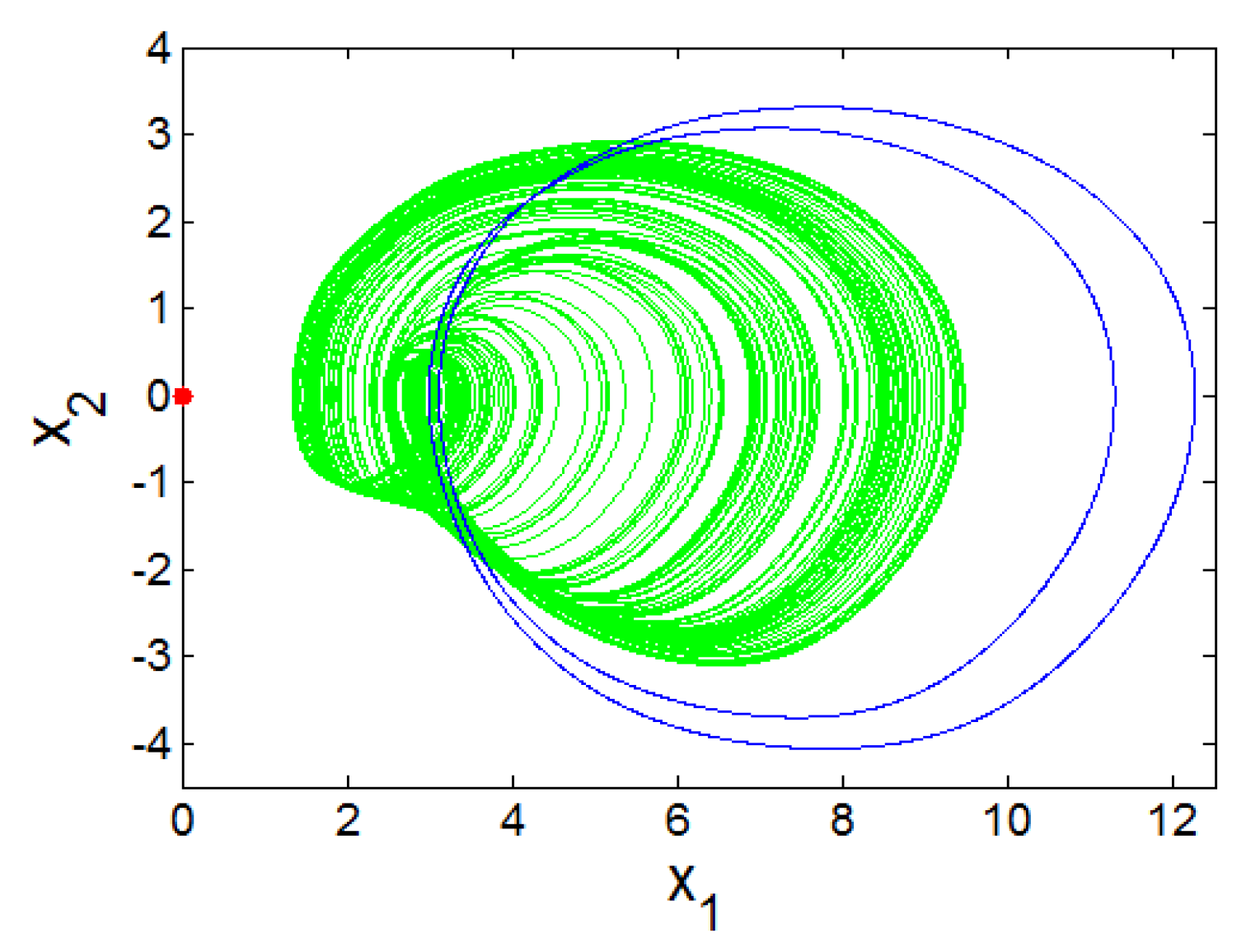
| 8 | One cycle and a chaotic attractor with fixed point | 2.9 | (4,0,0,0,0,0), (6,0,0,0,0,0) |
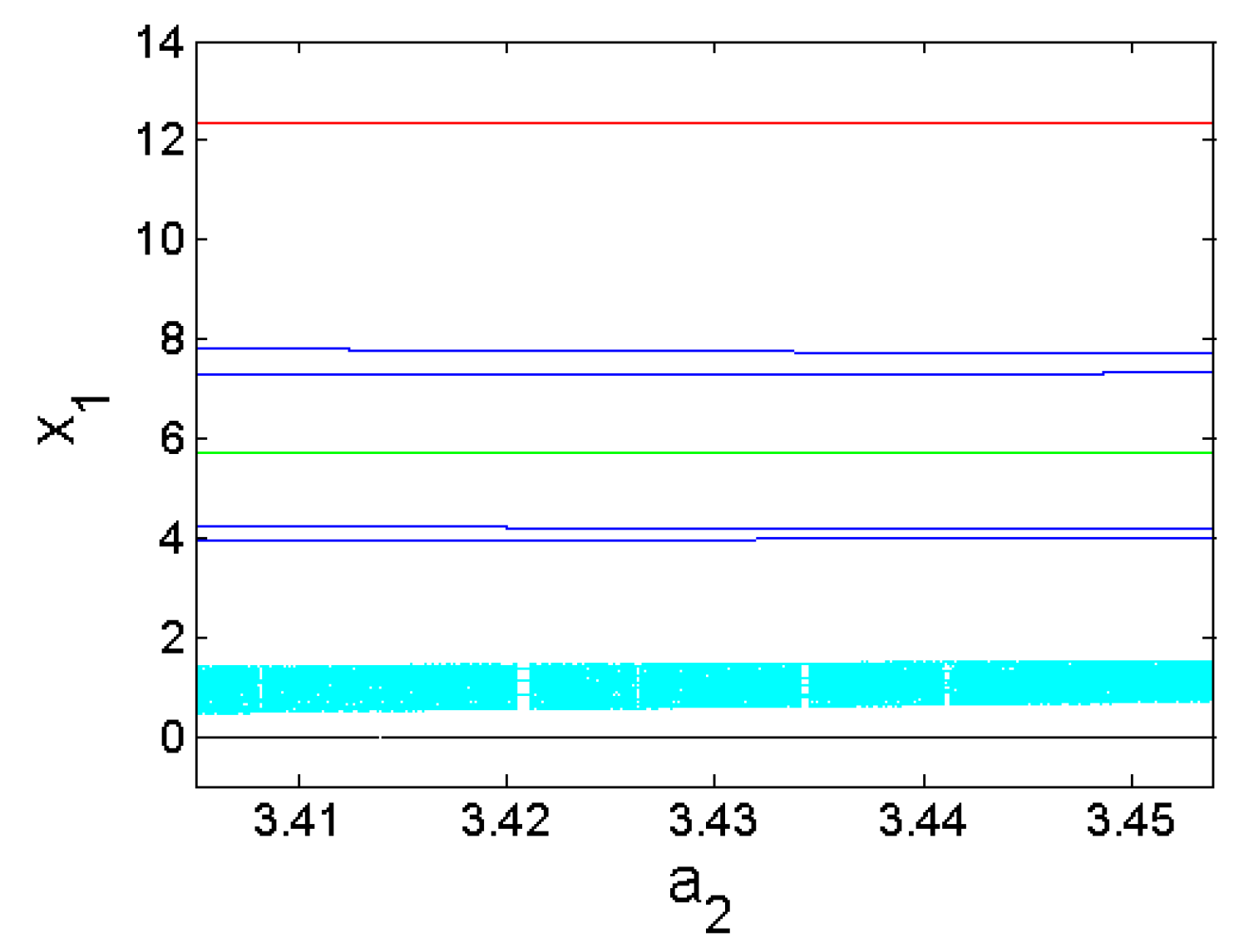
| 11 | Three different limit cycles and a chaotic attractor with fixed point | 3.454 | (a) (0.4,0,0,0,0), (1.2,0,0,0,0); (b) (5.2,0,0,0,0); (c) (4,0,0,0,0); (d) (4.4,0,0,0,0) |
| Components | Property | Rating |
|---|---|---|
| R | Resistance | 10 kΩ |
| Ra0 | Resistance | 6.66 kΩ |
| Ra1 | Resistance | 3.33 kΩ |
| Ra2 | Resistance | 3.5 kΩ |
| Ra3 | Resistance | 10 kΩ |
| Rb | Resistance | 3.33 kΩ |
| R1 | Resistance | 3.85 kΩ |
| R2 | Resistance | 277.77 kΩ |
| R3 | Resistance | 0.1 kΩ |
| Ci(i = 1,…5) | Capacitance | |
| Ui(i = 1,…5) | Operational Amplifier | TL084 |
| Correlation Coefficients | ||||||
|---|---|---|---|---|---|---|
| Image | Plain Image | Cipher Version | ||||
| Direction | Diagonal | Horizontal | Vertical | Diagonal | Horizontal | Vertical |
| [10] | 0.9466 | 0.9839 | 0.9526 | −0.0474 | −0.033 | 0.0068 |
| [11] | 0.9116 | 0.9282 | 0.9644 | −0.0319 | 0.0245 | 0.0295 |
| [55] | 0.8888 | 0.9567 | 0.9239 | −0.00012 | 0.0006 | −0.0052 |
| Proposed method | ||||||
| Boats | 0.9452 | 0.9266 | 0.8855 | −0.0007 | 0.0007 | −0.0015 |
| Bridge | 0.9203 | 0.9403 | 0.8866 | −0.0027 | 0.0008 | −0.001 |
| Clock | 0.9767 | 0.9578 | 0.9426 | −0.0001 | 0.0007 | −0.0023 |
| Encryption Algorithm | Entropy |
|---|---|
| [10] Greyscale flower image | 7.9969 |
| [11] Cameraman image | 7.9455 |
| Proposed method | |
| Boats | 7.9976 |
| Bridge | 7.9974 |
| Clock | 7.9975 |
| Encryption Algorithm | NPCR (%) | UACI (%) |
|---|---|---|
| [10] Grey flower image | 99.15 | 33.21 |
| [11] Cameraman image | 99.34 | 33.61 |
| Proposed method | ||
| Boats | 99.62 | 33.69 |
| Bridge | 99.60 | 33.24 |
| Clock | 99.64 | 35.26 |
| Process | Image Size | |||||
|---|---|---|---|---|---|---|
| 32 × 32 | 64 × 64 | 128 × 128 | 256 × 256 | 512 × 512 | 1024 × 1024 | |
| Iterations for 5DHO chaos generation | 0.000166 | 0.000728 | 0.002900 | 0.010600 | 0.041200 | 0.178700 |
| Constructing permutation sequences (Ph and Pw) | 0.000105 | 0.000172 | 0.000433 | 0.002200 | 0.009500 | 0.032100 |
| Constructing substitution sequence (Sb) | 0.000730 | 0.000730 | 0.000730 | 0.000730 | 0.000730 | 0.000730 |
| Encryption process | 0.001100 | 0.004500 | 0.014900 | 0.053700 | 0.062700 | 0.968700 |
| Total time | 0.002100 | 0.006130 | 0.018963 | 0.067230 | 0.114130 | 1.180230 |
| Encryption Algorithm | Image Size | |||||
|---|---|---|---|---|---|---|
| 32 × 32 | 64 × 64 | 128 × 128 | 256 × 256 | 512 × 512 | 1024 × 1024 | |
| [43] | N.R | 0.0045 | 0.0163 | 0.0629 | 0.2673 | 1.2157 |
| [52] | N.R | N.R | N.R | 0.0460 | 0.2300 | 0.9530 |
| [53] | N.R | N.R | N.R | 0.0790 | 0.2454 | N.R |
| [54] | N.R | N.R | N.R | N.R | 0.2141 | N.R |
| Proposed method | 0.0021 | 0.0062 | 0.0190 | 0.0672 | 0.1141 | 1.1802 |
| Test-Name | P-Value | Result |
|---|---|---|
| Frequency | 0.890240 | Passed |
| Block-frequency | 0.563092 | Passed |
| DFT | 0.378341 | Passed |
| Rank | 0.236565 | Passed |
| Runs | 0.089504 | Passed |
| Longest runs of ones | 0.172795 | Passed |
| Overlapping templates | 0.320178 | Passed |
| No overlapping templates | 0.465065 | Passed |
| Universal | 0.518372 | Passed |
| Approximate entropy | 0.844091 | Passed |
| Linear complexity | 0.042035 | Passed |
| Cumulative sums (forward) | 0.793995 | Passed |
| Cumulative sums (reverse) | 0.899532 | Passed |
| Serial test 1 | 0.179396 | Passed |
| Serial test 2 | 0.662233 | Passed |
| Random excursions x = 1 | 0.207249 | Passed |
| Random excursions variant x = 1 | 0.042985 | Passed |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nestor, T.; De Dieu, N.J.; Jacques, K.; Yves, E.J.; Iliyasu, A.M.; Abd El-Latif, A.A. A Multidimensional Hyperjerk Oscillator: Dynamics Analysis, Analogue and Embedded Systems Implementation, and Its Application as a Cryptosystem. Sensors 2020, 20, 83. https://doi.org/10.3390/s20010083
Nestor T, De Dieu NJ, Jacques K, Yves EJ, Iliyasu AM, Abd El-Latif AA. A Multidimensional Hyperjerk Oscillator: Dynamics Analysis, Analogue and Embedded Systems Implementation, and Its Application as a Cryptosystem. Sensors. 2020; 20(1):83. https://doi.org/10.3390/s20010083
Chicago/Turabian StyleNestor, Tsafack, Nkapkop Jean De Dieu, Kengne Jacques, Effa Joseph Yves, Abdullah M. Iliyasu, and Ahmed A. Abd El-Latif. 2020. "A Multidimensional Hyperjerk Oscillator: Dynamics Analysis, Analogue and Embedded Systems Implementation, and Its Application as a Cryptosystem" Sensors 20, no. 1: 83. https://doi.org/10.3390/s20010083
APA StyleNestor, T., De Dieu, N. J., Jacques, K., Yves, E. J., Iliyasu, A. M., & Abd El-Latif, A. A. (2020). A Multidimensional Hyperjerk Oscillator: Dynamics Analysis, Analogue and Embedded Systems Implementation, and Its Application as a Cryptosystem. Sensors, 20(1), 83. https://doi.org/10.3390/s20010083


.png)


