1. Introduction
Along with the continuous development of industrial technology, networked control systems (NCSs) have gradually become a new trend and attracted much attention [
1,
2,
3]. Compared with traditional point-to-point control systems, NCSs have advantages such as high reliability, reduced weight, low cost, and ease of maintenance [
4,
5]. The NCSs provide the low-level processing function via intelligent unit and are more conductive to the implementation of complex control algorithms [
6,
7,
8,
9]. However, the signal of NCSs is transmitted via bus network, which brings new challenges to algorithm design, such as networked-induced time-delay, packet dropout, and packet disordering.
Due to the strong nonlinear fitting characteristics of complex nonlinear systems, the Takagi-Sugeno (T-S) fuzzy model has been widely used in the study of nonlinear systems since it was proposed [
10,
11,
12]. In [
13], a new fuzzy Lyapunov function for stability analysis which depends on both fuzzy weighting functions and their first-order derivatives is proposed, and less conservative results can be obtained by the proposed method. Additionally, the filtering problem for T-S fuzzy systems with redundant channels and noise is investigated in [
14]. The T-S fuzzy model provides a method of stability analysis and performance synthesis which is based on the linear approach for nonlinear systems.
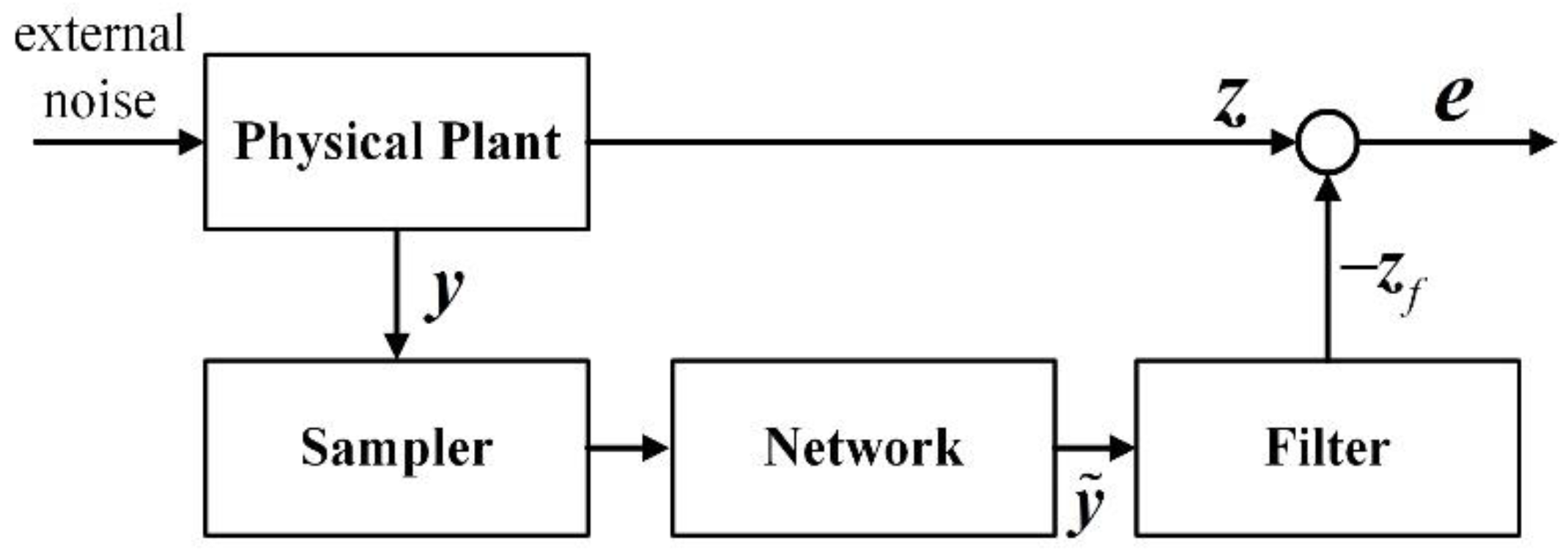
In addition, the estimation of unmeasured system parameters is significantly important, since the estimated parameters can not only be used in the design of controller but also for on-line monitoring [
15,
16]. For this kind of problem, the current method is mainly based on filtering technology, and a simple diagram of filtering for NCSs is shown in
Figure 1. Among the filters, the
H∞ filter stands out because it has robust stability against external noise without priori knowledge of noise and precise mathematical model [
17,
18,
19]. However, the gain perturbation of the filter is inevitable in practice, such as the error in analog-to-digital conversion and the finite word length of computer, which may affect the accuracy of the filtering results. Thus, it is desirable to design a non-fragile filter which can maintain precision with the gain perturbation of the filter.
At the same time, the parameter estimation is based on the assumption that the signal of the sensors is accurate. However, in practical applications, the sensors may fail due to electromagnetic interference or poor working environment, which will result in inaccurate filtering results or even an accident [
20,
21,
22]. A robust
H∞ filter is designed for a class of Markovian jump neural networks with random sensor failure in [
23], but in the literature, the gain of sensor failure is only
, which does not match the actual situation. In [
24], the sensor failure is described as a random variable obeying the Bernoulli distribution, but the probability distribution cannot be accurately obtained. In addition, most researches only focus on a fixed mode of sensor failures, which brings limitation to the application of filter. Therefore, it has great significance and practical value to design a non-fragile filter with sensor fault tolerance to improve the safety and reliability of system.
In this paper, the robust non-fragile H∞ filtering problem for T-S fuzzy networked control systems with time-delay, parameter uncertainties and sensor failures is studied. The main contributions of this paper can be concluded as follows: (i) the gain perturbation of the filter is considered, so that the designed non-fragile filter has a certain range of margins for disturbance; (ii) the unknown gain matrix of sensor failures is converted into a dynamic interval, which expands the range of allowed sensor failures; (iii) the free-weighting matrix method and related linear matrix inequalities (LMIs) method are used to reduce the conservativeness of the results.
The remainder of this paper is organized as follows:
Section 2 introduces the modeling method of NCSs with sensor failure and the design method of filter based on the T-S fuzzy model. The main results are presented in
Section 3, including the analysis and synthesis of the filtering error system. Numerical simulation results are shown in
Section 4 and finally the conclusion is presented.
2. Problem Formulation
Consider the NCSs with time-delay, which can be described by the T-S fuzzy model as follows:
Plant rule
i: If
is
and
and
is
, then
where
denotes the fuzzy set,
r denotes the number of IF-THEN rules and
denotes the premise variable.
is state variables;
is measured outputs;
is unmeasured parameters and
is the noise signal which belongs to
.
are matrices with appropriate dimension and
are unknown matrices which represent time-varying uncertainties.
is the health parameters of system, which represents the physical characteristics of each component.
Remark 1. The health parameters are considered in this paper because the performance degradation of the components in the system is inevitable during the working process. If the health parameters move away from their nominal values, the shift in other variables will be induced. In most cases, the health parameter is defined as the efficiency or capacity of each component and can be obtained by empirical formula or testing equipment. They may be treated as a set of biases and can be augmented to the system state.
By fuzzy blending, the final augmented dynamic fuzzy model can be rewritten as
where
and
is the grade of the membership value of
in
with
and
. Then, there is
It is assumed that the uncertainties of system can be described in the following form:
where
are known matrices and
is a time-varying unknown matrix which satisfies
Since time-delay depends heavily on variable network conditions [
4], they are usually time-varying, random, and unknown. In general, the time-delay
can be divided into queuing delay
, transmission delay
and reception delay
.
and
depend on the physical characteristics of the network, and for a given networked structure, they are regular. The uncertainties of
mainly come from
, which is affected by the network protocol. Because the load capacity of the bus is constant, there is an upper bound
of
for a certain network protocol, and
is a random variable that is only related to the time-delay in the previous moment. The upper bound
is constant for a certain networked structure and network protocol. It is assumed that both the sensors and actuators are time driven. The data has timestamp and are transmitted in a single-packet, and incorrect order of the data packet does not exist. Then the upper bound
of
may be estimated; see [
25] for more detail.
As a consequence,
can be modeled as a finite state Markov stochastic process on a finite set
. The transition probability from
at time
t to
(
j ≠
i) at time
t+Δ
t is
where
and
.
is the transition probability rates from
at time
t to
(
j ≠
i) at time
t+Δ
t, and there is
.
Then a more general model of sensor failures is introduced.
is the measured outputs with sensor failures, which has the form
Define , and is the output gain of i-th sensor signal. and are the upper and lower bounds of output gain, respectively, and denotes that the i-th sensor is normal.
Then, the following non-fragile fuzzy filter is considered.
Filter rule
i: If
is
and
and
is
, then
where
is filter state and
is filter output.
are the filter parameters to be determined. Similarly,
and
are variations of filter parameters, which satisfy
Hence, the dynamic model of non-fragile T-S fuzzy filter can be constructed as:
Define
and
, and the filtering error system is given by
where
Define the following parameters
The goal is to design a filter in the form of Equation (10) so that when there are sensor failures, the filtering error system (11) can still meet the following requirements simultaneously:
- (1)
The filtering error system is asymptotically stable when ;
- (2)
Under the zero initial condition, the filtering error system satisfies
for any nonzero
.
3. Main Results
In this section, the analysis and synthesis of the filtering error system is conducted. Before proceeding with the study, the following Lemma is needed.
Lemma 1 ([
26])
. are real matrices with appropriate dimensions, and is a time-varying unknown matrix which satisfies . Then for a scalar , the following inequalityalways holds. Theorem 1. If there exist positive matricesandsuch that the following inequality holds:wherethen the filtering error system (11) is asymptotically stable and the prescribed H∞ performanceis guaranteed under the zero initial condition. Proof. Select a Lyapunov function as
where
When
, the derivation of
is
It is obvious that there is
Then,
can be rewritten as
where
By the Schur complement, if inequality (14) holds, there is . So it can be obtained that there is and the filtering error system (11) is asymptotically stable when .
Secondly, a new function is defined
where
. So under the zero initial condition, there is
Similarly, referring to the derivation of Equation (18), there is
where
By the Schur complement, it follows that
If the inequality holds, it can be obtained that there is , which implies that Equation (12) holds for any nonzero . The proof is completed. □
Theorem 2. For a given constant scalar, the filtering error system (11) is asymptotically stable with a H∞ performance levelif there exist positive definite matrices, matricesand scalarssuch that the following inequalities hold:where Moreover, the parameters of fuzzy
H∞ filter can be solved by
Proof. According to [
27],
can be rewritten as
where
The gain matrix of sensor signal is an unknown matrix for various fault modes, which makes the design of the filter complex. However, since is bounded, can be transformed into a class of dynamic interval matrices.
Let
and
, and the output gain can be rewritten as
. So, we define
Then, the dynamic interval matrices of
is
Similarly, we can define
, and the gain matrix can be rewritten as
where
in which
is the
i-th column of identity matrix
. Additionally, it is obvious that there is
.
Substituting Equation (27) into Equation (24),
can be decomposed into
where
in which
Then by the Schur complement,
is equivalent to
For time-varying uncertainties of the filtering error system, based on Equations (4), (9) and Lemma 1, Equation (30) can be rewritten as
By applying the Schur complement to Equations (22) and (23), there are
and
Then based on Equations (31)–(33), there is
which is the same as Equation (21). The proof is completed. □
Remark 2. The fault-tolerant filter designed by Theorem 2 has robustness against any sensor failures with gain matrix, whereandare composed of the minimum and maximum allowable value of sensors failures, respectively. Obviously, the sensor failures are not limited to a given finite interval and converted into a dynamic interval, which expands the range of the allowed sensor failure and improves the reliability of the system.
4. Simulation Example
In this section, a simulation example is given to illustrate the effectiveness of the proposed method in this paper. The system parameters are defined as follows:
Furthermore, the membership functions are
The state space of time delay is
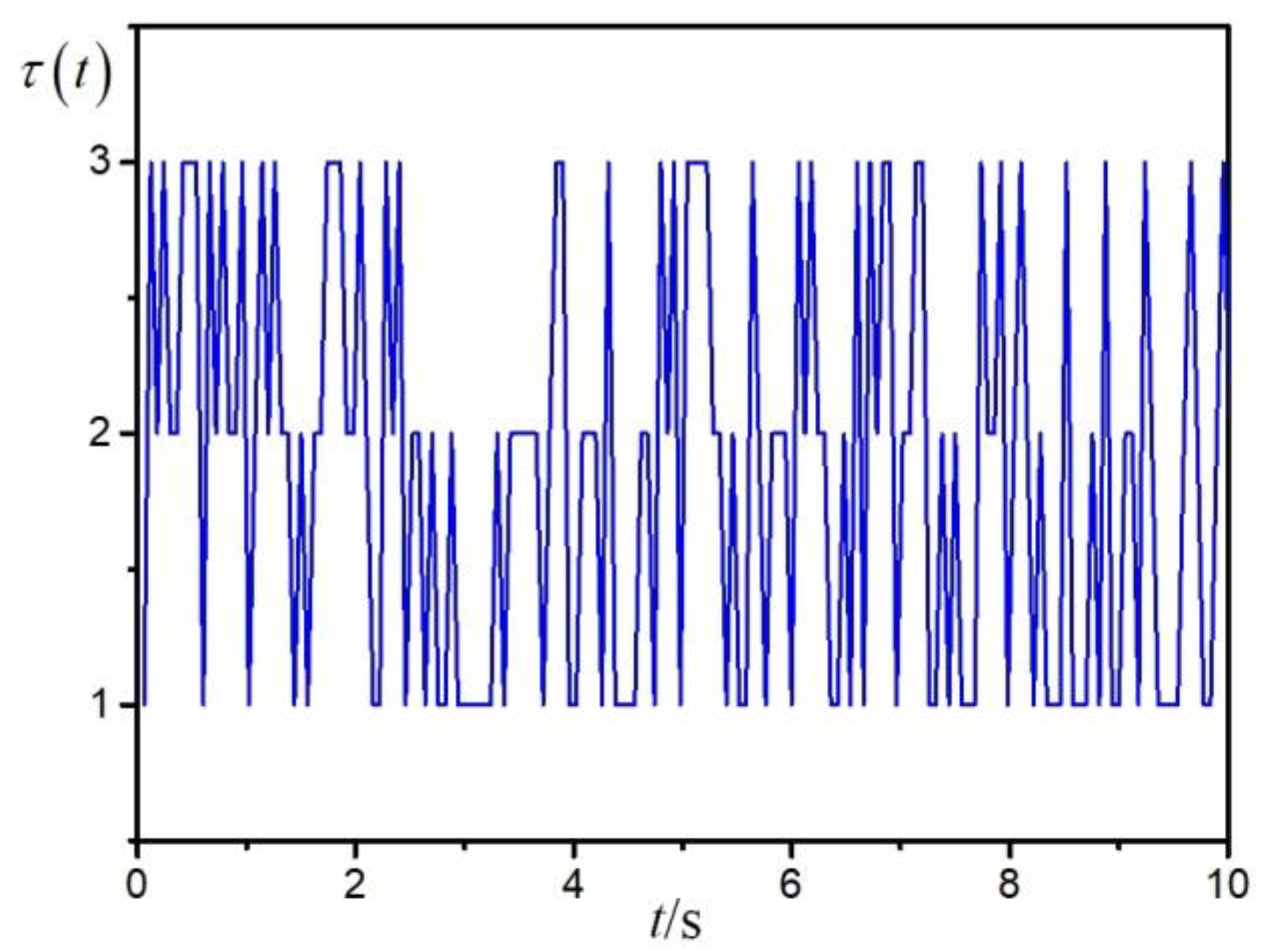
, and the state transition matrix of
is
Based on the matrix
, the distribution of the Markov chain-type time-delay is shown in
Figure 2. The range of sensor failures is assumed as
. The given value of
is
and then the filter parameters can be solved by Theorem 2:
The system sampling period is set as
. The initial condition is defined as
and the external disturbance
is
Furthermore, the health parameter is defined as follows to represent the performance degradation during the simulation:
.
Figure 3 is the filtering error response
. It can be seen that the filter designed in this paper can remain stable under the influence of sensor failures, parameter uncertainties and external disturbance. And
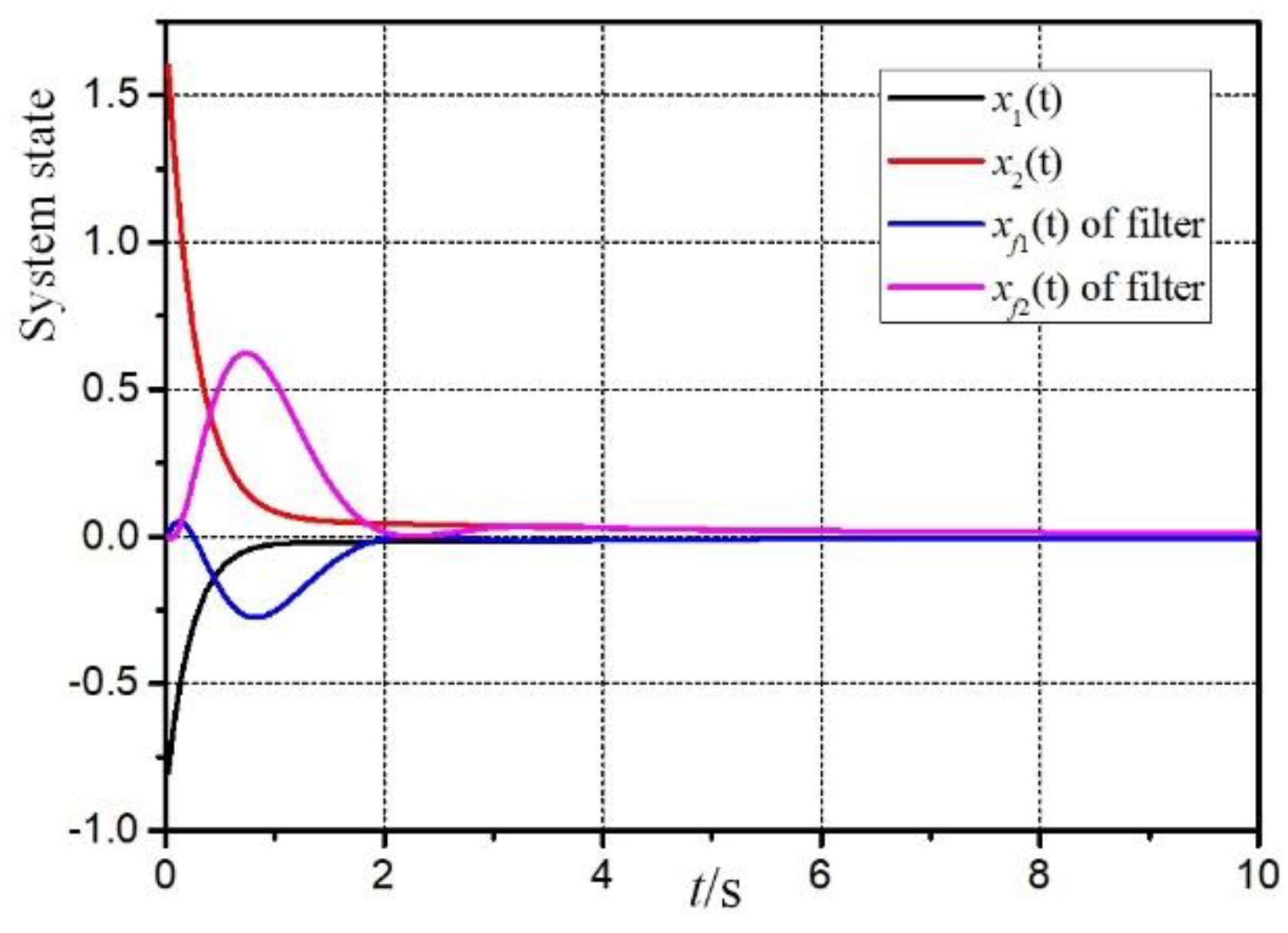
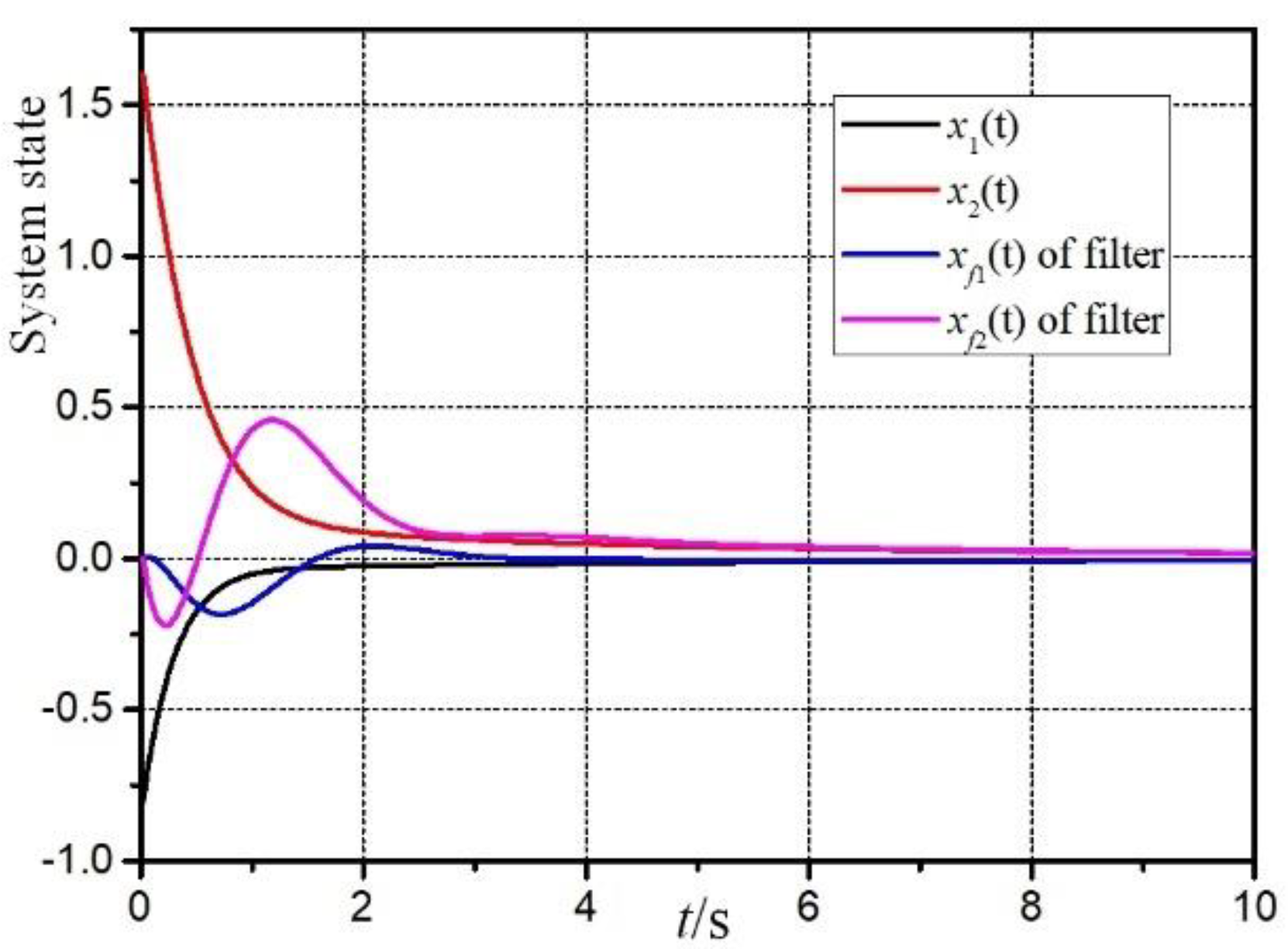
Figure 4 and
Figure 5 are the responses of the system and filter state.
To inspect the conservativeness of the sufficient condition proposed in this paper, the minimum
obtained by the method in this paper (defined as
) is compared with the results solved by the method in [
28] (defined as
), as shown in
Table 1. Note that, in [
28] different
values may lead to a different minimum
, and
has no influence on
. It can be seen that the non-fragile filter sacrifices some conservativeness to obtain robustness against perturbation of filter parameters and sensor failures. However, from the comparison results,
is close to the minimum
, which indicates that the method in this paper involves fewer sacrifices regarding conservativeness.