Optimal Energy Aware Clustering in Sensor Networks

Abstract

Sensor networks is among the fastest growing technologies that have the potential of changing our lives drastically. These collaborative, dynamic and distributed computing and communicating systems will be self organizing. They will have capabilities of distributing a task among themselves for efficient computation. There are many challenges in implementation of such systems: energy dissipation and clustering being one of them. In order to maintain a certain degree of service quality and a reasonable system lifetime, energy needs to be optimized at every stage of system operation. Sensor node clustering is another very important optimization problem. Nodes that are clustered together will easily be able to communicate with each other. Considering energy as an optimization parameter while clustering is imperative. In this paper we study the theoretical aspects of the clustering problem in sensor networks with application to energy optimization. We illustrate an optimal algorithm for clustering the sensor nodes such that each cluster (which has a master) is balanced and the total distance between sensor nodes and master nodes is minimized. Balancing the clusters is needed for evenly distributing the load on all master nodes. Minimizing the total distance helps in reducing the communication overhead and hence the energy dissipation. This problem (which we call balanced k-clustering) is modeled as a mincost flow problem which can be solved optimally using existing techniques.

1. Introduction

Wireless ad-hoc sensor networks are a prime example of a second generation distributed system. Such dynamic, adaptive and distributive systems will find wide applications in our daily lives, including, medical applications, data collection and monitoring, military and space. There are many fundamental problems that sensor networks research will have to address in order to ensure a reasonable degree of cost and system quality. Some of these problems include sensor node clustering, master selection and energy dissipation. The research community is actively looking into these challenges. [6] describes an optimal sensor node scheduling methodology for energy optimization during intruder detection. [14] discusses the importance of energy dissipation in these systems. [2] contains a detailed outline of the design and challenges of these systems and also discusses the importance of localized power optimization/aware algorithms. Information routing on sensor networks especially in a power aware fashion is extremely important. [3,4,5] are some of the publications in this direction. [4] studies online power aware routing in large sensor networks. They seek to optimize the system lifetime and develop and approximation algorithm to achieve this. [1,7,13] emphasize the importance of low power communication, computation and partitioning (clustering) in sensor networks. In this paper we look at the theoretical aspects of the sensor node clustering problem. The proposed algorithms could be used for partitioning the sensor nodes into subgroups for task subdivision or energy management.

Clustering is defined as the grouping of similar objects or the process of finding a natural association among some specific objects or data. It finds applications in many fields. Clustering, specifically in sensor networks, could be used to solve a verity of problems. [19] uses clusters to transmit processed data to base stations, hence minimizing the number of nodes that take part in long distance communication. This directly affects the overall system energy dissipation. Apart from sensor networks, clustering has been applied tremendously in fields like VLSI-CAD and data mining [10]. A classical analytic VLSI placer [12] uses clustering for efficient standard cell placement. In this work we solve some interesting instances of the clustering problem optimally and study many others. These problem instances have many applications in sensor networks, specially in master node selection and energy management.

Specifically, we solve the balanced k-clustering problem optimally, where k signifies the specific master nodes in the system. The balanced k-clustering problem tries to group the sensor nodes such that each cluster is balanced (in terms of number of sensor nodes) and has exactly one master. The proposed algorithm is based on min-weight matching and optimizes the total spatial distance between sensor and master nodes. This would help in balancing the system load on each master since all the clusters are balanced. Minimizing the total distance between sensor and master nodes would reduce the energy dissipated by sensor nodes while making communication with the corresponding masters. Other interesting extensions of related clustering problems are also discussed.

The rest of the paper is organized as follows. Section 2 describes the energy aware clustering problem that we solve optimally along with a formal statement of the problem.

The optimal method for solving this problem is described in section 3. Section 4 discusses some interesting extensions in cost functions and algorithms. Section 5 presents the result of some preliminary experiments and section 6 concludes the paper.

2. Problem Description

In this section, we describe a sensor network framework. We show the effect of clustering quality on communication energy dissipation in such networks and Hence, We formulate a clustering problem to minimize the communication energy dissipation. Throughout the paper, we assume that sensors are distributed in a spatial region and hence can be represented using points in two dimensional plane.

In most of the applications, sensors are required to communicate with one another to transfer the collected data to base stations. They also need to collaborate to route the control information from the base stations to a specific sensor. Communication is usually the main source of energy dissipation in sensors, which greatly depends on the distance between the source and destination of a communication link. Previous research have shown that energy dissipation e to transmit a message to a receiver at distance d can be estimated by the following formula:

$$\begin{array}{l}e=k{d}^c[3,4,19]\end{array}$$

where k and c are constants for a specific wireless system (usually 2 < c < 4).

Since message transmission energy consumption is proportional to d^c where c > 2, significant amount of energy savings can be made by partitioning the sensor nodes into clusters and transmitting the information in a hierarchical fashion [4,19]. Moreover clustering can drastically relax the resource requirements at the base stations.

Cluster formation, hence, is one of the pivotal problems in sensor network applications and can drastically affect the network's communication energy dissipation. Clustering is performed by assigning each sensor node to a specific master node. All communication to (from) each sensor node is carried out through its corresponding master node. Obviously one would like to have each sensor to communicate with the closest master node to conserve its energy, however master nodes can usually handle a specific number of communication channels. Therefore there is a maximum number of sensors that each master node can handle. This does not allow each sensor to communicate to its closest master node, as that master node might have already reached its service capacity.

Figure 1. Partitioning the nodes into clusters A and B leads to a solution dissipating less communication energy compared to clusters C and D.

Figure 1. Partitioning the nodes into clusters A and B leads to a solution dissipating less communication energy compared to clusters C and D.

Figure 1 demonstrates an example of clustering affect on communication energy consumption. In this figure, black filled points indicate master nodes while the empty circles represent the sensor nodes. Assuming the capacity constraint of 3 for each master node, two sample clustering options, namely A-B and C-D have been shown. The total square of distances between master nodes and sensors in clustering A-B is 65 unit, while it is 117 units for clustering C-D. Considering the relation of energy dissipation and this simplified metric (total square of distances), Figure 1 highlights the effect of clustering quality on network's total energy dissipation.

Therefore, an important optimization question to be answered is: to which master node each sensor has to communicate such that the capacity constraint for the master nodes is met and the total energy dissipation of the sensors is minimized. This problem can be formally stated as follows:

Given n sensors and k master nodes, we would like to form sets S₁,…,S_k (clusters) such that:

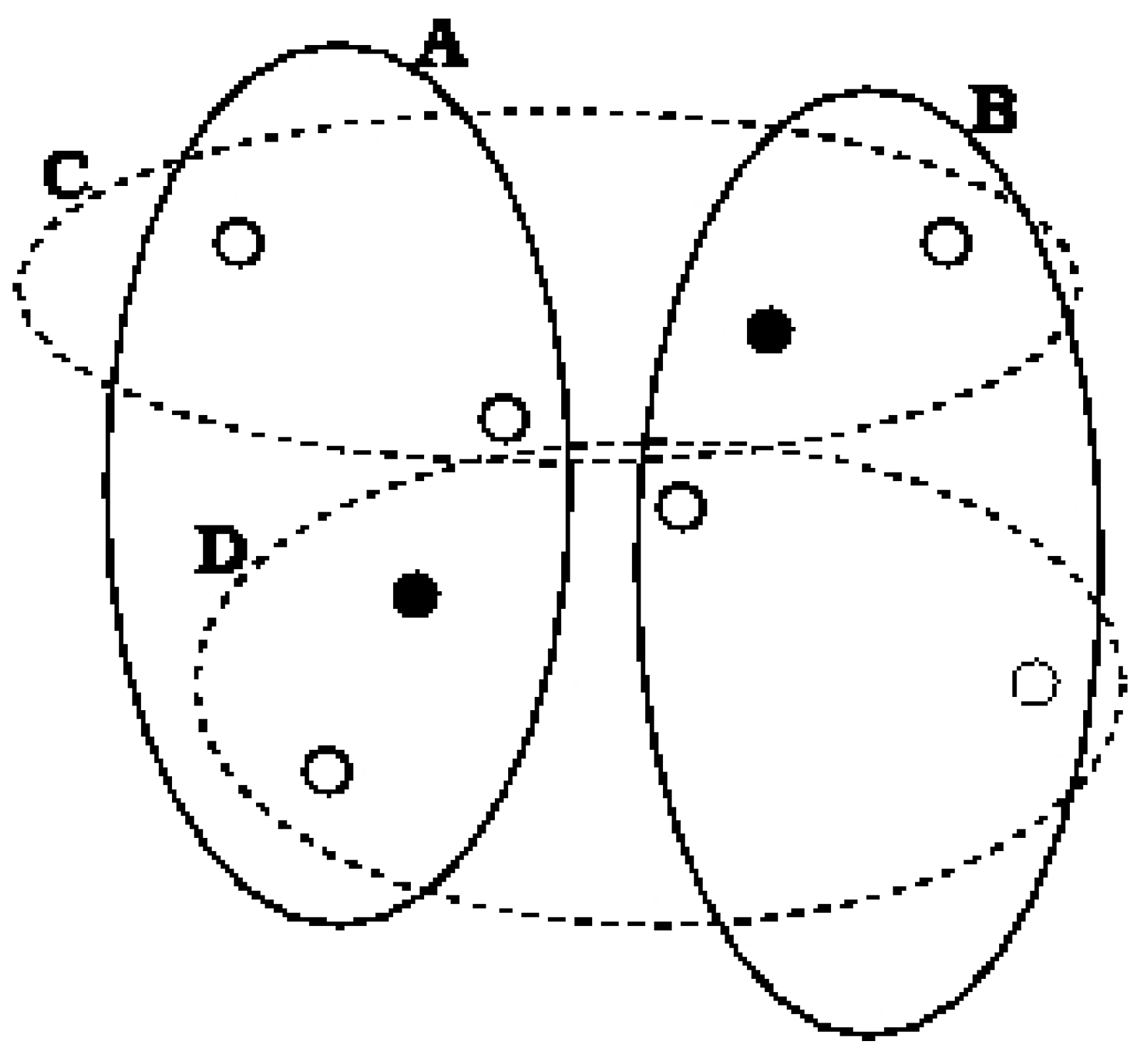
• Each point belongs to exactly one of clusters.
• Clusters are balanced, i.e.:

  $$\frac{1}{k}-\delta \le \frac{\left(S_i\right)}{n}\le \frac{1}{k}+\delta i=1,\dots ,k$$

  where 0 ≤ δ ≤ 1 / k is the unbalance factor. δ depends on n/k and the master nodes' actual capacity. In this paper, our focus is on strictly balanced clusters and we assume δ = 0. Therefore, we assume that n is a multiple of k.
• The total cost over all clusters is minimized. Specifically, the cost for each cluster S_i is:

  $$C_i={\displaystyle \sum _{x\subset S_i}f\left(x,a_i\right)}$$

  where x and a_i are the locations (x and y coordinates) of a sensor and the master node in cluster i. f(x, a_i) is the message transmission energy dissipation between a sensor and a master node. Function f can be as simple as the square of the distance between these two points. The balanced clustering feature makes the k-clustering problem in our work distinct from previous works [19,8,18]. In the next section, We solve this problem optimally by transforming it to matching on bipartite graphs.

3. Optimal k-Clustering for Energy Optimization

In this section, we present an optimal algorithm to solve the balanced k-clustering problem formulated in the previous section. Before explaining our method, we explain the optimal clustering algorithm when there is no balance constraint.

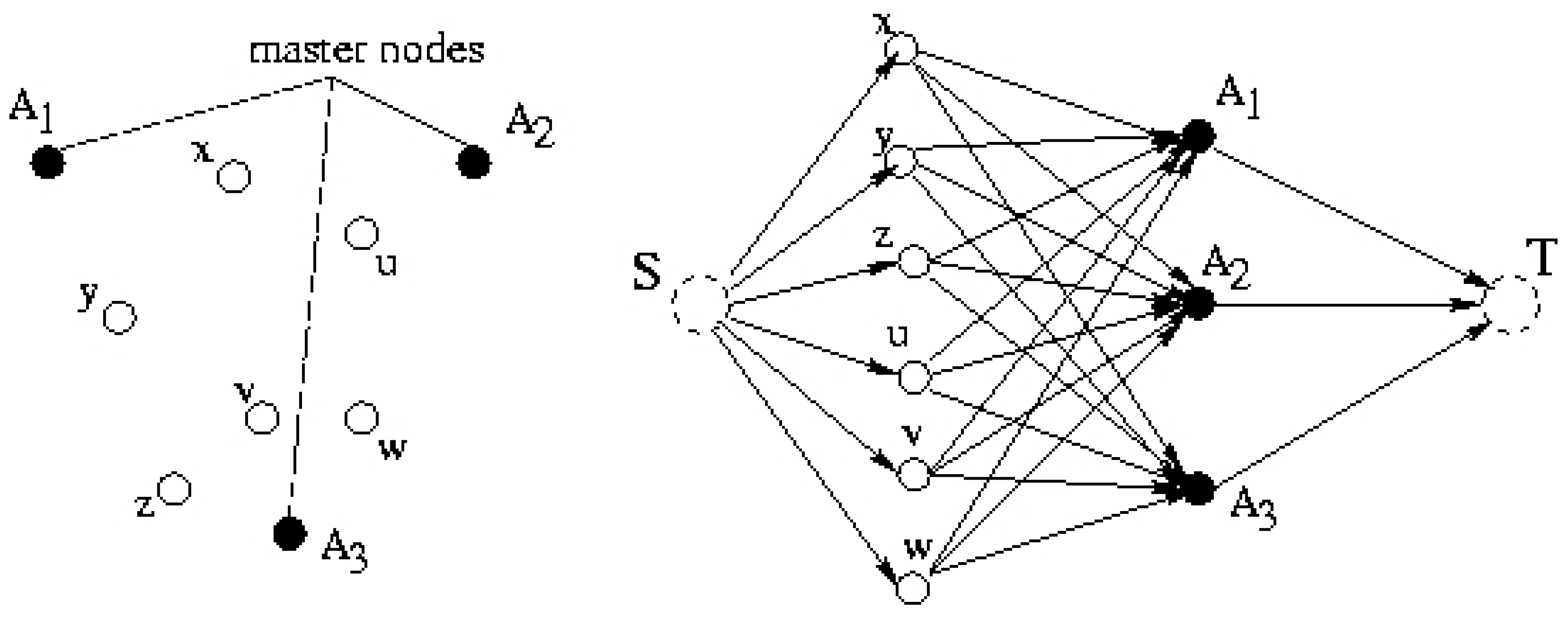
3.1 General Clustering (no balance constraint)

If there is no balance constraint in the aforementioned clustering problem, then the problem can be solved optimally using Voronoi diagrams. First we build Voronoi diagram of the k master nodes. These master nodes are also called anchor points and we use these two terms interchangeably. Then we locate every given point (sensor) in the constructed Voronoi diagram. A point located in one Voronoi region will be added to the cluster associated with the anchor point of that Voronoi region. k-clustering solution is obtained after locating and assigning each point. It is straightforward to prove that this solution is optimal, since we find the closest anchor point for every point in the problem. Constructing the Voronoi diagram of k anchor points, can be done optimally in O(k log k) time [9]. Moreover, locating n points in such a Voronoi diagram can be performed in O(n log n) time [9]. Therefore, the algorithm runs in O(n log n) time. Figure 2 shows an optimal k-clustering solution for an instance of the problem. Note that the balance constraint is not met.

Figure 2. k-clustering using Voronoi diagrams. Clusters are denoted by dashed lines.

Figure 2. k-clustering using Voronoi diagrams. Clusters are denoted by dashed lines.

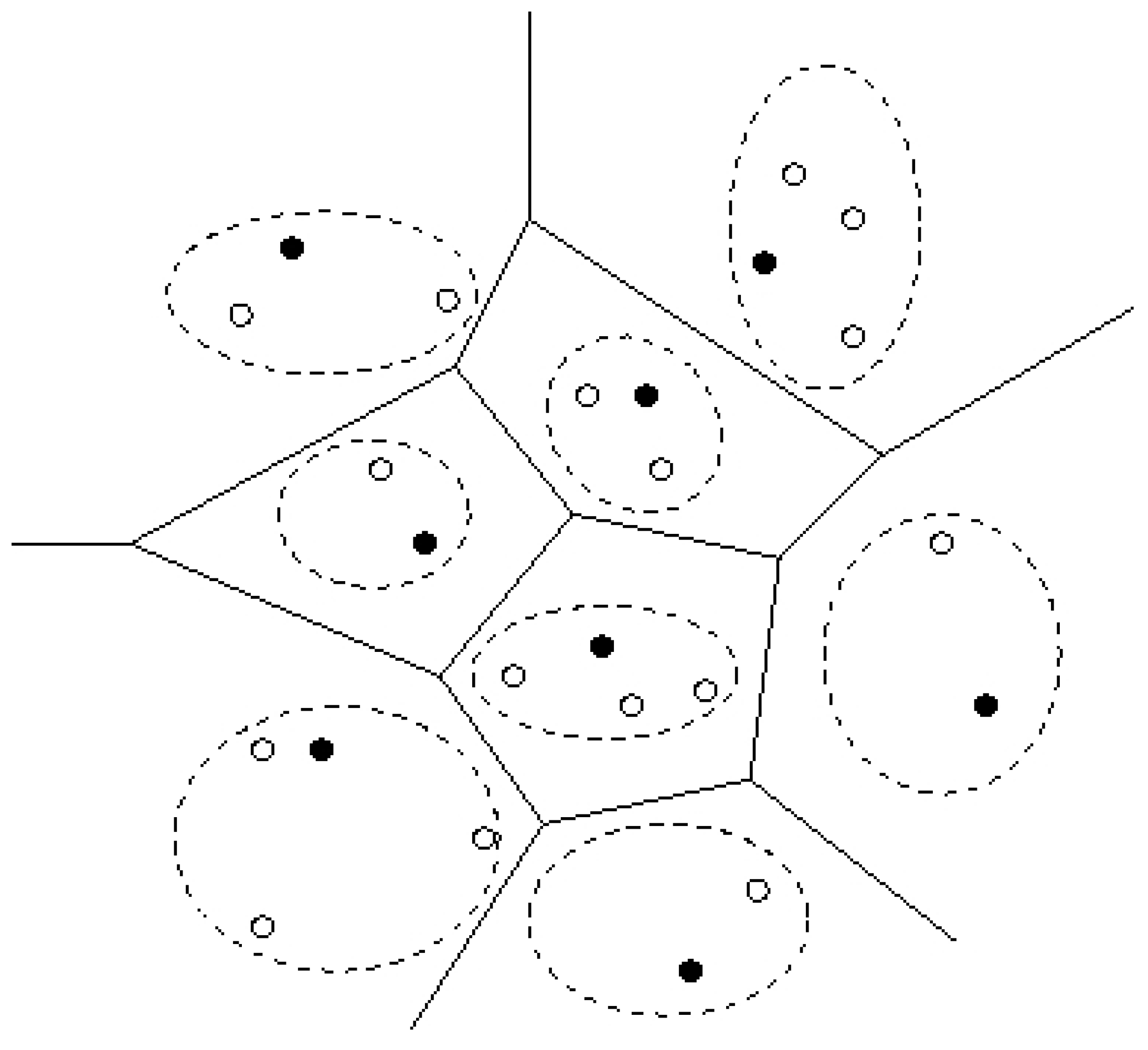
3.2 Balanced k-Clustering

As discussed earlier, each master node can handle a certain number of communication channels. This constrains the number of sensor nodes that can communicate with a master node, thus existing in a cluster. The above approach does not take this constraint into account, therefore it might lead to a solution that overloads some master nodes. Such a solution is not feasible in practice. The balanced clustering formulation can overcome this drawback by having an upper/lower bound on the size of each cluster.

In this section, we transform the balanced k-clustering problem to a min-cost flow instance. This instance, can be solved optimally using existing techniques.

Suppose we are given n points and we want to group them into k clusters. For the sake of simplicity, we assume that n is a multiple of k. We want to obtain a strictly balanced solution, i.e., each cluster has to contain exactly n/k points.

We build a directed graph, G, in the following way. For each sensor node and for each master node we put a vertex in G. Moreover, for any pair of sensor and master nodes, such as (x, a_i), we put a directed edge from x to a_i in G. Each edge has a weight equal to the message transmission energy dissipation between the two end vertices. For example, an edge connecting x and a_i has weight f(x, a_i). A source node S and a sink node T are also added to G. There are n directed edges from S to all vertices corresponding to sensors nodes. Similarly, there are k directed edges from vertices corresponding to master nodes to T. All edges incident to S or T have weight 0. Finally, nodes corresponding to sensors have capacity 1, while nodes corresponding to master nodes have capacity n/k. S and T both have infinite capacity. Figure 3 shows an example of G built for a sample network of sensors.

Figure 3. Transforming a balanced k-clustering instance to a minimum cost flow instance. Each sensor node has unit capacity, while each master nodes has capacity n/k.

Figure 3. Transforming a balanced k-clustering instance to a minimum cost flow instance. Each sensor node has unit capacity, while each master nodes has capacity n/k.

We pass n unit of flow from S to T. Since each vertex corresponding to a sensor node (or sensor node for short) has unit capacity, they all have to pass exactly one unit of flow. Otherwise, S can not send n units of flow towards T. Similarly, each vertex corresponding to a master node (or master node), has to pass exactly n/k units of flow. Considering that we solve the problem integrally, the flow passing from each sensor node has to pass through exactly one master node. Furthermore, there are exactly n/k sensor nodes passing their flow through each master node. Therefore, assigning each sensor to the master node collecting its flow, leads to a valid k-clustering solution. Therefore, each flow solution is corresponding to a k-clustering solution. Moreover, the cost of each flow solution is equal to the corresponding k-clustering solution, because all edges adjacent to S or T have no cost and other edges have costs equal to energy dissipation between the sensor node and its cluster master node. This is exactly the same cost for the corresponding k-clustering solution.

Similarly, any solution to the k-clustering problem is corresponding to a solution to the flow problem on the constructed graph and these two solutions have the same cost. The min-cost flow problem, can be optimally solved using existing techniques in O(|V|³) time [16,11] where |V| is the total number of vertices in the graph. Constructing G and the corresponding k-clustering solution can be done in O(n.k) time. Hence, the k-clustering problem can be optimally solved in O((n+k)³) time.

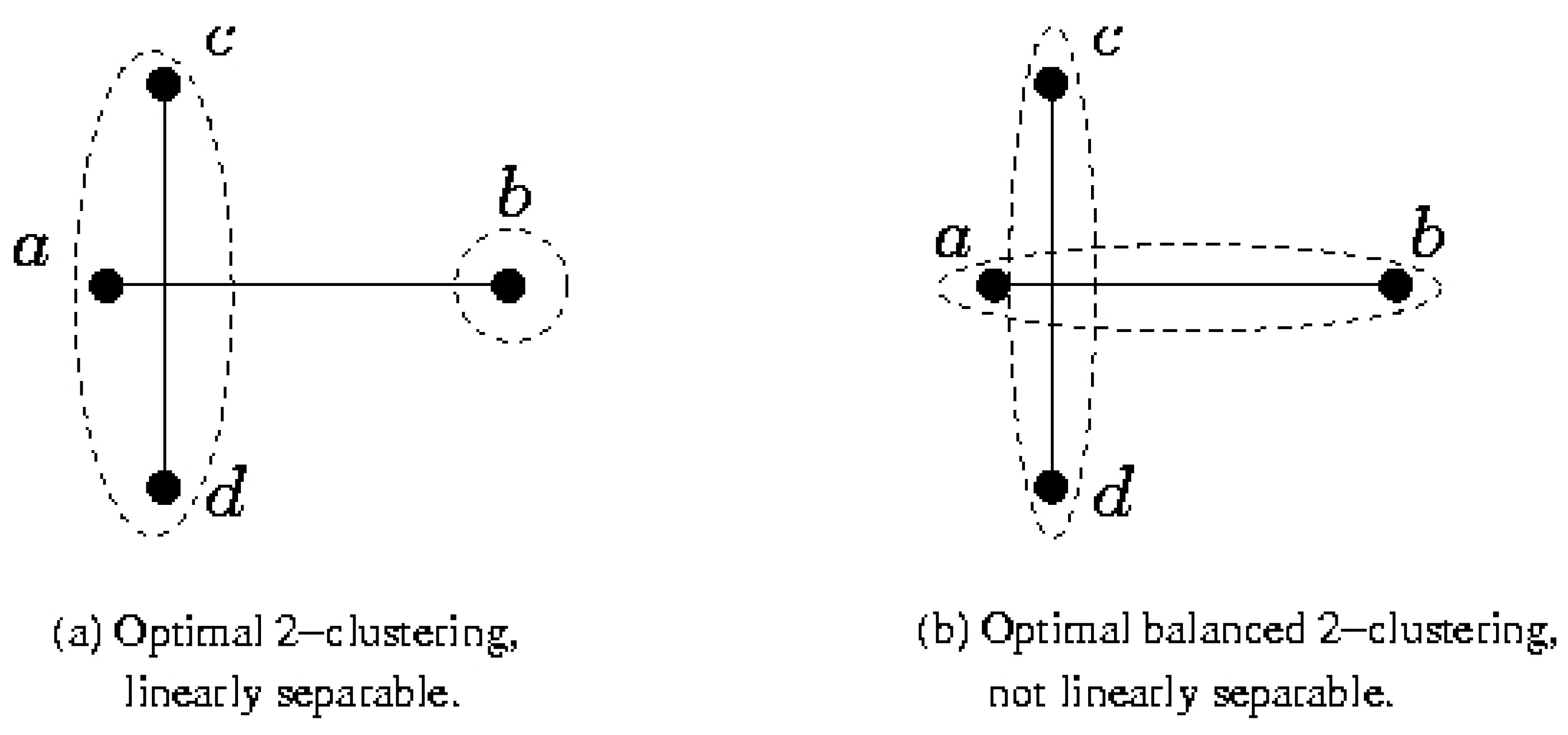
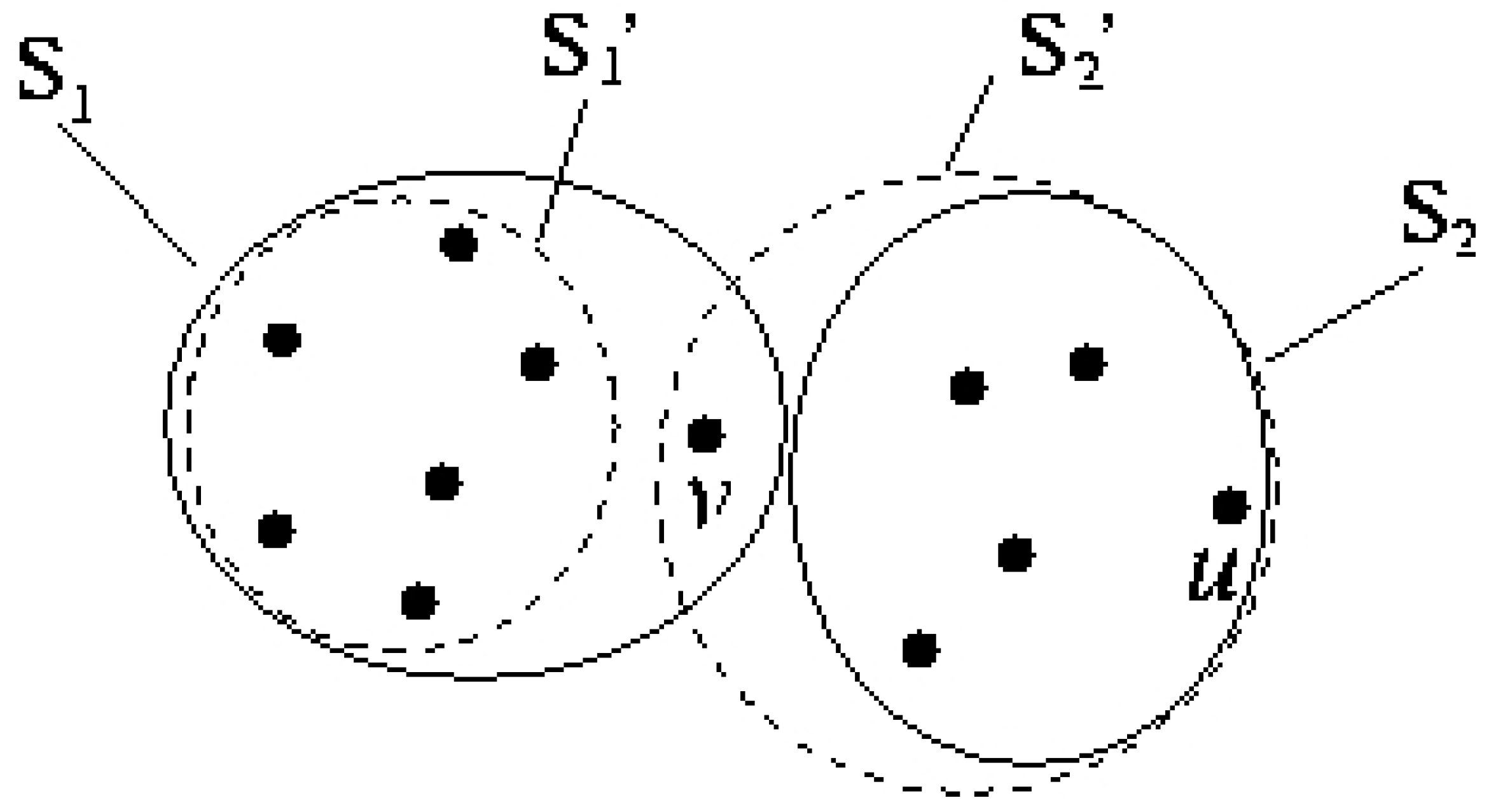
4. 2–Clustering to Minimize the Maximum Diameter

Some sensor network applications, require sensors in a cluster to talk to eachother. This might not be feasible if two sensors in a clusters are far from eachother, since there is a maximum communication range for each sensor. Forming clusters for such applications requires that distance between all pairs of sensors be less than a threshold. The problem of forming such clusters can be formally stated as a balanced minimum diameter k-clustering problem.

In this section, we present an optimal algorithm for balanced minimum diameter 2-clustering problem. We first mention the previous work on similar minimum diameter clustering problems and in particular [15] that solves the unbalanced version of our problem optimally. We build our algorithm based on it and prove its optimality.

4.1 2–Clustering for Minimizing the Maximum Diameter

The maximum distance between pairs of points in a cluster is called the diameter. Clustering to minimize the maximum diameter over all clusters is a well studied problem. If k is part of the input, the problem of minimizing the maximum diameter is NP-hard. It is even NP-hard to find a solution whose maximum radius (or maximum diameter) is within a factor of 1.82 (or 1.97, respectively) of the optimum solution [17]. However, for a fixed k, the min-max diameter (or radius) k-clustering problem becomes solvable in polynomial time. For 2-clustering problem, the solution was attributed to Avis et. al. [8], who found an algorithm that obtains a min-diameter separable bipartition in O(n² log² n) time. Asano, et. al. [15] proved that there exists an optimal solution that is linearly separable, and improved the algorithm performance to O(n log n) using the maximum spanning tree. Capoyleas [18] extended this work to k-clustering problem and found that the problem is polynomially solvable as long as the objective is a monotone increasing function of the diameters or radii of the clusters. The paper gave O(n^6k) for general k-clustering problem. Focusing on 2-clustering version of the problem, Asano et. al. [15] gave an algorithm which minimizes the larger diameter of two clusters in time O(n log n) and space O(n). The basis of the approach is a theorem which indicates that for any clustering P with the maximum diameter d, there exists a clustering P' with maximum diameter d', such that P' is linearly separable and d' ≤ d . Therefore the optimal clustering can be found by checking only the linearly separable clusters.

The algorithm first constructs a maximum spanning tree M for the point set S. Then it sorts the edges of the M in non-increasing order by length, and finds the threshold stabbing line L for these edges. A threshold stabbing line is defined as the following: assume the sequence of edges are e₁,e₂,…,e_p the maximum index i such that <e₁,e₂,…,e_i> allows a line intersecting with each edge while <e₁,e₂,…,e_i,e_i+1> does not is called a threshold stabbing line. The partitioning induced by this threshold stabbing line is the optimal clustering solution.

The above 2-clustering algorithm can not be extended to the problem with a balanced manner, since the linearly separable principle does not hold in balanced problem. Figure 4 illustrates a counter example.

However, the optimal balanced partition can be achieved based on the optimal unbalanced partition. The following simple greedy algorithm is designed for balanced bi-partitioning problem. Without loss of generality, for points set S, we require the number of points for a balanced partition to be |S|/2, if |S| is even, or one of [|S|/2] and [|S|/2] + 1, if |S| is odd.

Figure 5 depicts an algorithm that solves the problem optimally. It starts from an optimal 2-clustering obtained by Asano's algorithm [15], and then keeps moving points from the bigger partition to the smaller one. For each move, the algorithm greedily picks the point which causes the smallest increment on the diameter of the smaller partition. This step is repeated until a balanced partitioning is reached.

Figure 4. An example showing that an optimal balanced clustering is not necessarily a linearly separable partition. The point set contains four points, which are the endpoints of two unit-length segments $\overline{ab}$ and $\overline{cd}$, with a being slightly to the left of $\overline{cd}$. The optimal clustering is {a,b,c} and {d}, which is linearly separable; while the optimal balanced clustering is {a,b} and {c,d}, which is not linearly separable.

Figure 4. An example showing that an optimal balanced clustering is not necessarily a linearly separable partition. The point set contains four points, which are the endpoints of two unit-length segments $\overline{ab}$ and $\overline{cd}$, with a being slightly to the left of $\overline{cd}$. The optimal clustering is {a,b,c} and {d}, which is linearly separable; while the optimal balanced clustering is {a,b} and {c,d}, which is not linearly separable.

Figure 5. Balanced minimum diameter 2-clustering algorithm.

Figure 5. Balanced minimum diameter 2-clustering algorithm.

We use the term mn-clustering for bi-partitioning with m and n as the sizes of two clusters. To show that the algorithm produces optimal balanced 2-clustering, it suffices to prove the following theorem.

Theorem 4.1: 

Let S₁ and S₂ be the two partitions for an optimal minmax diameter mn-clustering with |S₁| = m, |S₂| = n and m − n ≥ 2. Let v be a point such that v ∈ S₁ and diam(S₂ ∪{v}) for any S₁∈S₂. Assume that there exists an optimal bi-partitioning $S_1^{*}$ and $S_2^{*}$ such that $S_1\subset S_1^{*}$ and $S_2^{*}\subset S_2$. Then the S₁ - {v} and S₂ ∪{v} form the optimal (m-1)(n+1)-clustering.

Proof: 

Let the diameters of S₁ and S₂ be d₁ and d₂, respectively. Assume S₁' = S₁ −{v} and S₂' = S₂ ∪{v}. Let d₁' and d₂' be the diameters of S₁' and S₂' . Obviously we have d₁' ≤ d₁ ≤ d₁^* and d₂`≥ d₂ ≥ d₂^*.

If d₂' < d₁^*, the proof is trivial since d₁' = d₁^*. Otherwise d₁' < d₁^*, causing max(diam(S₁' ),diam(S₂' )) < $d_1^{*}$, which contradicts with the optimal bi-partitioning $S_1^{*}$ and $S_2^{*}$.

We only consider d₂' ≥ d₁^*, meaning that the maximum diameter of partition S₁' and S₂' is determined by d₂' . We discuss two cases:

If d₂' > d₂, meaning the diameter of S₂ increases after including point v. Therefore v must belong to one of the farthest point pairs in S₂' . Assume that the other point in this point pair is u. We claim that S₁' and S₂' construct the optimal (m-1)(n+1)-clustering. If this is not the case, there exists a partitioning A and B with the larger diameter less than d₂' . Apparently u and v can not be in the same partition (otherwise the diameter of this partition is at least d₂' ). Moreover, there are m-1 points (except v) which have distance to u larger than or equal to d₂' . These points together with v have to be partitioned into the set other than the set containing u. Thus one partition has at least m points. Note that m-n>2, thus it contradicts with (m-1)(n+1) -clustering definition.

If d₂' = d₂, we can prove that v still belongs to one of the farthest point pairs in S₂' , otherwise v would be chosen earlier.

Now we analyze the time complexity of the algorithm. The initial partitioning is computed in O(n log n) time. For each move, we need to compare all the points in S₁, find the one with minimum diameter increasing on S₂ if it is added into S₂. This can be done in O(n²) time. There are at most [|S|/2]. Therefore the total running time of Algorithm 1 is O(n³).

Figure 6. Proof of Theorem 4.1.

Figure 6. Proof of Theorem 4.1.

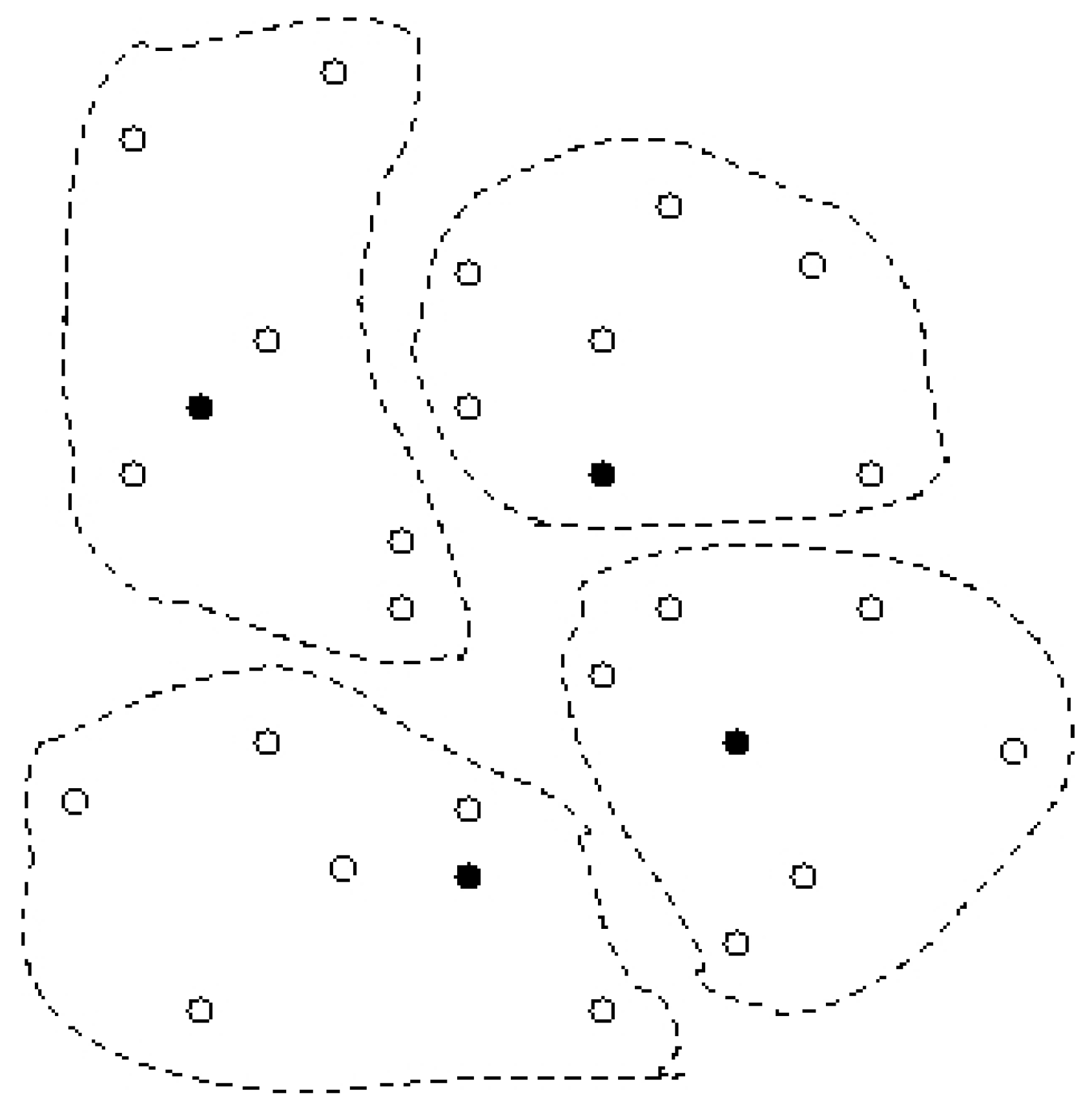
5. Preliminary Experiments

We have generated a sample sensor network with 24 sensor nodes. These sensors are randomly distributed on a small region. Similarly, we have randomly placed some master nodes in this region. We have applied our algorithm to form k clusters, such that the total square of the distances between sensors in a cluster and the corresponding master node, over all clusters is minimized. The number of master nodes depends on the capacity constraint of each of them. Figure 7 shows a case in which each master node can handle 6 sensor nodes. The dashed closed areas demonstrate the output of our algorithm, hence the optimal solution. Figure 8 shows the same sensor network with a different capacity constraint for master nodes. Each master node can handle 4 sensors in this example. Therefore the number of master nodes has been increased in order to cover all sensor nodes. Note that the optimal solution does not necessarily assign each sensor to its closest master node.

Figure 7. The output of the algorithm on a sample network. Each master node can handle 6 sensors.

Figure 7. The output of the algorithm on a sample network. Each master node can handle 6 sensors.

Figure 8. The effect of changing the master nodes' capacity constraint on the clustering. Each master node can handle 4 sensors in this example.

Figure 8. The effect of changing the master nodes' capacity constraint on the clustering. Each master node can handle 4 sensors in this example.

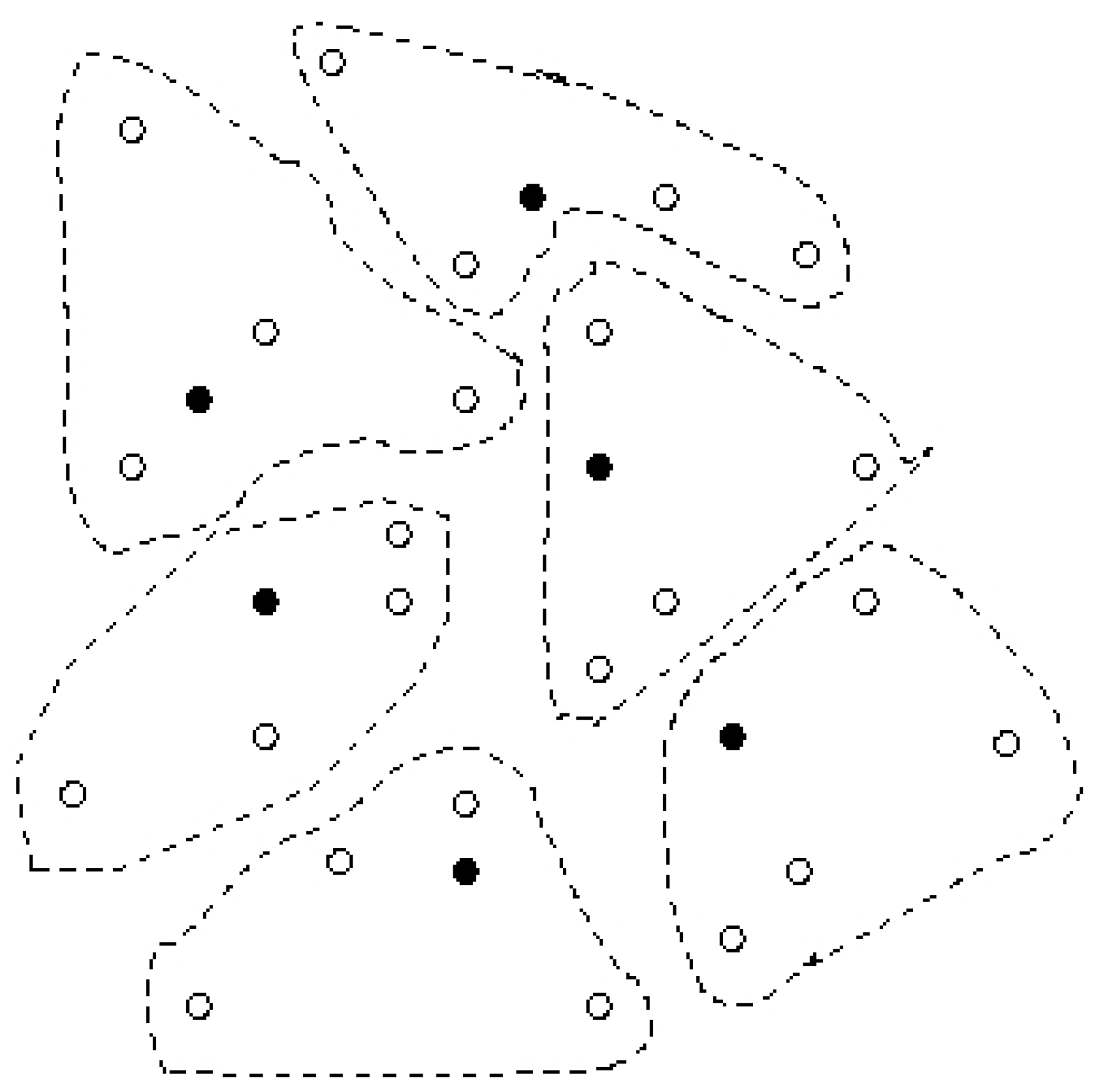
6. Conclusion

This paper discussed the theoretical issues in clustering problem. We showed that the balanced k-clustering problem can be solved optimally using min-cost network flow. This strategy could be used to evenly distribute the loading for all the master nodes and also minimize the communication energy dissipated by the sensors. We also discussed the 2-clustering problem which constraints the diameter of the clusters. Interesting extensions for current work would be extensions of these algorithms to incorporate the dynamic and distributed nature of these systems.