Visual IoT Security: Data Hiding in AMBTC Images Using Block-Wise Embedding Strategy †
Abstract
:1. Introduction
2. Related Work (AMBTC Compression)
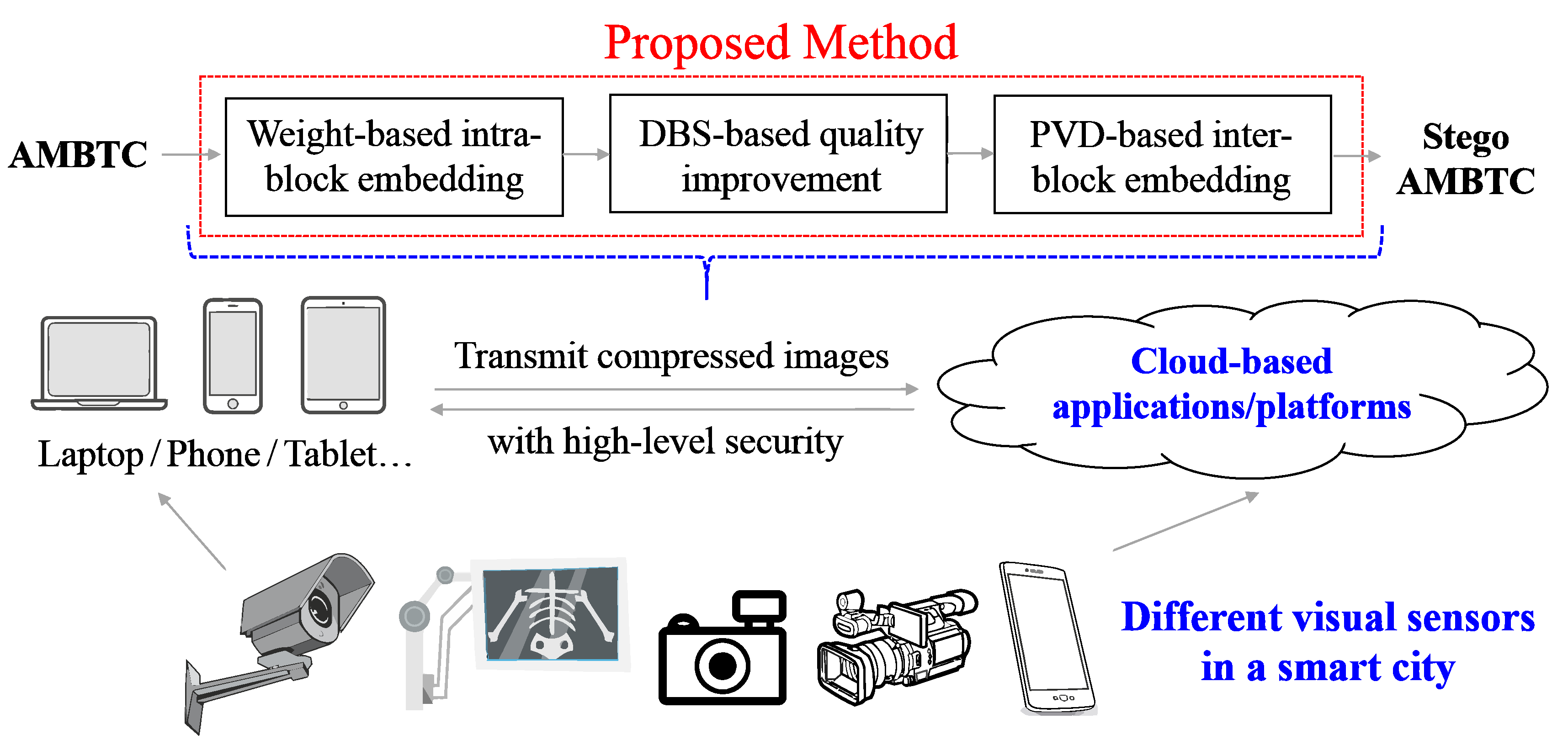
3. Proposed 2-Phase Intra- and Inter-Block Embedding Method
3.1. Intra-Block Embedding Phase
- (Candidate 1) ;
- (Candidate 2) ;
- (Candidate 3) ;
- (Candidate 4) ;
- (Candidate 5) ; and
- (Candidate 6) ,
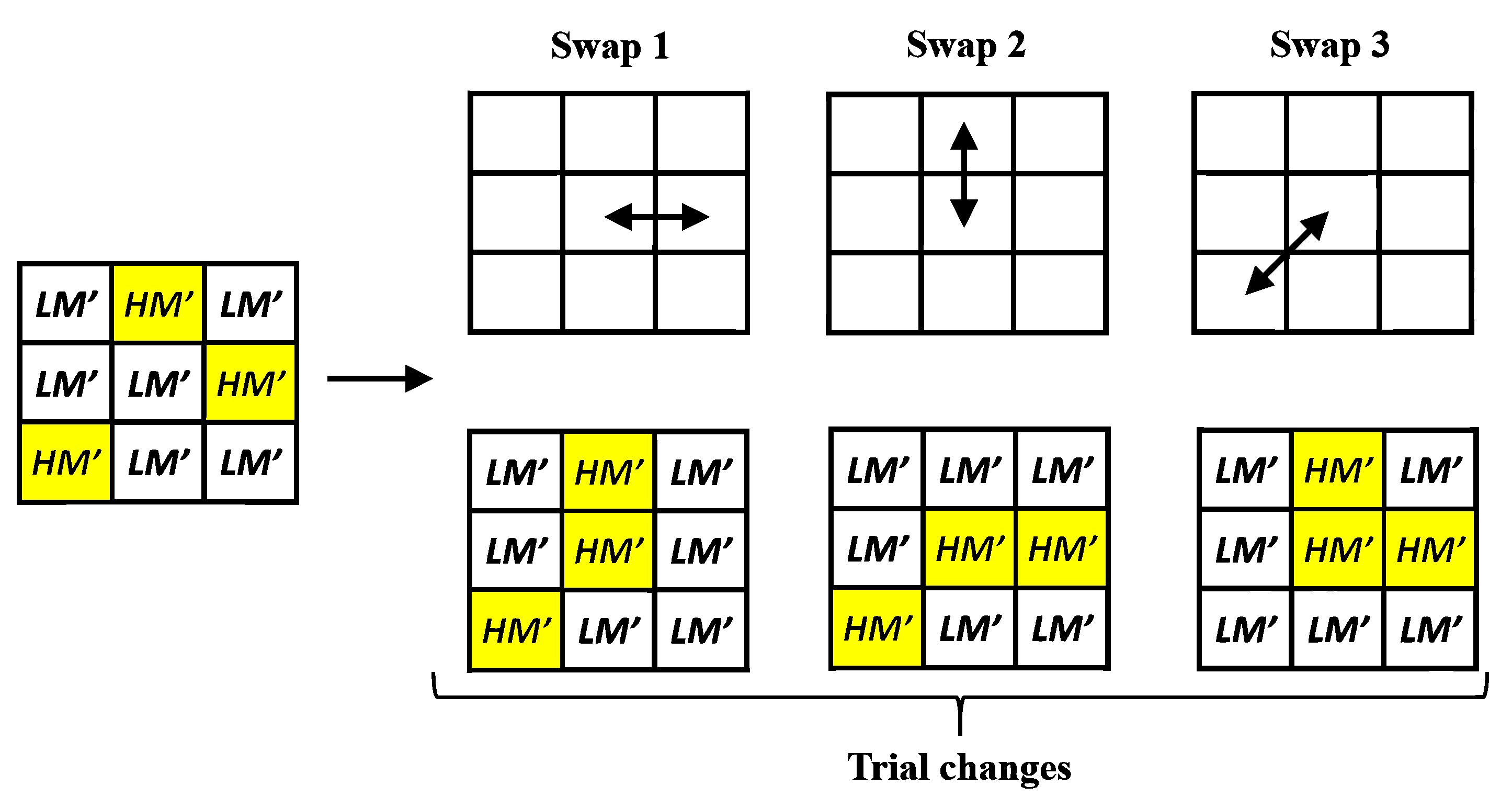
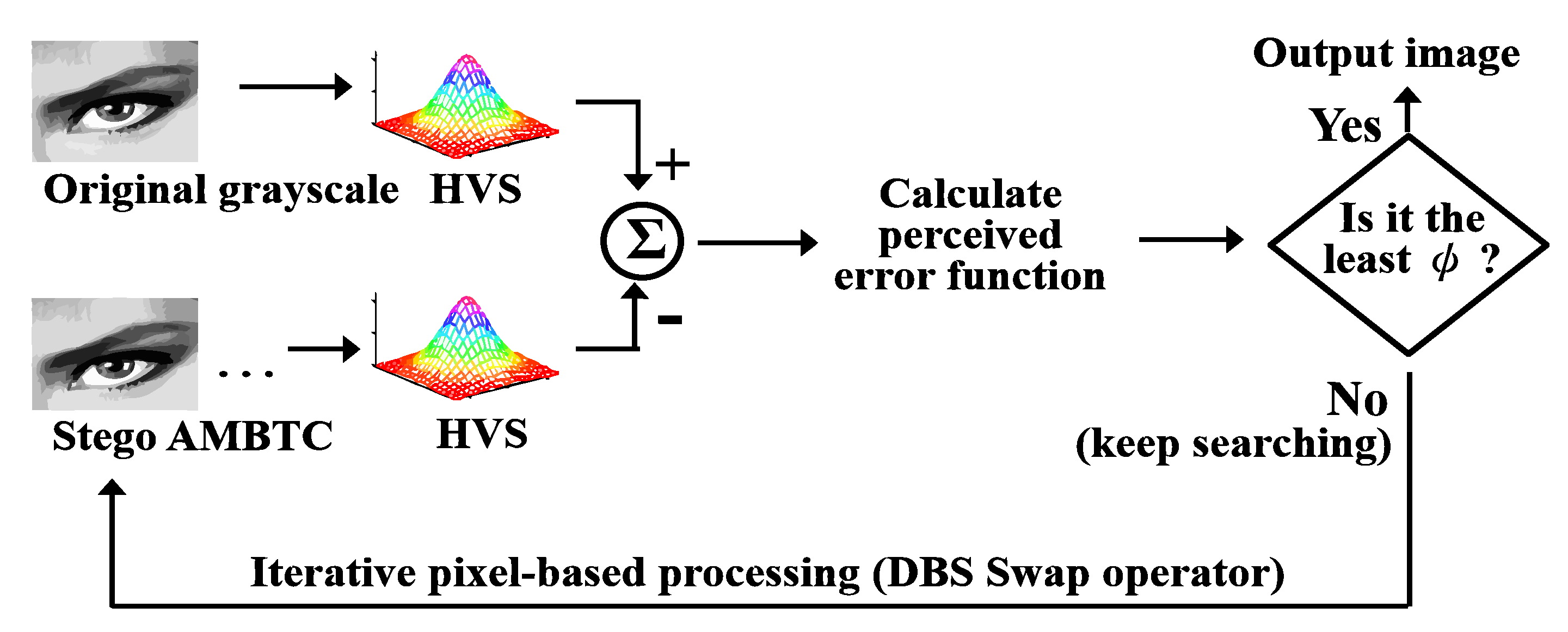
3.2. Quality Improvement Phase
3.3. Reversible Inter-Block Embedding Phase
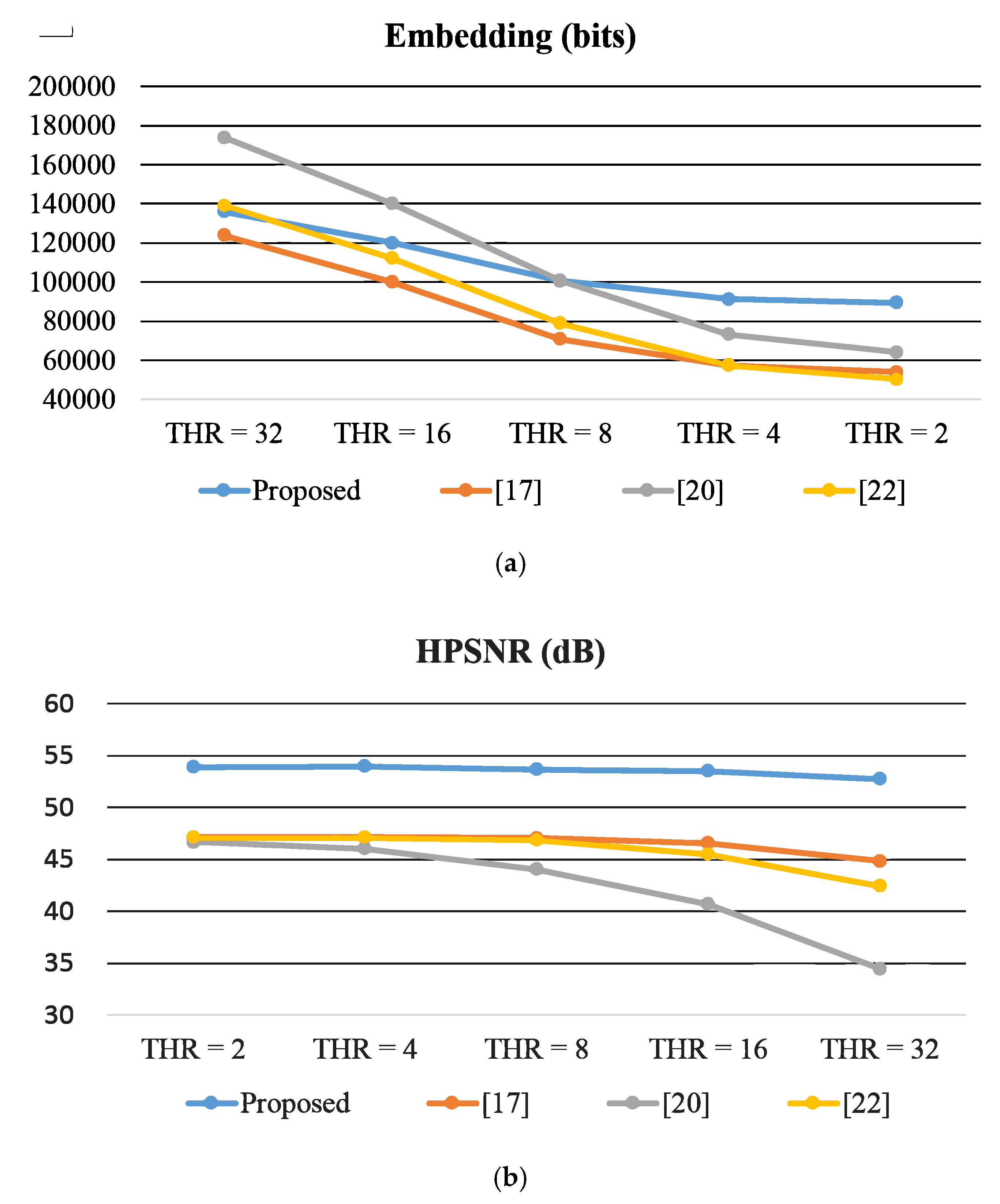
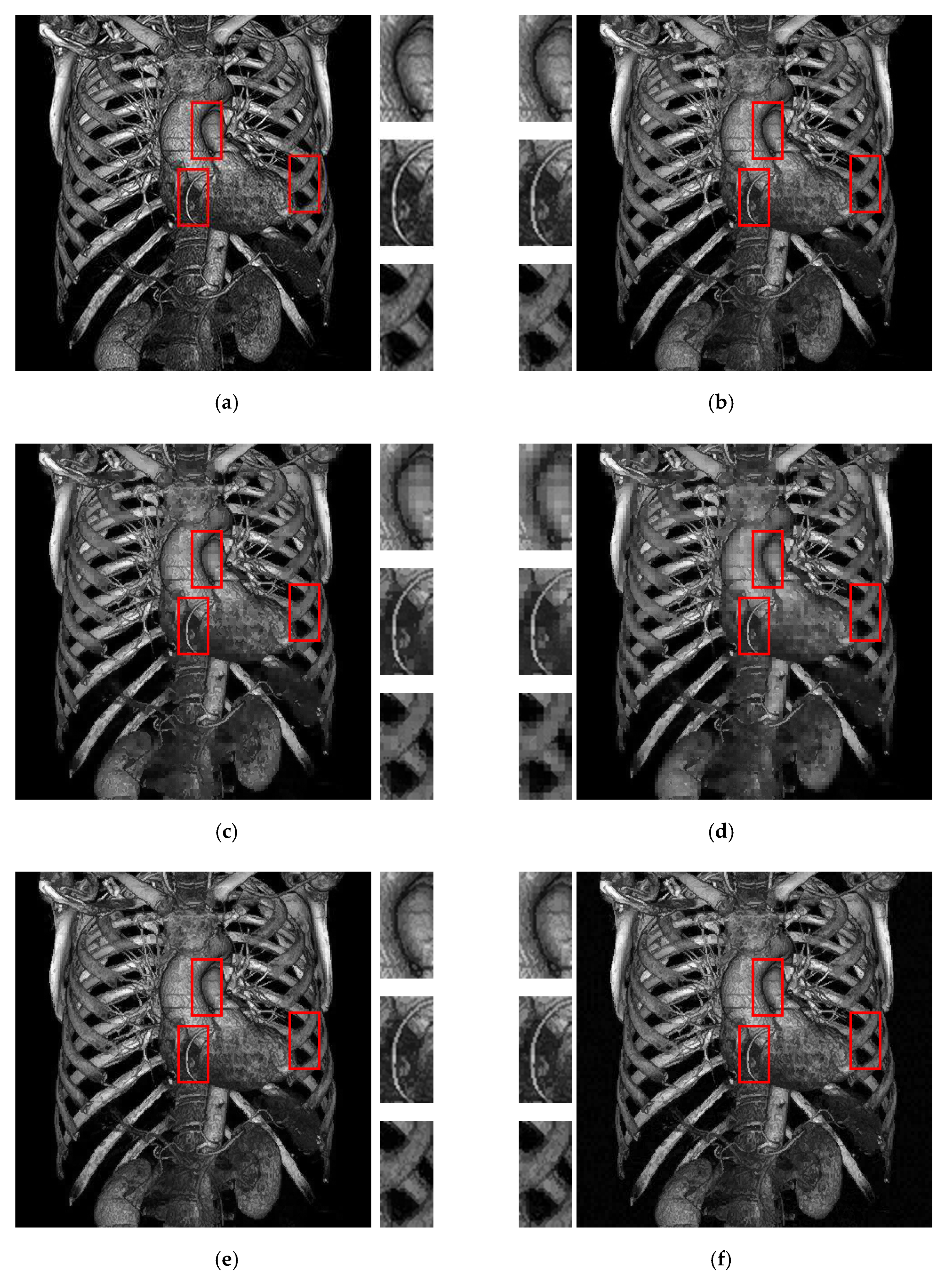
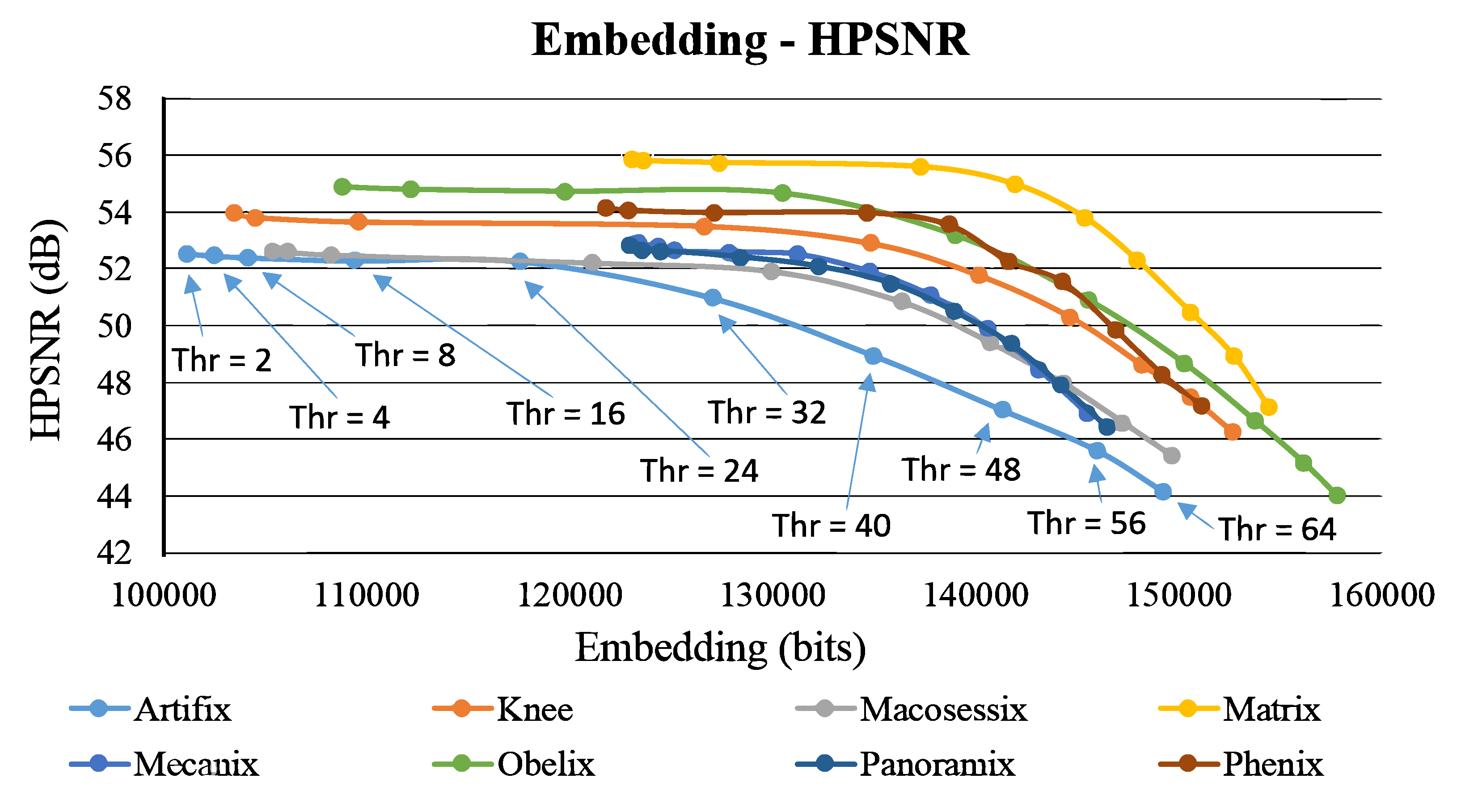
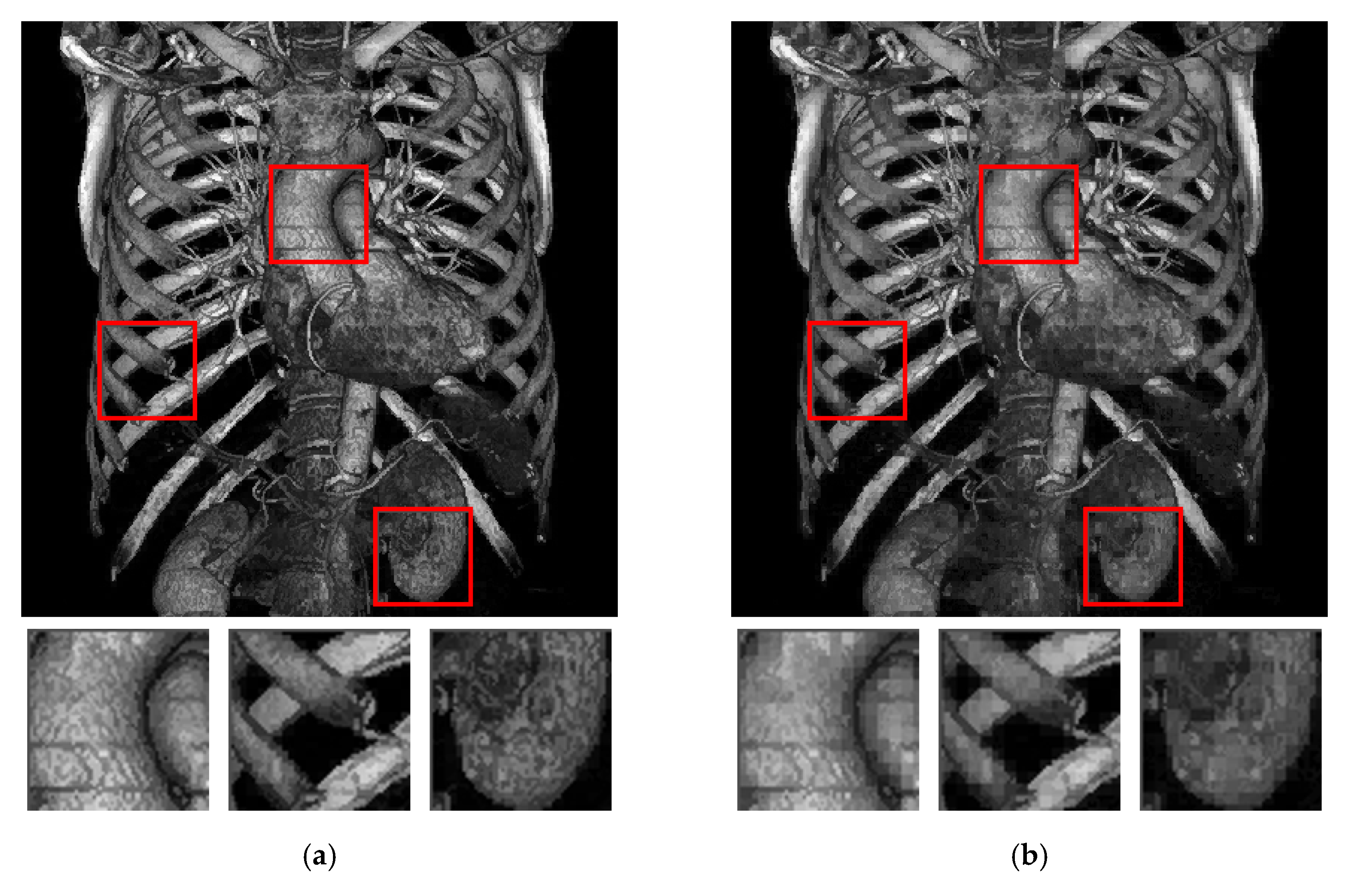
4. Experimental Results and Discussions
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Liao, X.; Yu, Y.; Li, Z.; Qin, Z. A new payload partition strategy in color image steganography. IEEE Trans. Circuits Syst. Video Technol. 2019. early access. [Google Scholar] [CrossRef]
- Li, C.; Lin, D.; Lu, J.; Hao, F. Cryptanalyzing an image encryption algorithm based on autoblocking and electrocardiography. IEEE Multimed. 2018, 25, 46–56. [Google Scholar] [CrossRef]
- Qin, C.; Zhang, X. Effective reversible data hiding in encrypted image with privacy protection for image content. J. Vis. Commun. Image Represent. 2015, 31, 154–164. [Google Scholar] [CrossRef]
- Xiong, L.; Xu, Z.; Shi, Y. An integer wavelet transform based scheme for reversible data hiding in encrypted images. Multidimens. Syst. Signal Process. 2018, 29, 1191–1202. [Google Scholar] [CrossRef]
- Huang, F.; Qu, X.; Kim, H.; Huang, J. Reversible data hiding in JPEG images. IEEE Trans. Circuits Syst. Video Technol. 2016, 26, 1610–1621. [Google Scholar] [CrossRef]
- Qian, Z.; Zhang, X. Reversible data hiding in encrypted images with distributed source encoding. IEEE Trans. Circuits Syst. Video Technol. 2016, 26, 636–646. [Google Scholar] [CrossRef]
- Li, W.; Lin, C.; Pan, J. Novel image authentication scheme with fine image quality for BTC-based compressed images. Multimed. Tools Appl. 2016, 75, 4771–4793. [Google Scholar] [CrossRef]
- Saha, S.; Ghosal, S.; Chakraborty, A.; Dhargupta, S.; Sarkar, R.; Mandal, J. Improved exploiting modification direction-based steganography using dynamic weightage array. Electron. Lett. 2018, 54, 498–500. [Google Scholar] [CrossRef]
- Sharma, D.; Saxena, R.; Singh, N. Dual domain robust watermarking scheme using random DFRFT and least significant bit technique. Multimed. Tools Appl. 2017, 76, 3921–3942. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, C.; Sun, Q. Enhance embedding capacity of generalized exploiting modification directions in data hiding. IEEE Access 2017, 6, 5374–5378. [Google Scholar] [CrossRef]
- Shukla, A.; Singh, A.; Singh, B.; Kumar, A. A secure and high-capacity data-hiding method using compression, encryption and optimized pixel value differencing. IEEE Access 2018, 6, 51130–51139. [Google Scholar] [CrossRef]
- Qian, Z.; Zhou, H.; Zhang, X.; Zhang, W. Separable reversible data hiding in encrypted JPEG bitstreams. IEEE Trans. Dependable Secur. Comput. 2018, 15, 1055–1067. [Google Scholar] [CrossRef]
- Qin, C.; Ji, P.; Chang, C.; Dong, J.; Sun, X. Non-uniform watermark sharing based on optimal iterative BTC for image tampering recovery. IEEE Multimed. 2018, 25, 36–48. [Google Scholar] [CrossRef]
- Rahmani, P.; Dastghaibyfard, G. Two reversible data hiding schemes for VQ-compressed images based on index coding. IET Image Process. 2018, 12, 1195–1203. [Google Scholar] [CrossRef]
- He, J.; Huang, S.; Tang, S.; Huang, J. JPEG image encryption with improved format compatibility and file size preservation. IEEE Trans. Multimed. 2018, 20, 2645–2658. [Google Scholar] [CrossRef]
- Li, X.; Meng, X.; Yang, X.; Yin, Y.; Wang, Y.; Peng, X.; He, W.; Dong, G.; Chen, H. Multiple-image encryption based on compressive ghost imaging and coordinate sampling. IEEE Photonics J. 2016, 8, 3900511. [Google Scholar] [CrossRef]
- Ou, D.; Sun, W. High payload image steganography with minimum distortion based on absolute moment block truncation coding. Multimed. Tools Appl. 2015, 74, 9117–9139. [Google Scholar] [CrossRef]
- Tang, M.; Zeng, S.; Chen, X.; Du, Y. An adaptive image steganography using AMBTC compression and interpolation technique. Optik 2016, 127, 471–477. [Google Scholar] [CrossRef]
- Lin, C.; Huang, Y.; Tai, W. A novel hybrid image authentication scheme based on absolute moment block truncation coding. Multimed. Tools Appl. 2017, 76, 463–488. [Google Scholar] [CrossRef]
- Huang, Y.; Chang, C.; Chen, Y. Hybrid secret hiding schemes based on absolute moment block truncation coding. Multimed. Tools Appl. 2017, 76, 6159–6174. [Google Scholar] [CrossRef]
- Al-Salhi, Y.; Lu, S. New steganography scheme to conceal a large amount of secret messages using an improved-AMBTC algorithm based on hybrid adaptive neural networks. In Proceedings of the IEEE 3rd Conference on Big Data Security on Cloud, Beijing, China, 26–28 May 2017; pp. 112–121. [Google Scholar]
- Hong, W.; Chen, T.; Yin, Z.; Luo, B.; Ma, Y. Data hiding in AMBTC images using quantization level modification and perturbation technique. Multimed. Tools Appl. 2017, 76, 3761–3782. [Google Scholar] [CrossRef]
- Liao, J. Theoretical bounds of direct binary search halftoning. IEEE Trans. Image Process. 2015, 24, 3478–3487. [Google Scholar] [CrossRef] [PubMed]
- Thomas, S.; Gharge, S. Halftone visual cryptography for grayscale images using error diffusion and direct binary search. In Proceedings of the 2nd International Conference on Trends in Electronics and Informatics (ICOEI 2018), Beijing, China, 11–12 May 2018; pp. 1091–1096. [Google Scholar]
- Osirix Database. Knowledge Base. Available online: https://www.osirix-viewer.com/support/knowledge-base/ (accessed on 10 March 2019).

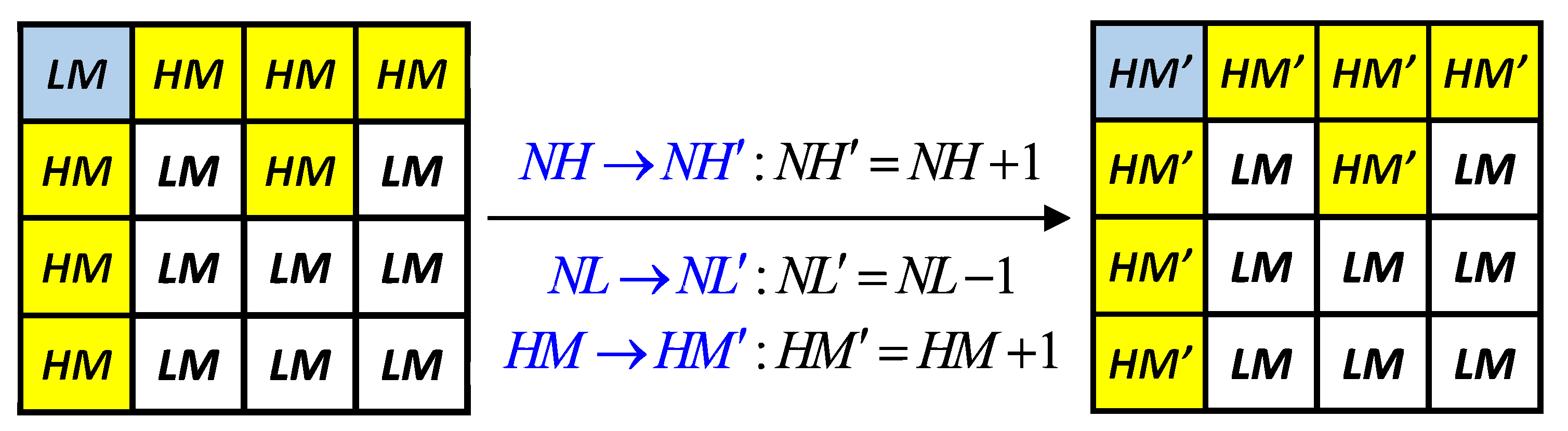



| Form of the Trio Code | Change of the Nominal Parameters | Change of the Hidden Function Value |
|---|---|---|
| 2-Bit Secret Code | Change of the Mean Value Difference (DH, DL) |
|---|---|
| code 00 | is maintained |
| code 01 | as |
| code 10 | as |
| code 11 | as and |
| Methods | Metrics | Test Images | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Figure 6a | Figure 6b | Figure 6c | Figure 6d | Figure 6e | Figure 6f | Figure 6g | Figure 6h | ||
| AMBTC | HPSNR | 52.386 | 53.714 | 52.327 | 56.880 | 51.947 | 55.782 | 51.997 | 53.398 |
| MSSIM | 0.999989 | 0.999993 | 0.999991 | 0.999998 | 0.999988 | 0.999996 | 0.999989 | 0.999992 | |
| [17] | Payload | 47140 | 54040 | 53500 | 113620 | 90940 | 134800 | 86230 | 86755 |
| HPSNR | 45.627 | 47.150 | 46.046 | 50.836 | 45.050 | 48.919 | 45.290 | 46.766 | |
| MSSIM | 0.985399 | 0.989024 | 0.991863 | 0.996137 | 0.991472 | 0.997172 | 0.992645 | 0.992822 | |
| [20] | Payload | 56285 | 64040 | 62915 | 119825 | 100625 | 144560 | 95705 | 95885 |
| HPSNR | 45.305 | 46.676 | 45.621 | 49.429 | 44.617 | 47.689 | 44.828 | 46.192 | |
| MSSIM | 0.983738 | 0.986889 | 0.990008 | 0.990257 | 0.986442 | 0.98905 | 0.988244 | 0.988436 | |
| [22] | Payload | 47140 | 50404 | 53500 | 113560 | 90940 | 134800 | 86230 | 86695 |
| HPSNR | 45.619 | 47.085 | 46.040 | 50.655 | 45.044 | 48.920 | 45.287 | 46.753 | |
| MSSIM | 0.985352 | 0.988626 | 0.99183 | 0.995239 | 0.991359 | 0.997161 | 0.992628 | 0.992788 | |
| Ours | Payload | 101136 | 89360 | 105416 | 133600 | 123408 | 147720 | 122944 | 121792 |
| HPSNR | 52.848 | 53.871 | 52.551 | 57.262 | 53.136 | 56.705 | 53.175 | 54.594 | |
| MSSIM | 0.999989 | 0.999993 | 0.999991 | 0.999998 | 0.999988 | 0.999996 | 0.999989 | 0.999992 | |
| Methods | Metrics | Test Images | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Figure 6a | Figure 6b | Figure 6c | Figure 6d | Figure 6e | Figure 6f | Figure 6g | Figure 6h | ||
| AMBTC | HPSNR | 52.386 | 53.714 | 52.327 | 56.880 | 51.947 | 55.782 | 51.997 | 53.398 |
| MSSIM | 0.999989 | 0.999993 | 0.999991 | 0.999998 | 0.999988 | 0.999996 | 0.999989 | 0.999992 | |
| [17] | Payload | 55705 | 70735 | 65290 | 139045 | 94285 | 138550 | 93385 | 99745 |
| HPSNR | 45.611 | 47.074 | 46.000 | 50.547 | 45.043 | 48.918 | 45.278 | 46.718 | |
| MSSIM | 0.985154 | 0.987358 | 0.99123 | 0.991295 | 0.991393 | 0.997105 | 0.992532 | 0.991948 | |
| [20] | Payload | 85225 | 100375 | 94090 | 168190 | 124075 | 168355 | 104503 | 111643 |
| HPSNR | 43.593 | 44.052 | 43.417 | 43.274 | 41.751 | 41.757 | 45.095 | 46.517 | |
| MSSIM | 0.944949 | 0.93087 | 0.944172 | 0.831976 | 0.840213 | 0.748125 | 0.992271 | 0.991502 | |
| [22] | Payload | 61799 | 78833 | 72662 | 156251 | 105523 | 155690 | 90355 | 93070 |
| HPSNR | 45.451 | 46.861 | 45.758 | 49.688 | 44.980 | 48.722 | 45.223 | 46.670 | |
| MSSIM | 0.984876 | 0.986678 | 0.990819 | 0.988496 | 0.991152 | 0.996853 | 0.992462 | 0.992346 | |
| Ours | Payload | 104152 | 100490 | 108296 | 148264 | 125192 | 148664 | 124464 | 128712 |
| HPSNR | 52.402 | 53.653 | 52.489 | 56.008 | 52.777 | 56.152 | 52.644 | 53.989 | |
| MSSIM | 0.999990 | 0.999994 | 0.999992 | 0.999998 | 0.999989 | 0.999996 | 0.999990 | 0.999993 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, Y.-H.; Hsia, C.-H.; Chen, B.-Y.; Chen, Y.-Y. Visual IoT Security: Data Hiding in AMBTC Images Using Block-Wise Embedding Strategy. Sensors 2019, 19, 1974. https://doi.org/10.3390/s19091974
Lin Y-H, Hsia C-H, Chen B-Y, Chen Y-Y. Visual IoT Security: Data Hiding in AMBTC Images Using Block-Wise Embedding Strategy. Sensors. 2019; 19(9):1974. https://doi.org/10.3390/s19091974
Chicago/Turabian StyleLin, Yu-Hsiu, Chih-Hsien Hsia, Bo-Yan Chen, and Yung-Yao Chen. 2019. "Visual IoT Security: Data Hiding in AMBTC Images Using Block-Wise Embedding Strategy" Sensors 19, no. 9: 1974. https://doi.org/10.3390/s19091974
APA StyleLin, Y.-H., Hsia, C.-H., Chen, B.-Y., & Chen, Y.-Y. (2019). Visual IoT Security: Data Hiding in AMBTC Images Using Block-Wise Embedding Strategy. Sensors, 19(9), 1974. https://doi.org/10.3390/s19091974







