A Submersible Printed Sensor Based on a Monopole-Coupled Split Ring Resonator for Permittivity Characterization
Abstract
1. Introduction
2. Materials and Methods
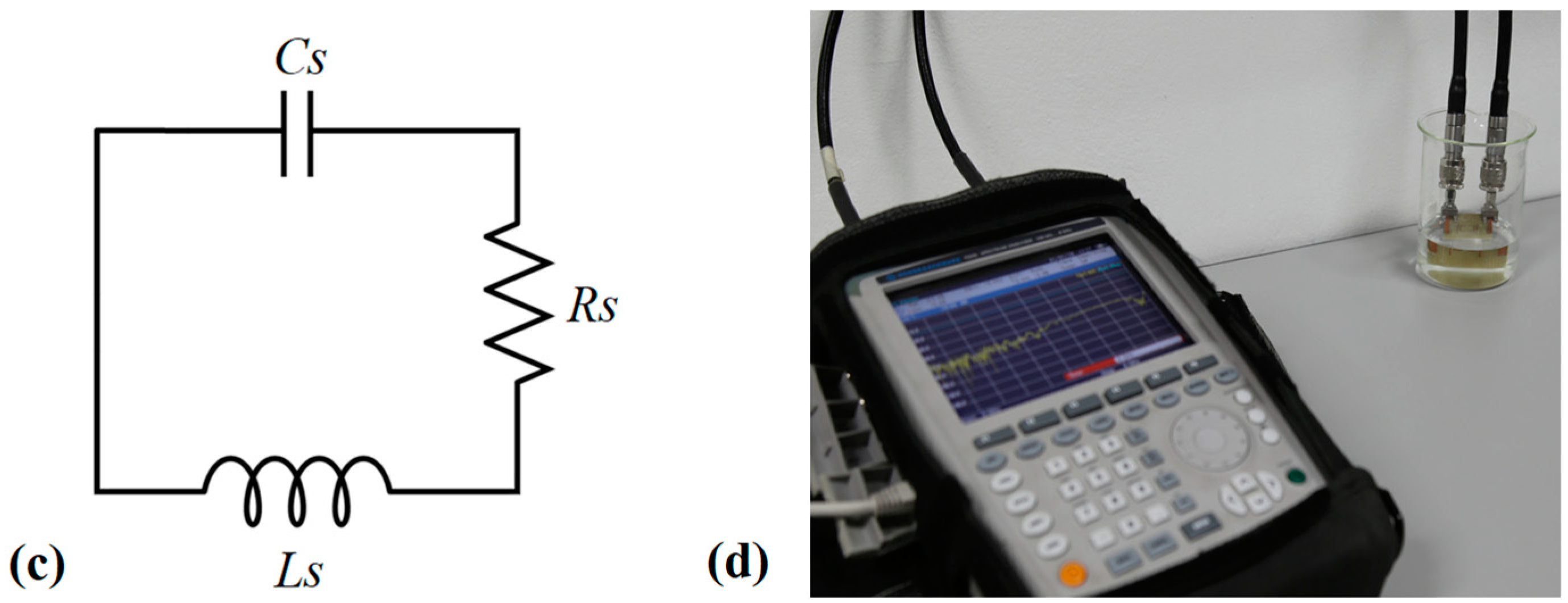
2.1. Theoretical Model
2.2. Sensor Design
2.3. Characterization of Sensor
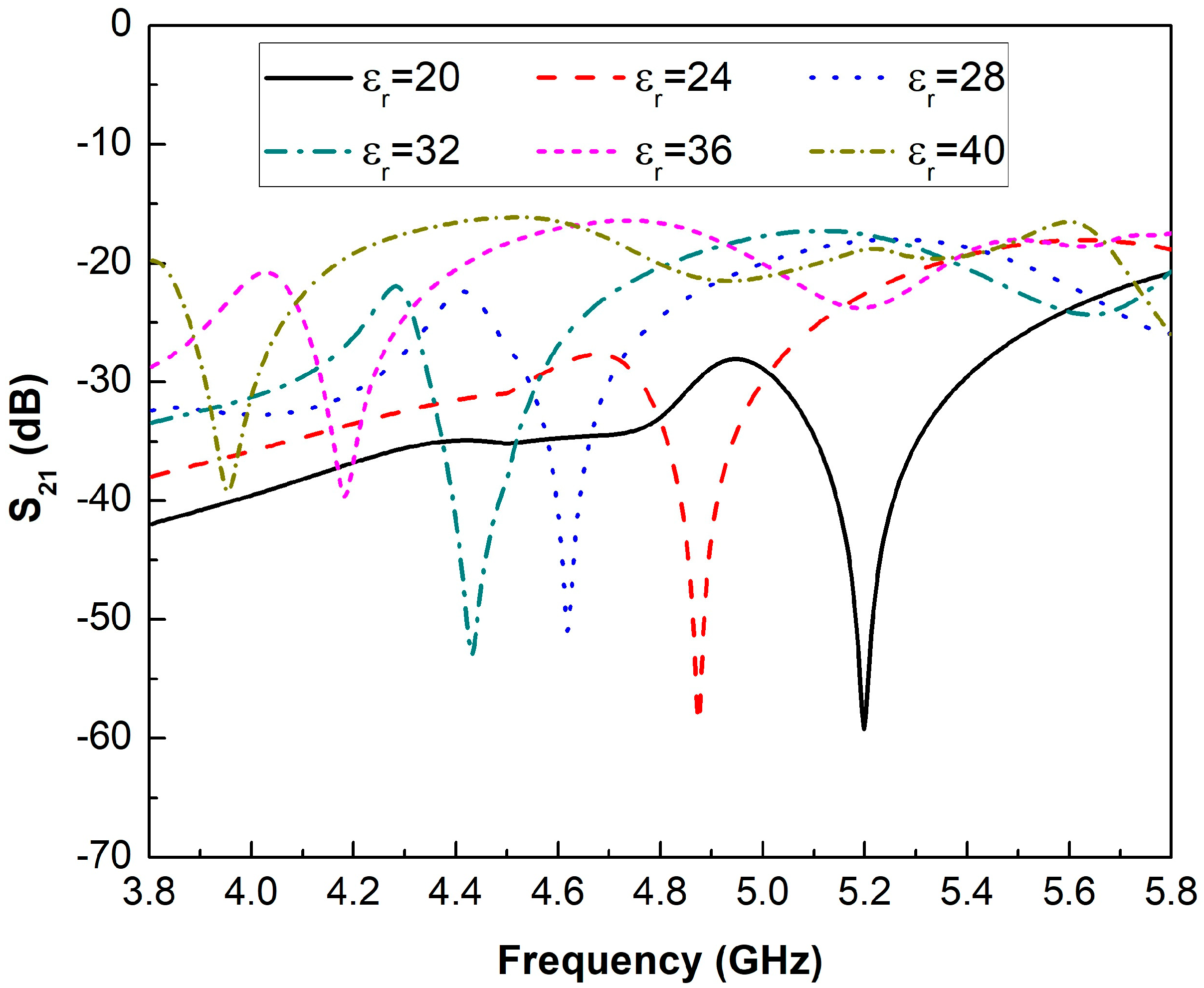
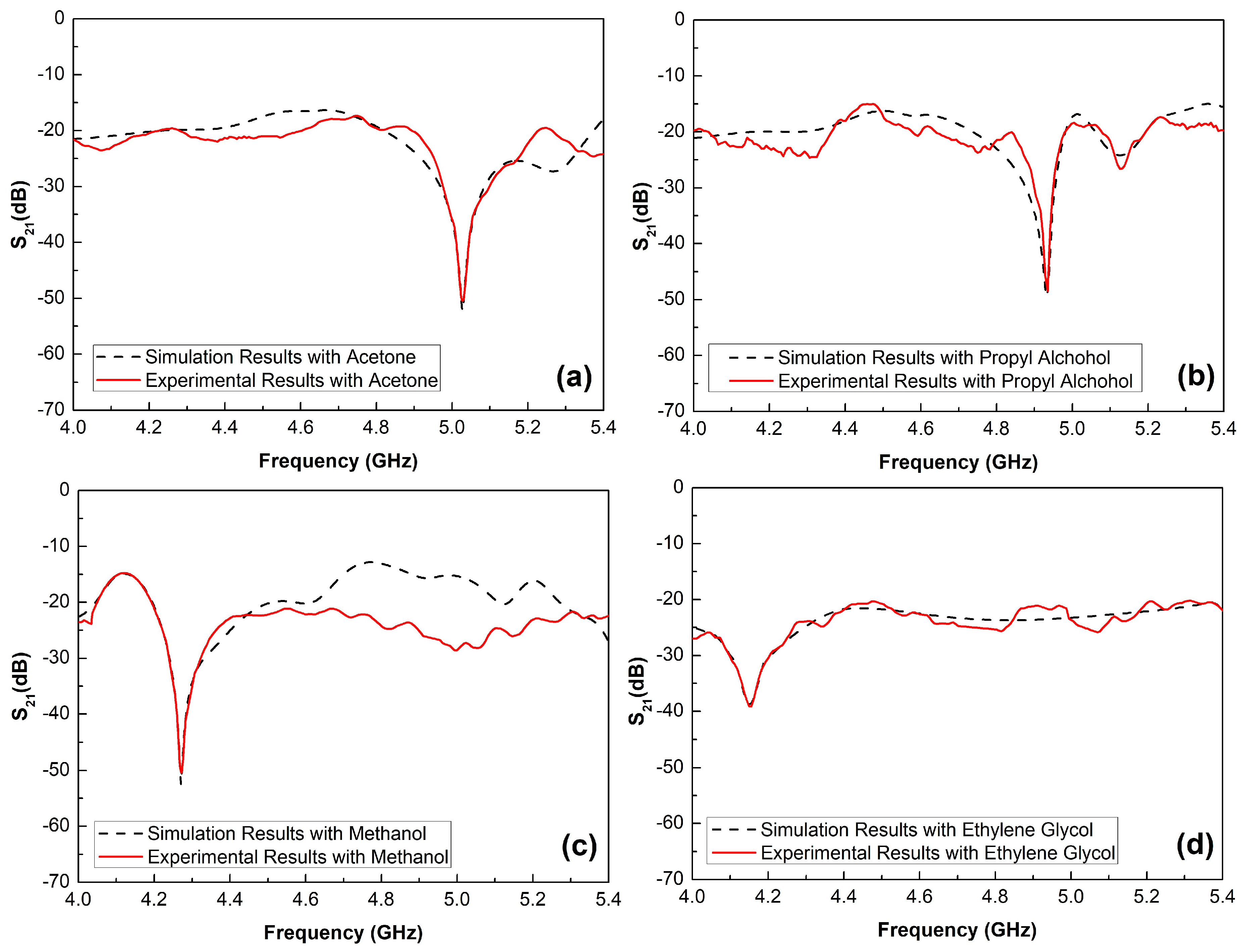
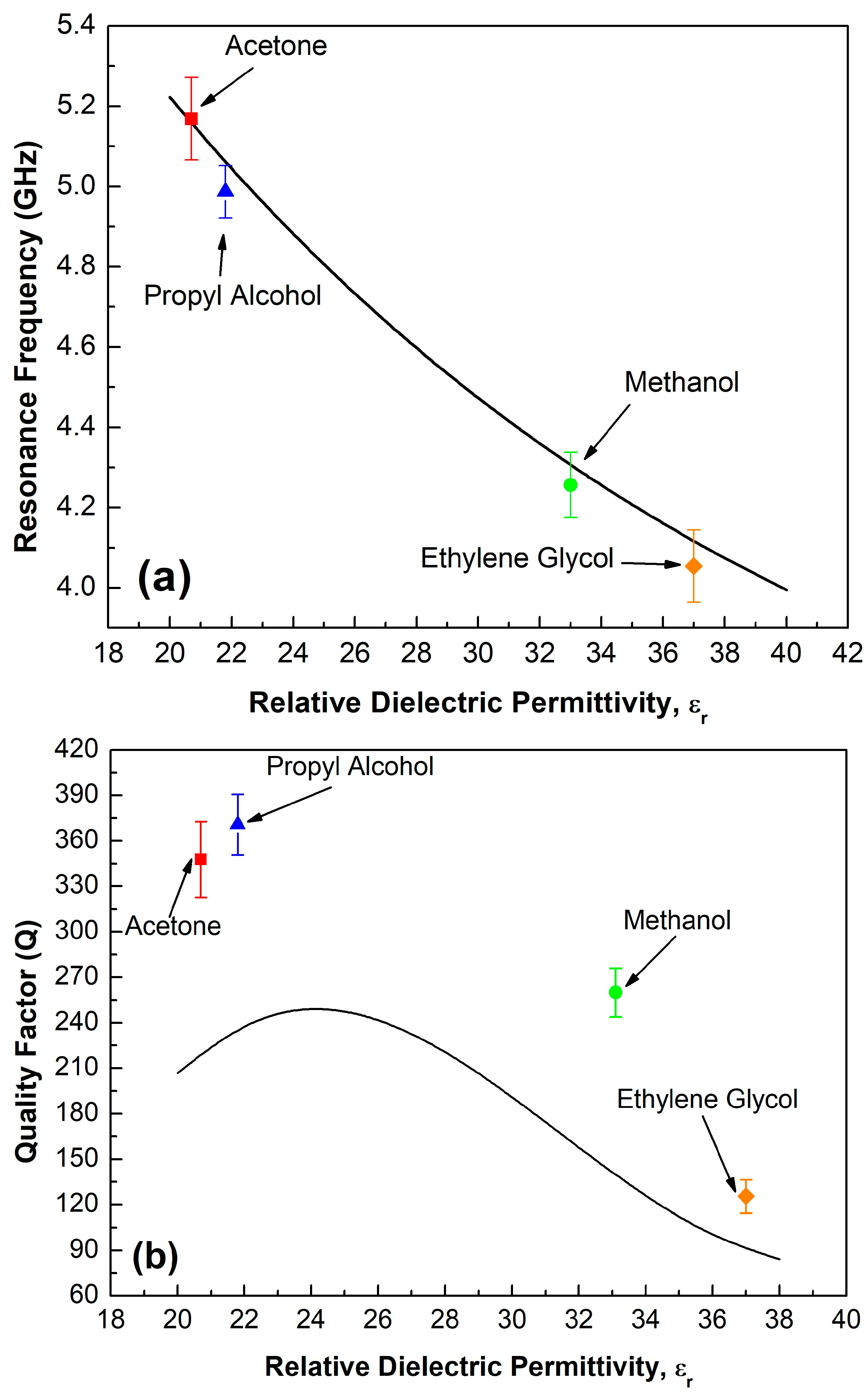
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zhou, H.; Hu, D.; Yang, C.; Chen, C.; Ji, J.; Chen, M.; Chen, Y.; Yang, Y.; Mu, X. Multi-Band Sensing for Dielectric Property of Chemicals Using Metamaterial Integrated Microfluidic Sensor. Sci. Rep. 2018, 8, 14801. [Google Scholar] [CrossRef] [PubMed]
- Kaatze, U. Measuring the dielectric properties of materials. Ninety-year development from low-frequency techniques to broadband spectroscopy and high-frequency imaging. Meas. Sci. Technol. 2013, 24, 012005. [Google Scholar] [CrossRef]
- Ansari, M.A.H.; Jha, A.K.; Akhtar, M.J. Design and Application of the CSRR-Based Planar Sensor for Noninvasive Measurement of Complex Permittivity. IEEE Sens. J. 2015, 15, 7181–7189. [Google Scholar] [CrossRef]
- Jilnai, M.; Wen, W.; Cheong, L.; Ur Rehman, M. A Microwave Ring-Resonator Sensor for Non-Invasive Assessment of Meat Aging. Sensors 2016, 16, 52. [Google Scholar] [CrossRef]
- Gutierrez, S.; Just, T.; Sachs, J.; Baer, C.; Vega, F. Field-Deployable System for the Measurement of Complex Permittivity of Improvised Explosives and Lossy Dielectric Materials. IEEE Sens. J. 2018, 18, 6706–6714. [Google Scholar] [CrossRef]
- Murata, K.I.; Hanawa, A.; Nozaki, R. Broadband complex permittivity measurement techniques of materials with thin configuration at microwave frequencies. J. Appl. Phys. 2005, 98. [Google Scholar] [CrossRef]
- Saeed, K.; Pollard, R.D.; Hunter, I.C. Substrate integrated waveguide cavity resonators for complex permittivity characterization of materials. IEEE Trans. Microw. Theory Tech. 2008, 56, 2340–2347. [Google Scholar] [CrossRef]
- Valencia-Balvín, C.; Pérez-Walton, S.; Osorio-Guillén, J.M. First principles calculations of the electronic and dielectric properties of λ-Ta2O5. TecnoLógicas 2018, 21, 43–52. [Google Scholar] [CrossRef][Green Version]
- Stacheder, M.; Koeniger, F.; Schuhmann, R. New Dielectric Sensors and Sensing Techniques for Soil and Snow Moisture Measurements. Sensors 2009, 9, 2951–2967. [Google Scholar] [CrossRef] [PubMed]
- Torrealba-Meléndez, R.; Sosa-Morales, M.E.; Olvera-Cervantes, J.L.; Corona-Chávez, A. Dielectric Properties of Beans at Ultra-Wide Band Frequencies. J. Microw. Power Electromagn. Energy 2014, 48, 104–112. [Google Scholar] [CrossRef]
- Lee, H.J.; Lee, H.S.; Yoo, K.H.; Yook, J.G. DNA sensing using split-ring resonator alone at microwave regime. J. Appl. Phys. 2010, 108. [Google Scholar] [CrossRef]
- Sun, J.; Huang, M.; Yang, J.-J.; Li, T.-H.; Lan, Y.-Z. A microring resonator based negative permeability metamaterial sensor. Sensors 2011, 11, 8060–8071. [Google Scholar] [CrossRef] [PubMed]
- Stevan, S.; Paiter, L.; Galvão, J.; Roque, D.; Chaves, E. Sensor and Methodology for Dielectric Analysis of Vegetal Oils Submitted to Thermal Stress. Sensors 2015, 15, 26457–26477. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.F.; Ong, C.K.; Neo, C.P.; Varadan, V.V.; Varadan, V.K. Microwave Electronics Measurement and Materials Characterization; John Wiley & Sons, Ltd: Chichester, UK, 2004; ISBN 9780470020463. [Google Scholar]
- Megriche, A.; Belhadj, A.; Mgaidi, A. Microwave dielectric properties of binary solvent water- alcohol, alcohol-alcohol mixtures at temperatures between −35 °C and + 35 °C and dielectric relaxation studies. Mediterr. J. Chem. 2012, 1, 200–209. [Google Scholar] [CrossRef]
- Saeed, K.; Shafique, M.F.; Byrne, M.B.; Hunter, I.C. Planar Microwave Sensors for Complex Permittivity Characterization of Materials and Their Applications; Haq, M.Z., Ed.; InTech: London, UK, 2012; ISBN 978-953-51-0103-1. [Google Scholar]
- Jilani, M.T.; Zaka, M.; Khan, A.M.; Khan, M.T.; Ali, S.M. A Brief Review of Measuring Techniques for Characterization of Dielectric Materials. Int. J. Inf. Technol. Electr. Eng. 2012, 1. [Google Scholar]
- Lobato-Morales, H.; Corona-Chávez, A.; Murthy, D.V.B.; Olvera-Cervantes, J.L. Complex permittivity measurements using cavity perturbation technique with substrate integrated waveguide cavities. Rev. Sci. Instrum. 2010, 81, 64704. [Google Scholar] [CrossRef] [PubMed]
- Li., S.; Akyel, C.; Bosisio, R.G. Precise Calculations and Measurements on the Complex Dielectric Constant of Lossy Materials Using TM/sub 010/ Cavity Perturbation Techniques. IEEE Trans. Microw. Theory Tech. 1981, 29, 1041–1048. [Google Scholar] [CrossRef]
- Galindo-Romera, G.; Javier Herraiz-Martinez, F.; Gil, M.; Martinez-Martinez, J.J.; Segovia-Vargas, D. Submersible Printed Split-Ring Resonator-Based Sensor for Thin-Film Detection and Permittivity Characterization. IEEE Sens. J. 2016, 16, 3587–3596. [Google Scholar] [CrossRef]
- Acevedo-Osorio, G.; Muñoz Ossa, H.; Reyes-Vera, E. Performance Analysis of Monopole Excited Split Ring Resonator for Permittivity Characterization. In 2017 42nd International Conference on Infrared, Millimeter, and Terahertz Waves (IRMMW-THz); IEEE: Cancun, Mexico, 2017; pp. 1–2. [Google Scholar]
- Lobato-Morales, H.; Corona-Chavez, A.; Olvera-Cervantes, J.L. Planar sensors for RFID wireless complex-dielectric-permittivity sensing of liquids. In 2013 IEEE MTT-S International Microwave Symposium Digest (MTT); IEEE: Berlin, Germany, 2013; pp. 1–3. [Google Scholar]
- Iqbal, A.; Smida, A.; Saraereh, O.A.; Alsafasfeh, Q.H.; Mallat, N.K.; Lee, B.M. Cylindrical Dielectric Resonator Antenna-Based Sensors for Liquid Chemical Detection. Sensors 2019, 19, 1200. [Google Scholar] [CrossRef]
- Xu, K.; Liu, Y.; Chen, S.; Zhao, P.; Peng, L.; Dong, L.; Wang, G. Novel Microwave Sensors Based on Split Ring Resonators for Measuring Permittivity. IEEE Access 2018, 6, 26111–26120. [Google Scholar] [CrossRef]
- Domínguez, M.; Cataño, D.; Reyes, E. Design a sensor of relative dielectric permittivity of a medium using an antenna microstrip with metamaterial structures. Actas Ing. 2015, 1, 110–114. [Google Scholar]
- Benkhaoua, L.; Benhabiles, M.T.; Mouissat, S.; Riabi, M.L. Miniaturized Quasi-Lumped Resonator for Dielectric Characterization of Liquid Mixtures. IEEE Sens. J. 2016, 16, 1603–1610. [Google Scholar] [CrossRef]
- Islam, M.T.; Hoque, A.; Almutairi, A.F.; Amin, N. Left-handed metamaterial-inspired unit cell for S-Band glucose sensing application. Sensors 2019, 19, 169. [Google Scholar] [CrossRef] [PubMed]
- Smith, D.; Padilla, W.; Vier, D.; Nemat-Nasser, S.; Schultz, S. Composite Medium with Simultaneously Negative Permeability and Permittivity. Phys. Rev. Lett. 2000, 84, 4184–4187. [Google Scholar] [CrossRef] [PubMed]
- Castellanos, L.M.; Lopez, F.; Reyes-Vera, E. Metamateriales: principales características y aplicaciones. Rev. la Acad. Colomb. Ciencias Exactas, Físicas y Nat. 2016, 40, 395. [Google Scholar] [CrossRef]
- Catano-Ochoa, D.; Senior, D.E.; Lopez, F.; Reyes-Vera, E. Performance analysis of a microstrip patch antenna loaded with an array of metamaterial resonators. In Proceedings of the 2016 IEEE Antennas and Propagation Society International Symposium, Fajardo, Puerto Rico, 26 June–1 July 2016. [Google Scholar]
- Raghavan, S.; Rajeshkumar, V. An overview of metamaterials in biomedical applications. Prog. Electromagn. Res. Symp. 2013, 368–371. [Google Scholar]
- Chen, T.; Li, S.; Sun, H. Metamaterials application in sensing. Sensors 2012, 12, 2742–2765. [Google Scholar] [CrossRef]
- Cheng, X.; Shi, J.; Jao, P.; Senior, D.E.; Yoon, Y.-K. Reconfigurable split ring resonator array loaded waveguide for insitu tuning. In Proceedings of the 2011 IEEE International Symposium on Antennas and Propagation (APSURSI), Spokane, WA, USA, 3–8 July 2011; pp. 2947–2950. [Google Scholar]
- Reyes-Vera, E.; Senior, D.E.; Luna-Rivera, J.M.; Lopez, F. Advances in electromagnetic applications and communications. TecnoLógicas 2018, 21, 9–13. [Google Scholar] [CrossRef]
- Rusni, I.; Ismail, A.; Alhawari, A.; Hamidon, M.; Yusof, N. An Aligned-Gap and Centered-Gap Rectangular Multiple Split Ring Resonator for Dielectric Sensing Applications. Sensors 2014, 14, 13134–13148. [Google Scholar] [CrossRef]
- Lobato-Morales, H.; Corona-Chavez, A.; Olvera-Cervantes, J.L.; Chavez-Perez, R.A.; Medina-Monroy, J.L. Wireless Sensing of Complex Dielectric Permittivity of Liquids Based on the RFID. IEEE Trans. Microw. Theory Tech. 2014, 62, 2160–2167. [Google Scholar] [CrossRef]
- Lee, H.J.; Lee, J.H.; Choi, S.; Jang, I.S.; Choi, J.S.; Jung, H. Il Asymmetric split-ring resonator-based biosensor for detection of label-free stress biomarkers. Appl. Phys. Lett. 2013, 103. [Google Scholar] [CrossRef]
- Lee, H.J.; Yook, J.G. Biosensing using split-ring resonators at microwave regime. Appl. Phys. Lett. 2008, 92, 2011–2014. [Google Scholar] [CrossRef]
- Lee, C.-S.; Yang, C.-L. Thickness and Permittivity Measurement in Multi-Layered Dielectric Structures Using Complementary Split-Ring Resonators. IEEE Sens. J. 2014, 14, 695–700. [Google Scholar] [CrossRef]
- Salim, A.; Lim, S. Complementary split-ring resonator-loaded microfluidic ethanol chemical sensor. Sensors 2016, 16, 1802. [Google Scholar] [CrossRef] [PubMed]
- Ebrahimi, A.; Withayachumnankul, W.; Al-Sarawi, S.; Abbott, D. High-Sensitivity Metamaterial-Inspired Sensor for Microfluidic Dielectric Characterization. IEEE Sens. J. 2014, 14, 1345–1351. [Google Scholar] [CrossRef]
- Withayachumnankul, W.; Jaruwongrungsee, K.; Tuantranont, A.; Fumeaux, C.; Abbott, D. Metamaterial-based microfluidic sensor for dielectric characterization. Sens. Actuators, A Phys. 2013, 189, 233–237. [Google Scholar] [CrossRef]
- Velez, P.; Su, L.; Grenier, K.; Mata-Contreras, J.; Dubuc, D.; Martin, F. Microwave Microfluidic Sensor Based on a Microstrip Splitter/Combiner Configuration and Split Ring Resonators (SRRs) for Dielectric Characterization of Liquids. IEEE Sens. J. 2017, 17, 6589–6598. [Google Scholar] [CrossRef]
- Chretiennot, T.; Dubuc, D.; Grenier, K. A Microwave and Microfluidic Planar Resonator for Efficient and Accurate Complex Permittivity Characterization of Aqueous Solutions. IEEE Trans. Microw. Theory Tech. 2013, 61, 972–978. [Google Scholar] [CrossRef]
- Velez, P.; Grenier, K.; Mata-Contreras, J.; Dubuc, D.; Martin, F. Highly-Sensitive Microwave Sensors Based on Open Complementary Split Ring Resonators (OCSRRs) for Dielectric Characterization and Solute Concentration Measurement in Liquids. IEEE Access 2018, 6, 48324–48338. [Google Scholar] [CrossRef]
- Velez, P.; Munoz-Enano, J.; Grenier, K.; Mata-Contreras, J.; Dubuc, D.; Martin, F. Split Ring Resonator-Based Microwave Fluidic Sensors for Electrolyte Concentration Measurements. IEEE Sens. J. 2019, 19, 2562–2569. [Google Scholar] [CrossRef]
- Boratay, K. Miniaturized negative permeability materials. Appl. Phys. Lett. 2007, 137–139. [Google Scholar] [CrossRef]
- Zahertar, S.; Yalcinkaya, A.D.; Torun, H. Rectangular split-ring resonators with single-split and two-splits under different excitations at microwave frequencies. AIP Adv. 2015, 5, 117220. [Google Scholar] [CrossRef]
- Baena, J.D.; Bonache, J.; Martin, F.; Sillero, R.M.; Falcone, F.; Lopetegi, T.; Laso, M.A.G.; Garcia-Garcia, J.; Gil, I.; Portillo, M.F.; et al. Equivalent-circuit models for split-ring resonators and complementary split-ring resonators coupled to planar transmission lines. IEEE Trans. Microw. Theory Tech. 2005, 53, 1451–1461. [Google Scholar] [CrossRef]
- Alahnomi, R.A.; Zakaria, Z.; Ruslan, E.; Ab Rashid, S.R.; Mohd Bahar, A.A. High-Q Sensor Based on Symmetrical Split Ring Resonator With Spurlines for Solids Material Detection. IEEE Sens. J. 2017, 17, 2766–2775. [Google Scholar] [CrossRef]
- Alahnomi, R.A.; Zakaria, Z.; Ruslan, E.; Bahar, A.A.M. A Novel Symmetrical Split Ring Resonator Based on Microstrip for Microwave Sensors. Meas. Sci. Rev. 2016, 16, 21–27. [Google Scholar] [CrossRef]
- Kumari, R.; Patel, P.N.; Yadav, R. An ENG Resonator-Based Microwave Sensor for the Characterization of Aqueous Glucose. J. Phys. D. Appl. Phys. 2018, 51, 075601. [Google Scholar] [CrossRef]
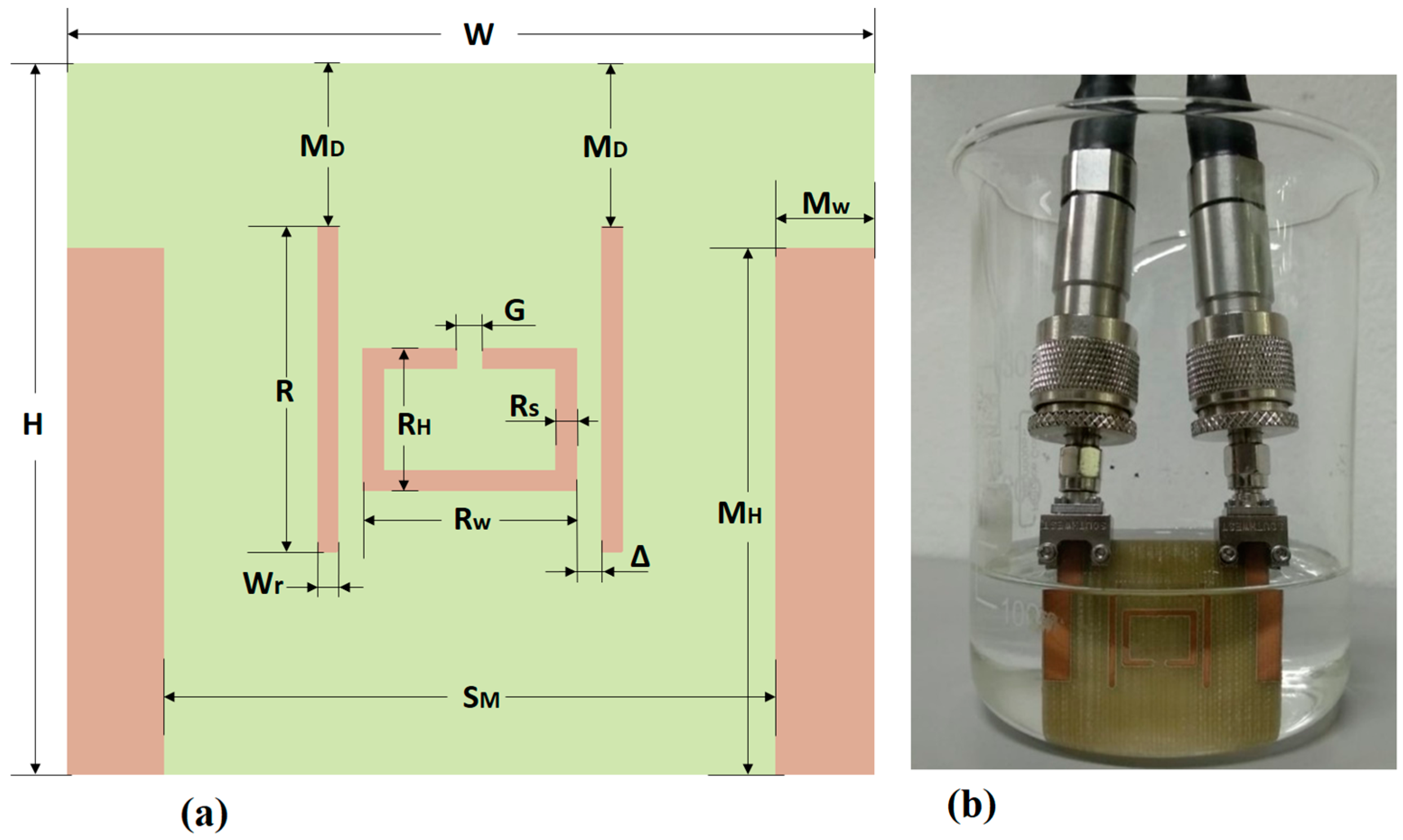
| Variable | Dimension (mm) |
|---|---|
| Substrate width (W) | 40.0 |
| Substrate height (H) | 35.0 |
| Monopole width (Mw) | 1.5 |
| Monopole height (MH) | 28.0 |
| Rectangle height (R) | 16.0 |
| Resonator width (RW) | 10.5 |
| Rectangle width (WR) | 1.0 |
| Resonator height (RH) | 7.0 |
| Resonator separation (Rs) | 1.0 |
| Gap (G) | 1.5 |
| Monopoles separation (SM) | 24.5 |
| Separation between resonator and monopole (Δ) | 1.25 |
| Monopole distance (MD) | 8 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Reyes-Vera, E.; Acevedo-Osorio, G.; Arias-Correa, M.; Senior, D.E. A Submersible Printed Sensor Based on a Monopole-Coupled Split Ring Resonator for Permittivity Characterization. Sensors 2019, 19, 1936. https://doi.org/10.3390/s19081936
Reyes-Vera E, Acevedo-Osorio G, Arias-Correa M, Senior DE. A Submersible Printed Sensor Based on a Monopole-Coupled Split Ring Resonator for Permittivity Characterization. Sensors. 2019; 19(8):1936. https://doi.org/10.3390/s19081936
Chicago/Turabian StyleReyes-Vera, Erick, G. Acevedo-Osorio, Mauricio Arias-Correa, and David E. Senior. 2019. "A Submersible Printed Sensor Based on a Monopole-Coupled Split Ring Resonator for Permittivity Characterization" Sensors 19, no. 8: 1936. https://doi.org/10.3390/s19081936
APA StyleReyes-Vera, E., Acevedo-Osorio, G., Arias-Correa, M., & Senior, D. E. (2019). A Submersible Printed Sensor Based on a Monopole-Coupled Split Ring Resonator for Permittivity Characterization. Sensors, 19(8), 1936. https://doi.org/10.3390/s19081936






