Low-Complexity and Hardware-Friendly H.265/HEVC Encoder for Vehicular Ad-Hoc Networks
Abstract
1. Introduction
- We propose a low-complexity and hardware-friendly H.265/HEVC encoder. The proposed encoder allows the encoding complexity to be reduced significantly so that low delay requirements for video transmission in power-limited VANETs nodes are satisfied.
- A novel spatiotemporal neighboring set is used to predict the depth range of the current coding tree unit. The prior probability of coding unit splitting or non-splitting is calculated with the spatiotemporal neighboring set. Moreover, the Bayesian rule and Gibbs Random Field (GRF) are used to reduce the encoding complexity for H.265/HEVC encoder with the combination of the coding tree unit depth decision and prediction unit modes decision.
- The proposed algorithm can balance the encoding complexity and encoding efficiency successfully. The encoding time can be reduced by 50% with negligible encoding efficiency loss, and the proposed encoder is suitable for real-time video applications.
2. Related Work
2.1. Video Streaming in Vehicular Ad-Hoc Networks
2.2. Low Complexity Algorithm for H.265/HEVC Encoder
3. Technical Background
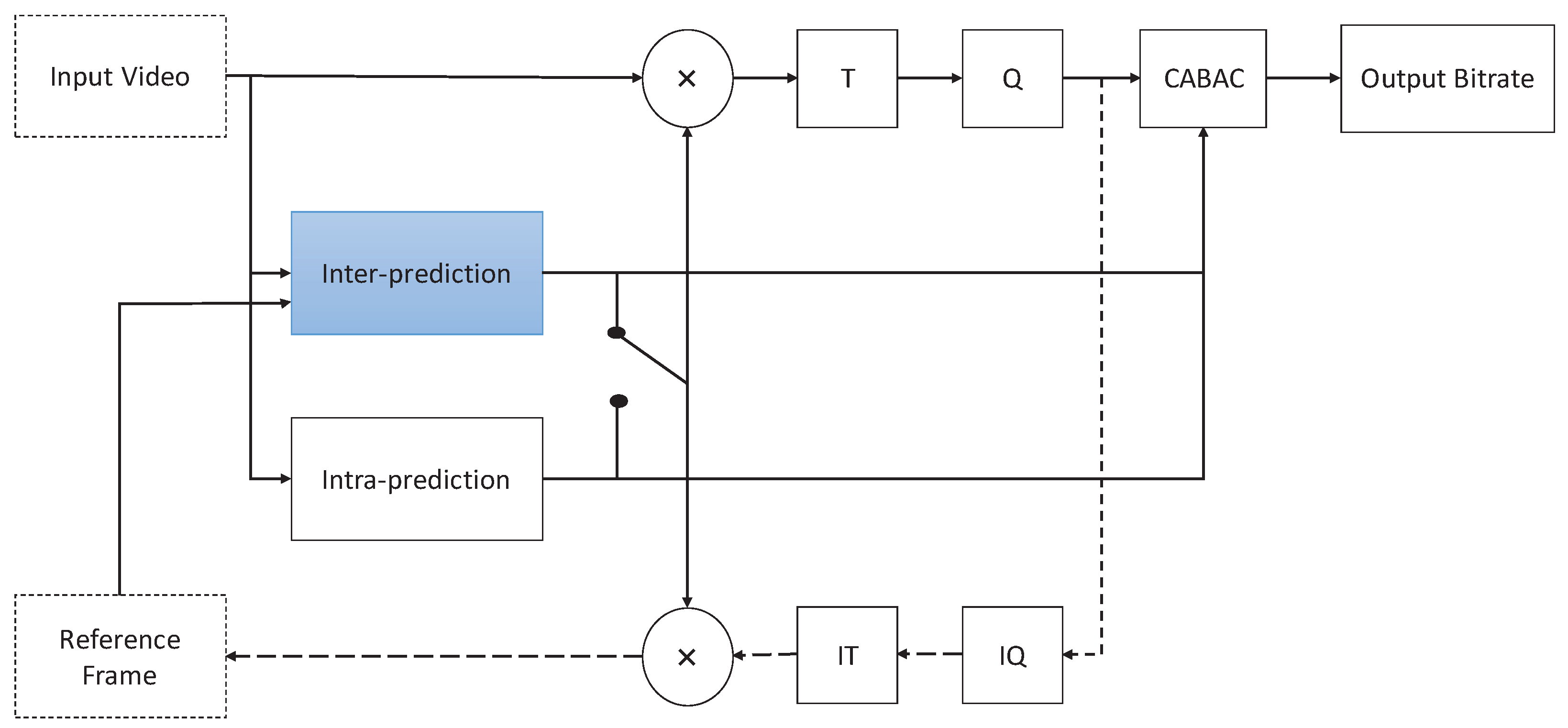
H.265/HEVC
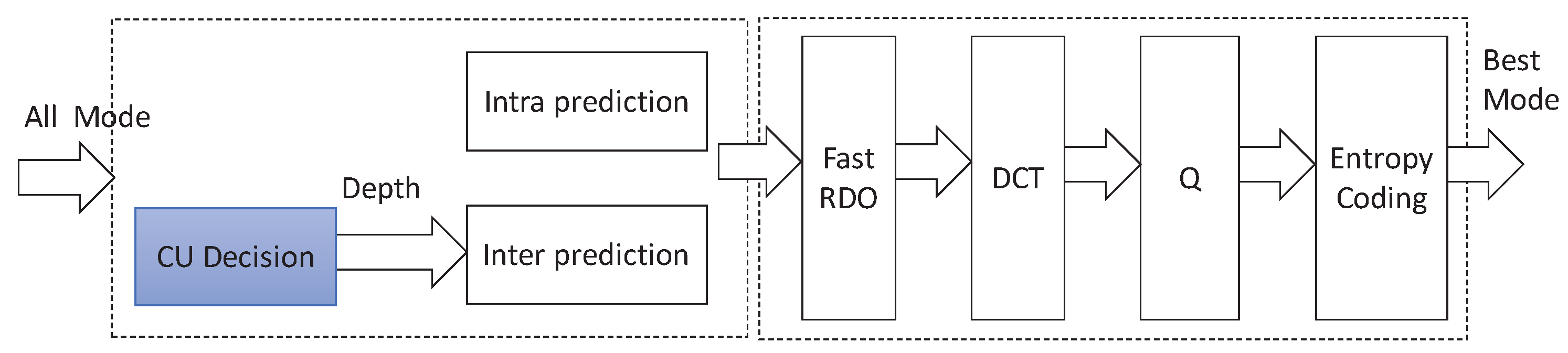
4. The Proposed Low-Complexity and Hardware-Friendly H.265/HEVC Encoder for VANETs
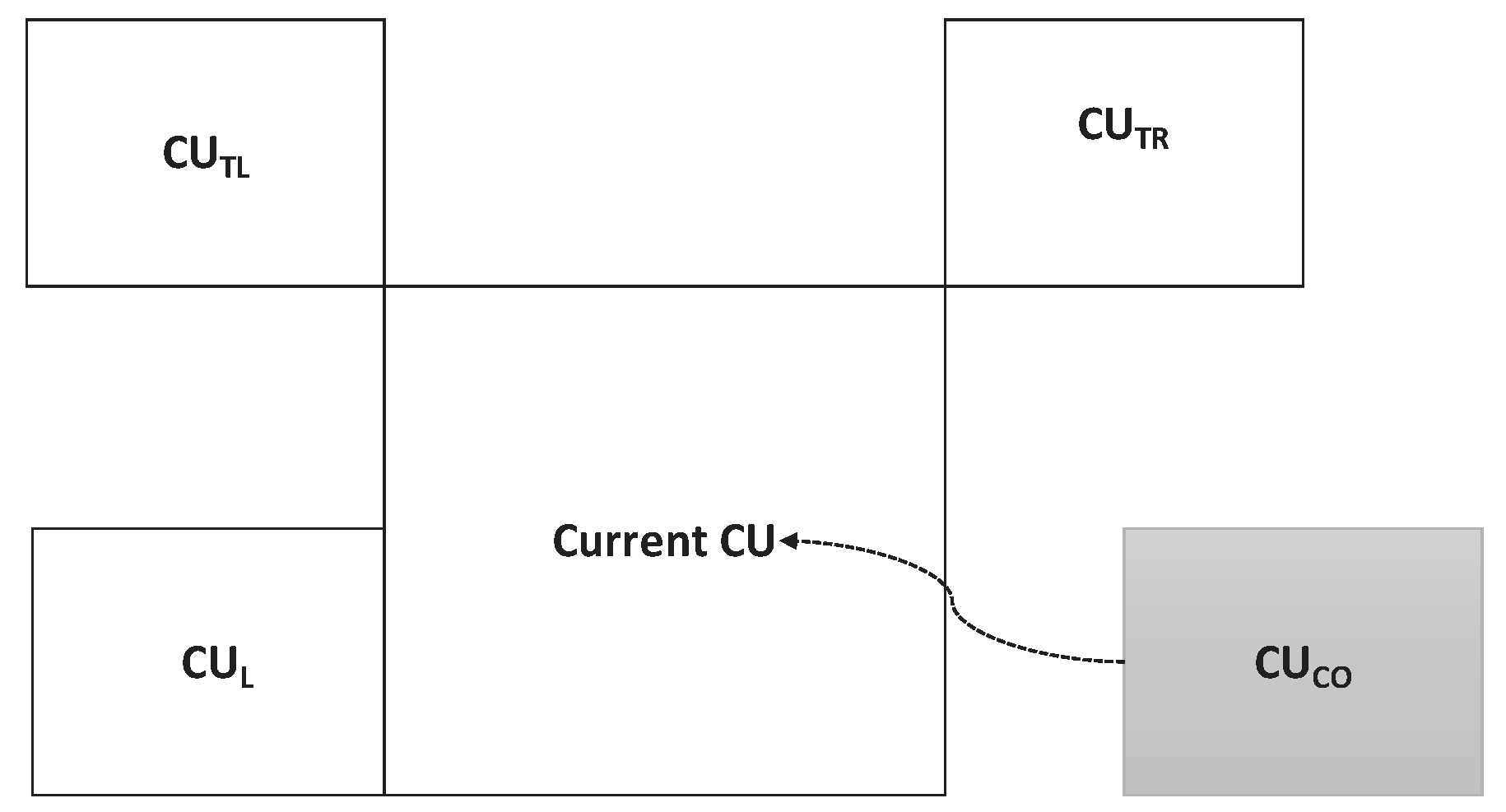
4.1. The Novel Spatiotemporal Neighborhood Set
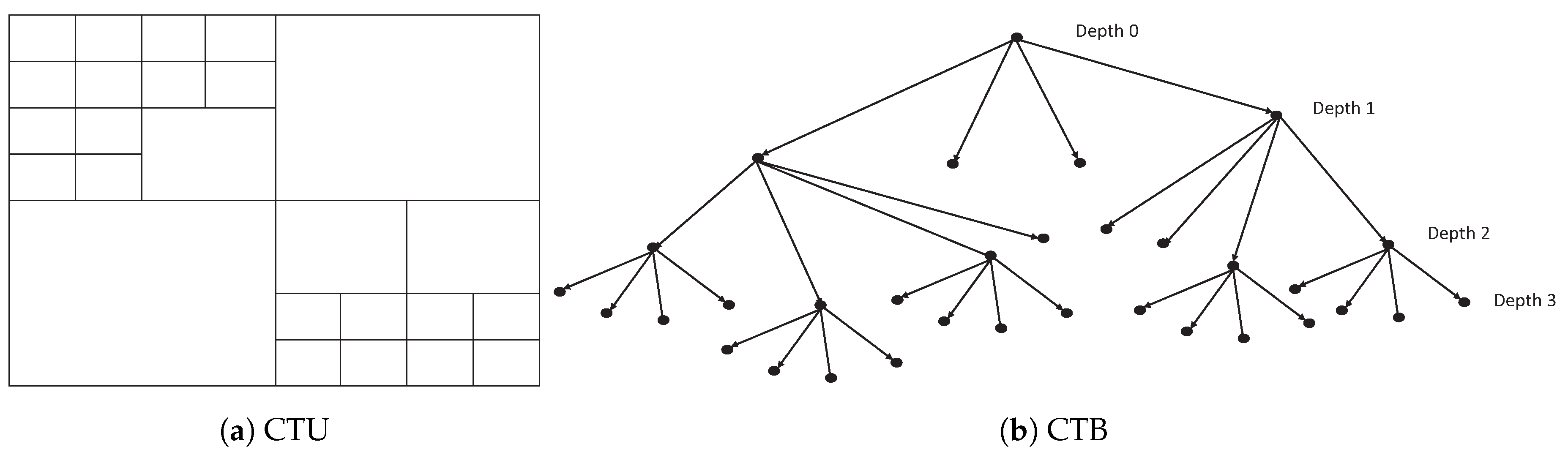
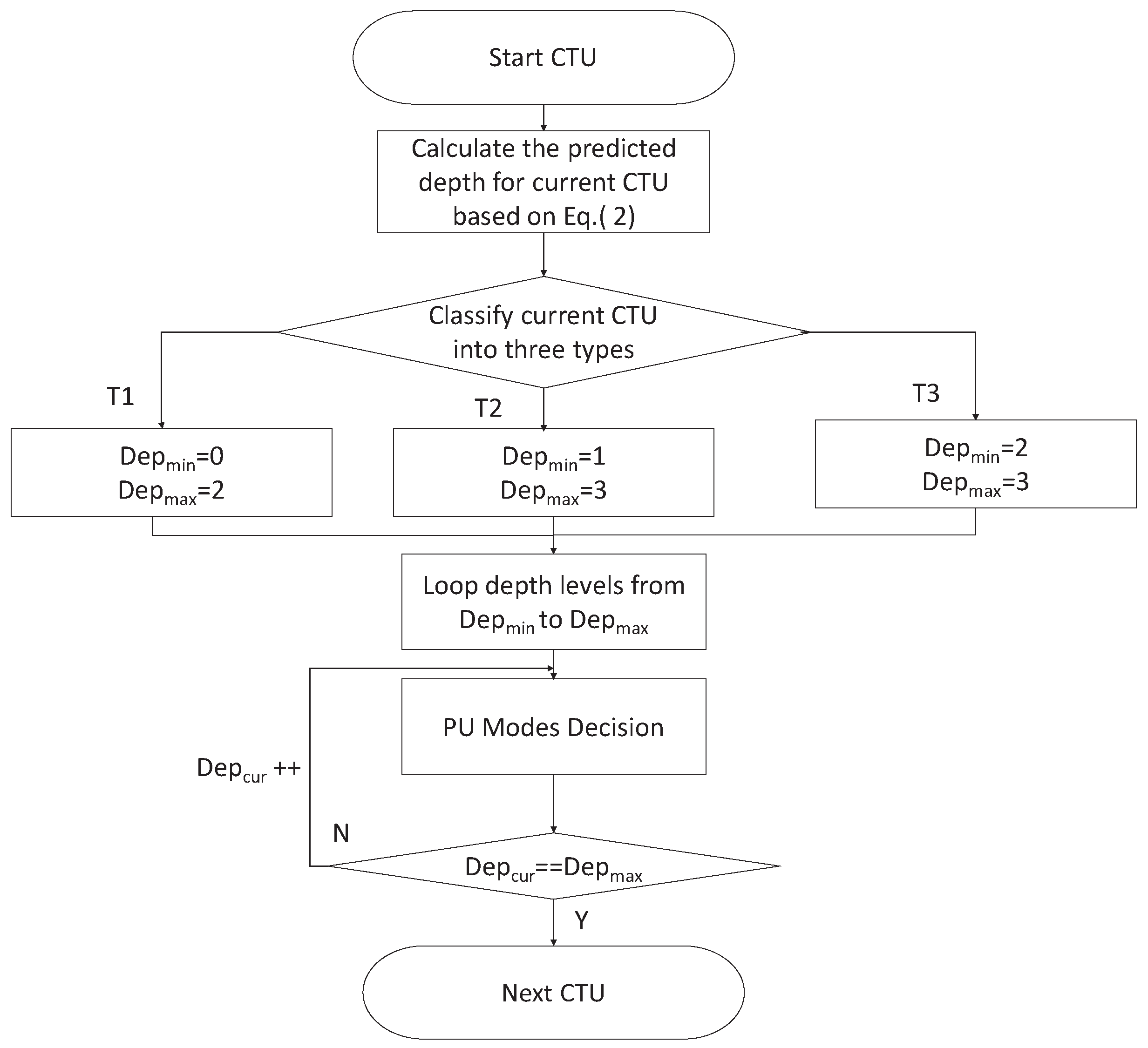
4.2. CTU Depth Decision
- (1)
- when the predicted depth of current CTU satisfies ≤ 1.5, it means that the motions of neighboring CTUs are smooth and the depths of neighboring CTUs are small. The current CTU belongs to the still or homogeneous motion region and is classified as type . In this case, the minimum depth of current CTU is equal to “0”, and the maximum depth of current CTU is equal to “2”.
- (2)
- when the predicted depth of current CTU satisfies 1.5 < ≤ 2.5, it means that the depths of neighboring CTUs are middle. The current CTU belongs to the moderate motion region and is classified as type . In this case, the minimum depth of current CTU is equal to “1”, and the maximum depth of current CTU is equal to “3”.
- (3)
- when the predicted depth of current CTU satisfies 2.5 < ≤ 3, it means that the motions of neighboring CTUs are intense and the depths of neighboring CTUs are high. The current CTU belongs to the fast motion region and is classified as type .
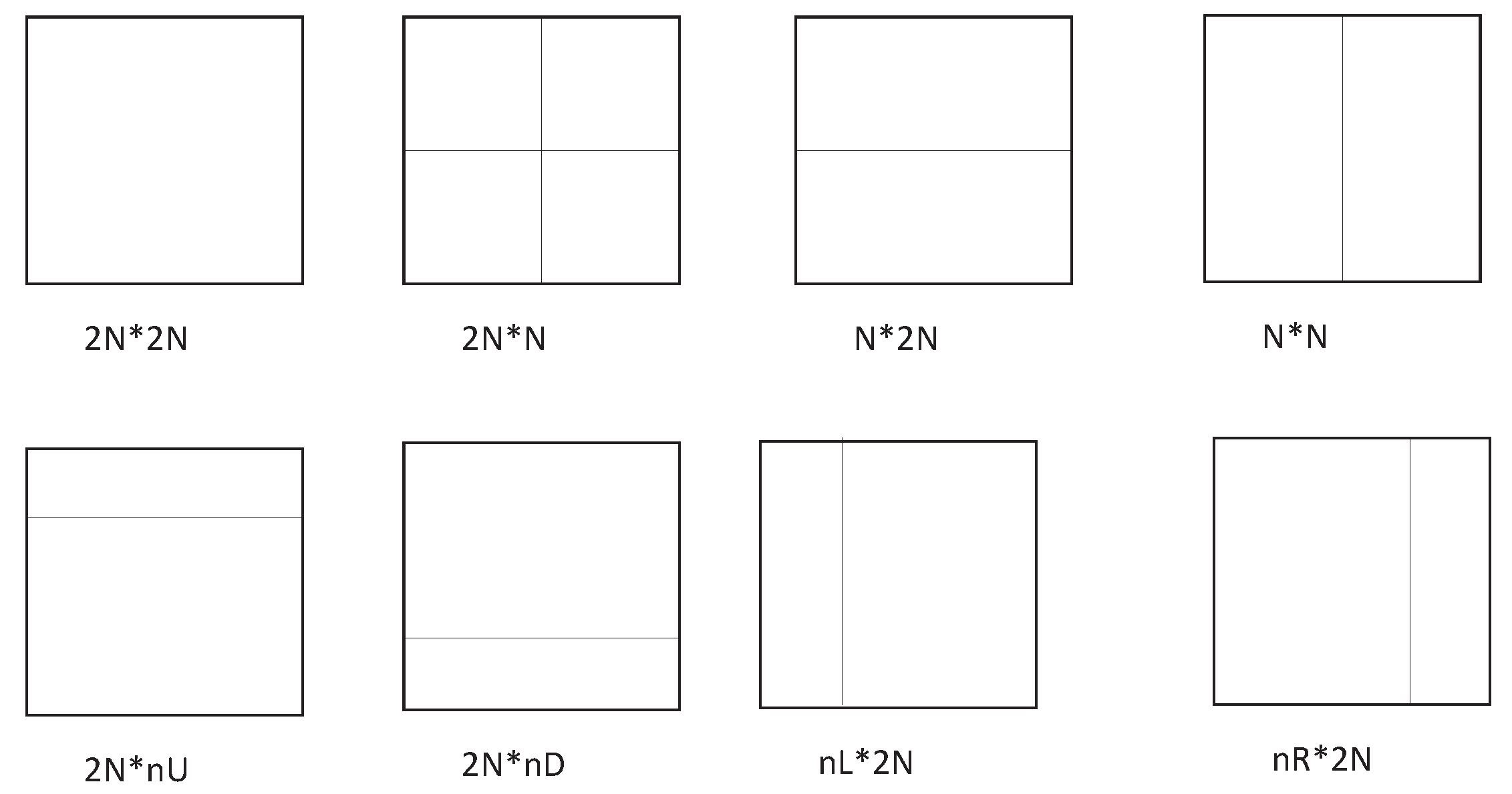
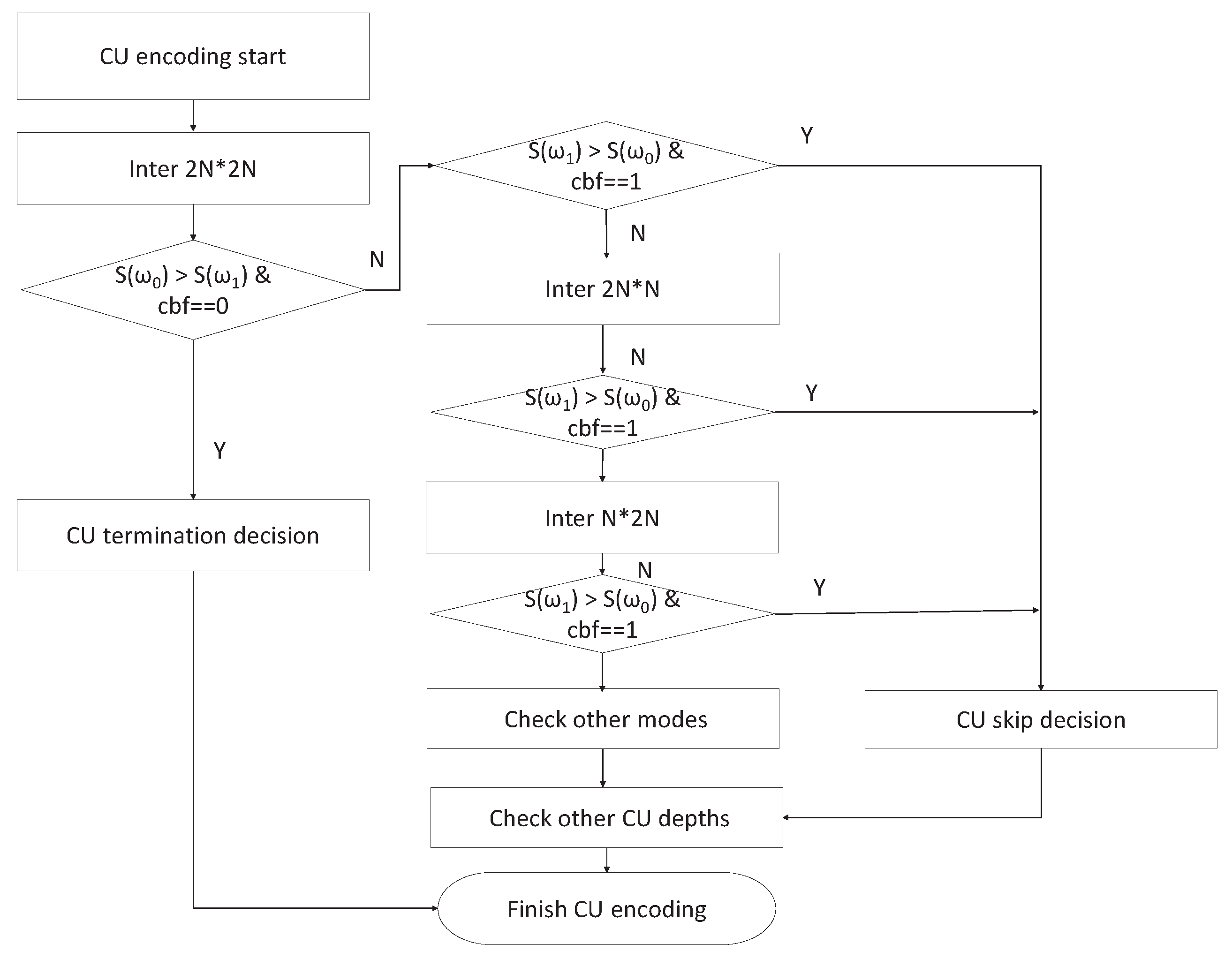
4.3. PU Mode Decision
- (1)
- At the encoding time for inter prediction, first of all, look up the statistical parameters in LUT. Then, the RD cost of the inter PU mode is checked. If the condition satisfies > and cbf = 0, the CU termination decision is processed. Otherwise, if the condition is satisfying > and cbf = 1, a CU skip decision is made.
- (2)
- RD cost of the inter PU mode is checked. If the condition is satisfying > and cbf = 1, a CU skip decision is made.
- (3)
- RD cost of the inter PU mode is checked. If the condition is satisfying > and cbf = 1, a CU skip decision is made.
- (4)
- Other PU modes are checked according to the H.265/HEVC reference model.
4.4. The Overall Framework
4.5. Encoder Hardware Architecture
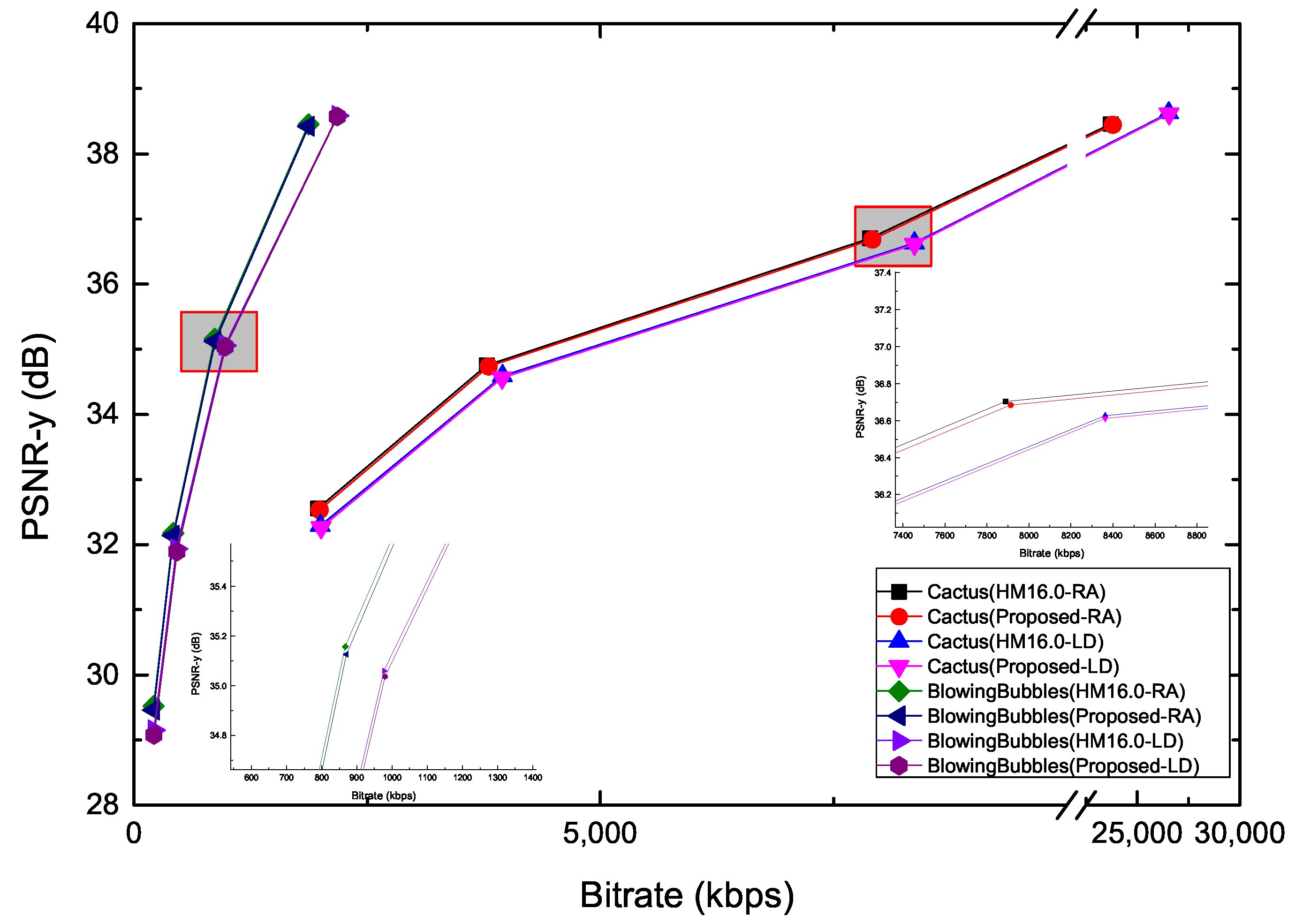
5. Experimental Results
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Bazzi, A.; Masini, B.M.; Zanella, A.; De Castro, C.; Raffaelli, C.; Andrisano, O. Cellular aided vehicular named data networking. In Proceedings of the 2014 IEEE International Conference on Connected Vehicles and Expo (ICCVE), Vienna, Austria, 3–7 November 2014; pp. 747–752. [Google Scholar]
- Paredes, C.I.; Mezher, A.M.; Igartua, M.A. Performance Comparison of H. 265/HEVC, H. 264/AVC and VP9 Encoders in Video Dissemination over VANETs. In Proceedings of the International Conference on Smart Objects and Technologies for Social Good, Venice, Italy, 30 November–1 December 2016; pp. 51–60. [Google Scholar]
- Shaibani, R.F.; Zahary, A.T. Survey of Context-Aware Video Transmission over Vehicular Ad-Hoc Networks (VANETs). EAI Endorsed Trans. Mob. Commun. Appl. 2018, 4, 1–11. [Google Scholar] [CrossRef][Green Version]
- Torres, A.; Piñol, P.; Calafate, C.T.; Cano, J.C.; Manzoni, P. Evaluating H.265 real-time video flooding quality in highway V2V environments. In Proceedings of the 2014 IEEE Wireless Communications and Networking Conference (WCNC), Istanbul, Turkey, 6–9 April 2014; pp. 2716–2721. [Google Scholar]
- Mammeri, A.; Boukerche, A.; Fang, Z. Video streaming over vehicular ad hoc networks using erasure coding. IEEE Syst. J. 2016, 10, 785–796. [Google Scholar] [CrossRef]
- Pan, Z.; Chen, L.; Sun, X. Low complexity HEVC encoder for visual sensor networks. Sensors 2015, 15, 30115–30125. [Google Scholar] [CrossRef] [PubMed]
- Laude, T.; Adhisantoso, Y.G.; Voges, J.; Munderloh, M.; Ostermann, J. A Comparison of JEM and AV1 with HEVC: Coding Tools, Coding Efficiency and Complexity. In Proceedings of the 2018 Picture Coding Symposium (PCS), San Francisco, CA, USA, 24–27 June 2018; pp. 36–40. [Google Scholar]
- Bossen, F.; Bross, B.; Suhring, K.; Flynn, D. HEVC complexity and implementation analysis. IEEE Trans. Circuits Syst. Video Technol. 2012, 22, 1685–1696. [Google Scholar] [CrossRef]
- Jiang, X.; Song, T.; Zhu, D.; Katayama, T.; Wang, L. Quality-Oriented Perceptual HEVC Based on the Spatiotemporal Saliency Detection Model. Entropy 2019, 21, 165. [Google Scholar] [CrossRef]
- Xu, Z.; Min, B.; Cheung, R.C. A fast inter CU decision algorithm for HEVC. Signal Process. Image Commun. 2018, 60, 211–223. [Google Scholar] [CrossRef]
- Duan, K.; Liu, P.; Jia, K.; Feng, Z. An Adaptive Quad-Tree Depth Range Prediction Mechanism for HEVC. IEEE Access 2018, 6, 54195–54206. [Google Scholar] [CrossRef]
- Zhang, J.; Kwong, S.; Wang, X. Two-stage fast inter CU decision for HEVC based on bayesian method and conditional random fields. IEEE Trans. Circuits Syst. Video Technol. 2018, 28, 3223–3235. [Google Scholar] [CrossRef]
- Zhu, L.; Zhang, Y.; Pan, Z.; Wang, R.; Kwong, S.; Peng, Z. Binary and multi-class learning based low complexity optimization for HEVC encoding. IEEE Trans. Broadcast. 2017, 63, 547–561. [Google Scholar] [CrossRef]
- Ahn, S.; Lee, B.; Kim, M. A novel fast CU encoding scheme based on spatiotemporal encoding parameters for HEVC inter coding. IEEE Trans. Circuits Syst. Video Technol. 2015, 25, 422–435. [Google Scholar] [CrossRef]
- Sharma, P.; Kaul, A.; Garg, M.L. Performance analysis of video streaming applications over VANETs. Int. J. Comput. Appl. 2015, 112, 13–18. [Google Scholar]
- Yaacoub, E.; Filali, F.; Abu-Dayya, A. QoE enhancement of SVC video streaming over vehicular networks using cooperative LTE/802.11 p communications. IEEE J. Sel. Top. Signal Process. 2015, 9, 37–49. [Google Scholar] [CrossRef]
- Rezende, C.; Boukerche, A.; Almulla, M.; Loureiro, A.A. The selective use of redundancy for video streaming over Vehicular Ad Hoc Networks. Comput. Netw. 2015, 81, 43–62. [Google Scholar] [CrossRef]
- Yousef, W.S.M.; Arshad, M.R.H.; Zahary, A. Vehicle rewarding for video transmission over VANETs using real neighborhood and relative velocity (RNRV). J. Theor. Appl. Inf. Technol. 2017, 95, 242–258. [Google Scholar]
- Jiang, X.; Wang, X.; Song, T.; Shi, W.; Katayama, T.; Shimamoto, T.; Leu, J.S. An efficient complexity reduction algorithm for CU size decision in HEVC. Int. J. Innov. Comput. Inf. Control 2018, 14, 309–322. [Google Scholar]
- Jiang, X.; Song, T.; Shi, W.; Katayama, T.; Shimamoto, T.; Wang, L. Fast coding unit size decision based on probabilistic graphical model in high efficiency video coding inter prediction. IEICE Trans. Inf. Syst. 2016, 99, 2836–2839. [Google Scholar] [CrossRef]
- Zhang, J.; Kwong, S.; Zhao, T.; Pan, Z. CTU-level complexity control for high efficiency video coding. IEEE Trans. Multimed. 2018, 20, 29–44. [Google Scholar] [CrossRef]
- Jiang, X.; Song, T.; Katayama, T.; Leu, J.S. Spatial Correlation-Based Motion-Vector Prediction for Video-Coding Efficiency Improvement. Symmetry 2019, 11, 129. [Google Scholar] [CrossRef]
- Li, Y.; Yang, G.; Zhu, Y.; Ding, X.; Sun, X. Unimodal stopping model-based early SKIP mode decision for high-efficiency video coding. IEEE Trans. Multimed. 2017, 19, 1431–1441. [Google Scholar] [CrossRef]
- Goswami, K.; Kim, B.G. A Design of Fast High-Efficiency Video Coding Scheme Based on Markov Chain Monte Carlo Model and Bayesian Classifier. IEEE Trans. Ind. Electron. 2018, 65, 8861–8871. [Google Scholar] [CrossRef]
- Tai, K.H.; Hsieh, M.Y.; Chen, M.J.; Chen, C.Y.; Yeh, C.H. A fast HEVC encoding method using depth information of collocated CUs and RD cost characteristics of PU modes. IEEE Trans. Broadcast. 2017, 43, 680–692. [Google Scholar] [CrossRef]
- Xiong, J.; Li, H.; Meng, F.; Wu, Q.; Ngan, K.N. Fast HEVC inter CU decision based on latent SAD estimation. IEEE Trans. Multimed. 2015, 17, 2147–2159. [Google Scholar] [CrossRef]
- Liu, Z.; Lin, T.L.; Chou, C.C. Efficient prediction of CU depth and PU mode for fast HEVC encoding using statistical analysis. J. Vis. Commun. Image Represent. 2016, 38, 474–486. [Google Scholar] [CrossRef]
- Chen, M.J.; Wu, Y.D.; Yeh, C.H.; Lin, K.M.; Lin, S.D. Efficient CU and PU Decision Based on Motion Information for Interprediction of HEVC. IEEE Trans. Ind. Inform. 2018, 14, 4735–4745. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, H.; Li, Z. Fast coding unit depth decision algorithm for interframe coding in HEVC. In Proceedings of the IEEE Data Compression Conference, Snowbird, UT, USA, 20–22 March 2013; pp. 53–62. [Google Scholar]
- Clifford, P. Markov random fields in statistics. In Disorder in Physical Systems: A Volume in Honour of John M. Hammersley; Oxford University Press: Oxford, UK, 1990; p. 19. [Google Scholar]
- Kruis, J.; Maris, G. Three representations of the Ising model. Sci. Rep. 2016, 6, 34175. [Google Scholar] [CrossRef]
- Rosewarne, C. High Efficiency Video Coding (HEVC) Test Model 16 (HM 16); Document JCTVC-V1002, JCT-VC. October 2015. Available online: http://phenix.int-evry.fr/jct/ (accessed on 15 March 2019).
- Bjontegaard, G. Calculation of Average PSNR Differences between RD-Curves. In Proceedings of the ITU-T Video Coding Experts Group (VCEG) Thirteenth Meeting, Austin, TX, USA, 2–4 April 2001; Available online: https://www.itu.int/wftp3/av-arch/video-site/0104_Aus/ (accessed on 15 March 2019).
- Bossen, F. Common Test Conditions and Software Reference Configurations, Joint Collaborative Team on Video Coding (JCT-VC), Document JCTVC-L1110, Geneva. January 2014. Available online: https://www.itu.int/wftp3/av-arch/video-site/0104_Aus/ (accessed on 15 March 2019).

| CTU Type | Range | The CTU Depth Range |
|---|---|---|
| ≤ 1.5 | [0, 1, 2] | |
| 1.5 < ≤ 2.5 | [1, 2, 3] | |
| 2.5 < ≤ 3 | [2, 3] |
| Items | Descriptions |
|---|---|
| Software | HM16.0 |
| Video Size | , , , , |
| Configurations | random access (RA), low delay (LD) |
| Quantization Parameter (QP) | 22, 27, 32, 37 |
| Maximum CTU size |
| CTU Depth Decision | PU Mode Decision | Overall (Proposed) | |||||
|---|---|---|---|---|---|---|---|
| Size | Sequence | BDBR(%) | TS(%) | BDBR(%) | TS(%) | BDBR(%) | TS(%) |
| Traffic | 0.19 | 12.46 | 1.15 | 58.03 | 1.00 | 52.31 | |
| SteamLocomotive | 0.12 | 13.79 | 0.82 | 56.32 | 0.72 | 52.65 | |
| ParkScene | 0.14 | 12.83 | 1.03 | 56.93 | 0.83 | 51.76 | |
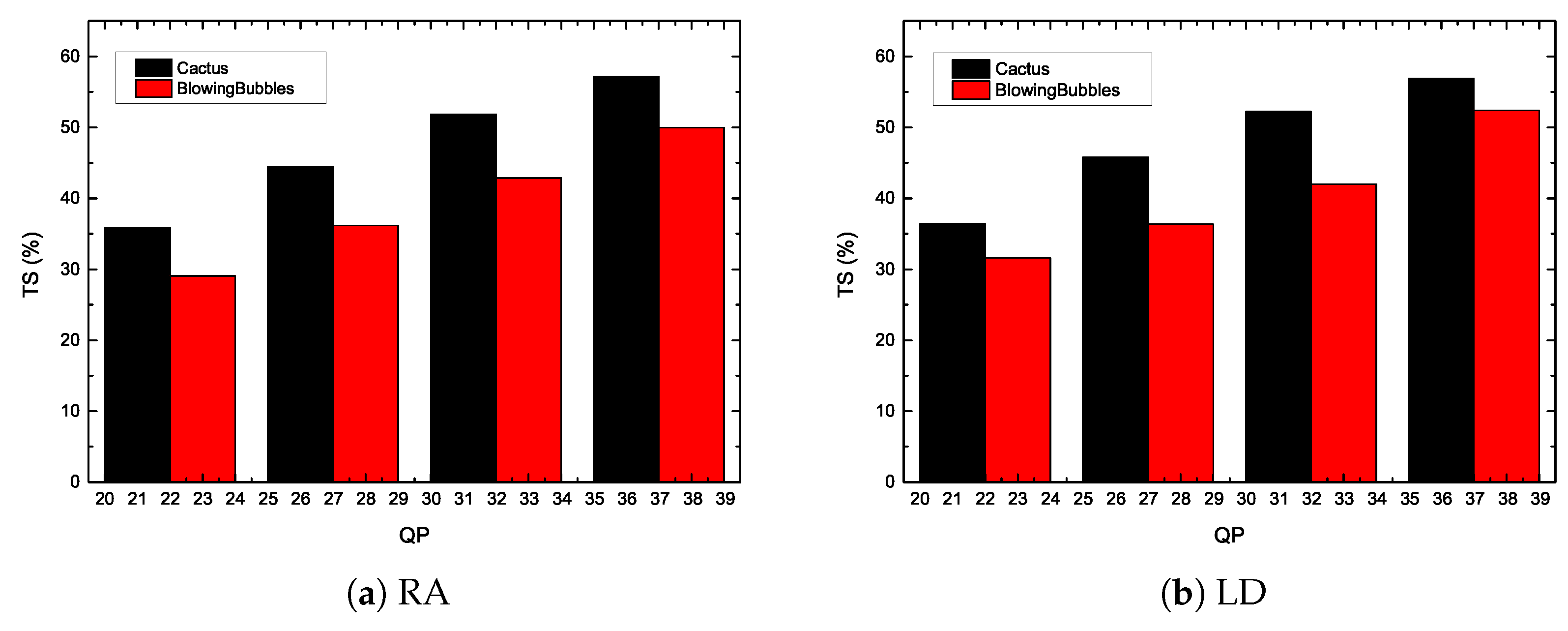
| Cactus | 0.13 | 12.25 | 1.34 | 52.57 | 1.19 | 47.31 | |
| BQTerrace | 0.02 | 14.18 | 0.84 | 57.54 | 0.69 | 54.09 | |
| BasketballDrill | −0.13 | 14.11 | 0.73 | 51.55 | 0.50 | 46.10 | |
| BQMall | 0.18 | 15.97 | 0.92 | 56.76 | 0.73 | 51.37 | |
| PartyScene | 0.06 | 17.34 | 0.75 | 50.09 | 0.61 | 44.96 | |
| RaceHorses | 0.02 | 13.59 | 1.31 | 44.27 | 1.08 | 37.10 | |
| BasketballPass | 0.26 | 7.09 | 0.90 | 54.73 | 0.60 | 46.40 | |
| BQSquare | 0.05 | 14.37 | 0.57 | 54.08 | 0.44 | 45.93 | |
| BlowingBubbles | 0.17 | 8.54 | 1.26 | 48.12 | 1.09 | 39.53 | |
| Vidyo1 | 0.11 | 16.19 | 1.18 | 66.60 | 0.77 | 63.30 | |
| Vidyo3 | 0.11 | 14.81 | 0.57 | 63.90 | 0.75 | 61.74 | |
| Vidyo4 | 0.20 | 16.29 | 1.04 | 65.36 | 1.04 | 63.96 | |
| Average | 0.11 | 13.59 | 0.96 | 55.79 | 0.80 | 50.96 | |
| CTU Depth Decision | PU Mode Decision | Overall (Proposed) | |||||
|---|---|---|---|---|---|---|---|
| Size | Sequence | BDBR(%) | TS(%) | BDBR(%) | TS(%) | BDBR(%) | TS(%) |
| Traffic | 0.12 | 9.34 | 0.92 | 54.54 | 0.89 | 54.81 | |
| SteamLocomotive | −0.19 | 11.65 | 0.33 | 51.62 | 0.29 | 51.84 | |
| ParkScene | 0.11 | 10.15 | 1.07 | 52.66 | 1.08 | 53.02 | |
| Cactus | 0.06 | 10.19 | 1.03 | 47.47 | 0.85 | 47.82 | |
| BQTerrace | 0.01 | 12.83 | 0.58 | 54.33 | 0.62 | 54.46 | |
| BasketballDrill | 0.18 | 10.75 | 0.71 | 43.95 | 0.79 | 44.22 | |
| BQMall | 0.42 | 8.09 | 0.93 | 51.06 | 0.86 | 49.39 | |
| PartyScene | 0.22 | 9.16 | 0.58 | 40.92 | 0.55 | 41.29 | |
| RaceHorses | 0.02 | 6.73 | 0.79 | 37.04 | 0.89 | 37.03 | |
| BasketballPass | 0.94 | 6.99 | 0.91 | 51.21 | 0.91 | 51.80 | |
| BQSquare | 0.10 | 4.33 | 0.54 | 44.85 | 0.36 | 42.24 | |
| BlowingBubbles | 0.24 | 3.92 | 1.16 | 40.16 | 1.15 | 40.57 | |
| Vidyo1 | 0.18 | 20.30 | 0.68 | 64.11 | 0.70 | 64.13 | |
| Vidyo3 | 0.25 | 12.33 | 1.04 | 58.55 | 1.01 | 58.95 | |
| Vidyo4 | −0.37 | 14.03 | 0.55 | 61.67 | 0.48 | 61.95 | |
| Average | 0.15 | 14.05 | 0.79 | 50.28 | 0.76 | 50.23 | |
| (BDBR, TS) | |||
|---|---|---|---|
| = 0.5 | = 0.75 (Proposed) | = 0.85 | |
| Random Access | (1.01, 55.25) | (0.80, 50.96) | (0.98, 51.83) |
| Low Delay | (0.86, 50.63) | (0.76, 50.23) | (0.82, 50.55) |
| Method | (BDBR, TS) | |
|---|---|---|
| RA | Proposed | (0.80, 50.96) |
| Zhang’s [12] | (1.19, 54.93) | |
| Zhu’s [13] | (3.67, 65.60) | |
| Ahn’s [14] | (1.40, 49.60) | |
| Goswami’s [24] | (1.11, 51.68) | |
| Tai’s [25] | (1.41, 45.70) | |
| Xiong’s [26] | (2.00, 58.40) | |
| LD | Proposed | (0.76, 50.23) |
| Zhu’s [13] | (3.84, 67.30) | |
| Ahn’s [14] | (1.00, 42.70) | |
| Tai’s [25] | (0.75, 37.90) | |
| Xiong’s [26] | (1.61, 52.00) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, X.; Feng, J.; Song, T.; Katayama, T. Low-Complexity and Hardware-Friendly H.265/HEVC Encoder for Vehicular Ad-Hoc Networks. Sensors 2019, 19, 1927. https://doi.org/10.3390/s19081927
Jiang X, Feng J, Song T, Katayama T. Low-Complexity and Hardware-Friendly H.265/HEVC Encoder for Vehicular Ad-Hoc Networks. Sensors. 2019; 19(8):1927. https://doi.org/10.3390/s19081927
Chicago/Turabian StyleJiang, Xiantao, Jie Feng, Tian Song, and Takafumi Katayama. 2019. "Low-Complexity and Hardware-Friendly H.265/HEVC Encoder for Vehicular Ad-Hoc Networks" Sensors 19, no. 8: 1927. https://doi.org/10.3390/s19081927
APA StyleJiang, X., Feng, J., Song, T., & Katayama, T. (2019). Low-Complexity and Hardware-Friendly H.265/HEVC Encoder for Vehicular Ad-Hoc Networks. Sensors, 19(8), 1927. https://doi.org/10.3390/s19081927





